17 авг. 2022 г.
читать 2 мин
Вы можете использовать функцию ЛИНЕЙН , чтобы быстро найти уравнение регрессии в Excel.
Эта функция использует следующий базовый синтаксис:
LINEST(known_y's, known_x's)
куда:
- known_y’s : столбец значений для переменной ответа.
- known_x’s : один или несколько столбцов значений для переменных-предикторов.
В следующих примерах показано, как использовать эту функцию для поиска уравнения регрессии для простой модели линейной регрессии и модели множественной линейной регрессии .
Пример 1: Найдите уравнение для простой линейной регрессии
Предположим, у нас есть следующий набор данных, который содержит одну предикторную переменную (x) и одну переменную ответа (y):

Мы можем ввести следующую формулу в ячейку D1 , чтобы вычислить простое уравнение линейной регрессии для этого набора данных:
=LINEST( A2:A15 , B2:B15 )
Как только мы нажмем ENTER , будут показаны коэффициенты для простой модели линейной регрессии:

Вот как интерпретировать вывод:
- Коэффициент на перехват 3,115589.
- Коэффициент наклона равен 0,479072.
Используя эти значения, мы можем написать уравнение для этой простой модели регрессии:
у = 3,115589 + 0,478072 (х)
Примечание.Чтобы найти p-значения для коэффициентов, значение r-квадрата модели и другие показатели, следует использовать функцию регрессии из пакета анализа данных. В этом руководстве объясняется, как это сделать.
Пример 2: найти уравнение для множественной линейной регрессии
Предположим, у нас есть следующий набор данных, который содержит две переменные-предикторы (x1 и x2) и одну переменную ответа (y):

Мы можем ввести следующую формулу в ячейку E1 , чтобы вычислить уравнение множественной линейной регрессии для этого набора данных:
=LINEST( A2:A15 , B2:C15 )
Как только мы нажмем ENTER , будут показаны коэффициенты для модели множественной линейной регрессии:

Вот как интерпретировать вывод:
- Коэффициент на перехват 1.471205
- Коэффициент для x1 равен 0,047243.
- Коэффициент для x2 равен 0,406344.
Используя эти значения, мы можем написать уравнение для этой модели множественной регрессии:
у = 1,471205 + 0,047243 (х1) + 0,406344 (х2)
Примечание.Чтобы найти p-значения для коэффициентов, значение r-квадрата модели и другие показатели для модели множественной линейной регрессии в Excel, следует использовать функцию регрессии из пакета анализа данных. В этом руководстве объясняется, как это сделать.
Дополнительные ресурсы
В следующих руководствах представлена дополнительная информация о регрессии в Excel:
Как интерпретировать вывод регрессии в Excel
Как добавить линию регрессии на диаграмму рассеяния в Excel
Как выполнить полиномиальную регрессию в Excel
Содержание
- Подключение пакета анализа
- Виды регрессионного анализа
- Линейная регрессия в программе Excel
- Разбор результатов анализа
- Вопросы и ответы

Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
- Перемещаемся во вкладку «Файл».
- Переходим в раздел «Параметры».
- Открывается окно параметров Excel. Переходим в подраздел «Надстройки».
- В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
- Открывается окно доступных надстроек Эксель. Ставим галочку около пункта «Пакет анализа». Жмем на кнопку «OK».





Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».

Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
- Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
- Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».

С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.

После того, как все настройки установлены, жмем на кнопку «OK».




Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.

Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Видео занятия
Строим корреляционную матрицу. Для этого используем надстройку «Анализ данных»
Выбираем в диалоговом окне «Анализа данных» – корреляция.
Далее заполняем диалоговое окно:
Получим корреляционную матрицу:
Наблюдается тесная связь между переменной Y и Х1, Y и X2, так как попарные коэффициенты корреляции составляют 0,8602 и 0,7479 соответственно. Это выше 0,7 – связь достаточно тесная.
Межу объясняющими переменными Х1 и Х2 коэффициент составляет 0,6311. Он ниже других, но имеет значение больше 0,6. Значит между объясняющими переменными, может быть корреляционная связь (явление мультиколлинеарности). Для обнаружения мультиколлинеарности есть ряд критериев, например VIF-критерий.
Парные коэффициенты корреляции можно ещё найти с помощью статистической функции КОРРЕЛ.
Заполняем диалоговое окно статистической функции КОРРЕЛ.
Получаем тоже значение, что и корреляционной матрице для Y и X1: 0,860227
Аналогично по отдельности можем найти и другие парные коэффициенты корреляции.
Строим множественную регрессию. Для этого в надстройке «Анализ данных» выбираем регрессия. Заполняем диалоговое окно.
Выбираем уровень надёжности 98%. Для коэффициентов регрессии будет найден доверительный интервал с уровнем с доверительной вероятностью 98%. Так же выбираем остатки, график остатков. Эти данные необходимы нам для дальнейшего анализа во второй части.
Получим.
Проведём анализ полученных данных.
Здесь выводятся: множественный коэффициент корреляции, коэффициент детерминации (R-квадрат), скорректированный коэффициент детерминации (нормированный R-квадрат), стандартная ошибка регрессии (S).
R-квадрат = RSS/TSS
Стандартная ошибка = (ESS/(n-m-1))^0.5
ESS (error sum of squares) – остаточная сумма квадратов.
Построенное уравнение регрессии объясняет изменение результативного показателя Y на 80,99%. Остальные 10,01% приходятся на случайные факторы и факторы не включённые в модель.
Здесь даны столбцы: со степенями свободы (df); суммой квадратов (SS), суммой квадратов, делённых на степень свободы (MS=SS/df). Так же дано значение F-критерия Фишера и вероятность принятия нулевой гипотезы о равенстве коэффициента детерминации нулю (Значимость F).
TSS (total sum of squares) – общая сумма квадратов отклонений зависимой переменной от средней или вся дисперсия зависимой переменной;
RSS (regression sum of squares) – сумма квадратов, обусловленная регрессией или объясненная часть всей дисперсии;
ESS (error sum of squares) – остаточная сумма квадратов, характеризующая влияние неучтенных факторов или необъясненная дисперсия.
F= (ESS/m)/(RSS/(n-m-1)), n=32 m=2
Значимость F= 3,51562998617576E-11 <<<<0.01. Не можем принять нулевую гипотезу, принимаем альтернативную. Коэффициент детерминации отличен от нуля. Уравнение значимо в целом.
Так же можно сравнить наблюдаемое значение F-критерия с критическим. Берём уровень значимости 0,01, число степеней свободы 2 и 29. И с помощью статистической функции F.ОБР.ПХ находим критическое значение распределения Фишера
F.ОБР.ПХ(0,01;2;29) = 5,420445
Наблюдаемое значение оказалось выше критического (61,766> 5,420445), отвергаем нулевую гипотезу – уравнение значимо в целом.
В данной таблице выводятся столбцы: коэффициентов регрессии; стандартных ошибок коэффициентов регрессии; t-статистик; вероятности принятия нулевой гипотезы для коэффициентов (Р-значение); доверительные интервалы для коэффициентов регрессии (95% интервал считается по умолчанию, 98% – мы задали сами в диалоговом окне регрессия).
Запишем полученное уравнение множественной регрессии.
Если P-значение < 0.05, то коэффициент регрессии можем принять значимым при 5% уровне.
Т. е. отвергаем нулевую гипотезу при 5% уровне значимости. Т. е. все коэффициенты полученного уравнения статистически значимы при 5% уровне, т. к. для них всех р-значение меньше 0,05.
Так же можем определить значимость коэффициентов, сравнивая наблюдаемые значения t-статистик с критическими. Находим критическое значения с помощью статистической функции СТЬЮДЕНТ.ОБР.2Х.
СТЬЮДЕНТ.ОБР.2Х(0,05;29)= 2,04523
Наблюдаемые значения t-статистик из таблицы, выше критического значения при 5% уровне значимости, отвергаем нулевую гипотезу. Коэффициенты регрессии являются статистически значимыми.
Так же можем получить расчёт для множественной регрессии, используя статистическую функцию Excel – ЛИНЕЙН.
Для неё берётся число столбцов, равное количеству объясняющих переменных плюс один (в нашем случае три), а количество строк всегда пять.
Выделяем диапазон: E37:G41. Ставим знак равно и находим функцию ЛИНЕЙН в статистических функциях.
Заполняем диалоговое окно:
Нажимаем клавиши
Получаем результат:
t-статистики определим делением коэффициента регрессии на стандартную ошибку.
Получим следующую таблицу.
Кроме t-статистики в этой таблице считает функция ЛИНЕЙН. t-статистики мы подсчитали сами дополнительно.
Принципиальное отличие функции ЛИНЕЙН от регрессии в пакете «Анализ данных» заключается в том, что при изменении самих данных, все значения в таблице ЛИНЕЙН пересчитываются автоматически сразу. А при работе с пакетом «анализа данных» надо запускать процесс ещё раз, т. е. вызывать диалоговое окно, заполнять его и нажимать «ок».
В следующей части мы рассмотрим тестирование полученной модели на наличие автокорреляции остатков и на наличие гетероскедастичности.
Материал подготовлен сайтом: https://pro-smysl.ru/
Онлайн помощь в решении задач, консультации, создание обучающих роликов.
Подписывайтесь на наши каналы:
https://vk.com/sm_smysl
https://www.youtube.com/@SMYS_L
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.

Модель линейной регрессии имеет следующий вид:
У = а0 + а1х1 +…+акхк.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.



После активации надстройка будет доступна на вкладке «Данные».

Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).



В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.

Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» – первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» – второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.

Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:

Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:

- Строим корреляционное поле: «Вставка» – «Диаграмма» – «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».




Теперь стали видны и данные регрессионного анализа.
Регрессионный анализ – это набор статистических методов, позволяющих изучить влияние одной или нескольких независимых переменных на зависимую. Давайте разберемся, каким образом можно выполнить данный анализ в программе Excel.
Содержание
- Включение функции анализа в программе
- Линейный регрессионный анализ
- Анализ полученных результатов
- Заключение
Включение функции анализа в программе
Для начала нужно активировать функцию программы, с помощью которой мы будем проводить анализ. Для этого делаем следующее:
- Открываем меню “Файл”.

- Щелкаем по пункту “Параметры”.

- В нижней части содержимого подраздела “Надстройки” выбираем значение “Надстройки Excel” для параметра “Управление”, после чего кликаем “Перейти”.

- В окне управления надстройками выбираем “Пакет анализа” и щелкаем OK.

- Переходим во вкладку “Данные”, чтобы проверить, появилась ли функция “Анализ данных” в группе инструментов “Анализ”.

Линейный регрессионный анализ
Выделяют несколько разновидностей регрессий: линейная, гиперболическая, множественная, логарифмически линейная, нелинейная, обратная, парная.
В рамках данной статьи мы рассмотрим линейную регрессию. В общем виде ее функция выглядит так:
y = a0+a1x1+a2x2+…anxn
В данном уравнении:
- Y – переменная, влияние на которую нужно найти;
- X – факторы, влияющие на переменную;
- A – коэффициенты регрессии, определяющие значимости факторов;
- N – общее количество факторов.
Чтобы было понятнее, давайте разберем конкретный практический пример. Допустим, у нас есть таблица, в которой представлена информация по среднесуточной температуре и количеству осадков с разбивкой по месяцам.

Наша задача – выяснить, как температура влияет на осадки. Приступи к ее выполнению.
- Щелкаем по кнопке “Анализ данных”.
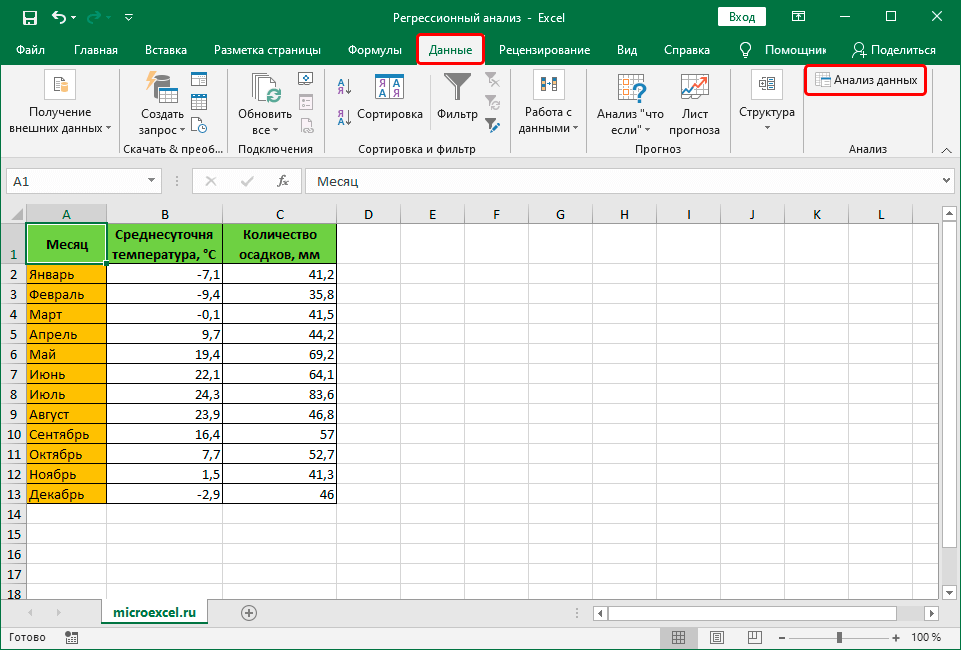
- В открывшемся окошке отмечаем пункт “Регрессия”, после чего щелкаем OK.

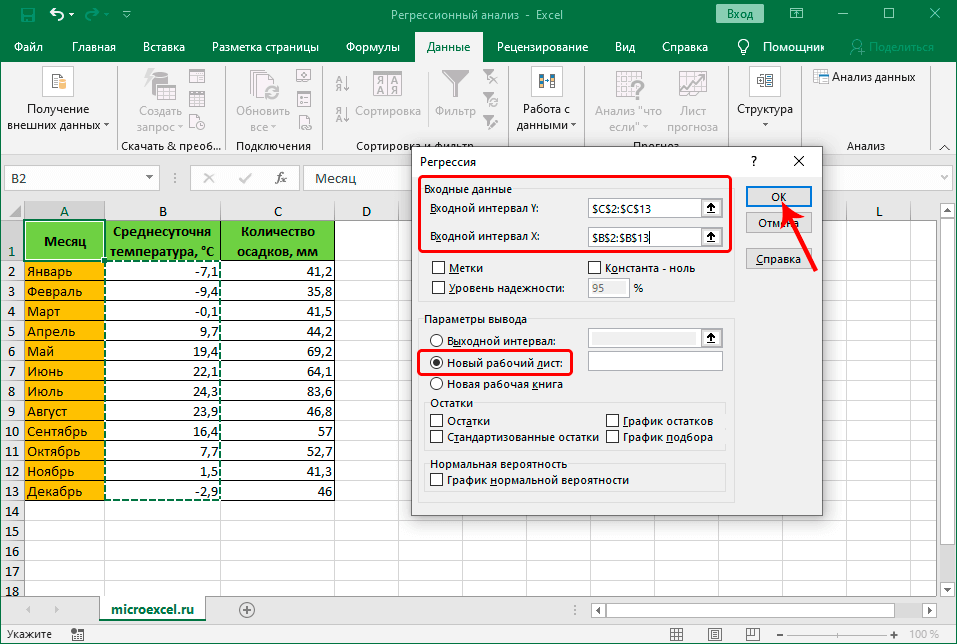
- Перед нами появится окно, в котором нужно настроить параметры регрессии:
- в поле “Входной интервал_Y” пишем координаты диапазона ячеек, в которых находятся переменные, влияние на которые нам нужно выяснить. У нас это столбец “Количество осадков, мм”. Координаты диапазона можно указать как вручную, используя клавиши на клавиатуре, так и выделив его в самой таблице с помощью зажатой левой кнопки мыши.
- в поле “Входной интервал_X” указываем координаты диапазона ячеек с данными, влияние которых нам нужно найти. В нашем случае – это столбец “Среднесуточная температура”.
- Остальные параметры не являются обязательными и, чаще всего, остаются незаполненными. У нас есть возможность установить метки, значения уровня надежности в процентах, константу-ноль, график нормальной вероятности и т.д. Пожалуй, самым важным здесь является способ вывода результатов анализа. Доступны следующие варианты: на новом листе (по умолчанию), в новой книге или в указанном диапазоне на этом же листе. Мы оставим все как есть и жмем кнопку OK.
Анализ полученных результатов
После корректного заполнения всех параметров и нажатия кнопки OK отобразятся результаты анализа (в зависимости от выбранного способа). В нашем случае – на отдельном листе.

Ключевым показателем здесь является R-квадрат (коэффициент детерминации), значение которого характеризует качество модели. Приемлемым считается значение не менее 0,5 (или 50%).
Также следует обратить внимание на ячейку, расположенную на пересечении строки “Y-пересечение” и столбца “Коэффициенты”. Здесь показывается, каким будет значение Y (количество осадков), если все остальные факторы будут равны нулю.
Ячейка на пересечении строки “Переменная X 1” и столбца “Коэффициенты” содержит значение, характеризующее степень зависимости Y от X. Коэф. 0,89 в нашем случае говорит о достаточно сильной связи между переменными.
Заключение
Регрессионный анализ – сложная и трудоемкая задача, которая требует определенных математических и статистических знаний. Но с помощью стандартных инструментов Эксель ее выполнение можно значительно облегчить.

