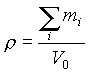Как найти рентгеновскую плотность

Если
известен тип структуры исследуемого
кристалла и определены параметры его
элементарной ячейки, то можно найти
плотность кристалла по формуле:

(33)

где 
–
суммарная масса всех атомов, приходящихся
на одну элементарную ячейку, V₀ –
объем элементарной ячейки.

В
случае простейших металлических
кристаллов, состоящих из атомов одного
сорта,

(34)

где n –
число атомов с массой m,
приходящихся на одну элементарную
ячейку.

Для
определения массы атома m воспользуемся
значениями атомной единицы массы A₀ =
1,66056 10^-27 кг (она
равна 1/12 массы нуклида углерода C¹²)
и атомной массы А (безразмерной
величины) атома:

m=(A
A₀)
кг.

Массу
атома можно определить и другим способом.
В периодической системе Д. И. Менделеева
под символами элементов приведена масса
каждого элемента, приведенная в граммах.
Поскольку в одном грамм-атоме вещества
содержится количество атомов равное
числу Авогадро, то массу одного атома
можно найти как:

(в
граммах) (35)

Пример: M _Cu =
63,54 г/моль,

Следует
заметить, что плотность кристалла,
найденная рентгеновским методом, может
отличаться от истинной плотности, т. к.
рентгеновская плотность определяется
в предположении идеальности кристаллической
решетки, т.е. без учета примесей и дефектов
решетки.

Порядок выполнения работы

1. Получить
   дифрактограмму поликристаллического
   образца с кубической структурой (при
   возможности можно использовать и
   дифрактограмму многофазного образца,
   выделив из нее соответствующую
   совокупность линий).

2. Графическим
   и аналитическим способами найти индексы
   отражающих плоскостей и по ним определить
   тип элементарной ячейки.

3. Вычислить
   параметр элементарной ячейки и
   погрешность определения.

4. Определить
   плотность материала и радиус атомов.

5. Оформить
   отчет по работе; результаты проставить
   в табл.4.

Таблица
4

Данные
индицирования дифрактограммы кристалла
кубической сингонии

N	d,A	(hkl)	Тип элементарной ячейки	Результаты расчета  a, r, p

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

    При прохождении света через узкую щель происходит дифракция световых лучей, при которой они способны интерферировать, т. е. усиливать или поглощать друг друга. При этом между длиной волны излучения, углом падения лучей и постоянной дифракционной решетки существуют простые соотношения, вытекающие из волновой теории света. Именно эти закономерности и лежат в основе так называемых дифракционных методов изучения структуры кристаллов. В настоящее время применяют два основных метода получения дифракционных рентгенограмм кристаллов порошковый и метод вращения кристалла. И в том и в другом методе используют монохроматическое рентгеновское излучение. Анализ получаемых рентгенограмм не всегда прост, тем не менее удается определить не только размеры и форму элементарной ячейки, но и число частиц, входящих в ее состав. Так, ориентируя кристалл определенным образом, можно установить постоянные решетки,а следовательно, и размеры элементарной ячейки. Зная плотность кристалла, можно рассчитать массу эле- [c.91]

    Часто, особенно в сложных сплавах, рентгеновским исследованием можно выявить образовавшиеся в процессе кристаллизации фазы, которые нельзя получить в изолированном, чистом состоянии (карбиды, нитриды, карбонитриды и т. д.). Данные рентгенографического исследования можно использовать для определения плотности кристалла. Эта так называемая рентгенографическая плотность не зависит от нарушений кристаллической структуры реального вешества (поры, несплошности, вакансии, дислокации и т. д.) и принимается эталонной. [c.110]

    При использовании рентгеновского излучения меди с длиной волны 1,54 А отражение первого порядка от грани кристалла хлористого калия при 25° С происходит под углом 0=14°12. Вычислить а) ребро элементарной ячейки для этой взаимопроникающей гранецентрированной решетки и б) плотность кристалла. [c.598]

    Рентгеновский метод. Общая масса М элементарной ячейки кристалла легко может быть получена из рентгеновских измерений объема ячейки V и плотности кристалла р. При умножении pV на чнсло Авогадро N получают массу в обычных единицах атомного веса С-12  [c.48]

    Так, например, при оценке содержания кристаллической фазы в полиэтилене по плотности предполагается, что плотности кристаллов полиэтилена и обычных кристаллических парафинов равны. Оценка плотности на основании рентгеновских данных страдает тем же дефектом, что и определение параметров ячейки кристаллов, так как основана на вычислении этих параметров. [c.82]

    Такие результаты обычно представляются в виде карт электронной плотности. Поскольку рентгеновские лучи рассеиваются электронами, кристалл при рентгеноструктурном исследовании ведет себя как трехмерное периодическое распределение электронов с большей плотностью [c.314]

    Ориентируя кристалл определенным образом, можно определить постоянные решетки, а, следовательно, и размеры элементарной ячейки. Зная плотность кристалла, можно рассчитать массу элементарной ячейки, а зная химический состав кристалла и атомный вес элементов, можно определить число атомов в элементарной ячейке. Наконец, дифракционная картина позволяет установить тип симметрии кристалла. Получаемой таким путем информации часто достаточно для определения структуры кристалла, по крайней мере в простых системах (для более сложных структур требуется более тщательный анализ). Атомы различного сорта в зависимости от числа электронов обладают различной способностью рассеивать рентгеновские лучи, что выражается фактором рассеяния . Общая интенсивность пучка, дифрагированного элементарной ячейкой, состоит из вкладов различных атомов, а усиление или ослабление интенсивности объясняется тем или иным геометрическим расположением атомов или различием факторов рассеяния. [c.26]

    Первый физический метод, который попытались применить для определения зарядов на атомах, был рентгеноструктурный анализ. Карты рентгеновской плотности, получаемые в ходе структурного исследования кристаллов, казалось бы, давали в руки исследователей объективную картину распределения электронной плотности кристаллов. Однако в дальнейшем выяснилось, что для количественного решения этой задачи необходима такая высокая точность эксперимента и чувствительность приборов, что достоверные данные о зарядах па атомах могли появиться только в последнее время. В табл. 49 дана сводка результатов рентгенографического определения степени ионности связи в кристаллах. Ионность связи [c.102]

    Основным методом определения положения атомов является построение электронной плотности кристаллов. В настоящем сообщении на основе данных, полученных в рентгеновской лаборатории Физико-химического института имени Л. Я. Карпова, рассматриваются методические вопросы, связанные с определением электронной плотности в кристаллических соединениях. [c.144]

    Сравнение рентгеновской и пикнометрической плотности. Зная параметр кристаллической решетки и число атомов в единичной ячейке, можно вычислить плотность кристалла. Если найденная пикнометрическая плотность больше вычисленного значения, это указывает на междоузельные дефекты или дефекты замещения тяжелого атома легким, в противном случае — на наличие вакансий или замещение легких атомов тяжелыми. Пустоты и трещины в кристалле будут давать аномальную низкую величину для пикнометрической плотности, поэтому целесообразней проводить измерения плотности как функции состава. Рост плотности [c.21]

    Если известен тип кристаллической решетки и число ионов или атомов в элементарной ячейке, то из плотности кристалла и известных атомных весов можно вычислить размер элементарной ячейки, не пользуясь рентгеновскими данными. Как можно видеть на рис. 22-11, элементарная ячейка хлористого натрия состоит из четырех ионов натрия и четырех ионов хлора. В гранецентрированной решетке хлора ион, нахо-дяш,ийся в углу элементарной ячейки, фактически экранирован восемью соседними элементарными ячейками, так что только одна восьмая его массы связана с одной элементарной ячейкой. В элементарной ячейке имеется восемь таких угловых ионов, причем каждый вносит одну восьмую своей массы в элементарную ячейку поэтому все угловые ионы составляют в сумме один ион хлора в каждом элементарном кубе решетки, состоящей из ионов хлора. Кроме того, у каждого элементарного куба решетки хлора на каждой из его шести граней есть один ион, который экранируется соседним кубом. В соответствии с этим половина от шести ионов, т. е. три иона, могут быть приписаны данному кубу. Таким образом, элементарная ячейка решетки хлористого натрия содержит [c.667]

    При использовании рентгеновских лучей (Х=1,54 A ) от медного антикатода найдено, что отражение первого порядка от грани кристалла хлористого калия при 25° происходит под углом 14°12. Вычислить а) длину стороны элементарной ячейки для этой взаимопроникающей гранецентрированной решетки б) плотность кристалла. [c.678]

    Наиболее полная и строгая теория дифракционного муара основана на динамической теории рассеяния коротких волн в кристаллах. Исходная модель динамического рассеяния заключается в следующем. Под влиянием падающей из вакуума электронной (или рентгеновской) волны в кристалле возникает волновое поле, которое описывается в случае электронов уравнением Шредингера [4, 5] и в случае рентгеновских лучей — уравнением Максвелла [6] . Решением этих уравнений для периодического потенциала или электронной плотности кристалла является так называемая блоховская волна, которая может быть представлена совокупностью плоских волн. Хотя с теоретической точки зрения количество упомянутых плоских волн в кристалле должно быть велико, в реальных условиях эксперимента можно рас- [c.176]

    Важную информацию о связи в кристаллах можно получить с помощью так называемого фурье-преобразования рассеяния рентгеновских лучей на электронах кристаллической решетки монокристалла. Так как в кристалле электронная плотность периодически изменяется, снимают диаграммы электронной плотности, на которых проводят линии одинаковой электронной плотности. [c.111]

    Оценки показывают, что показатель преломления рентгеновских лучей меньше единицы и отличается от единицы на несколько миллионных. Проведенный расчет относится к кристаллу и аморфному веществу того же состава и плотности. При возникновении селективных отражений нужно учитывать их взаимодействие с первичным пучком, что приводит к небольшим отклонениям от простой формулы Вульфа — Брегга. [c.93]

    Помимо направлений, по которым происходит рассеяние, последнее характеризуется интенсивностью рассеянного пучка. Она может быть измерена, например, по степени почернения рентгеновской плен- ки, на которую падает рассеянный пучок. Интенсивность рассеянных пучков (интенсивность их изображений на пленке, рефлексов) содержит информацию о распределении электронной плотности в пределах элементарной ячейки. Поясним это на примере того же кристалла хлористого цезия. Для этого учтем рассеяние от ионов хлора, которое в несколько раз слабее, чем рассеяние от ионов цезия, но все же вполне измеримо. [c.163]

    В отличие от кристаллов, в жидкостях при практически той же средней плотности распределения вещества дальний порядок отсутствует. Есть только ближний порядок, т. е. правильность расположения молекул или атомов в непосредственной близости от данной центральной молекулы, резко нарушающаяся с расстоянием. Такой ближний порядок, как и дальний порядок в кристаллах, может быть количественно изучен с помощью современных методов структурного анализа — по дифракции рентгеновских лучей или электронных пучков с длиной волны, соизмеримой с межмолекулярными расстояниями. [c.171]

    Важное значение для химика-неорганика имеют радиусы ионов ионные радиусы). Если кристалл состоит из ионов, например Ка С1, (Га Р5, то межионное (межъядерное) расстояние можно рассматривать как сумму ионных радиусов л. Предложены различные способы разделения межионных расстояний на слагаемые, отвечающие отдельным ионам. Соответственно известен ряд шкал ионных радиусов (Гольдшмидта, Полинга и др). Наиболее распространена в настоящее время шкала так называемых физических радиусов ионов, предложенная физиками Шенноном и Прюиттом в 1969 г. В этой системе радиусов границей между ионами считается точка минимума электронной плотности иа линии, соединяющей центры ионов. Такую систему радиусов удалось разработать благодаря появлению метода точного определения электронной плотности в кристаллах по рассеянию кристаллами рентгеновского излучения. Ионные радиусы по шкале Шеннона и Прюитта представлены в табл. 1.5 (указаны значения радиуса иона в кристаллической решетке при окружении его шестью ближайшими соседями). [c.51]

    Зная число частиц, необходимых для построения элемента кристаллической решетки, массу этих частиц и плотность кристалла можно определить сторону куба, а следовательно, и значения d, входящих в уравнение Брэггов, а это, в свою очередь, было необходимо для определения длины волны Я рентгеновских лучей, получаемых от различных антикатодов. Если бы этого не было сделано, то Мозли не смог бы открыть свой закон. [c.102]

    Рентгеновские лучи способны к дифракции (рассешию), а кристаллы служат естественной дифракционной решеткой. Расстояния между плоскостями трехмерной кристаллической решетки (определяющие параметры элементарной ячейки) имеют такой же порядок, как и длина волны рентгеновского излучения, поэтому кристаллическая решетка и ведет себя подобно дифракционной решетке. Если монохроматический пучок рентгеновских лучей направить на кристалл, рентгеновские лучи рассеиваются когерентно, т е. при сохранении во времени постоянства соотношения между фазами волн и, следовательно, длины волны. Это создает возможность интерференции (сложения амплитуд волн) дифрагированного (вторичного) излучения, возникающего при взаимодействии первичного излучения с электронными орбиталями атомов кристаллической решетки. Получаемая дифракционная картина отражает трехмерную периодичности распределения электронных плотностей в кристаллической решетке, характеризующих расположение атомов. [c.145]

    Другой метод определения электронного заряда основывается на измерении угла диффракцин рентгеновских лучей в кристалле известного строения. В выражение для е входят угол скольжения при отражении рентгеновского луча (см. стр. 224), молекулярный вес вещества, плотность кристалла, число Фарадея и длина волны рентгеновских г>ией. Последняя определяется из опытов диффракцин, проведенных соЛ>аидартными решетками. [c.17]

    Исходя из тетрагональной симметрии наиболее хорошо образованных кристаллов, определили кристаллическую систему при помощи графика для тетрагональных кристаллов. Хорошее совпадение было получено для отношения с/а = 1,73. Оно дает следующие значения параметров а = 6,28 A с = 10,84 A, откуда расчетная плотность de = 0,722 п, где п — число молекул в ячейке объемом а с. При n = 4 рентгеновская плотность кристаллов N0BrF4 оказалась равной 2,89, что хорошо совпадает с величиной 2,83—2,85, найденной пикнометрически, и позволяет сделать вывод о наличии четырех молекул в элементарной кристаллической ячейке вещества. [c.179]

    Применение рентгенографического метода определения электронной плотности кристаллов сложных химических соединений можно показать на примере расшифровки серии структур комплексных роданидов металлов. В кристалле КгС(1(5СН)4.2Н20 моноклинной сингонии, содержащем 84 атома на элементарную ячейку, требовалось определить 27 параметров координат атомов. Построением проекций электронной плотности по -рядам, включающим до 200 членов ряда, установлено положение всех атомов структуры. Методический интерес представляет определение положения легких атомов азота и кислорода в присутствии тяжелого атома кад-мия. Эти атомы дают различное рассеивание рентгеновских лучей. Возникновение волны [c.146]

    При образовании точечных дефектов в их окрестности происходят заметные деформапии рещетки атомы вокруг вакансии сдвигаются в направлении этого дефекта, межузельный атом раздвигает близлежащие атомы (рис. 14.1, 14.2). Благодаря этому образование дефекта по Шоттки с перемещением атома на поверхность увеличивает объем кристалла менее, чем на один атомный объем, при этом плотность дефектного кристалла должна быть меньше по сравнению с идеальным кристаллом. Образование дефекта по Френкелю практически не меняет объем кристалла, вследствие чего его плотность останется неизменной. Поэтому сравнение измеренной экспериментально плотности кристалла с ее значением, вычисленным исходя из размеров элементарной ячейки ( рентгеновская плотность), приннипиально позволяет определить разность числа межузельных атомов и вакансий. [c.315]

    Ввиду расхождения в результатах, несомненно, является желательным проведение дальнейших исследований по этому вопросу. При измерении интенсивности рентгеновских лучей явно трудно достичь требуемой точности было бы чрезвычайно полезно независимое решение вопроса. Такое независимое решение существовало бы, если бы размеры элементарной ячейки кристаллического каучука можно было определить с достаточной точностью методом рентгеновских лучей. Тогда можно было бы вычислить плотность кристаллов. Если бы она была известна, то измерения плотности, которые легко проводятся с нужной точностью, можно было бы использовать для определения процента кристалличности. Самая надежная оценка плотности каучукового кристалла, вероятно, сделана Бунном [14], который получил значение 1,00. К сожалению, температура, к которой относится результат, не указана. Это довольно важное упущение, поскольку плотность меняется на 1 % при изменении температуры на 15° С. Если считать, что эта плотность относится к температуре 20° С, то плотность, определенная при помощи рентгеновских лучей, будет на 10% больше, чем плотность аморфного каучука, подвергшегося очистке. Она по данным Макферсона [90] равна 0,909 при 20° С. На этом основании изменение в плотности, вычисленное по плотности в аморфном состоянии, которое соответствует 100% кристаллизации, будет равно 10,0%. Типичная экспериментальная величина для роста плотности при затвердевании при 0°С будет 2,7% [5], что будет соответствовать поэтому только 27% кристаллизации. Это значение совпадает с оценкой Гоппеля для задубевшего каучука. Значение для растянутого кристаллического каучука немного выше. Автор [129] измерил плотность сырого каучука и нашел, что при 700% растяжения она меняется более чем на 3%. Из измерений двойного лучепреломления он вычислил, что максимальная полученная кристаллизация отвечает изменению плотности на 3,75%, что эквивалентно 37% кристаллизации. Однако это число, вероятно, завышено, так как не принималось во внимание двойное лучепреломление, связанное с деформацией. Невозможно строгое сравнение этих количественных результатов, полученных для сырого каучука, растянутого при 0°С, с данными Гоппеля, характеризующими вулканизованный каучук при комнатной температуре. Но если их все-таки сопоставить, то они скорее подтверждают точность его данных и наводят на мысль, что максимально возможная степень кристаллизации ближе к 30%, чем к 90%. [c.163]

    Размер кристаллов вольфраиа, рассчитанный по данным дифракционного рентгеновского анализа по методу уширения дифракционных колец, оказался 170 – 200 Эти данные хорошо согласуются с оценкой дисперсности порошка по измеренной его удельной поверхности ( 9 = 19-23 м /г), которую определяли методом тепловой адсорбции азота. Данные электронно-мю ско-пического анализа порошка показали четкую кубическую форму у большинства частиц, имеющих размеры в пределах 20-300 Плотность порошка, измеренная пикнометром, составляла 19,24 – 19 28 г/см теоретическая плотность кристаллов вольфрама 19,3 г/см . [c.75]

    Плотность упаковки молекул в структуре молекулярного кристалла характеризуется коэффициентом упаковки к, который представляет собой частное отделения объема молекулы, вычисленного по величине межмолекулярного радиуса, на объем той же молекулы, установленный по данным рентгеновских измерений. Значения коэффициента упаковки для молекулярных кристаллов находятся в пределах от 0,65 до 0,77, как и для плотных укладок эллипсоидов и шаров. Вещества, имеющие молекулы такой формы, что любая их укладка не может иметь коэффициент упаковки больше 0,6, при отвердевании образуют не молекулярные кристаллы, а стекла. Для молекулярных кристаллов бензола, нафталина и знтрацена [c.22]

    В последние десятилетия наблюдалось бурное развитие рентгеноструктурного анализа (в первую очередь с использованием монокристаллов), а также других дифракционных методов исследования. Это обусловлено рядом причин. Одной из них явилось кардинальное усовершенствование рентгеновской аппаратуры, включая разработку ряда типов дифрактометров, управляемых ЭВМ, для съемки монокристаллов, внедрение новых способов регистрации рентгеновского излучения, использование монохроматоров. В результате точность экспериментальных данных резко возросла и появилась возможность решения принципиально новых задач (локализация легких атомов, определение деталей распределения электронной плотности на базе совместных данных нейтронографического и рентгеновского методов). Не менее важным обстоятельством явилась разработка комплексов программ обработки результатов измерений и определения структуры кристаллов, зачастую с недостаточно охарактеризованным химическим составом. Этой области применения рентгеноструктурного ана 1иза в химии посвящено несколько прекрасных монографий и учебников, и структурные разделы почти обязательно включаются в работы по синтезу новых соединений, так как дают непосредственные данные о пространственном расположении атомов в кристаллах а иногда являются и удобным способом определения химического состава, в особенности если известен качественный состав. [c.3]

    Общую схему рентгеноструктурного анализа можно сравнить с работой обычного микроскопа. Роль объектива, разлагающего в спектр лучи, рассеянные предметом, играет рентгеновская камера (или дифрактометр) с исследуемым кристаллом первичный пучок лучей, создаваемый рентгеновским аппаратом, разлагается кристаллом в дифракционный спектр. Роль окуляра, собирающего лучи спектра в увеличенное изображение предмета, играет вычислительная машина путем математической обработки дифракционных характеристик —направлений и интенсивности дифракционных лучей, она воссоздает увеличенное изображетше распределения электронной плотности по элементарной ячейке кристалла позиции максимумов плотности отвечают размещению [c.47]

---

Рентгенологическая плотность

Полезное

Методика исследования кристаллической структуры Порошковый рентгеновский дифрактометр в движении

Рентгеновская кристаллография (XRC ) – это экспериментальная наука, определяющая атомную и молекулярную структуру кристалла , в котором кристаллическая структура вызывает луч падающего рентгеновского излучения на рассеивать во многих конкретных направлениях. Путем измерения углов и интенсивности этих дифрагированных лучей кристаллограф может создать трехмерное изображение плотности электронов внутри кристалла. Из этой электронной плотности можно определить средние положения атомов в кристалле, а также их химические связи, их кристаллографический беспорядок и различные другие Информация.

Поскольку многие материалы могут образовывать кристаллы, такие как соли, металлы, минералы, полупроводники, а также различные неорганические, органические и биологические молекулы. Рентгеновская кристаллография сыграла фундаментальную роль в развитии многих научных областей. В первые десятилетия использования этот метод определял размер атомов, длину и типы химических связей, а также различия в атомном масштабе между различными материалами, особенно минералами и сплавами. Метод также выявил структуру и функцию многих биологических молекул, включая витамины, лекарства, белки и нуклеиновые кислоты, такие как ДНК. Рентгеновская кристаллография по-прежнему является основным методом определения атомной структуры новых материалов и выявления материалов, которые кажутся похожими в других экспериментах. Рентгеновские кристаллические структуры также могут объяснять необычные электронные или упругие свойства материала, проливать свет на химические взаимодействия и процессы или служить основой для разработка лекарственных средств против болезней.

При измерении дифракции рентгеновских лучей на монокристалле кристалл устанавливается на гониометре. Гониометр используется для позиционирования кристалла в выбранной ориентации. Кристалл освещается тонко сфокусированным монохроматическим пучком рентгеновских лучей, создавая дифракционную картину из регулярно расположенных пятен, известных как отражения. Двумерные изображения, полученные при различных ориентациях, преобразуются в трехмерную модель плотности электронов внутри кристалла с использованием математического метода преобразования Фурье в сочетании с химическими данными, известными для образца. Плохое разрешение (нечеткость) или даже ошибки могут возникнуть, если кристаллы слишком малы или недостаточно однородны по своему внутреннему составу.

Рентгеновская кристаллография связана с несколькими другими методами определения атомных структур. Подобные дифракционные картины могут быть получены путем рассеяния электронов или нейтронов, которые аналогично интерпретируются с помощью преобразования Фурье. Если монокристаллы достаточного размера не могут быть получены, могут быть применены различные другие рентгеновские методы для получения менее подробной информации; такие методы включают дифракцию на волокне, порошковую дифракцию и (если образец не кристаллизован) малоугловое рассеяние рентгеновских лучей (SAXS). Если исследуемый материал доступен только в форме нанокристаллических порошков или страдает плохой кристалличностью, методы электронной кристаллографии могут быть применены для определения атомной структуры.

Для всех вышеупомянутых методов дифракции рентгеновских лучей рассеяние является упругим ; Рассеянные рентгеновские лучи имеют ту же длину волны, что и входящие рентгеновские лучи. Напротив, методы неупругого рассеяния рентгеновских лучей полезны при изучении возбуждений образца, таких как плазмоны, кристаллическое поле и орбитальные возбуждения, магноны и фононы, а не распределение его атомов.

Содержание

• 1 История
  • 1.1 Ранняя научная история кристаллов и рентгеновских лучей
  • 1.2 Дифракция рентгеновских лучей
  • 1.3 Рассеяние
  • 1.4 Развитие от 1912–1920
  • 1.5 Культурное и эстетическое значение
• 2 Вклад в химию и материаловедение
  • 2.1 Минералогия и металлургия
  • 2.2 Ранние органические и малые биологические молекулы
  • 2.3 Биологическая кристаллография макромолекул
• 3 Рассеяние методы
  • 3.1 Упругое и неупругое рассеяние
  • 3.2 Другие рентгеновские методы
  • 3.3 Дифракция электронов и нейтронов
• 4 Методы
  • 4.1 Обзор дифракции рентгеновских лучей на монокристаллах
    • 4.1. 1 Процедура
    • 4.1.2 Ограничения
  • 4.2 Кристаллизация
  • 4.3 Сбор данных
    • 4.3.1 Монтаж кристалла
    • 4.3.2 Рентгеновское кислое ces
      • 4.3.2.1 Вращающийся анод
      • 4.3.2.2 Синхротронное излучение
      • 4.3.2.3 Лазер на свободных электронах
    • 4.3.3 Регистрация отражений
  • 4.4 Анализ данных
    • 4.4.1 Кристаллическая симметрия, элементарная ячейка и масштабирование изображения
    • 4.4.2 Начальное фазирование
    • 4.4.3 Построение модели и уточнение фазы
    • 4.4.4 Беспорядок
    • 4.4.5 Анализ прикладных вычислительных данных
  • 4.5 Отложение структура
• 5 Теория дифракции
  • 5.1 Интуитивное понимание закона Брэгга
  • 5.2 Рассеяние как преобразование Фурье
  • 5.3 Фридел и Бийвоет
  • 5.4 Сфера Эвальда
  • 5.5 Функция Паттерсона
  • 5.6 Преимущества кристалла
• 6 Нобелевских премий по рентгеновской кристаллографии
• 7 Области применения
  • 7.1 Идентификация лекарств
  • 7.2 Характеристика текстильных волокон и полимеров
  • 7.3 Исследование костей
  • 7.4 Интегральные схемы
• 8 См. Также
• 9 Ссылки
• 10 Дополнительная литература
  • 10.1 Международные таблицы для кристаллографии
  • 10.2 Связанные сборники статей
  • 10.3 Учебники
  • 10. 4 Прикладной анализ вычислительных данных
  • 10.5 Исторический
• 11 Внешние ссылки
  • 11.1 Учебные пособия
  • 11.2 Первичные базы данных
  • 11.3 Производные базы данных
  • 11.4 Структурная проверка

История

Ранний научная история кристаллов и рентгеновских лучей

Рисунок квадратной (рисунок A, вверху) и гексагональной (рисунок B, внизу) упаковки из работы Кеплера, Strena seu de Nive Sexangula.

Кристаллы, хотя их давно восхищали своей регулярностью и симметрией, они не исследовались научно до 17 века. Иоганн Кеплер предположил в своей работе Strena seu de Nive Sexangula (Новогодний подарок шестиугольного снега) (1611), что шестиугольная симметрия кристаллов снежинок была вызвана регулярной упаковкой сферических частицы воды.

Как показывает рентгеновская кристаллография, гексагональная симметрия снежинок является результатом тетраэдрического расположения водородных связей вокруг каждой молекулы воды. Молекулы воды расположены аналогично атомам кремния в полиморфе тридимита SiO 2. Полученная кристаллическая структура имеет гексагональную симметрию, если смотреть вдоль главной оси.

Датский ученый Николас Стено (1669) впервые провел экспериментальные исследования симметрии кристаллов. Стено показал, что углы между гранями одинаковы в каждом образце кристалла определенного типа, а Рене Жюст Хаю (1784) обнаружил, что каждую грань кристалла можно описать простым набором блоков блоков. такой же формы и размера. Следовательно, Уильям Хэллоуз Миллер в 1839 году смог присвоить каждой грани уникальную метку из трех небольших целых чисел, индексов Миллера, которые до сих пор используются для идентификации граней кристаллов. Исследование Хая привело к правильной идее, что кристаллы представляют собой регулярный трехмерный массив (решетка Браве ) атомов и молекул ; одиночная элементарная ячейка повторяется бесконечно по трем основным направлениям, которые не обязательно перпендикулярны. В 19 веке полный каталог возможных симметрий кристалла был разработан Йоханом Хесселем, Огюстом Браве, Евграфом Федоровым, Артуром Шенфлис и (с опозданием) Уильям Барлоу (1894). На основе имеющихся данных и физических соображений Барлоу предложил несколько кристаллических структур в 1880-х годах, которые позже были подтверждены рентгеновской кристаллографией; однако доступных данных в 1880-х годах было слишком мало, чтобы считать его модели убедительными.

Рентгеновская кристаллография показывает расположение молекул воды во льду, выявляя водородные связи (1), которые удерживают твердое тело вместе. Немногие другие методы могут определить структуру материи с такой точностью (разрешением).

Вильгельм Рентген открыл рентгеновские лучи в 1895 году, как раз в то время, когда завершались исследования симметрии кристаллов. Физики не были уверены в природе рентгеновских лучей, но вскоре заподозрили, что это волны электромагнитного излучения, формы света. Теория Максвелла электромагнитного излучения была хорошо принята учеными, а эксперименты Чарльза Гловера Баркла показали, что рентгеновские лучи демонстрируют явления, связанные с электромагнитными волнами, включая поперечные поляризационные и спектральные линии, аналогичные наблюдаемым в видимых длинах волн. Эксперименты с одной щелью в лаборатории Арнольда Зоммерфельда показали, что рентгеновские лучи имели длину волны примерно 1 ангстрем. Рентгеновские лучи – это не только волны, но также фотоны и обладают свойствами частиц. Альберт Эйнштейн представил концепцию фотона в 1905 году, но она не была широко принята до 1922 года, когда Артур Комптон подтвердил ее путем рассеяния рентгеновских лучей на электронах. Подобные частицам свойства рентгеновских лучей, такие как ионизация газов, побудили Уильяма Генри Брэгга в 1907 году утверждать, что рентгеновские лучи не являются электромагнитным излучением. Точка зрения Брэгга оказалась непопулярной, и наблюдение дифракции рентгеновских лучей, сделанное Максом фон Лауэ в 1912 году, подтвердило для большинства ученых, что рентгеновские лучи являются формой электромагнитного излучения.

Дифракция рентгеновских лучей

Входящий луч (идущий сверху слева) заставляет каждый рассеиватель повторно излучать небольшую часть своей интенсивности в виде сферической волны. Если рассеиватели расположены симметрично с расстоянием d, эти сферические волны будут синхронизированы (сложить конструктивно) только в направлениях, где разность их длины пути 2d sin θ равна целому числу, кратному длине волны λ. В этом случае часть входящего луча отклоняется на угол 2θ, создавая пятно отражения на дифракционной картине .

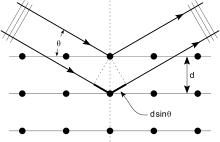
. Кристаллы представляют собой регулярные массивы атомов, а рентгеновские лучи можно рассматривать как волны электромагнитного излучения. Атомы рассеивают рентгеновские волны, в основном, через электроны атомов. Подобно тому, как океанская волна, ударяющаяся о маяк, производит вторичные круговые волны, исходящие от маяка, так и рентгеновские лучи, падающие на электрон, создают вторичные сферические волны, исходящие от него. Это явление известно как упругое рассеяние, а электрон (или маяк) известен как рассеиватель. Регулярный массив рассеивателей создает регулярный массив сферических волн. Хотя эти волны подавляют друг друга в большинстве направлений за счет деструктивной интерференции, они конструктивно складываются в нескольких конкретных направлениях, определяемых законом Брэгга :

2 d sin ⁡ θ = n λ { displaystyle 2d sin theta = n lambda}

Здесь d – расстояние между дифрагирующими плоскостями, θ { displaystyle theta}– угол падения, n – любое целое число, а λ – длина волны луча. Эти конкретные направления появляются в виде пятен на дифракционной картине , называемых отражениями. Таким образом, дифракция рентгеновских лучей возникает в результате падения электромагнитной волны (рентгеновских лучей) на регулярный массив рассеивателей (повторяющееся расположение атомов внутри кристалла).

Рентгеновские лучи используются для создания дифракционной картины, потому что их длина волны λ обычно того же порядка величины (1–100 ангстрем), что и расстояние d между плоскостями в кристалле. В принципе, любая волна, падающая на регулярный массив рассеивателей, вызывает дифракцию, как впервые предсказал Франческо Мария Гримальди в 1665 году. Для получения значительной дифракции необходимо расстояние между рассеивателями и длина волны падающей волны должны быть одинаковыми по размеру. Например, дифракция солнечного света через птичье перо впервые была описана Джеймсом Грегори в конце 17 века. Первые искусственные дифракционные решетки для видимого света были построены Дэвидом Риттенхаусом в 1787 году и Джозефом фон Фраунгофер в 1821 году. Однако видимый свет имеет слишком большую длину волны. (обычно 5500 ангстрем) для наблюдения дифракции на кристаллах. До первых экспериментов по дифракции рентгеновских лучей расстояния между плоскостями решетки в кристалле точно не были известны.

Идея использования кристаллов в качестве дифракционной решетки для рентгеновского излучения возникла в 1912 году в разговоре между Полом Питером Эвальдом и Макс фон Лауэ в Английском саду в Мюнхене. Эвальд предложил модель кристаллов резонатора для своей диссертации, но эта модель не могла быть подтверждена с использованием видимого света, так как длина волны была намного больше, чем расстояние между резонаторами. Фон Лауэ понял, что для наблюдения таких малых расстояний необходимо электромагнитное излучение с более короткой длиной волны, и предположил, что рентгеновские лучи могут иметь длину волны, сравнимую с расстоянием между элементарными ячейками в кристаллах. Фон Лауэ работал с двумя техниками, Вальтером Фридрихом и его помощником Полем Книппингом, чтобы направить луч рентгеновских лучей через кристалл сульфата меди и записать его дифракцию на фотопластинке. После проявления пластина показала большое количество четко определенных пятен, расположенных в виде пересекающихся кругов вокруг пятна, созданного центральным лучом. Фон Лауэ разработал закон, который связывает углы рассеяния, размер и ориентацию расстояний между элементарными ячейками в кристалле, за что он был удостоен Нобелевской премии по физике в 1914 году.

Рассеяние

Как описано в математическом выводе ниже, рассеяние рентгеновских лучей определяется плотностью электронов внутри кристалла. Поскольку энергия рентгеновского излучения намного больше, чем энергия валентного электрона, рассеяние может быть смоделировано как томсоновское рассеяние, взаимодействие электромагнитного луча со свободным электроном. Эта модель обычно применяется для описания поляризации рассеянного излучения.

Интенсивность томсоновского рассеяния для одной частицы с массой m и элементарным зарядом q составляет:

I o = I e (q 4 m 2 c 4) 1 + cos 2 ⁡ 2 θ 2 знак равно I e 7.94.10 – 26 1 + cos 2 ⁡ 2 θ 2 = I ef { displaystyle I_ {o} = I_ {e} left ({ frac {q ^ {4}} {m ^ {2} c ^ {4}}} right) { frac {1+ cos ^ {2} 2 theta} {2}} = I_ {e} 7.94.10 ^ {- 26} { frac { 1+ cos ^ {2} 2 theta} {2}} = I_ {e} f}

Следовательно, атомные ядра, которые намного тяжелее электрона, вносят незначительный вклад в рассеянное рентгеновское излучение.

Развитие с 1912 по 1920 год

Хотя алмазы (вверху слева) и графит (вверху справа) идентичны по химическому составу – оба являются чистыми углерод – рентгеновская кристаллография показала, что расположение их атомов (внизу) объясняет их различные свойства. В алмазе атомы углерода расположены тетраэдрически и удерживаются вместе одинарными ковалентными связями, что делает его прочным во всех направлениях. В отличие от графита, он состоит из сложенных листов. Внутри листа соединение ковалентно и имеет гексагональную симметрию, но между листами нет ковалентных связей, благодаря чему графит легко раскалывается на чешуйки.

После новаторских исследований Фон Лауэ область быстро развивалась, в первую очередь физиками Уильям Лоуренс Брэгг и его отец Уильям Генри Брэгг. В 1912–1913 годах младший Брэгг разработал закон Брэгга, который связывает наблюдаемое рассеяние с отражениями от равномерно расположенных плоскостей внутри кристалла. Брэгги, отец и сын, разделили Нобелевскую премию 1915 года по физике за свои работы в области кристаллографии. Самые ранние конструкции в целом были простыми и отличались одномерной симметрией. Однако по мере совершенствования вычислительных и экспериментальных методов в течение следующих десятилетий стало возможным вывести надежные положения атомов для более сложных двух- и трехмерных расположений атомов в элементарной ячейке.

Потенциал рентгеновской кристаллографии для определения структуры молекул и минералов – тогда еще смутно известный из химических и гидродинамических экспериментов – был реализован немедленно. Самые ранние структуры были простыми неорганическими кристаллами и минералами, но даже они раскрывали фундаментальные законы физики и химии. Первой структурой с атомным разрешением, которая была «решена» (т.е. определена) в 1914 году, была структура поваренной соли. Распределение электронов в структуре поваренной соли показало, что кристаллы не обязательно состоят из ковалентно связанных молекул, и доказало существование ионных соединений. Структура алмаза была решена в том же году, что доказало тетраэдрическое расположение его химических связей и показало, что длина одинарной связи C – C составляет 1,52 ангстрем. Другие ранние структуры включали медь, фторид кальция (CaF 2, также известный как флюорит), кальцит (CaCO 3) и пирит (FeS 2) в 1914 году; шпинель (MgAl 2O4) в 1915 г.; формы рутила и анатаза из диоксида титана (TiO 2) в 1916 году; Mn (OH) 2 и, соответственно, брусит Mg (OH) 2 в 1919 году. Также в 1919 году нитрат натрия ( NaNO 3) и дихлорийодид цезия (CsICl 2) были определены Ральфом Уолтером Грейстоуном Вайкоффом, а структура вюрцита (гексагональный ZnS) стало известно в 1920 году.

Структура графита была решена в 1916 году родственным методом порошковой дифракции, который был разработан Питером Дебаем и Пол Шеррер и, независимо, Альберт Халл в 1917 году. Структура графита была определена методом дифракции на монокристаллах в 1924 году двумя группами независимо. Халл также использовал порошковый метод для определения структуры различных металлов, таких как железо и магний.

Культурное и эстетическое значение

В 1951 году группа Festival Pattern Group на фестивале Великобритания принимала у себя группу производителей текстиля и опытных кристаллографов для создания кружева и принтов на основе рентгеновской кристаллографии инсулина, фарфоровой глины и гемоглобина. Одним из ведущих ученых проекта была д-р Хелен Мэгоу (1907–2002), в то время заместитель директора по исследованиям в Кавендишской лаборатории в Кембридже. Мегоу считается одной из центральных фигур, которая черпалавдохновение из кристаллических диаграмм и увидела их потенциал в дизайне. В 2008 году коллекция Wellcome в Лондоне организовала выставку в рамках Festival Pattern Group под названием «От атома к узорам».

Вклад в химию и материаловедение

Рентгеновская кристаллография привела к лучшему пониманию химические связи и нековалентных взаимодействий. Первоначальные исследования выявили типичные радиусы и подтвердили многие теоретические модели химической связи, такие как тетраэдрическая связь углерода в структуре алмаза, октаэдрическая связь металлов, наблюдаемая в гексахлороплатинате (IV) аммония, и резонанс, наблюдаемая в плоской карбонатной группе и в ароматических молекулах. Структура гексаметилбензола, составленная Кэтлин Лонсдейл в 1928 году, установила гексагональную симметрию бензола и показала четкую разницу в длине связи между алифатическими связями C – C и ароматическими связями C – C; это открытие привело к идее резонанса между химическими связями, что имело глубокие последствия для развития химии. Ее выводы были предвосхищены Уильямом Генри Брэггом, опубликовавшим в 1921 году модели нафталина и антрацена на основе других форм, ранней молекулярной замены..

Также в 1920-х годах Виктор Мориц Гольдшмидт и позже Линус Полинг разработал правила устранения химически маловероятных структур и определения относительных размеров элементов. Эти правила привели к структуре брукита (1928) и пониманию относительной стабильности форм рутила, брукита и анатаза. из диоксида титана.

Расстояние между двумя связанными атомами является чувствительной мерой прочности связи и его порядка связи ; Таким образом, рентгеноструктурные исследования приводят к открытию еще более экзотических типов связей в неорганической химии, таких как двойные металл-связь-металл, четверные металл-связь-металл и трехцентровые, двух- электронные связи. Рентгеновская кристаллография – или, строго говоря, эксперимент по неупругому комптоновскому рассеянию – также предоставила доказательства частично ковалентного характера водородных связей. В области металлоорганической химии рентгеновская структура ферроцена положила начало научным исследованиям сэндвич-соединения, а соли Цейса стимулировали исследования в области “обратных связей” и комплексов металл-пи. Наконец, рентгеновская кристаллография сыграет новаторскую роль в развитии супрамолекулярной химии, особенно в прояснении структуры краун-эфиров и принципы химии хозяин-гость.

Рентгеновская дифракция очень мощным инструментом при помощи разработка катализатора . Измерения ex-situ обычно проводятся для проверки кристаллической структуры материалов или для обнаружения новых структур. Эксперименты in-situ дают полное представление о структурной стабильности катализаторов в условиях реакции.

В области развития многих сложных неорганические и металлоорганические системы были проанализированы с использованием одного -кристаллические методы, такие как фуллерены, металлопорфирины и другие сложные соединения. Монокристаллическая дифракция также используется в фармацевтической промышленности из-за недавних проблем с полиморфами . Основными факторами, влияющими на качество монокристаллических структур, являются размер кристалла и его форма; перекристаллизация – широко используется метод для улучшения этих факторов в кристаллах с небольшими молекулами. Кембриджская база данных по конструкциям содержит более 1000000 структур по состоянию на июнь 2019 г.; более 99% этих структур были использованы дифракции рентгеновских лучей.

Минералогия и металлургия

Первый снимок дифракции рентгеновских лучей марсианской почвы – CheMin-анализ выявил полевой шпат, пироксены, оливин и другие (марсоход Curiosity в «Rocknest », 17 октября 2012 г.)

С 1920-х годов дифракция рентгеновских лучей был основным методом определения расположения элементов в минералах и металлах. Применение рентгеновской кристаллографии в минералогии началось со структуры граната, которая была определена в 1924 году Менцером. Систематическое рентгеноструктурное исследование силикатов было предпринято в 1920-х годах. Это исследование показало, что при изменении отношения Si /O кристаллы силиката демонстрируют значительные изменения в их расположении объектов. Мачацки распространил эти идеи на минералы, в которых алюминий заменяет атомы кремния силикатов. Первое применение рентгеновской кристаллографии в металлургии также произошло в середине 1920-х годов. В частности, структура сплава Mg 2 Sn Линусом Полингом привела к его теории стабильности и структуры ионных кристаллов.

17 октября В 2012 году марсоход Curiosity на планете Марс в «Rocknest » провел первый рентгеноструктурный анализ марсианской почвы. Результаты анализатора CheMin марсохода показали присутствие нескольких минералов, включая полевой шпат, пироксены и оливин, и предположили, что марсианин почва в образце была похожа на «выветрившиеся базальтовые почвы » гавайских вулканов.

Ранние органические и небольшие биологические молекулы

Трехмерная структура пенициллина, решено Дороти Кроуфут Ходжкин в 1945 году. Зеленые, красные, желтые и синие сферы представляют атомы углерода, кислорода, серы и азот соответственно. Белые сферы предоставляют собой водород, который был определен математически, а не с помощью рентгеновского анализа.

Первая структура органического соединения, гексаметилентетрамин, была решена в 1923 году. за этим последовало несколько исследований длинноцепочечных жирных кислот, которые являются важным компонентом биологических мембран. В 1930-х годах начали собираться игрушки, большие молекулы с двумерной сложностью. Значительным достижением стала структура фталоцианина, большая плоской молекулы, которая связями с молекулами порф, важными в биологии, такими как гем, коррин. и хлорофилл.

Рентгеновская кристаллография биологических молекул была начата с Дороти Кроуфут Ходжкин, которая решила структуры холестерина (1937), пенициллин ( 1946) и витамин B 12 (1956), за что она была удостоена Нобелевской программы по химии в 1964 году. В 1969 году ей удалось решить проблему инсулин, над которым она работала более тридцати лет.

Биологическая макромолекулярная кристаллография

Ленточная диаграмма структуры миоглобина, показывающая цветные альфа спирали. Такие белки представляют собой длинные линейные молекулы с тысячами элементов; Все же относительное положение каждого атома было определено с субатомным разрешением с помощью рентгеновской кристаллографии. Трудно визуализировать все атомы одновременно, лента показывает грубый путь основной цепи белка от его N-конца (синий) до его C-конца (красный).

Кристаллические структуры белков, которые нерегулярны и в сотни раз больше, чем холестерин, начали решаться в конце 1950-х годов, начиная со структур кашалота миоглобина сэра Джона Каудери Кендрю, за которую он разделил Нобелевскую премию по химии с Максом Перуцем в 1962 году. С тех пор было создано более 130 000 рентгеновских кристаллических структур белков, нуклеиновых кислот и других биологических молекулы. Ближайшим конкурирующим методом количеству проанализированных структур является спектроскопия ядерного магнитного резонанса (ЯМР), которая разрешает менее одной десятой этого числа. Кристаллография может определять структуру произвольно больших молекул, тогда как ЯМР в растворе ограничивается относительно небольшими молекулами (менее 70 k Da ). Рентгеновская кристаллография обычно используется для определения того, как фармацевтический препарат взаимодействует со своей белковой мишенью и какие изменения могут его улучшить. Однако внутренние белки мембраны по-прежнему сложно кристаллизовать, потому что требуются детергенты или другие денатуранты для их изолирования солюбилизировать, и такие детергенты часто препятствуют кристаллизации. Мембранные белки являются крупным компонентом генома и включают в себя многие белки, имеющие большое физиологическое значение, такие как ионные каналы и рецепторы. Гелиевая криогенная техника используются для предотвращения радиационного повреждения кристаллов белка.

С другой стороны, даже относительно небольшие молекулы создают проблемы для разрешающей способности рентгеновской кристаллографии. Структура, присвоенная в 1991 г. антибиотику, выделенному из морского организма (C 40H34Cl2N6O6, молярная масса 765,65 г / моль), оказалась неверной классическим доказательством структуры: синтетический образец не был идентичен натуральному продукту. Ошибка была приписана неспособности рентгеновской кристаллографии различить правильные -ОН / -NH и замененные -NH 2 / -O- группы в неправильной структуре. Однако с помощью электронных устройств группы можно использовать с помощью современных монокристаллических рентгеновских дифрактометров.

Несмотря на то, что кристаллография белков является бесценным инструментом структурологии, в ее методологии есть некоторые проблемы, которые затрудняют интерпретацию данных. Кристаллическая решетка, которая образуется в процессе кристаллизации, создает набор очищенного белка, который плотно и симметрично упакованы в кристалле. При поиске ранее неизвестного экспериментального метода определение его формы и границ внутри кристаллической решетки может быть сложной задачей. Белки обычно состоят из более мелких субъединиц, и задача различения субъединицы и идентификации фактического белка может быть сложной даже для опытных кристаллографов. Небиологические интерфейсы, используемые для использования в различных технологиях, используются как контакты упаковки кристаллов (или просто контакты кристаллов). Когда новая структура белка определяет с помощью рентгеновской кристаллографии и помещается в банк данных по белкам, ее авторов просят указать «биологическую сборку», которая будет составлять функциональный, биологически значимый белок. Однако ошибки, недостающие данные и неточные аннотации во время представления данных приводят к неясным структурам и ставят под угрозу надежность базы данных. Сообщается, что частота ошибок только в случае ошибочных аннотаций составляет 6,6% или приблизительно 15%, что, возможно, нетривиальным размером, указанным количеством размещенных структур. Эта «проблема границ раздела» обычно решается с помощью вычислительных подходов и стала признанной темой в структурной биоинформатике.

Методы рассеяния

Упругое и неупругое рассеяние

Рентгеновская кристаллография представляет собой форму упругого рассеяния ; исходящие рентгеновские лучи имеют ту же энергию и, следовательно, ту же длину волны, что и входящие рентгеновские лучи, только с измененным направлением. Напротив, неупругое рассеяние происходит, когда энергия передается от входящего рентгеновского излучения к кристаллу, например, путем возбуждения электрона внутренней оболочки на более высокий энергетический уровень. Такое неупругое рассеяние снижает энергию (увеличение длины волны) выходящего лучача. Неупругое рассеяние полезно для исследования таких возбуждений вещества, но не для определения распределения рассеивателей в веществе, что является целью рентгеновской кристаллографии.

рентгеновское излучение в диапазоне длин волн от 10 до 0,01 нанометров ; типичная длина волны, используемая для кристаллографии, составляет 1 Å (0,1 нм), что соответствует шкале ковалентных химических связей и радиуса одиночного атома. Более длинноволновые фотоны (такие как ультрафиолетовое излучение ) не будут иметь достаточного разрешения для определения положения атомов. С другой стороны, более коротковолновые фотоны, такие как гамма-лучи, трудно производить в больших количествах, их трудно сфокусировать, и они слишком сильно взаимодействуют с материей, создавая пары частиц-античастиц. Следовательно, рентгеновские лучи являются «сладким пятном» для длины волны при определении структур с атомным разрешением по рассеянию электромагнитного излучения.

Другие методы рентгеновского излучения

Другие формы упругого рассеяния рентгеновских лучей помимо Монокристаллическая дифракция включает порошковую дифракцию, малоугловое рассеяние рентгеновских лучей (SAXS ) и несколько типов дифракции рентгеновских лучей на волокнах, которые использовались Розалинда Франклин при определении структуры двойной спирали ДНК. В общем, дифракция рентгеновских лучей на монокристаллах дает больше структурной информации, чем эти другие методы; однако для этого требуется достаточно большой и обычный кристалл, который не всегда доступен.

В этих методах рассеяния обычно используются монохроматические рентгеновские лучи, которые ограничены одной длиной волны с небольшими отклонениями. Широкий спектр рентгеновских лучей (то есть смесь рентгеновских лучей с разными длинами волн) также может использоваться для проведения дифракции рентгеновских лучей, метод, известный как метод Лауэ. Это метод, использованный в первоначальном открытии дифракции рентгеновских лучей. Рассеяние Лауэ дает много структурной информации только при кратковременном воздействии рентгеновского луча и поэтому используется в структурных исследованиях очень быстрых событий (кристаллография с временным разрешением ). Однако оно не так хорошо подходит для определения полной атомной структуры кристалла, как монохроматическое рассеяние, и поэтому лучше работает с кристаллами с относительно простым расположением атомов.

В режиме обратного отражения Лауэ регистрируются рентгеновские лучи, рассеянные назад от источника широкого спектра. Это полезно, если образец слишком толстый для прохождения через него рентгеновских лучей. Плоскости дифрагирования в кристалле определяются, зная, что нормаль к плоскости дифрагирования делит угол между падающим лучом и дифрагированным лучом пополам. Диаграмма Гренингера может использоваться для интерпретации фотографии Лауэ с обратным отражением.

Дифракция электронов и нейтронов

Другие частицы, такие как электроны и нейтроны, могут быть использованы для создания дифракционной картины. Хотя рассеяние электронов, нейтронов и рентгеновских лучей основано на разных физических процессах, полученные дифракционные картины анализируются с использованием тех же методов построения изображений когерентной дифракции.

Как показано ниже, электронная плотность внутри кристалла и дифракционные картины связаны простым математическим методом, преобразованием Фурье, которое позволяет относительно легко вычислять плотность по образцам.. Однако это работает, только если рассеяние слабое, т. Е. Если рассеянные пучки намного менее интенсивны, чем приходящий пучок. Слабо рассеянные пучки проходят через остальную часть кристалла, не подвергаясь второму рассеянию. Такие повторно рассеянные волны называются «вторичным рассеянием» и затрудняют анализ. Любой достаточно толстый кристалл будет вызывать вторичное рассеяние, но поскольку рентгеновские лучи относительно слабо взаимодействуют с электронами, это обычно не вызывает серьезного беспокойства. Напротив, электронные лучи могут вызывать сильное вторичное рассеяние даже для относительно тонких кристаллов (>100 нм). Поскольку эта толщина соответствует диаметру многих вирусов, многообещающим направлением является дифракция электронов на изолированных макромолекулярных ансамблях, таких как вирусные капсиды и молекулярные машины, которые могут быть с помощью крио- электронного микроскопа. Кроме того, сильное взаимодействие электронов с веществом (примерно в 1000 раз сильнее, чем для рентгеновских лучей) позволяет определять того, насколько хорошо пронизывают размеры. Область применения электронной кристаллографии изменяется от биомолекул, таких как мембранные белки, на тонких пленках до сложных структур (нанокристаллических) интерметаллических соединений и цеолитов.

Нейтронная дифракция – отличный метод определения структуры, хотя было трудно получить интенсивные монохроматические пучки нейтронов в достаточных количествах. Традиционно используются ядерные реакторы, источники, вырабатывающие нейтроны путем расщепления, становятся все более доступными. Будучи незаряженными, нейтроны намного легче рассеиваются на ядрах атомов, чем на электронах. Следовательно, рассеяние нейтронов очень полезно для наблюдения положения легких с небольшим количеством электронов, особенно водорода, который практически невидим при дифракции рентгеновских лучей. Рассеяние нейтронов также имеет замечательное свойство, заключающееся в том, что происходит, регулируемое соотношение нормальной воды, H 2 O и тяжелой воды, D 2 О.

Методы

Обзор дифракции рентгеновских лучей на монокристаллах

Рабочий процесс для определения структуры молекулы с помощью рентгеновской кристаллографии.

Самый старый и самый точный метод рентгеновского исследования -лучевая кристаллография – это дифракция рентгеновских лучей на монокристалле, при которой луч рентгеновских лучей попадает на монокристалл, создаваемую рассеянные лучи. Когда они попадают на кусок пленки или другой детектор, эти лучи образуют дифракционную картину из пятен; сила и углы этих лучей регистрируются по мере следящего поворота кристалла. Каждое пятно называется отражением, поскольку оно соответствует отражению рентгеновских лучей от одного наборано равномерно плоскостей внутри кристалла. Для монокристаллов достаточной чистоты и регулярности данных дифракции рентгеновских лучей можно определить средние длины и углы химических связей с точностью до нескольких тысяч долей ангстрема и до нескольких десятых долей градуса соответственно. Атомы в кристалле не статичны, а колеблются вокруг своего среднего положения, обычно менее чем на несколько десятых ангстрема. Рентская кристаллография позволяет измерить этих колебаний.

Процедура

Методика рентгеновской кристаллографии монокристаллов состоит из трех основных этапов. Первый – и часто самый трудный – шаг – получить адекватный кристалл исследуемого материала. Кристалл должен быть достаточно большим (обычно более 0,1 мм по всем размерам), чистым по составу и правильной структуре, без значительных внутренних дефектов, таких как трещины или двойникование.

во втором На шаге кристалл помещают в интенсивный пучок рентгеновских лучей, обычно с одной длиной волны (монохроматические рентгеновские лучи), создавая регулярную картину отражений. Измеряются углы и интенсивности дифрагированных рентгеновских лучей, при этом каждое соединение имеет уникальную дифракционную картину. По мере того, как кристалл постепенно поворачивается, предыдущие отражения исчезают и появляются новые; интенсивность каждого пятна записывается при каждой ориентации кристалла. Может потребоваться сбор нескольких наборов данных, каждый из которых охватывает чуть больше половины полного оборота кристалла и обычно содержит десятки тысяч отражений.

На третьем этапе эти данные комбинируются с помощью вычислений с дополнительной химической информацией для создания и уточнения модели расположения атомов внутри кристалла. Окончательная, уточненная модель атомного устройства – теперь называемая кристаллической структурой – обычно хранится в общедоступной базе данных.

Ограничения

По мере того, как повторяющаяся единица кристалла, его элементарная ячейка, становится больше и сложнее, изображение атомного уровня, полученное с помощью рентгеновской кристаллографии, становится менее разрешенным (более “нечетким”) для заданного числа наблюдаемых отражений. Часто различают два предельных случая рентгеновской кристаллографии – «низкомолекулярная» (которая включает сплошные неорганические твердые тела) и «макромолекулярная» кристаллография. Кристаллография малых молекул обычно включает кристаллы, содержащие менее 100 атомов в их асимметричной единице ; такие кристаллические структуры обычно настолько хорошо разрешены, что атомы можно различить как изолированные «капли» электронной плотности. Напротив, кристаллография макромолекул часто включает в себя десятки тысяч атомов в элементарной ячейке. Такие кристаллические структуры обычно менее разрешены (более «размыты»); атомы и химические связи выглядят как трубки электронной плотности, а не как изолированные атомы. В общем, небольшие молекулы также легче кристаллизовать, чем макромолекулы; тем не менее, рентгеновская кристаллография оказалась возможной даже для вирусов и белков с сотнями тысяч атомов благодаря усовершенствованной кристаллографической визуализации и технологии. Хотя обычно рентгеновская кристаллография может выполняться только в том случае, если образец находится в кристаллической форме, были проведены новые исследования по отбору образцов некристаллических форм.

Кристаллизация

Кристалл белка, видимый под микроскоп. Кристаллы, используемые в рентгеновской кристаллографии, могут быть меньше миллиметра в поперечнике.

Хотя кристаллографию можно использовать для характеристики беспорядка в нечистых или нерегулярных кристаллах, кристаллография обычно требует чистого кристалла высокой регулярности для определения структуры сложной структуры. расположение атомов. Чистые, правильные кристаллы иногда можно получить из природных или синтетических материалов, таких как образцы металлов, минералов или других макроскопических материалов. Регулярность таких кристаллов иногда можно улучшить с помощью отжига макромолекулярных кристаллов и других методов. Однако во многих случаях получение кристалла дифракционного качества является главным препятствием на пути решения его структуры с атомным разрешением.

Кристаллография малых молекул и макромолекул различается по диапазону возможных методов, используемых для получения кристаллов дифракционного качества.. Небольшие молекулы обычно имеют несколько степеней конформационной свободы и могут быть кристаллизованы с помощью широкого диапазона методов, таких как химическое осаждение из паровой фазы и перекристаллизация. Напротив, макромолекулы обычно имеют много степеней свободы, и их кристаллизация должна осуществляться таким образом, чтобы поддерживать стабильную структуру. Например, белки и более крупные молекулы РНК не могут кристаллизоваться, если их третичная структура была развернута ; поэтому диапазон условий кристаллизации ограничен условиями раствора, в которых такие молекулы остаются свернутыми.

Три метода изготовления кристаллов, A: висящая капля. B: Падение сидя. C: Микродиализ

Кристаллы белка почти всегда выращиваются в растворе. Наиболее распространенный подход – очень постепенно снижать растворимость составляющих его молекул; если это сделать слишком быстро, молекулы будут выпадать в осадок из раствора, образуя бесполезную пыль или аморфный гель на дне контейнера. Рост кристаллов в растворе характеризуется двумя стадиями: зарождение микроскопического кристаллита (возможно, имеющего только 100 молекул), за которым следует рост этого кристаллита, в идеале до кристалла дифракционного качества. Условия решения, благоприятствующие первой стадии (зародышеобразование), не всегда совпадают с условиями, благоприятствующими второй стадии (последующему росту). Цель кристаллографа – определить условия раствора, которые способствуют развитию одного большого кристалла, поскольку более крупные кристаллы обеспечивают улучшенное разрешение молекулы. Следовательно, условия раствора не должны благоприятствовать первому этапу (зародышеобразование), но благоприятствовать второму (росту), так что на каждую каплю образуется только один большой кристалл. Если зародышеобразование будет слишком благоприятным, в капле будет формироваться поток мелких кристаллитов, а не один большой кристалл; если одолжить слишком мало, никакой кристалл не образуется. Другие подходы включают кристаллизацию белков под маслом, когда водные растворы белков распределяются под жидким маслом, а вода испаряется через слой масла. Различные масла имеют разную проницаемость к испарению, что приводит к изменениям в скоростях концентрации из разных смесей перципиент / белок.

Крайне трудно предсказать хорошие условия для зарождения или роста хорошо упорядоченных кристаллов. На практике благоприятные условия выявляются путем скрининга; готовят очень большую партию молекул и испытывают большое количество растворов для кристаллизации. Сотни, даже тысячи условий решения обычно пробуются, прежде чем найти удачное. В различных условиях можно использовать один или несколько физических механизмов для снижения растворимости молекулы; например, некоторые из них могут изменять pH, некоторые содержат соли серии Хофмейстера или химические вещества, снижающие диэлектрическую проницаемость раствора, а третьи содержат крупные полимеры, такие как полиэтиленгликоль, который выгнать молекулу из раствора за счет энтропийных эффектов. Также принято пробовать несколько температур для стимулирования кристаллизации или постепенно понижать температуру, чтобы раствор стал перенасыщенным. Эти методы требуют больших количеств целевой молекулы, так как они используют высокую концентрацию молекулы (молекул) для кристаллизации. Из-за сложности получения таких больших количеств (миллиграммов ) кристаллизационного белка были разработаны роботы, способные точно дозировать кристаллизационные пробные капли, размер которых составляет порядка 100 нанолитров <568.>в объеме. Это означает, что в эксперименте используется в 10 раз меньше белка по сравнению с испытаниями по кристаллизации, проводимыми вручную (порядка 1 микролитр ).

Известно несколько факторов, препятствующих или нарушающих кристаллизацию. Растущие кристаллы обычно удерживаются при постоянной температуре и защищенных от ударов или вибраций, которые могут нарушить их кристаллизацию. Примеси в молекулах или в кристаллизационных растворах часто препятствуют кристаллизации. Конформационная гибкость молекулы также имеет тенденцию к снижению вероятности кристаллизации из-за энтропии. Молекулы, которые имеют тенденцию к самоорганизации в регулярные спирали, часто не желают собираться в кристаллы. Кристаллы могут быть испорчены двойникованием, которое может происходить, когда элементарная ячейка может одинаково выгодно упаковываться в нескольких ориентациях; хотя недавние достижения в вычислительных методах может позволить решить структуру некоторых двойниковых кристаллов. Не сумев кристаллизовать целевую молекулу, кристаллограф может попробовать еще раз. с немного измененным вариантом молекулы; даже небольшие изменения молекулярных свойств могут привести к большим различиям в поведении кристаллизации.

Сбор данных

Установка кристалла

Воспроизведение мультимедиа Анимация, показывающая пять возможных движений с помощью четырехкружного каппа-гониометра. Вращения вокруг каждого из четырех углов φ, κ, ω и 2θ покидают кристалл в пределах рентгеновского луча, но меняют ориентацию кристалла. Детектор (красный прямоугольник) можно сдвинуть ближе или дальше от кристалла, что позволит получать данные с более высоким разрешением (если они ближе) или лучше различать пики Брэгга (если они находятся дальше).

Кристалл устанавливается для измерений так что его можно держать в рентгеновском луче и вращать. Есть несколько способов крепления. Раньше кристаллы загружали в стеклянные капилляры с раствором для кристаллизации (маточный раствор ). В настоящее время кристаллы малых молекул обычно прикрепляются маслом или клеем к стекловолокну или петле, которая сделана из нейлона или пластика и прикреплена к твердому стержню. Кристаллы белка захватывают петлей, затем быстро замораживают жидким азотом. Это замораживание снижает радиационное повреждение рентгеновских лучей, а также шум в пиках Брэгга из-за теплового движения (эффект Дебая-Валлера). Однако необработанные кристаллы протеина часто трескаются при мгновенной заморозке; поэтому перед замораживанием их обычно предварительно замачивают в растворе криопротектора. К сожалению, это предварительное замачивание само по себе может привести к растрескиванию кристалла, разрушив его для кристаллографии. Как правило, успешные криоусловия определяются методом проб и ошибок.

Капилляр или петля устанавливаются на гониометре, что позволяет точно позиционировать его в пределах луча рентгеновского излучения и вращать. Поскольку и кристалл, и луч часто очень малы, кристалл должен быть центрирован внутри луча с точностью ~ 25 микрометров, чему способствует камера, сфокусированная на кристалле. Наиболее распространенным типом гониометров является «каппа-гониометр», который предлагает три угла поворота: угол ω, который вращается вокруг оси, перпендикулярной лучу; угол κ вокруг оси, находящейся под углом ~ 50 ° к оси ω; и, наконец, угол φ относительно оси петли / капилляра. Когда угол κ равен нулю, оси ω и φ выровнены. Вращение κ обеспечивает удобную установку кристалла, поскольку рычаг, в котором установлен кристалл, может быть повернут в сторону кристаллографа. Колебания, возникающие во время сбора данных (упомянутые ниже), касаются только оси ω. Более старый тип гониометра – это гониометр с четырьмя кругами и его родственники, такие как гониометр с шестью кругами.

Источники рентгеновского излучения

Вращающийся анод

Мелкомасштабная кристаллография может выполняться с помощью местного источника рентгеновской трубки, обычно соединенного с электронная матрица детектор. Их преимущество заключается в том, что они относительно недороги и просты в обслуживании, а также позволяют проводить быстрый скрининг и сбор образцов. Однако длина волны излучаемого света ограничена доступностью различных материалов анода. Кроме того, интенсивность ограничивается прилагаемой мощностью и доступной охлаждающей способностью, чтобы избежать расплавления анода. В таких системах электроны выкипают из катода и ускоряются за счет сильного электрического потенциала ~ 50 кВ ; достигнув высокой скорости, электроны сталкиваются с металлической пластиной, испуская тормозное излучение и некоторые сильные спектральные линии, соответствующие возбуждению электронов внутренней оболочки металла. Наиболее распространенным используемым металлом является медь, которую можно легко хранить в холодном состоянии благодаря высокой теплопроводности, и которая дает прочный Kα и K β линий. Линия K β иногда подавляется тонкой (~ 10 мкм) никелевой фольгой. Самая простая и дешевая разновидность герметичной рентгеновской трубки имеет стационарный анод (трубка Крукса ) и работает с мощностью электронного луча ~ 2 кВт. Более дорогая разновидность имеет источник типа с вращающимся анодом, который работает с мощностью электронного луча ~ 14 кВт.

Рентгеновские лучи обычно фильтруются (с использованием рентгеновских фильтров ) до одной длины волны (становятся монохроматическими) и коллимируются в одном направлении, прежде чем они будут позволил ударить кристалл. Фильтрация не только упрощает анализ данных, но также удаляет излучение, ухудшающее кристалл, не предоставляя полезной информации. Коллимация выполняется либо с помощью коллиматора (в основном, длинной трубки), либо с помощью хитроумной компоновки слегка изогнутых зеркал. Зеркальные системы предпочтительны для небольших кристаллов (менее 0,3 мм) или с крупными элементарными ячейками (более 150 Å).

Вращающиеся аноды использовались Джоанной (Джока) Марией Ванденберг в первых экспериментах, которые продемонстрировали мощность рентгеновских лучей для быстрого (в реальном времени) скрининга больших InGaAsP тонкопленочные пластины для контроля качества лазеров с квантовыми ямами.

Синхротронное излучение

Источники синхротронного излучения – одни из самых ярких источников света на Земле и являются одними из самых мощных инструментов, доступных для рентгеновских кристаллографов. Рентгеновские лучи, генерируемые в больших машинах, называемых синхротронами, которые ускоряют электрически заряженные частицы, часто электроны, почти до скорости света и удерживают их в (примерно) круговой петле с использованием магнитных полей.

Синхротроны, как правило, являются национальными объектами, каждое из которых имеет несколько выделенных линий передачи, где данные собираются непрерывно. Первоначально синхротроны были разработаны для использования физиками высоких энергий, изучающими субатомные частицы и космические явления. Самый большой компонент каждого синхротрона – это электронное накопительное кольцо. Это кольцо на самом деле не идеальный круг, а многогранный многоугольник. В каждом углу многоугольника или сектора точно выровненные магниты изгибают электронный поток. Поскольку путь электронов искривляется, они излучают всплески энергии в виде рентгеновских лучей.

Использование синхротронного излучения часто требует определенных требований для рентгеновской кристаллографии. Интенсивное ионизирующее излучение может вызвать радиационное повреждение образцов, особенно макромолекулярных кристаллов. Криокристаллография защищает образец от радиационного повреждения, замораживая кристалл при температуре жидкого азота (~ 100 K ). Однако синхротронное излучение часто имеет преимущество в виде выбираемых пользователем длин волн, что позволяет проводить эксперименты по аномальному рассеянию, которые максимизируют аномальный сигнал. Это очень важно в таких экспериментах, как SAD и MAD.

Лазер на свободных электронах

Лазеры на свободных электронах были разработаны для использования в рентгеновской кристаллографии. Это самые яркие источники рентгеновского излучения, доступные в настоящее время; с рентгеновскими лучами, приходящими всплесками фемтосекунд. Интенсивность источника такова, что дифракционные картины с атомным разрешением могут быть разрешены для кристаллов, иначе они слишком малы для сбора. Однако интенсивный источник света также разрушает образец, что требует снятия нескольких кристаллов. Поскольку каждый кристалл случайным образом ориентирован в луче, необходимо собрать сотни тысяч отдельных дифракционных изображений, чтобы получить полный набор данных. Этот метод, последовательная фемтосекундная кристаллография, использовался для определения структуры ряда структур белковых кристаллов, иногда отмечены различия с эквивалентными структурами, полученными из синхротронных источников.

Запись отражений

Картина дифракции рентгеновских лучей кристаллизованного фермента. Рисунок пятен (отражений) и относительная сила каждого пятна (интенсивности) могут использоваться для определения структуры фермента.

Когда кристалл устанавливается и подвергается воздействию интенсивного пучка рентгеновских лучей, он рассеивает Рентгеновские лучи превращаются в узор из пятен или отражений, которые можно наблюдать на экране за кристаллом. Аналогичный узор можно увидеть, посветив лазерной указкой на компакт-диск. Относительная интенсивность этих пятен дает информацию для определения расположения молекул внутри кристалла в атомных деталях. Интенсивность этих отражений может быть записана с помощью фотопленки, детектора области (такого как пиксельный детектор ) или с помощью устройства с зарядовой связью (CCD). датчик изображений. Пики под малыми углами соответствуют данным с низким разрешением, тогда как пики под большими углами представляют данные с высоким разрешением; таким образом, верхний предел возможного разрешения структуры может быть определен по первым нескольким изображениям. На этом этапе можно определить некоторые показатели качества дифракции, такие как мозаичность кристалла и его общий беспорядок, как это наблюдается по ширине пиков. Некоторые патологии кристалла, которые могут сделать его непригодным для определения структуры, также могут быть быстро диагностированы на этом этапе.

Одного изображения пятен недостаточно, чтобы восстановить весь кристалл; он представляет собой лишь небольшую часть полного преобразования Фурье. Чтобы собрать всю необходимую информацию, кристалл необходимо пошагово повернуть на 180 ° с записью изображения на каждом шаге; фактически, для покрытия обратного пространства требуется чуть больше 180 ° из-за кривизны сферы Эвальда. Однако, если кристалл имеет более высокую симметрию, может быть зарегистрирован меньший угловой диапазон, такой как 90 ° или 45 °. Ось вращения следует менять хотя бы один раз, чтобы избежать образования «мертвого пятна» в обратном пространстве вблизи оси вращения. Принято слегка покачивать кристалл (на 0,5–2 °), чтобы охватить более широкую область обратного пространства.

Для определенных методов фазирования может потребоваться несколько наборов данных. Например, фазировка MAD требует, чтобы рассеяние регистрировалось по крайней мере на трех (а обычно на четырех для избыточности) длинах волн входящего рентгеновского излучения. Монокристалл может слишком сильно разложиться во время сбора одного набора данных из-за радиационного повреждения; в таких случаях необходимо брать наборы данных по множеству кристаллов.

Анализ данных

Симметрия кристаллов, элементарная ячейка и масштабирование изображения

Записанные серии двумерной дифракции паттерны, каждая из которых соответствует разной ориентации кристаллов, преобразуются в трехмерную модель электронной плотности; при преобразовании используется математический метод преобразования Фурье, который поясняется ниже. Каждое пятно соответствует разному типу изменения электронной плотности; кристаллограф должен определить, какая вариация соответствует какому пятну (индексация), относительная сила пятен на разных изображениях (слияние и масштабирование) и как вариации должны быть объединены для получения общей электронной плотности (фазировка).

Обработка данных начинается с индексации отражений. Это означает определение размеров элементарной ячейки и пик изображения, соответствующий положению в обратном пространстве. Побочным продуктом индексации является определение симметрии кристалла, то есть его пространственной группы. Некоторые космические группы можно исключить с самого начала. Например, в хиральных молекулах невозможно наблюдать симметрию отражения; таким образом, только 65 пространственных групп из 230 возможных допускаются для белковых молекул, которые почти всегда хиральны. Индексирование обычно выполняется с помощью процедуры автоиндексирования. После назначения симметрии данные интегрируются. Этопреобразует изображения, тысячи тысяч отражений, один файл записей, состоящий из (как минимум) индекс Миллера каждого отражения и каждого отражения (в этом состоянии файл часто также включает оценки и меры пристрастности (какая часть) данного отражения была записана на этом изображении)).

Полный набор данных может состоять из сотен отдельных изображений, сделанных при разных ориентациях кристалла. Первый шаг – объединить и масштабировать эти различные изображения, то есть определить, какие пики появляются на двух или более изображениях (слияние), и масштабировать относительные изображения так, чтобы они имели согласованный масштаб изображения. Оптимизация шкалы интенсивности имеет решающее значение, поскольку относительная интенсивность ключевой информации, на основе которой определяется структура. Повторяющийся метод сбора кристаллографических данных часто приводит к многократному множеству эквивалентных по симметрии отражений. Это позволяет рассчитать связанный с симметрией R-фактор, индекс надежности, основанный на том, показатели надежности, измеренные значения отражений, эквивалентных симметрии, что позволяет оценить качество.

Начальное фазирование

Данные, собранные в результате дифракционного эксперимента, представляют собой представление кристаллической решетки в обратном космическом пространстве. Расположение каждого дифракционного «пятна» определяется размером и формой элементарной ячейки, а также внутренней симметрией внутри кристалла. Регистрируется интенсивность каждого дифракционного «пятна», и эта интенсивность пропорциональна квадрату структурного фактора амплитуды. Структурный фактор представляет собой комплексное число , содержащее информацию, относящуюся как к амплитуду, так и к фазе волны . Чтобы получить модель интерпретируемой карты электронной плотности, которая может быть известна как амплитуда, так и фаза (карта электронной плотности позволяет кристаллографу построить начальную молекулы). Фазу нельзя напрямую записать во время дифракционного эксперимента: это известно как фазовая проблема . Оценки начальной фазы могут быть получены разными способами:

• Ab initio phasing или прямыми методами – обычно это метод выбора для малых молекул. (<1000 non-hydrogen atoms), and has been used successfully to solve the phase problems for small proteins. If the resolution of the data is better than 1.4 Å (140 pm ), прямые методы использовать информацию о фазе через использование фазовых методов между определенными группами отражений.
• Молекулярная замена – если родственная структура известна, ее можно использовать в качестве модели поиска в молекулярном замещении для определения ориентации и положения молекул в элементарной ячейке. Полученные таким образом фазы можно использовать для создания электронной электронной почты.
• Аномальное рассеяние рентгеновских лучей (MAD или фазировка SAD ) – длина волны рентгеновского излучения может быть сканирована за пределы крайнего атома, который известным образом изменяет рассеяние. Регистрируя полные наборы отражений на трех длинах волн (намного ниже и в середине концевых элементов), можно определить субструктуру аномально дифрагирующих элементов и, следовательно, преобразовать всю молекулы. Самый популярный метод аномальных возбудителей в белки – это экспрессия белка в ауксотрофе метионина (неспособный синтезировать метионин) в среде, богатой селенометионином, который содержит селен атомы. Затем можно провести эксперимент MAD вокруг элемента, который затем должен определить положение любых остатков метионина в белке, начальные фазы.
• Методы тяжелых атомов (множественные изоморфные замены ) – Если электронно-плотные атомы могут быть введены в кристалл, можно использовать прямые методы или методы пространства Паттерсона для определения их местоположения и получения начальных значений. Такие тяжелые атомы могут быть введены либо путем вымачивания кристаллов в растворе, либо путем совместной кристаллизации (выращивания кристаллов в тяжелого атома). Как и в случае фазирования MAD, амплитуды амплитуды рассеяния можно интерпретировать как получение фаз. Хотя это первоначальный метод, с помощью которого были решены кристаллические структуры белка, он в степени был заменен фазированием MAD селенометионином.

Построение модели и уточнение фаз

Структура альфа-спирали белка с фигурными фигурами для ковалентного связывания в пределах электронной плотности для кристаллической структуры при сверхвысоком разрешении (0,91 Å). Контуры плотности показаны серым цветом, остов спирали – белым, боковые цепи – голубым, атомы O – красным, атомы N – синим, а водородные связи – зелеными пунктирными линиями. Трехмерное изображение электронной плотности (синий) лиганда (оранжевый), связанное с сайтом связывания в белке (желтый). Электронная плотность получается из экспериментальных данных, и лиганд создается в этой электронной плотности.

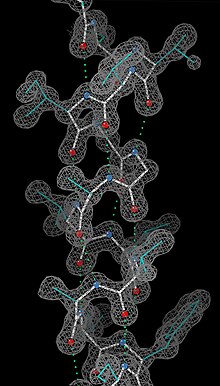
Получив начальные фазы, можно построить начальную модель. Позиции элементов в моделях и соответствующие им факторы Дебая-Валлера (или B -факторы, учитывающие тепловое движение атома) могут быть уточнены, чтобы соответствовать наблюдаемым дифракционным данным, в идеале дает лучший набор фаз. Затем модель может быть приспособлена к новой карте электронной плотности, и будут выполнены последовательные раунды уточнения. Этот процесс взаимодействия продолжается до тех пор, пока корреляция между дифракционными данными и моделью не станет максимальной. Согласованность измеряется с помощью R-фактора определяемого как

R = ∑ все отражения | F obs – F calc | ∑ все размышления | F obs |, { displaystyle R = { frac { sum _ { text {все отражения}} left | F _ { text {obs}} – F _ { text {calc}} right |} { sum _ { text {все отражения}} left | F _ { text {obs}} right |}},}

где F – структурный фактор . Аналогичным критерием качества является R бесплатный, который рассчитывается из подмножества (~ 10%) отражений, которые не включены в уточнение структуры. Оба фактора R зависят от разрешения данных. Как показывает практика, R бесплатно быть равным разрешению в ангстремах, деленному на 10; таким образом, набор данных с разрешением 2 Å должен дать окончательное R бесплатно ~ 0,2. Характеристики химической связи, такие как стереохимия, водородная связь и распределение связей, дополнительными длинными показателями качества модели. Фазовый сдвиг – серьезная проблема при построении такой итеративной модели. Пропуск карты – распространенный метод, использование для проверки этого.

Возможно, наблюдать каждый атом в асимметричном блоке. Во многих случаях Кристаллографический беспорядок смазывает карту электронной плотности. Слабо рассеивающие атомы, такие как водород, обычно невидимы. Также возможно, что один атом несколько раз появляется на карте электронной плотности, например, если боковая цепь белка имеет несколько (<4) allowed conformations. In still other cases, the crystallographer may detect that the covalent structure deduced for the molecule was incorrect, or changed. For example, proteins may be cleaved or undergo post-translational modifications that were not detected prior to the crystallization.

Беспорядок

Обычная проблема при уточнении кристаллических структур беспорядка. Ловушки неправильного моделирования демонстрируют дисконтированную гипотезой изомерии растяжения связей. Неупорядоченность моделируется относительно относительной совокупности компонентов, часто только двух, неупорядоченность предполагает сосуществование двух видов или конформаций.

Анализ прикладных вычислительных данных

Использование вычислительных методов для обработки данных порошковой дифракции рентгеновских лучей обобщено. эксперим ентальные данные сравниваются с смоделированной дифрактограммой модели s. структурирует, используя во внимание инструментальные параметры, уточняют структурные или модроструктурные параметры модели, алгоритм минимизации на основе наименьших квадратов. Большинство доступных инструментов позволяют идентифицировать фазы и структурное уточнение, основаны на методе Ритвельда, некоторые из них являются открытыми и бесплатными программами, такими как FullProf Suite, Jana2006, MAUD, Rietan, GSAS и т. Д., В то время как другие доступны под коммерческие лицензии, такие как Diffrac.Suite TOPAS, Match!, И т. д. Эти инструменты также позволяют уточнять Le Bail r (также называемое сопоставлением профилей), есть уточнять параметры ячеек на основе Положения пиков Брэгга и профили пиков без учета самой кристаллографической структуры. Более современные инструменты позволяют уточнять как структурные, так и микроструктурные данные, такие как программа FAULTS, включенная в FullProf Suite, которая позволяет уточнять структуры с плоскими дефектами (например, дефекты упаковки, двойникование, срастания).

Создание структуры

После того, как модель структуры молекулы завершена, она часто депонируется в кристаллографической базе данных, такой как Кембриджская структурная база данных (для малых молекул), База данных неорганической кристаллической структуры (ICSD) (для неорганических соединений) или Банк данных по белкам (для белков и иногда нуклеиновых кислот). Многие структуры, полученные в частных коммерческих предприятиях для кристаллизации белков, имеющих медицинское значение, не депонируются в публичных кристаллографических базах данных.

Теория дифракции

Основная цель рентгеновской кристаллографии – определить плотность электронов f (r ) по всему кристаллу, где r представляет трехмерное положение вектор внутри кристалла. Для этого с помощью рассеяния рентгеновских лучей собираются данные о его преобразовании Фурье F (q ), которое математически инвертируется для получения плотности, определенной в реальном пространстве, с использованием формулы

f (r) Знак равно 1 (2 π) 3 ∫ F (q) eiq ⋅ rdq, { displaystyle f ( mathbf {r}) = { frac {1} { left (2 pi right) ^ {3}} } int F ( mathbf {q}) e ^ { mathrm {i} mathbf {q} cdot mathbf {r}} mathrm {d} mathbf {q},}

где интеграл берется по всем значениям q . Трехмерный действительный вектор q представляет собой точку в обратном пространстве, то есть конкретное колебание электронной плотности при движении в направлении, в котором q баллов. Длина q соответствует 2 π { displaystyle 2 pi}, деленному на длину волны колебаний. Соответствующая формула для преобразования Фурье будет использоваться ниже

F (q) = ∫ f (r) e – iq ⋅ rdr, { displaystyle F ( mathbf {q}) = int f ( mathbf {r }) mathrm {e} ^ {- mathrm {i} mathbf {q} cdot mathbf {r}} mathrm {d} mathbf {r},}

где интеграл суммируется по всем возможным значениям вектора положения r внутри кристалла.

Преобразование Фурье F (q ) обычно является комплексным числом и, следовательно, имеет величину | F (q ) | и фаза φ(q), связанные уравнением

F (q) = | F (q) | e i ϕ (q). { Displaystyle F ( mathbf {q}) = left | F ( mathbf {q}) right | mathrm {e} ^ { mathrm {i} phi ( mathbf {q})}.}

Интенсивность отражений, наблюдаемых при дифракции рентгеновских лучей, дает нам величины | F (q ) | но не фазы φ (q ). Для получения фаз собираются полные наборы отражений с известными изменениями в рассеянии, либо путем модуляции длины волны за определенным краем поглощения, либо путем добавления сильно рассеивающих (т.е. электронно-плотных) атомов металла, таких как ртуть. Комбинирование величин и фаз дает полное преобразование Фурье F (q ), которое можно инвертировать для получения электронной плотности f (r ).

Кристаллы часто идеализируются как совершенно периодические. В этом идеальном случае атомы расположены на идеальной решетке, плотность электронов идеально периодична, а преобразование Фурье F (q ) равно нулю, за исключением случаев, когда q принадлежит обратная решетка (так называемые пики Брэгга). В действительности, однако, кристаллы не являются идеально периодическими; атомы колеблются вокруг своего среднего положения, и может быть беспорядок различных типов, такой как мозаичность, дислокации, различные точечные дефекты и неоднородность в конформации кристаллизованные молекулы. Следовательно, пики Брэгга имеют конечную ширину и может иметь место значительное диффузное рассеяние, континуум рассеянных рентгеновских лучей, которые попадают между пиками Брэгга.

Интуитивное понимание закона Брэгга

Интуитивное понимание дифракции рентгеновских лучей может быть получено из модели дифракции Брэгга. В этой модели данное отражение связано с набором равномерно расположенных листов, проходящих через кристалл, обычно проходящих через центры атомов кристаллической решетки. Чт

Истинной плотностью называют величину, характеризующую массу единицы объема тела, то есть истинная плотность представляет собой отношение массы тела (минерала) к его объему:

где р — плотность, m — масса, V — объем.

Истинная плотность минералов изменяется от величин, близких к 1 г/см3, до 23 г/см3 (для металлов группы платины). Больше половины всех минералов, в том числе почти все породообразующие, имеют плотность от 2 до 4 г/см3. Еще 1/3 минералов, часто содержащих элементы с большой атомной массой, имеет плотность от 4 до 8 г/см3. Количество минералов с очень высокой плотностью, так же как и с весьма низкой, незначительно.

Истинная плотность кристаллических веществ, к которым относятся и почти все минералы, зависит от их химического состава и закономерностей внутреннего строения. Примерами взаимосвязи между плотностью и структурой минералов служат любые полиморфные модификации: алмаз (плотностью 3,51 г/см3) и графит (2,23 г/см3); пирит (5,013 г/см3) и марказит (4,875 г/см3); а-кварц (2,65 г/см3) и Р-кварц (2,51 г/см3) и многие другие. При одинаковом химическом составе на истинную плотность влияют межатомные расстояния и координационные числа, часто зависящие от характера химической связи, а при прочих равных условиях — и взаимное расположение групп атомов в разных полиморфных модификациях.

Влияние химического состава минералов на их плотность неоднозначно: в изоструктурных минералах и изоморфных рядах минералообразующий элемент с большей атомной массой увеличивает плотность, а элемент с большим ионным радиусом уменьшает ее. Влияние ионного радиуса более существенно при одинаковой относительной величине изменения обеих характеристик.

Истинную плотность минералов находят чаще всего по пробе, состоящей из большинства мелких или ограниченного количества более крупных зерен. Определенная в этом случае величина характеризует среднее значение плотности.

Сведения об истинной плотности минералов помогают при решении следующих задач:

– диагностика минералов, похожих по другим свойствам;

– определение химического состава представителей изоморфных рядов;

– выделение мономинеральных фракций;

– определение режимов гравитационного обогащения руд;

– изучение однородности мономинеральных фракций;

– выяснение концентрации дефектов структуры в зернах;

– расшифровка структурных особенностей минералов и другие.

При исследовании неоднородного материала (например, смеси минеральных фаз, руды) определяют среднюю плотность — средневзвешенное значение плотностей отдельных фаз с учетом их фактических количественных соотношений.

При изучении пористых и рыхлых пород определение плотности должно проводиться с учетом объема пор или пространства между зернами. При исследовании образцов пород с ненарушенной или восстановленной текстурой измеряется объемная или насыпная масса. Отличие ее от плотности заключается в том, что здесь измеряется суммарный объем вещества и пор, а масса определяется практически лишь для самого вещества. Объемная масса тем меньше по сравнению с плотностью, чем больше пористость вещества.

Методы определения истинной плотности твердых веществ сводятся в две основные группы: объемно-весовые и основанные на использовании физических констант.

Существующие объемно-весовые методы определения истинной плотности минерального сырья в настоящее время сводятся к измерению объема и массы навески пробы, измельченной до крупности -0,16 мм. Наиболее трудная операция — определение объема твердой фазы навески. При этом пользуются методом пропитки испытуемой пробы порозаполняющей жидкостью или газом.

Порозаполняющая жидкость хорошо смачивает пробу, не взаимодействуя с материалом пробы, имеет постоянную плотность и по возможности минимальные упругость паров, вязкость и размер молекул. Увеличение вязкости или размера молекул порозаполняющей жидкости приводит, например, к занижению значения истинной плотности исследуемого материала в связи с тем, что такая жидкость не заполнит тонкие трещины и поры. Газ лучше проникает в тонкие поры и трещины, однако измерение объема газа требует более сложной аппаратуры, поэтому большее распространение получили методы с пропиткой жидкостью.

Из наиболее широко используемых объемно-весовых методов определения истинной плотности следует отметить гидростатическое взвешивание, пикнометрический, микропоплавковый, объемометрический (в барометрической трубе) и с защитным (парафиновым или другим пленочным) покрытием. Выбор любого метода определения истинной плотности зависит от задачи исследования, количества и качества исследуемого материала.

Для технологических исследований широко используют пикнометрический метод, позволяющий с высокой точностью определять истинную плотность любых минералов, но требующий достаточно больших навесок проб (100—200 мг). Для определения истинной плотности объемометрическим способом также необходима достаточная навеска (15—100 мг). Микропоплавковым способом можно измерить плотность одного зерна минерала размером 30—40 мкм и более, но возможности применения этого способа ограничены максимальной плотностью жидкой среды. Также с помощью специальных микропоплавков с точно установленным объемом измеряют плотность тяжелых жидкостей, которые применяют для фракционирования проб.

Гидростатическое взвешивание основано на измерении объема пробы по массе вытесненной ею жидкости (чаще всего воды). Метод прост в применении, не требует дорогостоящего или уникального оборудования, дает достаточно высокую точность, хорошую производительность и может быть применен практически для любого материала во всем диапазоне значений истинной плотности.

Объем минерала (Vм) при гидростатическом взвешивании находят по разности результатов взвешивания его в воздухе (m) и в жидкости (mж) известной плотности (Dж):

Истинная плотность минерала находится по формуле:

Гидростатическое взвешивание чаще всего проводят в дистиллированной воде, плотность которой в первом приближении можно принять равной единице. Тогда формула расчета истинной плотности твердого вещества упрощается:

где mв — масса твердого вещества в воде.

Наиболее удобен, а часто и незаменим метод гидростатического взвешивания для определения истинной плотности крупных кристаллов или кусков руды. Такие объекты промывают спиртом или ацетоном для снятия загрязнений и улучшения смачиваемости поверхности и подсушивают. Гидростатическое взвешивание применяют и для зернистых фракций с размером зерна > 0,5-0,1 мм. Однако при работе с такой пробой приходится прибегать к сложной процедуре удаления пузырьков воздуха, а возможность потери части вещества из-за флотации зерен в жидкости возрастает пропорционально степени измельчения.

Для удобства взвешивания в воде исследуемую пробу помещают в какую-либо тару или подвешивают непосредственно на проволоке. Крупный кристалл оплетают тонкой (диаметром 0,1—0,2 мм) медной или платиновой проволочкой. С помощью петельки на верхнем конце проволоку с минералом прикрепляют к серьге на коромысле весов. Для размещения пробы используют также часовое стекло с просверленными для закрепления подвеса отверстиями. При взвешивании в жидкости проволочку с пробой надо опускать всегда до одного и того же уровня, что необходимо для уменьшения погрешности из-за влияния выталкивающей силы, капиллярного взаимодействия и смачиваемости подвеса.

Для взвешивания в жидкости проволочку с пробой подвешивают к левому коромыслу весов, как и при взвешивании в воздухе, но над чашкой весов помещают стакан с жидкостью. Его обычно устанавливают на профильной подставке или треноге, не соприкасающейся с чашкой и не мешающей свободному колебанию коромысла.

Гидростатическое взвешивание проводят, как правило, на лабораторных аналитических весах, позволяющих получать отсчет массы с точностью до 0,0001 г.

Если аналитические весы используются только для гидростатического взвешивания, их можно усовершенствовать (рис. 3.1). Левую чашку весов снимают с коромысла, к серьге подвешивают равноценный груз (железную шайбу или свинцовый шарик). Весы уравновешивают, подгоняя этот груз, подвесную систему прикрепляют к грузу.

Определение истинной плотности минералов и отдельных кусков руды методом гидростатического взвешивания можно проводить в любой жидкости с плотностью не выше плотности исследуемого объекта. Чаще всего используют дистиллированную воду, главный недостаток которой — относительно плохая смачивающая способность. Для минералов, растворимых в воде, необходимо брать другие жидкости (этиловый спирт, керосин, бензол, толуол, четыреххлористый углерод, разные тяжелые жидкости. Тяжелые жидкости непригодны, если их плотность больше истинной плотности минерала или даже одной подвесной системы.

Важное значение при взвешивании в воде приобретает точное измерение ее температуры, по которой и устанавливают плотность воды. Наиболее простой путь — выравнивание температур воды и минерала (кусков руды или породы или продукта обогащения) с температурой воздуха в помещении или футляре весов путем выдержки пробы исследуемого материала и сосуда с водой близ весов в течение 25—35 мин. Тогда температуру воды находят измерением температуры воздуха, располагая термометр непосредственно около пробы.

Для определения истинной плотности твердого вещества гидростатическим взвешиванием рекомендуется следующая последовательность операций взвешивания: 1) подвесной системы в воздухе (P), 2) системы с минералом в воздухе (Рм), 3) системы с минералом в жидкости (Pмж), 4) подвесной системы в жидкости (Рж).

Из мелкозернистых проб воздух целесообразно удалять либо прогревом жидкости с пробой в сосуде при погружении нижней его части в водяную баню, либо отсасыванием воздуха в эксикаторе, соединенном с водяным или масляным вакуумным насосом.

По результатам взвешивания минерала в воздухе и воде находят значение истинной плотности без поправок на условия определения:

В случае гидростатического взвешивания твердого вещества в любой жидкости истинная плотность рассчитывается по формуле:

Ареометры постоянного объема, пружинные гидростатические весы Жали и рычажные измерители плотности, квадрантные весы Марголина приспособлены для быстрого определения плотности твердых тел вообще, минералов и горных пород в частности, с точностью до 0,005—0,010 г/см3 при навесках в десятки и сотни граммов. Ареометр постоянного объема показан на рис. 3.2 и состоит из поплавка-луковицы, стержня и двух чашек для размещения навески и гирь. Одна чашка располагается на верхнем конце стержня, другая, предназначенная для определения объема пробы, — под луковицей; эта чашка погружена в жидкость. Ареометр опускают в жидкость до определенной постоянной метки на стержне и стабилизируют это положение, размещая на верхней чашке необходимое количество гирь с массой P1. На эту же чашку кладут пробу, сохраняя объем погруженной части ареометра снятием части гирь. Оставшиеся гири массой P2 вместе с пробой уравновешивают ареометр в жидкости. По разности (P1-P2) находят массу пробы вещества m. Затем пробу перекладывают на нижнюю чашку ареометра, добавляя груз на верхнюю, чтобы уравновесить ареометр в жидкости в том же положении. Если P3 — груз на верхней чашке, то объем пробы:

Для определения истинной плотности руды, концентратов, окатышей, продуктов их переработки и шлиховых материалов используют также пикнометрический метод. Основной прибор, применяемый в этом методе, — стеклянный пикнометр может иметь разную форму и вместимость (рис. 3.3). Реже встречаются пикнометры из кварцевого стекла и металлические.

По объему различают большие пикнометры, вмещающие 25-100 см3 жидкости, обычные минералогические вместимостью 1-5 см3 и микропикнометры с внутренним объемом 0,2-0,1 см3 и меньше. Уровень жидкости в пикнометре, то есть его номинальный внутренний объем, фиксируют преимущественно двумя способами. У пикнометров с относительно широким горлышком (диаметр 3-5 мм) на трубке горлышка имеется кольцевая риска, при заполнении пикнометра жидкостью нижний край мениска устанавливают по этой риске. В зависимости от смачиваемости стенок сосуда жидкостью мениск может быть вогнутым или выпуклым. Сравнительно большое поперечное сечение горла пикнометра и трудность точного фиксирования положения мениска ограничивают применение крупнообъемных пикнометров. Для минералогических исследований удобнее пикнометры со вставленным капилляром. Через широкое горлышко в пикнометр засыпают пробу минерала и заливают жидкость. Постоянство объема жидкости достигается совпадением ее уровня с верхним торцом капиллярной пробки. Небольшой диаметр капилляра повышает точность определения объема пикнометра. Иногда с этой целью используют пикнометры с двумя горлышками разного диаметра: широкое после заполнения пикнометра минералом закрывают сплошной пробкой, а по узкому капиллярному контролируют объем. Микропикнометры закрывают тщательно подогнанной пробкой с капилляром или пришлифованной стеклянной пластинкой, полностью ограничивающей внутренний объем сосуда.

Для определения истинной плотности твердого тела пикнометрическим методом необходимы также: вакуум-эксикатор с водоструйным или масляным насосом, обеспечивающим разрежение 532 Па (4 мм рт. ст.) (рис. 3.4) или водяная баня (рис. 3.5; весы технические с погрешностью взвешивания не более 0,001 г; водяной термостат и сушильный шкаф с терморегулятором; пипетка с тонковытянутым капилляром для доведения уровня жидкости в пикнометре до метки; воронка стеклянная; совочек или шпатель.

Перед испытанием определяют вместимость пикнометра. Для этого предварительно отмытый и высушенный пикнометр заполняют дистиллированной водой до метки, помещают в термостат и выдерживают в течение 30 мин при температуре (20 ± 0,1) °С. Доводят мениск воды до метки, вытирают насухо пикнометр и определяют его массу с водой (m1). Выполняют три определения m1, расхождение между которыми не должно превышать 0,01 г.

Вместимость пикнометра V (м3) рассчитывают по выражению:

где m1 — масса пикнометра с водой, кг; т — масса пустого пикнометра, кг; 998 — плотность воды при 20°С, кг/м3.

При определении истинной плотности тонкодисперсных руд, гидрофобных материалов или материалов, содержащих растворимые компоненты, применяют не дистиллированную воду, а этиловый спирт или керосин. Плотность этилового спирта или керосина (рc) определяют в пикнометре и вычисляют с точностью до 1 кг/м3:

где m2 — масса пикнометра с жидкостью, кг.

Вычисляют среднее арифметическое результатов трех испытаний рc, расхождение между которыми не должно превышать 5 кг/м3.

От высушенной в сушильном шкафу до постоянной массы представительной пробы исследуемого материала отбирают навеску массой примерно 14 г (объемом примерно 25 % вместимости пикнометра) и крупностью -0,16 мм. Пробы флотационных концентратов перед сушкой отмывают от реагентов ксилолом или этиловым спиртом.

С помощью совочка (шпателя) и сухой воронки заполняют пикнометр подготовленной для испытания навеской, взвешивают (m3), заполняют на 1/3 дистиллированной водой (керосином, этиловым спиртом) и помещают его в вакуумный шкаф (эксикатор или водяную баню) на 30 мин для удаления пузырьков воздуха. Затем пикнометр доливают вакуумированной дистиллированной водой до метки и помещают в термостат при температуре (20+-0,1) °С на 30 мин. Доводят мениск жидкости до метки на пикнометре, который затем вытирают насухо и взвешивают (m4).

Истинная плотность материала р (кг/м3) рассчитывается по формуле:

Полученный результат записывают с точностью до 10 кг/м3. За окончательный результат принимают среднее арифметическое двух определений, расхождение между которыми не должно превышать 20 кг/м3. Время проведения анализа, исключая пробоподготовку, составляет 2 часа. Погрешность измерений — 0,5 %.

Длительность описанного циклометрического метода с использованием порозаполняющих жидкостей не удовлетворяет исследователей. Сконструированы приборы, в которых вместо порозаполняющей жидкости используется газ и в основу работы которых положен закон Бойля—Мариотта. К таким приборам относят воздушный пикнометр ПДМ-1 (рис. 3.6), воздушный пикнометр Бекмана (рис. 3.7) и автопикнометр модели 1320 (рис. 3.8), детальные сведения о которых приведены в табл. 3.1.

Прибор ПДМ-1 (см. рис. 3.6) состоит из двух сообщающихся камер: рабочей 1 и измерительной 5; кюветы 2 для размещения испытуемого образца; манометра 6 для измерения давления в измерительной камере; соединительных трубок 4; вентилей: 3 — для прекращения доступа воздуха из измерительной камеры в рабочую, 8 — для нагнетания, 7 — выпуска воздуха из системы и 9— выпуска воздуха из микрокомпрессора 10.

Вместимость кюветы для пробы — 30 см3. Время проведения измерения, исключая пробоподготовку, составляет 5—10 мин. Погрешность измерений — 0,5 %.

Воздушный пикнометр Бекмана (см. рис. 3.7) для определения истинной плотности материалов состоит из двух сообщающихся цилиндров А и В, в которых перемещаются при помощи специального устройства поршни. К поршню цилиндра В присоединяют кювету с пробой. Цилиндры сообщаются между собой при помощи соединительных трубок и вентиля 3, а при помощи вентиля 2 могут быть соединены с атмосферой для выравнивания давления. При помощи дифференциального индикатора 1 контролируется постоянный перепад давления в цилиндрах. Положение поршня цилиндра В прокалибровано в см3 при помощи счетчика 4. Кювета с пробой 5 устанавливается и герметизируется специальным устройством. Для проверки исправной работы прибора и его калибровки применяют два стальных шарика с известным объемом 8,58 и 28,96 см3. Вместимость кюветы для пробы — 50 см3.

Погрешность измерения при работе на приборе Бекмана колеблется в зависимости от навыков оператора от 0,5 до 0,1 см3.

Автопикнометр модели 1320 (см. рис. 3.8) повторными перемещениями газа в камеру для пробы измеряет объем измельченных твердых тел в сухом виде и проводит автоматический расчет истинной плотности в зависимости от массы испытуемого образца. Результат испытаний выводится в цифровой индикатор в г/см3. Вместимость измерительной кюветы для образца — 9 см3. Дегазация образца выполняется автоматически первичным вакуумным насосом. Время проведения испытания несколько минут.

К объемометрическим методам, широко применяемым в минералогических и технологических лабораториях для определения истинной плотности минералов, горных пород и руд, относят группу методов, в которых массу пробы определяют взвешиванием, а объем — линейными измерениями (если проба имеет правильную геометрическую форму), по изменению давления в замкнутой системе (вызванному помещением в эту систему пробы), по объему жидкости, вытесненной пробой. Такие методы не дают обычно высокой точности (±0,01 г/см3) по сравнению с весовыми, но отличаются простотой и большой скоростью определения. Точность определения плотности объемометрическими методами возрастает с увеличением массы навески пробы и не зависит от плотности применяемой жидкости.

Особое достаточно широкое распространение получил метод микробюреток (метод М. М. Василевского), позволяющий измерять плотность при весьма небольших количествах материала в течение 10—12 мин. Объем пробы измеряют в микробюретке — капиллярной трубке длиной 6—10 см, запаянной с одного конца и воронкообразной с другого. Удобно иметь несколько микробюреток внутренним диаметром от 0,5 до 2—3 мм, пригодных для разных навесок и зерен разного размера. Взвешенную на аналитических (или торсионных типа ВТ-20) весах микронавеску (несколько зерен общей массой от 5 до 50 мг) осторожно высыпают в микробюретку, заполненную до известного уровня прокипяченным и охлажденным до комнатной температуры этиловым спиртом. Объем пробы соответствует приросту столба жидкости в трубке:

где d — внутренний диаметр капилляра; А — высота подъема мениска в капиллярной трубке после погружения минерала в жидкость.

Положение мениска находят под микроскопом при увеличении в 10— 20 раз, изменение уровня определяют с помощью окуляр-микрометра AM-9-2, MOB-1 или катетометра КМ-8. Посредством окуляр-микрометра берут отсчет положения мениска в микробюретке до погружения минерала (n1), а затем — после введения пробы (n2). Тогда

где С — цена деления окуляр-микрометра (величины d и С — в мм при массе пробы в мг; в см при массе пробы в долях грамма).

Тогда плотность минерала (породы, руды) составляет:

где K= 4/(пd2Q — константа данной микробюретки при работе с постоянными объективом и окуляром; т — масса навески пробы.

Чаще всего при работе с микробюретками используют биологический микроскоп M-10 с объективом, дающим минимальное увеличение, что позволяет увидеть отрезок микробюретки длиной 5—7 мм. Тубус микроскопа устанавливают горизонтально, а на столике (обычно на препаратоводителе CT-12) закрепляют микробюретку в вертикальном положении. Перед началом замеров микробюретку ставят так, чтобы мениск находился в верхней части поля зрения (так как изображение перевернутое). Фокусируя микроскоп на середину нижнего края мениска, берут отсчет его положения с помощью окуляр-микрометра либо, перемещая бюретку препаратоводителем, ставят край мениска на начало отсчетной шкалы. После погружения зерен минерала берут второй отсчет положения мениска, уже не перемещая и даже не трогая микробюретку.

Одним из наиболее простых способов приближенной оценки плотности зерен является их поочередное погружение в серию жидкостей с разной плотностью. В зависимости от соотношения плотностей минерала и жидкости, в которую погружено зерно, оно займет одно из трех возможных положений: всплывет, опустится на дно или останется в жидкости в равновесном состоянии. Уравновешивание зерна, наблюдающееся при равенстве его веса и гидростатической силы, позволяет определить его плотность с той же точностью, с какой известна плотность жидкости.

Погружаемые в жидкость зерна не должны иметь твердых или газовожидких включений, трещинок и прилипающих к зернам пузырьков воздуха. Для определения плотности используют зерна диаметром от 0,5 до 2—3 мм, хорошо заметные при их движении в жидкости. Более крупные зерна чаще имеют трещинки, заполненные воздухом, а очень мелкие медленно перемещаются в жидкости, подчиняясь ее турбулентному движению.

Наборы тяжелых жидкостей размещают в пробирках вместимостью 5— 10 мл или во флакончиках из-под оптических иммерсионных препаратов. Интервалы значений плотности (г/см3) между соседними жидкостями могут быть: 0,2—0,1 — для диагностических измерений; 0,01—0,005 — для более точных измерений отдельных минеральных групп. Для приготовления набора тяжелых жидкостей используют, как правило, смеси концентрированной жидкости (Клеричи и Туле) и разбавителя (вода), не анализируя их соотношений и лишь констатируя получившиеся величины плотности мик-ропоплавковым методом. Для получения жидкости с заранее заданной плотностью вычисляют нужный объем растворителя Vр с известной плотностью Dp, который добавляется в определенное количество концентрированной жидкости (Vк) с плотностью Dк:

где Dж — заданная плотность жидкости.

Например, для получения тяжелой жидкости плотностью Dж = 3,89 г/см3 из 10 мл жидкости Клеричи (Dк = 4,27 г/см3) в нее надо добавить воды:

Если из 5 мл полученной жидкости необходимо приготовить раствор плотностью Dж = 3,79 г/см3, то

Путем преобразований можно найти

Процесс уравновешивания зерна в жидкости несложен и при некотором опыте занимает 5—15 мин. Отобранное для исследования зерно (< 3—4 штук) погружают в жидкость с предположительно близкой плотностью. При всплывании зерна необходимо добавить разбавитель или жидкость меньшей плотности, проверив отсутствие пузырька воздуха на зерне. Если зерно тонет, добавляют более концентрированную жидкость, тщательно перемешивая полученную смесь.

Для работы пригодны небольшие стаканчики вместимостью 10—30 мл, широкие пробирки, мензурки и т.д. Сосуд по размерам и форме должен быть удобен для жидкости и для измерения ее плотности.

Для экспрессного определения плотности жидкостей предназначен микропоплавковый метод. Применяемый при этом «поплавок» представляет собой пустотелый или монолитный цилиндр с конусными основаниями, на одном из которых находится ушко с отверстием – 0,2 мм для подвешивания поплавка на тонкой, диаметром 0,1 мм, нихромовой проволоке (ее длина 150—200 мм, в зависимости от типа применяемых весов). Объем откалиброванного микропоплавка равен 100 мм3, масса пустотелого микропоплавка 480 мг, монолитного 800 мг. Суммарные массы каждого из поплавков вместе с подвесками должны быть 500 и 1000 мг соответственно, что обеспечивает соответствие градуировке торсионных весов и создает необходимые удобства в работе. Точность определения плотности жидкости с микропоплавком ±0,01 г/см3 при использовании торсионных весов типа ВТ-500 или ВТ-1000 и ±0,005 г/см3 — аналитических весов.

Применение микропоплавков позволяет определить плотность любых жидкостей в сосудах объемом 2 мл, плотность жидкости в процессе ее разбавления в различных емкостях, в том числе в центрифужных пробирках. Определение плотности жидкости производится по уменьшению значения массы поплавка с известным объемом при его погружении в анализируемую жидкость.

При работе с торсионными или аналитическими весами поплавок подвешивают на коромысле весов, погружают в жидкость на глубину 5—7 мм и взвешивают по правилам, предусмотренным для работы с весами данного типа. Повторив погружение поплавка и его взвешивание 2—3 раза, находят среднее значение массы поплавка в жидкости (m2). Плотность жидкости Dx (в г/см3) рассчитывают по формуле:

где m1 — масса поплавка в воздушной среде; m2 — масса поплавка в жидкости; V — объем поплавка.

Для быстрого определения плотности жидкости с помощью грузила удобны специальные неравноплечные весы для гидростатического взвешивания — весы Вестфаля (рис. 3.9).

Массивный штатив со стойкой и выдвижным стержнем удерживает планку с коромыслом. На одном конце планки закреплены в вилке опорные подпятники для коромысла, на другом — шкала для отсчета или указатель равновесного положения. Коромысло — неравноплечно: короткое плечо имеет противовес с указателем равновесного положения; длинное плечо — от опорной призмы до серьги с крючком, к которому подвешивают грузило, — имеет шкалу, разделенную на 10 частей. Начало шкалы совпадает с ребром опорной призмы, последнее (десятое) деление — с призмой серьги.

К серьге на подвесе прикрепляют такое грузило, чтобы при нахождении его в воздухе коромысло было бы в равновесном положении. Высоту подвеса грузила регулируют выдвижным стержнем, закрепляемым стопорным винтом. В основании штатива, со стороны, противоположной нагружаемому концу коромысла, имеется установочный винт (иногда два). Он позволяет выравнивать стойку по отвесу или слегка наклонять ее в ту или иную сторону при установке в рабочее положение. Такой наклон позволяет фиксировать установку весов по строгому совпадению указателей равновесия или по нулевому отсчету шкалы.

Когда грузило опускают в сосуд с жидкостью, на него действует гидростатическая сила выталкивания и равновесие нарушается. Для восстановления равновесного положения на длинное коромысло весов помещают специальные гири — рейтеры. Они бывают разного типа: гири А должны быть по массе равны вытесненной грузилом воде при температуре градуировки весов, гири В — в 10 раз меньше, а разновесы С — еще в 10 раз меньше. Показания гидростатических весов зависят от типа рейтера и от его положения на том или ином делении шкалы коромысла. Показание гидростатических весов при уравновешивании грузила в жидкости соответствует ее плотности. Показанные на рис. 3.9 весы Вестфаля уравновешены в жидкости с плотностью 1,824 г/см3.

Для определения плотности твердых тел в воздушной среде из навесок массой 15—100 мг используют устройство, показанное на рис. 3.10. Устройство состоит из измерительной ячейки 5, соединенной с калиброванным измерительным капилляром 6 и через него с промежуточным компенсационным резервуаром 1, заполненным металлической ртутью, к которому через воздушную подушку 2 и капилляр 3 присоединяются вакуумметр 4 и вакуум-насос. Таким образом, измерительная ячейка в данном приборе не имеет прямого соединения с системой измерения давления, что позволяет существенно повысить точность измерения объема вводимой в ампулу навески.

Один из способов измерения объема с помощью данного прибора — измерение длин перемещения ртутного столба в измерительном капилляре, определяемых при строго одинаковом во всех случаях разрежении в компенсационном резервуаре и измерительной ячейке, вначале пустой (длина перемещения ртутного столба lп), затем заполненной эталоном (длина перемещения ртутного столба lэт) и заполненной точно взятой навеской (от) исследуемого материала (длина перемещения ртутного столба lобр.

Получив необходимые данные, плотность вещества рассчитывают по формуле:

где m — масса навески, г; Vэт — объем эталона, см3; Аlэт и Alобр — разницы длин перемещения ртути в измерительном капилляре при пустой ячейке и ячейке, заполненной эталоном или образцом, мм.

Из методов определения истинной плотности твердых веществ, основанных на использовании физических констант, наиболее распространены рентгенографический и химический анализы. Они используют связь значения плотности минерала с атомными массами составляющих его элементов и объемом, ими занимаемым. Плотность принимается равной отношению массы элементарной ячейки кристаллической структуры минерала к объему элементарной ячейки:

где Z — число молекул (или атомов для одноатомных минералов) в элементарной ячейке; М — молекулярная масса минерала (масса структурной единицы); mн — атомная (углеродная) единица массы, равная 1,6603*10в-27 кг; V — объем элементарной ячейки минерала, нм3.

Величину Z для минералов с известной кристаллической структурой можно найти в справочной литературе; M рассчитывают по данным химического анализа из реальной формулы минерала, то есть из формулы, учитывающей имеющиеся в минерале изоморфные замещения; V рассчитывают по данным рентгеноструктурного анализа параметров ячейки.

Простейший пример расчета рентгеновской плотности минерала. Ильменорутил имеет состав (%): FeO 10,56; ТiO2 53,40; Nb2O3 21,73; Ta2O3 14,70. Расчет дает кристаллохимическую формулу (Ti0,64 Nb0,16, Ta0,06 Fe0,06 (II)O2]. Формула позволяет определить молекулярную’ массу изучаемого минерала, которая равна сумме произведений атомной массы элемента на его содержание:

В элементарной ячейке ильменорутила содержатся две молекулы (Z= 2); элементарная ячейка минерала тетрагональна и для данного образца ее размеры (нм) определяются величинами а = 0,458, с = 0,297. Так как объем элементарной ячейки

Рентгеновская плотность называется идеализированной, так как отнесена к микрообъему. Как правило, эта плотность больше определяемой непосредственно на реальном материале. Трещины, пустоты, газово-жидкие включения не оказывают влияния на рентгеновскую плотность. He исключены, однако, случаи, когда р рентгеновская меньше р экспериментальной. Это может иметь место, если изучаемый минерал загрязнен механической примесью с большей, чем у него, плотностью.

Для простых минералов, построенных одним типом атомов (самородные элементы), может быть предложен расчетный метод определения плотности, учитывающий тот факт, что плотность вещества зависит от атомной массы слагающих его атомов, их размеров и характера упаковки. В предположении сферической формы атомов и заданного типа их упаковки плотность может быть определена по формуле:

где р — плотность минерала; Р — плотность упаковки атомов; А — атомная плотность элемента; R— атомный радиус; N — число Авогадро, равное 0,602*1024.

Эта формула относится только к самородным минералам, построенным однотипными атомами преимущественно с металлическим характером связи. Описанный метод определения плотности применим только к минералам, имеющим кристаллическое строение.

При определении объема, занимаемого минеральным сырьем, инженерных расчетах бункеров и емкостей для его хранения и перевозки, давления сырья на стенки емкостей, вагонов и т.д. используют насыпную плотность.

Под насыпной плотностью измельченного продукта понимают его массу в единице объема, включая промежутки между отдельными зернами и поры. Она зависит от истинной плотности, минерального и гранулометрического состава материала, степени его уплотнения, влажности.

При определении насыпной плотности определяют объем пробы минерального сырья, насыпая его в мерный сосуд, и вычисляют отношение ее массы к занимаемому объему. Проба должна быть достаточной для трехразового заполнения мерного сосуда.

Для испытаний применяют мерные сосуды цилиндрической формы, изготовленные из металлического листа, не подвергающегося коррозии, толщиной 1,5—2 мм (табл. 3.2); технические весы с погрешностью взвешивания не более 0,005 кг; сушильный шкаф с терморегулятором; сита с квадратными отверстиями размером: 1, 10, 16, 25, 50 мм.

Для определения вместимости мерный сосуд взвешивают, наполняют водой и снова взвешивают с погрешностью до 0,01 кг. По разности результатов взвешивания определяют массу воды в сосуде, соответствующую его вместимости в м3. Определение повторяют 5 раз и вычисляют среднее арифметическое.

Насыпную плотность пробы определяют в воздушно-сухом или сухом состоянии, реже при определенной заданной влажности. В случае определения насыпной плотности в сухом состоянии пробу высушивают в сушильном шкафу при (105±5) °С до постоянной массы и определяют ее влажность. Пробу, если определение необходимо выполнить при естественной влажности, предварительно отбирают на влагу. В предварительно взвешенный мерный сосуд с высоты < 50 мм над поверхностью совком или лопатой засыпают пробу до образования конуса над верхом сосуда. Образовавшийся конус срезают металлической планкой вровень с краями сосуда (без уплотнения). После этого сосуд с пробой взвешивают с погрешностью < 0,01 кг.

Насыпная плотность пробы рн (кг/м3) в воздушно-сухом состоянии

где m1 — масса сосуда с материалом, кг; m — масса пустого сосуда, кг; V— вместимость сосуда, м3.

Насыпная плотность рн.с. (кг/м3) пробы в сухом состоянии

где W — массовая доля влаги в пробе, %.

За окончательный результат испытания принимают среднее арифметическое результатов двух наиболее близких определений, расхождение между которыми не превышает 5 %. При расхождении результатов параллельных определений, которые превышают допустимые значения, производят третье определение. За окончательный результат принимают среднее арифметическое двух наиболее близких результатов в пределах допустимых расхождений. Если результат третьего определения находится в пределах допустимых расхождений по отношению к результатам каждого из двух предыдущих определений, то за окончательный результат испытания принимают среднее арифметическое результатов трех определений. Вычисление выполняют с погрешностью < 1 кг/м3, а результат округляют до 10 кг/м3.

Для определения насыпной плотности руд и агломератов крупностью 50 мм используют контейнер, в качестве которого служит кузов автомобиля или железнодорожного вагона правильной геометрической формы или другая подобная емкость. Длина, ширина и высота контейнера должны превышать размер максимального куска руды не менее чем в 10 раз. Для взвешивания применяют автомобильные или вагонные весы с погрешностью взвешивания < 0,5 % массы пробы. Предварительно определяют вместимость выбранной емкости, измеряя ее геометрические параметры, с погрешностью < 0,5 %. Затем во взвешенный контейнер засыпают пробу с небольшой высоты, избегая дробления и сегрегации по крупности. Поверхность выравнивают с помощью планки. Контейнер с пробой взвешивают. Насыпную плотность рн.с. и рн (кг/м3) руды или агломерата соответственно в воздушно-сухом состоянии или с заданной влажностью и в сухом состоянии определяют по тем же формулам, что и для мерного материала. За окончательный результат принимают среднее арифметическое результатов двух параллельных определений, расхождение между которыми не должно превышать 100 кг/м3. Если расхождение между результатами параллельных определений превышает допустимое значение, то производят третье определение и за окончательный принимают среднее арифметическое значение двух наиболее близких результатов анализа в пределах допустимых расхождений. Вычисление производят с погрешностью 10 кг/м3, а результат записывают с точностью до 100 кг/м3.

Большинство измельченных материалов склонно к самоуплотнению и слеживаемости, особенно в больших емкостях, силосах, конусах и т.д., где вышележащая толща материала оказывает давление на нижние слои. Значение давления можно ориентировочно рассчитать. По приведенной выше методике определяют насыпную плотность пробы материала без уплотнения, то есть насыпную плотность поверхностного слоя. Зная высоту насыпной толщины руды или концентрата, рассчитывают его давление на дно емкости. Для определения насыпной плотности материала в нижнем слое пробу уплотняют, приложив груз, соответствующий рассчитанному давлению. Материал выдерживают под нафузкой в течение суток, а затем определяют объем спрессованной пробы.

Установлено, что до 10 м в глубину наблюдается пропорциональность между глубиной слоя и ростом насыпной плотности. На основании этого можно приближенно находить и промежуточные значения насыпной плотности рнi (кг/м3) путем линейной интерполяции на глубину А:

где рн — насыпная плотность поверхностного слоя, кг/м3; ра — насыпная плотность нижнего слоя, кг/м3.

Для определения усредненной насыпной плотности рср материала на складе, имеющего примерно форму усеченной пирамиды, И.Е. Пестов предложил следующую формулу:

где S1 — площадь верхнего основания, м2; S2 — площадь нижнего основания, м2;

Методы определения истинной плотности позволяют найти объем вещества горной породы или минерального агрегата без учета его текстурных особенностей, то есть объем лишь самой минеральной массы. При изучении пористых пород бывает необходимо узнать и объемную массу — массу единицы объема горной породы вместе с характерными для этого объема порами. По методике процессы определения объемной массы и плотности аналогичны.

Объемная масса может быть определена для пористой породы с естественной влажностью или при насыщенности ее, например, нефтью. В этом случае масса единицы объема высушенной породы — это кажущаяся объемная масса. Объемная масса всегда меньше плотности, так как в первом случае возрастает объем при учете пор и практически сохраняется общая масса. Плотность р и объемная масса Mоб взаимосвязаны:

где Kп — пористость образца (в долях единицы объема).

Объемную массу ищут в первую очередь для оценки пористости исследуемого материала:

Различают открытую пористость, закрытую (или изолированную) и общую. Надежнее всего определяется открытая пористость.

Объем породы с ненарушенной текстурой можно найти разными способами. Например, для монолитов породы любой правильной формы объем узнают линейны ми измерениями. Более распространен метод гидростатического взвешивания насыщенного водой или парафинированного образца. Последовательность работы при гидростатическом взвешивании парафинированного образца следующая. Образец взвешивают на лабораторных весах (обычно с точностью до 0,01 г), обвязывают ниткой или проволочкой и погружают в расплавленный при 70 °С парафин. После застывания парафина образец снова взвешивают, сначала в воздухе, а затем в воде.

Объем парафина составляет:

Объем парафинированного образца

где mгидр — масса образца, покрытого парафином, в воде; рз — плотность воды.

При повышенной точности измерений из величины mгидр вычитают массу подвесной системы в воде. Объем и массу проволоки или подвесной нити учитывают, взвесив их отдельно от образца в воздухе и воде.

Объем образца составляет:

Формула для расчета объемной массы при подстановке всех экспериментальных значений приобретает следующий вид:

При определении объемной массы образца с крупными порами парафин может их частично заполнить. В таких случаях образец предварительно обертывают бумагой, а затем парафинируют либо сразу обертывают образец тонким слоем парафина, подготовленного на поверхности воды в плоском сосуде типа кристаллизатора. Возникающие под пленкой парафина воздушные пузыри необходимо проколоть и сгладить. Сохранение общей массы образца в воздухе после гидростатического взвешивания свидетельствует о том, что под парафиновую оболочку вода не проникла.

Открытую пористость можно определить и методом насыщения образца жидкостью. Образец массой 2 100 г высушивают при 100—105 °C и взвешивают с точностью до 0,01 г. Затем погружают его в воду или керосин (вода растворяет некоторые минералы и хуже проникает в тонкие поры). Для лучшего проникновения жидкости в поры образец, погруженный в жидкость, выдерживают в вакууме не менее 30 мин. Рекомендуется также образец заливать жидкостью после частичного вакуумирования, которое следует продолжать до прекращения выделения пузырьков. При использовании воды можно нагревать образец вместе с жидкостью для удаления воздуха из пор.

После этих процедур образец взвешивают в той же жидкости на гидростатических весах, просушивают с поверхности фильтровальной бумагой и взвешивают в воздухе. Открытая пористость рассчитывается:

где P — масса сухого образца в воздухе; Рж — масса образца, насыщенного жидкостью, в воздухе; Pгодр — масса образца в жидкости.

Иногда приводят коэффициент пористости (е), представляющий собой отношение пористости к объему минерального скелета породы

Поправки на условия определения обычно не вводят, так как точность измерений меньше поправок и между повторными определениями допускается расхождение 1 %. В первом приближении пористость насыщенных водой пород можно определять и по изменению их удельного сопротивления.

Большую роль для объяснения некоторых физических констант (проницаемости, характера свободного водонасыщения) играет дифференцированная пористость, то есть наличие в породе пор того или иного размера. Из известных методов определения дифференцированной пористости наиболее широко применяют метод вдавливания ртути, метод малопроницаемых мембран, микроскопический и адсорбционный.

Определение дифференцированной пористости методом вдавливания ртути производится на специальном поромере, где количество вдавленной в образец ртути учитывается по изменению сопротивления платиновой проволоки, погруженной в ртуть, на которую передается давление. Метод основан на свойстве ртути не смачивать твердые тела. По связи между давлением, капиллярным сопротивлением и смачиваемостью рассчитывают эффективный радиус пор породы, заполненных ртутью, при соответствующем давлении:

где r — радиус пор; a — поверхностное натяжение ртути; 0 — краевой угол смачивания ртути; р — примененное давление.

Метод малопроницаемых мембран заключается в том, что поры образца перед испытанием заполняются жидкостью, которая далее выдавливается под различными давлениями на малопроницаемые мембраны. Расчет эффективного радиуса пор породы производится по формуле (3.1).

Все встречающиеся поры делятся на несколько групп по их размерам: 1) 0,02 поры 0,002 мм, определяемые микроскопическим методом; 2) поры < 0,0002 мм, определяемые методом капиллярной конденсации при адсорбции и десорбции; 3) поры 0,002 — 0,0002 мм, определяемые по разности между суммой указанных групп пор и общей пористостью.

Метод определения пор < 0,0002 мм по адсорбции и десорбции и полузамкнутых бутылочных пор по разности между адсорбцией и десорбцией — адсорбционный метод, основанный на применении формулы Томсона при капиллярной конденсации. Капиллярная конденсация — процесс, которым заканчивается адсорбция, — происходит в порах не под действием сил притяжения со стороны поверхности пор, а вследствие понижения упругости насыщенного пара в узких капиллярах (закон Бернулли) и под действием капиллярных сил, возникающих вследствие большой кривизны мениска жидкости (вогнутости его).

Соотношение между капиллярностью, относительной упругостью пара над мениском, поверхностным натяжением и радиусом кривизны мениска выражается формулой Томсона:

где р — давление пара жидкости над вогнутым мениском, Па; рo — давления насыщенного пара жидкости (над поверхностью в сосуде для той же температуры), мм рт.ст.; о — поверхностное натяжение жидкости, Н/м2; R — газовая постоянная, 8,315 Дж/(мольК); Т — абсолютная температура, К; г— радиус кривизны мениска в капилляре, см; M — молекулярная масса жидкости; р — плотность жидкости, г/см3.

Поскольку молекулярный объем сконденсированной жидкости V = М/r, формула (3.2) принимает вид:

При постоянной температуре опыта

Для цилиндрического капилляра в случае полного смачивания радиус кривизны мениска равен радиусу капилляра. Таким образом, по радиусу кривизны мениска получается радиус капилляра.

Пользуясь формулой Томсона, вычисляют любое значение r в зависимости от р/рo (относительной упругости пара), причем нужно иметь в виду, что по мере возрастания температуры при одинаковом равновесном давлении пара уменьшается максимальный радиус пор, заполняемых жидкостью при капиллярной конденсации.

Определение выполняется следующим образом: образцы горной породы размером -1 см3 с пришлифованными поверхностями (чтобы исключить влияние поверхности образца на величину адсорбции) помещаются в изолированное пространство (вакуумный эксикатор) над раствором электролита. В вакууме при постоянной температуре создается определенная упругость пара, при которой образцы выдерживаются в течение 21 дня.

Обычно определяется равновесная концентрация воды как при адсорбции, так и при десорбции, для чего образцы каждой породы подбираются парами с одинаковой объемной массой. Одни поступают на испытания полностью насыщенные водой, другие — в абсолютно сухом состоянии. Затем все кубики (сухие и водонасыщенные) помещаются в вакуумный эксикатор на сетку, подвешенную над насыщенным раствором сернокислого калия, имеющего при 293 К относительную упругость пара 0,98. По истечении 21 дня образцы извлекаются и быстро взвешиваются (образцы после извлечения из эксикатора следует поместить в отдельные бюксы с крышками и взвешивать вместе с бюксами).

Расчет ведется по обычной формуле подсчета количества пор, заполненных влагой, в объемных процентах, то есть определяется массовое держание сконденсированной влаги в образцах, умноженное на объемную массу этого кусочка породы, которое дает величину адсорбции или объем пор размером 0,0002 мм.

При этом определении имеется расхождение в данных, полученных при адсорбции и при десорбции (образцы сухие и водонасыщенные). Это объясняется тем, что в породах имеются полузамкнутые поры с входами менее 0,0002 мм. Такие входы, заполненные водой, при данной упругости пара образуют как бы «водяные пробки» и мешают полузамкнутым порам десорбировать влагу.