Универсальный способ решения: составить систему уравнений, подставить известные значения и вычислить неизвестные. Раз у нас 2 объекта, то 2 уравнения описывают движение этих объектов, а остальные уравнения берутся из условий задачи.
- s1 = v1 ⋅ t, формула движения, где s1 – длина пути автобуса №1, v1 – скорость автобуса №1, t – время движения каждого объекта.
- s2 = v2 ⋅ t, формула движения, где s2 – длина пути автобуса №2, v2 – скорость автобуса №2, t – время движения каждого объекта.
Отметим, что время движения у них одинаковое, поэтому мы его обозначили одинаково как t.
Базовыми единицами измерения возьмём км для пути, ч для времени и км/ч для скорости.
Итак, у нас в формулах есть 5 величин, из которых 3 известные (s1=100, v1=25, v2=50) и 2 неизвестные (s2, t), которые предстоит найти для получения результата.
Для успешного решения неизвестных должно быть столько же или меньше, чем уравнений. В нашем случае одинаково – 2, то есть скорее всего решение найдётся.
КАК НАУЧИТЬСЯ РЕШАТЬ ТЕКСТОВЫЕ ЗАДАЧИ
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Чернышов С.В. 1
1МБОУ Гимназия №3
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Введение
С простейшими текстовыми задачами учащиеся встречаются уже в первом классе. Переходя из класса в класс, ребята постепенно осваивают задачи на отношения «на …больше, на…меньше», «в…раз больше, в…раз меньше», причем заданных как в прямой, так и косвенной форме.
Новой ступенью развития умений решать текстовые задачи, является введение физической формулы равномерного движения: S=V*T. С помощью этой формулы можно решать несколько разновидностей задач: на прямую и обратную пропорциональные зависимости; такие процессы как «купля-продажа», «целое, разбитое на равные части», «работа», «площадь прямоугольника» и т.д.
Новый, очень серьёзный класс задач появляется при изучении процентов, обыкновенных и десятичных дробей. И начинается он с элементарных задач (процент или дробь от числа, число по его процентам или дроби) и заканчивается достаточно сложными для понимания и решения учащимися задачами на растворы, смеси, сплавы.
В курсе математики обязательно встречаются разного рода задачи, вот они и вызывают у многих затруднения. Все дело в том, что необходимо отработать и автоматизировать эти процессы. Чтобы получить правильный ответ на задачу, необходимо понять ее суть, поэтому тренироваться необходимо на простейших примерах для младшей школы.
Решение задач – это работа несколько необычная, а именно умственная работа. А чтобы научиться какой-либо работе, нужно предварительно хорошо изучить тот материал, над которым придется работать, те инструменты, с помощью которых выполняется эта работа.
Значит, для того, чтобы научиться решать задачи, надо разобраться в том, что собой они представляют, как они устроены, из каких основных частей они состоят, каковы инструменты, с помощью которых производится решение задач.
Итак, что же такое задача? Любая текстовая задача представляет собой описание какого-либо явления (ситуации, процесса). С этой точки зрения текстовая задача есть словесная модель явления (ситуации, процесса). И, как во всякой модели, в текстовой задаче описывается не все явление в целом, а лишь некоторые его стороны, главным образом, его количественные характеристики.
Любая текстовая задача состоит из двух частей – условия и требования (вопроса). В условии сообщаются сведения об объектах и некоторые числовые данные объекта, об известных и неизвестных значениях между ними. Требования задачи – это указание того, что нужно найти. Оно выражено предложением в повелительной или вопросительной форме.
Начинается работа над любой задачей с того, что:
1) Ученики самостоятельно знакомятся с условием задачи.
2) Далее один из учащихся читает задачу вслух. Ученик должен прочитать задачу так, чтобы условие задачи стало доступно каждому.
2) После четкого, разборчивого и выразительного чтения задачи учащихся должны рассказать о той ситуации, которая происходит в данной задаче.
3) Выделить главные слова, так как одним из важнейших этапов в работе над задачей является умение записать условие задачи в виде краткой записи.
4) Составить краткий план для записи решения задачи.
5) Выбрать модель задачи (рисунок, чертёж, таблица).
6) Спланировать способ решения.
7) Ответить на вопрос задачи.
8) Проверить решение.
Основная часть
2. 1 Классификация текстовых задач
Текстовые задачи делятся на группы, которые объединяет либо метод решения, либо количество действий, которые необходимо выполнить для решения задачи, либо схожий сюжет. Задачи можно классифицировать:
1. По числу действий, которые необходимо выполнить для решения задачи;
2. По соответствию числа данных и искомых;
3. По фабуле задачи;
4. По способам решения и др.
По числу действий:
простые;
составные задачи.
Задачу, для решения которой нужно выполнить одно арифметическое действие, называют простой.
Пример.Один кг яблок стоит 50 рублей. Сколько стоит один кг груш, если груши весят на 15, 5 рубля дороже?
Задачу, для которой нужно выполнить два или большее число действий, называют составной.
Пример. Ширина прямоугольника составляет 8/9 его длины. Найдите площадь и периметр прямоугольника, если его ширина равна 32 см.
Разделение задач на простые и составные не может быть проведено вполне строго. Например: задача на сложение нескольких слагаемых может быть решена одним действием сложения или несколькими действиями сложения, т.е. может быть причислена к простым или составным. Задачи на нахождение числа по его части могут решаться одним действием – делением на дробь, как задачи простые, или двумя действиями (деление на числитель дроби и умножением на ее знаменатель), т. е. могут быть отнесены к составным задачам.
Решение составной задачи сводится к разложению ее на простые задачи и к решению этих простых задач.
По соответствию числа данных и искомых;
определенные задачи;
неопределенные задачи;
Число условий должно соответствовать числу данных и искомых. Тогда задача имеет одно решение и является задачей определенной.
Пример. Два переплетчика должны переплести 384 книги. Один из них переплетает по пять книг в день и уже переплел 160 книг. Сколько книг в день должен переплетать другой переплетчик, чтобы закончить работу в один день с первым?
Если число условий в задаче недостаточно, то задача может иметь несколько решений и называется задачей неопределенной.
Пример. На складе было 392 банки вишневого, малинового и клубничного варенья. Банок с вишневым вареньем было в 3 раза больше, чем малинового. Какова масса вишневого варенья, если в каждой банке его 800 г?
По фабуле задачи:
«на движение»;
«на работу»;
«на смеси и сплавы»;
«на смешение и концентрацию»;
«на проценты»;
«на части»;
«на время»;
«на покупку и продажу» и т. п.
По способу решения задач:
задачи на тройное правило;
задачи на нахождение неизвестных по результатам действий;
задачи на пропорциональное деление;
задачи на исключение одного из неизвестных;
задачи на среднее арифметическое;
задачи на проценты и части;
задачи, решаемые с конца, или «обратным ходом».
При обучении математике в средних классах, кроме приведенной классификации задач по их месту при изучении нового материала используются классификации по другим основаниям:
По методам поиска решения – алгоритмические, типовые, эвристические;
По требованию задачи – на построение, вычисление, доказательство;
По трудности — легкие и трудные;
По сложности – простые и сложные;
По применению математических методов – уравнений, подобия, арифметический, алгебраический, графический, практический методы и т. д.
Все эти классификации позволяют рассматривать математические задачи под разными углами зрения и уточнять, совершенствовать методику работы с учащимися над задачей.
2.2 Методы и способы решения тестовых задач
Существуют различные методы решения текстовых задач:
арифметический,
алгебраический,
геометрический,
логический,
практический,
табличный,
комбинированный,
метод проб и ошибок.
В основе каждого метода лежат различные виды математических моделей.
При алгебраическом методе решения задачи составляются уравнения или неравенства, при геометрическом – строятся диаграммы или графики. Решение задачи логическим методом начинается с составления алгоритма.
Практически каждая задача в рамках выбранного метода допускает решение с помощью различных моделей. Используя алгебраический метод, ответ на требование одной и той же задачи можно получить, составив и решив совершенно разные уравнения; используя логический метод – построив разные алгоритмы. В этих случаях мы так же имеем дело с различными методами решения конкретной задачи, которые называют способы решения.
Арифметический метод. Решить задачу арифметическим методом – значит найти ответ на требование задачи посредством выполнения арифметических действий над числами. Одну и ту де задачу во многих случаях можно решить различными арифметическими способами.
Алгебраический метод. Решить задачу алгебраическим методом – это значит найти ответ на требование задачи, составив и решив уравнение или системы уравнений (или неравенств). Одну и ту же задачу можно так же решить различными алгебраическими способами.
Геометрический метод. Решить задачу геометрическим методом – значит найти ответ на требование задачи, используя геометрические построения или свойства геометрических фигур.
Логический метод. Решить задачу логическим методом – это значит найти ответ на требование задачи, как правило, не выполняя вычислений, а только используя логические рассуждения.
Практический метод. Решить задачу практическим методом – значит найти ответ на требования задачи, выполнив практические действия с предметами или их копиями (моделями, макетами).
Табличный методпозволяет видеть задачу целиком это- решение путем занесения содержания задачи в соответствующим образом организованную таблицу.
Комбинированный метод позволяет получить ответ на требование задачи более простым путем.
Метод проб и ошибок (самый примитивный), в нем ответ на вопрос задачи угадывается.
Методы решения могут быть разные, но способ решения, лежащий в их основе, может быть только один.
2.3 Практическая часть
В практической части научно-исследовательской работы для 5-го и 6-го классов были предложены следующие задачи:
Арифметический метод решения задачи. В этой задаче необходимо знать формулу: S=V*T.
Задача 1: Воробей за два часа пролетел 14 километров, а орел за три часа пролетел 210 километров. Во сколько раз скорость орла больше?
Условие
Воробей: 2ч – 14 км
в ? раз б
Орел: 3ч -210 км
Решение:
14 :2=7 (км/ч) – скорость воробья;
210 :3=70 (км/ч) – скорость орла;
70 :7=10 – во столько раз скорость орла превосходит скорость воробья.
Ответ: в 10 раз больше.
Задача 2.Найдем 12 % от 7000 рублей
1 способ: Найдем 1 %, а потом 12 %.
1) 7000:100 = 70(р.) – 1%
2) 70 * 12 = 840(р.) – 12%
2 способ: Перевод % в десятичную дробь
1) 12% = 0,12
2) 7000 * 0,12 = 840(р.)
Ответ: 840р.
Задача 3. Два мальчика выбежали одновременно навстречу друг другу по спортивной дорожке, длина которой 100 м. Они встретились через 10 с. Первый мальчик бежал со скоростью 4 м /с. С какой скоростью бежал второй мальчик?
План решения задачи:
І способ.
1.Найти путь, который пробежал первый мальчик до встречи.
2. Найти путь, который пробежал второй мальчик до встречи.
3. Найти скорость, с которой бежал второй мальчик.
II способ.
1. Найти скорость сближения.
2. Найти скорость, с которой бежал второй мальчик до встречи.
Задача 4.(2 уровень.) Цена книги понизилась на 15%. Найдите новую цену книги, если прежняя составляла 60 рублей?
Вот наглядный пример решения задачи на составление уравнения с использованием вспомогательной таблицы. Она значительно упрощает восприятие
Задача5. На первой полке книг в три раза больше, чем на второй. Если с первой полки убрать восемь книг, а на вторую поставить 32, то их станет поровну. Сколько книг было первоначально на каждой полке?
Условие
|
1 полка |
2 полка |
|
|
Было |
3х |
3х-8 |
|
Стало |
х |
х+32 |
Решение:
3х-8=х+32;
3х-х=32+8;
2х=40;
х=20
20 (книг) – было на второй полке;
20*3=60 (книг) – было на первой полке.
Ответ:60 книг;20книг.
Задача6. На солнышке грелось несколько кошек. У них вместе лап на 10 больше, чем ушей. Сколько кошек грелось на солнышке?
Решение.
1 способ.
|
Лапы |
Ушки |
|
|
1 кошка |
4х |
2х |
|
Кошки |
На 10 больше |
? |
Так как лап на 10 больше чем ушей.
Составим и решим уравнение:4х – 2х = 102х= 10 │: 2х = 5
Ответ: 5 кошек грелось на солнышке.
способ
1. На сколько лап больше чем ушей у одной кошки?4 – 2 = 2 (шт.)
2. Сколько кошек грелось на солнышке?10 : 2 = 5 (шт.)
Ответ: 5 кошек грелось на солнышке.
Задача7. В хозяйстве имеются куры и овцы. Сколько тех и других, если известно, что у них вместе 19 голов и 46 ног?
Составленное уравнение учащиеся решают самостоятельно, с последующей проверкой.
2х + 76 – 4х = 46-2х = -30 │: (-2)х= 1515 шт. – куры19 – 15 = 4 (шт.) – овцы
Ответ: 15 кур, 4 овцы
Логический метод.
Задача 8. Кто из учеников Саша, Сергей, Дима и Андрей играет, а кто не играет в шахматы, если известно следующее:
а) если Саша и Сергей играет, то Дима не играет;
б) если Сергей не играет, то играют Дима и Андрей;
в) Дима играет.
Решение:
Если Саша и Сережа играют, то Дима не играет.
Если играют Дима и Андрей, то Сережа не играет.
Так как Дима по условию играет в шахматы, значит – это Дима и Андрей играют в шахматы.
Ответ: в шахматы играют ученики Дима и Андрей, а Саша и Сергей – не играют.
Задача 9. Поют в хоре и занимаются танцами 82 ученика, занимаются танцами и художественной гимнастикой 32 ученика, а поют в хоре и занимаются художественной гимнастикой 78 учеников. Сколько учеников поют в хоре, занимаются танцами и художественной гимнастикой отдельно, если известно, что каждый ученик занимается только чем-то одним?
Решение:
1-й способ.
1) 82 32 + 78 = 192 (чел.) – удвоенное число учеников, поющих в хоре, занимающихся танцами и художественной гимнастикой;
2) 192 : 2 = 96 (чел.) – поют в хоре, занимаются танцами и художественной гимнастикой;
3) 96 – 32 = 64 (чел.) – поют в хоре;
4) 96 – 78 = 18 (чел.) – занимаются танцами;
5) 96 – 82 = 14 (чел.) – занимаются художественной гимнастикой.
2-й способ.
1) 82 – 32 = 50 (чел.) –на столько больше учеников поют в хоре, чем
занимаются художественной гимнастикой;
2) 50 + 78 = 128 (чел.) – удвоенное число учеников, поющих в хоре;
3) 128 : 2 = 64 (чел.) – поют в хоре;
4) 78 – 64 = 14 (чел.) — занимаются художественной гимнастикой;
5) 82 – 64 = 18 (чел.) – занимаются танцами.
Ответ: 64 ученика поют в хоре, 14 учеников занимаются художественной гимнастикой, 18 учеников занимаются танцами.
Среди учащихся 5 и 6 классов, в количестве 33 человек с предложенными задачами справилось 12 человек. Задачи на проценты в 5 классе учащиеся ещё не умеют решать. Обратились за помощью 8 учащихся, и потом они тоже справились с предложенными задачами.
Отсюда можно сделать вывод, что 37% успешно решили все задачи. Прибегнув к помощи, ещё 24% учащихся смогли справиться с данными задачами. Особые затруднения вызвали логические задачи.
Подводим итог: с задачами более простыми в целом ученики 5-го и 6-го классов справляются, но если добавляются немного больше элементов в рассуждениях, то справляются с такими заданиями не все.
Так же был проведён соц. Опрос среди учащихся 5-6 классов. Всем задавали вопрос: «Какие задачи легче решать: математические или логические?» В опросе участвовали 33 ученика. 25 учеников ответили – математические, 3 ученика – логические, 5 учеников – ни какие не могут решить.
Вывод: математические задачи легче решить 76-ти % опрошенных, логические – 10% и 14% не смогут решить никакую задачу.
Заключение
Для достижения цели данного исследования были выполнены следующие задачи:
1.Был произведен анализ некоторой методической и школьной литературы с точки зрения изучения методов решения задач в школе на уроках математики.
2.На основе изученного материла, были описаны методы и способы решения текстовых задач, в основной школе. С кратким описанием и приведением примеров.
3. В результате были описаны наиболее часто встречающиеся методы используемые в школьном курсе математики в 5 – 6 классах.
Таким образом, была достигнута цель данного исследования: описать методы и способы решения текстовой задачи в курсе изучения математики 5 – 6 классов.
Литература
1.Виленкин Н.Я. Математика: Учебник для 5 класса общеобразовательных учреждений// Н.Я.Виленкин, В.И. Жохов, А.С.Чесноков, С.И.Шварцбурд. – М.: Мнемозина: 1999-2004. – 384 с.
2.Виленкин Н.Я. Математика: Учебник для 6 класса общеобразовательных учреждений// Н.Я.Виленкин, В.И. Жохов, А.С.Чесноков, С.И.Шварцбурд. – М.: Мнемозина, 1999-2004. – 384 с.
3.Дорофеев Г.В. Математика 6 класс.-Просвещение,:2013.
4.Матвеева Г. Логические задачи // Математика. – 1999. № 25. – С. 4-8.
5. Фридман, Л.М. Как научиться решать задачи [Текст] : Кн. для учащихся ст. кл. средн. шк. / Л.М. Фридман, Е.Н. Турецкий.– 3-е изд., дораб.– М.: Просвещение, 1989.– 192 с.: ил.
6. Целищева, И. Как помочь каждому ученику самост-но решать текстовые задачи [Текст] / И. Целищева, С. Зайцева // Нач. шк.: еженед. прил. к газ. “Первое сентября”.– 2001.– 00.05 (№ 18).– С. 2-5.
7. Шарыгин И.Ф. , Шевкин Е.А. Задачи на смекалку.-Москва,:Просвещение,1996.-65с.
Приложение
«ПАМЯТКА «КАК РЕШАТЬ ТЕКСТОВЫЕ ЗАДАЧИ»
1. Прочитай задачу и представь себе то, о чем в ней говорится.
2. Выдели условие и вопрос.
3. Запиши условие кратко или выполни чертёж.
4. Подумай можно ли сразу ответить на вопрос задачи. Если нет, то почему. Что надо узнать сначала, что потом?
5. Составь план решения.
6. Выполни решение.
7. Проверь решение и запиши ответ задачи.Примерный план ответа-рассуждения при решении задачи:
1.Арифметический метод.
Анализ задачи.
1. Известно, что … (расскажи условие задачи)
2. Надо узнать… (повтори вопрос)
3. Чтобы ответить на вопрос задачи, надо …
4. Сразу мы не можем ответить на вопрос задачи, так как не знаем…
5. Поэтому в первом действии мы узнаем …
6. Во втором действии мы ответим на вопрос задачи. Для этого … ( какое действие выполняем)
7. Ответ …
2. Алгебраический метод:
Одним из важнейших направлений улучшения качества обучения математике является совершенствование его практической составляющей. К средствам реализации этого направления можно отнести использование текстовых задач и метода уравнений. Действительно, решение текстовых задач с помощью уравнений иллюстрирует применение математики к исследованию явлений реальной действительности, обеспечивает реализацию общих принципов прикладной направленности курса математики. Поэтому необходимо уделять внимание решению текстовых алгебраических задач. Схема работы над задачей:1 этап – анализ и запись условия задачи. Выполнение чертежа, если он необходим.
Содержание данного этапа включает:
Установление объекта наблюдения (исследования);
Выделение процессов, подлежащих рассмотрению;
Выявление величин, входящих в каждый процесс;
Выяснение функциональной зависимости между величинами и составление формул этой зависимости;
Схематическая запись условия задачи с обозначение неизвестных величин;
2 этап – нахождение плана решения.
Выявление основания для составления уравнения или системы уравнений;
Составление уравнения или системы уравнений;
3 этап – осуществление плана решения задачи.
Решение уравнения или системы;
Исследование корней уравнения (системы) с целью установления решений задачи. Проверка расчетов и обоснований;
Запись ответа;
4 этап – анализ решения задачи.Комментирование решения задачи. Возвращение к решению задачи (ретроспективный подход) с целью уточнения идей и методов решения задачи, упрощение расчетов. Поиск более рациональных приёмов решения задачи.
Пример № 1.На середине пути между станциями А и В поезд был задержан на 10 минут. Чтобы прибыть вВ по расписанию, машинисту пришлось первоначальную скорость поезда увеличить на 12 км/ч. Найти первоначальную скорость поезда, если известно, что расстояние между А и В равно 120 км. 1 – Пусть Х км/ч – первоначальная скорость поезда (умение выделять величины и обозначать их буквами).2 – Найдем зависимость между зафиксированной величиной и другими, участвующими в задаче (умение формулировать зависимости между величинами и выражать посредством букв).ч – время прохождения поездом пути от А до середины;(х + 12) км/ч – скорость поезда от середины пути до В;ч – время прохождения второго участка пути; 3 – По условию задачи поезд прошел вторую часть пути на ч меньше, чем предполагалось по расписанию. Время прохождения поезда по расписанию от середины до конца пути – 60 км/ч, поезд из-за стоянки ч должен был увеличить первоначальную скорость на 12 км/ч , чтобы прибыть по расписанию, т.е. время, затраченное им на втором участке пути, равно ( + ) ч (умение выражать одну и ту же зависимость разными способами, умение составлять уравниваемые выражения). 4 – Составляем уравнениеРешив данное уравнение, получаем: х1 = 60, х2 = – 72. Условию задачи, отвечает х = 60. Таким образом первоначальная скорость поезда – 60 км/ч. (умение интерпретировать результат решения задачи на языке данной задачи).5 – Заметим, что словесная формулировка условия задачи довольно громоздка. В таких случаях осуществления анализа может помочь рисунок.На рисунок вынесены величины, содержащиеся в условии задачи (умение использовать графические модели условия задачи, осуществлять переход от одной модели к другой).
Памятка для лучшего усвоения решения задач с помощью уравнений.
Тщательно изучи условие задачи, если надо, сделай чертёж.
Выясни, о каких величинах идет речь в задаче.
Выбери любую из этих величин для правой части уравнения.
Установи, каким действием и над какими величинами её можно получить.
Выясни, какие из них известны, какие нет. Введи обозначение переменной.
Запиши уравнение.
Реши данное уравнение.
Сделай анализ уравнения.
20
Просмотров работы: 14541
Методы решения текстовых задач
Содержание
1. Введение……………………………………………………………………2
2. Задачи на
движение………………………………………………………..3
3. Задачи «на работу»…………………………………………………………6
4. Заключение………………………………………………………………..20
5. Список литературы………………………………………………………..20
Текстовые
задачи на составление уравнений
1.
Введение
Текстовые задачи
являются традиционным разделом на вступительных экзаменах. Как правило,
основная трудность при решении текстовой задачи состоит в переводе её условий
на математический язык уравнений. Общего способа такого перевода не существует.
Однако многие задачи на вступительных экзаменах, достаточно типичны.
Для
начала узнаем, что такое задача:
- Задача – это требование или вопрос, на который надо
найти ответ, опираясь или учитывая те условия, которые в ней указаны. - Любая задача состоит из трёх частей: условие, объект, требование (вопрос) задачи.
- Приступая
к решению какой-либо задачи, надо её внимательно
изучить, установить, в чем состоят её требования, каковы условия, исходя
из которых надо её решать. Всё
это называется анализом
задачи.
Весь процесс решения задачи можно
разделить на восемь этапов:
1-й этап: анализ;
2-й этап: схематическая запись;
3-й этап: поиск способа решения;
4-й этап: осуществление решения:
5-й этап: проверка решения;
6-й этап: исследование задачи;
7-й этап: формулировка ответа;
8-й этап: анализ решения.
Стандартная
схема решения таких задач включает в себя:
1.Выбор и обозначение неизвестных.
2.Составление уравнений (возможно неравенств) с использованием
неизвестных и всех условий задачи.
3.Решение полученных уравнений (неравенств).
4.Отбор решений по смыслу задачи.
Задачи на движение
В задачах на движение
используются обычно формулы, выражающие законы равномерного движения: S=V·t , где S– пройденное расстояние, V– скорость
равномерного движения, t – время движения.
При составлении
уравнений в таких задачах часто бывает удобно прибегнуть к геометрической иллюстрации
процесса движения: путь изображается в виде отрезка прямой, место встречи
движущихся с разных сторон объектов точкой на отрезке и т.д.
Часто для усложнения
задачи её условие формулируется в различных единицах измерения(метры, километры,
часы, минуты и т.д.). В этом случае при выписывании уравнений необходимо
пересчитывать все данные задачи в одинаковых единицах измерения:
1.
Если расстояние между двумя движущимися
навстречу друг другу телами равно S, а их скорости V1 и V2, то время t через
которое они встретятся , находиться по формуле t= S V1+V2 .
2.
Если движение вдогонку , то есть первое тело
следует за вторым , то время t , через которое
первое тело догонит второе , находится по формуле t=SV1-V2 .
3.
В задачах на движение по воде скорость
течения считается неизменной . При движении по течению скорость течения
прибавляется к скорости плывущего тела , при движении против течения –
вычитается из скорости тела . Скорость плота считается равной скорости
течения.
4.
Средняя скорость вычисляется по формуле V=St , где S– путь , пройденный телом , а t– время, за
которое этот путь пройден . Если путь состоит из нескольких участков ,
то следует вычислить всю длину пути и всё время движения .
Задача 1. Велосипедист ехал 2 часа по лесной дороге и 1 час по шоссе,
всего он проехал 40 км. Скорость его по шоссе была на 4
км/ч больше, чем скорость на лесной дороге. С какой скоростью велосипедист
ехал по лесной дороге, и с какой по шоссе?
Решение:
Пусть x км/ч скорость велосипедиста на лесной
дороге. Тогда его скорость на шоссе будет (x+4) км/ч. За 2 часа по лесной
дороге велосипедист проехал 2·x км., а за час по шоссе (x+4) км. Весь путь по условию равен 40км.
Составляем уравнение:
2x+(x+4) = 40;
2x+x = 40 – 4;
3x = 36;
x = 36:3;
x=12.
Значит скорость на
лесной дороге 12 км/ч, а на шоссе 12+4=16 (км/ч).
Ответ: 12
км/ч ; 16 км/ч.
Задача 2. От пристани против течения реки отправилась моторная лодка,
собственная скорость которой 10 км/ч. Через 45 минут после выхода у лодки
испортился мотор, и лодку течением реки через 3 часа принесло обратно к
пристани. Какова скорость течения реки?
Решение:
Пусть x км/ч скорость течения реки.
Моторная лодка против течения реки шла со скоростью (10-x) км/ч. В пути была 45
минут.
часа.
Путь против течения
равен
Далее лодка с испорченным двигателем плыла по течению со скоростью x км/ч 3 часа обратно к
пристани. Весь этот путь равен 3∙x км. Но расстояния туда и обратно
равны:
Ответ: 2 км/ч.
Задача 3. Из двух городов, расстояние между которыми 200
км, одновременно навстречу друг другу выехали легковой автомобиль и грузовик и
встретились через 2 часа. Скорость легкового автомобиля 60
км/ч. Найти скорость грузовика.
Решение:
Пусть скорость
грузовика равна x км/ч. Поскольку машины выехали
одновременно навстречу друг другу, то скорость сближения (сумма скоростей)
равна (x+60) км/ч. Каждый из них до встречи
находится в пути 2 часа.
Поэтому:
2(x+60) = 200
x+60 = 100
x = 100-60
x = 40
Скорость грузовика 40
км/ч.
Ответ: 40
км/ч.
Задача 4. Из пунктов А и В, расстояние между которыми 94км, отправились
одновременно навстречу друг другу пешеход и велосипедист. Скорость пешехода на 16
км/ч меньше скорости велосипедиста. Найти скорость каждого, если известно, что
встретились они через 4ч и пешеход сделал в пути получасовую остановку.
Решение:
Пусть скорость
пешехода равна х км/час, тогда скорость велосипедиста (х+16) км/ч. Отправляются навстречу друг
другу одновременно. Встречаются через 4 часа. Пешеход делал в пути получасовую
остановку. Значит шел до встречи 4-0,5=3,5 часа, велосипедист до встречи ехал 4
час.
Итак, путь пешехода 3,5х км, а путь велосипедиста 4(х+16) км. Сумма по условию 94.
Составляем уравнение:
4(x+16)+3,5x=94;
4x+64+3,5x=94;
7,5x=30;
x=30:7,5;
x=300:75
x=4.
Скорость пешехода
4км/ч, велосипедиста 16+4=20км/час
Ответ: 4км/ч; 20км/ч.
Задача 5. Пароход прошел 4
км против течения реки, а затем прошел еще 33
км по течению, затратив на весь путь один час. Найдите собственную скорость
парохода, если скорость течения реки равна 6,5
км/ч.
Решение. Пусть х км/ч – собственная скорость
парохода. Тогда (х +
6,5) км/ч –
скорость парохода по течению, а (х
– 6,5) км/ч – скорость
парохода против течения.
Так как против течения пароход прошел 4 км со скоростью (х – 6,5) км/ч, то 4 / (х – 6,5 ) – время движения парохода против
течения.
А так как по течению пароход прошел 33 км со скоростью (х+6,5) км/ч,
то 33 / (х
+ 6,5 ) – время
движения парохода по течению.
По условию 4 / (х – 6,5) = 33 / (х + 6,5) = 1.
Решая это уравнение, получим х2 – 37х + 146,25 = 0; х1=4,5 км/ч и х2=32,5 км/ч.
Осуществим отбор
полученных решений. Через х мы обозначили собственную скорость
парохода, при этом скорость течения реки 6,5
км/ч, поэтому х1=4,5
км/ч не подходит по смыслу задачи (при
такой скорости пароход не выплыл бы против течения). Поэтому, собственная
скорость парохода равна 32,5 км/ч. Ответ: v=32,5 км/ч.
Задачи на совместную работу
Между величинами,
описывающими равномерное движение и величинами, характеризующими процесс работы,
имеется полная аналогия.
Представим это так:
Вся работа – А;
Время работы – t;
Производительность
При совместной работе
нескольких объектов, выполняющих одновременно работу, их общая
производительность равна сумме производительностей отдельных объектов.
Во многих задачах на
работу точный характер этой работы не определен, тогда удобно принять объем
всей работы за единицу и измерять части такой работы в долях от единицы.
Иногда в задачах
на совместную работу можно обойтись без решения уравнений , используя
только арифметический способ .
Рассмотрим примеры решения задач из
Открытого банка заданий для подготовки к ЕГЭ
по математике:
Задание B13
Даша и Маша пропалывают грядку за 12 минут, а одна
Маша — за 20 минут. За сколько минут пропалывает грядку одна Даша?
Про Машу нам все известно: время ее работы равно
20, следовательно, ее производительность равна .
Пусть Даша пропалывает грядку за х минут, тогда ее
производительность равна .
Тогда совместная
производительность равна
Объем работы примем равным 1.
Время совместной работы равно 12 минут, отсюда получаем уравнение:
Решим его:
Ответ: 30
Классическая задача на совместную работу:
Задание B13
Первая труба наполняет резервуар на 6 минут дольше,
чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут
наполняет этот резервуар одна вторая труба?
1. Введем неизвестные:
Пусть
х – время заполнения резервуара первой трубой
y – время заполнения резервуара второй трубой
– производительность первой трубы
– производительность второй трубы
– совместная производительность
2. Примем объем резервуара равным 1.
3.
У нас 2 неизвестных, поэтому будем
составлять систему из двух уравнений.
По условию задачи, первая труба наполняет
резервуар на 6 минут дольше, чем вторая, следовательно, время работы
первой трубы на 6 минут больше, чем второй:
Обе трубы наполняют этот же резервуар за 4 минуты, следовательно, время совместной работы равно 4
минуты. Получаем второе уравнение системы:
Получили систему уравнений:
,
– не подходит по
смыслу задачи.
Ответ: 6 мин
Рассмотрим
примеры решения задач:
Задача 1. Заказ по выпуску машин завод должен выполнить за 20 дней, но уже
за 18 дней завод перевыполнил план на 6 машин, так как ежедневно выпускал на 3
машины сверх плана. Сколько машин выпустил завод?
1способ
Проведём анализ
задачи, cоставив таблицу . Пусть х машин выпустил завод.
|
А (шт.) |
N (шт. в |
t (дни) |
|
|
По плану |
x-6 |
|
20 |
|
Фактически |
х |
|
18 |
Тогда
х+54=3·180; х+54=540; х=540-54;
х=486
Ответ: 486
штук.
2 способ
Пусть х – количество
машин в день по плану.
|
А (шт.) |
N(шт. в |
t(дни) |
|
|
По плану |
20х |
х |
20 |
|
Фактически |
18(х+3) |
х+3 |
18 |
Тогда
18∙(x+3) – 20x =
6;
18x + 54 – 20x=6;
-2x=-54+6;
-2x = -48;
x=24;
18∙(24+3)=18∙27=486.
Ответ: 486
штук.
Задача 2. Две бригады, работая вместе, могут закончить уборку урожая
за 8 дней. Если первая бригада будет работать 3 дня, а вторая 12 дней, то они
выполнят всей работы. За сколько дней может
закончить уборку урожая каждая бригада, работая отдельно?
Решение:
Примем весь объем
работы за 1. Тогда две бригады, работая вместе за один день выполнят часть работы. Это
их общая производительность.
Пусть
производительность первой бригады равна х, тогда второй . (Это часть
работы, выполненная за 1 день).
За три дня, работая
отдельно первая бригада сделает 3х часть работы, а вторая за 12 дней: . Обе бригады
при этом выполнят
от 1.
Составляем уравнение:
Так как А=p·t, то p–
производительность.
Время работы первой
бригады: отдельно.
Вторая бригада,
работая сама, потратит время:
производительность второй бригады.
Ответ: 12 дней, 24 дня.
Задача 3. Один инструктор может выполнить задание на 5 ч.
быстрее другого. Оба вместе они выполняют это задание за 6ч. За сколько часов каждый
из них выполнит задание?
В задачах “на работу” три величины:
1) работа; 2)время; 3)производительность – работа, выполненная
за единицу времени.
Проведем анализ задачи, составив таблицу.
|
Вид деятельности |
Работа (1) |
Время (ч) |
Производительность |
|
Первый инструктор |
1 |
X |
|
|
Второй инструктор |
1 |
Х+5 |
|
|
Совместно |
1 |
6 |
|
Заметив по таблице, что совместная производительность
выражается как или
как ,
составим и решим уравнение.
1) =
Умножим
обе части на 6Х (Х + 5) ? 0, при Х ? 0 и Х ? -5, получим:
6 (Х+5) + 6Х = Х (Х+5),
6Х + 30 + 6Х = Х2 +
5Х,
Х2 –
7Х – 30 = 0;
Х1 =
-3; Х2 = 10.
2) -3 и 10являются корнями уравнения =
.
3) -3 не удовлетворяет условию задачи, т.к. время не может
быть отрицательным, значит, первый инструктор выполнит задание за 10 ч, а горой
за 15 ч.
Ответ: 10ч; 15ч.
Задача 4. Можно
предложить учащимся решить самостоятельно.
Двое рабочих выполнили работу за 12 дней. За сколько дней
может выполнить каждый рабочий, если одному из них для выполнения всей работы
потребуется на 10 дней больше, чем другому?
Проведем анализ задачи, составив таблицу.
|
Вид деятельности |
Работа (1) |
Время (дни) |
Производительность |
|
Первый рабочий |
1 |
X |
|
|
Второй рабочий |
1 |
Х+10 |
|
|
Совместно |
1 |
6 |
|
Заметив по таблице, что совместная производительность
выражается как или
как ,
составим и решим уравнение.
1) =
Умножим обе части на 12Х (Х + 10)
12Х + 120 + 12Х = Х2 +
10Х;
Х2 –
14Х – 120 =0;
Х1 =
-6; Х2 = 20;
2) -6 не удовлетворяет условию задачи, значит, за 20 дней
выполнит всю работу первый рабочий, а второй – за 30 дней.
Ответ: 20дней, 30 дней.
Задача 5. Предложить
задачу на дом.
Две бригады, работая совместно, закончили отделку квартир в
доме за 6 дней. Сколько дней потребовалось бы каждой бригаде на выполнение этой
работы, если одной для этого требуется на 5 дней больше чем другой?
Проведем анализ задачи, составив таблицу.
|
Вид деятельности |
Работа (1) |
Время (дни) |
Производительность |
|
Первая бригада |
1 |
X |
|
|
Вторая бригада |
1 |
Х+5 |
|
|
Совместно |
1 |
6 |
|
Заметив по таблице, что совместная производительность
выражается как или
как ,
составим и решим уравнение.
1) =
;
Ответ: 10 дней, 15 дней.
Используя этот способ, можно решить задачу.
Задача 6.
Два хлопкоуборочных комбайна могут собрать хлопок с поля на 9
дней скорее, чем один первый комбайн, и на 4 дня скорее, чем один второй. За
сколько дней каждый комбайн может собрать весь хлопок?
Проведем анализ задачи, составив таблицу.
|
Вид деятельности |
Работа (1) |
Время (дни) |
Производительность |
|
Первый комбайн |
1 |
X+9 |
|
|
Второй комбайн |
1 |
Х+4 |
|
|
Совместно |
1 |
6 |
|
1) Составим и решим уравнение
=
; умножив на Х (Х+9) + (Х+4) ? 0, получим:
2Х2 +
13Х = Х2 + 4Х +9Х +
36,
Х2 =
36;
Х1,2 =
+6;
2) – 6 не удовлетворяет условию задачи. За 6 дней соберут весь
хлопок два комбайна; за 10 дней – второй комбайн и за 15 дней – первый.
Ответ: 15 и 10 дней.
Задача7.
Для наполнения бассейна через первую трубу потребуется на 9ч.
больше времени, чем при пополнении через первую и вторую трубы, и на семь
меньше, чем через одну вторую трубу. За сколько часов наполниться бассейн через
обе трубы?
Проведем анализ задачи, составив таблицу.
|
Вид деятельности |
Работа (1) |
Время (ч) |
Производительность |
|
Первая труба |
1 |
X+9 |
|
|
Вторая труба |
1 |
(Х+9)+7 |
|
|
Совместно |
1 |
6 |
|
1) Составим и решим уравнение
=
;
х1,2 =
+12.
x = -12 – не удовлетворяет условию задачи. За 12 часов
наполнится бассейн.
Ответ: 12ч.
Задача 8.
Два слесаря получили заказ. Сначала 1ч работал первый слесарь,
затем 4ч они работали вместе. В результате было выполнено 40% заказа. За
сколько часов мог выполнить заказ каждый слесарь, если первому для этого
понадобилось бы на 5 ч больше, чем второму?
Проведем анализ задачи, составив таблицу.
|
Вид деятельности |
Работа (1) |
Время (ч) |
Производительность |
|
Первый слесарь |
1 |
X |
|
|
Второй слесарь |
1 |
(Х – 9) |
|
|
Совместно |
|
4 |
|
1) Первый слесарь, работая один, за 1 час выполнил работу , и работая
совместно, выполнили работу , что по условию равно 40% всего заказа, т.е.
2,5 не удовлетворяет условию задачи, т.к. второй слесарь
работал на 5 ч меньше, то есть 2,5 – 5 = – 2,5, что не выполнимо.
2) За 25 ч. может выполнить заказ первый слесарь и за 20 ч.
второй слесарь.
Ответ: 25ч и 20ч.
Алгебра 9 класс. Учебник авторов Ю.Н. Макарычев, Н.Г. Миндюк,
К.И Нешков, СБ. Суворова.
Задача 9. (Задачи
повышенной трудности).
За сколько часов может выполнить работу каждый из трех
рабочих, если производительность труда третьего рабочего равна полусумме
производительностей труда первого и второго? Известно, что если бы третий
рабочий проработал один 48 ч., то для окончания работы первому требовалось бы
10ч., а второму 15ч.
Проведем анализ задачи, составив таблицу.
|
Вид деятельности |
Работа (1) |
Время (ч) |
Производительность |
|
Первый рабочий |
1 |
10 |
Х |
|
Второй рабочий |
1 |
15 |
Y |
|
Третий рабочий |
1 |
48 |
|
1) работа,
выполненная вторым и третьим рабочими.
работа,
выполненная первым и третьим рабочими.
Составим и решим систему:
2)
Таким образом,
–
производительность первого рабочего,
–
производительность второго рабочего,
–
производительность третьего рабочего.
3) = 50ч – время первого рабочего,
= 75ч – время
второго рабочего,
= 60ч – время
третьего рабочего.
Ответ: 50ч; 75ч; 60ч.
Задача 10
Бассейн наполняется через первую трубу на 5ч быстрее, чем
через вторую. Бассейн можно наполнить, если открыть сначала одну первую трубу
на 5ч, а затем одну вторую на 7,5ч. За сколько часов наполнится бассейн при
совместной работе обеих труб?
Проведем анализ задачи, составив таблицу.
|
Вид деятельности |
Работа (1) |
Время (ч) |
Производительность |
Выполненная работа |
|
|
Время (ч) |
Работа (1) |
||||
|
Первая труба |
1 |
X |
|
5 |
|
|
Вторая труба |
1 |
Х+5 |
|
7,5 |
|
Составим и решим уравнение:
– 2,5 не удовлетворяет условию задачи.
Тогда первая труба заполняет бассейн за 10 ч и производительность
первой трубы.
Вторая труба заполняет бассейн за 15 ч и ее производительность .
– совместная
производительность.
Следовательно, две трубы наполняют бассейн при совместной
работе за 6ч.
Ответ: 6ч.
Решим задачу на производительность труда.
Задача11
Три каменщика разной квалификации
выложили кирпичную стену, причём первый каменщик работал 6 часов, второй – 4
часа, а третий – 7 часов. Если бы первый каменщик работал 4 часа, второй – 2
часа и третий – 5 часов, то было бы выполнено 2/3 всей работы. За сколько часов
каменщики закончили бы кладку, если бы они работали вместе одно и то же время?
Решение.
Решим эту задачу путём составления
системы уравнений.
Пусть х – скорость выполнения работы
первого каменщика, y – второго, z – третьего. Всю работу примем за 1. Составим
систему уравнений по условию задачи

Надо найти
, то есть
Умножим (2) на -2 и сложим почленно
с (1). Получим :
Затем умножим (2) на -1,5 и сложим почленно
с (1). Получим :
y=0,5z
Следовательно, подставим в искомое
выражение полученные значения для x, y, z . В итоге получим 6.
Ответ: каменщики выполнят эту работу
за 6 часов.
Мы решили эту задачу путём
составления систем уравнений и решая их методом Гаусса.
Задачи «на работу сложны тем», что в
них абстрактное понятие «работа» приобретает различное конкретное содержание. В
первой задаче работа выражалась в виде производительности труда каменщиков. В
следующей задаче мы рассмотрим случай, в котором идёт речь о работе по
наполнению бассейна.
Задача 12
При одновременной работе двух
насосов разной мощности бассейн наполняется водой за 8 часов. После ремонта
насосов производительность первого из них увеличилась в 1,2 раза., а второго –
в 1,6 раза, и при одновременной работе насосов бассейн стал наполняться за 6
часов. За какое время наполнится бассейн при работе только первого насоса после
ремонта?
Решение.
Пусть объём бассейна равен 1, тогда
время его заполнения до ремонта первым насосом – x, а вторым – y часов.
Следовательно,
– производительность первого
насоса до ремонта, а – производительность второго
насоса до ремонта. Зная, что бассейн до ремонта насосов заполняется за 8 часов,
то составим первое уравнение . – производительность первого
насоса до ремонта, а – производительность второго
насоса после ремонта. Зная, что бассейн после ремонта насосов заполняется за 6
часов, то составим второе уравнении .
Решив оба уравнения можно составить
систему:
Умножим (1) на 0,9 и вычтем из него
(2).
В итоге получим y=24, x=12.
Из найденных значений для x и y
вычислим производительность первого насоса после ремонта:
По формуле
найдём время наполнения бассейна при
работе только первого насоса после ремонта: ч.
Ответ: 10 ч.
Вывод: в большинстве случаев задачи решаются
путём составления систем уравнений. В результате решения задач двух разных
видов мы выяснили, что все задачи на работу решаются по одной общей формуле
(А=P
t)
Заключение
Решение текстовых задач
является неотъемлемой частью изучения математики и выносится на ГИА и ЕГЭ
по математике. Нередко с ними приходится сталкиваться и в повседневной
жизни. Однако, как показывает практика, при решении задач у учеников
часто возникают трудности, связанные с непониманием смысла самой задачи
. Решение задач развивает логическое и интеллектуальное мышление. Однако
времени на их решение в школьном курсе математики отводится очень
немного. Постоянно на уроках математики 5-11классов необходимо решать
текстовые задачи . При выполнении задачи В13 ученики допускают очень
много вычислительных ошибок . Проводя апробирование по решению текстовых
задач в 9-х классах я вижу , что только 50% учащихся решают задачи В13 .
Список литературы
- Макарычев
Ю.Н., Миндюк Н. Г., Нешков К. И. и др. «Алгебра. Учебник для 8 класса
общеобразовательных учреждений»; Москва, «Просвещение» 2010г. - Лахова
Н. В. «Математика в школе» - Потапов
М. К., Олехник С., Нестеренко Ю. «Математика. Методы решения задач для
поступающих в вузы»; Москва, «Дрофа» 2005г. - Соловейчик
И. «Математика»; Москва, «Первое сентября» 2009г. - Фридман
Л. М., Турецкий Е. Н. «Как научиться решать задачи»; Москва «Просвещение» 1984
г. - Шестаков С.
А., Гущин Д. Д. Задачи на составление уравнений . Москва. МЦНМО 2012г.
В этом уроке мы с вами займёмся классическими школьными задачами! Да-да, теми самыми старыми добрыми задачками про трубы и бассейны, автомобили и поезда, лодки и катера, велосипедистов и лыжников, строителей и маляров — и так далее.) По-другому их ещё называют текстовыми задачами.
Название говорит само за себя: условие задачи дано словами. То есть, в виде текста. Но текста не простого, а золотого… пардон… наполненного математическим смыслом! И наша с вами основная задача будет уловить этот самый смысл да грамотно перевести обычные русские слова в чистую математику. А той — всё по плечу! Именно этим увлекательным процессом (переводом слов в математику) мы большей частью и будем заниматься на протяжении всех уроков этого раздела. Приступим?)
Какие бывают задачи по математике?
Задач в математике очень и очень много. Самых разных — простых и сложных, коротких и навороченных. Но всё богатое многообразие текстовых задач можно условно разделить на четыре основные группы.
1) Задачи на движение.
2) Задачи на работу.
3) Задачи на проценты (в т.ч. на смеси, сплавы и т.д.).
4) Прочие…
Из текста задачи сразу становится понятно, к какой именно группе она принадлежит. Если что-то или кто-то куда-то движется (едут поезда, автобусы, велосипеды, плывут лодки, идут туристы и т.д.), то перед вами типичная задача на движение. Если же кто-то что-то делает (строители строят дом, маляр красит забор, труба наполняет бассейн, землекоп роет канаву, писатель пишет книгу и т.д.) — задача на работу. Если речь идёт о процентах (а также долях, частях, концентрациях и т.п.) — соответственно задача на проценты (или на части, на дроби). Ну а если что-то кардинально другое (например, покупки в магазине, целые числа и т.п.) или же несколько групп в одном флаконе (скажем, одновременно работа и проценты), то эта задачка уже из разряда “прочие”. Всего и не предугадаешь. Математика — она большая, да…)
А зачем вообще делить задачи на какие-то группы?! Решай себе, да и дело с концом! А вот зачем. Дело всё в том, что для каждой группы текстовых задач существует своя ключевая формула для решения. Эта формула-ключ — едина для всей группы. Разумеется, за исключением задач из группы “Прочие”. Там свои порядки. Можно и вовсе без ключей обойтись, а может пригодиться и несколько ключей сразу. Всё от конкретной задачи зависит.
Что же такое формула-ключ? Это основная формула для решения задач из конкретной группы, которую надо знать железно! Ибо без этой формулы-ключа — никак. Причём никак от слова “совсем”… Зато с ключом — всё легко и просто! Зная формулу-ключ, вы будете в состоянии решать любые задачи из конкретной группы: простые, сложные — всякие! Заманчивая перспектива, правда?)
Как решать задачи из конкретной группы, подробно будет разобрано в соответствующих уроках. А в этом уроке мы с вами разберём самый общий принцип решения задач по математике любой группы. Краеугольный камень, если можно так выразиться. Который лежит в основе победы даже над самой-самой злой задачкой.)
Как решать текстовые задачи?
Так как же решать задачи?
Решение любой (да-да, именно любой!) текстовой задачи всегда состоит из двух основных этапов. На первом этапе надо по условию задачи составить уравнение (или систему уравнений). А на втором этапе надо это самое уравнение или систему (вы не поверите) решить.)
Как решать уравнения — переходим по ссылке и постигаем. А вот как составлять эти самые уравнения для любых текстовых задач по математике, этим мы займёмся прямо здесь и сейчас.
Как составить уравнение для задачи?
Рецепт здесь универсальный. Сначала (всегда!) определяем группу, к которой относится задача. Вспоминаем формулу-ключ для этой группы и записываем рядышком с условием. Пригодится.)
А вот дальше начинается самое интересное. Нам что нужно? Правильно, составить уравнение! Для составления уравнения надо что-то взять за икс. А вот дальше, читая задачу, делать с иксом все те действия, которые описаны в условии. При этом икс выступает как бы известной величиной. Вот в результате всего этого набора действий и получается уравнение.
Что же брать за икс? Этот момент — стратегический. Это самая важная часть решения любой текстовой задачи. Именно ответ на этот вопрос и является основной проблемой в решении текстовых задач. Ибо от удачного выбора того, что взять за икс, зависит и общий итог решения: получится/не получится. Многие ученики на этом вопросе решение задачи и заканчивают. А зря…
Возьмите за икс вопрос задачи!
Да-да! Вот, что спрашивают в задаче, то и берите за икс! Спрашивают, сколько километров проехал велосипедист? Вот и пишем: “Пусть велосипедист проехал х километров!” Сколько часов работал слесарь? Нет проблем! Слесарь работал х часов! Сколько килограммов золота в сплаве? Да х килограммов! И так далее…
Всегда ли такой выбор икса срабатывает? В подавляющем большинстве текстовых задач — да. Разумеется, думать головой никто не отменял, да.) Иногда вопрос простой, но за икс никак не берётся. Например, в задаче могут фигурировать Саша, Петя и Вася. Допустим, они занимаются чем-то полезным (скажем, красят забор). Даны все соотношения, но вопрос задачи поставлен так: “Кто из мальчиков красит быстрее всех?”
И что? Как нам такой вопрос за икс брать? Никак. В таких случаях приходится брать за икс что-нибудь конкретное. Производительность Саши, например. Вычислить все остальные производительности, а затем дать и окончательный ответ задачи.
Отсюда простое правило: если не знаете, что именно брать за икс — берите вопрос задачи! Чаще всего этого вполне достаточно. Что-то не срастается — не беда. Делаем вторую попытку, пробуем брать за икс другую величину, третью… Подбираем варианты как ключики к замку. Что-то да сработает!
Кстати, это относится не только к текстовым задачам, а ко всей математике вообще. Кто пробует, у того и получается. Рано или поздно, но — получается! А вот кто не пробует, тому ничего и не светит. Увы…
Учимся составлять уравнения!
Итак, для составления уравнения нам нужно просто перевести условие задачи из текста в формулы. Допустим, мы определились и что-то выбрали за икс. Удачно, неудачно — неважно. Выясним при составлении уравнения для задачи. Кстати, эта увлекательная процедура (перевод словесного описания задачи в математическую форму) носит название составление математической модели задачи.
Что же нам делать с иксом-то? Ну выбрали и выбрали — и что из этого?
А вот что. Как только мы что-то выбрали за икс, с этого момента наш икс становится как бы известной величиной. Да! Именно так. Покажу на конкретном примере, как это выглядит. Ибо, как говорится, лучше один раз увидеть, чем сто раз услышать, да…)
Итак, задачка:
Настя пошла в магазин за продуктами и купила батон хлеба, пакет молока и пачку масла, а на оставшиеся деньги купила мороженое. На молоко Настя потратила на 20 рублей меньше, чем на масло, но на 50 рублей больше, чем на хлеб. За мороженое Настя заплатила 40 рублей, а все продукты обошлись Насте в 250 рублей. Сколько стоит молоко?
Что, круто, да?)
Ничего не боимся и работаем строго по этапам. Первым этапом определяем группу, к которой относится задача. Движение есть? Нет его. Работы тоже нет. Да и процентами, к счастью, не пахнет. Значит, задача из группы “прочие”. Стало быть, никаких формул-ключей применять не надо.
Вторым этапом выбираем, что взять за икс. Думаем, прикидываем и так и сяк, а потом просто машем рукой и пишем вопрос задачи:
Пусть молоко стоит х рублей.
Ну вот. Начало положено. А теперь внимательно читаем условие задачи ещё раз и выкачиваем из текста всю ценную информацию. Первое предложение никакой математической нагрузки не несёт. Зато во втором предложении натыкаемся на слова: “На молоко Настя потратила на 20 рублей меньше, чем на масло…”
А вот эту фразу уже можно в дело пустить! Напоминаю, что икс (стоимость молока) мы считаем как бы известной величиной. С которой можно делать всё что угодно. Вот о чём говорится в задаче, то и делаем! Раз нам сказано, что на молоко Настя потратила на 20 рублей меньше, чем на масло, то сколько же она потратила на масло? Правильно! На 20 рублей больше, чем на молоко (х рублей)! То есть (х+20) рублей.
Вот и пишем:
х+20 — стоимость масла.
Отлично! Процесс идёт.) Читаем условие дальше: “…, но на 50 рублей больше, чем на хлеб.” Стоп! Это важно. Можно записать стоимость хлеба. Ведь стоимость молока нам как бы известна! Это икс рублей. А хлеб на 50 рублей дешевле.
Записываем:
х-50 — стоимость хлеба.
Вот и ещё одну величину скачали и перевели из текста в математику. Читаем внимательно дальше. Мороженое пока что никак в нашу модель не вписывается, ну и ладно. Его учтём в самом конце. А вот следующие слова: “… все продукты обошлись Насте в 250 рублей.” – сразу ставят всё на свои места! Ведь у нас все продукты уже записаны: и хлеб, и молоко, и масло! Сложим всё вместе, да мороженку-то не забываем:
(х-50) + х + (х+20) + 40 = 250
Всё! Уравнение составилось и записалось само собой.)
Решаем этого монстра и получаем:
х = 80
Это и есть ответ. Молоко стоит 80 рублей.
Что, примитивная задачка? Что ж, можно и усложнить. Задать вопрос по-другому. Например, так: “На сколько рублей молоко дороже мороженого?”
“А чего тут думать-то?” — спросите вы… На 40 рублей, конечно же!
Согласен, элементарно… когда задача уже решена. Для молока. А если не решена? Что тогда брать за икс? Вопрос задачи? Не канает! По той простой причине, что этот вопрос — разницу в цене — никуда не пристегнёшь. Ничего у нас не запишется, уравнение не составится…
Здесь как раз тот самый случай, когда вопрос задачи не годится в качестве икса. Что делать? Да просто взять за икс что-нибудь конкретное! Не обязательно брать именно молоко, можно хлеб, например. Решить задачу для хлеба, отыскать все остальные цены, а уж потом и нужную разницу в цене сосчитать.
Кроме того, такая постановка вопроса — наглядный пример той ситуации, когда выбранный икс (неважно, молоко это, хлеб, масло…) не будет служить ответом на вопрос задачи! Да-да! Многие про эту фишку забывают, записывают радостно найденный икс в ответ и… все труды идут коту под хвост… Посему железно запомните элементарное, но глобальное правило:
Перед записью окончательного ответа ещё раз прочитайте условие задачи! Это гарантированная защита от очередного источника досадных ошибок.
Выполняйте это простое правило всегда, в любых заданиях, на автомате! И не только в текстовых задачах. Пять секунд – и вы спасены от дурацких и обидных ляпов на 100%.
Итак, вот он, универсальный алгоритм решения любых текстовых задач:
1. Определяем, к какой группе относится задача. Вспоминаем формулу-ключ для этой группы и записываем рядышком с условием на всякий случай.
2. Вводим неизвестную величину. Для этого выбираем, что взять за икс. Если с выбором сложности, то берём за икс вопрос задачи. Чаще всего этого достаточно.
3. Используя формулу-ключ (или здравый смысл и житейскую логику), переводим текст задачи в математическую форму, считая икс как известную величину. Расписываем все остальные величины через икс и строим математическую модель задачи. Или, что то же самое, составляем уравнение. Если что-то не стыкуется, то, скорее всего, выбор икса неудачный. Пробуем выбрать другую величину, третью…
4. Записываем уравнение и решаем его. Находим икс.
5. Читаем ещё раз условие! Чего спрашивают-то… Используя найденный икс, отвечаем на нужный вопрос задачи и записываем окончательный ответ.
Специально ещё раз заостряю ваше внимание на самом последнем пункте. Забывают про него частенько. А потом начинают на себе волосья драть, подавать необоснованные жалобы, апелляции за вполне заслуженно сниженные баллы на ЕГЭ или ОГЭ…
Ну что, я считаю, что пришла пора потренироваться в составлении уравнений для простеньких задачек! А вы что думаете?) Сразу обрадую, что никаких специальных формул-ключей здесь применять не надо, достаточно расписать условие, составить математическую модель и… готово дело.) Но вынужден и огорчить: в каких-то задачах хорошо брать за икс сам вопрос, а в каких-то нет. Тут уж вы сами.)
Решите задачи:
1. Турист путешествует пешком по Карелии, по болотам и тайге, и за три дня одолел целых 100 км! В первый день он прошёл на 5 км меньше, чем во второй, но на 10 км больше, чем в третий. Сколько километров прошёл турист в первый день?
2. У кассира набралось мелочи на общую сумму 800 рублей, состоящую из рублёвых, двухрублёвых, пятирублёвых и десятирублёвых монеток. Известно, что пятирублёвых монет было в два раза больше, чем десятирублёвых, но на 20 меньше, чем двухрублёвых, а количество рублёвых монет было 40 штук. Сколько всего монет у кассира?
3. У Ани день рождения! Такое радостное событие Аня решила отметить в хорошем ресторане. Внимательно изучив меню, на первое Аня заказала себе суп-пюре из шампиньонов, на второе — спагетти с морепродуктами, на десерт — торт “Тирамису”, а в качестве напитка — безалкогольный мохито. Попраздновав от души, Аня отдала 1500 рублей официанту, после чего, попрощавшись и не беря сдачи, довольная покинула ресторан. Сколько стоит самое дорогое блюдо, если известно, что:
1) Тирамису на 100 рублей дороже супа-пюре, но на 120 рублей дешевле спагетти, а мохито дешевле спагетти в 2,5 раза?
2) Добровольные чаевые официанту за безупречное обслуживание составили 140 рублей.
Ответы (в беспорядке): 210; 500; 35.
Ну а где километры, монеты, рубли — это уж вы сами как-нибудь…)
Определение
текстовой задачи.
Математические
задачи, в которых есть хотя бы один
объект, являющийся
реальным предметом, принято называть
текстовыми
{сюжетными, практическими, арифметическими
и
т.д.). Перечисленные
названия берут начало от способа записи
(задача представлена в виде текста),
сюжета (описываются реальные объекты,
явления, события), характера математических
выкладок (устанавливаются
количественные отношения между значениями
некоторых
величин, связанные чаще всего с
вычислениями). В последнее время
наиболее распространенным является
термин «текстовая задача».
Текстовой
задачей как
правило, называется описание некоторой
ситуации
(явления, процесса) на естественном и
(или) математическом
языке с требованием либо дать количественную
характеристику
какого-то компонента этой ситуации
(определить числовое значение некоторой
величины по известным числовым значениям
других величин и зависимостям между
ними), либо установить наличие
или отсутствие некоторого отношения
между ее компонентами или определить
вид этого отношения, либо найти
последовательность
требуемых действий.
Придерживаясь
современной терминологии, можно сказать,
что
текстовая задача представляет собой
словесную
модель ситуации,
явления, события, процесса и т.п. Как в
любой модели, в текстовой
задаче описывается не все событие или
явление, а лишь его
количественные и функциональные
характеристики. Основная
особенность текстовых задач состоит в
том, что в них не
указывается прямо, какое именно действие
(или действия) должно
быть выполнено для получения ответа на
требование задачи.
Виды текстовых
задач.
Множество
задач, в которых имеется одинаковая
зависимость между величинами, входящими
в эти задачи, при возможном различии
их числовых данных и фабул образуют
определенный вид задач.
Задачи
одного вида имеют одну и ту же алгебраическую
модель.
Положив в основание классификации
способы решения задач,
можно выделить такие группы задач:
-
задачи на тройное
правило; -
задачи на нахождение
неизвестных по результатам действий; -
задачи на
пропорциональное деление; -
задачи на исключение
одного из неизвестных; -
задачи на среднее
арифметическое; -
задачи на проценты
и части; -
задачи на движение;
-
задачи,
решаемые с конца, или «обратным ходом»,
и
т.д.
Можно
рассмотреть и следующую классификацию
задач: задачи на движение, задачи на
работу, задачи на проценты и части,
задачи на концентрацию, логические
задачи и т.д.
Методы решения
текстовых задач.
Существуют
различные методы решения текстовых
задач: арифметический,
алгебраический, геометрический,
логический, практический
и др. В основе каждого метода лежат
различные виды математических моделей.
Например, при алгебраическом методе
решения задачи составляются уравнения
или неравенства,
при геометрическом — строятся диаграммы
или графики. Решение
задачи логическим методом начинается
с составления алгоритма.
Следует
иметь в виду, что практически каждая
задача в рамках выбранного
метода допускает решение с помощью
различных моделей. Так, используя
алгебраический метод, ответ на требование
одной и той же задачи можно получить,
составив и решив совершенно разные
уравнения, используя логический метод
— построив разные алгоритмы. Ясно,
что и в этих случаях мы также имеем дело
с различными методами решения конкретной
задачи, которые
(с целью избежать разночтения и
неоднозначность трактовки термина
«метод решения») будем называть способами
решения.
Арифметический
метод.
Решить
задачу арифметическим методом
— значит найти ответ на требование
задачи посредством выполнения
арифметических действий над числами.
Одну и ту же задачу
во многих случаях можно решить различными
арифметическими
способами. Задача считается решенной
различными способами,
если ее решения отличаются связями
между данными и искомыми, положенными
в основу решений, или последовательностью
использования этих связей.
Алгебраический
метод.
Решить
задачу алгебраическим методом — это
значит
найти ответ на требование задачи,
составив и решив уравнение
или систему уравнений (или неравенств).
Одну и ту же задачу
можно
также решить различными алгебраическими
способами.
Задача считается решенной различными
способами, если для
ее
решения составлены различные уравнения
или системы уравнений (неравенств), в
основе составления которых лежат
различные
соотношения между данными и искомыми.
Геометрический
метод.
Решить
задачу геометрическим методом — значит
найти ответ на требование задачи,
используя геометрические построения
или свойства геометрических фигур. Одну
и ту же задачу
можно
также решить различными геометрическими
способами.
Задача считается решенной различными
способами, если для ее решения
используются
различные построения или свойства
фигур.
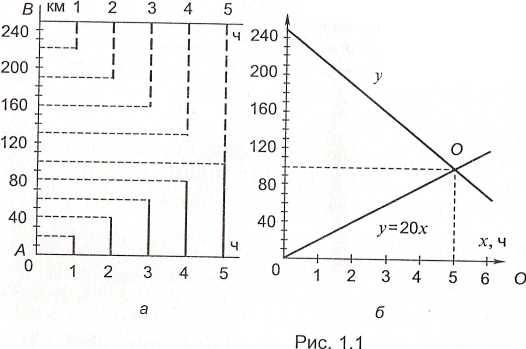
Задача:
Из двух городов Аи В, расстояние между
которыми 250 км, навстречу
друг другу выехали два туриста. Скорость
движения первого равна 20км/ч,
второго — 30 км/ч. Через сколько часов
туристы встретятся?
Решение:

способ. Математическую модель задачи
представим в виде диаграммы. Примем
длину одного отрезка по вертикали за
10 км, а длину одно
отрезка по горизонтали — за 1 ч. Отложим
на вертикальной прямой отрезок АВ,
равный 250 км. Он будет изображать
расстояние между городами. Для
удобства проведем еще одну ось времени
через точку В. Затем на вертикальных
прямых станем откладывать отрезки пути,
пройденные каждым туристом за 1 ч, 2
ч, 3 ч и т.д. (рис. 1.1, а). Из чертежа видим,
что через 5 ч они встретятся.
2-й способ. В
прямоугольной системе координат по
горизонтали отложим время движения (в
часах), по вертикали — расстояние (в
километрах).
Примем длину одного
отрезка по вертикали за 10 км, а длину
одного отрезка по горизонтали — за 1 ч.
Построим графики, характеризующие
движение каждого туриста. Движение
первого туриста определяется функцией
у = 20х, второго — у = 250 – 30х. Абсцисса
точки их пересечения (точки О) указывает,
через сколько часов туристы встретятся
(рис. 1.1, б). Из чертежа видно, что ее
значение равно 5. Ордината указывает,
на каком расстоянии от пункта А
произойдет встреча. Ее значение равно
100.

способ. Пусть время движения туристов
до встречи изображается отрезком ОТ, а
скорость сближения — отрезком OS (рис.
1.1, в). Тогда площадь S прямоугольника
OSO1Т (она равна OS∙ОТ) соответствует
расстоянию между городами А и В
(пройденный путь есть произведение
скорости движения на время движения).
Учитывая, что туристы сближаются каждый
час на 20 + 30 = 50 (км), расстояние между
городами равно 250 км, имеем уравнение
250 = 50 • ОТ, решив которое находим ОТ = 5
(ч). Итак, туристы встретятся через 5 ч.
Ответ: через 5 ч.
в
Логический
метод.
Решить
задачу логическим методом — это значит
найти ответ на требование задачи, как
правило, не выполняя
вычислений, а только используя логические
рассуждения. Примерами таких задач
могут служить задачи «на переправы»,
классическим
представителем которых является задача
о волке, козе и капусте,
или задачи «на взвешивание».
Практический
метод.
Решить
задачу практическим методом — значит
найти ответ на требование задачи,
выполнив практические
действия с предметами или их копиями
(моделями, макетами и
т.п.).
Иногда
в ходе решения задачи применяются
несколько методов:
алгебраический и арифметический;
геометрический, алгебраический
и арифметический; арифметический и
практический
и т.п. В этом случае считают, что задача
решается комбинированным
(смешанным) методом.
Методы
решения могут быть разными, но способ
решения, лежащий
в их основе,
может
быть один.
Этапы решения
текстовых задач.
Теперь
ознакомимся с этапами решения текстовых
задач.
Деятельность
по решению задачи включает следующие
этапы независимо
от выбранного метода решения:
-
Анализ содержания
задачи. -
Поиск пути решения
задачи и составление плана ее решения. -
Осуществление
плана решения задачи.
4.Проверка решения
задачи.
В
реальном процессе решения задачи
названные этапы не имеют четких
границ, и человек, решающий задачу, не
всегда выделяет
их в явном виде, переходя от одного к
другому незаметно для себя. Вместе с
тем решение каждой отдельно взятой
задачи обязательно
должно содержать все указанные этапы,
осмысленное прохождение
которых (вместе со знанием приемов их
выполнения) делает
процесс решения любой задачи осознанным
и целенаправленным,
а значит, более успешным. Игнорирование
одних этапов (например, поиска пути
решения) может привести к решению
методом «проб и ошибок», игнорирование
других (например,
проверки решения задачи) — к получению
неверного ответа и
т.д.
Рассмотрим
более подробно каждый этап решения
задачи.
1.
Анализ задачи.
Основное назначение этапа — осмыслить
ситуацию,
отраженную в задаче; выделить условия
и требования, назвать
данные и искомые, выделить величины и
зависимости между
ними (явные и неявные). На этом этапе
решения задачи можно
использовать такие приемы:
а) представление
той жизненной ситуации, которая описана
в
задаче;
б) постановка
специальных вопросов и поиск ответов
на них;
в) «переформулировка»
задачи;
г) моделирование
ситуации, описанной в задаче, с
помощью
реальных
предметов, предметных или графических
моделей и др.
Первый
прием —
представление той жизненной ситуации,
которая
описана в задаче, — выполняется фактически
при чтении или
слушании задачи. Вместе с тем мысленное
воспроизведение всех
объектов задачи и связей между ними
может проводиться и позже.
Цель такого воспроизведения — выявление
основных количественных и качественных
характеристик ситуации, представленной
в задаче.
Второй
прием — постановка
специальных вопросов и поиск ответов
на них — включает следующий «стандартный»
набор вопросов,
ответы на которые позволяют детально
разобраться в содержании
задачи:
-
О чем говорится
в задаче? -
Что известно в
задаче? -
Что требуется
найти в задаче? -
Что в задаче
неизвестно? и др.
Третий
прием — переформулировка
текста задачи — состоит в замене
данного в задаче описания некоторой
ситуации другим описанием,
сохраняющим все отношения, связи,
качественные характеристики,
но более явно их выражающим. Вся лишняя,
несущественная
информация при этом отбрасывается,
текст задачи преобразуется
в форму, облегчающую поиск пути решения.
В ходе переформулировки
выделяются основные ситуации, о которых
идет речь
в задаче, при необходимости строится
вспомогательная модель
задачи: краткая запись условия, таблица,
рисунок, чертеж,
диаграмма и т.п.
Моделирование
ситуации, описанной в задаче, с помощью
реальных
предметов, предметных моделей или
графических моделей является еще одним,
четвертым,
приемом
анализа задачи.
Вспомогательные
модели являются действенным средством
поиска
пути решения задачи и составления плана
ее решения.
2.
Поиск пути решения задачи и составление
плана ее решения.
Назначение
этапа — завершить установление связей
между данными и искомыми величинами
и указать последовательность использования
этих связей.
Проведя
анализ задачи, не всегда просто найти
путь ее решения.
Поиск пути решения задачи является
довольно трудным процессом,
для которого нет точного предписания.
Укажем некоторые
приемы, помогающие осуществлять этот
этап.
Одним
из приемов поиска пути решения задачи
является анализ задачи по тексту или
по ее вспомогательной модели. Поиск
пути
решения задачи можно осуществлять от
вопроса задачи к данным
(аналитический
путь) или
от данных к вопросу (синтетический
путь).
В
первом
случае
(аналитический
путь) на
основе анализа задачи
необходимо уточнить, что требуется
найти в задаче и определить,
что достаточно знать для ответа на этот
вопрос. Для этого следует
выяснить, какие из нужных данных есть
в условии задачи. Если
они (или одно из них) отсутствуют, надо
определить, что нужно
знать, чтобы найти недостающие данные
(или одно недостающее
данное), и т.д., пока для определения
очередного неизвестного
оба данных будут известны.
Во
втором случае (синтетический
путь) решающий
выделяет в тексте
задачи два каких-либо данных и на основе
связи между ними,
установленной при анализе, определяет,
какое неизвестное
может быть найдено по этим данным и с
помощью какого действия.
Затем, считая полученное число данным,
решающий
опять
выделяет два взаимосвязанных данных и
определяет, какое неизвестное может
быть найдено по ним и с помощью какого
действия,
и т.д., пока выполнение очередного
действия не приведет к определению
искомого.
При
решении задач анализ и синтез в
рассуждениях, как правило,
переплетаются. Осуществляя поиск пути
решения задачи синтетически,
анализ часто производят «про себя». В
то же время, каким бы приемом мы ни вели
поиск пути решения составной задачи,
ее предварительный анализ (хотя бы
подсознательный) неизбежен.
Еще
одним из приемов поиска пути решения
задачи является разбиение
задачи на смысловые части. Сущность
этой работы заключается в том, чтобы
научиться различать в данной задаче
отдельные, менее сложные задачи,
последовательное решение которых
позволяет получить ответ на требование
данной.
3.
Осуществление
плана решения задачи.
Назначение
этапа — найти
ответ на требование задачи. Немаловажную
роль при решении задач играет запись
найденного решения. Прежде всего,
остановимся на используемых сокращениях
при записи действий с именованными
числами. При записи именованных чисел,
выраженных в метрических мерах,
используются наименования, принятые в
международной системе единиц СИ,
например, «м» — метр, «км/ч» — километров
в час. Названия таких мер, как квадратный
метр, кубический метр, записываются
«м2»,
«м3».
Вес названия метрических мер, употребляемых
без чисел, выписываются полностью
словами, например: «сколько гектаров
земли…»,а не «сколько га земли…».
Принято названия метрических мер
выписывать полностью и в случае буквенной
символики, например, «а литров», «b
метров» и т.д. Однако часто этого не
делают, а используют более удобную
запись «х км/ч», «у м3»
и т.д. Что касается других наименований,
то здесь нет общеустановленных условных
обозначений. Вместе с тем, в последнее
время как правило вместо «руб.» принято
писать «р.», вместо «коп.» — «к.» и др.
Рассмотрим
пример на задаче, решаемой геометрическим
методом.
Геометрический
метод. Осуществление
плана решения задачи выполняется
письменно. Обычно в этом случае описывают
и выполняют построение графика или
диаграммы. Затем ответы на требование
задачи
считываются с чертежа (если используется
конструктивный прием) или находятся в
результате аналитического решения
задачи (если
используется графико-вычислительный
прием).
Задача:
Имеются
два сплава золота и серебра; в одном
количество этих металлов находится
в отношении 2 : 3, в другом — в отношении
3:
7. Сколько нужно взять каждого сплава,
чтобы получить 8 кг нового сплава,
в котором золото и серебро были бы в
отношении 5:11?
Решение:
Математическую модель задачи представим
в виде диаграммы
(рис. ниже). По горизонтали будем
откладывать массу сплава (в килограммах),
по вертикали — число долей серебра в
сплаве.
Рассмотрим
вначале доли какого-либо одного металла
в сплаве, например
доли серебра. Серебро составляет 3/5
первого сплава, 7/10 второго и 11/16
искомого. Общий знаменатель этих дробей
— 80, Следовательно, на каждые 80 частей
в первом сплаве приходится 48 частей
серебра,
во втором — 56 частей, в искомом — 55
частей.
Проведем
горизонтальный отрезок АВ,
изображающий
8 кг (массу искомого сплава). По
вертикали для уменьшения размера
чертежа наносим на луче АС
деления,
начиная
не с нуля, а с 48 (48 — наименьшее число
долей серебра в сплавах). Соединяем
прямолинейным отрезком точки В
(8
кг) и С (56 долей серебра) и проводим через
точку с отметкой 55 горизонтальную
прямую
до пересечения с ВС
в
точке D,
а
через D
—
вертикальную прямую до
пересечения с АВ
в
точке Е.
Отрезки
АЕ
и
ЕВ
указывают
ответ: надо взять
1 кг первого сплава (отрезок АЕ)
и
7 кг второго сплава (отрезок ЕВ).
Ответ: 1 кг; 7кг.
А Е 2 4 6 8 х,кг
4.Проверка
решения задачи.
Назначение
этапа — установить, правильно
ли понята задача, и выяснить, не
противоречит ли полученный
ответ всем другим условиям задачи. Этот
этап является
обязательным при решении задач. Следует
помнить, что логичные
рассуждения на других этапах решения
задачи не гарантируют
правильности ее решения.
Проверку
решения задачи можно проводить
различными способами. Перечислим их.
I.
Установление соответствия между числами,
полученными в результате решения задачи
и данными в условии задачи.
-
Составление и
решение задачи, обратной данной. -
Решение задачи
различными способами.
IV.
Решение
задачи различными методами.
V.
Прикидка (грубая проверка).
Планирование
решения текстовых задач в
VII
– VIII
классах.
Решение
текстовых задач занимает в курсе алгебры
VII
– VIII
классов значительное место.
Авторы: Ю. Н.
Макарычев, Н. Г. Миндюк, К.И. Нешков, С. Б.
Суворова.
Алгебра
VII
кл.
Глава
I.
Выражения, тождества, уравнения. (45 + 8
на повторение)
Глава
II.Функции.
(33 + 10 на повторение)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #