Прежде чем разбираться, как решать квадратное неравенство,
давайте рассмотрим, какое неравенство называют квадратным.
Запомните!
![]()
Неравенство называют квадратным, если старшая (наибольшая) степень неизвестного «x»
равна двум.
Потренируемся определять тип неравенства на примерах.
| Неравенство | Тип |
|---|---|
|
x − 7 < 0
|
линейное |
| x2 + 5x ≥ 0 | квадратное |
| 2x − 7 > 5 | линейное |
| x2 + x − 12 ≤ 0 |
квадратное
|
Как решить квадратное неравенство
В предыдущих уроках мы разбирали, как решать
линейные неравенства.
Но в отличие от линейных неравенств квадратные решаются совсем иным образом.
Важно!

Решать квадратное неравенство таким же образом как и линейное нельзя!
Для решения квадратного неравенства используется специальный способ, который называется методом интервалов.
Что такое метод интервалов
Методом интервалов называют специальный способ решения квадратных неравенств. Ниже мы объясним, как использовать
этот метод и почему он получил такое название.
Запомните!
![]()
Чтобы решить квадратное неравенство методом интервалов нужно:
- перенести все члены неравенства в левую часть, так чтобы в правой остался только ноль;
- сделать так, чтобы при неизвестном «x2» стоял положительный коэффициент;
- приравнять левую часть неравенства к нулю и решить полученное квадратное уравнение;
- полученные корни уравнения разместить на числовой оси в порядке возрастания;
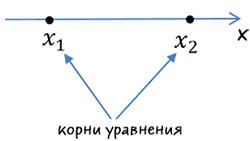
- нарисовать «арки» для интервалов. Справа налево,
начиная с «+», проставить чередуя знаки «+»
и «−»;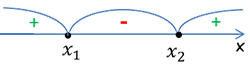
- выбрать необходимые интервалы и записать их в ответ.
Мы понимаем, что правила, описанные выше, трудно воспринимать только в теории, поэтому сразу рассмотрим пример решения
квадратного неравенства по алгоритму выше.
Требуется решить квадратное неравенство.
x2 + x − 12 < 0
Итак, согласно п.1 мы должны перенести
все члены неравенства в левую часть, так чтобы в правой остался только ноль.
В заданном неравенстве
«x2 + x − 12 < 0» ничего дополнительно делать не требуется,
так как в правой части и так уже стоит ноль.
Переходим к п.2. Необходимо сделать так, чтобы перед «x2»
стоял положительный коэффициент. В неравенстве
«x2 + x − 12 < 0»
при «x2» стоит положительный коэффициент «1»,
значит, снова нам ничего делать не требуется.
Согласно п.3 приравняем левую часть неравенства к нулю и решим полученное квадратное уравнение.
x2 + x − 12 = 0
x1;2 =
| −1 ± √12 − 4 · 1 · (−12) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
|
x1 = |
x2 = |
|
x1 = |
x2 = |
|
x1 = −4 |
x2 = 3 |
Теперь по п.4 отметим полученные корни на числовой оси в порядке возрастания.

Помните, что, исходя их того, какое перед нами неравенство (строгое или нестрогое) мы отмечаем точки на числовой оси
разным образом.
Теперь, как сказано в п.5, нарисуем «арки» над интервалами между отмеченными точками.

Проставим знаки внутри интервалов.
Справа налево чередуя, начиная с «+», отметим знаки.
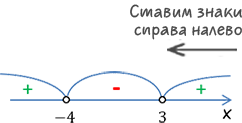
Нам осталось только выполнить пункт 6, то есть выбрать нужные интервалы и записать их в ответ.
Вернемся к нашему неравенству.
Так как в нашем неравенстве
«x2 + x − 12 < 0»,
значит, нам требуются отрицательные интервалы.
Заштрихуем все отрицательные области на числовой оси и выпишем их в ответ.

Отрицательным интервалом оказался лишь один, который находится между числами
«−4» и «3», поэтому
запишем его в ответ в виде двойного неравенства
−4 < x < 3.
Запишем полученный ответ квадратного неравенства.
Ответ: −4 < x < 3
Именно из-за того, что при решении квадратного неравенства мы рассматриваем интервалы между числами,
метод интервалов и получил свое название.
После получения ответа имеет смысл сделать его проверку, чтобы убедиться в правильности решения.
Выберем любое число, которое находится в заштрихованной области полученного ответа −4 < x < 3
и подставим его вместо «x» в исходное неравенство.
Если мы получим верное неравенство,
значит мы нашли ответ квадратного неравенства верно.
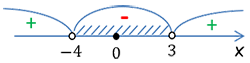
Возьмем, например, из интервала число «0». Подставим его в исходное неравенство
«x2 + x − 12 < 0».
x2 + x − 12 < 0
02 + 0 − 12 < 0
−12 < 0
(верно)
Мы получили верное неравенство при подстановке числа из области решений, значит ответ найден правильно.
Краткая запись решения методом интервалов
Сокращенно запись решения квадратного неравенства
«x2 + x − 12 < 0»
методом интервалов будет выглядеть так:
x2 + x − 12 < 0
x2 + x − 12 = 0
x1;2 =
| −1 ± √12 − 4 · 1 · (−12) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
|
x1 = |
x2 = |
|
x1 = |
x2 = |
|
x1 = −4 |
x2 = 3 |

Ответ: −4 < x < 3
Другие примеры решения квадратных неравенств
Рассмотрим решение других примеров квадратных неравенств. Требуется решить квадратное неравенство:
2x2 − x ≥ 0
В правой части неравенство уже стоит ноль. При «x2»
стоит «2» (положительный коэффициент), значит можно сразу переходить
к поиску корней.
2x2 − x ≥ 0
2x2 − x = 0
x1;2 =
| −(−1) ± √(−12) − 4 · 2 · 0 |
| 2 · 2 |
x1;2 =
x1;2 =
| x1 = |
x2 = |
| x1 = |
x2 = |
| x1 = |
x2 = 0 |
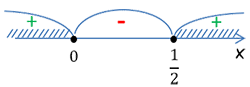
Ответ: x ≤ 0; x ≥
Рассмотрим пример, где перед «x2» в квадратном неравенстве стоит
отрицательный коэффициент.
−x2 − 3x + 4 ≥ 0
По п.2 общих правил решения методом интервалов нам нужно сделать так, чтобы
перед «x2» стоял положительный
коэффициент. Для этого умножим все неравенство на «−1».
−x2 − 3x + 4 ≥ 0 | ·(−1)
x2 + 3x − 4 ≤ 0
Можно переходить к п.4 и п.5. Приравняем левую часть неравенства к нулю и решим полученное квадратное уравнение.
Затем расположим полученные корни на числовой оси и проведем между ними «арки».
x2 + 3x − 4 ≤ 0
x2 + 3x − 4 = 0
x1;2 =
| −3 ± √32 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
|
x2 = |
x1 = |
|
x2 = |
x1 = |
| x2 = −4 | x1 = 1 |
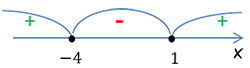
Важно!

При определении того какие интервалы нам нужно брать в ответ, исходить нужно из самого последнего изменения неравенства
перед нахождением его корней.
В нашем случае самая последняя версия неравенства перед поиском корней уравнения это
«x2 + 3x − 4 ≤ 0».
Значит для ответа нужно выбирать интервалы со знаком «−».
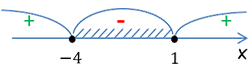
Ответ: −4 ≤ x ≤ 1
К сожалению, при решении квадратного неравенства не всегда получаются два корня и все идет по общему плану выше.
Возможны случаи, когда получается один корень или даже ни одного корня.
Как решить квадратные неравенства в таких случаях, мы разберем в следующем уроке
«Квадратные неравенства
с одним корнем или без корней».
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
5 апреля 2019 в 8:15
Gulnara Muslimova

Профиль
Благодарили: 0
Сообщений: 1

Gulnara Muslimova
Профиль
Благодарили: 0
Сообщений: 1
Помогите решить неравенство (желательно подробно и с пояснениями):
(x2+3x+3)x^2 -1<(8x-3)x^2 -1
0
Спасибо
Ответить
6 апреля 2019 в 16:12
Ответ для Gulnara Muslimova
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Логарифмируем
ac < bc <=> c·ln(a/b) < 0
и метод интервалов.
0
Спасибо
Ответить
15 сентября 2018 в 22:11
Vlad Lukashenok

Профиль
Благодарили: 0
Сообщений: 1

Vlad Lukashenok
Профиль
Благодарили: 0
Сообщений: 1
Решите неравенство:
x · sin2(πx)>=0
0
Спасибо
Ответить
17 сентября 2018 в 23:05
Ответ для Vlad Lukashenok
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
x = k ∈ Ζ; x > 0.
0
Спасибо
Ответить
Продолжим разбираться с решением неравенств.
В прошлой статье подробно рассмотрели решение линейных неравенств.
Какие неравенства называют квадратными?
Это неравенства, содержащие в левой части квадратный трехчлен, а в правой – “0”
Где, a≠0. Т.к. при a=0 получим конечно же линейное неравенство.
Напомню, неравенство, содержащее знак “><” называется строгим, содержащее “≥≤” – нестрогим.
Рассмотрим в качестве примера два неравенства.
1. Приводим к стандартному виду
Если первое неравенство в условии уже записано в стандартном виде (левая часть неравенства квадратный трехчлен, правая част – нуль), то второе неравенство необходимо привести к такому виду.
2. Находим корни уравнения, полученного приравниванием левой части нулю
Тут на дзене возникал вопрос про “корни”.
Нахождение корней уравнения и извлечение корня – это разные математические понятия. Так что не путайте !
Корень уравнения – это число, при подстановке которого в уравнение получается верное равенство.
Извлечение корня — это действие, обратное возведению в степень, с помощью которого по данной степени и по данному показателю степени находят основание степени.
Будем искать КОРЕНЬ УРАВНЕНИЯ, т.е. число при котором левая часть окажется равна нулю. Обычно пользуются формулами или подбором корней по обратной теореме Виета.
Здесь покажу расчет по формулам.
3. Отмечаем найденные корни на числовой прямой
4. Проводим условно “параболу” через точки на прямой
Направление веток параболы определяется коэффициентом “а”, входящим в квадратный трехчлен левой части неравенства.
В первом неравенстве а=1>0,
во втором неравенстве а=-5<0.
5. Выбираем интервалы, являющиеся решением неравенства
Теперь еще раз посмотрим на знак неравенства. Если знак “меньше нуля”, то выбираем интервалы, где функция расположена ниже числовой прямой. Если знак “больше нуля”, то выбираем интервалы, где парабола находится выше числовой прямой.
6. Записываем ответ
А вот в какие скобки заключены интервалы кратко можно пояснить так:
“> → ○→(“
“≥→●→[“
Если вы знаете того, кто готовится к ОГЭ не забудьте поделиться с ним этой информацией. Всегда пригодится.
Продолжение следует…
Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность
(✿◠‿◠)
В данном разделе мы собрали информацию о квадратных неравенствах и основных подходах к их решению. Закрепим материал разбором примеров.
Что представляет собой квадратное неравенство
Давайте посмотрим, как по виду записи различать неравенства различных видов и выделять среди них квадратные.
Квадратное неравенство – это такое неравенство, которое имеет вид a·x2+b·x+c<0, где a, b и c – некоторые числа, причем a не равно нулю. x – это переменная, а на месте знака < может стоять любой другой знак неравенства.
Вторым названием квадратных уравнений является название «неравенства второй степени». Объяснить наличие второго названия можно следующим образом. В левой части неравенства находится многочлен второй степени – квадратный трехчлен. Применение к квадратным неравенствам термина «квадратичные неравенства» некорректен, так как квадратичными являются функции, которые задаются уравнениями вида y=a·x2+b·x+c.
Приведем пример квадратного неравенства:
Возьмем 5·x2−3·x+1>0. В этом случае a=5, b=−3 и c=1.
Или вот такое неравенство:
−2,2·z2−0,5·z−11≤0, где a=−2,2, b=−0,5 и c=−11.
Покажем несколько примеров квадратных неравенств:
Здесь коэффициенты этого квадратного неравенства есть ; 123·x2-x+57<0, в этом случае a=123, b=-1, c=57.
Особое внимание нужно обратить на тот факт, что коэффициент при x2 считается неравным нулю. Объясняется это тем, что иначе мы получим линейное неравенство вида b·x+c>0, так как квадратная переменная при умножении на ноль сама станет равной нулю. При этом, коэффициенты b и c могут быть равны нулю как вместе, так и по отдельности.
Пример такого неравенства x2−5≥0.
Способы решения квадратных неравенств
Основным метода три:
- графический;
- метод интервалов;
- через выделение квадрата двучлена в левой части.
Графический метод
Метод предполагает проведение построения и анализа графика квадратичной функции y=a·x2+b·x+c для квадратных неравенств a·x2+b·x+c<0 (≤, >, ≥). Решением квадратного неравенства являются промежутки или интервалы, на которых указанная функция принимает положительные и отрицательные значения.
Метод интервалов
Решить квадратное неравенство с одной переменной можно методом интервалов. Метод применим для решения любого вида неравенств, не только квадратных. Суть метода в том, чтобы определить знаки промежутков, на которые разбивается ось координат нулями трехчлена a·x2+b·x+c при их наличии.
Для неравенства a·x2+b·x+c<0 решениями являются промежутки со знаком минус, для неравенства a·x2+b·x+c>0, промежутки со знаком плюс. Если мы имеем дело с нестрогими неравенствами, то решением становится интервал, который включает точки, которые соответствуют нулям трехчлена.
Выделение квадрата двучлена
Принцип выделения квадрата двучлена в левой части квадратного неравенства состоит в выполнении равносильных преобразований, которые позволяют перейти к решению равносильного неравенства вида (x−p)2<q (≤, >, ≥), где p и q – некоторые числа.
Неравенства, сводящиеся к квадратным
К квадратным неравенствам с помощью равносильных преобразований можно прийти от неравенств других видов. Сделать это можно разными способами. Например, перестановкой в данном неравенства слагаемых или переносом слагаемых из одной части в другую.
Приведем пример. Рассмотрим равносильное преобразование неравенства 5≤2·x−3·x2. Если мы перенесем все слагаемые из правой части в левую, то получим квадратное неравенство вида 3·x2−2·x+5≤0.
Необходимо найти множество решений неравенства 3·(x−1)·(x+1)<(x−2)2+x2+5.
Решение
Для решения задачи используем формулы сокращенного умножения. Для этого соберем все слагаемые в левой части неравенства, раскроем скобки и приведем подобные слагаемые:
3·(x−1)·(x+1)−(x−2)2−x2−5<0, 3·(x2−1)−(x2−4·x+4)−x2−5<0, 3·x2−3−x2+4·x−4−x2−5<0, x2+4·x−12<0.
Мы получили равносильное квадратное неравенство, которое можно решить графическим способом, определив дискриминант и точки пересечения.
D’=22−1·(−12)=16, x1=−6, x2=2
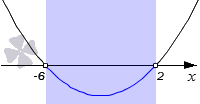
Построив график, мы можем увидеть, что множеством решений является интервал (−6, 2).
Ответ: (−6, 2).
Примером неравенств, которые часто сводятся к квадратным, могут служить иррациональные и логарифмические неравенства. Так, например, неравенство 2·x2+5<x2+6·x+14
равносильно квадратному неравенству x2−6·x−9<0, а логарифмическое неравенство log3(x2+x+7)≥2 – неравенству x2+x−2≥0.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c < 0 a x 2 + b x + c ≤ 0 где a, b, c – некоторые числа, причем a ≠ 0, x – переменная.
Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.
Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения.
Алгоритм решения квадратного неравенства методом интервалов
- Решить уравнение a x 2 + b x + c = 0 и найти корни x 1 и x 2 .
- Отметить на числовой прямой корни трехчлена.
Если знак неравенства строгий > , < , точки будут выколотые.

Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).

- Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A) и подставить её значение в выражение a x 2 + b x + c вместо x.
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

- Выбрать подходящие интервалы (или интервал).
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.
Если знак неравенства < или ≤ в ответ выбираем интервалы со знаком -.
- Записать ответ.
Примеры решения квадратных неравенств:
№1. Решить неравенство x 2 ≥ x + 12.
№2. Решить неравенство − 3 x − 2 ≥ x 2 .
№3. Решить неравенство 4 < x 2 + 3 x .
№4. Решить неравенство x 2 − 5 x < 6.
№5. Решить неравенство x 2 < 4.
№6. Решить неравенство x 2 + x ≥ 0.
Квадратными неравенствами называют неравенства, которые можно привести к виду (ax^2+bx+c) (⋁) (0), где (a),(b) и (с) – любые числа (причем (a≠0)), (x) – неизвестная переменная, а (⋁) – любой из знаков сравнения ((>),(<),(≤),(≥)).
Проще говоря, такие неравенства выглядят как квадратные уравнения, но со знаком сравнения вместо знака равно.
Примеры:
(x^2+2x-3>0)
(3x^2-x≥0)
((2x+5)(x-1)≤5)
Как решать квадратные неравенства?
Квадратные неравенства обычно решают методом интервалов. Ниже приведен алгоритм, как решать квадратные неравенства с дискриминантом больше нуля. Решение квадратных неравенств с дискриминантом равным нулю или меньше нуля – разобраны отдельно.
-
Приведите неравенство к виду (ax^2+bx+c⋁0).
Примеры:(x^2-6x-16<0) (-9x^2+x+8≤0)
-
Разложите выражение слева на множители. Для этого приравняйте его к нулю и решите получившееся уравнение, найдя корни (x_1) и (x_2). Затем запишите исходное выражение в виде (a(x-x_1 ) (x-x_2 )) Подробнее об этом можно почитать здесь.
(x^2-6x-16=0) (-9x^2+x+8=0)
(D=36-4 cdot 1 cdot (-16)=100=10^2) (D=1-4 cdot (-9) cdot 8=289)
(x_1=frac{6-10}{2}=-2) (x_1=frac{-1+17}{-18}=frac{16}{-18}=-frac{8}{9}) (x_2=frac{6+10}{2}=8) (x_2=frac{-1-17}{-18}=frac{-18}{-18}=1)
((x-8)(x+2)<0) (-9(x+frac{8}{9})(x-1)≤0) -
Начертите числовую ось и отметьте на ней найденные корни. Если неравенство строгое (со знаком (<) или (>)) то точки должны быть выколоты, если неравенство нестрогое (со знаком (≤) или (≥)), то точки должны быть закрашены.


-
Нанесенные корни разбивают числовую ось на несколько интервалов.
В первом справа интервале поставьте:
(-) знак плюс если перед скобками ничего не стоит или стоит положительное число
(-) знак минус если перед скобками стоит знак минус.
В следующих за ним интервалах поставьте чередующиеся знаки.

-
Заштрихуйте подходящие интервалы, то есть числовые промежутки:
(-) со знаком «(+)», если в неравенстве стояло «(>0)» или «(≥0)»
(-) со знаком «(-)», если в неравенстве стояло «(<0)» или «(≤0)»

-
Выпишите в ответ те интервалы, которые вы заштриховали.
Внимание! При строгих знаках неравенства ((<) или (>)) границы интервала НЕ ВХОДЯТ в решение, при этом в ответе сам интервал записывается в виде ((x_1;x_2)) – скобки круглые. При нестрогих знаках неравенства ((≤) или (≥)) – границы интервала ВХОДЯТ в решение, и ответ записывается в виде ([x_1;x_2]), с квадратными скобками на точках.Ответ: ((-2;8)) Ответ: ((-∞;frac{8}{9}]∪[1;∞))
Пример. Решите квадратное неравенство (frac{x^2}{5}+frac{2x}{3})(≥) (frac{8}{15})
Решение:
|
(frac{x^2}{5}+frac{2x}{3})(≥) (frac{8}{15}) |
Чтобы избавиться от дробей, умножим обе части неравенство на (15). |
|
|
(3x^2+10x≥8) |
Перенесем (8) влево. |
|
|
(3x^2+10x-8≥0) |
Вот мы и привели неравенство к виду (ax^2+bx+c⋁0). Запишем квадратное уравнение вида (ax^2+bx+c=0). |
|
|
(3x^2+10x-8=0) |
Решим полученное квадратное уравнение. |
|
|
(D=100+4⋅3⋅8=196=14^2) |
Когда корни найдены, запишем неравенство в разложенном на множители виде. |
|
|
(3(x+4)(x-frac{2}{3})≥0) |
Теперь начертим числовую ось, отметим на ней корни и расставим знаки на интервалах. |
|

|
Выпишем в ответ интересующие нас интервалы . Так как знак неравенства (≥), то нам нужны интервалы со знаком (+), при этом сами корни мы включаем в ответ (скобки на этих точках – квадратные). |
Ответ: (x∈(-∞;-4]∪[ frac{2}{3};∞))
Квадратные неравенства с отрицательным и равным нулю дискриминантом
Алгоритм выше работает, когда дискриминант больше нуля, то есть квадратный трехчлен имеет (2) корня. Что делать в остальных случаях? Например, таких:
|
(1) x^2+2x+9>0) |
(2) x^2+6x+9≤0) |
(3)-x^2-4x-4>0) |
(4) -x^2-64<0) |
|
(D=4-36=-32<0) |
(D=36-36=0) |
(D=16-16=0) |
(D=-4 cdot 64<0) |
Если (D<0), то квадратный трехчлен имеет постоянный знак, совпадающий со знаком коэффициента (a) (тем, что стоит перед (x^2)).
То есть, выражение:
(x^2+2x+9) – положительно при любых (x), т.к. (a=1>0)
(-x^2-64) – отрицательно при любых (x), т.к. (a=-1<0)
Если (D=0), то квадратный трехчлен при одном значении (x) равен нулю, а при всех остальных имеет постоянный знак, который совпадает со знаком коэффициента (a).
То есть, выражение:
(x^2+6x+9) – равно нулю при (x=-3) и положительно при всех остальных иксах, т.к. (a=1>0)
(-x^2-4x-4) – равно нулю при (x=-2) и отрицательно при всех остальных, т.к. (a=-1<0).
Как найти икс, при котором квадратный трехчлен равен нулю? Нужно решить соответствующее квадратное уравнение.
С учетом этой информации давайте решим квадратные неравенства:
|
1) (x^2+2x+9>0) |
Неравенство, можно сказать, задает нам вопрос: «при каких (x) выражение слева больше нуля?». Выше мы уже выяснили, что при любых. В ответе можно так и написать: «при любых (x)», но лучше туже самую мысль, выразить на языке математики. |
|
|
Ответ: (x∈(-∞;∞)) |
||
|
2) (x^2+6x+9≤0) |
Вопрос от неравенства: «при каких (x) выражение слева меньше или равно нулю?» Меньше нуля оно быть не может, а вот равно нулю – вполне. И чтобы выяснить при каком иске это произойдет, решим соответствующие квадратное уравнение. |
|
|
(x^2+6x+9=0) |
Давайте соберем наше выражение по формуле (a^2+2ab+b^2=(a+b)^2). |
|
|
((x+3)^2=0) |
Сейчас нам мешает только квадрат. Давайте вместе подумаем – какое число в квадрате равно нулю? Ноль! Значит, квадрат выражения равен нулю только если само выражение равно нулю. |
|
|
(x+3=0) |
Это число и будет ответом. |
|
|
Ответ: (-3) |
||
|
3)(-x^2-4x-4>0) |
Когда выражение слева больше нуля? Как выше уже было сказано выражение слева либо отрицательно, либо равно нулю, положительным оно быть не может. Значит ответ – никогда. Запишем «никогда» на языке математике, с помощью символа «пустое множество» – (∅). |
|
|
Ответ: (x∈∅) |
||
|
4) (-x^2-64<0) |
Когда выражение слева меньше нуля? Всегда. Значит неравенство выполняется при любых (x). |
|
|
Ответ: (x∈(-∞;∞)) |
Смотрите также:
Дробно-рациональные неравенства
