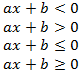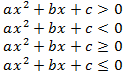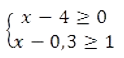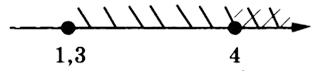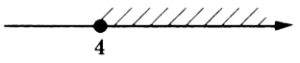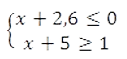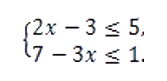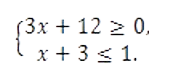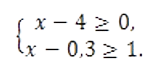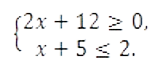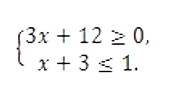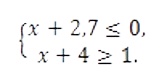Несмотря на то, что решение неравенств очень напоминает решение уравнений, все-таки неравенства вызывают у школьников больше затруднений.
Ученики часто спрашивают как решать неравенства те или иные, просят оценить решение неравенства, полученное у доски в школе или помочь в решении домашнего задания с неравенством. В основном они связаны не с решением неравенства как такового, а с проблемой записи решения и с проблемой знака неравенства, которое в определенные моменты заменяется на противоположный.
Решение неравенств – это материал, который помогает выявить у экзаменуемого сразу несколько умений и навыков: умение решать уравнения, работать со знаком неравенства, оценить полученное решение с точки зрения постановки неравенства. Поэтому неравенства включены в ОГЭ (ГИА).
Как решать простейшие неравенства из ОГЭ (ГИА)
Итак, первое неравенство:
3х-4<6x-6
Решаем неравенство как уравнение – перенесем все неизвестные в левую часть, а все числа – в правую. Неизвестные – это все выражения с х: 3х и 6х.
3х уже находится слева, а вот 6х – справа, и 6х мы перенесем в левую часть нашего неравенства. Не забываем, что когда мы переносим любые выражения и числа из одной части неравенства, как и равенства, в другую, то мы обязательно меняем знак. То есть слева у нас запишется:
3х-6х.
Что будет справа? Справа останется число -6 (со знаком минус), и еще мы перенесем 4 из левой части в правую. Перед четверкой в левой части неравенства стоит знак минус, значит, при переносе мы получим четверку со знаком +. Смотрите, что получилось:
3х-6х<-6+4
Упростим левую и правую части, получим:
-3х<-2
Если бы у нас вместо неравенства было уравнение: -3х=-2, то x мы бы нашли разделив -2 на -3. Точно также поступают и в неравенстве, но, помнят одно простое правило,
если мы делим или умножаем на отрицательное число (число со знаком минус), то знак неравенства меняется на противоположный.
То есть мы запишем решение нашего неравенства вот так:
Мы поменяли знак, так как делили на отрицательное число – -3. При этом знак бы не менялся, если бы мы делили отрицательное число на положительное. Знак неравенства меняется только тогда – когда отрицательным является число на которое делят или умножают.
Итак, ответ у нас будет таким:
.
Как решать нестрогое неравенство
Нестрогим неравенством называется неравенство, у которого вместо строгого знака “больше” или “меньше”, стоит знак “больше или равно” или “меньше или равно”. Например, давайте решим нестрогое неравенство. Возьмем простое неравенство, чтобы вы поняли суть вопроса.
Решаем аналогично – только сначала упростим правую часть нашего неравенства. Переносим неизвестные в левую часть неравенства, а известные (числа) в правую часть неравенства:
Упрощаем правую часть:
Посчитаем, получим:
Ответ: .
Обратите внимание на запись ответа. Так как у нас неравенство нестрогое, то число 2 будет входить в решение этого неравенства, поэтому мы его включаем в ответ, отмечая квадратной скобкой.
Вот так:
Решение неравенств из сборника ОГЭ по математике ФИПИ
Неравенство 1
Укажите решение неравенства
Решение:
Перенесем неизвестные в левую часть неравенства, а известные – в правую часть неравенства:
Посчитаем:
, отсюда
искомый интервал: . Таким образом, из списка предложенных интервалов нам подходит интервал под номером 2.
Ответ 2.
Неравенство 2
Укажите множество решений неравенства:
Решение:
Как обычно, переносим неизвестные влево от знака неравенства, а известные величины – вправо:
Обратите внимание – здесь мы делим отрицательное число. Но делим то мы его на положительное число 6. Поэтому знак неравенства остается прежним!
или
Нам подходит вариант решения 4.
Ответ: 4.
Неравенство 3
Укажите решение неравенства
Решение:
Подходит вариант решения 2.
Ответ: 2
Неравенство 4
Укажите множество решений неравенства
Решение:
Итак, решение неравенство иллюстрируется графиком 3.
Ответ: 3.
Теперь вы знаете, как решать неравенства, которые даны в части “Алгебра” ОГЭ (ГИА).
Решению неравенств посвящены два задания в ОГЭ по математике: в задании 7 (хотите повторить, читайте статью по ссылке) в основном применяются свойства неравенств, а уже в 13 задании нужно решить неравенство: линейное, квадратное, рациональное или систему неравенств.
Вообще решение неравенств — слабое место школьников, их часто путают с уравнениями — при решении заменяют вдруг знак неравенств на «=», либо, даже если решают правильно, не могут интерпретировать получившийся ответ, показать его на координатной прямой и т.д. В этой статье я напомню вам, как решаются линейные неравенства и их системы.
Прежде всего, вспомним 2 свойства числовых неравенств, которыми будем пользоваться:
1. Если обе части верного неравенства умножить или разделить на одно и то же положительное число, то получится верное неравенство.
2. Если обе части верного неравенства умножить или разделить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.
Пример 1.
Решение:
20 – 3(x – 5) ˂ 19 – 7x
Раскроем скобки в левой части неравенства:
20 – 3x + 15 ˂ 19 – 7x
Перенесём неизвестные слагаемые в одну часть неравенства, известные в другую, как и при решении уравнения, не забывая менять знаки при переносе:
– 3x + 7x ˂ – 20 – 15 + 19
4x ˂ – 16
x ˂ (– 16) : 4
x ˂ – 4
Осталось интерпретировать ответ. Лучше всего показать на числовой прямой:
Обращаю внимание, что неравенство строгое (˂, «меньше»), поэтому число (– 4) в наш промежуток не включается, и точка (– 4) на прямой не закрашена. Меньше (– 4), значит, решением неравенства будет являться множество чисел слева от (– 4) (на рис. показано штриховкой).
Решением неравенства будет интервал: (– ∞; – 4). Скобка у числа (–4) круглая. В ответе указываем номер правильного варианта. Это 4.
Ответ: 4.
Пример 2.
То же неравенство, что и в примере 1, только в качестве вариантов ответов представлены числовые прямые:
Здесь правильным будет ответ под номером 1.
Ответ: 1.
Пример 3.
Решение:
Задание сформулировано так, что прежде, чем решать неравенство, нужно его составить, часто этот шаг вызывает затруднения у школьников. Итак, составим неравенство:
6x – 2 > 7x + 8
Решаем так же, как и в примере 1:
6x – 7x > 8 + 2
– x > 10
!!!!! Вот здесь используем правило 2, приведённое в начале статьи: разделим обе части неравенства на (– 1), при этом знак неравенства изменится на противоположный.
x ˂ – 10.
В данном случае, варианты ответов представлены в виде неравенства, правильный вариант по номером 2.
Обратите внимание, что, если бы вы забыли поменять знак неравенства на противоположный и сделали ошибку, то вы бы нашли свой вариант ответа под номером 1. Не забывайте, что каждая ваша ошибка отражена в одном из вариантов ответа.
Ответ: 2.
Пример 4.
Решение:
Решить систему 2 неравенств — значит найти множество общих решений этих двух неравенств. Решаем пошагово каждое неравенство:
Осталось соединить решения на одной числовой прямой. Обращаю внимание, что оба неравенства нестрогие, обе точки будут закрашены на прямой и включаться в решения.
Оба числа отрицательные, поэтому необходимо определить какое из них больше (а, значит, расположено правее, ближе к 0).
На числовой прямой решение первого неравенство (множество чисел) показано красной штриховкой, второго — синей. Эти 2 множества пересекаются — их пересечение, т.е. общее решение показано розовым цветом. Это и есть решение системы: отрезок [– 4; – 13/5].
Правильный вариант ответа под номером 2.
Обращаю внимание, что под номером 1 — неправильный ответ, который вы могли бы получить, если бы неправильно определили взаимное расположение чисел на прямой. Как могли бы получиться другие варианты ответов — порассуждайте сами.
Ответ: 2.
Пример 5
Решение:
Ещё один вариант системы неравенств, которую решаем так же, как и предыдущую. Но по-другому сформулировано само задание, и вариантов ответов здесь нет. Но давайте сначала решим систему:
Итак, решением системы неравенств является множество чисел — отрезок [– 6; – 3].
Теперь вернёмся к вопросу задачи: найти наибольшее значение x, удовлетворяющее системе. Это значит, мы должны найти наибольшее x из отрезка [– 6; – 3]. Это число (– 3).
Ответ: – 3.
Надеюсь, мой, очень подробный разбор решения неравенств и систем неравенств, поможет вам при подготовке к экзамену. В следующей статье мы рассмотрим неравенства посложнее: квадратные.
Если найдёте ошибку или опечатку, пишите в комментариях, буду благодарна.
Автор: Чудневцева Ирина, координатор и соавтор канала Хакнем Школа.
Читайте нас также в телеграм — по этой ссылке
Другие статьи автора:
Другие статьи для подготовки к ОГЭ по математике, вы найдёте в подборке
Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Неравенства
Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:
> больше,
≥ больше или равно,
< меньше,
≤ меньше или равно,
то получится неравенство.
Линейные неравенства
Линейные неравенства – это неравенства вида:
a x < b a x ≤ b a x > b a x ≥ b
где a и b – любые числа, причем a ≠ 0, x – переменная.
Примеры линейных неравенств:
3 x < 5 x − 2 ≥ 0 7 − 5 x < 1 x ≤ 0
Решить линейное неравенство – получить выражение вида:
x < c x ≤ c x > c x ≥ c
где c – некоторое число.
Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.
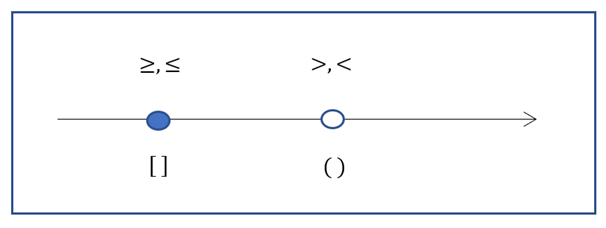
- Если знак неравенства строгий > , < , точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой.
Смысл выколотой точки в том, что сама точка в ответ не входит.
- Если знак неравенства нестрогий ≥ , ≤ , точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной.
Смысл жирной точки в том, что сама точка входит в ответ.
- Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.
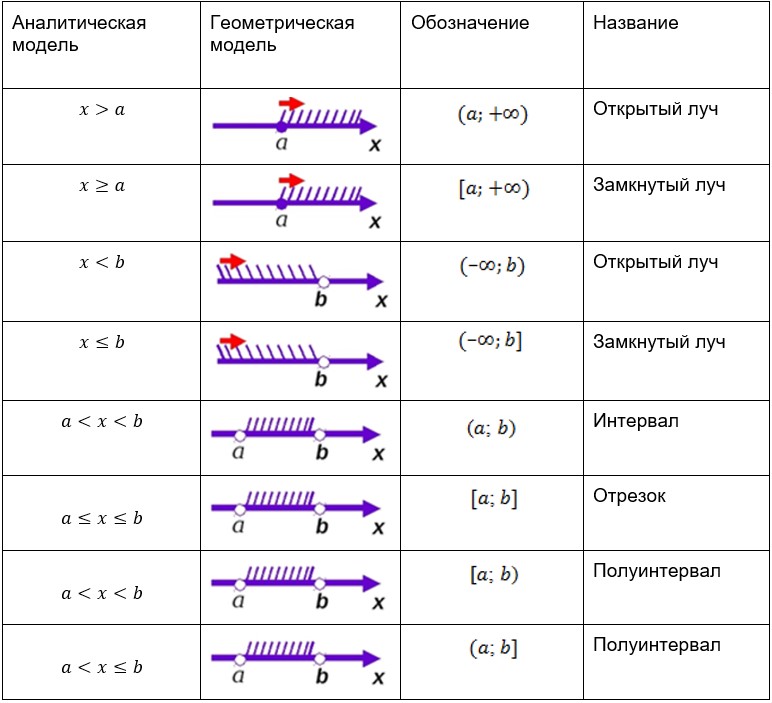
Таблица числовых промежутков
| Неравенство | Графическое решение | Форма записи ответа |
|---|---|---|
| x < c |
|
x ∈ ( − ∞ ; c ) |
| x ≤ c |
|
x ∈ ( − ∞ ; c ] |
| x > c |
|
x ∈ ( c ; + ∞ ) |
| x ≥ c |
|
x ∈ [ c ; + ∞ ) |
Алгоритм решения линейного неравенства
- Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов:
a x < b a x ≤ b a x > b a x ≥ b
- Пусть получилось неравенство вида a x ≤ b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.
- Если a > 0 то неравенство приобретает вид x ≤ b a .
- Если a < 0 , то знак неравенства меняется на противоположный, неравенство приобретает вид x ≥ b a .
- Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.
Примеры решения линейных неравенств:
№1. Решить неравенство 3 ( 2 − x ) > 18.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 − 3 x > 18
− 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 )
Делим обе части неравенства на (-3) – коэффициент, который стоит перед x. Так как − 3 < 0 , знак неравенства поменяется на противоположный. x < 12 − 3 ⇒ x < − 4 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x ∈ ( − ∞ ; − 4 )
№2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x + 4 ≥ 3 x + 3 − 14
6 x − 3 x ≥ 3 − 14 − 4
3 x ≥ − 15 | ÷ 3 Делим обе части неравенства на (3) – коэффициент, который стоит перед x. Так как 3 > 0, знак неравенства после деления меняться не будет.
x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x ∈ [ − 5 ; + ∞ )
Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).
Примеры:
№1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x − 1 ≤ 6 x − 1
6 x − 6 x ≤ − 1 + 1
0 ≤ 0
Получили верное неравенство, которое не зависит от переменной x. Возникает вопрос, какие значения может принимать переменная x, чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.
Ответ:
- x – любое число
- x ∈ ( − ∞ ; + ∞ )
- x ∈ ℝ
№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
x + 6 − 9 x > − 8 x + 48
− 8 x + 8 x > 48 − 6
0 > 42
Получили неверное равенство, которое не зависит от переменной x. Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ.
Ответ: x ∈ ∅
Квадратные неравенства
Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c < 0 a x 2 + b x + c ≤ 0 где a, b, c – некоторые числа, причем a ≠ 0, x – переменная.
Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.
Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).
Алгоритм решения квадратного неравенства методом интервалов
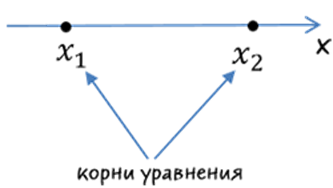
- Решить уравнение a x 2 + b x + c = 0 и найти корни x 1 и x 2 .
- Отметить на числовой прямой корни трехчлена.
Если знак неравенства строгий > , < , точки будут выколотые.
Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).
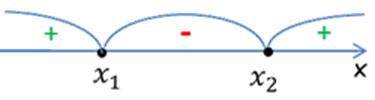
- Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A) и подставить её значение в выражение a x 2 + b x + c вместо x.
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
- Выбрать подходящие интервалы (или интервал).
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.
Если знак неравенства < или ≤ в ответ выбираем интервалы со знаком -.
- Записать ответ.
Примеры решения квадратных неравенств:
№1. Решить неравенство x 2 ≥ x + 12.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
x 2 ≥ x + 12
x 2 − x − 12 ≥ 0
x 2 − x − 12 = 0
a = 1, b = − 1, c = − 12
D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6. Подставляем эту точку в исходное выражение:
x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0
Это значит, что знак на интервале, в котором лежит точка 6 будет +.
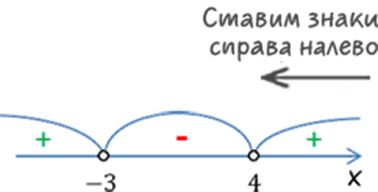
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪ .
Точки -3 и 4 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ )
№2. Решить неравенство − 3 x − 2 ≥ x 2 .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
− 3 x − 2 ≥ x 2
− x 2 − 3 x − 2 ≥ 0
− x 2 − 3 x − 2 = 0
a = − 1, b = − 3, c = − 2
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1
x 1 = − 2, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение:
− x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 < 0
Это значит, что знак на интервале, в котором лежит точка 0 будет − .
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервал со знаком +.
Точки -2 и -1 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ [ − 2 ; − 1 ]
№3. Решить неравенство 4 < x 2 + 3 x .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
4 < x 2 + 3 x
− x 2 − 3 x + 4 < 0
− x 2 − 3 x + 4 = 0
a = − 1, b = − 3, c = 4
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1
x 1 = − 4, x 2 = 1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение:
− x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 < 0
Это значит, что знак на интервале, в котором лежит точка 2, будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервалы со знаком − .
Точки -4 и 1 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ )
№4. Решить неравенство x 2 − 5 x < 6.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
x 2 − 5 x < 6
x 2 − 5 x − 6 < 0
x 2 − 5 x − 6 = 0
a = 1, b = − 5, c = − 6
D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1
x 1 = 6, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:
x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0
Это значит, что знак на интервале, в котором лежит точка 10 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервал со знаком -.
Точки -1 и 6 будут в круглых скобках, так как они выколотые
Ответ: x ∈ ( − 1 ; 6 )
№5. Решить неравенство x 2 < 4.
Решение:
Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.
x 2 < 4
x 2 − 4 < 0
x 2 − 4 = 0
( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2
x 1 = 2, x 2 = − 2
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3. Подставляем эту точку в исходное выражение:
x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0
Это значит, что знак на интервале, в котором лежит точка 3 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервал со знаком − .
Точки -2 и 2 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 2 ; 2 )
№6. Решить неравенство x 2 + x ≥ 0.
Решение:
Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0.
x 2 + x ≥ 0
x 2 + x = 0
x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1
x 1 = 0, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1. Подставляем эту точку в исходное выражение:
x 2 + x = 1 2 + 1 = 2 > 0
Это значит, что знак на интервале, в котором лежит точка 1 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ )
Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.
Дробно рациональные неравенства
Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:
f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).
Примеры дробно рациональных неравенств:
x − 1 x + 3 < 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3
Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.
Алгоритм решения дробно рациональных неравенств:
- Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):
f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
- Приравнять числитель дроби к нулю f ( x ) = 0. Найти нули числителя.
- Приравнять знаменатель дроби к нулю g ( x ) = 0. Найти нули знаменателя.
В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.
- Нанести нули числителя и нули знаменателя на ось x.
Вне зависимости от знака неравенства
при нанесении на ось x нули знаменателя всегда выколотые.
Если знак неравенства строгий,
при нанесении на ось x нули числителя выколотые.
Если знак неравенства нестрогий,
при нанесении на ось x нули числителя жирные.
- Расставить знаки на интервалах.
- Выбрать подходящие интервалы и записать ответ.
Примеры решения дробно рациональных неравенств:
№1. Решить неравенство x − 1 x + 3 > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравниваем числитель к нулю f ( x ) = 0.
x − 1 = 0
x = 1 – это ноль числителя. Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.
- Приравниваем знаменатель к нулю g ( x ) = 0.
x + 3 = 0
x = − 3 – это ноль знаменателя. При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0,
Это значит, что знак на интервале, в котором лежит точка 2 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.
Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )
№2. Решить неравенство 3 ( x + 8 ) ≤ 5.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Привести неравенство к виду f ( x ) g ( x ) ≤ 0.
3 ( x + 8 ) ≤ 5
3 ( x + 8 ) − 5 x + 8 ≤ 0
3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 x − 40 x + 8 ≤ 0
− 5 x − 37 x + 8 ≤ 0
- Приравнять числитель к нулю f ( x ) = 0.
− 5 x − 37 = 0
− 5 x = 37
x = − 37 5 = − 37 5 = − 7,4
x = − 7,4 – ноль числителя. Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.
- Приравнять знаменатель к нулю g ( x ) = 0.
x + 8 = 0
x = − 8 – это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 < 0
Это значит, что знак на интервале, в котором лежит точка 0 будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -.
В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.
Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )
№3. Решить неравенство x 2 − 1 x > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравнять числитель к нулю f ( x ) = 0.
x 2 − 1 = 0
( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1
x 1 = 1, x 2 = − 1 – нули числителя. Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.
- Приравнять знаменатель к нулю g ( x ) = 0.
x = 0 – это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )
Системы неравенств
Сперва давайте разберёмся, чем отличается знак { системы от знака [ совокупности. Система неравенств ищет пересечение решений, то есть те точки, которые являются решением и для первого неравенства системы, и для второго. Проще говоря, решить систему неравенств – это найти пересечение решений всех неравенств этой системы друг с другом. Совокупность неравенств ищет объединение решений, то есть те точки, которые являются решением либо для первого неравенства, либо для второго, либо одновременно и для первого неравенства, и для второго. Решить совокупность неравенств означает объединить решения обоих неравенств этой совокупности. Более подробно об этом смотрите короткий видео-урок.
Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.
Пример системы неравенств:
{ x + 4 > 0 2 x + 3 ≤ x 2
Алгоритм решения системы неравенств
- Решить первое неравенство системы, изобразить его графически на оси x.
- Решить второе неравенство системы, изобразить его графически на оси x.
- Нанести решения первого и второго неравенств на ось x.
- Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.
Примеры решений систем неравенств:
№1. Решить систему неравенств { 2 x − 3 ≤ 5 7 − 3 x ≤ 1
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x − 3 ≤ 5
2 x ≤ 8 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x ≤ 4 ;
Графическая интерпретация:
Точка 4 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
7 − 3 x ≤ 1
− 3 x ≤ 1 − 7
− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 < 0, знак неравенства после деления меняется на противоположный.
x ≥ 2
Графическая интерпретация решения:
Точка 2 на графике жирная, так как знак неравенства нестрогий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на отрезке от 2 до 4. Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные.
Ответ: x ∈ [ 2 ; 4 ]
№2. Решить систему неравенств { 2 x − 1 ≤ 5 1 < − 3 x − 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x − 1 ≤ 5
2 x ≤ 6 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x ≤ 3
Графическая интерпретация:
Точка 3 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
1 < − 3 x − 2
3 x < − 1 − 2
3 x < − 3 | ÷ 3 , поскольку 3 > 0, знак неравенства после деления сохраняется.
x < − 1
Графическая интерпретация решения:
Точка -1 на графике выколотая, так как знак неравенства строгий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая.
Ответ: x ∈ ( − ∞ ; − 1 )
№3. Решить систему неравенств { 3 x + 1 ≤ 2 x x − 7 > 5 − x
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
3 x + 1 ≤ 2 x
3 x − 2 x ≤ − 1
x ≤ − 1
Графическая интерпретация решения:
- Решаем второе неравенство системы
x − 7 > 5 − x
x + x > 5 + 7
2 x > 12 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x > 6
Графическая интерпретация решения:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.
Ответ: x ∈ ∅
№4. Решить систему неравенств { x + 4 > 0 2 x + 3 ≤ x 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
x + 4 > 0
x > − 4
Графическая интерпретация решения первого неравенства:
- Решаем второе неравенство системы
2 x + 3 ≤ x 2
− x 2 + 2 x + 3 ≤ 0
Решаем методом интервалов.
− x 2 + 2 x + 3 = 0
a = − 1, b = 2, c = 3
D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16
D > 0 – два различных действительных корня.
x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1
Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.
Графическая интерпретация решения второго неравенства:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪ .
Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные.
Ответ: x ∈ ( − 4 ; − 1 ] ∪ [ 3 ; + ∞ )
Скачать домашнее задание к уроку 8.
Краткий ответ, к ак решать задания на неравенства из ОГЭ по математике
Для того чтобы научиться решать задания экзамена ОГЭ, где встречаются линейные неравенства и их системы, следует основательно знать теорию. А именно – основные понятия, обозначения и правила преобразования неравенств.
Задание 20 ОГЭ математика линейные неравенства – теория
Линейными неравенствами называются неравенства вида:
где a и b — любые числа, причем a≠0, x – неизвестная переменная.
Обозначения на координатной прямой и в записи ответа в виде множества:
Сводная таблица числовых промежутков
Правила преобразования неравенств – задание 20 ОГЭ математика
Правило 1. Любой член неравенства можно переносить из одной части неравенства в другую, меняя при этом знак на противоположный (т.е. при переносе через знак неравенства знаки при слагаемых меняются на противоположные, как в уравнении).
Правило 2. Обе части неравенства можно умножить/разделить на одно и то же положительное число, при этом получится неравенство, равносильное данному.
Правило 3. Обе части неравенства можно умножить/разделить на одно и то же отрицательное число, меняя знак неравенства на противоположный (т.е. знак > на знак < и наоборот; знак ≥ на знак ≤ и наоборот).
Пример
Укажите решение неравенства:
Решение
Для решения линейного неравенства достаточно выполнить действия, аналогичные действию решений линейных уравнений. Однако, в отличие от линейных уравнений, следует проявлять внимательность при выполнении операций деления или умножения на отрицательное число — в этих случаях знак неравенства будет меняться на противоположный!
Для решения этого примера вначале раскроем скобки, не забывая, что -3 умножается на -7 и дает +27:
Затем приводим подобные, перенося числа в правую сторону:
Нам необходимо умножить неравенство на -1, чтобы получить диапазон x, не забывая, что при этом меняется знак неравенства:
Таким образом, мы получаем, что x должен быть больше либо равен 18.
Ответ:
Разбор 20 задания ОГЭ по математике
Квадратное неравенство — это неравенство вида:
где a, b, c – числа, x≠0, x – переменная.
Для решения квадратного неравенства используется специальный способ, который называется методом интервалов.
Чтобы решить квадратное неравенство методом интервалов, нужно:
- Перенести все члены неравенства в левую часть так, чтобы в правой остался только нуль.
- Сделать так, чтобы при неизвестном «x2» стоял положительный коэффициент.
- Приравнять левую часть неравенства к нулю и решить полученное квадратное уравнение.
- Записать разложенное на множители выражение по формуле a(x-x1)(x-x2) . Полученные корни уравнения разместить на числовой оси в порядке возрастания.
- Нарисовать «арки» для интервалов. Справа налево, начиная с «+», проставить, чередуя знаки «+» и «−».
- Выбрать необходимые интервалы и записать их в ответ.
Пример
Требуется решить квадратное неравенство: x2 +x-12 <0
Итак, согласно пункту 1 мы должны перенести все члены неравенства в левую часть, так чтобы в правой части остался только нуль. В заданном неравенстве ничего дополнительно делать не требуется, так как в правой части и так уже стоит нуль.
Переходим к пункту 2. Необходимо сделать так, чтобы перед «x2 » стоял положительный коэффициент. В неравенстве x2 +x-12 <0 при «x2» стоит положительный коэффициент «1», значит, снова нам ничего делать не требуется.
Согласно пункту 3 приравняем левую часть неравенства к нулю и решим полученное квадратное уравнение:
x2 +x-12 =0
Получим корни уравнения:
x1=4, x2=-3
(x-4)(x+3)<0
Теперь согласно пункту 4 отметим полученные корни на числовой оси в порядке возрастания.
Необходимо помнить, что, исходя их того, какое перед нами неравенство (строгое или нестрогое) мы отмечаем точки на числовой оси соответствующим способом.
Теперь, как сказано в пункте 5, нарисуем «арки» над интервалами между отмеченными точками.
Проставим знаки внутри интервалов. Справа налево, чередуя, начиная с «+», отметим знаки.
Нам осталось только выполнить пункт 6, то есть выбрать нужные интервалы и записать их в ответ. Вернемся к нашему неравенству.
Так как в нашем неравенстве знак неравенства < значит, нам требуются отрицательные интервалы. Заштрихуем все отрицательные области на числовой оси и выпишем их в ответ.
Отрицательным интервалом оказался лишь один, который находится между числами «−3» и «4», поэтому запишем его в ответ в виде двойного неравенства -3<x<4.
Ответ: -3<x<4
Решение 20 задания ОГЭ по математике — системы неравенств
Система неравенств состоит из нескольких неравенств с одной переменной. Эти неравенства объединяются фигурной скобкой (так же, как и уравнения в системах уравнений).
Задача состоит в том, чтобы найти все общие решения заданных неравенств.
Значение переменной, при котором каждое из неравенств системы становится верным числовым неравенством, называют решением системы неравенств.
Множество всех решений системы неравенств является общим решением (чаще всего — просто решением системы неравенств.)
Решить систему неравенств — это найти все её решения. Чтобы решить систему неравенств нужно:
- решить отдельно каждое неравенство;
- сравнить полученные решения каждого неравенства и получить общий ответ системы.
Пример
Укажите множество системы неравенств:
Решение
Решение системы линейных неравенств сводится к решению линейного неравенства с дальнейшим анализом промежутков. В начале действуем аналогично первому случаю: переносим числа в правую часть, оставляя x слева:
Сравним промежутки и выберем общий. Первое неравенство требует, чтобы x был больше 4, а второе — более 1,3. На координатной прямой это будет выглядеть следующим образом:
Промежутки перекрывают друг друга, начиная с 4. Значит, ответ выглядит следующим образом (не забываем, что неравенство нестрогое): [4;+∞ ] или
Пример
Решите систему неравенств:
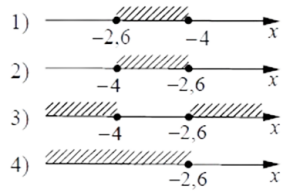
На каком рисунке изображено множество ее решений?
Решение
Итак, решим систему неравенств — оставим x в левой части, а остальное перенесем в правую, получим:
Вычислив, получаем ответ:
Найдем его на координатной прямой. Это №2.
Ответ: 2.
![Якорь Якорь]() Прототипы задания 20 ОГЭ по математике 2023 года
Прототипы задания 20 ОГЭ по математике 2023 года
Задание 1
Решите систему неравенств
Задание 2
Найдите наименьшее значение x , удовлетворяющее системе неравенств
Задание 3
Решите систему неравенств
Задание 4
Найдите наименьшее значение x, удовлетворяющее системе неравенств
Задание 5
Найдите наибольшее значение x, удовлетворяющее системе неравенств
Задание 6
Решите систему неравенств
Ответы к заданиям
- Ответ: 2;4 .
- Ответ: -4.
- Ответ: 4;+∞ .
- Ответ: -6.
- Ответ: -2.
- Ответ: -3;-2,7 .
СДАМ ГИА: РЕШУ ОГЭ
Образовательный портал для подготовки к экзаменам
Математика
математика
Математика
Информатика
≡ Русский язык
Письменный экзамен
Устное собеседование
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
сайты – меню – вход – новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Справочник
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
НАШИ БОТЫ
 |
 |
На сайте что-то не так? Отключите адблок
Новости
1 мая
Новый сервис: можно исправить ошибки!
29 апреля
Разместили актуальные шкалы ОГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
21 апреля
Разместили варианты из заданий открытого банка ФИПИ ОГЭ по русскому языку
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
6 марта
Изменения ВПР 2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
ЧУЖОЕ НЕ БРАТЬ!
Зайчиков и Поваляев стащили наши тесты
Наша группа
Каталог заданий.
Неравенства
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 20 № 177
i
Решите неравенство
Аналоги к заданию № 177: 125 314589 314591 … Все
Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1317
Решение
·
Критерии
·
Помощь
2
Тип 20 № 311237
i
Решите неравенство
Аналоги к заданию № 311237: 311256 339005 Все
Решение
·
Критерии
·
Помощь
3
Тип 20 № 314563
i
Решите неравенство
Аналоги к заданию № 151: 314563 314576 314578 … Все
Источник: Банк заданий ФИПИ
Решение
·
Критерии
·
1 комментарий
·
Помощь
4
Тип 20 № 314574
i
Решите неравенство
Аналоги к заданию № 314574: 314582 314588 314595 Все
Источник: Банк заданий ФИПИ
Решение
·
Критерии
·
Помощь
5
Тип 20 № 333318
Решите неравенство
Аналоги к заданию № 333318: 333344 338628 338918 … Все
Решение
·
Критерии
·
Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023