Время чтения: 8 минут.
Задание 6 решается за несколько секунд, если ты умеешь работать с графиками и таблицами. Давай разберемся, как легко и быстро разбираться в данных, представленных графически.
Диаграммы и графики – что это?📈
Для начала давай разберемся, что такое графики и диаграммы.
График – это отражение зависимости одной величины от другой. Пример: график зависимости температуры воздуха от времени суток.
Диаграмма – показывает соотношение каких-либо величин. Пример: доля населения Азии в общей численности населения Земли.
Чаще всего данные на диаграмме представлены в процентах (%).
Решение заданий из ВПР📝
Столбчатые диаграммы📊
Задачи со столбчатыми диаграммами решаются проще всего. Обычно нужно подсчитать общее количество чего-либо, либо определить наибольшее/наименьшее число из общего количества.
Пример №1: На диаграмме показаны виды кровли домов жителей поселка. По вертикальной оси указано количество домов. Сколько домов в данном поселке?
Решение: По диаграмме можно определить, сколько домов с каждым видом кровли. С железной крышей – 5 домов, с соломенной крышей – 9 домов, с черепичной – 8 домов и с деревянной – 7 домов. Складываем и получаем ответ!
Пример №2: На диаграмме показаны результаты проверочной работы, проведенной в 6 «А» классе. По вертикальной оси указано число учеников. Назовите средний балл по классу за эту проверочную работу.
Решение: Для расчета среднего балла используем формулу среднего арифметического – сумму всех оценок делим на число учеников.
Круговые диаграммы🔘
Задания с круговыми диаграммами решаются как задачи на проценты: находится процент от числа или число по его проценту.
Разбор задач на части представлен в статье:
Пример №3: На диаграмме представлен отчет о тратах семьи за прошедший месяц. По данным диаграммы, определите, сколько рублей потратила семья на одежду, если известно, что на коммунальные услуги было истрачено 7000 рублей?
Решение: Сначала находим число по его проценту – сколько семья потратила за месяц в целом. Затем из общего числа определяем, сколько денег было потрачено конкретно на одежду.
Формулы для решения ниже👇
Пример №4: На диаграмме показаны результаты контрольной работы в 6 «В» классе. Сколько процентов ребят получило отметку выше «3»?
Решение: Данная задача отличается тем, что нужно найти, какую часть одно число составляет от другого (в процентах). Для этого используется третья формула из задач на проценты.
На этом все! Остались вопросы? Напиши о них в комментариях!👇
Обязательно подпишись на канал, чтобы не пропустить больше полезных статей!🧠
#впр #огэ #егэ #математика #репетитор #6класс #алгебра #геометрия #диаграммы #задачинапроценты
Некоторые задачи удобно и наглядно решать с помощью диаграмм Эйлера-Венна. Например, задачи на множества. Если Вы не знаете, что такое диаграммы Эйлера-Венна и как их строить, то сначала прочтите эту статью.
Теперь разберем типовые задачи о множествах.
Задача 1.
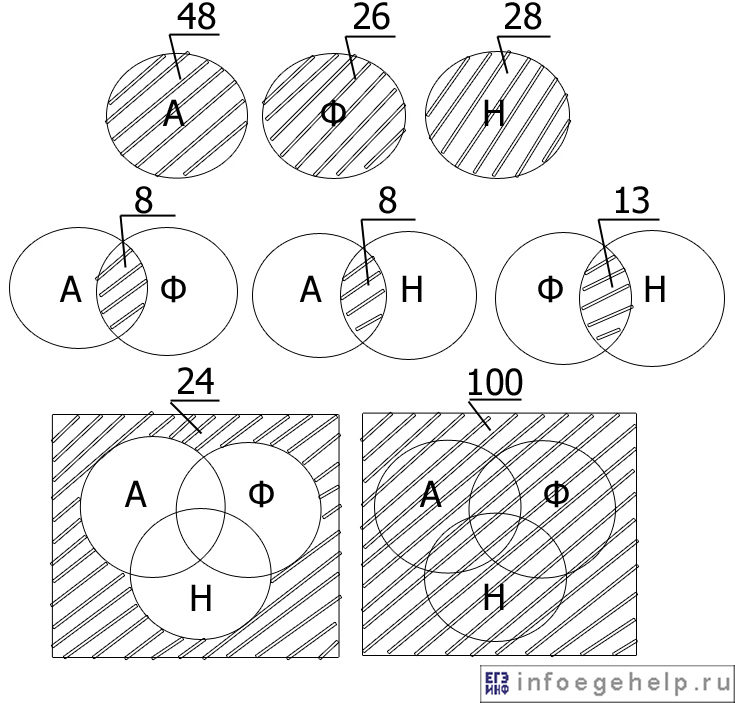
В школе с углубленным изучением иностранных языков провели опрос среди 100 учащихся. Ученикам задали вопрос: “Какие иностранные языки вы изучаете?”. Выяснилось, что 48 учеников изучают английский, 26 – французский, 28 – немецкий. 8 школьников изучают английский и немецкий, 8 – английский и французский, 13 – французский и немецкий. 24 школьника не изучают ни английский, ни французский, ни немецкий. Сколько школьников, прошедших опрос, изучают одновременно три языка: английский, французский и немецкий?
Ответ: 3.
Решение:
Сначала определим множества и введем обозначения. Их три:
- множество школьников, изучающих английский (“А”);
- множество школьников изучающих французский (“Ф”);
- множество школьников изучающих немецкий (“Н”).
Изобразим с помощью диаграммы Эйлера-Венна то, что нам дано по условию.
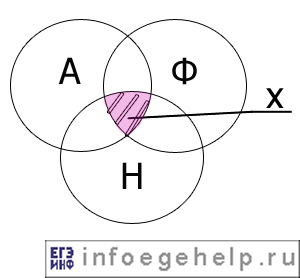
Изобразим то, что нам надо найти:
Определим количество школьников для всех возможных областей.
Обозначим искомую область А=1, Ф=1, Н=1 как “х” (в таблице ниже область №7). Выразим остальные области через х.
0) Область А=0, Ф=0, Н=0: 24 школьника – дано по условию задачи.
1) Область А=0, Ф=0, Н=1: 28-(8-х+х+13-х)=7+х школьников.
2) Область А=0, Ф=1, Н=0: 26-(8-х+х+13-х)=5+х школьников.
3) Область А=0, Ф=1, Н=1: 13-х школьников.
4) Область А=1, Ф=0, Н=0: 48-(8-х+х+8-х)=32+х школьников.
5) Область А=1, Ф=0, Н=1: 8-х школьников.
6) Область А=1, Ф=1, Н=0: 8-х школьников.
Запишем значения областей в таблицу:
| № области |
А | Ф | Н | Количество школьников |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 24 |
| 1 | 0 | 0 | 1 | 7+х |
| 2 | 0 | 1 | 0 | 5+х |
| 3 | 0 | 1 | 1 | 13-х |
| 4 | 1 | 0 | 0 | 32+х |
| 5 | 1 | 0 | 1 | 8-х |
| 6 | 1 | 1 | 0 | 8-х |
| 7 | 1 | 1 | 1 | х |
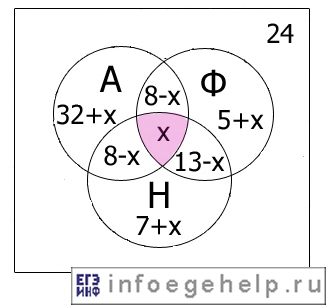
Изобразим значения для всех областей с помощью диаграммы:
Определим х:
24+7+(х+5)+х+(13-х)+(32+х)+(8-х)+(8-х)+х=100.
х=100-(24+7+5+13+32+8+8)=100-97=3.
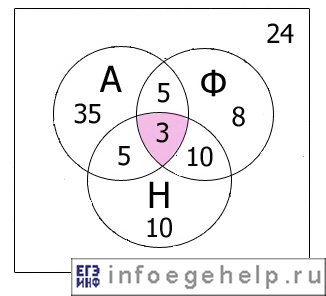
Получили, что 3 школьника изучают одновременно три языка: английский, французский и немецкий.
Так будет выглядеть диаграмма Эйлера-Венна при известном х:
Задача 2.
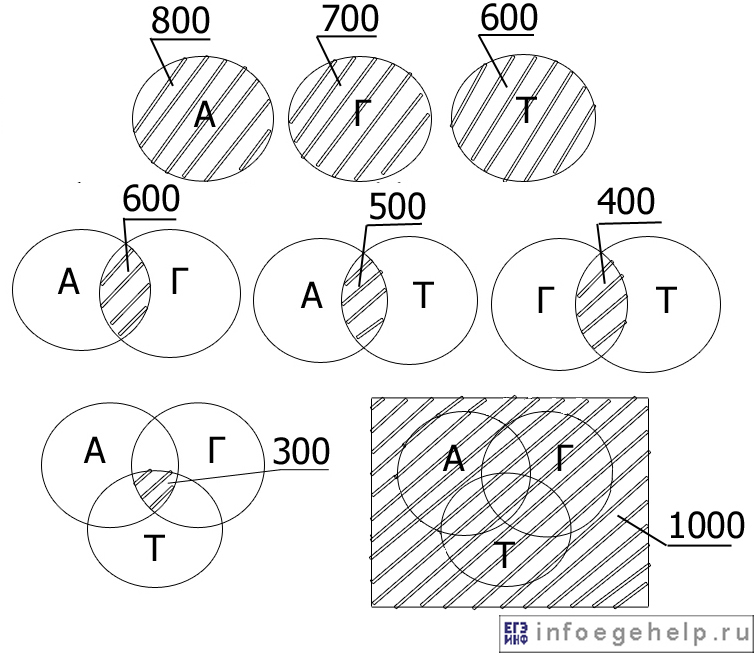
На олимпиаде по математике школьникам предложили решить три задачи: одну по алгебре, одну по геометрии, одну по тригонометрии. В олимпиаде участвовало 1000 школьников. Результаты олимпиады были следующие: задачу по алгебре решили 800 участников, по геометрии – 700, по тригонометрии – 600. 600 школьников решили задачи по алгебре и геометрии, 500 – по алгебре и тригонометрии, 400 – по геометрии и тригонометрии. 300 человек решили задачи по алгебре, геометрии и тригонометрии. Сколько школьников не решило ни одной задачи?
Ответ: 100.
Решение:
Сначала определим множества и введем обозначения. Их три:
- множество задач по алгебре (“А”);
- множество задач по геометрии (“Г”);
- множество задач по тригонометрии (“Т”).
Изобразим с помощью диаграммы Эйлера-Венна то, что нам дано по условию:
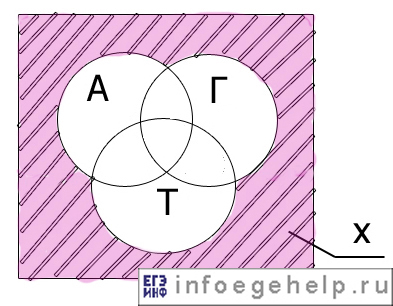
Изобразим то, что нам надо найти:
Определим количество школьников для всех возможных областей.
Обозначим искомую область А=0, Г=0, Т=0 как “х” (в таблице ниже область №0).
Найдем остальные области:
1) Область А=0, Г=0, Т=1: школьников нет.
2) Область А=0, Г=1, Т=0: школьников нет.
3) Область А=0, Г=1, Т=1: 100 школьников.
4) Область А=1, Г=0, Т=0: школьников нет.
5) Область А=1, Г=0, Т=1: 200 школьников.
6) Область А=1, Г=1, Т=0: 300 школьников.
7) Область А=1, Г=1, Т=1: 300 школьников.
Запишем значения областей в таблицу:
| № области |
А | Г | Т | Количество школьников |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | х |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 |
| 3 | 0 | 1 | 1 | 100 |
| 4 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 200 |
| 6 | 1 | 1 | 0 | 300 |
| 7 | 1 | 1 | 1 | 300 |
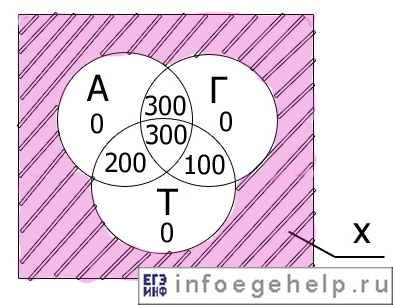
Изобразим значения для всех областей с помощью диаграммы:
Определим х:
х=U-(A V Г V Т), где U-универсум.
U=1000.
A V Г V Т=0+0+0+300+300+200+100=900.
x=1000-900=100.
Получили, что 100 школьников не решило ни одной задачи.
Задача 3.
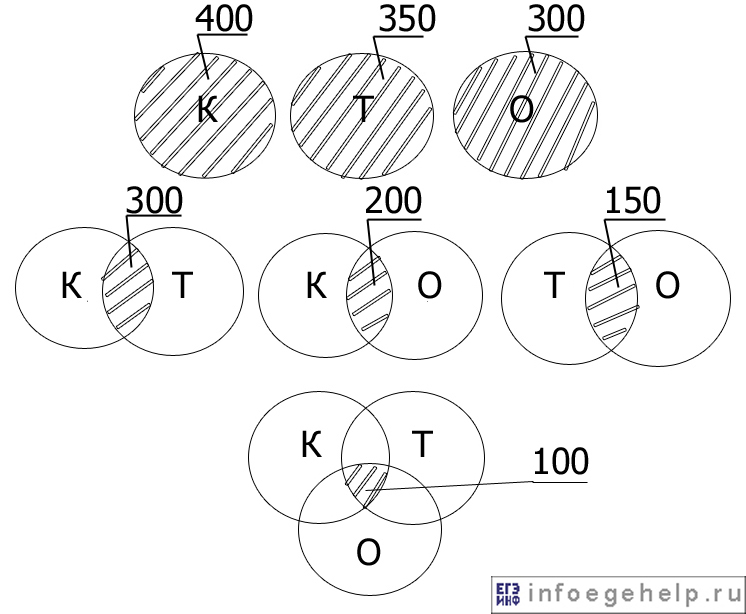
На олимпиаде по физике школьникам предложили решить три задачи: одну по кинематике, одну по термодинамике, одну по оптике. Результаты олимпиады были следующие: задачу по кинематике решили 400 участников, по термодинамике – 350, по оптике – 300. 300 школьников решили задачи по кинематике и термодинамике, 200 – по кинематике и оптике, 150 – по термодинамике и оптике. 100 человек решили задачи по кинематике, термодинамике и оптике. Сколько школьников решило две задачи?
Ответ: 350.
Решение:
Сначала определим множества и введем обозначения. Их три:
- множество задач по кинематике (“К”);
- множество задач по термодинамике (“Т”);
- множество задач по оптике (“О”).
Изобразим с помощью диаграммы Эйлера-Венна то, что нам дано по условию:
Изобразим то, что нам надо найти:
Определим количество школьников для всех возможных областей:
0) Область К=0, Т=0, О=0: не определено.
1) Область К=0,Т=0, О=1: 50 школьников.
2) Область К=0, Т=1, О=0: школьников нет.
3) Область К=0, Т=1, О=1: 50 школьников.
4) Область К=1, Т=0, О=0: школьников нет.
5) Область К=1, Т=0, О=1: 100 школьников.
6) Область К=1, Т=1, О=0: 200 школьников.
7) Область К=1, Т=1, О=1: 100 школьников.
Запишем значения областей в таблицу:
| № области |
К | Т | О | Количество школьников |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | – |
| 1 | 0 | 0 | 1 | 50 |
| 2 | 0 | 1 | 0 | 0 |
| 3 | 0 | 1 | 1 | 50 |
| 4 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 100 |
| 6 | 1 | 1 | 0 | 200 |
| 7 | 1 | 1 | 1 | 100 |
Изобразим значения для всех областей с помощью диаграммы:
Определим х.
х=200+100+50=350.
Получили, 350 школьников решило две задачи.
Задача 4.
Среди прохожих провели опрос. Был задан вопрос: “Какое домашнее животное у Вас есть?”. По результатам опроса выяснилось, что у 150 человек есть кошка, у 130 – собака, у 50 – птичка. У 60 человек есть кошка и собака, у 20 – кошка и птичка, у 30 – собака и птичка. У 70 человек вообще нет домашнего животного. У 10 человек есть и кошка, и собака, и птичка. Сколько прохожих приняли участие в опросе?
Ответ: 300.
Решение:
Сначала определим множества и введем обозначения. Их три:
- множество людей, у которых есть кошка (“К”);
- множество людей, у которых есть собака (“С”);
- множество людей, у которых есть птичка (“П”).
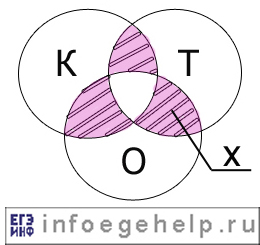
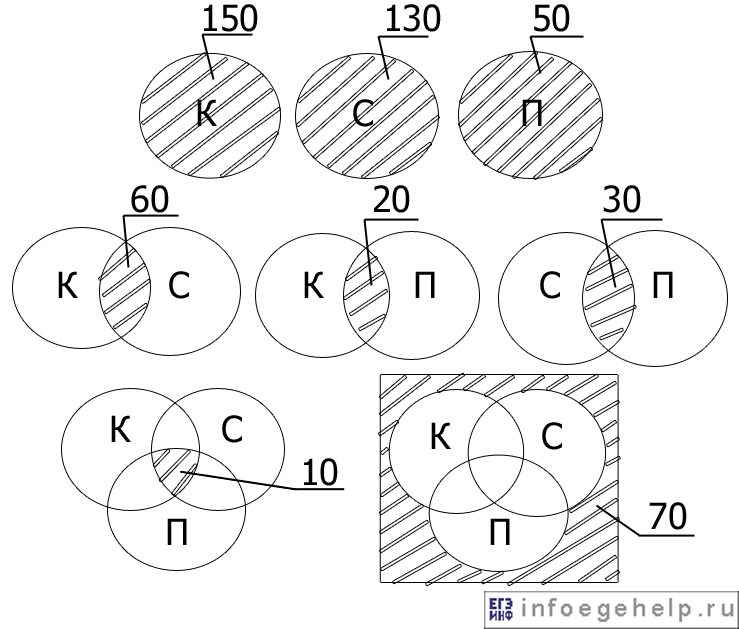
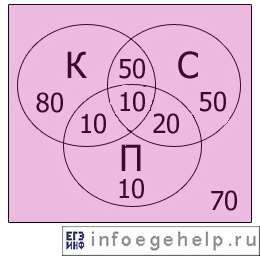
Изобразим с помощью диаграммы Эйлера-Венна то, что нам дано по условию:
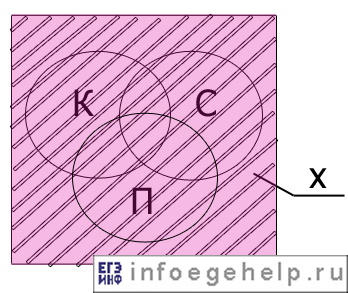
Изобразим то, что нам надо найти:
Определим количество человек для всех возможных областей:
0) Область К=0, С=0, П=0: 70 человек.
1) Область К=0, С=0, П=1: 10 человек.
2) Область К=0, С=1, П=0: 50 человек.
3) Область К=0, С=1, П=1: 20 человек.
4) Область К=1, С=0, П=0: 80 человек.
5) Область К=1, Т=0, О=1: 10 человек.
6) Область К=1, Т=1, О=0: 50 человек.
7) Область К=1, Т=1, О=1: 10 человек.
Запишем значения областей в таблицу:
| № области |
К | C | П | Количество человек |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 70 |
| 1 | 0 | 0 | 1 | 10 |
| 2 | 0 | 1 | 0 | 50 |
| 3 | 0 | 1 | 1 | 20 |
| 4 | 1 | 0 | 0 | 80 |
| 5 | 1 | 0 | 1 | 10 |
| 6 | 1 | 1 | 0 | 50 |
| 7 | 1 | 1 | 1 | 10 |
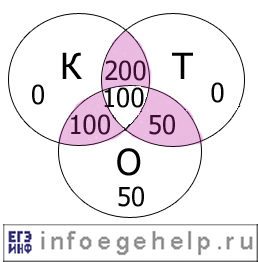
Изобразим значения для всех областей с помощью диаграммы:
Определим х:
х=U (универсум)
U=70+10+50+20+80+10+50+10=300.
Получили, что 300 человек приняли участие в опросе.
Задача 5.
На одну специальность в одном из ВУЗов поступало 120 человек. Абитуриенты сдавали три экзамена: по математике, по информатике и русскому языку. Математику сдали 60 человек, информатику – 40. 30 абитуриентов сдали математику и информатику, 30 – математику и русский язык, 25 – информатику и русский язык. 20 человек сдали все три экзамена, а 50 человек – провалили. Сколько абитуриентов сдали русский язык?
Ответ: 35.
Решение:
Сначала определим множества и введем обозначения. Их три:
- множество абитуриентов, сдавших математику (“М”);
- множество абитуриентов, сдавших информатику (“И”);
- множество абитуриентов, сдавших русский язык (“Р”);
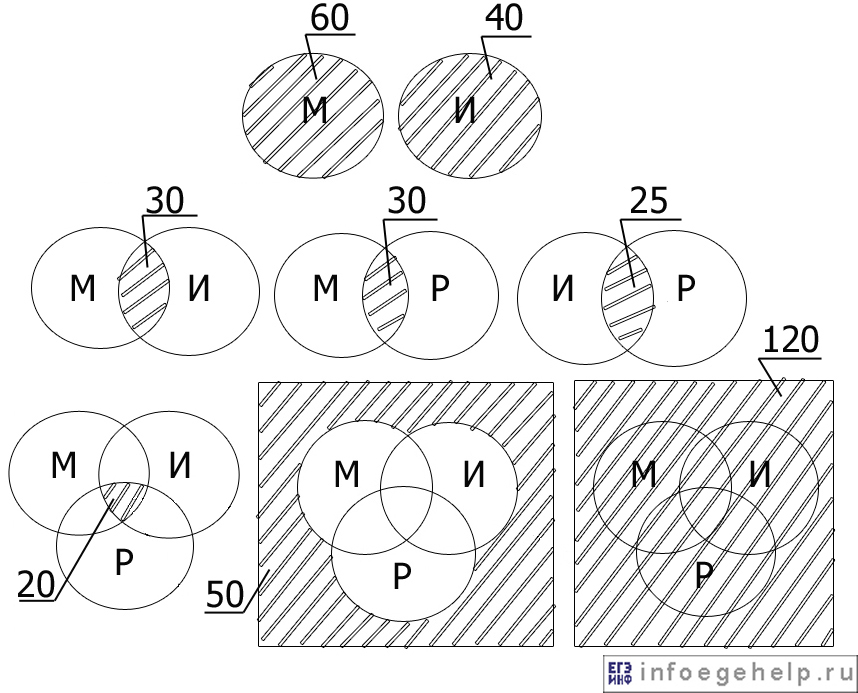
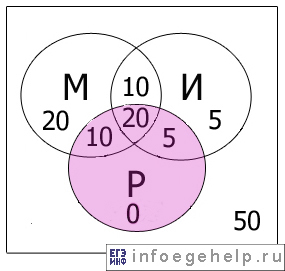
Изобразим с помощью диаграммы Эйлера-Венна то, что нам дано по условию:
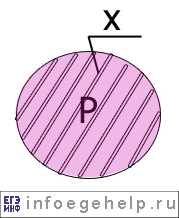
Изобразим то, что нам надо найти:
Определим количество абитуриентов для всех возможных областей.
Обозначим искомую область как “х”.
0) Область М=0, И=0, Р=0: 50 абитуриентов.
1) Область М=0, И=0, Р=1: х-35 абитуриентов.
2) Область М=0, И=1, Р=0: 5 абитуриентов.
3) Область М=0, И=1, Р=1: 20 абитуриентов.
4) Область М=1, И=0, Р=0: 80 абитуриентов.
5) Область М=1, И=0, Р=1: 10 абитуриентов.
6) Область М=1, И=1, Р=0: 50 абитуриентов.
7) Область М=1, И=1, Р=1: 10 абитуриентов.
Запишем значения областей в таблицу:
| № области |
М | И | Р | Количество абитуриентов |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 50 |
| 1 | 0 | 0 | 1 | х-35 |
| 2 | 0 | 1 | 0 | 5 |
| 3 | 0 | 1 | 1 | 5 |
| 4 | 1 | 0 | 0 | 20 |
| 5 | 1 | 0 | 1 | 10 |
| 6 | 1 | 1 | 0 | 10 |
| 7 | 1 | 1 | 1 | 20 |
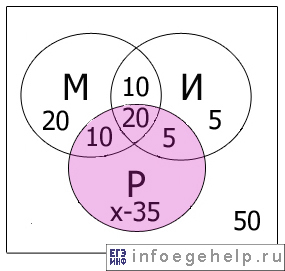
Изобразим значения для всех областей с помощью диаграммы:
Определим х:
х=120-50-(20+10+5)=35.
Получили, что 35 абитуриентов сдали русский язык.
Так будет выглядеть диаграмма Эйлера-Венна при известном х:
Перейти к разбору задач на множества из демо ЕГЭ (определение количества страниц по запросу поискового сервера):
- В12-2012
- В9-2011
- В10-2010
- В10-2009
Перейти к другим задачам демо ЕГЭ.
Решение
задач с помощью чертежей – диаграмм
Диаграмма
– это чертеж или рисунок, на котором условно изображены в виде отдельных фигур
различные значения одной и той же величины или несколько сравнимых величин.
Графико-вычислительные
приемы помогают решать разнообразные арифметические и геометрические задачи.
Построение этих чертежей дает возможность «увидеть» задачу, установить и
исследовать связи, существующие между величинами, входящими в задачу, выбрать
кратчайший путь решения.
Применяя
диаграммы к решению задач, будем изображать отрезками численные значения
величин, входящих в условие задачи. Действия над числами заменяют соответствующими
построениями на диаграмме.
Самостоятельное
решение задач таким путем требует определенного навыка, изобретательности. В
некоторых случаях этот путь может заменить чисто вычислительные приемы, в
других – облегчить наилучший выбор неизвестного для составления уравнения, или
подсказать ход рассуждений для отыскания арифметического решения.
Очень важное
достоинство такого пути – в наглядности: на рисунке сразу видна связь между
величинами, входящими в условие задачи; чертеж помогает расширить задачу –
поставить и решить более общие вопросы, глубже проникнуть в существо задачи,
оценить реальность результата и промежуточных действий. Особенно целесообразно
применять этот путь в тех случаях, когда требуется ответить не на один, а на
несколько вопросов.
Задача.
В одном бидоне вдвое больше молока, чем в другом. Когда из обоих бидонов отлили
по 20 литров молока, то в первом бидоне оказалось втрое больше молока, чем во
втором. Сколько литров молока было первоначально в каждом бидоне?
Решение.
Начертим
два вертикальных отрезка «бидоны», один по высоте в два раза больше, чем
другой, т.к. одном бидоне вдвое больше молока, чем в другом.
Допустим:
8 и 4 клетки.
Сколько
взять клеток, чтобы показать, что отлили по 20 литров молока, учтем условие: в
первом бидоне оказалось втрое больше молока, чем во втором. На рисунке должна
остаться одна часть во втором «бидоне» и три части в первом.
Тогда
20 л молока – это две клетки. Останется во втором «бидоне» две клетки, в первом
– шесть клеток.
Выходит, что 20
литров – это часть, таких частей в первом бидоне 4, тогда 4∙20=80 л, во втором
бидоне – две части 2∙20= 40 л.
Эту задачу легко
решить, используя алгебраический метод.
|
I бидон |
II бидон |
|
|
Было |
2x |
x |
|
стало |
2x-20 |
x-20 |
Составить
уравнение помогает фраза «в первом бидоне оказалось втрое больше молока, чем во
втором».
2х
– 20= 3(х-20), х=40, 40∙20=80
Ответ:
в первом бидоне 80 л, во втором -40 л молока.
Ученик 7класса
справится с такой задачей, используя введение переменной, и решит уравнение.
Но интересен другой факт: ученик 5, 6 классов тоже способен решить такую
задачу, используя рисунок и логически рассуждая.
Задача.
Коля уплатил в кассу кафе за три блюда, Саша – за два блюда (все пять блюд
одинаковой стоимости). Когда они сели за стол, к ним присоединился Юра, и они
втроем съели все пять блюд поровну. При расчете приятелей между собой
выяснилось, что Юра должен уплатить за съеденный им обед 500 рублей. Сколько из
этих денег следует отдать Коле и сколько Саше?
Решение.
Пусть отрезок в 15
клеток – это вся стоимость обеда (Юра должен отдать 500 рублей), ведь они
втроем съели поровну блюда, то поровну и заплатили за обед. Из рисунка
очевидно, что 1 клетка – 100 рублей. И Коля за три блюда заплатил 900 рублей,
Саша – 600 рублей. Полный обед из пяти блюд стоил 1500 рублей. Следовательно,
Коле нужно отдать 900-500=400 рублей, Саше 600-500=100 рублей.
Ответ:
Коле нужно отдать 400 рублей, Саше 100 рублей.
Задача.
На трех деревьях уселось 36 галок. Когда с первого дерева перелетели на второе
6 галок, а со второго перелетели на третье 4 галки, то на всех трех деревьях
галок стало поровну. Сколько галок сидело первоначально на деревьях?
Решение.
Рисунок
подсказывает, что на втором дереве после перелетов добавились две птицы, и их
стало 12, следовательно, первоначально их было 12-2=10. Конечно, если на
рисунок вынести общее число галок, то решение будет еще более очевидным.
Ответ:
1 дерево -18 галок, 2-10 галок, 3 – 8 галок.
Задача.
Рабочие отремонтировали дорогу длиной 820 метров за три дня. Во вторник они
отремонтировали этой дороги, в среду
остальной части дороги.
Сколько метров дороги отремонтировали рабочие в четверг?
Решение.
Возьмем отрезок длиной в 15 клеток – это длина всей отремонтированной дороги
(НОК (5;3)=15). Ведь нам нужно показать сначала две части из пяти, а потом две
части из трех.
Из рисунка
становится очевидным, что вся дорога разделена на пять частей, и, чтобы узнать,
какая часть осталась на четверг (это одна часть), нужно 820:5=164 метра.
Обычный путь
решения:
1)
820 ∙ =328 м была
отремонтирована во вторник,
2)
820-328=492 м осталось отремонтировать в среду и четверг,
3)
492∙=328 м отремонтировали в
среду,
4)
(820-328) -328=164 м отремонтировали в четверг.
Рисунок
позволяет решить задачу без громоздких вычислений.
Ответ.
164 метра дороги отремонтировали в четверг.
Графики
можно использовать для геометрической иллюстрации движения (перемещения).
Например, расписание движения поездов раньше разрабатывались при помощи
графиков, которые назывались «графики движения поездов». Наиболее просто
графиком изображается равномерное движение.
На
графике обычно, но не всегда, по направлению оси ОХ отсчитывают время, а по
направлению оси OY – расстояние. В
таком случае абсцисса всякой точки графика движения любого тела указывает
момент времени, а ордината – положение этого тела. Следовательно, график дает
возможность ответить на вопрос: «Где в данный момент находится тело? Когда оно
находилось или будет находиться в данном месте?»
Если
на одном чертеже построить два графика движения пешеходов, и если эти два
графика пересекаются в некоторой точке, то координаты этой точки показывают
место и время встречи пешеходов. Вот две задачи на движение, которые можно
решить с помощью графика равномерного движения. Геометрия придет на помощь
алгебре.
Задача.
Два туриста выезжают одновременно навстречу друг другу из двух пунктов А и В.
При встрече оказалось, что первый проехал на 30 км больше второго и что через
четыре дня он будет в В. Второй попадет в А через 9 дней после встречи. Найти
расстояние АВ.
Решение.
Берем произвольный отрезок АВ, изображающий расстояние между пунктами Аи В.
Отрезки АВꞌ и ВАꞌ – это графики движения первого и второго туриста (№1, №2).
Место и момент встречи определяются точкой О пересечения графиков.
Через точку О
проведем KL ‖ AB.
По условию KAꞌ =9 дней и LBꞌ =4 дня. Обозначим число дней от момента выхода туристов до их встречи
через х, тогда x=AK=BL.
Имеем
две пары подобных треугольников:
▲AOK
∞ ▲Bꞌ OL,
откуда x:4=OK:
OL
▲Aꞌ
OK ∞ ▲BOL, откуда 9:х= OK:
OL.
Отсюда
получаем x:4=9:х,
решая,
получим х=6 дней.
Обозначим
расстояние BC через y.
Тогда
LO=BC=y,
AC=KO=y+30.
Из
подобия треугольников AOK , BꞌOL
следует OK:OL=AK:
Bꞌ L или (y+30):y=6:4.
Упрощая
эту пропорцию, получим 30:y=2:4,
y=60
км.
Таким
образом, AB=2y+30=150
км.
Ответ:
расстояние между пунктами 150 км
Кроме
того, мы можем определить скорость каждого туриста.
Скорость
первого: v1=OL:LBꞌ
=60:4=15 км в день.
Скорость
второго v2
=OL:LB=60:6=10
км в день.
Задача.
Два пешехода идут навстречу друг другу, один из пункта А, другой из пункта В.
Первый выходит из А на 6 часов позже, чем второй из В. При встрече оказывается,
что он прошел на 12 км меньше второго. Продолжая после встречи дальней путь с
той же скоростью, первый приходит в В через 8 часов, второй в А – через 9
часов. Найти скорость каждого пешехода.
Решение.
Изобразим расстояние между пунктами А и В произвольным отрезком АВ. Ось времени
теперь направим вертикально. На перпендикуляре АЕ отмечаем точку С, принимая,
что АС=6 часам. Пусть прямая СD является
графиком движения первого пешехода, а прямая ВЕ – графиком движения второго. F
– точка пересечения графиков – это место встречи пешеходов, G
– проекция на АВ точки F.
Через
точку F проведем HJ ‖ AB.
По
условию, HE=9 часов, JD=
8 часов, JB – AG=12
км.
Пусть
CH=y,
тогда BJ=AH=(y+6)
часов.
▲BGF∞▲FHE
и ▲FJD∞▲
FHC
(▲FGB=▲FBJ)
Отсюда
получаем (y+6) : 9=FJ : FH=8 : y,
Следовательно,
(y+6)
∙y=8
∙ 9
или
y2+6y
– 72=0 , y=6 часов.
Далее,
,
,
, FH=36
км,
FJ=48
км.
FH
– это путь, который прошел первый пешеход за время, равное y=6
часов; FJ – путь, который прошел
второй пешеход за y+6=12 часов.
Следовательно,
первый пешеход шел со скоростью 36:6=6 км/час,
а
второй – со скоростью 48:12=4 км/час.
Ответ:
6 км/час – скорость первого пешехода, 4 км/час – скорость второго пешехода.
Вот второй вариант
решения данной задачи – алгебраический, привычный для ученика и учителя. Пусть
х – путь, пройденный первым пешеходом до встречи.
|
S, км |
V, км/ч |
t, час |
||
|
До |
1-й |
x |
|
|
|
2-й |
x+12 |
|
|
|
|
После |
1-й |
x+12 |
|
8 |
|
2-й |
x |
|
9 |
Составить
уравнение поможет фраза «первый выходит из А на 6 часов позже, чем второй из
В», следовательно, разница во времени между ними 6 часов:
После
преобразований получим: 5х2 – 12∙12х – 12∙12∙9=0, решив квадратное
уравнение, получаем х=36.
Следовательно,
второй пешеход прошел после встречи 36 км, а до встречи 36+12=48 км. Эти же 48
км прошел первый пешеход после встречи.
Первый пешеход шел
со скоростью 48:8=6 км/ч, второй – 36:9=4 км/ч.
Невозможно пройти
мимо интереснейшей задачи из рассказа Чехова «Репетитор». Чтобы освежить в
памяти, о чем идет речь, вот небольшой отрывок из этого рассказа.
«Теперь
по арифметике… Берите доску. Какая следующая задача?
Петя
плюет на доску и стирает рукавом. Учитель берет задачник и диктует:
—
«Купец купил 138 арш. черного и синего сукна за 540 руб. Спрашивается, сколько
аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное 3
руб.?» Повторите задачу.
Петя
повторяет задачу и тотчас же, ни слова не говоря, начинает делить 540 на 138.
—
Для чего же это вы делите? Постойте! Впрочем, так… продолжайте. Остаток
получается? Здесь не может быть остатка. Дайте-ка я разделю!
Зиберов
делит, получает 3 с остатком и быстро стирает.
«Странно…
— думает он, ероша волосы и краснея. — Как же она решается? Гм!.. Это задача на
неопределенные уравнения, а вовсе не арифметическая»…
Учитель
глядит в ответы и видит 75 и 63.
«Гм!..
странно… Сложить 5 и 3, а потом делить 540 на 8? Так, что ли? Нет, не то».
—
Решайте же! — говорит он Пете.
—
Ну, чего думаешь? Задача-то ведь пустяковая! — говорит Удодов Пете. — Экий ты
дурак, братец! Решите уж вы ему, Егор Алексеич.
Егор
Алексеич берет в руки грифель и начинает решать. Он заикается, краснеет,
бледнеет.
—
Эта задача, собственно говоря, алгебраическая, — говорит он. — Ее с иксом и
игреком решить можно. Впрочем, можно и так решить. Я, вот, разделил…
понимаете? Теперь, вот, надо вычесть… понимаете? Или, вот что… Решите мне
эту задачу сами к завтраму… Подумайте…
Петя
ехидно улыбается. Удодов тоже улыбается. Оба они понимают замешательство
учителя. Ученик VII класса еще пуще конфузится, встает и начинает ходить из
угла в угол.
—
И без алгебры решить можно, — говорит Удодов, протягивая руку к счетам и
вздыхая. — Вот, извольте видеть…
Он
щелкает на счетах, и у него получается 75 и 63, что и нужно было.
—
Вот-с… по-нашему, по-неученому.
Учителю становится
нестерпимо жутко. С замиранием сердца поглядывает он на часы и видит, что до
конца урока остается еще час с четвертью — целая вечность!»
Задачу из рассказа
А. П. Чехова можно решать по-разному.
Для учеников,
осваивающих тему «Решение задач с помощью системы уравнений», можно предложить
такой способ.
Пусть
х – количество аршин синего сукна,
y
– количество аршин черного сукна,
тогда
5х – стоимость синего сукна,
3y
– стоимость черного сукна.
Учитывая
условие задачи, составим систему уравнений
Выразим
х через y,
получим x=138-y,
5∙(138-y)+3y=540,
y=75,
138-75=63.
Ответ:
купец
купил 75 аршин черного сукна и 63 аршина синего сукна.
Еще вариант
размышлений: если бы купец приобрел только 138 аршин синего сукна, то ему
пришлось бы заплатить 138 ∙ 5 = 690 рублей. А он заплатил 540 рублей, на 150
рублей меньше. Заменяя один аршин синего сукна на аршин черного, можно
уменьшить стоимость сукна на 2 рубля. А чтобы уменьшить стоимость 138 аршин
сукна на 150 рублей, надо заменить 150 : 2 = 75 аршин синего сукна на такое же
количество черного. Выходит, что купец купил 75 аршин черного сукна и 138-75 =
63 аршина синего.
Есть ли
какой-то смысл в действиях чеховских героев? Петя разделил 540 на 138. У него
получилось 3 и 126 в остатке. Если купить 138 аршин черного сукна, то 138∙3=414
– стоимость черного сукна, и при делении его стоимости на 138, получается 3 без
остатка. Замена 1 аршина черного сукна на аршин синего увеличивает общую
стоимость сукна 2 рубля, и остаток от деления общей стоимости на 138
увеличивается на 2. Для того, чтобы остаток стал равен 126, надо 126 : 2 = 63
аршина черного сукна заменить таким же количеством синего. Следовательно, было
куплено 63 аршина синего сукна и 138 – 63 = 75 аршин черного.
Учитель-гимназист
хотел сложить пять и три, а потом 540:3. Посмотрим, что из этого получается.
540: (5 + 3) = 67 и 1/2 аршина черного и синего сукна, Как купить на те же
деньги 138 аршин? Для того, чтобы купить еще 3 аршина черного сукна, нужно 3 ∙
3 = 9 рублей. Эти 9 рублей можно выиграть от замены 9: 2 = 4 и 1/2 аршина
синего сукна на такое же количество черного. При этом синего сукна останется 63
аршина, а черного 75 аршин.
Вот еще одно
решение с применением ломаных графиков.
Один
аршин синего сукна стоит 5 рублей, следовательно, 100 аршин стоят 500 рублей.
Отмечаем точку М и строим луч ОМ – это график стоимости синего сукна.
Один
аршин черного сукна стоит 3 рубля, следовательно, 100 аршин стоят 300 рублей.
Отмечаем точку N и строим
луч ON – это график стоимости
черного сукна.
Т.к.
точка С (138 аршин, 540 рублей) оказывается между лучами OM и ON, то,
следовательно, купили и черное, и синее сукно.
Проведем
CA‖
NO до пересечения с OM,
получим точку А. Ломаная OAС – график
нарастающей стоимости сукон – синего (OA)
и черного (AC).
Проекции
точки А на оси OX и OY
указывают, что синего сукна купили 63 аршина на 315 рублей. Задача решена.
Найти количество и стоимость черного сукна уже легко.
Можно поступить и
немного иначе: провести CB ‖ MO;
тогда ломаная OBC -график нарастающей
стоимости сукон – черного (OB)
и синего (BC). Проекции точки В на
оси OX,
OY показывают, что черного сукна купили 75 аршин на 225 рублей. Проверка:
63+75=138 аршин и 315+225=540 рублей.
Приведенные
выше пути решения задач на первый взгляд могут показаться неожиданными и
непривычными. И возникает закономерный вопрос: «Зачем нужно использовать
нестандартные приемы задач, если для усвоения стандартного пути решения очень
мало времени и не все учащиеся отрабатывают каждый прием до конца?»
Показывать
нестандартные приемы решений задач можно на факультативных занятиях, кружковых,
а самые простые рисунки и схемы для понимания смысла задачи обязательно
включать в урочную деятельность.
Если
включить в уроки, кружки, факультативы подобные пути решения заданий, то
появляется вероятность привлечь учащихся в реальную для них творческую
деятельность. И это будет важным условием формирования разных творческих
качеств мышления школьников. Это один из путей развития креативности.
Школьники, которые готовятся к сдаче ЕГЭ по математике и рассчитывают на получение достойных баллов по итогам прохождения аттестационного испытания, обязательно должны уметь справляться с заданиями, где требуется выполнить анализ данных с помощью диаграмм. Подобные задачи включаются в экзамен ежегодно. Если задания ЕГЭ на выполнение анализа данных по диаграммам вызывают у вас определенные затруднения, рекомендуем вам повторить эту тему.
Вместе с образовательным проектом «Школково» вы сможете восполнить пробелы в знаниях. Наши специалисты подготовили и систематизировали весь необходимый материал, который может потребоваться вам для выполнения заданий ЕГЭ на проведение анализа данных с помощью диаграмм.
Прежде всего мы рекомендуем выпускникам на этапе подготовки к прохождению аттестационного испытания вспомнить основные понятия и правила. Для этого необходимо посетить раздел «Теоретическая справка».
Для закрепления полученных знаний и приобретения практического навыка предлагаем выполнить задания по темам «Построение графиков и диаграмм и анализ статических данных» и «Определение величины по графикам ЕГЭ» подобные тем, которые присутствуют в ЕГЭ. Для каждого упражнения на сайте представлены алгоритм решения и правильный ответ. При этом учащиеся могут попрактиковаться как с простыми, так и с более сложными заданиями по теме «Анализ данных с помощью диаграмм».
В случае необходимости школьники имеют возможность сохранить упражнение в «Избранное», чтобы затем обсудить алгоритм нахождения правильного ответа с преподавателем. Практиковаться в решении задач, в которых требуется выполнить анализ данных по диаграммам и графикам, имеют возможность учащиеся из Москвы и любого другого российского города.
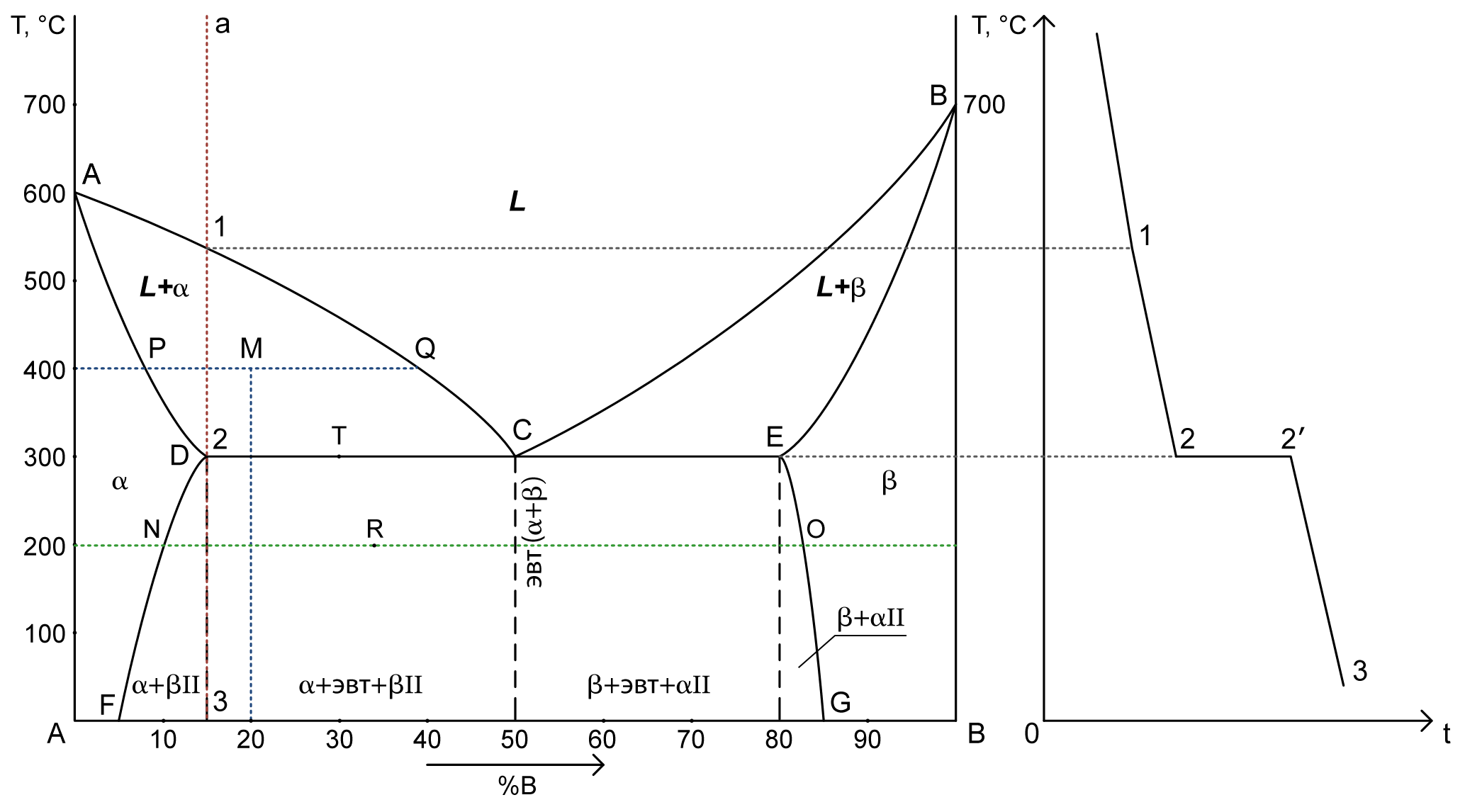
Задание 1
- Описать все превращения по диаграмме(название диаграммы, описание всех
точек, линий, фаз и структур). - Определить с помощью правила отрезков:
a. структуру сплава с 20%В при Т= 400°C
b. химический состав сплава по структуре Qβ= 33%, Qα= 67% при Т= 200°C
Определить химический состав найденных (задание а) и заданных (заданиеb) фаз. - Начертить кривую охлаждения для сплава содержащего15%В.
- Определить число степеней свободы для сплава с 30%В при Т= 300°C
Решение
1. Диаграмма состояния сплавов, испытывающих фазовые превращения в твердом состоянии.
2 компонента:
- A – температура плавления компонента A
- B – температура плавления компонента B
3 фазы:
- L – жидкость
- α – кристаллы твердого раствора A
- β – кристаллы твердого раствора B
ACB – ликвидус
ADCEB – солидус
DF – линия предельной растворимоси компонента B в A
EG – линия предельной растворимоси компонента A в B
2. a) Структура сплава 20%В при Т= 400°C – точка M.
PM – твердый раствор α: 7% B => 93% A. Cα= 7% B+ 93% A
MQ – жидкость: 40% B => 60% A. Cж= 40% B+ 60% A
Qα= (MQ/PQ)·100% = (40-20)/(40-7)·100% = 60,6%
Qж= 100%-60,6% = 39,4% (Или: (PM/PQ)·100% = (20-7)/(40-7)·100% = 39,4%)
b) химический состав сплава по структуре Qβ= 33%, Qα= 67% при Т= 200°C – точка R.
Qβ/Qобщ= RN/NO = 33%/100%
RN/(83-10) = 33/100
RN ≈ 24
B = 10+24=34% => A = 66%
Cсплава= 34%B + 66%A
Cα= 10%B + 90%A
Cβ= 83%B + 17%A
3. Кривая охаждения для сплава 15%В – a
4. Число степеней свободы для сплава с 30%В при Т= 300°C – точка T.
C = 2-3+1 = 0 (компоненты (A, B) – фазы (α, β, эвтектика) + 1)
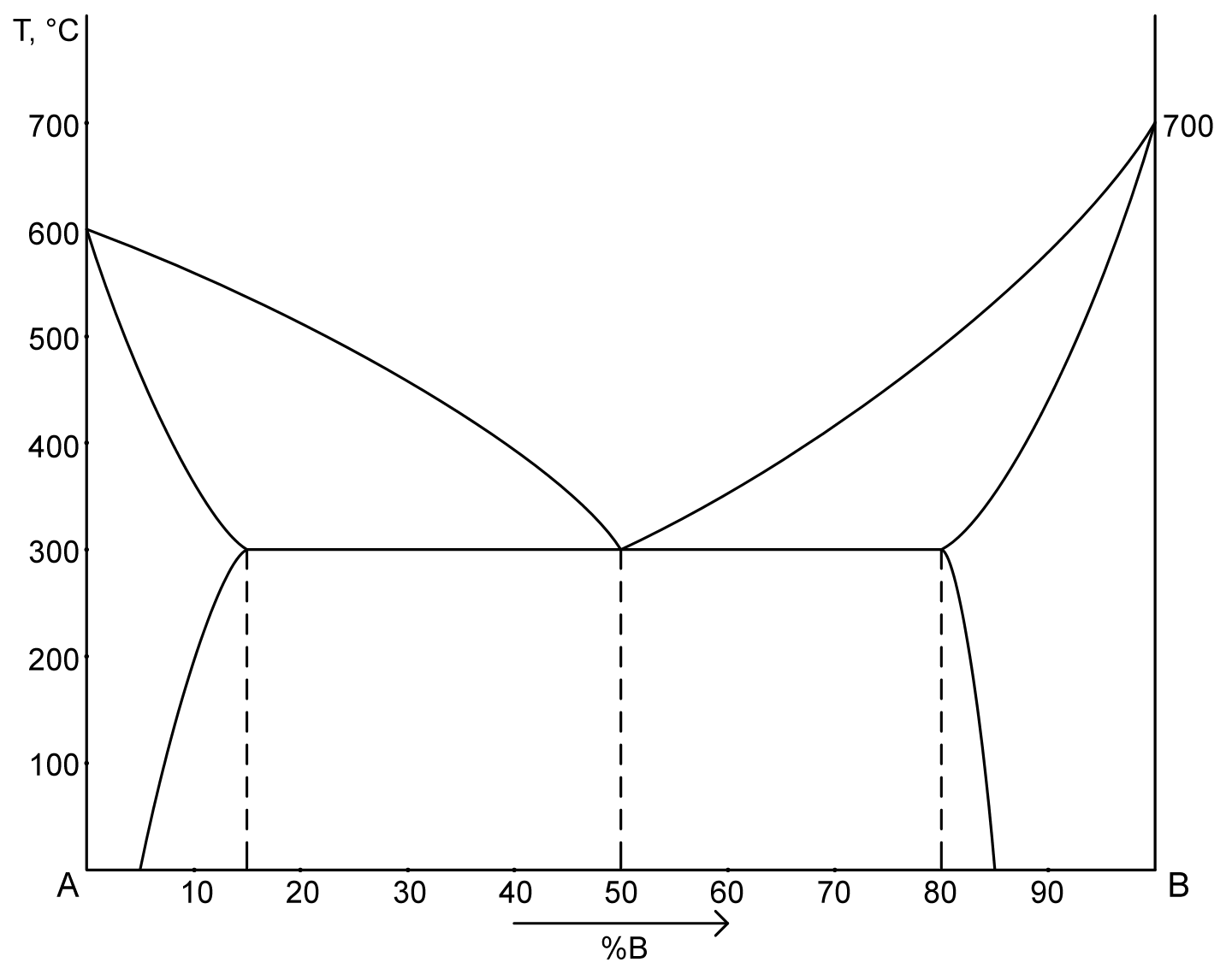
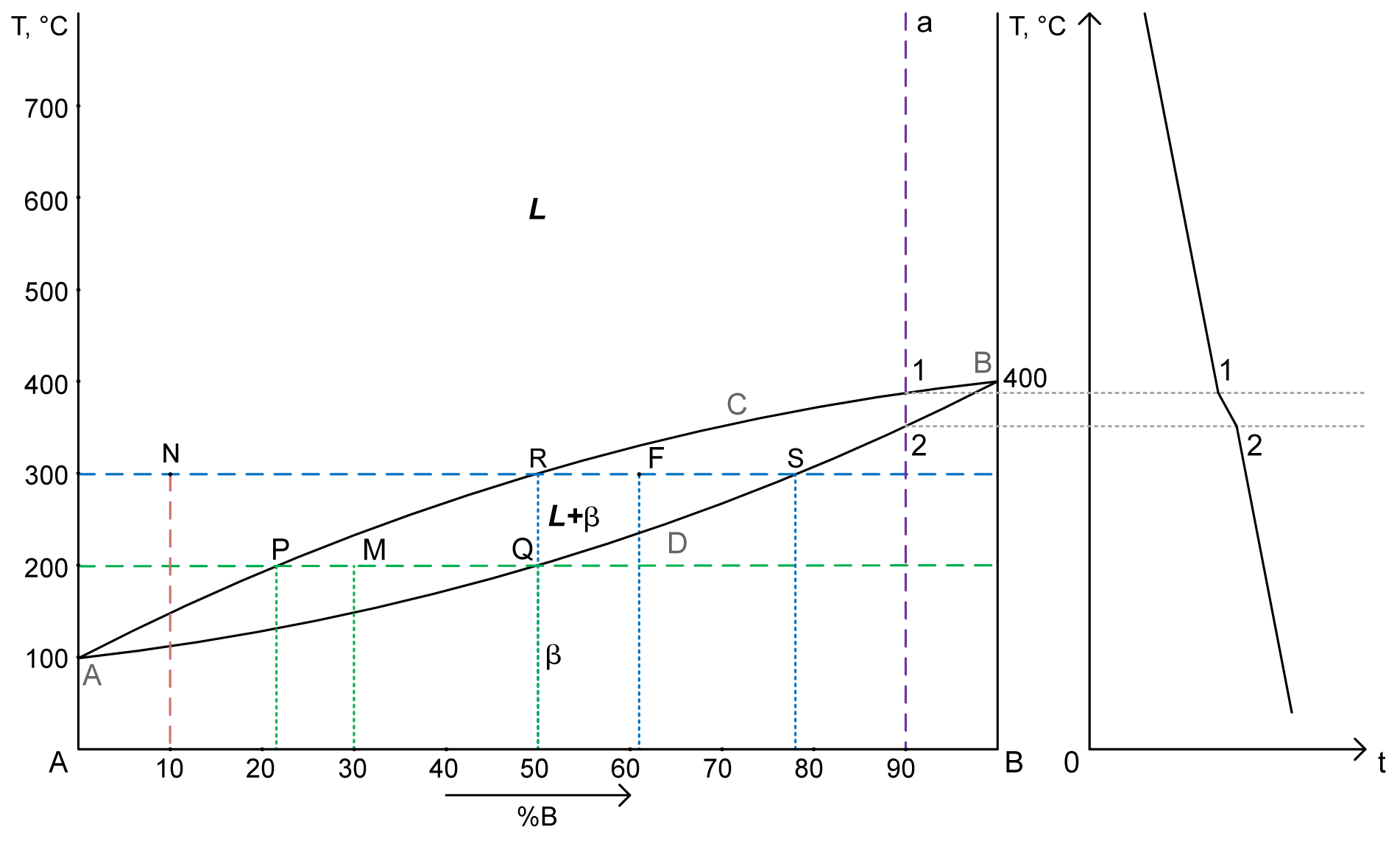
Задание 2
- Описать все превращения по диаграмме(название диаграммы, описание всех
точек, линий, фаз и структур). - Определить с помощью правила отрезков:
a. структуру сплава с 30%В при Т= 200°C
b. химический состав сплава по структуре Qβ= 40%, Qж= 60% при Т= 300°C
Определить химический состав найденных (задание а) и заданных (заданиеb) фаз. - Начертить кривую охлаждения для сплава содержащего 90%В.
- Определить число степеней свободы для сплава с 10%В при Т= 300°C
Решение
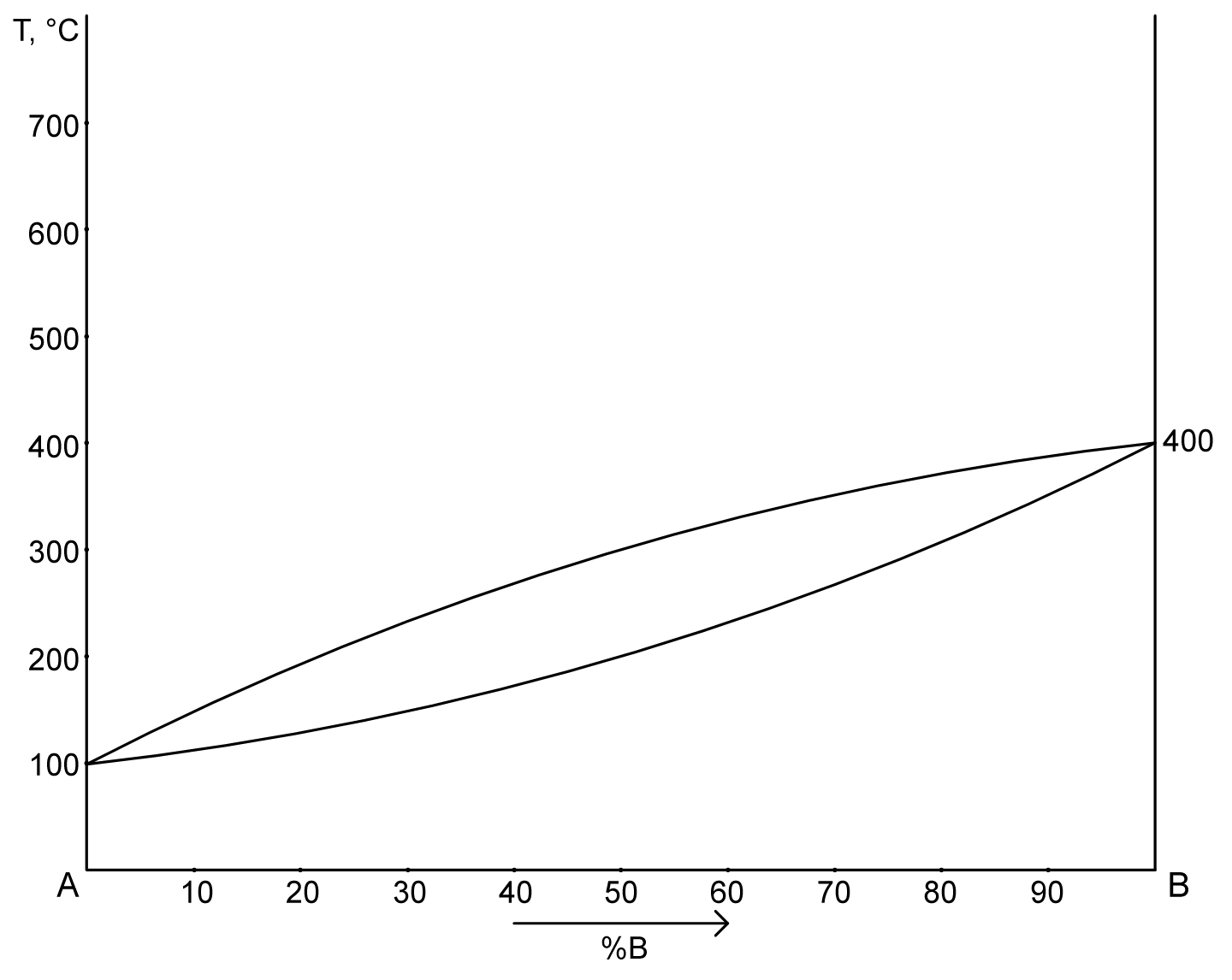
1. Диаграмма состояния сплавов с неограниченной растворимостью в твердом состоянии.
2 компонента:
- A – температура плавления компонента A
- B – температура плавления компонента B
2 фазы:
- L – жидкость
- β – кристаллы твердого раствора
ACB – ликвидус
ADB – солидус
2. a) Структура сплава 30%В при Т= 200°C – точка M.
PM – жидкость: 21% B => 79% A. Cж= 21% B+ 79% A
MQ – кристаллы твердого раствора: 50% B => 50% A. Cтв= 50% B+ 50% A
Qж= (MQ/PQ)·100% = (50-30)/(50-21)·100% = 69%
Qтв= 100%-69% = 31% (Или: (PM/PQ)·100% = (30-21)/(50-21)·100% = 31%)
b) химический состав сплава по структуре Qβ= 40%, Qж= 60% при Т= 300°C – точка F.
Qβ/Qобщ= RF/RS = 40%/100%
RF/(78-50) = 40/100
RF ≈11
B = 50+11=61% => A = 39%
Cсплава= 61%B + 39%A
Cβ= 78%B + 22%A
Cж= 50%B + 50%A
3. Кривая охаждения для сплава 90%В – a
4. Число степеней свободы для сплава с 10%В при Т= 300°C – точка N.
C = 2-1+1 = 2 (компоненты (A, B) – фазы (жидкость) + 1)
По Лукашова Т.В. Варианты заданий и пример решения по двухкомпонентным диаграммам состояния [Текст]: Методическое указание / Т.В.Лукашова, М.М.Сычев, С.И. Гринева. – СПб.: СПбГТИ(ТУ), 2008. – 41 с.