Решаем СЛАУ методом обратной матрицы:
2×1-4×2+3×3=1×1-2×2+4×3=33×1-x2+5×3=2
Как решить?
- Записываем систему в виде матричного уравнения АX=B, где
А=2-431-243-15, X=x1x2x3, B=132.
- Выражаем из этого уравнения X:
X=A-1×B
- Находим определитель матрицы А:
det A= 2-431-243-15=2×(-2)×5+3×(-4)×4+3×(-1)×1-3×(-2)×3–1×(-4)×5-2×4-(-1)=-20-48-3+18+20+8=-25
det А не равняется 0, следовательно, для этой системы подходит метод решения обратной матрицей.
- Находим обратную матрицу А-1 при помощи союзной матрицы. Вычисляем алгебраические дополнения Аij к соответствующим элементам матрицы А:
А11=(-1)(1+1)-24-15=-10+4=-6,
А12=(-1)1+21435=-(5-12)=7,
А13=(-1)1+31-23-1=-1+6=5,
А21=(-1)2+1-43-15=-(-20+3)=17,
А22=(-1)2+22335-10-9=1,
А23=(-1)2+32-43-1=-(-2+12)=-10,
А31=(-1)3+1-43-24=-16+6=-10,
А32=(-1)3+22314=-(8-3)=-5,
А33=(-1)3+32-41-2=-4+4=0.
- Записываем союзную матрицу А*, которая составлена из алгебраических дополнений матрицы А:
А*=-675171-10-10-50
- Записываем обратную матрицу согласно формуле:
A-1=1detA(A*)T: А-1=-125-617-1071-55-100,
- Умножаем обратную матрицу А-1 на столбец свободных членов В и получаем решение системы:
X=A-1×B=-125-617-1071-55-100132=-125-6+51-207+3-105-30+0=-101
Ответ: x1=-1; x2=0; x3=1
Перед тем как перейти к решению систем линейных уравнений методом обратной матрицы вспомним, что такое обратная матрица, какие способы ее нахождения существуют, что такое матричные уравнения и как они решаются.
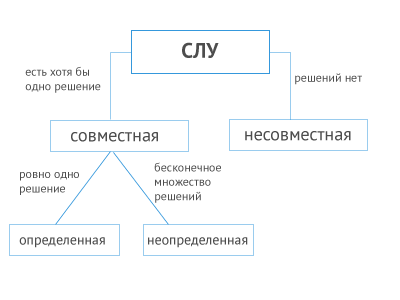
Система линейных уравнений (СЛУ)
Под системой линейных уравнений (СЛУ) будем понимать систему {a11x1+a12x2+a13x3+…+a1nxn=b1,a21x1+a22x2+a23x3+…+a2nxn=b2,………………………………….am1x1+am2x2+am3x3+…+amnxn=bm.begin{cases}a_{11}x_{1}+a_{12}x_{2}+a_{13}x_{3}+ldots+a_{1n}x_{n}=b_{1},\a_{21}x_{1}+a_{22}x_{2}+a_{23}x_{3}+ldots+a_{2n}x_{n}=b_{2},\ldotsldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots.\a_{m1}x_{1}+a_{m2}x_{2}+a_{m3}x_{3}+ldots+a_{mn}x_{n}=b_{m}.end{cases},
содержащую mm уравнений и nn неизвестных.Линейность означает, что все неизвестные в уравнении содержатся в первой степени.
Рассмотрим на схеме основные понятия, связанные с понятием системы линейных уравнений.
Матричная форма записи СЛУ
С каждой системой линейных уравнений
{a11x1+a12x2+a13x3+…+a1nxn=b1,a21x1+a22x2+a23x3+…+a2nxn=b2,………………………………….am1x1+am2x2+am3x3+…+amnxn=bm.begin{cases}a_{11}x_{1}+a_{12}x_{2}+a_{13}x_{3}+ldots+a_{1n}x_{n}=b_{1},\a_{21}x_{1}+a_{22}x_{2}+a_{23}x_{3}+ldots+a_{2n}x_{n}=b_{2},\ldotsldotsldotsldotsldotsldotsldotsldotsldotsldotsldotsldotsldots.\a_{m1}x_{1}+a_{m2}x_{2}+a_{m3}x_{3}+ldots+a_{mn}x_{n}=b_{m}.end{cases} можно связать несколько матриц.
-
Матрица системы, состоящая из коэффициентов заданной системы линейных уравнений: A=(a11a12a13…a1na21a22a23…a2n……………am1am2am3…amn)A=begin{pmatrix}a_{11}&a_{12}&a_{13}&ldots&a_{1n}\a_{21}&a_{22}&a_{23}&ldots&a_{2n}\ldots&ldots&ldots&ldots&ldots\a_{m1}&a_{m2}&a_{m3}&ldots&a_{mn}end{pmatrix}.
-
Матрица неизвестных, состоящая из столбца, который содержит неизвестные x1,x2,…,xn:x_{1}, x_{2}, … , x_{n}:
X=(x1x2…xn)X=begin{pmatrix}x_{1}\x_{2}\…\x_{n}end{pmatrix}.
- Матрица свободных членов, состоящая из столбца, который содержит свободные члены b1,b2,…,bm:b_{1}, b_{2}, … , b_{m}:
B=(b1b2…bm)B=begin{pmatrix}b_{1}\b_{2}\ … \b_{m}end{pmatrix}.
Используя введенные обозначения (AA — матрица системы, XX — матрица неизвестных, BB — матрица свободных членов) СЛУ можно записать в виде матричного уравнения A⋅X=BAcdot X=B, поэтому метод обратной матрицы, по существу, является частным случаем матричного уравнения.
Метод обратной матрицы может применяться только для тех систем линейных уравнений, у которых определитель матрицы системы отличен от нуля, а именно ∣A∣≠0begin{vmatrix}Aend{vmatrix}neq0. Если же ∣A∣=0begin{vmatrix}Aend{vmatrix}=0, то решить СЛУ матричным методом невозможно (в таком случае СЛУ может быть решена методом Гаусса).
Алгоритм решения СЛУ методом обратной матрицы
- Записать систему линейных уравнений в матричной форме: A⋅X=BAcdot X=B, где
A=(a11a12a13…a1na21a22a23…a2n……………am1am2am3…amn)A=begin{pmatrix}a_{11}&a_{12}&a_{13}&ldots&a_{1n}\a_{21}&a_{22}&a_{23}&ldots&a_{2n}\ ldots&ldots&ldots&ldots&ldots\a_{m1}&a_{m2}&a_{m3}&ldots&a_{mn}end{pmatrix} — матрица системы,
X=(x1x2…xn)X=begin{pmatrix}x_{1}\x_{2}\…\x_{n}end{pmatrix} — матрица неизвестных,
B=(b1b2…bm)B=begin{pmatrix}b_{1}\b_{2}\…\b_{m}end{pmatrix} — матрица свободных членов.
- Решить матричное уравнение A⋅X=BAcdot X=B:
2.1 Найти обратную матрицу A−1A^{-1} одним из способов.
2.2 Найти XX, используя равенство X=(x1x2…xn)=A−1⋅BX=begin{pmatrix}x_{1}\x_{2}\…\x_{n}end{pmatrix}=A^{-1}cdot B.
Рассмотрим примеры решения СЛУ методом обратной матрицы.
Пример 1
Решить систему {x1−2×2+x3=1,2×1−x2+x3=2,3×1+2×2+2×3=−2.begin{cases}x_{1}-2x_{2}+x_{3}=1,\2x_{1}-x_{2}+x_{3}=2,\3x_{1}+2x_{2}+2x_{3}=-2.end{cases} с помощью обратной матрицы.
Запишем систему в матричной форме A⋅X=BAcdot X=B, где
A=(1−212−11322)A=begin{pmatrix}1&-2&1\2&-1&1\3&2&2end{pmatrix},
X=(x1x2x3)X=begin{pmatrix}x_{1}\x_{2}\x_{3}end{pmatrix},
B=(12−2):B=begin{pmatrix}1\2\-2end{pmatrix}:
(1−212−11322)⋅(x1x2x3)=(12−2)begin{pmatrix}1&-2&1\2&-1&1\3&2&2end{pmatrix}cdot begin{pmatrix}x_{1}\x_{2}\x_{3}end{pmatrix}=begin{pmatrix}1\2\-2end{pmatrix}.
∣1−212−11322∣=5≠0begin{vmatrix}1&-2&1\2&-1&1\3&2&2end{vmatrix}=5neq0, значит, уравнение можно решить методом обратной матрицы.
Найдем обратную матрицу A−1A^{-1} методом элементарных преобразований.
Составим расширенную матрицу:
(1−212−11322∣100010001)begin{pmatrix}left.begin{matrix}1&-2&1\2&-1&1\3&2&2end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}.
Прибавим к строке №2 строку №1, умноженную на -2:
(1−212−11322∣100010001)∼(1−2103−1322∣100−210001)begin{pmatrix}left.begin{matrix}1&-2&1\2&-1&1\3&2&2end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-2&1\0&3&-1\3&2&2end{matrix}right|begin{matrix}1&0&0\-2&1&0\0&0&1end{matrix}end{pmatrix}.
Прибавим к строке №3 строку №1, умноженную на -3:
(1−2103−1322∣100−210001)∼(1−2103−108−1∣100−210−301)begin{pmatrix}left.begin{matrix}1&-2&1\0&3&-1\3&2&2end{matrix}right|begin{matrix}1&0&0\-2&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-2&1\0&3&-1\0&8&-1end{matrix}right|begin{matrix}1&0&0\-2&1&0\-3&0&1end{matrix}end{pmatrix}.
Прибавим к строке №2 строку №3, умноженную на -1:
(1−2103−108−1∣100−210−301)∼(1−210−5008−1∣10011−1−301)begin{pmatrix}left.begin{matrix}1&-2&1\0&3&-1\0&8&-1end{matrix}right|begin{matrix}1&0&0\-2&1&0\-3&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-2&1\0&-5&0\0&8&-1end{matrix}right|begin{matrix}1&0&0\1&1&-1\-3&0&1end{matrix}end{pmatrix}.
Умножим строку №2 на −15-frac{1}{5}:
(1−210−5008−1∣10011−1−301)∼(1−2101008−1∣100−15−1515−301)begin{pmatrix}left.begin{matrix}1&-2&1\0&-5&0\0&8&-1end{matrix}right|begin{matrix}1&0&0\1&1&-1\-3&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-2&1\0&1&0\0&8&-1end{matrix}right|begin{matrix}1&0&0\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\-3&0&1end{matrix}end{pmatrix}.
Прибавим к строке №3 строку №2, умноженную на -8:
(1−2101008−1∣100−15−1515−301)∼(1−2101000−1∣100−15−1515−7585−35)begin{pmatrix}left.begin{matrix}1&-2&1\0&1&0\0&8&-1end{matrix}right|begin{matrix}1&0&0\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\-3&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-2&1\0&1&0\0&0&-1end{matrix}right|begin{matrix}1&0&0\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\-frac{7}{5}&frac{8}{5}&-frac{3}{5}end{matrix}end{pmatrix}.
Умножим строку №3 на -1:
(1−2101000−1∣100−15−1515−7585−35)∼(1−21010001∣100−15−151575−8535)begin{pmatrix}left.begin{matrix}1&-2&1\0&1&0\0&0&-1end{matrix}right|begin{matrix}1&0&0\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\-frac{7}{5}&frac{8}{5}&-frac{3}{5}end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-2&1\0&1&0\0&0&1end{matrix}right|begin{matrix}1&0&0\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\frac{7}{5}&-frac{8}{5}&frac{3}{5}end{matrix}end{pmatrix}.
Прибавим к строке №1 строку №3, умноженную на -1:
(1−21010001∣100−15−151575−8535)∼(1−20010001∣−2585−35−15−151575−8535)begin{pmatrix}left.begin{matrix}1&-2&1\0&1&0\0&0&1end{matrix}right|begin{matrix}1&0&0\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\frac{7}{5}&-frac{8}{5}&frac{3}{5}end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-2&0\0&1&0\0&0&1end{matrix}right|begin{matrix}-frac{2}{5}&frac{8}{5}&-frac{3}{5}\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\frac{7}{5}&-frac{8}{5}&frac{3}{5}end{matrix}end{pmatrix}.
Прибавим к строке №1 строку №2, умноженную на 2:
(1−20010001∣−2585−35−15−151575−8535)∼(100010001∣−4565−15−15−151575−8535)begin{pmatrix}left.begin{matrix}1&-2&0\0&1&0\0&0&1end{matrix}right|begin{matrix}-frac{2}{5}&frac{8}{5}&-frac{3}{5}\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\frac{7}{5}&-frac{8}{5}&frac{3}{5}end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}right|begin{matrix}-frac{4}{5}&frac{6}{5}&-frac{1}{5}\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\frac{7}{5}&-frac{8}{5}&frac{3}{5}end{matrix}end{pmatrix}.
A−1=(−4565−15−15−151575−8535)=15(−46−1−1−117−83)A^{-1}=begin{pmatrix}-frac{4}{5}&frac{6}{5}&-frac{1}{5}\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\frac{7}{5}&-frac{8}{5}&frac{3}{5}end{pmatrix}=frac{1}{5}begin{pmatrix}-4&6&-1\-1&-1&1\7&-8&3end{pmatrix}.
Подставим матрицы в равенство X=A−1⋅BX=A^{-1}cdot B:
(x1x2x3)=15(−46−1−1−117−83)⋅(12−2)=15(10−5−15)=(2−1−3)begin{pmatrix}x_{1}\x_{2}\x_{3}end{pmatrix}=frac{1}{5}begin{pmatrix}-4&6&-1\-1&-1&1\7&-8&3end{pmatrix}cdot begin{pmatrix}1\2\-2end{pmatrix}=frac{1}{5}begin{pmatrix}10\-5\-15end{pmatrix}=begin{pmatrix}2\-1\-3end{pmatrix}.
Получили равенство (x1x2x3)=(2−1−3)begin{pmatrix}x_{1}\x_{2}\x_{3}end{pmatrix}=begin{pmatrix}2\-1\-3end{pmatrix}. Исходя из этого, имеем: x1=2,x2=−1,x3=−3x_{1}=2, x_{2}=-1, x_{3}=-3.
Ответ: x1=2,x2=−1,x3=−3x_{1}=2, x_{2}=-1, x_{3}=-3.
Пример 2
Решить систему {3×1+2×2+x3=5,2×1+3×2+x3=1,2×1+x2+3×3=11.begin{cases}3x_{1}+2x_{2}+x_{3}=5,\2x_{1}+3x_{2}+x_{3}=1,\2x_{1}+x_{2}+3x_{3}=11.end{cases} с помощью обратной матрицы.
Запишем систему в матричной форме A⋅X=BAcdot X=B,
где A=(321231213)A=begin{pmatrix}3&2&1\2&3&1\2&1&3end{pmatrix},
X=(x1x2x3)X=begin{pmatrix}x_{1}\x_{2}\x_{3}end{pmatrix},
B=(5111):B=begin{pmatrix}5\1\11end{pmatrix}:
(321231213)⋅(x1x2x3)=(5111)begin{pmatrix}3&2&1\2&3&1\2&1&3end{pmatrix}cdot begin{pmatrix}x_{1}\x_{2}\x_{3}end{pmatrix}=begin{pmatrix}5\1\11end{pmatrix}.
∣321231213∣=12≠0begin{vmatrix}3&2&1\2&3&1\2&1&3end{vmatrix}=12neq0, значит, уравнение можно решить методом обратной матрицы.
Найдем обратную матрицу A−1A^{-1} по формуле A−1=1∣A∣⋅A∗TA^{-1}=frac{1}{|A|}cdot A_{*}^{T}, где A∗TA_{*}^{T} — транспонированная матрица алгебраических дополнений.
A∗T=(a11a21a31a12a22a32a13a23a33)A_{*}^{T}=begin{pmatrix}a_{11}&a_{21}&a_{31}\a_{12}&a_{22}&a_{32}\a_{13}&a_{23}&a_{33}end{pmatrix}, aija_{ij} — алгебраические дополнения матрицы AA.
A∗T=(8−5−1−47−1−415)A_{*}^{T}=begin{pmatrix}8&-5&-1\-4&7&-1\-4&1&5end{pmatrix}.
A−1=112⋅(8−5−1−47−1−415)A^{-1}=frac{1}{12}cdot begin{pmatrix}8&-5&-1\-4&7&-1\-4&1&5end{pmatrix}.
Подставим матрицы в равенство X=A−1⋅BX=A^{-1}cdot B:
(x1x2x3)=112(8−5−1−47−1−415)⋅(5111)=112(24−2436)=(2−23)begin{pmatrix}x_{1}\x_{2}\x_{3}end{pmatrix}=frac{1}{12}begin{pmatrix}8&-5&-1\-4&7&-1\-4&1&5end{pmatrix}cdot begin{pmatrix}5\1\11end{pmatrix}=frac{1}{12}begin{pmatrix}24\-24\36end{pmatrix}=begin{pmatrix}2\-2\3end{pmatrix}.
Получили равенство (x1x2x3)=(2−23)begin{pmatrix}x_{1}\x_{2}\x_{3}end{pmatrix}=begin{pmatrix}2\-2\3end{pmatrix}.
Исходя из этого, имеем: x1=2,x2=−2,x3=3x_{1}=2, x_{2}=-2, x_{3}=3.
Ответ: x1=2,x2=−2,x3=3x_{1}=2, x_{2}=-2, x_{3}=3.
Возникают трудности с решением уравнений с помощью обратной матрицы? Советуем вам заказать решение задачи у наших экспертов!
Тест по теме “Линейные уравнения и и метод обратной матрицы”
Решение систем линейных алгебраических уравнений с помощью обратной матрицы.
Решение систем линейных алгебраических уравнений (СЛАУ) с помощью обратной матрицы (иногда этот способ именуют ещё матричным методом или методом обратной матрицы) требует предварительного ознакомления с таким понятием как матричная форма записи СЛАУ. Метод обратной матрицы предназначен для решения тех систем линейных алгебраических уравнений, у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Суть метода обратной матрицы можно выразить в трёх пунктах:
- Записать три матрицы: матрицу системы $A$, матрицу неизвестных $X$, матрицу свободных членов $B$.
- Найти обратную матрицу $A^{-1}$.
- Используя равенство $X=A^{-1}cdot B$ получить решение заданной СЛАУ.
Почему $X=A^{-1}cdot B$? показатьскрыть
Перед переходом к чтению примеров рекомендую ознакомиться с методами вычисления обратных матриц, изложенными здесь.
Пример №1
Решить СЛАУ $
left { begin{aligned}
& -5x_1+7x_2=29;\
& 9x_1+8x_2=-11.
end{aligned} right.$ с помощью обратной матрицы.
Решение
Запишем матрицу системы $A$, матрицу свободных членов $B$ и матрицу неизвестных $X$.
$$
A=left(begin{array} {cc} -5 & 7\ 9 & 8 end{array}right);;
B=left(begin{array} {c} 29\ -11 end{array}right);;
X=left(begin{array} {c} x_1\ x_2 end{array}right).
$$
Найдём обратную матрицу к матрице системы, т.е. вычислим $A^{-1}$. В примере №2 на странице, посвящённой нахождению обратных матриц, обратная матрица была уже найдена. Воспользуемся готовым результатом и запишем $A^{-1}$:
$$
A^{-1}=-frac{1}{103}cdotleft(begin{array}{cc} 8 & -7\ -9 & -5end{array}right).
$$
Теперь подставим все три матрицы ($X$, $A^{-1}$, $B$) в равенство $X=A^{-1}cdot B$. Затем выполним умножение матриц в правой части данного равенства.
$$
left(begin{array} {c} x_1\ x_2 end{array}right)=
-frac{1}{103}cdotleft(begin{array}{cc} 8 & -7\ -9 & -5end{array}right)cdot
left(begin{array} {c} 29\ -11 end{array}right)=\
=-frac{1}{103}cdot left(begin{array} {c} 8cdot 29+(-7)cdot (-11)\ -9cdot 29+(-5)cdot (-11) end{array}right)=
-frac{1}{103}cdot left(begin{array} {c} 309\ -206 end{array}right)=left(begin{array} {c} -3\ 2end{array}right).
$$
Итак, мы получили равенство $left(begin{array} {c} x_1\ x_2 end{array}right)=left(begin{array} {c} -3\ 2end{array}right)$. Из этого равенства имеем: $x_1=-3$, $x_2=2$.
Ответ: $x_1=-3$, $x_2=2$.
Пример №2
Решить СЛАУ $
left{begin{aligned}
& x_1+7x_2+3x_3=-1;\
& -4x_1+9x_2+4x_3=0;\
& 3x_2+2x_3=6.
end{aligned}right.$ методом обратной матрицы.
Решение
Запишем матрицу системы $A$, матрицу свободных членов $B$ и матрицу неизвестных $X$.
$$
A=left(begin{array} {ccc} 1 & 7 & 3\ -4 & 9 & 4 \0 & 3 & 2end{array}right);;
B=left(begin{array} {c} -1\0\6end{array}right);;
X=left(begin{array} {c} x_1\ x_2 \ x_3 end{array}right).
$$
Теперь настал черёд найти обратную матрицу к матрице системы, т.е. найти $A^{-1}$. В примере №3 на странице, посвящённой нахождению обратных матриц, обратная матрица была уже найдена. Воспользуемся готовым результатом и запишем $A^{-1}$:
$$
A^{-1}=frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right).
$$
Теперь подставим все три матрицы ($X$, $A^{-1}$, $B$) в равенство $X=A^{-1}cdot B$, после чего выполним умножение матриц в правой части данного равенства.
$$
left(begin{array} {c} x_1\ x_2 \ x_3 end{array}right)=
frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)cdot
left(begin{array} {c} -1\0\6end{array}right)=\
=frac{1}{26}cdot left(begin{array} {c} 6cdot(-1)+(-5)cdot 0+1cdot 6 \ 8cdot (-1)+2cdot 0+(-16)cdot 6 \ -12cdot (-1)+(-3)cdot 0+37cdot 6 end{array}right)=frac{1}{26}cdot left(begin{array} {c} 0\-104\234end{array}right)=left(begin{array} {c} 0\-4\9end{array}right)
$$
Итак, мы получили равенство $left(begin{array} {c} x_1\ x_2 \ x_3 end{array}right)=left(begin{array} {c} 0\-4\9end{array}right)$. Из этого равенства имеем: $x_1=0$, $x_2=-4$, $x_3=9$.
Ответ: $x_1=0$, $x_2=-4$, $x_3=9$.
Естественно, что решение систем линейных уравнений с помощью обратной матрицы без применения специальных программ вроде Mathcad возможно лишь при сравнительно небольшом количестве переменных. Если СЛАУ содержит четыре и более переменных, то гораздо удобнее в таком случае применить метод Гаусса или метод Гаусса-Жордана.
Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).
Пусть
система линейных алгебраических
уравнений задана в матричной форме
,
где матрицаAимеет размерностьnнаnи ее определитель отличен от
нуля.
Так
как
,
то матрицаА– обратима, то есть,
существует обратная матрица.
Если умножить обе части равенствана
слева,
то получим формулу для нахождения
матрицы-столбца неизвестных переменных.
Так мы получили решение системы линейных
алгебраических уравнений матричным
методом.
Пример.
Решите
систему линейных уравнений

методом.
Решение.
Перепишем
систему уравнений в матричной форме:
Так
как

СЛАУ можно решать матричным методом. С
помощью обратной матрицы решение этой
системы может быть найдено как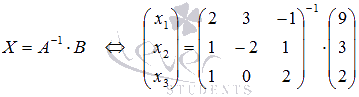
Построим
обратную матрицу
с
помощью матрицы из алгебраических
дополнений элементов матрицыА(при
необходимости смотрите статьюметоды
нахождения обратной матрицы):
Осталось
вычислить

матрицу неизвестных переменных, умножив
обратную матрицу
матрицу-столбец свободных членов
необходимости смотрите статьюоперации
над матрицами):
Ответ:

в другой записи x1 = 4, x2
= 0, x3 = -1.
Основная
проблема при нахождении решения систем
линейных алгебраических уравнений
матричным методом заключается в
трудоемкости нахождения обратной
матрицы, особенно для квадратных матриц
порядка выше третьего.
Более
подробное описание теории и дополнительные
примеры смотрите в статье матричный
метод решения систем линейных уравнений.
К
началу страницы
Решение систем линейных уравнений методом Гаусса.
Пусть
нам требуется найти решение системы из
nлинейных уравнений сnнеизвестными
переменными
основной матрицы которой отличен от
нуля.
Суть
метода Гауссасостоит в последовательном
исключении неизвестных переменных:
сначала исключаетсяx1из
всех уравнений системы, начиная со
второго, далее исключаетсяx2из всех уравнений, начиная с третьего,
и так далее, пока в последнем уравнении
останется только неизвестная переменнаяxn. Такой процесс преобразования
уравнений системы для последовательного
исключения неизвестных переменных
называетсяпрямым ходом метода Гаусса.
После завершения прямого хода метода
Гаусса из последнего уравнения находитсяxn, с помощью этого значения
из предпоследнего уравнения вычисляетсяxn-1, и так далее, из первого
уравнения находитсяx1.
Процесс вычисления неизвестных переменных
при движении от последнего уравнения
системы к первому называетсяобратным
ходом метода Гаусса.
Кратко
опишем алгоритм исключения неизвестных
переменных.
Будем
считать, что
,
так как мы всегда можем этого добиться
перестановкой местами уравнений системы.
Исключим неизвестную переменнуюx1из всех уравнений системы, начиная со
второго. Для этого ко второму уравнению
системы прибавим первое, умноженное на,
к третьему уравнению прибавим первое,
умноженное на,
и так далее, кn-омууравнению прибавим
первое, умноженное на.
Система уравнений после таких
преобразований примет вид

а
К
такому же результату мы бы пришли, если
бы выразили x1через другие
неизвестные переменные в первом уравнении
системы и полученное выражение подставили
во все остальные уравнения. Таким
образом, переменнаяx1исключена из всех уравнений, начиная
со второго.
Далее
действуем аналогично, но лишь с частью
полученной системы, которая отмечена
на рисунке
Будем
считать, что
(в
противном случае мы переставим местами
вторую строку сk-ой, где).
Приступаем к исключению неизвестной
переменнойx2из всех
уравнений, начиная с третьего.
Для
этого к третьему уравнению системы
прибавим второе, умноженное на
,
к четвертому уравнению прибавим второе,
умноженное на,
и так далее, кn-омууравнению прибавим
второе, умноженное на.
Система уравнений после таких
преобразований примет вид

а
Таким образом, переменнаяx2исключена из всех уравнений, начиная с
третьего.
Далее
приступаем к исключению неизвестной
x3, при этом действуем
аналогично с отмеченной на рисунке
частью системы
Так
продолжаем прямой ход метода Гаусса
пока система не примет вид
С
этого момента начинаем обратный ход
метода Гаусса: вычисляем xnиз последнего уравнения как
с помощью полученного значенияxnнаходимxn-1из предпоследнего
уравнения, и так далее, находимx1из первого уравнения.
Пример.
Решите
систему линейных уравнений

Гаусса.
Решение.
Исключим
неизвестную переменную x1из второго и третьего уравнения системы.
Для этого к обеим частям второго и
третьего уравнений прибавим соответствующие
части первого уравнения, умноженные на
на
Теперь
из третьего уравнения исключим x2,
прибавив к его левой и правой частям
левую и правую части второго уравнения,
умноженные на
На
этом прямой ход метода Гаусса закончен,
начинаем обратный ход.
Из
последнего уравнения полученной системы
уравнений находим x3:
Из
второго уравнения получаем

Из
первого уравнения находим оставшуюся
неизвестную переменную и этим завершаем
обратный ход метода Гаусса
.
Ответ:
x1
= 4, x2 = 0, x3 =
-1.
Более
детальную информацию и дополнительные
примеры смотрите в разделе решение
элементарных систем линейных алгебраических
уравнений методом Гаусса.
К
началу страницы
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Метод обратной матрицы (матричный способ)
Пусть задана система линейных алгебраических уравнений $$begin{cases} a_{11}x_1 + a_{12}x_2 + a_{13}x_3 = b_1 \ a_{21}x_1 + a_{22}x_2 + a_{23}x_3 = b_2 \ a_{31}x_1 + a_{32}x_2 + a_{33}x_3 = b_3 end{cases}.$$
Метод обратной матрицы подходит для решения систем линейных алгебраических уравнений в которых число строк совпадает с числом неизвестных переменных. Формула матричного метода выглядит следующим образом $$X = A^{-1} cdot B$$
Здесь $A^{-1}$ – это обратная матрица к матрице $A$, составленной из коэфициентов $a_{ij}$ в системе уравнений. $B$ – это вектор свободных членов, взятых из системы $$begin{pmatrix} x_1\x_2\x_3 end{pmatrix} = A^{-1} cdot begin{pmatrix} b_1 \ b_2 \ b_3 end{pmatrix}.$$
Важное замечание!
Для данного метода определитель матрицы $A$ не должен равняться нулю $det A neq 0$, так как это условие для существования обратной матрицы $A^{-1}$.
| Пример 1 |
| Решить систему уравнений методом обратной матрицы $$begin{cases} x_1+2x_2-x_3=2 \ 2x_1-3x_2 + 2x_3 = 2 \ 3x_1 + x_2 + x_3 = 8 end{cases}.$$ |
| Решение |
|
Составляем матрицу $$A = begin{pmatrix} 1&2&-1 \ 2&-3&2 \ 3&1&1 end{pmatrix}.$$ Прежде чем искать обратную матрицу, необходимо вычислить определитель и проверить то, что он неравен нулю. $$det A = begin{vmatrix} 1&2&-1 \ 2&-3&2 \ 3&1&1 end{vmatrix} = -3+12-2-9-2-4=-8 neq 0$$ Найдем обратную матрицу $A^{-1}$ с помощью единичной матрицы. Добавляем её к основной матрице сбоку. $$begin{pmatrix} 1&2&-1&|&1&0&0 \ 2&-3&2&|&0&1&0 \ 3&1&1&|&0&0&1 end{pmatrix}$$ Выполняем элементарные преобразования со строками приводим матрицу $A$ слева к единичной, а справа получаем обратную матрицу. Из второй строки вычитаем первую строчку, умноженную на 2. Из третьей строки вычитаем первую, умноженную на 3. $$begin{pmatrix} 1&2&-1&|&1&0&0 \ 2&-3&2&|&0&1&0 \ 3&1&1&|&0&0&1 end{pmatrix} sim begin{pmatrix} 1&2&-1&|&1&0&0 \ 0&-7&4&|&-2&1&0 \ 0&-5&4&|&-3&0&1 end{pmatrix}$$ Умножаем третью строку на 7 и вычитаем из неё вторую строчку, умноженную на 5. $$begin{pmatrix} 1&2&-1&|&1&0&0 \ 0&-7&4&|&-2&1&0 \ 0&0&8&|&-11&-5&7 end{pmatrix}$$ Теперь запускаем обратный ход. Умножаем вторую строку на 2 и вычитаем из неё третью. Умножаем первую строку на 8 и прибавляем к ней третью. $$begin{pmatrix} 8&16&0&|&-3&-5&7 \ 0&-14&0&|&7&7&-7 \ 0&0&8&|&-11&-5&7 end{pmatrix}$$ Умножаем первую строчку на 14 и прибавляем к ней вторую строчку, умноженную на 16. $$begin{pmatrix} 112&0&0&|&70&42&-14 \ 0&-14&0&|&7&7&-7 \ 0&0&8&|&-11&-5&7 end{pmatrix}$$ Теперь делим кажду строку на элемент стоящий на главной диагонали левой матрицы, чтобы получилась единичная. Первую строку делим на 112, вторую на (-14) и третью на 8. $$begin{pmatrix} 1&0&0&|&frac{70}{112}&frac{42}{112}&frac{-14}{112} \ 0&1&0&|&-frac{7}{14}&-frac{7}{14}&frac{7}{14} \ 0&0&1&|&-frac{11}{8}&-frac{5}{8}&frac{7}{8} end{pmatrix}$$ Итак, слева получилась обратная матрица $$A^{-1} = begin{pmatrix} frac{70}{112}&frac{42}{112}&frac{-14}{112} \ -frac{7}{14}&-frac{7}{14}&frac{7}{14} \ -frac{11}{8}&-frac{5}{8}&frac{7}{8} end{pmatrix}.$$ Теперь воспользуемся формулой $X = A^{-1} cdot B$, чтобы найти $x_1,x_2,x_3$ и тем самым решить поставленную задачу. Производим умножение обратной матрицы на столбец свободных членов $$begin{pmatrix} x_1\x_2\x_3 end{pmatrix} = begin{pmatrix} frac{70}{112}&frac{42}{112}&frac{-14}{70} \ -frac{7}{14}&-frac{7}{14}&frac{7}{14} \ -frac{11}{8}&-frac{5}{8}&frac{7}{8} end{pmatrix} cdot begin{pmatrix} 2\2\8 end{pmatrix} =$$ Произведение ищем по правилу умножения двух матриц. Напоминаем, находим сумму произведения элементов строк на столбец. $$=begin{pmatrix} frac{2cdot70}{112} + frac{2cdot42}{112} -frac{8cdot14}{112} \ -frac{2cdot7}{14} – frac{2cdot7}{14} + frac{8cdot7}{14} \ -frac{2cdot11}{8} -frac{2cdot5}{8} + frac{8cdot7}{8} end{pmatrix} = begin{pmatrix} 1\2\3 end{pmatrix}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$x_1 = 1, x_2=2, x_3=3$$ |
| Пример 2 |
| Решить систему уравнений матричным методом $$begin{cases} x_1+2x_2=10 \ 3x_1+2x_2+x_3=23 \ x_2+2x_3=13 end{cases}.$$ |
| Решение |
|
Составляем матрицу из коэффициентов $$A = begin{pmatrix} 1&2&0 \ 3&2&1 \ 0&1&2 end{pmatrix}$$ Находим обратную матрицу с помощью единичной матрицы. $$begin{pmatrix} 1&2&0 &|& 1&0&0 \ 3&2&1 &|& 0&1&0 \ 0&1&2 &|& 0&0&1 end{pmatrix}$$ Из второй строки вычитаем первую, умноженную на 3. $$begin{pmatrix} 1&2&0 &|& 1&0&0 \ 0&-4&1 &|& -3&1&0 \ 0&1&2 &|& 0&0&1 end{pmatrix}$$ Умножаем третью строчку на 4 и прибавляем к ней вторую. $$begin{pmatrix} 1&2&0 &|& 1&0&0 \ 0&-4&1 &|& -3&1&0 \ 0&0&9 &|& -3&1&4 end{pmatrix}$$ Начинаем обратный ход элементарных преобразований. Умножаем вторую строку на 9 и вычитаем третью. $$begin{pmatrix} 1&2&0 &|& 1&0&0 \ 0&-36&0 &|& -24&8&-4 \ 0&0&9 &|& -3&1&4 end{pmatrix}$$ Умножаем первую строку на 18 и прибавляем к ней вторую. $$begin{pmatrix} 18&0&0 &|& -6&8&-4 \ 0&-36&0 &|& -24&8&-4 \ 0&0&9 &|& -3&1&4 end{pmatrix}$$ Остаётся получить единицы на главной диагонали. Для этого делим первую строку на 18, вторую на (-36) и третью 9. $$begin{pmatrix} 1&0&0 &|& -frac{6}{18}&frac{8}{18}&-frac{4}{18} \ 0&1&0 &|& frac{24}{36}&-frac{8}{36}&frac{4}{36} \ 0&0&1 &|& -frac{3}{9}&frac{1}{9}&frac{4}{9} end{pmatrix}$$ Итак, выписываем полученную обратную матрицу $$A^{-1} = begin{pmatrix} -frac{6}{18}&frac{8}{18}&-frac{4}{18} \ frac{24}{36}&-frac{8}{36}&frac{4}{36} \ -frac{3}{9}&frac{1}{9}&frac{4}{9} end{pmatrix}.$$ Теперь пользуйся формулой $X = A^{-1} cdot B$ вычисляем $$begin{pmatrix} x_1\x_2\x_3 end{pmatrix} = begin{pmatrix} -frac{6}{18}&frac{8}{18}&-frac{4}{18} \ frac{24}{36}&-frac{8}{36}&frac{4}{36} \ -frac{3}{9}&frac{1}{9}&frac{4}{9} end{pmatrix} cdot begin{pmatrix} 10\23\13 end{pmatrix} = $$ Умножение производится по правилу произведения двух матриц: сумма произведений элементов строк первой матрицы на элементы второй матрицы. $$ = begin{pmatrix} -frac{6cdot10}{18}+frac{8cdot23}{18}-frac{4cdot13}{18} \ frac{24cdot10}{36}-frac{8cdot23}{36}+frac{4cdot13}{36} \ -frac{3cdot10}{9}+frac{23}{9}+frac{4cdot13}{9} end{pmatrix} = begin{pmatrix} 4\3\5 end{pmatrix}$$ Вот таким вот образом матричный метод помогает решать системы линейных алгебраических уравнений. Главное не забывать что данный способ работает, если определитель матрицы $A$ не равен нулю и число переменных в системе совпадает с числом уравнений. |
| Ответ |
| $$x_1 = 4, x_2 = 3, x_3 = 5$$ |