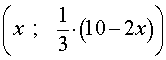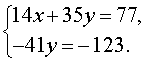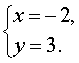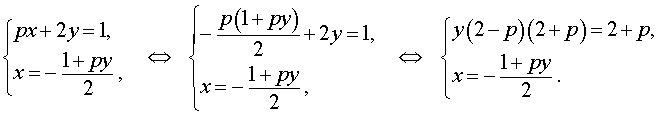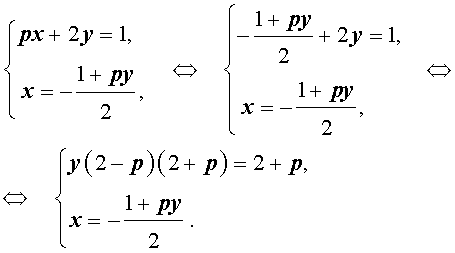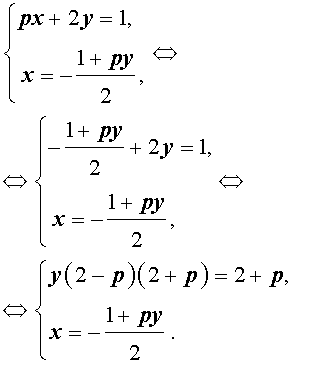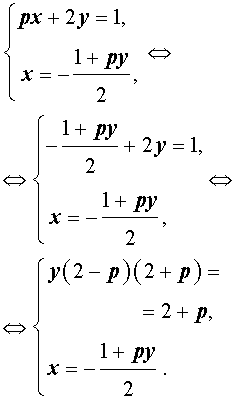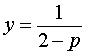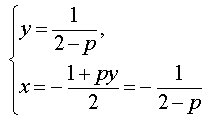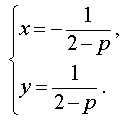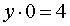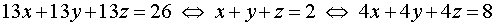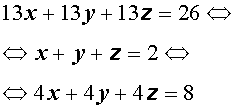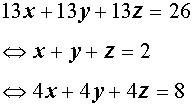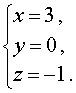Как найти решение системы с тремя неизвестными

Линейное уравнение с тремя переменными и его решение

Уравнение вида ax+by+cz = d , где a, b, c, d – данные числа, называется линейным уравнением с тремя переменными x, y и z.

Например: $2x+5y+z = 8; -x+1, 5y+2z = 0; frac{1}{2} x-8y-5z = 7$

Уравнение с тремя переменными может быть не только линейным, т.е. содержать не только первые степени переменных x,y и z.

Например: $2x^2+xz+y^2+yz^2 = 3,x-5y^2+z^3 = 1, 7x^3+y+xyz = 7$

Решением уравнения с тремя переменными называется упорядоченная тройка значений переменных (x,y,z), обращающая это уравнение в тождество.

О тождествах – см. §3 данного справочника

Например: для уравнения 2x+5y+z=8 решениями являются тройки x = -2, y = 1, z = 7; x = -1, y = 1, 6 , z = 2; x = -3, y = 2, 4, z = 2 и т.д. Уравнение имеет бесконечное множество решений.

Геометрическим представлением линейного уравнения с тремя переменными является плоскость в трёхмерном координатном пространстве.

Решение системы линейных уравнений с тремя переменными методом подстановки

Алгоритм метода подстановки для системы уравнений с тремя переменными аналогичен алгоритму для двух переменных (см.§45 данного справочника)

Например: решить систему

$$ {left{ begin{array}{c} 3x+2y-z = 8 \ x-y+z = -2 \ 2x-3y-5z = 1 end{array} right.} Rightarrow {left{ begin{array}{c} 3(y-z-2)+2y-z = 8 \ x = y-z-2 \ 2(y-z-2)-3y-5z = 1 end{array} right.} Rightarrow $$

$$ Rightarrow {left{ begin{array}{c} x = y-z-2 \ 5y-4z = 14 \ -y-7z = 5 end{array} right.} Rightarrow {left{ begin{array}{c} x = y-z-2 \ y = -7z-5 \ 5(-7z-5)-4z = 14 end{array} right.} Rightarrow {left{ begin{array}{c} x = y-z-2 \ y = -7z-5 \ -39z = 39 end{array} right.} Rightarrow $$

$$ Rightarrow {left{ begin{array}{c} x = 2-(-1)-2 = 1 \ y = -7cdot(-1)-5 = 2 \ z = -1 end{array} right.} Rightarrow {left{ begin{array}{c} x = 1 \ y = 2 \ z = -1 end{array} right.} $$

Ответ: (1;2;-1)

Решение системы линейных уравнений с тремя переменными методом Крамера

Метод Крамера для системы уравнений с 2-мя переменными рассмотрен в §48 данного справочника.

Для системы с 3-мя переменными действуем по аналогии.

Дана система 3-х линейных уравнений с 3-мя переменными:

$$ {left{ begin{array}{c} a_1 x+b_1 y+c_1 z = d_1 \ a_2 x+b_2 y+c_2 z = d_2 \ a_3 x+b_3 y+c_3 z = d_3 end{array} right.} $$

Определим главный определитель системы:

$$ Delta = begin{vmatrix} a_1 & b_1 & c_1 \ a_2 & b_2 & c_2 \ a_3 & b_3 & c_3 end{vmatrix} $$

и вспомогательные определители:

$$ Delta_x = begin{vmatrix} d_1 & b_1 & c_1 \ d_2 & b_2 & c_2 \ d_3 & b_3 & c_3 end{vmatrix}, Delta_y = begin{vmatrix} a_1 & d_1 & c_1 \ a_2 & d_2 & c_2 \ a_3 & d_3 & c_3 end{vmatrix}, Delta_z = begin{vmatrix} a_1 & b_1 & d_1 \ a_2 & b_2 & d_2 \ a_3 & b_3 & d_3 end{vmatrix} $$

Тогда решение системы:

$$ {left{ begin{array}{c} x = frac{Delta_x}{Delta} \ y = frac{Delta_y}{Delta} \ z = frac{Delta_z}{Delta} end{array} right.} $$

Соотношение значений определителей, расположения плоскостей и количества решений:

Осталось определить правило вычисления определителя 3-го порядка.

Таких правил несколько, приведём одно из них (так называемое «раскрытие определителя по первой строке»):

$$ Delta = begin{vmatrix} a_1 & b_1 & c_1 \ a_2 & b_2 & c_2 \ a_3 & b_3 & c_3 end{vmatrix} = a_1 = begin{vmatrix} b_2 & c_2 \ b_3 & c_3 end{vmatrix} – b_1 = begin{vmatrix} a_2 & c_2 \ a_3 & c_3 end{vmatrix} + c_1 = begin{vmatrix} a_2 & b_2 \ a_3 & b_3 end{vmatrix} = $$

$$ = a_1 (b_2 c_3-b_3 c_2 )-b_1 (a_2 c_3-a_3 c_2 )+c_1 (a_2 b_3-a_3 b_2 )$$

Примеры

Пример 1. Найдите решение системы уравнений методом подстановки:

$ а) {left{ begin{array}{c} 3x+2y-z = 13 \ 2x-y+3z = -2 \ x+2y-z = 9 end{array} right.} $

$${left{ begin{array}{c} z = 3x+2y-13 \ 2x-y+3(3x+2y-13) = -2 \ x+2y-(3x+2y-13) = 9 end{array} right.} Rightarrow {left{ begin{array}{c} z = 3x+2y-13 \ 11x+5y = 37 \ -2x = -4 end{array} right.} Rightarrow $$

$$Rightarrow {left{ begin{array}{c} z = 3cdot2+2cdot3-13 = -1 \ y = frac{37-11cdot2}{5} = 3 \ x = 2 end{array} right.} Rightarrow {left{ begin{array}{c} x = 2 \ y = 3 \ z = -1 end{array} right.} $$

Ответ: (2;3;-1)

$ б) {left{ begin{array}{c} x+y+3z = 6 \ 2x-5y-z = 5 \ x+2y-5z = -11 end{array} right.} $

$$ {left{ begin{array}{c} x = -y-3z+6 \ 2(-y-3z+6)-5y-z = 5\ (-y-3z+6)+2y-5z = -11 end{array} right.} Rightarrow {left{ begin{array}{c} x = -y-3z+6 \ -7y-7z = -7 |:(-7) \ y-8z = -17 end{array} right.} Rightarrow $$

$$ Rightarrow {left{ begin{array}{c} x = -y-3z+6 \ y+z = 1 \ y-8z = -17 end{array} right.} Rightarrow {left{ begin{array}{c} x = -y-3z+6 \ 9z = 18 \ y = 1-z end{array} right.} Rightarrow {left{ begin{array}{c} x = 1-6+6 = 1 \ z = 2 \ y = 1-2 = -1 end{array} right.} Rightarrow$$

$$ Rightarrow {left{ begin{array}{c} x = 1 \ y = -1 \ z = 2 end{array} right.} $$

Ответ: (1;-1;2)

Пример 2. Найдите решение системы уравнений методом Крамера:

$а) {left{ begin{array}{c}3x+2y-z = 13 \ 2x-y+3z = -2 \ x+2y-z = 9 end{array} right.} $

$$ Delta = begin{vmatrix} 3 & 2 & -1 \ 2 & -1 & 3\ 1 & 2 & -1 end{vmatrix} = 3 = begin{vmatrix} -1 & 3 \ 2 & -1 \ end{vmatrix} – 2 = begin{vmatrix} 2 & 3 \ 1 & -1 \ end{vmatrix} – 1 = begin{vmatrix} 2 & -1 \ 1 & 2 \ end{vmatrix} = $$

$$= 3(1-6)-2(-2-3)-(4+1) = -15+10-5 = -10$$

$$ Delta_x = begin{vmatrix} 13 & 2 & -1 \ -2 & -1 & 3 \ 9 & 2 & -1 \ end{vmatrix} = 13 = begin{vmatrix} -1 & 3 \ 2 & -1 \ end{vmatrix} – 2 = begin{vmatrix} -2 & 3 \ 9 & -1 \ end{vmatrix} – 1 = begin{vmatrix} -2 & -1 \ 9 & 2 \ end{vmatrix} = $$

$$ = 13(1-6)-2(2-27)-(-4+9) = -65+50-5=-20 $$

$$ Delta_y = begin{vmatrix} 3 & 13 & -1 \ 2 & -2 & 3 \ 1 & 9 & -1 \ end{vmatrix} = 3 = begin{vmatrix} -2 & 3 \ 9 & -1 \ end{vmatrix} – 13 = begin{vmatrix} 2 & 3 \ 1 & -1 \ end{vmatrix} – 1 = begin{vmatrix} 2 & -2 \ 1 & 9 \ end{vmatrix} = $$

$$ = 3(2-27)-13(-2-3)-(18+2) = -75+65-20 = -30 $$

$$ Delta_z = begin{vmatrix} 3 & 2 & 13 \ 2 & -1 & -2 \ 1 & 2 & 9 \ end{vmatrix} = 3 = begin{vmatrix} -1 & -2 \ 2 & 9 \ end{vmatrix} – 2 = begin{vmatrix} 2 & -2 \ 1 & 9 \ end{vmatrix} + 13 = begin{vmatrix} 2 & -1 \ 1 & 2 \ end{vmatrix} = $$

$$ = 3(-9+4)-2(18+2)+13(4+1) = -15-40+65 = 10 $$

$$ x = frac{Delta_x}{Delta} = frac{-20}{-10} = 2, y = {Delta_y}{Delta} = frac{-30}{-10} = 3, z = {Delta_z}{Delta} = frac{10}{-10} = -1$$

Ответ: (2;3;-1)

$б) {left{ begin{array}{c} x+y+3z = 6 \ 2x-5y-z = 5 \ x+2y-5z = -11 end{array} right.} $

$$ Delta = begin{vmatrix} 1 & 1 & 3 \ 2 & -5 & -1\ 1 & 2 & -5 end{vmatrix} = 1 = begin{vmatrix} -5 & -1 \ 2 & -5 \ end{vmatrix} – 1 = begin{vmatrix} 2 & -1 \ 1 & -5 \ end{vmatrix} + 3 = begin{vmatrix} 2 & -5 \ 1 & 2 \ end{vmatrix} = $$

$$= (25+2)—(-10+1)+3(4+5) = 27+9+27 = 63$$

$$ Delta_x = begin{vmatrix} 6 & 1 & 3 \ 5 & -5 & -1 \ -11 & 2 & -5 \ end{vmatrix} = 6 = begin{vmatrix} -5 & -1 \ 2 & -5 \ end{vmatrix} – 1 = begin{vmatrix} 5 & -1 \ -11 & -5 \ end{vmatrix} + 3 = begin{vmatrix} 5 & -5 \ -11 & 2 \ end{vmatrix} = $$

$$ = 6(25+2)—(-25-11)+3(10-55) = 162+36-135 = 63 $$

$$ Delta_y = begin{vmatrix} 1 & 16 & 3 \ 2 & 5 & -1 \ 1 & -11 & -5 \ end{vmatrix} = 1 = begin{vmatrix} 5 & -1 \ -11 & -5 \ end{vmatrix} – 6 = begin{vmatrix} 2 & -1 \ 1 & -5 \ end{vmatrix} + 3 = begin{vmatrix} 2 & 5 \ 1 & -11 \ end{vmatrix} = $$

$$ = (-25-11)—6(-10+1)+3(-22-5) = -36+54-81 = -63 $$

$$ Delta_z = begin{vmatrix} 1 & 1 & 6 \ 2 & -5 & 5 \ 1 & 2 & -11 \ end{vmatrix} = 1 = begin{vmatrix} -5 & 5 \ 2 & -11 \ end{vmatrix} – 1 = begin{vmatrix} 2 & 5 \ 1 & -11 \ end{vmatrix} + 6 = begin{vmatrix} 2 & -5 \ 1 & 2 \ end{vmatrix} = $$

$$ = (55-10)—(-22-5)+6(4+5) = 45+27+54 = 126 $$

$$ x = frac{Delta_x}{Delta} = frac{63}{63} = 1, y = {Delta_y}{Delta} = frac{-63}{63} = -1, z = {Delta_z}{Delta} = frac{126}{63} = 2$$

Ответ: (1;-1;2)

Пример 3*. Решите систему уравнений относительно x,y,и z:

$$ {left{ begin{array}{c} a^3+a^2 x+ay+z = 0 \ b^3+b^2 x+by+z = 0 \ c^3+c^2 x+cy+z = 0 end{array} right.} $$

$$ a neq b, b neq c, a neq c $$

Решаем методом замены:

$$ {left{ begin{array}{c} z = -(a^3+a^2 x+ay)\ b^3+b^2 x+by-(a^3+a^2 x+ay) = 0 \ c^3+c^2 x+cy-(a^3+a^2 x+ay) = 0 end{array} right.} Rightarrow {left{ begin{array}{c}z = -(a^3+a^2 x+ay)\ (b^2-a^2 )x+(b-a)y = a^3-b^3 \ (c^2-a^2 )x+(c-a)y = a^3-c^3 end{array} right.} $$

Т.к. $ a neq b$ второе уравнение можно сократить на $(a-b) neq 0$

Т.к.$ a neq c$ третье уравнение можно сократить на $(a-с) neq 0 $. В третьем уравнении после сокращения поменяем знаки:

$$ {left{ begin{array}{c} z = -(a^3+a^2 x+ay) \ -(a-b)(a+b)x-(a-b)y = (a-b)(a^2+ab+b^2 ) \ -(a-c)(a+c)x-(a-c)y = (a-c)(a^2+ac+c^2 ) end{array} right.} $$

$$ {left{ begin{array}{c} z = -(a^3+a^2 x+ay) \ -(a+b)x-y = a^2+ab+b^2 \ (a+c)x+y = -(a^2+ac+c^2 ) end{array} right.} $$

$$ {left{ begin{array}{c} z = -(a^3+a^2 x+ay) \ -(a+b)x+(a+c)x = (a^2+ab+b^2 ) – (a^2+ac+c^2 ) \ y = -(a+c)x-(a^2+ac+c^2 ) end{array} right.} $$

Из второго уравнения получаем:

$$x = frac{ab+b^2-ac-c^2}{c-b} = -frac{a(b-c)+(b^2-c^2 )}{b-c} = – frac{(b-c)(a+b+c)}{b-c} $$

Т.к. $b neq c$ можно сократить на $(b-c) neq 0$:

$$ x = -(a+b+c)$$

Подставляем:

$$ y = -(a+c)x-(a^2+ac+c^2 ) = (a+c)(a+b+c)-(a^2+ac+c^2 ) = $$

$$ = a^2+ab+ac+ac+bc+c^2-a^2-ac-c^2 = ab+ac+bc $$

$$ z = -(a^3+a^2 x+ay) = -a^3+a^2 (a+b+c)-a(ab+ac+bc) = $$

$$ = -a^3+a^3+a^2 b+a^2 c-a^2 b-a^2 c-abc = -abc $$

Ответ:$ {left{ begin{array}{c} x = -(a+b+c) \ y = ab+ac+bc \ z = -abc end{array} right.} $

Системы линейных уравнений

Линейные уравнения (уравнения первой степени) с двумя неизвестными

Определение 1 . Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид

где a , b , c – заданные числа.

Определение 2 . Решением уравнения (1) называют пару чисел (x ; y) , для которых формула (1) является верным равенством.

Пример 1 . Найти решение уравнения

Решение . Выразим из равенства (2) переменную y через переменную x :

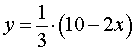(3)

Из формулы (3) следует, что решениями уравнения (2) служат все пары чисел вида

где x – любое число.

Замечание . Как видно из решения примера 1, уравнение (2) имеет бесконечно много решений. Однако важно отметить, что не любая пара чисел (x ; y) является решением этого уравнения. Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).

Системы из двух линейных уравнений с двумя неизвестными

Определение 3 . Системой из двух линейных уравнений с двумя неизвестными x и y называют систему уравнений, имеющую вид

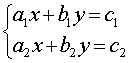(4)

Определение 4 . В системе уравнений (4) числа a₁ , b₁ , a₂ , b₂ называют коэффициентами при неизвестных , а числа c₁ , c₂ – свободными членами .

Определение 5 . Решением системы уравнений (4) называют пару чисел (x ; y) , являющуюся решением как одного, так и другого уравнения системы (4).

Определение 6 . Две системы уравнений называют равносильными (эквивалентными) , если все решения первой системы уравнений являются решениями второй системы, и все решения второй системы являются решениями первой системы.

Равносильность систем уравнений обозначают, используя символ «»

Системы линейных уравнений решают с помощью метода последовательного исключения неизвестных , который мы проиллюстрируем на примерах.

Пример 2 . Решить систему уравнений

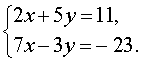(5)

Решение . Для того, чтобы решить систему (5) исключим из второго уравнения системы неизвестное х .

С этой целью сначала преобразуем систему (5) к виду, в котором коэффициенты при неизвестном x в первом и втором уравнениях системы станут одинаковыми.

Если первое уравнение системы (5) умножить на коэффициент, стоящий при x во втором уравнении (число 7 ), а второе уравнение умножить на коэффициент, стоящий при x в первом уравнении (число 2 ), то система (5) примет вид

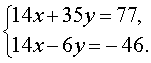(6)

Теперь совершим над системой (6) следующие преобразования:

• первое уравнение системы оставим без изменений;
• из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.

В результате система (6) преобразуется в равносильную ей систему

Из второго уравнения находим y = 3 , и, подставив это значение в первое уравнение, получаем

Пример 3 . Найти все значения параметра p , при которых система уравнений

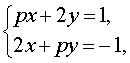(7)

а) имеет единственное решение;

б) имеет бесконечно много решений;

в) не имеет решений.

Решение . Выражая x через y из второго уравнения системы (7) и подставляя полученное выражение вместо x в первое уравнение системы (7), получим

Следовательно, система (7) равносильна системе

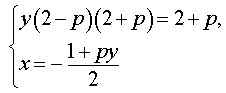(8)

Исследуем решения системы (8) в зависимости от значений параметра p . Для этого сначала рассмотрим первое уравнение системы (8):

y (2 – p) (2 + p) = 2 + p

(9)

Если , то уравнение (9) имеет единственное решение

Следовательно, система (8) равносильна системе

Таким образом, в случае, когда , система (7) имеет единственное решение

Если p = – 2 , то уравнение (9) принимает вид

,

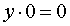
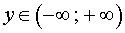
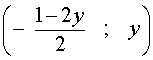
и его решением является любое число . Поэтому решением системы (7) служит бесконечное множество всех пар чисел

,

где y – любое число.

Если p = 2 , то уравнение (9) принимает вид

и решений не имеет, откуда вытекает, что и система (7) решений не имеет.

Системы из трех линейных уравнений с тремя неизвестными

Определение 7 . Системой из трех линейных уравнений с тремя неизвестными x , y и z называют систему уравнений, имеющую вид

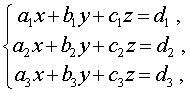(10)

Определение 9 . Решением системы уравнений (10) называют тройку чисел (x ; y ; z) , при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.

Пример 4 . Решить систему уравнений

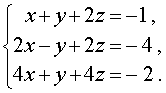(11)

Решение . Будем решать систему (11) при помощи метода последовательного исключения неизвестных .

Для этого сначала исключим из второго и третьего уравнений системы неизвестное y , совершив над системой (11) следующие преобразования:

• первое уравнение системы оставим без изменений;
• ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
• из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.

В результате система (11) преобразуется в равносильную ей систему

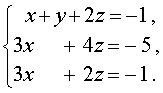(12)

Теперь исключим из третьего уравнения системы неизвестное x , совершив над системой (12) следующие преобразования:

• первое и второе уравнения системы оставим без изменений;
• из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.

В результате система (12) преобразуется в равносильную ей систему

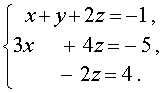(13)

Из системы (13) последовательно находим

Пример 5 . Решить систему уравнений

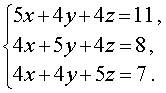(14)

Решение . Заметим, что из данной системы можно получить удобное следствие, сложив все три уравнения системы:

Если числа (x ; y ; z) являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа (x ; y ; z) должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):

Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) равносильными, то полученный результат нужно проверить. Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.

Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы с нелинейными уравнениями» и нашим учебным пособием «Системы уравнений».

Система линейных уравнений с тремя переменными

Линейное уравнение с тремя переменными и его решение

Уравнение вида ax+by+cz = d , где a, b, c, d – данные числа, называется линейным уравнением с тремя переменными x, y и z.

Например: $2x+5y+z = 8; -x+1, 5y+2z = 0; frac<1> <2>x-8y-5z = 7$

Уравнение с тремя переменными может быть не только линейным, т.е. содержать не только первые степени переменных x,y и z.

Например: $2x^2+xz+y^2+yz^2 = 3,x-5y^2+z^3 = 1, 7x^3+y+xyz = 7$

Решением уравнения с тремя переменными называется упорядоченная тройка значений переменных (x,y,z), обращающая это уравнение в тождество.

О тождествах – см. §3 данного справочника

Например: для уравнения 2x+5y+z=8 решениями являются тройки x = -2, y = 1, z = 7; x = -1, y = 1, 6 , z = 2; x = -3, y = 2, 4, z = 2 и т.д. Уравнение имеет бесконечное множество решений.

Геометрическим представлением линейного уравнения с тремя переменными является плоскость в трёхмерном координатном пространстве .

Решение системы линейных уравнений с тремя переменными методом подстановки

Алгоритм метода подстановки для системы уравнений с тремя переменными аналогичен алгоритму для двух переменных (см.§45 данного справочника)

Например: решить систему

$$ <left< begin 3x+2y-z = 8 \ x-y+z = -2 \ 2x-3y-5z = 1 end right.> Rightarrow <left< begin 3(y-z-2)+2y-z = 8 \ x = y-z-2 \ 2(y-z-2)-3y-5z = 1 end right.> Rightarrow $$

$$ Rightarrow <left< begin x = y-z-2 \ 5y-4z = 14 \ -y-7z = 5 end right.> Rightarrow <left< begin x = y-z-2 \ y = -7z-5 \ 5(-7z-5)-4z = 14 end right.> Rightarrow <left< begin x = y-z-2 \ y = -7z-5 \ -39z = 39 end right.> Rightarrow $$

$$ Rightarrow <left< begin x = 2-(-1)-2 = 1 \ y = -7cdot(-1)-5 = 2 \ z = -1 end right.> Rightarrow <left< begin x = 1 \ y = 2 \ z = -1 end right.> $$

Решение системы линейных уравнений с тремя переменными методом Крамера

Для системы с 3-мя переменными действуем по аналогии.

Дана система 3-х линейных уравнений с 3-мя переменными:

$$ <left< begin a_1 x+b_1 y+c_1 z = d_1 \ a_2 x+b_2 y+c_2 z = d_2 \ a_3 x+b_3 y+c_3 z = d_3 end right.> $$

Определим главный определитель системы:

$$ Delta = begin a_1 & b_1 & c_1 \ a_2 & b_2 & c_2 \ a_3 & b_3 & c_3 end $$

и вспомогательные определители :

$$ Delta_x = begin d_1 & b_1 & c_1 \ d_2 & b_2 & c_2 \ d_3 & b_3 & c_3 end, Delta_y = begin a_1 & d_1 & c_1 \ a_2 & d_2 & c_2 \ a_3 & d_3 & c_3 end, Delta_z = begin a_1 & b_1 & d_1 \ a_2 & b_2 & d_2 \ a_3 & b_3 & d_3 end $$

Тогда решение системы:

Соотношение значений определителей, расположения плоскостей и количества решений:

Три плоскости пересекаются в одной точке

Три плоскости параллельны

Две или три плоскости совпадают или пересекаются по прямой

Бесконечное множество решений

Осталось определить правило вычисления определителя 3-го порядка.

Таких правил несколько, приведём одно из них (так называемое «раскрытие определителя по первой строке»):

$$ Delta = begin a_1 & b_1 & c_1 \ a_2 & b_2 & c_2 \ a_3 & b_3 & c_3 end = a_1 = begin b_2 & c_2 \ b_3 & c_3 end – b_1 = begin a_2 & c_2 \ a_3 & c_3 end + c_1 = begin a_2 & b_2 \ a_3 & b_3 end = $$

$$ = a_1 (b_2 c_3-b_3 c_2 )-b_1 (a_2 c_3-a_3 c_2 )+c_1 (a_2 b_3-a_3 b_2 )$$

Примеры

Пример 1. Найдите решение системы уравнений методом подстановки:

$$<left< begin z = 3x+2y-13 \ 2x-y+3(3x+2y-13) = -2 \ x+2y-(3x+2y-13) = 9 end right.> Rightarrow <left< begin z = 3x+2y-13 \ 11x+5y = 37 \ -2x = -4 end right.> Rightarrow $$

$$Rightarrow <left< begin z = 3cdot2+2cdot3-13 = -1 \ y = frac<37-11cdot2> <5>= 3 \ x = 2 end right.> Rightarrow <left< begin x = 2 \ y = 3 \ z = -1 end right.> $$

$$ <left< begin x = -y-3z+6 \ 2(-y-3z+6)-5y-z = 5\ (-y-3z+6)+2y-5z = -11 end right.> Rightarrow <left< begin x = -y-3z+6 \ -7y-7z = -7 |:(-7) \ y-8z = -17 end right.> Rightarrow $$

$$ Rightarrow <left< begin x = -y-3z+6 \ y+z = 1 \ y-8z = -17 end right.> Rightarrow <left< begin x = -y-3z+6 \ 9z = 18 \ y = 1-z end right.> Rightarrow <left< begin x = 1-6+6 = 1 \ z = 2 \ y = 1-2 = -1 end right.> Rightarrow$$

Пример 2. Найдите решение системы уравнений методом Крамера:

$$ Delta = begin 3 & 2 & -1 \ 2 & -1 & 3\ 1 & 2 & -1 end = 3 = begin -1 & 3 \ 2 & -1 \ end – 2 = begin 2 & 3 \ 1 & -1 \ end – 1 = begin 2 & -1 \ 1 & 2 \ end = $$

$$ Delta_x = begin 13 & 2 & -1 \ -2 & -1 & 3 \ 9 & 2 & -1 \ end = 13 = begin -1 & 3 \ 2 & -1 \ end – 2 = begin -2 & 3 \ 9 & -1 \ end – 1 = begin -2 & -1 \ 9 & 2 \ end = $$

$$ Delta_y = begin 3 & 13 & -1 \ 2 & -2 & 3 \ 1 & 9 & -1 \ end = 3 = begin -2 & 3 \ 9 & -1 \ end – 13 = begin 2 & 3 \ 1 & -1 \ end – 1 = begin 2 & -2 \ 1 & 9 \ end = $$

$$ Delta_z = begin 3 & 2 & 13 \ 2 & -1 & -2 \ 1 & 2 & 9 \ end = 3 = begin -1 & -2 \ 2 & 9 \ end – 2 = begin 2 & -2 \ 1 & 9 \ end + 13 = begin 2 & -1 \ 1 & 2 \ end = $$

$$ Delta = begin 1 & 1 & 3 \ 2 & -5 & -1\ 1 & 2 & -5 end = 1 = begin -5 & -1 \ 2 & -5 \ end – 1 = begin 2 & -1 \ 1 & -5 \ end + 3 = begin 2 & -5 \ 1 & 2 \ end = $$

$$ Delta_x = begin 6 & 1 & 3 \ 5 & -5 & -1 \ -11 & 2 & -5 \ end = 6 = begin -5 & -1 \ 2 & -5 \ end – 1 = begin 5 & -1 \ -11 & -5 \ end + 3 = begin 5 & -5 \ -11 & 2 \ end = $$

$$ = 6(25+2)—(-25-11)+3(10-55) = 162+36-135 = 63 $$

$$ Delta_y = begin 1 & 16 & 3 \ 2 & 5 & -1 \ 1 & -11 & -5 \ end = 1 = begin 5 & -1 \ -11 & -5 \ end – 6 = begin 2 & -1 \ 1 & -5 \ end + 3 = begin 2 & 5 \ 1 & -11 \ end = $$

$$ Delta_z = begin 1 & 1 & 6 \ 2 & -5 & 5 \ 1 & 2 & -11 \ end = 1 = begin -5 & 5 \ 2 & -11 \ end – 1 = begin 2 & 5 \ 1 & -11 \ end + 6 = begin 2 & -5 \ 1 & 2 \ end = $$

Пример 3*. Решите систему уравнений относительно x,y,и z:

$$ a neq b, b neq c, a neq c $$

Решаем методом замены:

$$ <left< begin z = -(a^3+a^2 x+ay)\ b^3+b^2 x+by-(a^3+a^2 x+ay) = 0 \ c^3+c^2 x+cy-(a^3+a^2 x+ay) = 0 end right.> Rightarrow <left< beginz = -(a^3+a^2 x+ay)\ (b^2-a^2 )x+(b-a)y = a^3-b^3 \ (c^2-a^2 )x+(c-a)y = a^3-c^3 end right.> $$

Т.к. $ a neq b$ второе уравнение можно сократить на $(a-b) neq 0$

Т.к.$ a neq c$ третье уравнение можно сократить на $(a-с) neq 0 $. В третьем уравнении после сокращения поменяем знаки:

Из второго уравнения получаем:

Т.к. $b neq c$ можно сократить на $(b-c) neq 0$:

$$ z = -(a^3+a^2 x+ay) = -a^3+a^2 (a+b+c)-a(ab+ac+bc) = $$

$$ = -a^3+a^3+a^2 b+a^2 c-a^2 b-a^2 c-abc = -abc $$

Системы линейных уравнений с тремя переменными

Линейным уравнением называется уравнение вида:

В этом уравнении – неизвестные, а – действительные (или комплексные) числа. При этом называются коэффициентами уравнения, а – свободным членом.

Рассмотрим систему трех линейных уравнений с тремя неизвестными:

Из трех способов решения этих систем: графического, способа подстановки и способа сложения остается два последних способа. Графический способ уже не проходит, так как пришлось бы находить точку пересечения трех плоскостей. А это трудно изобразить.

Способ подстановки для трех уравнений похож на способ подстановки для двух уравнений с двумя неизвестными, только у этого способа на один шаг больше. Первое: выражаем одно из неизвестных из одного уравнения через два остальных неизвестных и подставляем это выражение в оставшиеся два уравнения. Эти оставшиеся два уравнения составляют систему из двух уравнений с двумя неизвестными. А дальше решаем эту полученную систему и находим два неизвестных, а затем, зная их, и третье неизвестное.

Пример 1 Решить систему уравнений: способом подстановки.

Выразим из первого уравнения через остальные неизвестные и свободный член. Найденное выражение подставим в остальные уравнения.

Далее, оставляя первое уравнение в покое, решаем систему из двух получившихся уравнений с неизвестными и (предварительно разделив обе части второго уравнения на ).

Получили единственное решение системы

Рассмотрим теперь способ сложения. Так же как и для двух уравнений с двумя неизвестными, нужно при помощи сложения уравнений добиться, чтобы одно из неизвестных пропало.Приведем пример.

Пример 2 Решить систему уравнений: способом сложения.

Постараемся получить два уравнения с двумя неизвестными. Избавимся от неизвестной . Для этого удвоенное первое уравнение сложим почленно с удвоенным вторым уравнением, а удвоенное второе уравнение прибавим к третьему уравнению:

Далее производим почленное сложение двух уравнений с двумя неизвестными, исключая неизвестную :

Из последнего уравнения системы находим . Подставляя найденное значение во второе уравнение, находим . Наконец из первого уравнения находим . Итак – единственное решение системы.

В заключении решим задачу, которая приводится к системе с тремя неизвестными.

Задача В трех урнах – шариков. В первой урне шариков больше чем во второй на столько, сколько шариков в третьей урне. Число шариков во второй урне относится к числу шариков в третьей урне как . Сколько шариков в каждой урне?

Обозначим число шариков в 1-й, 2-й и 3-й урнах через соответственно. Тогда первое условие задачи дает уравнение , второе условие – , а третье условие – . Запишем три полученные уравнения в систему, сделав предварительно третье уравнение линейным:

Складывая почленно первые два уравнения находим .Решаем систему из двух оставшихся уравнений:

Итак, в урнах соответственно и шариков.

Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.

Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.

Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.

Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).

В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.

В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.

Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.

Нужна помощь с курсовой или дипломной работой?

[spoiler title=”источники:”]

http://reshator.com/sprav/algebra/7-klass/sistema-linejnyh-uravnenij-s-tremya-peremennymi/

http://khab.work5.ru/spravochnik/matematika/sistemy-linejnykh-uravnenij-s-tremya-peremennymi

[/spoiler]

Литература: (1,
с. 18-34; 2, с. 82-100; 3, с. 286-275)

1. Основные
   понятия

Системой линейных
уравнений называется совокупность
рассматриваемых совместно нескольких
линейных уравнений.

В системе может
быть любое число уравнений с любым
числом неизвестных.

Решением системы
уравнений называется совокупность
значений неизвестных, удовлетворяющая
всем уравнениям системы, то есть
обращающая их в тождества.

Система, имеющая
решение, называется совместной, в
противном случае – несовместной.

Для решения системы
применяют различные методы.

1. Решение систем
   линейных уравнений снеизвестными

Пусть
(число уравнений равно числу неизвестных).

Метод Крамера

Рассмотрим решение
системы трёх линейных уравнений с тремя
неизвестными:

(7)

Для нахождения
неизвестных
применим формулу Крамера:

(8)

где
– определитель системы, элементы которого
есть коэффициенты при неизвестных:

.

получается путём
замены первого столбца определителя
столбцом свободных членов:

.

Аналогично:

;.

Пример 1. Решить
систему по формуле Крамера:

.

Решение: Воспользуемся
формулами (8):

;

;

;

;

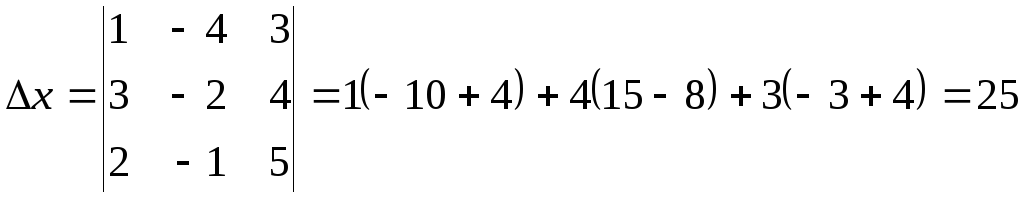
Тогда

Ответ:
.

Для любой системы
линейных уравнений снеизвестными можно утверждать:

1. Если определить
   системы
   ,
   то система имеет единственное решение,
   которое может быть найдено по формулам
   Крамера.

2. Если
   ,
   то правило Крамера неприменимо. В этом
   случае система может иметь бесчисленное
   множество решений, еслиили не иметь их, если хотя бы один из
   определителейне равен нулю.

Матричный способ
решения

Рассмотрим решение
системы (7) трёх линейных уравнений с
тремя неизвестными матричным способом.

Используя правила
умножения матриц, данную систему
уравнений можно записать в виде:
,
где

.

Пусть матрица
невырожденная, т.е..
Умножая обе части матричного уравнения
слева на матрицу,
обратную матрице,
получим:.

Учитывая, что
,
имеем

(9)

Пример 2. Решить
систему матричным способом:

.

Решение: Введём
матрицы:

–
из коэффициентов при неизвестных;

–
столбец свободных членов.

Тогда систему
можно записать матричным уравнением:
.

Воспользуемся
формулой (9). Найдём обратную матрицу
по формуле (6):

;

Тогда

.

Следовательно,

Получили:

.

Ответ:
.

Метод последовательного
исключения неизвестных (метод Гаусса)

Основная идея
применяемого метода заключается в
последовательном исключении неизвестных.
Поясним смысл этого метода на системе
трёх уравнений с тремя неизвестными:

.

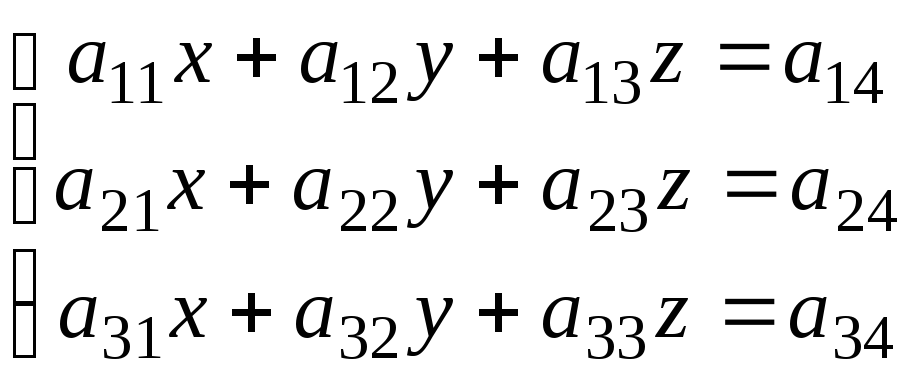
Допустим, что
(если,
то изменим порядок уравнений, выбрав
первым уравнением то, в котором коэффициент
прине равен нулю).

Первый шаг: а) делим
уравнение
на;
б) умножаем полученное уравнение наи вычитаем из;
в) затем полученное умножаем наи вычитаем из.
В результате первого шага будем иметь
систему:

причём

,

Второй шаг: поступаем
с уравнением
иточно так же, как с уравнениями.

В итоге исходная
система преобразуется к так называемому
ступенчатому виду:

Из преобразованной
системы все неизвестные определяются
последовательно без труда.

Замечание.
Практически удобнее приводить к
ступенчатому виду не саму систему
уравнений, а матрицу из коэффициентов,
при неизвестных, и свободных членов.

Пример 3. Решить
методом Гаусса систему:

.

Переход от одной
матрицы к другой будем записывать при
помощи знака эквивалентности ~.

~~~~

~.

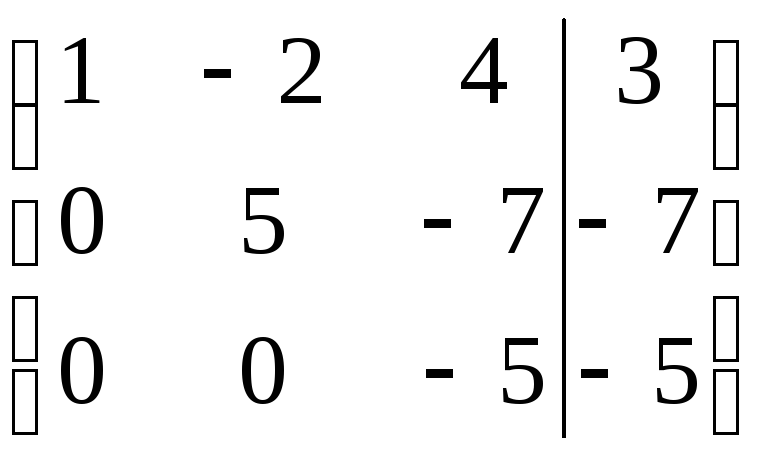
По полученной
матрице выписываем преобразованную
систему:

.

Тогда

Ответ:
.

Замечание: Если
система имеет единственное решение, то
ступенчатая система приводится к
треугольной, то есть к такой, в которой
последнее уравнение будет содержать
одно неизвестное. В случае неопределённой
системы, то есть такой, в которой число
неизвестных больше числа линейно
независимых уравнений, треугольной
системы не будет, так как последнее
уравнение будет содержать более одного
неизвестного (система имеет бесчисленное
множество решений). Когда же система
несовместна, то, после приведения её к
ступенчатому виду, она будет содержать
хотя бы одно
значение вида,
то есть уравнение, в котором все
неизвестные имеют нулевые коэффициенты,
а правая часть отлична от нуля (система
решений не имеет). Метод Гаусса применим
к произвольной системе линейных уравнений
(при любыхи).

1. Теорема
   существования решения системы линейных
   уравнений

При решении системы
линейных уравнений методом гаусса ответ
на вопрос, совместна или несовместна
данная система может быть дан лишь в
конце вычислений. Однако часто бывает
важно решить вопрос о совместности или
несовместности системы уравнений, не
находя самих решений. Ответ на этот
вопрос даёт следующая теорема
Кронекера-Капелли.

Пусть дана система
линейных уравнений снеизвестными:

(10)

Для того, чтобы
система (10) была совместной, необходимо
и достаточно чтобы ранг матрицы системы

.

был равен рангу
её расширенной матрицы

.

Причём, если
,
то система (10) имеет единственное решение;
если же,
то система имеет бесчисленное множество
решений.

1. Линейная,
   однородная система
   уравнений снеизвестными

Рассмотрим
однородную систему (все свободные члены
равны нулю) линейных уравнений:

.

Эта система всегда
совместна, так как она имеет нулевое
решение
.

В следующей теореме
даны условия, при которых система имеет
также решения, отличные от нулевого.

Терема. Для того,
чтобы однородная система линейчатых
уравнений имела нулевое решение,
необходимо и достаточно, чтобы её
определитель
был равен нулю:

.

Таким образом,
если
,
то решение– единственное. Если,
то существует бесконечноё множество
других ненулевых решений. Укажем один
из способов отыскания решений для
однородной системы трёх линейных
уравнений с тремя неизвестными в случае.

Можно доказать,
что если
,
а первое и второе уравнения непропорциональны
(линейно независимы), то третье уравнение
есть следствие первых двух. Решение
однородной системы трёх уравнений с
тремя неизвестными сводится к решению
двух уравнений с тремя неизвестными.
Появляется так называемое свободное
неизвестное, которому можно придавать
произвольные значения.

Пример 4. Найти
все решения системы:

.

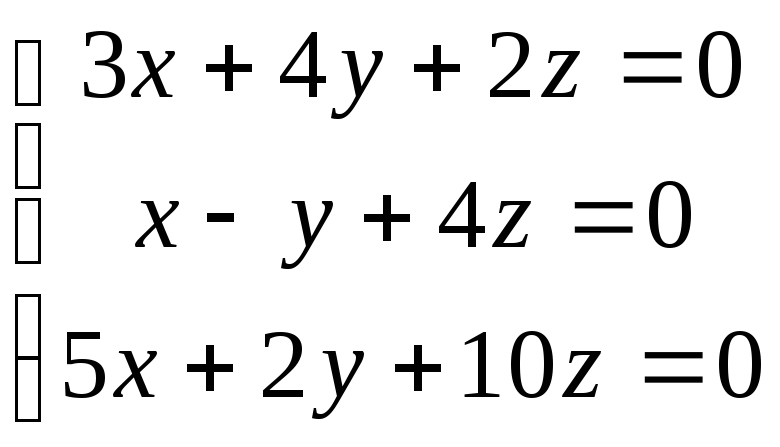
Решение. Определитель
этой системы

.

Поэтому система
имеет нулевые решения. Можно заметить,
что первые два уравнения, например,
непропорциональны, следовательно, они
линейно независимые. Третье является
следствием первых двух (получается,
если к первому уравнению прибавить
удвоенное второе). Отбросив его, получим
систему двух уравнений с тремя
неизвестными:

.

Полагая, например,
,
получим

.

Решая систему двух
линейных уравнений, выразим
ичерез:.
Следовательно, решение системы можно
записать в виде:,
где– произвольное число.

Пример 5. Найти
все решения системы:

.

Решение. Нетрудно
видеть, что в данной системе только одно
независимое уравнение (два других ему
пропорциональны). Система из трёх
уравнений с тремя неизвестными свелась
к одному уравнению с тремя неизвестными.
Появляются два свободных неизвестных.
Найдя, например, из первого уравнения
при произвольныхи,
получим решения данной системы. Общих
вид решения можно записать,
гдеи– произвольные числа.

1. Вопросы для
   самопроверки

Сформулируйте
правило Крамера для решения системы
линейных уравнений снеизвестными.

В чём сущность
матричного способа решения систем?

В чём заключается
метод Гаусса решения системы линейных
уравнений?

Сформулируйте
теорему Кронекера-Капелли.

Сформулируйте
необходимое и достаточноё условие
существования ненулевых решений
однородной системы линейных уравнений.

1. Примеры для
   самостоятельного решения

Найдите все решения
систем:

1.
; 2.;

3.
; 4.;

5.
; 6.;

7.
; 8.;

9.
; 10.;

11.
; 12.;

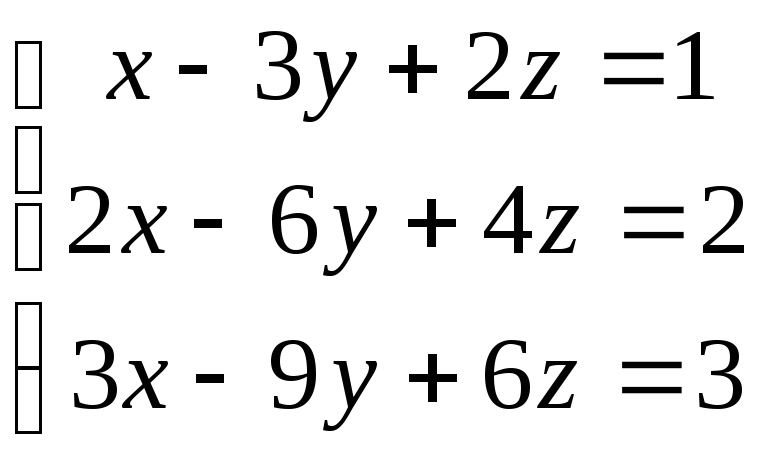
13.
;
14.
;

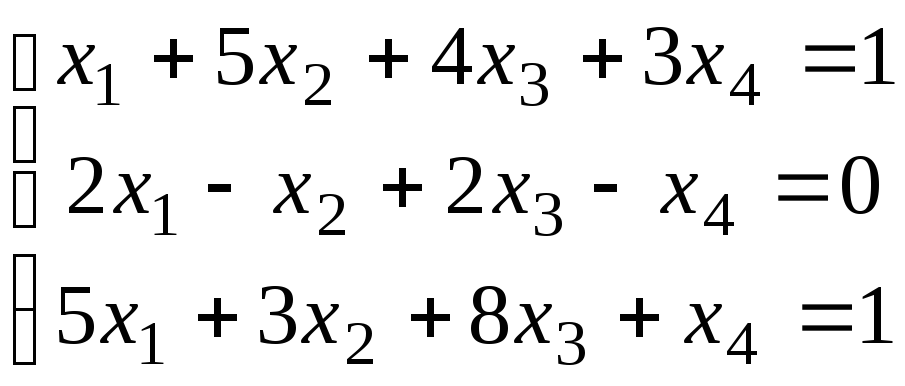
15.
.

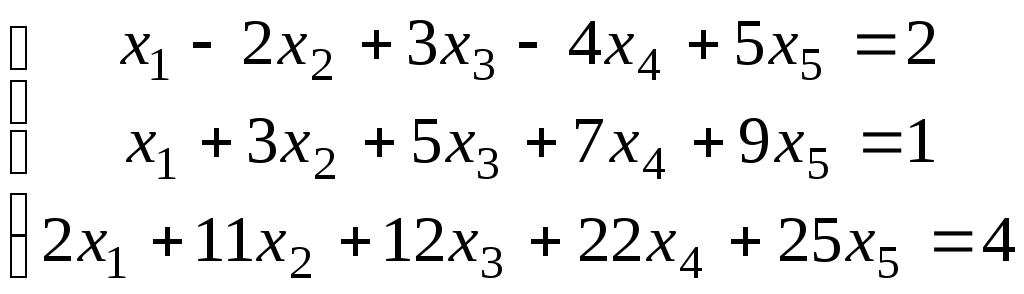
Определите, при
каких значениях
исистема уравнений

а) имеет единственное
решение;

б) не имеет решения;

в) имеет бесконечно
много решений.

16.
; 17.;

Найти все решения
следующих однородных систем:

18.
; 19.;

20.
; 21.;

22.
; 23.;

1. Ответы к
   примерам

1.
; 2.; 3.
Ǿ; 4. Ǿ;

5.
– произвольное число.

6.
,
где– произвольное число.

7.
; 8.; 9.
Ǿ; 10. Ǿ;

11.
,
где– произвольное число.

12.
,
гдеи– произвольные числа.

13.
; 14.гдеи– произвольные числа.

15. Ǿ; 16. а)
;
б);
в).

17. а)
;
б);
в);

18.
; 19.; 20.,
где– произвольное число.

21.
,
где– произвольное число.

22.
,
где– произвольное число.

23.
,
гдеи– произвольные числа.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Как решить систему с тремя неизвестными

Линейная система с тремя неизвестными имеет несколько способов решения. Найти решение системы можно с помощью правила Кремера через определители, методом Гаусса или используя простой способ подстановки. Метод подстановки является основным для решения систем линейных уравнений небольшого порядка. Он заключается в поочередном выражении из каждого уравнения системы одной неизвестной переменной, подстановки ее в следующее уравнение и упрощение получаемых выражений.

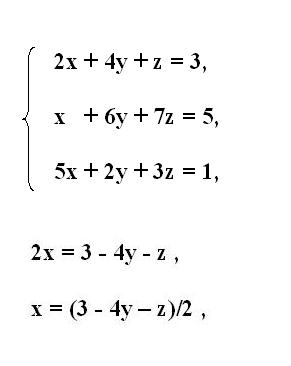
Инструкция

Запишите исходную систему уравнений третьего порядка. Из первого уравнения системы выразите первую неизвестную переменную х. Для этого перенесите члены, содержащие другие переменные за знак равенства. Перенесенным членам поменяйте знак на противоположный.

Если при множителе с выражаемой переменной присутствует коэффициент отличный от единицы, поделите на его значение все уравнение. Таким образом, вы получите переменную х, выраженную через остальные члены уравнения.

Подставьте во второе уравнение вместо х то выражение, которое вы получили из первого уравнения. Упростите полученную запись, произведя сложение или вычитание подобных членов. Аналогично предыдущему шагу выразите из второго уравнения следующую неизвестную переменную у. Также перенесите все другие члены за знак равенства и поделите все уравнение на коэффициент при у.

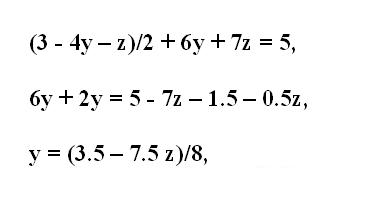
В последнее третье уравнение подставьте вместо двух неизвестных переменных х и у выраженные значения из первого и второго уравнений системы. Причем в выражении х также замените переменную у. Упростите полученное уравнение. В нем в качестве неизвестной величины останется лишь третья переменная z. Выразите ее из уравнения, как описано выше, и высчитайте ее значение.

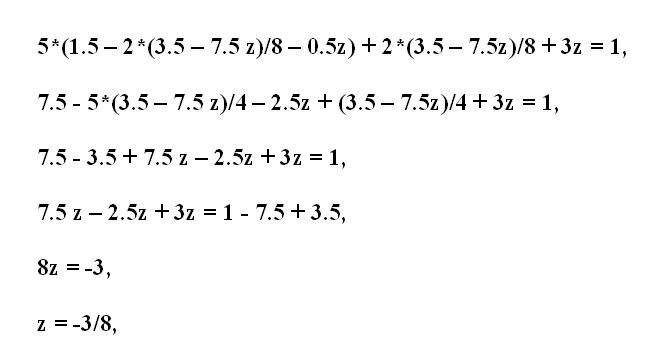
В выражение у из второго уравнения подставьте известное значение переменной z. Подсчитайте значение переменной у. Далее в выражение переменной х подставьте значения переменных у и z. Вычислите х. Запишите полученные значения х, у и z – это и есть решение системы с тремя неизвестными.

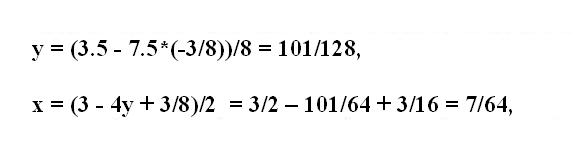
Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?