Как найти решение уравнений через матрицу

Решаем СЛАУ методом обратной матрицы:

2×1-4×2+3×3=1×1-2×2+4×3=33×1-x2+5×3=2

Как решить?

• Записываем систему в виде матричного уравнения АX=B, где

А=2-431-243-15, X=x1x2x3, B=132.  

• Выражаем из этого уравнения X:

X=A-1×B

• Находим определитель матрицы А:

det A= 2-431-243-15=2×(-2)×5+3×(-4)×4+3×(-1)×1-3×(-2)×3–1×(-4)×5-2×4-(-1)=-20-48-3+18+20+8=-25

det А не равняется 0, следовательно, для этой системы подходит метод решения обратной матрицей.

• Находим обратную матрицу А-1  при помощи союзной матрицы. Вычисляем алгебраические дополнения Аij к соответствующим элементам матрицы А:

А11=(-1)(1+1)-24-15=-10+4=-6,

А12=(-1)1+21435=-(5-12)=7,

А13=(-1)1+31-23-1=-1+6=5,

А21=(-1)2+1-43-15=-(-20+3)=17,

А22=(-1)2+22335-10-9=1,

А23=(-1)2+32-43-1=-(-2+12)=-10,

А31=(-1)3+1-43-24=-16+6=-10,

А32=(-1)3+22314=-(8-3)=-5,

А33=(-1)3+32-41-2=-4+4=0.

• Записываем союзную матрицу А*, которая составлена из алгебраических дополнений матрицы А:

А*=-675171-10-10-50

• Записываем обратную матрицу согласно формуле:

A-1=1detA(A*)T: А-1=-125-617-1071-55-100,

• Умножаем обратную матрицу А-1 на столбец свободных членов В и получаем решение системы:

X=A-1×B=-125-617-1071-55-100132=-125-6+51-207+3-105-30+0=-101

Ответ: x1=-1; x2=0; x3=1

Уравнения вообще, линейные алгебраические уравнения и их системы, а также методы их решения занимают в математике, как теоретической, так и прикладной, особое место.

Это связано с тем обстоятельством, что подавляющее большинство физических, экономических, технических и даже педагогических задач могут быть описаны и решены с помощью разнообразных уравнений и их систем. В последнее время особую популярность среди исследователей, ученых и практиков приобрело математическое моделирование практически во всех предметных областях, что объясняется очевидными его преимуществами перед другими известными и апробированными методами исследования объектов различной природы, в частности, так называемых, сложных систем. Существует великое многообразие различных определений математической модели, данных учеными в разные времена, но на наш взгляд, самое удачное, это следующее утверждение. Математическая модель – это идея, выраженная уравнением. Таким образом, умение составлять и решать уравнения и их системы – неотъемлемая характеристика современного специалиста.

Для решения систем линейных алгебраических уравнений наиболее часто используются методы: Крамера, Жордана-Гаусса и матричный метод.   

Матричный метод решения – метод решения с помощью обратной матрицы систем линейных алгебраических уравнений с ненулевым определителем.

Если выписать коэффициенты при неизвестных величинах xi в матрицу A, неизвестные величины собрать в вектор столбец X, а свободные члены в вектор столбец B, то систему линейных алгебраических уравнений можно записать в виде следующего матричного уравнения A · X = B, которое имеет единственное решение только тогда, когда определитель матрицы A не будет равен нулю. При этом решение системы уравнений можно найти следующим способом X = A^-1 · B, где A^-1 – обратная матрица.

Матричный метод решения состоит в следующем.

Пусть дана система линейных уравнений с nнеизвестными:

Её можно переписать в матричной форме: AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:

Умножим это матричное уравнение слева на A^-1 — матрицу, обратную к матрице A:  A^-1 (AX) = A^-1 B

Так как A^-1A = E, получаем X = A^-1B. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A: detA≠ 0.

Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть не нулевое) решение только если detA = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.

Пример решения неоднородной системы линейных алгебраических уравнений.

Убедимся в том, что определитель матрицы, составленный из коэффициентов при неизвестных системы линейных алгебраических уравнений не равен нулю.

Следующим шагом будет вычисление алгебраических дополнений для элементов матрицы, состоящей из коэффициентов при неизвестных. Они  понадобятся для нахождения обратной матрицы.

Теперь найдём союзную матрицу и транспонируем  её, потом подставим в формулу для нахождения обратной матрицы.

Подставляя переменные в формулу, получаем:

Найдем неизвестные. Для этого перемножим обратную матрицу  и столбец свободных членов.

Итак, x=2; y=1; z=4.

Если у Вас есть вопросы или Вам нужна помощь в решении линейных уравнений или систем, записывайтесь на мои занятия. Буду рад Вам помочь.  

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Матричный метод решения систем линейных уравнений.

В
этой статье поговорим о матричном методе
решения систем линейных алгебраических
уравнений вида

,
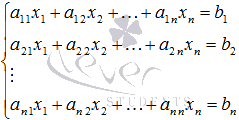
которые в матричной форме записываются
как

,
где

–
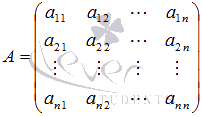
основная матрица системы,

–
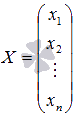
матрица-столбец неизвестных переменных,

–
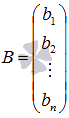
матрица свободных членов.

Сначала
опишем суть матричного метода, остановимся
на условии применимости этого метода,
далее подробно разберем решения
нескольких примеров.

Сразу
оговоримся, что решение систем линейных
алгебраических уравнений матричным
методом и решение СЛАУ с помощью обратной
матрицы есть одно и то же. Поэтому
рекомендуем освежить в памяти теорию
раздела обратная
матрица: определение, свойства, методы
нахождения.

Приступим.

Пусть
для матрицы А
порядка n
на n
существует обратная матрица

.
Умножим обе части матричного уравнения

слева
на

(порядки
матриц A
⋅
X
и В
позволяют произвести такую операцию,
смотрите статью операции
над матрицами, свойства операций).
Имеем

.
Так как для операции умножения матриц
подходящих порядков характерно свойство
ассоциативности, то последнее равенство
можно переписать как

,
а по определению обратной матрицы

(E
– единичная матрица порядка n
на n),
поэтому

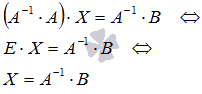
Таким
образом, решение
системы линейных алгебраических
уравнений по матричному методу
определяется равенством

.
Другими словами, решение СЛАУ находится
с помощью обратной матрицы

.

Мы
знаем, что квадратная матрица А
порядка n
на n
имеет обратную матрицу

только
тогда, когда ее определитель не равен
нулю. Следовательно, СИСТЕМУ n
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n
НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ
МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ
ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ
НУЛЯ.

Рассмотрим матричный
метод на примерах. В некоторых примерах
мы не будем подробно описывать процесс
вычисления определителей матриц, при
необходимости обращайтесь к статье
вычисление
определителя матрицы.

Пример.

С
помощью обратной матрицы найдите решение
системы линейных уравнений

.

Решение.

В
матричной форме исходная система
запишется как

,
где

.
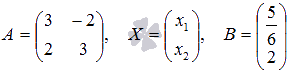
Вычислим определитель основной матрицы
и убедимся, что он отличен от нуля. В
противном случае мы не сможем решить
систему матричным методом. Имеем

,
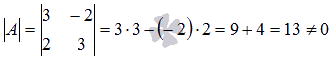
следовательно, для матрицы А
может быть найдена обратная матрица

.
Таким образом, если мы отыщем обратную
матрицу, то искомое решение СЛАУ определим
как

.
Итак, задача свелась к построению
обратной матрицы

.
Найдем ее.

Мы знаем, что для матрицы

обратная
матрица может быть найдена как

,
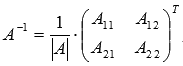
где

–
алгебраические дополнения элементов

.

В
нашем случае

Тогда

Выполним
проверку полученного решения

,
подставив его в матричную форму исходной
системы уравнений

.
Это равенство должно обратиться в
тождество, в противном случае где-то
была допущена ошибка.

Следовательно,
решение найдено верно.

Ответ:

или
в другой записи

.

Системы линейных уравнений: основные понятия

24 Июня 2011

Определение.
Система линейных уравнений — это
объединение из n линейных уравнений,
каждое из которых содержит k переменных.
Записывается это так:

Многие,
впервые сталкиваясь с высшей алгеброй,
ошибочно полагают, что число уравнений
обязательно должно совпадать с числом
переменных. В школьной алгебре так
обычно и бывает, однако для высшей
алгебры это, вообще говоря, неверно.

Определение.
Решение системы уравнений — это
последовательность чисел (k₁,
k₂, …, k_n),
которая является решением каждого
уравнения системы, т.е. при подстановке
в это уравнение вместо переменных x₁,
x₂, …, x_n
дает верное числовое равенство.

Соответственно,
решить систему уравнений — значит найти
множество всех ее решений или доказать,
что это множество пусто. Поскольку число
уравнений и число неизвестных может не
совпадать, возможны три случая:

1. Система
   несовместна, т.е. множество всех решений
   пусто. Достаточно редкий случай, который
   легко обнаруживается независимо от
   того, каким методом решать систему.

2. Система
   совместна и определена, т.е. имеет ровно
   одно решение. Классический вариант,
   хорошо известный еще со школьной скамьи.

3. Система
   совместна и не определена, т.е. имеет
   бесконечно много решений. Это самый
   жесткий вариант. Недостаточно указать,
   что «система имеет бесконечное множество
   решений» — надо описать, как устроено
   это множество.

Определение.
Переменная x_i
называется разрешенной, если она
входит только в одно уравнение системы,
причем с коэффициентом 1. Другими словами,
в остальных уравнениях коэффициент при
переменной x_i
должен быть равен нулю.

Если
в каждом уравнении выбрать по одной
разрешенной переменной, получим набор
разрешенных переменных для всей системы
уравнений. Сама система, записанная в
таком виде, тоже будет называться
разрешенной. Вообще говоря, одну и ту
же исходную систему можно свести к
разным разрешенным, однако сейчас нас
это не волнует. Вот примеры разрешенных
систем:

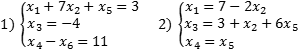
Обе
системы являются разрешенными относительно
переменных x₁,
x₃ и x₄.
Впрочем, с тем же успехом можно утверждать,
что вторая система — разрешенная
относительно x₁,
x₃ и x₅.
Достаточно переписать самое последнее
уравнение в виде x₅
= x₄.

Теперь
рассмотрим более общий случай. Пусть
всего у нас k переменных, из которых r
являются разрешенными. Тогда возможны
два случая:

1. Число
   разрешенных переменных r равно общему
   числу переменных k: r = k. Получаем систему
   из k уравнений, в которых r = k разрешенных
   переменных. Такая система является
   совместной и определенной, т.к. x₁
   = b₁, x₂
   = b₂, …,
   x_k = b_k;

2. Число
   разрешенных переменных r меньше общего
   числа переменных k: r < k. Остальные (k −
   r) переменных называются свободными —
   они могут принимать любые значения, из
   которых легко вычисляются разрешенные
   переменные.

Так,
в приведенных выше системах переменные
x₂, x₅,
x₆ (для
первой системы) и x₂,
x₅ (для
второй) являются свободными. Случай,
когда есть свободные переменные, лучше
сформулировать в виде теоремы:

Теорема.
Если в системе из n уравнений переменные
x₁, x₂,
…, x_r —
разрешенные, а x<sub>r
+ 1</sub>, x<sub>r
+ 2</sub>, …, x_k
— свободные, то:

1. Если
   задать значения свободным переменным
   (x<sub>r
   + 1</sub> = t<sub>r
   + 1</sub>, x<sub>r
   + 2</sub> = t<sub>r
   + 2</sub>, …, x_k
   = t_k), а
   затем найти значения x₁,
   x₂, …, x_r,
   получим одно из решений.

2. Если
   в двух решениях значения свободных
   переменных совпадают, то значения
   разрешенных переменных тоже совпадают,
   т.е. решения равны.

В
чем смысл этой теоремы? Чтобы получить
все решения разрешенной системы
уравнений, достаточно выделить свободные
переменные. Затем, присваивая свободным
переменным разные значения, будем
получать готовые решения. Вот и все —
таким образом можно получить все решения
системы. Других решений не существует.

Вывод:
разрешенная система уравнений всегда
совместна. Если число уравнений в
разрешенной системе равно числу
переменных, система будет определенной,
если меньше — неопределенной.

И
все бы хорошо, но возникает вопрос: как
из исходной системы уравнений получить
разрешенную? Для этого существует метод
Гаусса.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях». 

Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано. 

Краткое содержание прошлых частей: 

И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.

Что такое матричное уравнение

Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.

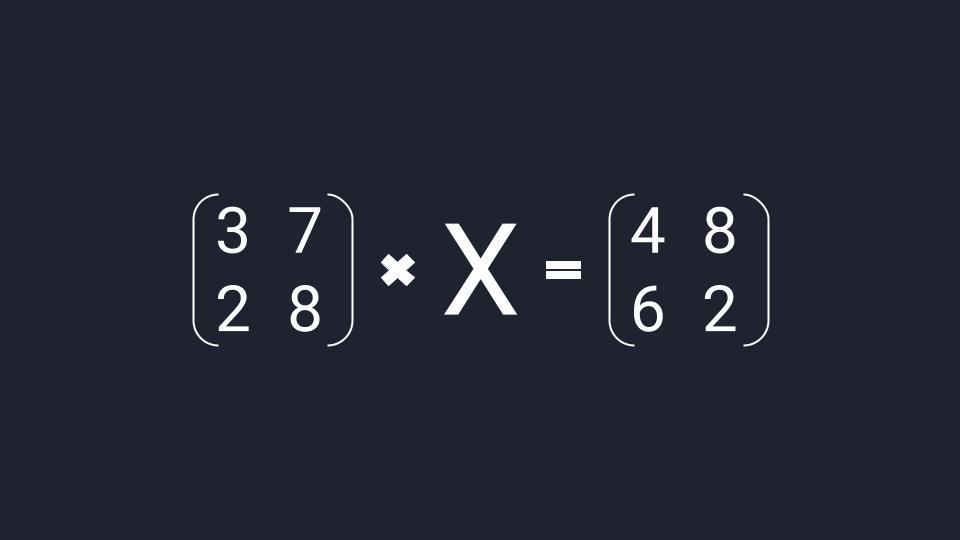
Шаг 1. Упрощаем уравнение 

Вместо известных числовых матриц вводим в уравнение буквы: первую матрицу обозначаем буквой A, вторую — буквой B. Неизвестную матрицу X оставляем. Это упрощение поможет составить формулу и выразить X через известную матрицу.

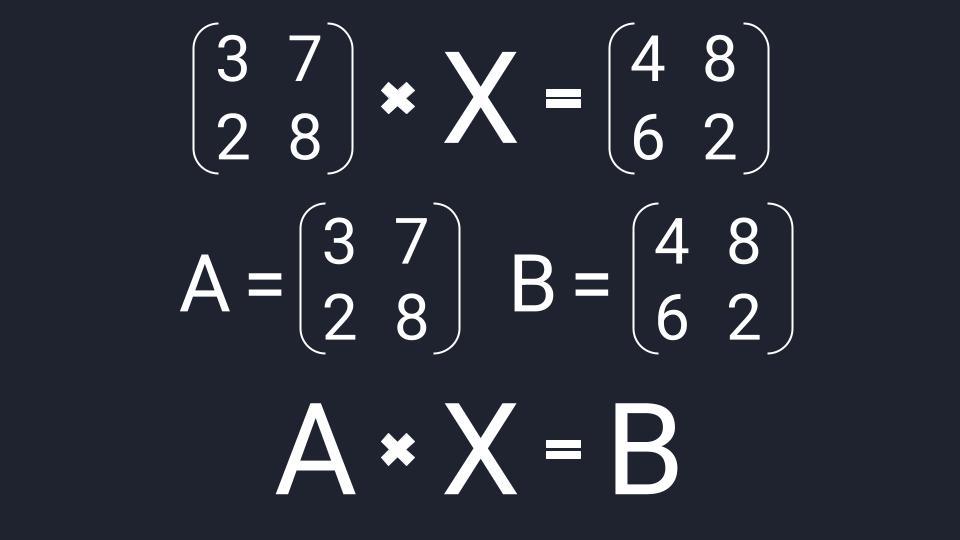
Шаг 2. Вводим единичную матрицу 

В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу. 

Можно представить, что есть число 100 — это «сто в первой степени», 100¹

И есть число 0,01 — это «сто в минус первой степени», 100^-1

При перемножении этих двух чисел получится единица:
100¹ × 100^-1 = 100 × 0,01 = 1. 

Вот такое, только в мире матриц. 

Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А^-1. Неизвестную матрицу Х оставляем без изменений и переписываем уравнение: 

А-1 × А × Х = А-1 × В  

Добавляем единичную матрицу и упрощаем запись: 

А-1 × А = E — единичная матрица 

E × Х = А-1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем

Х = А-1 × В — новая запись уравнения 

После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B. 

💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A^-1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто. 

Шаг 3. Находим обратную матрицу

Вспоминаем формулу и порядок расчёта обратной матрицы: 

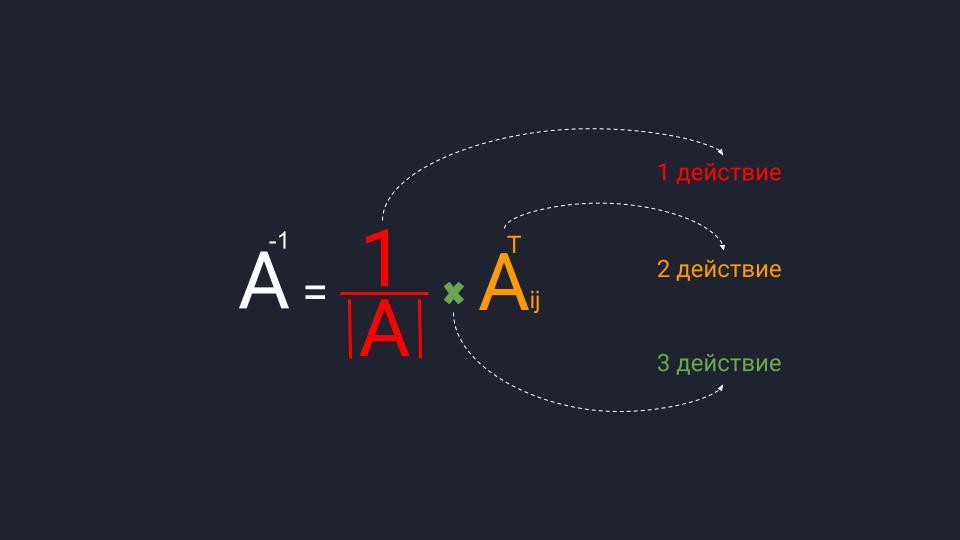
Собираем формулу и получаем обратную матрицу. Для удобства умышленно оставляем перед матрицей дробное число, чтобы было проще считать.

Шаг 4. Вычисляем неизвестную матрицу

Нам остаётся посчитать матрицу X: умножаем обратную матрицу А^-1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.

Шаг 5. Проверяем уравнение

Мы решили матричное уравнение и получили красивый ответ с целыми числами. Выглядит правильно, но в случае с матрицами этого недостаточно. Чтобы проверить ответ, нам нужно вернуться к условию и умножить исходную матрицу A на матрицу X. В результате должна появиться матрица B. Если расчёты совпадут — мы всё сделали правильно. Если будут отличия — придётся решать заново. 

👉 Часто начинающие математики пренебрегают финальной проверкой и считают её лишней тратой времени. Сегодня мы разобрали простое уравнение с двумя квадратными матрицами с четырьмя элементами в каждой. Когда элементов будет больше, в них легко запутаться и допустить ошибку.

Ну и что

Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика:

Этого котика не существует, а матрицы — существуют. 

Если вы перешли к изучению данной темы, то уже знаете, что такое матрица и определитель матрицы, умеете находить определители второго, третьего и высших порядков, а также обратные матрицы. Если какая-то из этих тем вам незнакома, то следует изучить сначала ее.

Приступим к рассмотрению понятия матричного уравнения.

Матричные уравнения

Матричные уравнения устроены практически также как и числовые, только вместо чисел в них содержатся числовые матрицы. Как правило, типовое матричное уравнение состоит из нескольких матриц и некоторой неизвестной матрицы XX, которую и требуется найти.

Рассмотрим примеры наиболее простых матричных уравнений и их решения.

Пример 1

Решить матричное уравнение

(1234)+x=(1101)begin{pmatrix}1&2\3&4end{pmatrix}+x=begin{pmatrix}1&1\0&1end{pmatrix}.

Перенесем матрицу из левой части в правую:

x=(1101)−(1234)x=begin{pmatrix}1&1\0&1end{pmatrix}-begin{pmatrix}1&2\3&4end{pmatrix}.

Найдем разность матриц в правой части уравнения:

x=(1−11−20−31−4)x=begin{pmatrix}1-1&1-2\0-3&1-4end{pmatrix}.

Значит, x=(0−1−3−3)x=begin{pmatrix}0&-1\-3&-3end{pmatrix}.

Можно провести проверку:

(1234)+(0−1−3−3)=(1+02−13−34−3)=(1101)begin{pmatrix}1&2\3&4end{pmatrix}+begin{pmatrix}0&-1\-3&-3end{pmatrix}=begin{pmatrix}1+0&2-1\3-3&4-3end{pmatrix}=begin{pmatrix}1&1\0&1end{pmatrix},

(1101)=(1101)begin{pmatrix}1&1\0&1end{pmatrix}=begin{pmatrix}1&1\0&1end{pmatrix}.

Пример 2

Решить матричное уравнение (58−469−5)−12x=(341212)begin{pmatrix}5&8&-4\6&9&-5end{pmatrix}-frac{1}{2}x=begin{pmatrix}3&4&1\2&1&2end{pmatrix}.

Перенесем матрицу из левой части в правую:

−12x=(341212)−(58−469−5)-frac{1}{2}x=begin{pmatrix}3&4&1\2&1&2end{pmatrix}-begin{pmatrix}5&8&-4\6&9&-5end{pmatrix}.

Найдем разность матриц в правой части уравнения:

−12x=(3−54−81−(−4)2−61−92−(−5))-frac{1}{2}x=begin{pmatrix}3-5&4-8&1-(-4)\2-6&1-9&2-(-5)end{pmatrix},

−12x=(−2−45−4−87)-frac{1}{2}x=begin{pmatrix}-2&-4&5\-4&-8&7end{pmatrix}.

Умножим обе части уравнения на -2:

x=−2(−2−45−4−87)x=-2begin{pmatrix}-2&-4&5\-4&-8&7end{pmatrix},

x=(48−10816−14)x=begin{pmatrix}4&8&-10\8&16&-14end{pmatrix}.

Можно провести проверку:

(58−469−5)−12(48−10816−14)=(58−469−5)−(24−548−7)=(341212)begin{pmatrix}5&8&-4\6&9&-5end{pmatrix}-frac{1}{2}begin{pmatrix}4&8&-10\8&16&-14end{pmatrix}=begin{pmatrix}5&8&-4\6&9&-5end{pmatrix}-begin{pmatrix}2&4&-5\4&8&-7end{pmatrix}=begin{pmatrix}3&4&1\2&1&2end{pmatrix},

(341212)=(341212)begin{pmatrix}3&4&1\2&1&2end{pmatrix}=begin{pmatrix}3&4&1\2&1&2end{pmatrix}.

Такие уравнения элементарны, поэтому они довольно редко встречаются на практике.

Простейшие матричные уравнения

Обычно решение матричных уравнений сводится к одному из двух видов:

1. A⋅X=BAcdot X=B;
2. X⋅A=BXcdot A=B.

Рассмотрим, как решается каждое из этих уравнений.

Рассмотрим примеры решения простейших матричных уравнений вида A⋅X=BAcdot X=B.

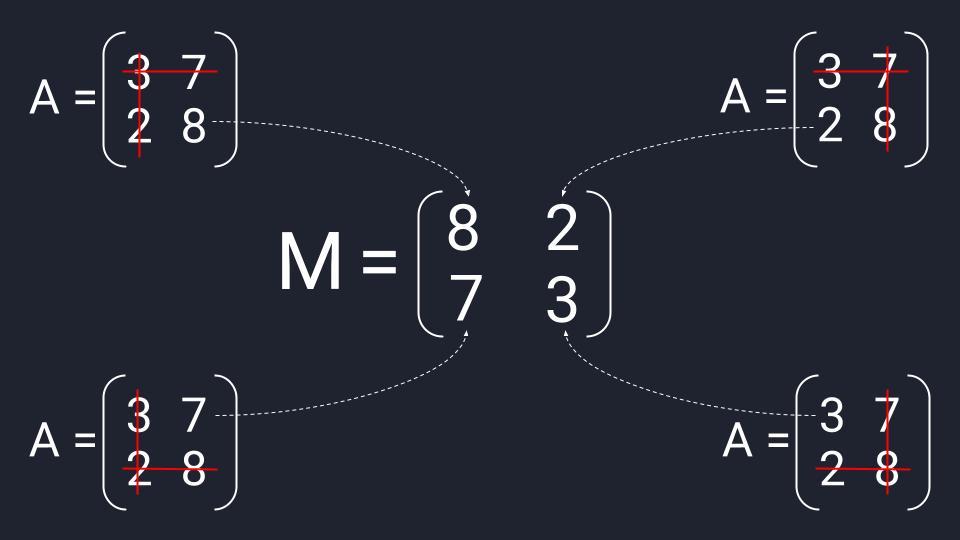
Пример 1

Решить матричное уравнение (3728)⋅X=(4862)begin{pmatrix}3&7\2&8end{pmatrix}cdot X=begin{pmatrix}4&8\6&2end{pmatrix}. Выполнить проверку.

Уравнение имеет вид A⋅X=BAcdot X=B, где A=(3728)A=begin{pmatrix}3&7\2&8end{pmatrix}, B=(4862)B=begin{pmatrix}4&8\6&2end{pmatrix}.

Умножим обе части уравнения на A−1A^{-1} слева:

A−1⋅A⋅X=A−1⋅BA^{-1}cdot Acdot X=A^{-1}cdot B,

E⋅X=A−1⋅BEcdot X=A^{-1}cdot B, EE — единичная матрица,

X=A−1⋅BX=A^{-1}cdot B.

Найдем матрицу A−1A^{-1}.

∣3728∣=3⋅8−2⋅7=24−14=10≠0begin{vmatrix}3&7\2&8end{vmatrix}=3cdot8-2cdot7=24-14=10neq 0, значит для матрицы AA существует обратная матрица. Найдем ее методом элементарных преобразований.

Составим расширенную матрицу:

(3728∣1001)begin{pmatrix}left.begin{matrix}3&7\2&8end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.

Вычтем из строки №1 строку №2:

(3728∣1001)∼(1−128∣1−101)begin{pmatrix}left.begin{matrix}3&7\2&8end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-1\2&8end{matrix}right|begin{matrix}1&-1\0&1end{matrix}end{pmatrix}.

Прибавим к строке №2 строку №1, умноженную на -2:

(1−128∣1−101)∼(1−1010∣1−1−23)begin{pmatrix}left.begin{matrix}1&-1\2&8end{matrix}right|begin{matrix}1&-1\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-1\0&10end{matrix}right|begin{matrix}1&-1\-2&3end{matrix}end{pmatrix}.

Умножим строку №1 на 10:

(1−1010∣1−1−23)∼(10−10010∣10−10−23)begin{pmatrix}left.begin{matrix}1&-1\0&10end{matrix}right|begin{matrix}1&-1\-2&3end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}10&-10\0&10end{matrix}right|begin{matrix}10&-10\-2&3end{matrix}end{pmatrix}.

Прибавим к строке №1 строку №2, умноженную на 1:

(10−10010∣10−10−23)∼(100010∣8−7−23)begin{pmatrix}left.begin{matrix}10&-10\0&10end{matrix}right|begin{matrix}10&-10\-2&3end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}10&0\0&10end{matrix}right|begin{matrix}8&-7\-2&3end{matrix}end{pmatrix}.

Умножим строку №1 и №2 на 110frac{1}{10}:

(100010∣8−7−23)∼(1001∣810−710−210310)begin{pmatrix}left.begin{matrix}10&0\0&10end{matrix}right|begin{matrix}8&-7\-2&3end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}frac{8}{10}&-frac{7}{10}\-frac{2}{10}&frac{3}{10}end{matrix}end{pmatrix}.

Значит, A−1=(810−710−210310)=110(8−7−23)A^{-1}=begin{pmatrix}frac{8}{10}&-frac{7}{10}\-frac{2}{10}&frac{3}{10}end{pmatrix}=frac{1}{10}begin{pmatrix}8&-7\-2&3end{pmatrix}.

A−1⋅B=110(8−7−23)⋅(4862)=110(−105010−10)=(−151−1)=XA^{-1}cdot B=frac{1}{10}begin{pmatrix}8&-7\-2&3end{pmatrix}cdotbegin{pmatrix}4&8\6&2end{pmatrix}=frac{1}{10}begin{pmatrix}-10&50\10&-10end{pmatrix}=begin{pmatrix}-1&5\1&-1end{pmatrix}=X.

Проверка:

(3728)⋅(−151−1)=(4862)begin{pmatrix}3&7\2&8end{pmatrix}cdotbegin{pmatrix}-1&5\1&-1end{pmatrix}=begin{pmatrix}4&8\6&2end{pmatrix}. — Верно.

Ответ: X=(−151−1)X=begin{pmatrix}-1&5\1&-1end{pmatrix}.

Пример 2

Решить матричное уравнение (0230)⋅X=(243−6)begin{pmatrix}0&2\3&0end{pmatrix}cdot X=begin{pmatrix}2&4\3&-6end{pmatrix}. Выполнить проверку.

Уравнение имеет вид A⋅X=BAcdot X=B, где A=(0230)A=begin{pmatrix}0&2\3&0end{pmatrix}, B=(243−6)B=begin{pmatrix}2&4\3&-6end{pmatrix}.

Умножим обе части уравнения на A−1A^{-1} слева:

A−1⋅A⋅X=A−1⋅BA^{-1}cdot Acdot X=A^{-1}cdot B,

E⋅X=A−1⋅BEcdot X=A^{-1}cdot B, EE — единичная матрица,

X=A−1⋅BX=A^{-1}cdot B.

Найдем матрицу A−1A^{-1}.

∣0230∣=0⋅0−3⋅2=0−6=−6≠0begin{vmatrix}0&2\3&0end{vmatrix}=0cdot0-3cdot2=0-6=-6neq 0, значит для матрицы AA существует обратная матрица. Найдем ее методом элементарных преобразований.

Составим расширенную матрицу:

(0230∣1001)begin{pmatrix}left.begin{matrix}0&2\3&0end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.

Поменяем местами строки №1 и №2:

(0230∣1001)∼(3002∣0110)begin{pmatrix}left.begin{matrix}0&2\3&0end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}3&0\0&2end{matrix}right|begin{matrix}0&1\1&0end{matrix}end{pmatrix}.

Умножим строку №1 на 13frac{1}{3}, а строку №2 на 12frac{1}{2}:

(3002∣0110)∼(1001∣013120)begin{pmatrix}left.begin{matrix}3&0\0&2end{matrix}right|begin{matrix}0&1\1&0end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}0&frac{1}{3}\frac{1}{2}&0end{matrix}end{pmatrix}.

Значит, A−1=(013120)=16(0230)A^{-1}=begin{pmatrix}0&frac{1}{3}\frac{1}{2}&0end{pmatrix}=frac{1}{6}begin{pmatrix}0&2\3&0end{pmatrix}.

A−1⋅B=16(0230)⋅(243−6)=16(6−12612)=(1−212)=XA^{-1}cdot B=frac{1}{6}begin{pmatrix}0&2\3&0end{pmatrix}cdot begin{pmatrix}2&4\3&-6end{pmatrix}=frac{1}{6}begin{pmatrix}6&-12\6&12end{pmatrix}=begin{pmatrix}1&-2\1&2end{pmatrix}=X.

Проверка:

(0230)⋅(1−212)=(243−6)begin{pmatrix}0&2\3&0end{pmatrix}cdotbegin{pmatrix}1&-2\1&2end{pmatrix}=begin{pmatrix}2&4\3&-6end{pmatrix}. — Верно.

Ответ: X=(1−212)X=begin{pmatrix}1&-2\1&2end{pmatrix}.

Рассмотрим примеры решения простейших матричных уравнений вида X⋅A=BXcdot A=B.

Пример 3

Решить матричное уравнение

X⋅(9711)=(201812)Xcdotbegin{pmatrix}9&7\1&1end{pmatrix}=begin{pmatrix}2&0\18&12end{pmatrix}. Выполнить проверку.

Уравнение имеет вид X⋅A=BXcdot A=B, где A=(9711)A=begin{pmatrix}9&7\1&1end{pmatrix}, B=(201812)B=begin{pmatrix}2&0\18&12end{pmatrix}.

Умножим обе части уравнения на A−1A^{-1} справа:

X⋅A⋅A−1=B⋅A−1Xcdot Acdot A^{-1}=Bcdot A^{-1},

X⋅E=B⋅A−1Xcdot E=Bcdot A^{-1}, EE — единичная матрица,

X=B⋅A−1X=Bcdot A^{-1}.

Найдем матрицу A−1A^{-1}.

∣9711∣=9⋅1−1⋅7=9−7=2≠0begin{vmatrix}9&7\1&1end{vmatrix}=9cdot1-1cdot7=9-7=2neq 0, значит для матрицы AA существует обратная матрица. Найдем ее методом элементарных преобразований.

Составим расширенную матрицу:

(9711∣1001)begin{pmatrix}left.begin{matrix}9&7\1&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.

Поменяем строки №1 и №2 местами:

(9711∣1001)∼(1197∣0110)begin{pmatrix}left.begin{matrix}9&7\1&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&1\9&7end{matrix}right|begin{matrix}0&1\1&0end{matrix}end{pmatrix}.

Прибавим к строке №2 строку №1, умноженную на -9:

(1197∣0110)∼(110−2∣011−9)begin{pmatrix}left.begin{matrix}1&1\9&7end{matrix}right|begin{matrix}0&1\1&0end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&1\0&-2end{matrix}right|begin{matrix}0&1\1&-9end{matrix}end{pmatrix}.

Умножим строку №2 на −12-frac{1}{2}:

(110−2∣011−9)∼(1101∣01−1292)begin{pmatrix}left.begin{matrix}1&1\0&-2end{matrix}right|begin{matrix}0&1\1&-9end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&1\0&1end{matrix}right|begin{matrix}0&1\-frac{1}{2}&frac{9}{2}end{matrix}end{pmatrix}.

Прибавим к строке №1 строку №2, умноженную на -1:

(1101∣01−1292)∼(1001∣12−72−1292)begin{pmatrix}left.begin{matrix}1&1\0&1end{matrix}right|begin{matrix}0&1\-frac{1}{2}&frac{9}{2}end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}frac{1}{2}&-frac{7}{2}\-frac{1}{2}&frac{9}{2}end{matrix}end{pmatrix}.

Значит, A−1=(12−72−1292)=12(1−7−19)A^{-1}=begin{pmatrix}frac{1}{2}&-frac{7}{2}\-frac{1}{2}&frac{9}{2}end{pmatrix}=frac{1}{2}begin{pmatrix}1&-7\-1&9end{pmatrix}.

B⋅A−1=(201812)⋅12⋅(1−7−19)=12(201812)⋅(1−7−19)=12(2−146−18)=(1−73−9)=XBcdot A^{-1}=begin{pmatrix}2&0\18&12end{pmatrix}cdot frac{1}{2}cdot begin{pmatrix}1&-7\-1&9end{pmatrix}=frac{1}{2}begin{pmatrix}2&0\18&12end{pmatrix}cdotbegin{pmatrix}1&-7\-1&9end{pmatrix}=frac{1}{2}begin{pmatrix}2&-14\6&-18end{pmatrix}=begin{pmatrix}1&-7\3&-9end{pmatrix}=X.

Проверка: (1−73−9)⋅(9711)=(201812).begin{pmatrix}1&-7\3&-9end{pmatrix}cdotbegin{pmatrix}9&7\1&1end{pmatrix}=begin{pmatrix}2&0\18&12end{pmatrix}. — Верно.

Ответ: X=(1−73−9)X=begin{pmatrix}1&-7\3&-9end{pmatrix}.

Пример 4

Решить матричное уравнение X⋅(1325)=(4−132)Xcdotbegin{pmatrix}1&3\2&5end{pmatrix}=begin{pmatrix}4&-1\3&2end{pmatrix}. Выполнить проверку.

Уравнение имеет вид X⋅A=BXcdot A=B, где A=(1325)A=begin{pmatrix}1&3\2&5end{pmatrix}, B=(4−132)B=begin{pmatrix}4&-1\3&2end{pmatrix}.

Умножим обе части уравнения на A−1A^{-1} справа:

X⋅A⋅A−1=B⋅A−1Xcdot Acdot A^{-1}=Bcdot A^{-1},

X⋅E=B⋅A−1Xcdot E=Bcdot A^{-1}, EE — единичная матрица,

X=B⋅A−1X=Bcdot A^{-1}.

Найдем матрицу A−1A^{-1}.

∣1325∣=1⋅5−2⋅3=5−6=−1≠0begin{vmatrix}1&3\2&5end{vmatrix}=1cdot5-2cdot3=5-6=-1neq 0, значит для матрицы AA существует обратная матрица. Найдем ее методом элементарных преобразований.

Составим расширенную матрицу:

(1325∣1001)begin{pmatrix}left.begin{matrix}1&3\2&5end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.

Прибавим к строке №2 строку №1, умноженную на -2:

(1325∣1001)∼(130−1∣10−21)begin{pmatrix}left.begin{matrix}1&3\2&5end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&3\0&-1end{matrix}right|begin{matrix}1&0\-2&1end{matrix}end{pmatrix}.

Прибавим к строке №1 строку №2, умноженную на 3:

(130−1∣10−21)∼(100−1∣−53−21)begin{pmatrix}left.begin{matrix}1&3\0&-1end{matrix}right|begin{matrix}1&0\-2&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&-1end{matrix}right|begin{matrix}-5&3\-2&1end{matrix}end{pmatrix}.

Умножим строку №2 на -1:

(100−1∣−53−21)∼(1001∣−532−1)begin{pmatrix}left.begin{matrix}1&0\0&-1end{matrix}right|begin{matrix}-5&3\-2&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}-5&3\2&-1end{matrix}end{pmatrix}.

Значит, A−1=(−532−1)A^{-1}=begin{pmatrix}-5&3\2&-1end{pmatrix}.

B⋅A−1=(4−132)⋅(−532−1)=(−2213−117)=XBcdot A^{-1}=begin{pmatrix}4&-1\3&2end{pmatrix}cdotbegin{pmatrix}-5&3\2&-1end{pmatrix}=begin{pmatrix}-22&13\-11&7end{pmatrix}=X.

Проверка:

(−2213−117)⋅(1325)=(4−132)begin{pmatrix}-22&13\-11&7end{pmatrix}cdotbegin{pmatrix}1&3\2&5end{pmatrix}=begin{pmatrix}4&-1\3&2end{pmatrix}. — Верно.

Ответ: X=(−2213−117).X=begin{pmatrix}-22&13\-11&7end{pmatrix}.

Существует третий вид матричных уравнений: A⋅X⋅B=CAcdot Xcdot B=C, но в действительности он встречается редко.

Обе части уравнения умножим на A−1A^{-1} слева: A−1⋅A⋅X⋅B=A−1⋅CA^{-1}cdot Acdot Xcdot B=A^{-1}cdot C.

Зная, что A−1⋅A=EA^{-1}cdot A=E, получим: E⋅X⋅B=A−1⋅CEcdot Xcdot B=A^{-1}cdot C.

Поскольку E⋅X=XEcdot X=X, то X⋅B=A−1⋅CXcdot B=A^{-1}cdot C.

Обе части уравнения умножим на B−1B^{-1} справа: X⋅B⋅B−1=A−1⋅C⋅B−1Xcdot Bcdot B^{-1}=A^{-1}cdot Ccdot B^{-1}.

Зная, что B⋅B−1=EBcdot B^{-1}=E, получим: X⋅E=A−1⋅C⋅B−1Xcdot E=A^{-1}cdot Ccdot B^{-1}.

Поскольку X⋅E=XXcdot E=X, то X=A−1⋅C⋅B−1X=A^{-1}cdot Ccdot B^{-1}.