Определение квадратного неравенства
Неравенство — алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Квадратное неравенство выглядит так:
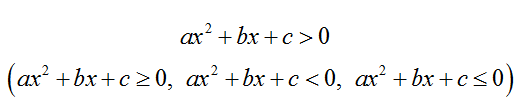
где x — переменная,
a, b, c — числа,
при этом а ≠ 0.
Квадратное неравенство можно решить двумя способами:
- графический метод;
- метод интервалов.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Решение неравенства графическим методом
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
Как дискриминант влияет на корни уравнения:
- D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
- D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два различных корня;
- D < 0. Если дискриминант меньше нуля, тогда у квадратного уравнения нет корней.
В зависимости от полученных корней и знака коэффициента a, возможно одно из шести расположений графика функции у = ax2 + bx + c.
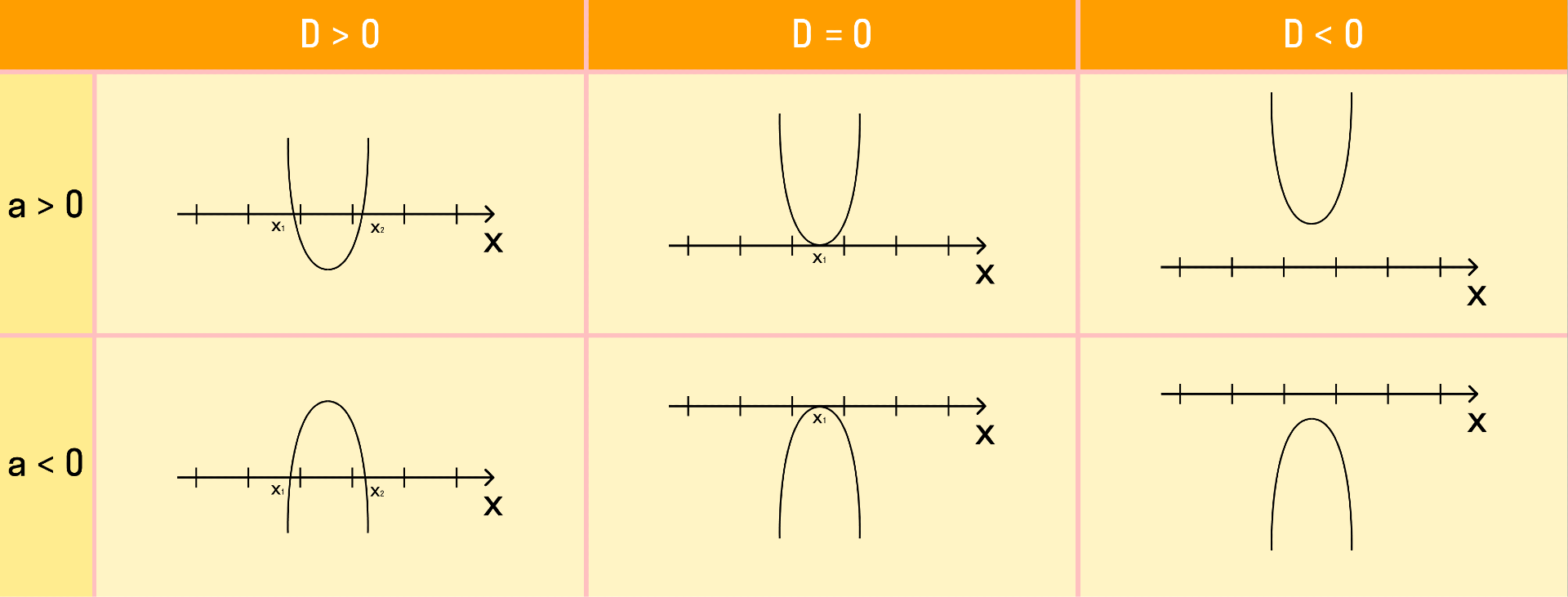
Если требуется найти числовой промежуток, на котором квадратный трехчлен ax2 + bx + c больше нуля, то этот числовой промежуток находится там, где парабола лежит выше оси ОХ.
Если нужно найти числовой промежуток, на котором квадратный трехчлен ax2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.
Если квадратное неравенство нестрогое, то корни входят в числовой промежуток. А если строгое — не входят.
Обучение на курсах по математике в онлайн-школе Skysmart сделает сложные темы понятными, а высокий балл на экзаменах — достижимым!
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.
Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, <, ≤, ≥.
Сейчас мы узнаем про интервалы в контексте решения квадратных неравенств.
Интервал — это некий промежуток числовой прямой, то есть все возможные числа, заключенные между двумя числами — концами интервала. Представить эти промежутки не так просто, поэтому интервалы принято рисовать.
Алгоритм решения квадратных неравенств методом интервалов:
- Найти нули квадратного трехчлена ax2 + bx + c из левой части квадратного неравенства.
- Изобразить координатную прямую и при наличии корней отметить их на ней.
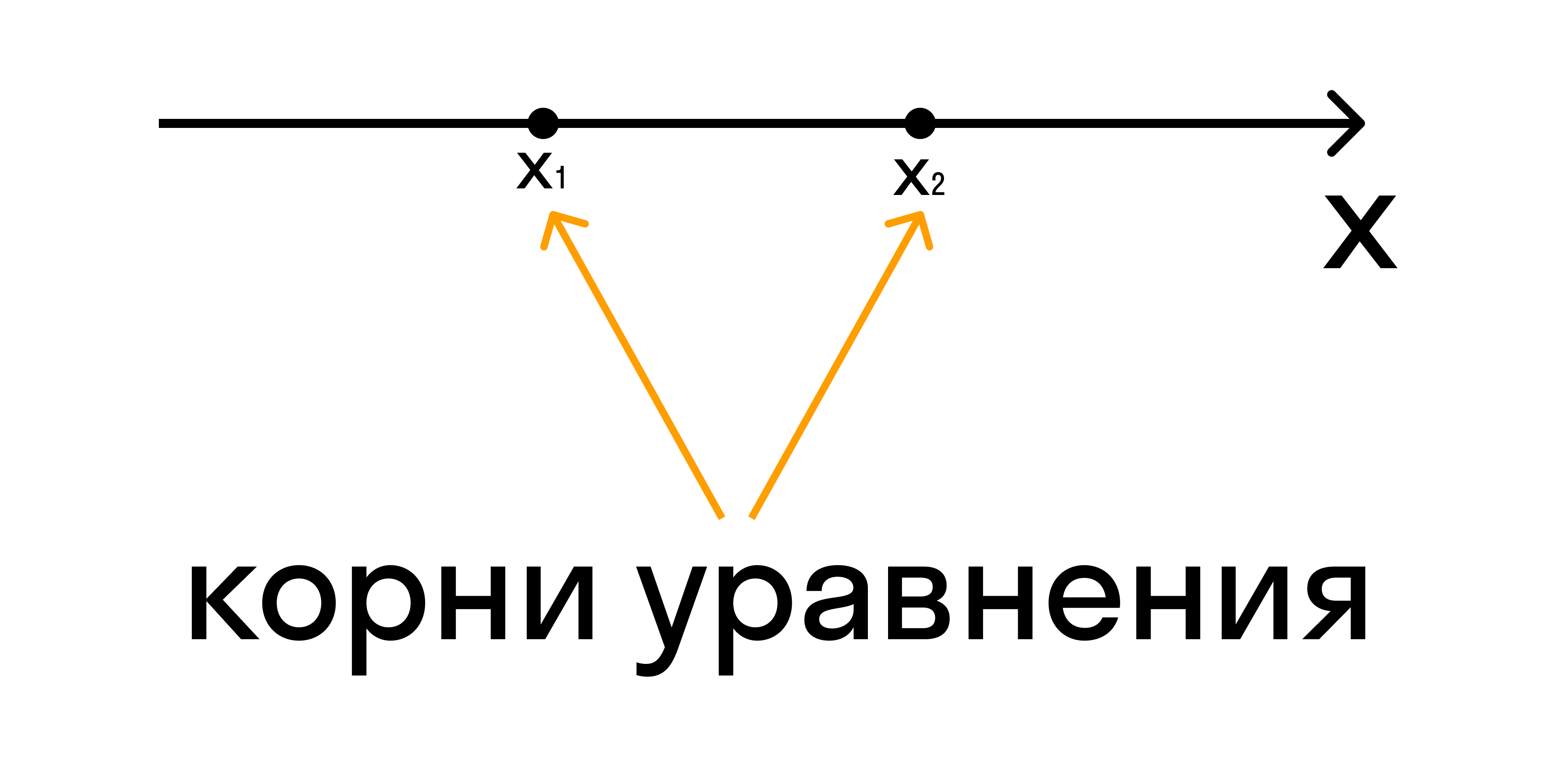
Если неравенство строгое, нужно отметить корни пустыми (выколотыми) точками. Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки.
- Определить, какие знаки имеют значения трехчлена на каждом промежутке (если на первом шаге нашли нули) или на всей числовой прямой (если нулей нет). И проставить над этими промежутками + или − в соответствии с определенными знаками.
- Если квадратное неравенство со знаком > или ≥ — наносим штриховку над промежутками со знаками +.
Если неравенство со знаком < или ≤, то наносим штриховку над промежутками со знаком −.
В результате получаем геометрический образ некоторого числового множества — это и есть решение неравенства.
Либо вместо штриховки можно нарисовать «арки» для интервалов. Справа налево, начиная с +, проставить чередуя знаки + и −.
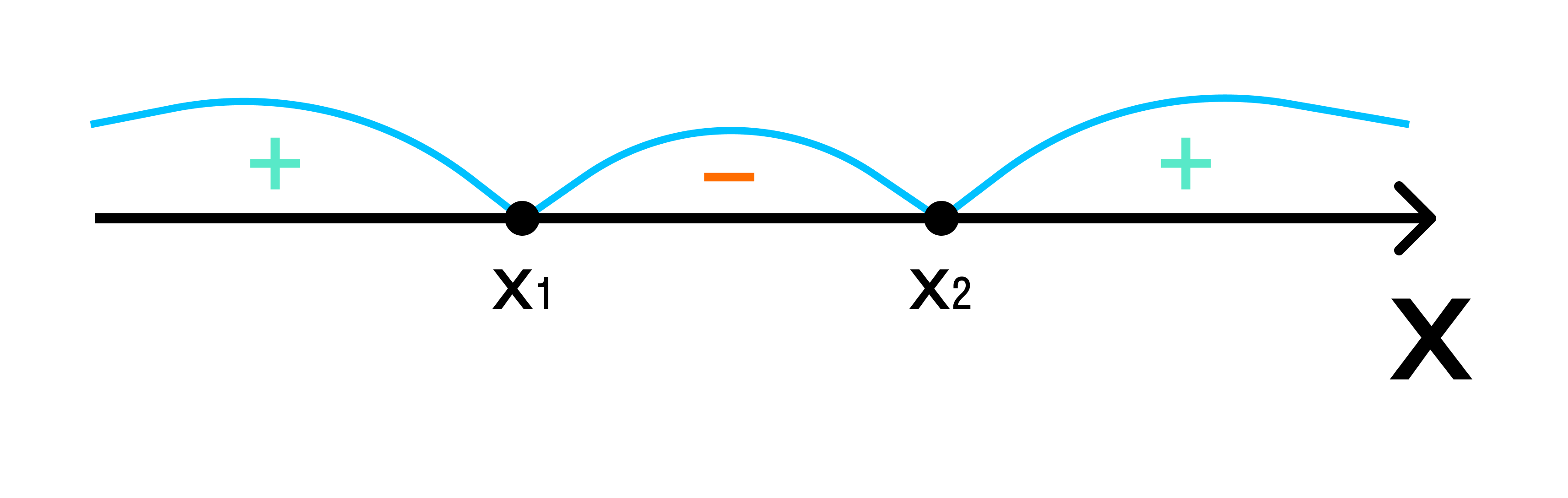
- Выбрать необходимые интервалы и записать ответ.
Расскажем подробнее про третий шаг алгоритма. Существует несколько подходов для определения знаков на промежутках.
Для примера возьмем трехчлен x2 + 4x – 5, его корнями являются числа -5 и 1, они разбивают числовую ось на три промежутка: (-∞, -5), (-5, 1) и (1, +∞).
Определим знак трехчлена x2 + 4x – 5 на промежутке (1, +∞). Для этого вычислим значение данного трехчлена при некотором значении x из этого промежутка. Можно брать любое значение переменной, главное — чтобы вычисления были простыми. В нашем случае, возьмем x = 2. Подставим его в трехчлен вместо переменной x:
- 22 + 4 * 2 – 5 = 4 + 8 – 5 = 7.
7 — положительное число. Это значит, что любое значение квадратного трехчлена на интервале (1, +∞) будет положительным. Так мы определили знак плюс.
Определим знаки на оставшихся двух промежутках. Начнем с интервала (-5, 1). Из этого интервала можем взять x = 0 и вычислить значение квадратного трехчлена при этом значении переменной:
- 02 + 4 * 0 – 5 = 0 + 0 – 5 = -5.
Так как -5 — отрицательное число, то на этом интервале все значения трехчлена будут отрицательными. Так мы определили знак минус.
Осталось определиться со знаком на промежутке (-∞, -5). Возьмем x = -6, подставляем:
- (-6)2 + 4 * (-6) – 5 = 36 – 24 – 5 = 7.
Следовательно, искомый знак — плюс.
Можно расставить знаки быстрее, если запомнить эти факты:
Плюс или минус: как определить знаки
Можно сделать вывод о знаках по значению старшего коэффициента a:
если a > 0, последовательность знаков: +, −, +,
если a < 0, последовательность знаков: −, +, −.
Можно также сделать вывод о знаках по значению старшего коэффициента a:
если a > 0, последовательность знаков: +, +,
если a < 0, последовательность знаков: −, −.
Например -4x2 – 7 не имеет корней и на промежутке (−∞, +∞) его значения отрицательны, так как коэффициент при x2 есть отрицательное число -4, и свободный член -7 тоже отрицателен.
- Когда квадратный трехчлен при D > 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.
- Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.
- Когда квадратный трехчлен корней не имеет (D < 0), то знаки его значений на всей числовой прямой совпадают как со знаком старшего коэффициента a, так и со знаком свободного члена c.
Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.
Пример 1. Решить неравенство методом интервалов: x^2 – 5x + 6 ≥ 0.
Как решаем:
-
Приравняем квадратный трехчлен к 0 и найдем нули:
x2 – 5x + 6 = 0
(x – 3) (x -2) = 0
x – 3 = 0
x – 2 = 0
x = 3
x = 2 -
Отметим полученные значения на числовой прямой:
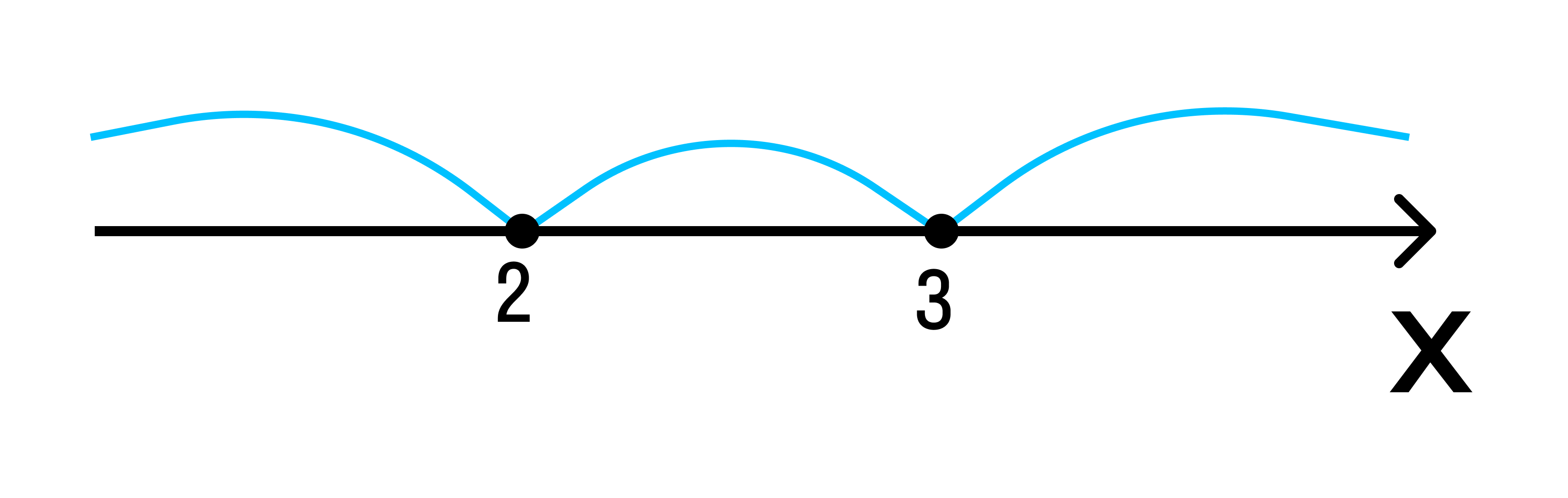
-
Расставим знаки на полученных промежутках:
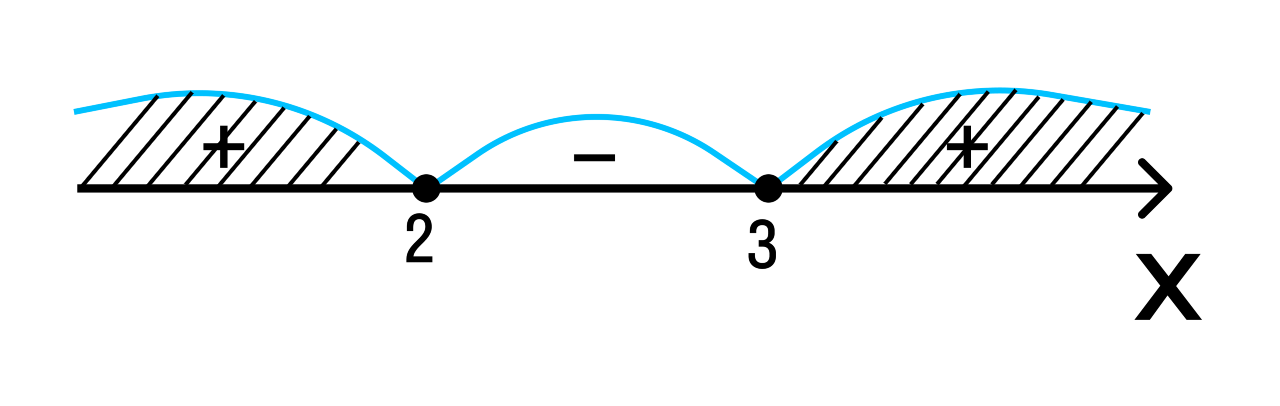
Ответ: х ≤ 2, х ≥ 3.
Пример 2. Применить метод интервалов для решения неравенства х2+4х+3 < 0.
Как решить неравенство методом интервалов, нам уже известно. Поэтому можем оформить решение кратко:
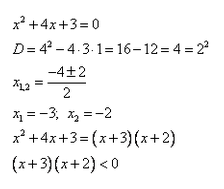
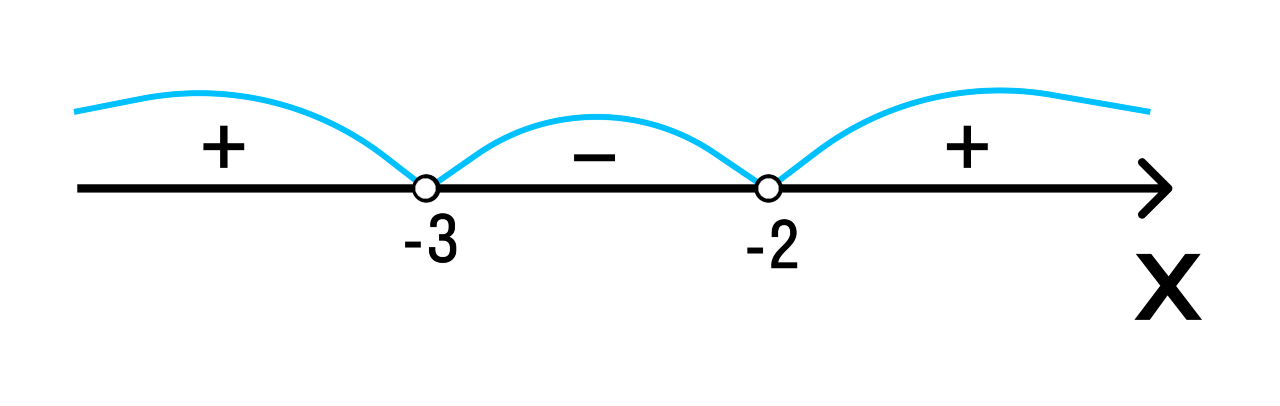
Ответ: -3 < x < -2.
Пример 3. Выполнить решение квадратного неравенства методом интервалов:
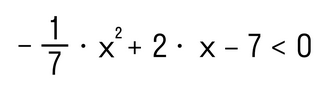
Как решаем:
- Находим корни квадратного трехчлена, который находится в левой части:
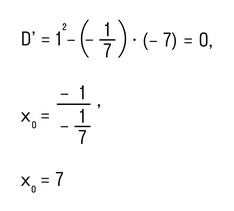
- Так как мы решаем строгое неравенство, то на координатной прямой изображаем выколотую точку с координатой 7:
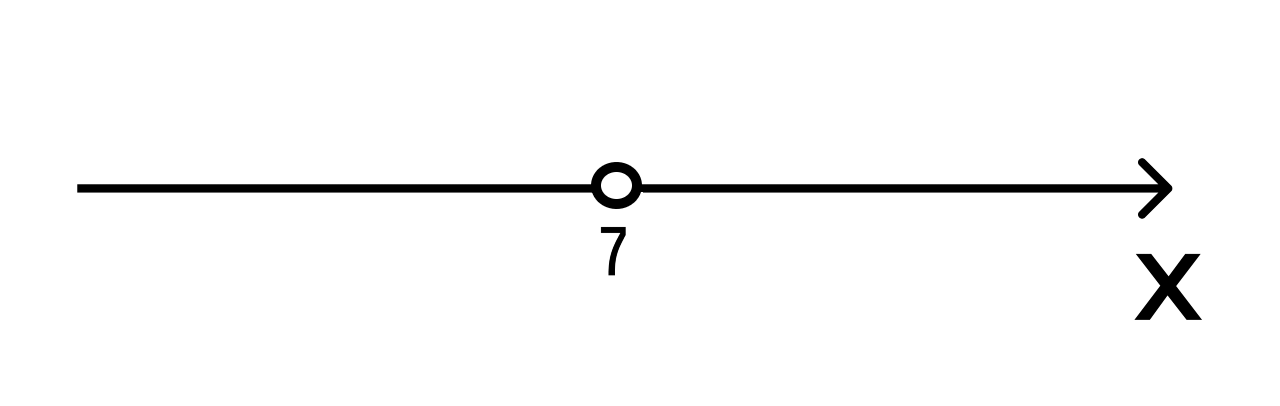
- Теперь определим знаки на двух полученных промежутках (−∞, 7) и (7, +∞).
Это легко сделать, потому что дискриминант квадратного трехчлена равен нулю, а старший коэффициент со знаком минус. Фиксируем знаки: −, −:
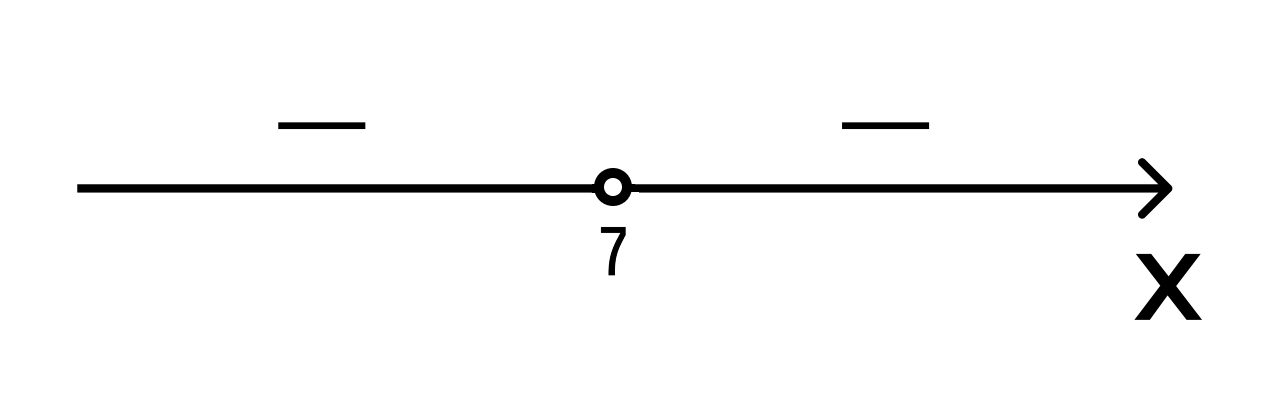
- Так как мы решаем неравенство со знаком <, то изобразим штриховку над интервалами со знаками минус:
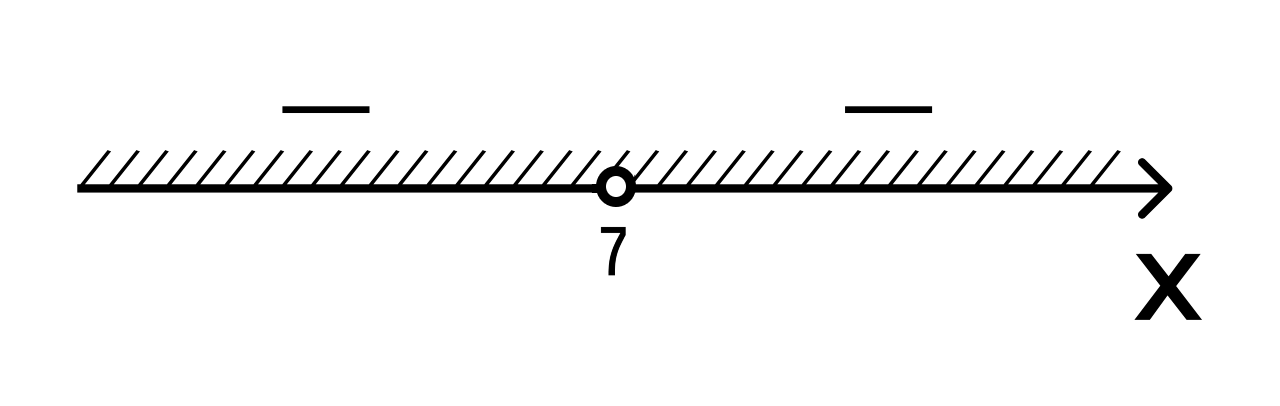
Очевидно, решениями являются оба промежутка (−∞, 7), (7, +∞).
Ответ: (−∞, 7), (7, +∞).
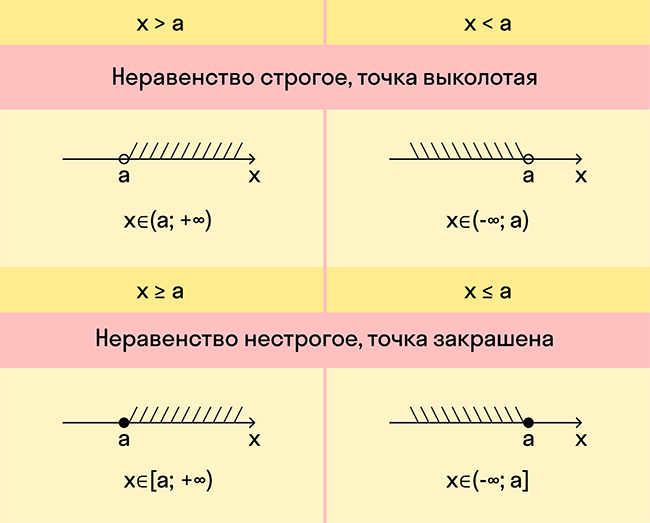
Метод интервалов: решение простейших строгих неравенств
12 ноября 2017
- Домашнее задание
- Ответы
Для начала — немного лирики, чтобы почувствовать проблему, которую решает метод интервалов. Допустим, нам надо решить вот такое неравенство:
(x − 5)(x + 3) > 0
Какие есть варианты? Первое, что приходит в голову большинству учеников — это правила «плюс на плюс дает плюс» и «минус на минус дает плюс». Поэтому достаточно рассмотреть случай, когда обе скобки положительны: x − 5 > 0 и x + 3 > 0. Затем также рассмотрим случай, когда обе скобки отрицательны: x − 5 < 0 и x + 3 < 0. Таким образом, наше неравенство свелось к совокупности двух систем, которая, впрочем, легко решается:
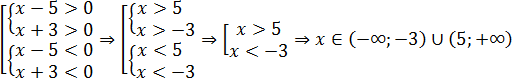
Более продвинутые ученики вспомнят (может быть), что слева стоит квадратичная функция, график которой — парабола. Причем эта парабола пересекает ось OX в точках x = 5 и x = −3. Для дальнейшей работы надо раскрыть скобки. Имеем:
x2 − 2x − 15 > 0
Теперь понятно, что ветви параболы направлены вверх, т.к. коэффициент a = 1 > 0. Попробуем нарисовать схему этой параболы:
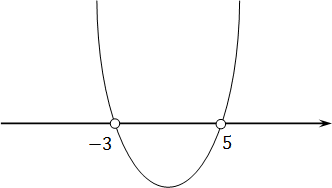
Функция больше нуля там, где она проходит выше оси OX. В нашем случае это интервалы (−∞ −3) и (5; +∞) — это и есть ответ.
Обратите внимание: на рисунке изображена именно схема функции, а не ее график. Потому что для настоящего графика надо считать координаты, рассчитывать смещения и прочую хрень, которая нам сейчас совершенно ни к чему.
Почему эти методы неэффективны?
Итак, мы рассмотрели два решения одного и того же неравенства. Оба они оказались весьма громоздкими. В первом решении возникает — вы только вдумайтесь! — совокупность систем неравенств. Второе решение тоже не особо легкое: нужно помнить график параболы и еще кучу мелких фактов.
Это было очень простое неравенство. В нем всего 2 множителя. А теперь представьте, что множителей будет не 2, а хотя бы 4. Например:
(x − 7)(x − 1)(x + 4)(x + 9) < 0
Как решать такое неравенство? Перебирать все возможные комбинации плюсов и минусов? Да мы уснем быстрее, чем найдем решение. Рисовать график — тоже не вариант, поскольку непонятно, как ведет себя такая функция на координатной плоскости.
Для таких неравенств нужен специальный алгоритм решения, который мы сегодня и рассмотрим.
Что такое метод интервалов
Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f (x) > 0 и f (x) < 0. Алгоритм состоит из 4 шагов:
- Решить уравнение f (x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
- Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;
- Выяснить знак (плюс или минус) функции f (x) на самом правом интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней;
- Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется.
Вот и все! После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f (x) > 0, или знаком «−», если неравенство имеет вид f (x) < 0.
На первый взгляд может показаться, что метод интервалов — это какая-то жесть. Но на практике все будет очень просто. Стоит чуть-чуть потренироваться — и все станет понятно. Взгляните на примеры — и убедитесь в этом сами:
Задача. Решите неравенство:
(x − 2)(x + 7) < 0
Работаем по методу интервалов. Шаг 1: заменяем неравенство уравнением и решаем его:
(x − 2)(x + 7) = 0
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:
x − 2 = 0 ⇒ x = 2;
x + 7 = 0 ⇒ x = −7.
Получили два корня. Переходим к шагу 2: отмечаем эти корни на координатной прямой. Имеем:
![]()
Теперь шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 (но никто не запрещает взять x = 4, x = 10 и даже x = 10 000). Получим:
f (x) = (x − 2)(x + 7);
x = 3;
f (3) = (3 − 2)(3 + 7) = 1 · 10 = 10;
Получаем, что f(3) = 10 > 0, поэтому в самом правом интервале ставим знак плюс.
Переходим к последнему пункту — надо отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс (мы убедились в этом на предыдущем шаге), поэтому слева обязан стоять минус.
Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс. Осталось отметить эти знаки на координатной оси. Имеем:
![]()
Вернемся к исходному неравенству, которое имело вид:
(x − 2)(x + 7) < 0
Итак, функция должна быть меньше нуля. Значит, нас интересует знак минус, который возникает лишь на одном интервале: (−7; 2). Это и будет ответ.
Задача. Решите неравенство:
(x + 9)(x − 3)(1 − x) < 0
Шаг 1: приравниваем левую часть к нулю:
(x + 9)(x − 3)(1 − x) = 0;
x + 9 = 0 ⇒ x = −9;
x − 3 = 0 ⇒ x = 3;
1 − x = 0 ⇒ x = 1.
Помните: произведение равно нулю, когда хотя бы один из множителей равен нулю. Именно поэтому мы вправе приравнять к нулю каждую отдельную скобку.
Шаг 2: отмечаем все корни на координатной прямой:
![]()
Шаг 3: выясняем знак самого правого промежутка. Берем любое число, которое больше, чем x = 1. Например, можно взять x = 10. Имеем:
f (x) = (x + 9)(x − 3)(1 − x);
x = 10;
f (10) = (10 + 9)(10 − 3)(1 − 10) = 19 · 7 · (−9) = − 1197;
f (10) = −1197 < 0.
Шаг 4: расставляем остальные знаки. Помним, что при переходе через каждый корень знак меняется. В итоге наша картинка будет выглядеть следующим образом:
![]()
Вот и все. Осталось лишь выписать ответ. Взгляните еще раз на исходное неравенство:
(x + 9)(x − 3)(1 − x) < 0
Это неравенство вида f (x) < 0, т.е. нас интересуют интервалы, отмеченные знаком минус. А именно:
x ∈ (−9; 1) ∪ (3; +∞)
Это и есть ответ.
Замечание по поводу знаков функции
Практика показывает, что наибольшие трудности в методе интервалов возникают на последних двух шагах, т.е. при расстановке знаков. Многие ученики начинают путаться: какие надо брать числа и где ставить знаки.
Чтобы окончательно разобраться в методе интервалов, рассмотрим два замечания, на которых он построен:
- Непрерывная функция меняет знак только в тех точках, где она равна нулю. Такие точки разбивают координатную ось на куски, внутри которых знак функции никогда не меняется. Вот зачем мы решаем уравнение f (x) = 0 и отмечаем найденные корни на прямой. Найденные числа — это «пограничные» точки, отделяющие плюсы от минусов.
- Чтобы выяснить знак функции на каком-либо интервале, достаточно подставить в функцию любое число из этого интервала. Например, для интервала (−5; 6) мы вправе брать x = −4, x = 0, x = 4 и даже x = 1,29374, если нам захочется. Почему это важно? Да потому что многих учеников начинают грызть сомнения. Мол, что если для x = −4 мы получим плюс, а для x = 0 — минус? А ничего — такого никогда не будет. Все точки на одном интервале дают один и тот же знак. Помните об этом.
Вот и все, что нужно знать про метод интервалов. Конечно, мы разобрали его в самом простом варианте. Существуют более сложные неравенства — нестрогие, дробные и с повторяющимися корнями. Для них тоже можно применять метод интервалов, но это тема для отдельного большого урока.
Теперь хотел бы разобрать продвинутый прием, который резко упрощает метод интервалов. Точнее, упрощение затрагивает только третий шаг — вычисление знака на самом правом куске прямой. По каким-то причинам этот прием не проходят в школах (по крайней мере, мне никто такого не объяснял). А зря — ведь на самом деле этот алгоритм очень прост.
Итак, знак функции на правом куске числовой оси. Этот кусок имеет вид (a; +∞), где a — самый большой корень уравнения f (x) = 0. Чтобы не взрывать мозг, рассмотрим конкретный пример:
(x − 1)(2 + x)(7 − x) < 0;
f (x) = (x − 1)(2 + x)(7 − x);
(x − 1)(2 + x)(7 − x) = 0;
x − 1 = 0 ⇒ x = 1;
2 + x = 0 ⇒ x = −2;
7 − x = 0 ⇒ x = 7;
Мы получили 3 корня. Перечислим их в порядке возрастания: x = −2, x = 1 и x = 7. Очевидно, что наибольший корень — это x = 7.
Для тех, кому легче рассуждать графически, я отмечу эти корни на координатной прямой. Посмотрим, что получится:
![]()
Требуется найти знак функции f (x) на самом правом интервале, т.е. на (7; +∞). Но как мы уже отмечали, для определения знака можно взять любое число из этого интервала. Например, можно взять x = 8, x = 150 и т.д. А теперь — тот самый прием, который не проходят в школах: давайте в качестве числа возьмем бесконечность. Точнее, плюс бесконечность, т.е. +∞.
«Ты че, обкурился? Как можно подставить в функцию бесконечность?» — возможно, спросите вы. Но задумайтесь: нам ведь не нужно само значение функции, нам нужен только знак. Поэтому, например, значения f (x) = −1 и f (x) = −938 740 576 215 значат одно и то же: функция на данном интервале отрицательна. Поэтому все, что от вас требуется — найти знак, который возникает на бесконечности, а не значение функции.
На самом деле, подставлять бесконечность очень просто. Вернемся к нашей функции:
f (x) = (x − 1)(2 + x)(7 − x)
Представьте, что x — это очень большое число. Миллиард или даже триллион. Теперь посмотрим, что будет происходить в каждой скобке.
Первая скобка: (x − 1). Что будет, если из миллиарда вычесть единицу? Получится число, не особо отличающееся от миллиарда, и это число будет положительным. Аналогично со второй скобкой: (2 + x). Если к двойке прибавить миллиард, по получим миллиард с копейками — это положительное число. Наконец, третья скобка: (7 − x). Здесь будет минус миллиард, от которого «отгрызли» жалкий кусочек в виде семерки. Т.е. полученное число мало чем будет отличаться от минус миллиарда — оно будет отрицательным.
Осталось найти знак всего произведения. Поскольку в первых скобках у нас был плюс, а в последней — минус, получаем следующую конструкцию:
(+) · (+) · (−) = (−)
Итоговый знак — минус! И неважно, чему равно значение самой функции. Главное, что это значение — отрицательное, т.е. на самом правом интервале стоит знак минус. Осталось выполнить четвертый шаг метода интервалов: расставить все знаки. Имеем:
![]()
Исходное неравенство имело вид:
(x − 1)(2 + x)(7 − x) < 0
Следовательно, нас интересуют интервалы, отмеченные знаком минус. Выписываем ответ:
x ∈ (−2; 1) ∪ (7; +∞)
Вот и весь прием, который я хотел рассказать. В заключение — еще одно неравенство, которое решается методом интервалов с привлечением бесконечности. Чтобы визуально сократить решение, я не буду писать номера шагов и развернутые комментарии. Напишу только то, что действительно надо писать при решении реальных задач:
Задача. Решите неравенство:
x(2x + 8)(x − 3) > 0
Заменяем неравенство уравнением и решаем его:
x(2x + 8)(x − 3) = 0;
x = 0;
2x + 8 = 0 ⇒ x = −4;
x − 3 = 0 ⇒ x = 3.
Отмечаем все три корня на координатной прямой (сразу со знаками):
![]()
Справа на координатной оси стоит плюс, т.к. функция имеет вид:
f (x) = x(2x + 8)(x − 3)
А если подставить бесконечность (например, миллиард), получим три положительных скобки. Поскольку исходное выражение должно быть больше нуля, нас интересуют только плюсы. Осталось выписать ответ:
x ∈ (−4; 0) ∪ (3; +∞)
Смотрите также:
- Метод интервалов: случай нестрогих неравенств

- Тест по методу интервалов для строгих неравенств

- Сводный тест по задачам B12 (2 вариант)

- Профильный ЕГЭ-2022, задание 6. Геометрический смысл производной

- Формулы приведения: ускоряем вычисления в тригонометрии

- Задачи B4: перевозка груза тремя фирмами

б) 2arccos 0 + 3 arccos 1. Ответ: ?
в) arcsin  + arcsin
+ arcsin  . Ответ:
. Ответ:  .
.
г) 5 arctg (- ) – arccos (-
) – arccos (- ). Ответ:–
). Ответ:–  .
.
– Проверим домашнее задание, откройте свои тетради с домашними работами.
Некоторые из вас нашли решение методом подбора, а некоторые с помощью графика.
2. Вывод о способах решения данных заданий и постановка проблемы, т. е. сообщение темы и цели урока.
– а) С помощью подбора решать сложно, если задан большой промежуток.
– б) Графический способ не даёт точных результатов, требует проверку, и занимает много времени.
– Поэтому должен быть ещё как минимум один способ, наиболее универсальный -попробуем его найти. Итак, чем мы будем заниматься сегодня на уроке? (Учиться выбирать корни тригонометрического уравнения на заданном промежутке.)
– Пример 1. (Ученик выходит к доске)
cos x = -0,5, где хI [-  ].
].
Вопрос: Отчего зависит ответ на данное задание? (От общего решения уравнения. Запишем решение в общем виде). Решение записывается на доске
х =
 + 2?k, где k
+ 2?k, где k  R.
R.
– Запишем это решение в виде совокупности:

– Как вы считаете, при какой записи решения удобно выбирать корни на промежутке? (из второй записи). Но это ведь опять способ подбора. Что нам необходимо знать, чтобы получить верный ответ? (Надо знать значения k).
(Составим математическую модель для нахождения k).
1 уровень: № 295 (а,б), № 317 (а,б)
2 уровень: № 307 (в), № 308 (б), № 326(б), № 327(б).
Метод интервалов, примеры, решения
Метод интервалов принято считать универсальным для решения неравенств. Иногда этот метод также называют методом промежутков. Применим он как для решения рациональных неравенств с одной переменной, так и для неравенств других видов. В нашем материале мы постарались уделить внимание всем аспектам вопроса.
Что ждет вас в данном разделе? Мы разберем метод промежутков и рассмотрим алгоритмы решения неравенств с его помощью. Затронем теоретические аспекты, на которых основано применение метода.
Особое внимание мы уделяем нюансам темы, которые обычно не затрагиваются в рамках школьной программы. Например, рассмотрим правила расстановки знаков на интервалах и сам метод интервалов в общем виде без его привязки к рациональным неравенствам.
Алгоритм
Кто помнит, как происходит знакомство с методом промежутков в школьном курсе алгебры? Обычно все начинается с решения неравенств вида f ( x ) 0 (знак неравенства может быть использован любой другой, например, ≤ , > или ≥ ). Здесь f ( x ) может быть многочленом или отношением многочленов. Многочлен, в свою очередь, может быть представлен как:
- произведение линейных двучленов с коэффициентом 1 при переменной х ;
- произведение квадратных трехчленов со старшим коэффициентом 1 и с отрицательным дискриминантом их корней.
Приведем несколько примеров таких неравенств:
( x + 3 ) · ( x 2 − x + 1 ) · ( x + 2 ) 3 ≥ 0 ,
( x – 2 ) · ( x + 5 ) x + 3 > 0 ,
( x − 5 ) · ( x + 5 ) ≤ 0 ,
( x 2 + 2 · x + 7 ) · ( x – 1 ) 2 ( x 2 – 7 ) 5 · ( x – 1 ) · ( x – 3 ) 7 ≤ 0 .
Запишем алгоритм решения неравенств такого вида, как мы привели в примерах, методом промежутков:
- находим нули числителя и знаменателя, для этого числитель и знаменатель выражения в левой части неравенства приравниваем к нулю и решаем полученные уравнения;
- определяем точки, которые соответствуют найденным нулям и отмечаем их черточками на оси координат;
- определяем знаки выражения f ( x ) из левой части решаемого неравенства на каждом промежутке и проставляем их на графике;
- наносим штриховку над нужными участками графика, руководствуясь следующим правилом: в случае, если неравенство имеет знаки или ≤ изображается, штрихуются «минусовые» промежутки, если же мы работаем с неравенством, имеющим знаки > или ≥ , то выделяем штриховкой участки, отмеченные знаком « + ».
Четреж, с которым мы будем работать, может иметь схематический вид. Излишние подробности могут перегружать рисунок и затруднять решение. Нас будет мало интересовать маштаб. Достаточно будет придерживаться правильного расположения точек по мере роста значений их координат.
При работе со строгими неравенствами мы будем использовать обозначение точки в виде круга с незакрашенным (пустым) центром. В случае нестрогих неравенств точки, которые соответствуют нулям знаменателя, мы будем изображать пустыми, а все остальные обычными черными.
Отмеченные точки разбивают координатную прямую на несколько числовых промежутков. Это позволяет нам получить геометрическое представление числового множества, которое фактически является решением данного неравенства.
Научные основы метода промежутков
Основан подход, положенный в основу метода промежутков, основан на следующем свойстве непрерывной функции: функция сохраняет постоянный знак на интервале ( a , b ) , на котором эта функция непрерывна и не обращается в нуль. Это же свойство характерно для числовых лучей ( − ∞ , a ) и ( a , + ∞ ) .
Приведенное свойство функции подтверждается теоремой Больцано-Коши, которая приведена во многих пособиях для подготовки к вступительным испытаниям.
Обосновать постоянство знака на промежутках также можно на основе свойств числовых неравенств. Например, возьмем неравенство x – 5 x + 1 > 0 . Если мы найдем нули числителя и знаменателя и нанесем их на числовую прямую, то получим ряд промежутков: ( − ∞ , − 1 ) , ( − 1 , 5 ) и ( 5 , + ∞ ) .
Возьмем любой из промежутков и покажем на нем, что на всем промежутке выражение из левой части неравенства будет иметь постоянный знак. Пусть это будет промежуток ( − ∞ , − 1 ) . Возьмем любое число t из этого промежутка. Оно будет удовлетворять условиям t − 1 , и так как − 1 5 , то по свойству транзитивности, оно же будет удовлетворять и неравенству t 5 .
Используя оба полученных неравенства и свойство числовых неравенств, мы можем предположить, что t + 1 0 и t − 5 0 . Это значит, что t + 1 и t − 5 – это отрицательные числа независимо от значения t на промежутке ( − ∞ , − 1 ) .
Используя правило деления отрицательных чисел, мы можем утверждать, что значение выражения t – 5 t + 1 будет положительным. Это значит, что значение выражения x – 5 x + 1 будет положительным при любом значении x из промежутка ( − ∞ , − 1 ) . Все это позволяет нам утверждать, что на промежутке, взятом для примера, выражение имеет постоянный знак. В нашем случае это знак « + ».
Нахождение нулей числителя и знаменателя
Алгоритм нахождения нулей прост: приравниваем выражения из числителя и знаменателя к нулю и решаем полученные уравнения. При возникновении затруднений можно обратиться к теме «Решение уравнений методом разложения на множители». В этом разделе мы ограничимся лишь рассмотрением примера.
Рассмотрим дробь x · ( x – 0 , 6 ) x 7 · ( x 2 + 2 · x + 7 ) 2 · ( x + 5 ) 3 . Для того, чтобы найти нули числителя и знаменателя, приравняем их к нулю для того, чтобы получить и решить уравнения: x · ( x − 0 , 6 ) = 0 и x 7 · ( x 2 + 2 · x + 7 ) 2 · ( x + 5 ) 3 = 0 .
В первом случае мы можем перейти к совокупности двух уравнений x = 0 и x − 0 , 6 = 0 , что дает нам два корня 0 и 0 , 6 . Это нули числителя.
Второе уравнение равносильно совокупности трех уравнений x 7 = 0 , ( x 2 + 2 · x + 7 ) 2 = 0 , ( x + 5 ) 3 = 0 . Проводим ряд преобразований и получаем x = 0 , x 2 + 2 · x + 7 = 0 , x + 5 = 0 . Корень первого уравнения 0 , у второго уравнения корней нет, так как оно имеет отрицательный дискриминант, корень третьего уравнения – 5 . Это нули знаменателя.
0 в данном случае является одновременно и нулем числителя, и нулем знаменателя.
В общем случае, когда в левой части неравенства дробь, которая не обязательно является рациональной, числитель и знаменатель точно также приравниваются к нулю для получения уравнений. Решение уравнений позволяет найти нули числителя и знаменателя.
Определение знаков на интервалах
Определить знак интервала просто. Для этого можно найти значение выражения из левой части неравенства для любой произвольно выбранной точки из данного интервала. Полученный знак значения выражения в произвольно выбранной точке промежутка будет совпадать со знаком всего промежутка.
Рассмотрим это утверждение на примере.
Возьмем неравенство x 2 – x + 4 x + 3 ≥ 0 . Нулей числителя выражение, расположенное в левой части неравенства, нулей не имеет. Нулем знаменателя будет число – 3 . Получаем два промежутка на числовой прямой ( − ∞ , − 3 ) и ( − 3 , + ∞ ) .
Для того, чтобы определить знаки промежутков, вычислим значение выражения x 2 – x + 4 x + 3 для точек, взятых произвольно на каждом из промежутков.
Из первого промежутка ( − ∞ , − 3 ) возьмем − 4 . При x = − 4 имеем ( – 4 ) 2 – ( – 4 ) + 4 ( – 4 ) + 3 = – 24 . Мы получили отрицательное значение, значит весь интервал будет со знаком « – ».
Для промежутка ( − 3 , + ∞ ) проведем вычисления с точкой, имеющей нулевую координату. При x = 0 имеем 0 2 – 0 + 4 0 + 3 = 4 3 . Получили положительное значение, что значит, что весь промежуток будет иметь знак « + ».
Можно использовать еще один способ определения знаков. Для этого мы можем найти знак на одном из интервалов и сохранить его или изменить при переходе через нуль. Для того, чтобы все сделать правильно, необходимо следовать правилу: при переходе через нуль знаменателя, но не числителя, или числителя, но не знаменателя мы можем поменять знак на противоположный, если степень выражения, дающего этот нуль, нечетная, и не можем поменять знак, если степень четная. Если мы получили точку, которая является одновременно нулем числителя и знаменателя, то поменять знак на противоположный можно только в том случае, если сумма степеней выражений, дающих этот нуль, нечетная.
Если вспомнить неравенство, которое мы рассмотрели в начале первого пункта этого материала, то на крайнем правом промежутке мы можем поставить знак « + ».
Теперь обратимся к примерам.
Возьмем неравенство ( x – 2 ) · ( x – 3 ) 3 · ( x – 4 ) 2 ( x – 1 ) 4 · ( x – 3 ) 5 · ( x – 4 ) ≥ 0 и решим его методом интервалов. Для этого нам необходимо найти нули числителя и знаменателя и отметить их на координатной прямой. Нулями числителя будут точки 2 , 3 , 4 , знаменателя точки 1 , 3 , 4 . Отметим их на оси координат черточками.
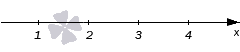
Нули знаменателя отметим пустыми точками.
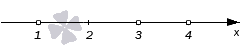
Так как мы имеем дело с нестрогим неравенством, то оставшиеся черточки заменяем обычными точками.
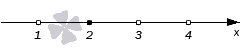
Теперь расставим точки на промежутках. Крайний правый промежуток ( 4 , + ∞ ) будет знак + .
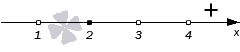
Продвигаясь справа налево будем проставлять знаки остальных промежутков. Переходим через точку с координатой 4 . Это одновременно нуль числителя и знаменателя. В сумме, эти нули дают выражения ( x − 4 ) 2 и x − 4 . Сложим их степени 2 + 1 = 3 и получим нечетное число. Это значит, что знак при переходе в данном случае меняется на противоположный. На интервале ( 3 , 4 ) будет знак минус.
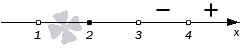
Переходим к интервалу ( 2 , 3 ) через точку с координатой 3 . Это тоже нуль и числителя, и знаменателя. Мы его получили благодаря двум выражениям ( x − 3 ) 3 и ( x − 3 ) 5 , сумма степеней которых равна 3 + 5 = 8 . Получение четного числа позволяет нам оставить знак интервала неизменным.
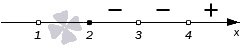
Точка с координатой 2 – это нуль числителя. Степень выражения х – 2 равна 1 (нечетная). Это значит, что при переходе через эту точку знак необходимо изменить на противоположный.
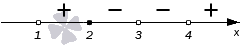
У нас остался последний интервал ( − ∞ , 1 ) . Точка с координатой 1 – это нуль знаменателя. Он был получен из выражения ( x − 1 ) 4 , с четной степенью 4 . Следовательно, знак остается прежним. Итоговый рисунок будет иметь вот такой вид:
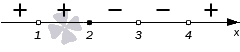
Применение метода интервалов особенно эффективно в случаях, когда вычисление значения выражения связано с большим объемом работы. Примером может стать необходимость вычисления значения выражения
x + 3 – 3 4 3 · x 2 + 6 · x + 11 2 · x + 2 – 3 4 ( x – 1 ) 2 · x – 2 3 5 · ( x – 12 )
в любой точке интервала 3 – 3 4 , 3 – 2 4 .
Будем считать, что с правилами определения знаков для промежутков мы разобрались. Идем дальше.
[spoiler title=”источники:”]
http://urok.1sept.ru/articles/419940
http://zaochnik.com/spravochnik/matematika/systems/metod-intervalov/
[/spoiler]
Метод интервалов принято считать универсальным для решения неравенств. Иногда этот метод также называют методом промежутков. Применим он как для решения рациональных неравенств с одной переменной, так и для неравенств других видов. В нашем материале мы постарались уделить внимание всем аспектам вопроса.
Что ждет вас в данном разделе? Мы разберем метод промежутков и рассмотрим алгоритмы решения неравенств с его помощью. Затронем теоретические аспекты, на которых основано применение метода.
Особое внимание мы уделяем нюансам темы, которые обычно не затрагиваются в рамках школьной программы. Например, рассмотрим правила расстановки знаков на интервалах и сам метод интервалов в общем виде без его привязки к рациональным неравенствам.
Алгоритм
Кто помнит, как происходит знакомство с методом промежутков в школьном курсе алгебры? Обычно все начинается с решения неравенств вида f(x)<0 (знак неравенства может быть использован любой другой, например, ≤, > или ≥). Здесь f(x) может быть многочленом или отношением многочленов. Многочлен, в свою очередь, может быть представлен как:
- произведение линейных двучленов с коэффициентом 1 при переменной х;
- произведение квадратных трехчленов со старшим коэффициентом 1 и с отрицательным дискриминантом их корней.
Приведем несколько примеров таких неравенств:
(x+3)·(x2−x+1)·(x+2)3≥0,
(x-2)·(x+5)x+3>0 ,
(x−5)·(x+5)≤0,
(x2+2·x+7)·(x-1)2(x2-7)5·(x-1)·(x-3)7≤0 .
Запишем алгоритм решения неравенств такого вида, как мы привели в примерах, методом промежутков:
- находим нули числителя и знаменателя, для этого числитель и знаменатель выражения в левой части неравенства приравниваем к нулю и решаем полученные уравнения;
- определяем точки, которые соответствуют найденным нулям и отмечаем их черточками на оси координат;
- определяем знаки выражения f(x) из левой части решаемого неравенства на каждом промежутке и проставляем их на графике;
- наносим штриховку над нужными участками графика, руководствуясь следующим правилом: в случае, если неравенство имеет знаки < или ≤ изображается, штрихуются «минусовые» промежутки, если же мы работаем с неравенством, имеющим знаки > или ≥, то выделяем штриховкой участки, отмеченные знаком «+».
Четреж, с которым мы будем работать, может иметь схематический вид. Излишние подробности могут перегружать рисунок и затруднять решение. Нас будет мало интересовать маштаб. Достаточно будет придерживаться правильного расположения точек по мере роста значений их координат.
При работе со строгими неравенствами мы будем использовать обозначение точки в виде круга с незакрашенным (пустым) центром. В случае нестрогих неравенств точки, которые соответствуют нулям знаменателя, мы будем изображать пустыми, а все остальные обычными черными.
Отмеченные точки разбивают координатную прямую на несколько числовых промежутков. Это позволяет нам получить геометрическое представление числового множества, которое фактически является решением данного неравенства.
Научные основы метода промежутков
Основан подход, положенный в основу метода промежутков, основан на следующем свойстве непрерывной функции: функция сохраняет постоянный знак на интервале (a, b), на котором эта функция непрерывна и не обращается в нуль. Это же свойство характерно для числовых лучей (−∞, a) и (a, +∞).
Приведенное свойство функции подтверждается теоремой Больцано-Коши, которая приведена во многих пособиях для подготовки к вступительным испытаниям.
Обосновать постоянство знака на промежутках также можно на основе свойств числовых неравенств. Например, возьмем неравенство x-5x+1>0 . Если мы найдем нули числителя и знаменателя и нанесем их на числовую прямую, то получим ряд промежутков: (−∞, −1), (−1, 5) и (5, +∞).
Возьмем любой из промежутков и покажем на нем, что на всем промежутке выражение из левой части неравенства будет иметь постоянный знак. Пусть это будет промежуток (−∞, −1). Возьмем любое число t из этого промежутка. Оно будет удовлетворять условиям t<−1, и так как −1<5, то по свойству транзитивности, оно же будет удовлетворять и неравенству t<5.
Используя оба полученных неравенства и свойство числовых неравенств, мы можем предположить, что t+1<0 и t−5<0. Это значит, что t+1 и t−5 – это отрицательные числа независимо от значения t на промежутке (−∞, −1).
Используя правило деления отрицательных чисел, мы можем утверждать, что значение выражения t-5t+1 будет положительным. Это значит, что значение выражения x-5x+1 будет положительным при любом значении x из промежутка (−∞, −1). Все это позволяет нам утверждать, что на промежутке, взятом для примера, выражение имеет постоянный знак. В нашем случае это знак «+».
Нахождение нулей числителя и знаменателя
Алгоритм нахождения нулей прост: приравниваем выражения из числителя и знаменателя к нулю и решаем полученные уравнения. При возникновении затруднений можно обратиться к теме «Решение уравнений методом разложения на множители». В этом разделе мы ограничимся лишь рассмотрением примера.
Рассмотрим дробь x·(x-0,6)x7·(x2+2·x+7)2·(x+5)3. Для того, чтобы найти нули числителя и знаменателя, приравняем их к нулю для того, чтобы получить и решить уравнения: x·(x−0,6)=0 и x7·(x2+2·x+7)2·(x+5)3=0.
В первом случае мы можем перейти к совокупности двух уравнений x=0 и x−0,6=0, что дает нам два корня 0 и 0,6. Это нули числителя.
Второе уравнение равносильно совокупности трех уравнений x7=0, (x2+2·x+7)2=0, (x+5)3=0. Проводим ряд преобразований и получаем x=0, x2+2·x+7=0, x+5=0. Корень первого уравнения 0, у второго уравнения корней нет, так как оно имеет отрицательный дискриминант, корень третьего уравнения -5. Это нули знаменателя.
0 в данном случае является одновременно и нулем числителя, и нулем знаменателя.
В общем случае, когда в левой части неравенства дробь, которая не обязательно является рациональной, числитель и знаменатель точно также приравниваются к нулю для получения уравнений. Решение уравнений позволяет найти нули числителя и знаменателя.
Определение знаков на интервалах
Определить знак интервала просто. Для этого можно найти значение выражения из левой части неравенства для любой произвольно выбранной точки из данного интервала. Полученный знак значения выражения в произвольно выбранной точке промежутка будет совпадать со знаком всего промежутка.
Рассмотрим это утверждение на примере.
Возьмем неравенство x2-x+4x+3≥0. Нулей числителя выражение, расположенное в левой части неравенства, нулей не имеет. Нулем знаменателя будет число -3. Получаем два промежутка на числовой прямой (−∞, −3) и (−3, +∞).
Для того, чтобы определить знаки промежутков, вычислим значение выражения x2-x+4x+3 для точек, взятых произвольно на каждом из промежутков.
Из первого промежутка (−∞, −3) возьмем −4. При x=−4 имеем (-4)2-(-4)+4(-4)+3=-24 . Мы получили отрицательное значение, значит весь интервал будет со знаком «-».
Для промежутка (−3, +∞) проведем вычисления с точкой, имеющей нулевую координату. При x=0 имеем 02-0+40+3=43. Получили положительное значение, что значит, что весь промежуток будет иметь знак «+».
Можно использовать еще один способ определения знаков. Для этого мы можем найти знак на одном из интервалов и сохранить его или изменить при переходе через нуль. Для того, чтобы все сделать правильно, необходимо следовать правилу: при переходе через нуль знаменателя, но не числителя, или числителя, но не знаменателя мы можем поменять знак на противоположный, если степень выражения, дающего этот нуль, нечетная, и не можем поменять знак, если степень четная. Если мы получили точку, которая является одновременно нулем числителя и знаменателя, то поменять знак на противоположный можно только в том случае, если сумма степеней выражений, дающих этот нуль, нечетная.
Если вспомнить неравенство, которое мы рассмотрели в начале первого пункта этого материала, то на крайнем правом промежутке мы можем поставить знак «+».
Теперь обратимся к примерам.
Возьмем неравенство (x-2)·(x-3)3·(x-4)2(x-1)4·(x-3)5·(x-4)≥0 и решим его методом интервалов. Для этого нам необходимо найти нули числителя и знаменателя и отметить их на координатной прямой. Нулями числителя будут точки 2, 3, 4, знаменателя точки 1, 3, 4. Отметим их на оси координат черточками.
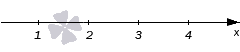
Нули знаменателя отметим пустыми точками.

Так как мы имеем дело с нестрогим неравенством, то оставшиеся черточки заменяем обычными точками.

Теперь расставим точки на промежутках. Крайний правый промежуток (4, +∞) будет знак +.

Продвигаясь справа налево будем проставлять знаки остальных промежутков. Переходим через точку с координатой 4. Это одновременно нуль числителя и знаменателя. В сумме, эти нули дают выражения (x−4)2 и x−4. Сложим их степени 2+1=3 и получим нечетное число. Это значит, что знак при переходе в данном случае меняется на противоположный. На интервале (3, 4) будет знак минус.

Переходим к интервалу (2, 3) через точку с координатой 3. Это тоже нуль и числителя, и знаменателя. Мы его получили благодаря двум выражениям (x−3)3 и (x−3)5, сумма степеней которых равна 3+5=8. Получение четного числа позволяет нам оставить знак интервала неизменным.

Точка с координатой 2 – это нуль числителя. Степень выражения х-2 равна 1 (нечетная). Это значит, что при переходе через эту точку знак необходимо изменить на противоположный.

У нас остался последний интервал (−∞, 1). Точка с координатой 1 – это нуль знаменателя. Он был получен из выражения (x−1)4, с четной степенью 4. Следовательно, знак остается прежним. Итоговый рисунок будет иметь вот такой вид:

Применение метода интервалов особенно эффективно в случаях, когда вычисление значения выражения связано с большим объемом работы. Примером может стать необходимость вычисления значения выражения
x+3-343·x2+6·x+112·x+2-34(x-1)2·x-235·(x-12)
в любой точке интервала 3-34,3-24.
Будем считать, что с правилами определения знаков для промежутков мы разобрались. Идем дальше.
Примеры решения неравенств методом интервалов
Теперь займемся применением полученных знаний и навыков на практике.
Решите неравенство (x-1)·(x+5)2(x-7)·(x-1)3≤0 .
Решение
Целесообразно применить для решения неравенства метод интервалов. Находим нули числителя и знаменателя. Нули числителя 1 и -5, нули знаменателя 7 и 1. Отметим их на числовой прямой. Мы имеем дело с нестрогим неравенством, поэтому нули знаменателя отметим пустыми точками, нуль числителя -5 отметим обычной закрашенной точкой.
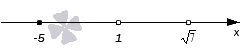
Проставим знаки промежутков, используя правила изменения знака при переходе через нуль. Начнем с крайнего правого промежутка, для которого вычислим значение выражения из левой части неравенства в точке, произвольно взятой из промежутка. Получим знак «+». Перейдем последовательно через все точки на координатной прямой, расставляя знаки, и получим:
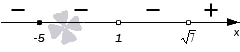
Мы работаем с нестрогим неравенством, имеющим знак ≤. Это значит, что нам необходимо отметить штриховкой промежутки, отмеченные знаком «-».
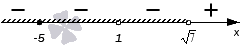
Ответ: (-∞,1)∪(1,7) .
Решение рациональных неравенств в большинстве случаев требует их предварительного преобразования к нужному виду. Только после этого появляется возможность использовать метод интервалов. Алгоритмы проведения таких преобразований рассмотрены в материале «Решение рациональных неравенств».
Рассмотрим пример преобразования квадратных трехчленов в записи неравенств.
Найдите решение неравенства (x2+3x+3)(x+3)x2+2·x-8>0.
Решение
Давайте посмотрим, действительно ли дискриминанты квадратных трехчленов в записи неравенства отрицательны. Это позволит нам определить, позволяет ли вид данного неравенства применить для решения метод интервалов.
Вычислим дискриминант для трехчлена x2+3·x+3: D=32−4·1·3=−3<0. Теперь вычислим дискриминант для трехчлена x2+2·x−8: D’=12−1·(−8)=9>0. Как видите, неравенство требует предварительного преобразования. Для этого представим трехчлен x2+2·x−8 как (x+4)·(x−2), а потом применим метод интервалов для решения неравенства (x2+3·x+3)·(x+3)(x+4)·(x-2)>0 .
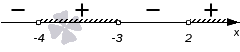
Ответ: (-4,-3)∪(2,+∞) .
Обобщенный метод интервалов
Обобщенный метод промежутков применяется для решения неравенств вида f(x)<0 (≤, >, ≥), где f(x) – произвольное выражение с одной переменной x.
Все действия проводятся по определенному алгоритму. При этом алгоритм решения неравенств обобщенным методом интервалов будет несколько отличаться от того, что мы разобрали ранее:
- находим область определения функции f и нули этой функции;
- отмечаем на координатной оси граничные точки;
- наносим на числовую прямую нули функции;
- определяем знаки промежутков;
- наносим штриховку;
- записываем ответ.
На числовой прямой необходимо отмечать в том числе и отдельные точки области определения. К примеру, областью определения функции служит множество (−5, 1]∪{3}∪[4, 7)∪{10}. Это значит, что нам необходимо отметить точки с координатами −5, 1, 3, 4, 7 и 10. Точки −5 и 7 изобразим пустыми, остальные можно выделить цветным карандашом для того, чтобы отличать их затем от нулей функции.
Нули функции в случае нестрогих неравенств наносятся обычными (закрашенными) точками, строгих – пустыми точками. Если нули совпадают с граничными точками или отдельными точками области определения, то их можно перекрасить в черный цвет, сделав пустыми или закрашенными в зависимости от вида неравенства.
Запись ответа представляет собой числовое множество, которое включает в себя:
- промежутки со штриховкой;
- отдельные точки области определения со знаком плюс, если мы имеем дело с неравенством, знак которого > или ≥ или со знаком минус, если в неравенстве есть знаки < или ≤.
Теперь стало понятно, что тот алгоритм, который мы привели в самом начале темы, является частным случаем алгоритма применения обобщенного метода интервалов.
Рассмотрим пример применения обобщенного метода интервалов.
Решите неравенство x2+2·x-24-34·x-3x-7<0 .
Решение
Вводим функцию f такую, что f(x)=x2+2·x-24-34·x-3x-7 . Найдем область определения функции f:
x2+2·x-24≥0x≠7D(f)=(-∞,-6]∪[4,7)∪(7,+∞) .
Теперь найдем нули функции. Для этого проведем решение иррационального уравнения:
x2+2·x-24-34·x-3=0
Получаем корень x=12.
Для обозначения граничных точек на оси координат используем оранжевый цвет. Точки -6,4 у нас будут закрашенными, а 7 оставляем пустой. Получаем:
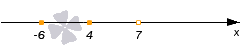
Отметим ноль функции пустой точкой черного цвета, так как мы работаем со строгим неравенством.
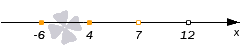
Определяем знаки на отдельных промежутках. Для этого возьмем по одной точке из каждого промежутка, например, 16, 8, 6 и −8, и вычислим в них значение функции f:
f(16)=162+2·16-24-34·16-316-7=264-159>0f(8)=82+2·8-24-34·8-38-7=56-9<0f(6)=62+2·6-24-34·6-36-7=24-152-1==15-2·242=225-962>0f(-8)=-82+2·(-8)-24-34·(-8)-3-8-7=24+3-15<0
Расставляем только что определенные знаки, и наносим штриховку над промежутками со знаком минус:
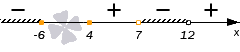
Ответом будет являться объединение двух промежутков со знаком «-»:(−∞, −6]∪(7, 12).
В ответ мы включили точку с координатой -6. Это не нуль функции, который мы бы не включили в ответ при решении строгого неравенства, а граничная точка области определения, которая входит в область определения. Значение функции в этой точке отрицательное, это значит, что она удовлетворяет неравенству.
Точку 4 мы в ответ не включили, точно также, как не включили весь промежуток [4, 7). В этой точке, точно также, как и на всем указанном промежутке значение функции положительно, что не удовлетворяет решаемому неравенству.
Запишем это еще раз для более четкого понимания: цветные точки необходимо включать в ответ в следующих случаях:
- эти точки являются частью промежутка со штриховкой,
- эти точки являются отдельными точками области определения функции, значения функции в которых удовлетворяют решаемому неравенству.
Ответ: (−∞, −6]∪(7, 12).
Цель урока:
а) закрепить умения решать
простейшие тригонометрические уравнения;
б) научить выбирать корни
тригонометрических уравнений из заданного
промежутка
Ход урока.
1. Актуализация знаний.
а)Проверка домашнего задания: классу
дано опережающее домашнее задание – решить
уравнение и найти способ выбора корней из
данного промежутка.
1)cos x = -0,5, где хI [-![]() ]. Ответ:
]. Ответ: ![]() .
.
2) sin x = ![]() , где хI [0;2?]. Ответ:
, где хI [0;2?]. Ответ: ![]() ;
; ![]() .
.
3)cos 2x = –![]() , где хI [0;
, где хI [0;![]() ]. Ответ:
]. Ответ:![]()
Ученики записывают решение на доске
кто-то с помощью графика, кто-то методом подбора.
В это время класс работает устно.
Найдите значение выражения:
а) tg ![]() –
–
sin ![]() + cos
+ cos ![]() + sin
+ sin ![]() . Ответ: 1.
. Ответ: 1.
б) 2arccos 0 + 3 arccos 1. Ответ: ?
в) arcsin ![]() + arcsin
+ arcsin ![]() . Ответ:
. Ответ:
![]() .
.
г) 5 arctg (-![]() ) – arccos (-
) – arccos (-![]() ). Ответ:–
). Ответ:– ![]() .
.
– Проверим домашнее задание, откройте
свои тетради с домашними работами.
Некоторые из вас нашли решение методом
подбора, а некоторые с помощью графика.
См. приложение 1
Приложение 2
Приложение 3
2. Вывод о способах решения данных
заданий и постановка проблемы, т. е. сообщение
темы и цели урока.
– а) С помощью подбора решать сложно,
если задан большой промежуток.
– б) Графический способ не даёт точных
результатов, требует проверку, и занимает много
времени.
– Поэтому должен быть ещё как минимум
один способ, наиболее универсальный -попробуем
его найти. Итак, чем мы будем заниматься сегодня
на уроке? (Учиться выбирать корни
тригонометрического уравнения на заданном
промежутке.)
– Пример 1. (Ученик выходит к доске)
cos x = -0,5, где хI [-![]() ].
].
Вопрос: Отчего зависит ответ на данное
задание? (От общего решения уравнения. Запишем
решение в общем виде). Решение записывается на
доске
х =![]()
![]() + 2?k, где k
+ 2?k, где k ![]() R.
R.
– Запишем это решение в виде
совокупности:

– Как вы считаете, при какой записи
решения удобно выбирать корни на промежутке? (из
второй записи). Но это ведь опять способ подбора.
Что нам необходимо знать, чтобы получить верный
ответ? (Надо знать значения k).
(Составим математическую модель для
нахождения k).
Ответ: ![]() .
.
Вывод: Чтобы выбрать корни
из заданного промежутка при решении
тригонометрического уравнения надо:
- для решения уравнения вида sin x = a, cos x = a
удобнее записать корни уравнения, как две серии
корней. - для решения уравнений вида tg x = a, ctg x = a
записать общую формулу корней. - составить математическую модель для каждого
решения в виде двойного неравенства и найти
целое значение параметра k или n. - подставить эти значения в формулу корней и
вычислить их.
3. Закрепление.
Пример №2 и №3 из домашнего задания
решить, используя полученный алгоритм.
Одновременно у доски работают два ученика, с
последующей проверкой работ.
4. Самостоятельная работа.
Самопроверка с выбором ответа. Выбрать №
правильного ответа, получив закодированное
число (312).
1) sin x = –![]() , x
, x ![]()
![]()
2) 3 tg x = –![]() , x I [0; 2
, x I [0; 2![]() ]
]
3) 2 cos ![]() ,
,
х ![]() [
[ ![]() ]
]
Приложение. Ответы
к примерам
5. Домашнее задание:
1 уровень: № 295 (а,б), № 317 (а,б)
2 уровень: № 307 (в), № 308 (б), № 326(б), № 327(б).
