Итак, с сегодняшнего дня мы начинаем вести новую рубрику: «Решение задач», в которой будем рассматривать задачи, взятые из сборника М.Э.Абрамяна «1000 ЗАДАЧ ПО ПРОГРАММИРОВАНИЮ».
Перейти на сайт с текстами задач
Открыв задачник и прочитав аннотацию, Вы, скорее всего, озадачитесь тем, что данное пособие предназначено для студентов механико-математического, физического и экономического факультетов, но смею Вас заверить, что это весьма универсальная книга, которая подходит как студентам, так и школьникам. Возможно, задачи из первых разделов книги покажутся Вам простыми — в этом случае используйте наш разбор только для проверки своих решений; но если же по каким-либо причинам решить задачи Вы не в состоянии, то тогда присоединяйтесь к нам.
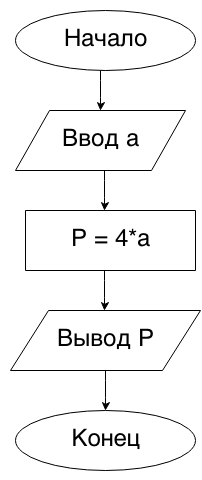
Begin1. Дана сторона квадрата a. Найти его периметр P = 4·a.
Прежде всего напомню, что для ввода и вывода информации, в Паскале используют следующие операторы:
- Read (Readln) — ввод значений с клавиатуры;
- Write (Writeln) — вывод результата (и вообще чего-либо) на экран.
Таким образом, решение задачи становится очевидным.
program Begin1;
var
a, P: real;
begin
write('Введите a:');
readln(a);
P := 4 * a;
write('P=', p);
end.
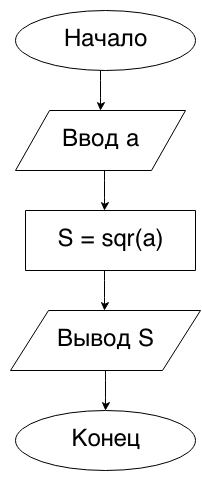
Begin2. Дана сторона квадрата a. Найти его площадь S = a2.
При решении данной задачи воспользуемся функцией sqr. Можно, конечно, вычислять квадрат, умножая число само на себя (S=a*a), но при вводе действительно больших чисел наша программа будет выполняться гораздо дольше, нежели при использовании sqr.
program Begin2;
var
a, s: real;
begin
write('Введите a: ');
readln(a);
s := sqr(a);
write('Площадь квадрата -- ', s);
end.
Begin3°. Даны стороны прямоугольника a и b. Найти его площадь S = a·b и периметр P = 2·(a + b).
Да, задача по сути своей проста и подобна предыдущим, поэтому поскорее составим к ней решение и перейдем к следующей.
program Begin3;
var
a, b, S, P: real;
begin
write('Введите a: ');
readln(a);
write('Введите b: ');
readln(b);
s := a * b;
p := 2 * (a + b);
write('Площадь прямоугольника -- ', s, '; Периметр прямоугольника -- ', p);
end.
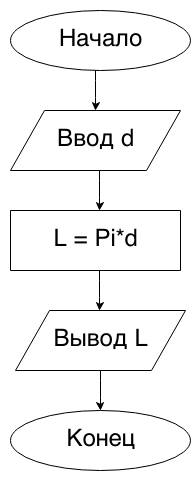
Begin4. Дан диаметр окружности d. Найти ее длину L = π·d. В качестве значения π использовать 3.14.
У вас, наверняка, возникает вопрос π — это константа или переменая? Так как π не изменяется в течение программы, π — константа. Вообще в Паскале уже встроена такая константа, но ее значение:
Pi = 3.14159265358979.
А так как в условии задачи указано, что в качестве значения π нужно использовать 3.14, то следует объявить π в разделе описания констант.
program Begin4;
const
pi = 3.14;
var
d, L: real;
begin
write('Введите диаметр окружности : ');
readln(d);
L := pi * d;
write('Длина окружности -- ', L);
end.
Begin5. Дана длина ребра куба a. Найти объем куба V = a3 и площадь его поверхности S = 6·a2.
Для решения задачи используем функцию power(x, a), где a — степень, x — число возводимое в степень (разумеется, использовать ее мы будем только для возведения числа в третью степень, квадрат числа по-прежнему находим с помощью sqr(x) ).
program Begin5;
var
v, a, s: real;
begin
write('Введите значение a: ');
readln(a);
v := power(a, 3);
s := 6 * sqr(a);
writeln('Объем куба -- ', v);
writeln('Площадь поверхности куба -- ', s);
end.
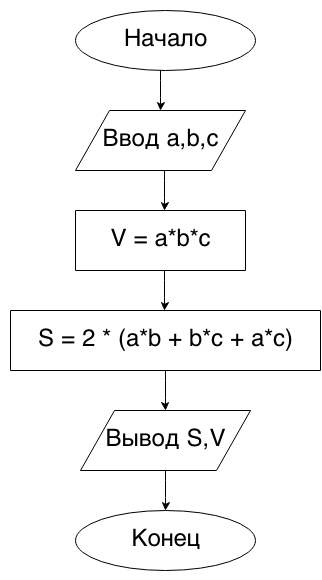
Begin6.Даны длины ребер a, b, c прямоугольного параллелепипеда. Найти его объем V = a·b·c и площадь поверхности S = 2·(a·b + b·c + a·c).
program Begin6;
var
v, a, b, c, s: real;
begin
write('Введите значения a, b, c: ');
readln(a, b, c);
v := a * b * c;
s := 2 * (a * b + b * c + a * c);
writeln('Объем параллелепипеда -- ', v);
writeln('Площадь поверхности параллелепипеда -- ', s);
end.
Begin7°. Найти длину окружности L и площадь круга S заданного радиуса R:
L = 2·π·R, S = π·R2.
В качестве значения π использовать 3.14.
program Begin7;
const
pi = 3.14;
var
l, s, r: real;
begin
write('Введите значение R: ');
readln(r);
l := 2 * pi * r;
s := pi * sqr(r);
writeln('Длина окружности -- ', l);
writeln('Площадь окружности -- ', s);
end.
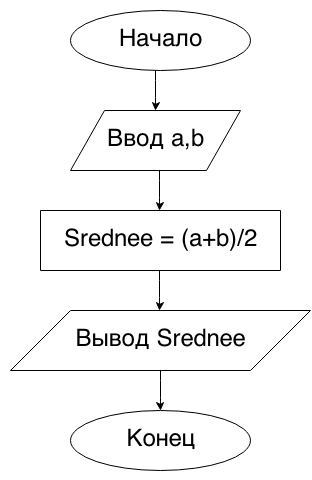
Begin8. Даны два числа a и b. Найти их среднее арифметическое: (a + b)/2.
program Begin8;
var
srednee, a, b: real;
begin
write('Введите значения a и b: ');
readln(a, b);
srednee := (a + b) / 2;
writeln('Среднее арифметическое -- ', srednee);
end.
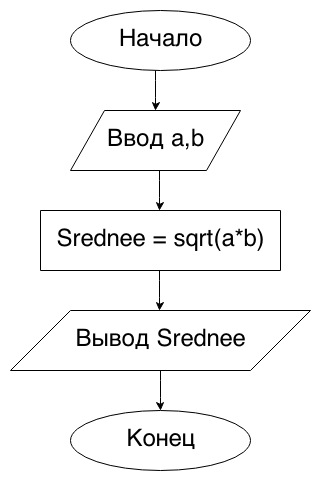
Begin9. Даны два неотрицательных числа a и b. Найти их среднее геометрическое, то есть квадратный корень из их произведения: √(a*b).
Напомню, что для нахождения квадратного корня мы используем функцию sqrt.
program Begin9;
var
a, b, srednee: real;
begin
write('Введите значения a и b: ');
readln(a, b);
srednee := sqrt(a * b);
writeln('Среднее геометрическое -- ', srednee);
end.
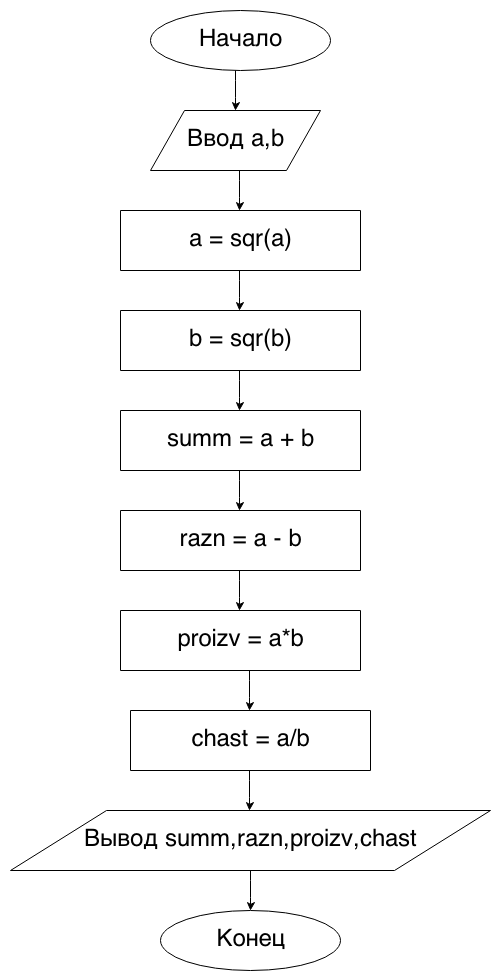
Begin10. Даны два ненулевых числа. Найти сумму, разность, произведение и частное их квадратов.
program Begin10;
var
a, b, summ, razn, proizv, chast: real;
begin
write('Введите значения a и b: ');
readln(a, b);
a := sqr(a); {квадрат первого числа}
b := sqr(b); {квадрат второго числа}
summ := a + b; {сумма квадратов}
razn := a - b; {разность квадратов}
proizv := a * b; {произведение квадратов}
chast := a / b; {частное квадратов}
writeln('Сумма квадратов -- ', summ);
writeln('Разность квадратов -- ', razn);
writeln('Произведение квадратов -- ', proizv);
writeln('Частное квадратов -- ', chast);
end.
Ну вот и все. Следующая публикация с решением задач выйдет в ближайшие дни.
Всем удачи и веселого Нового года:)
Данил Душистов
Решение 50 типовых
задач по программированию на языке Pascal
 |
Дата размещения сборника в сети: 31.08.2012
Онлайн-версия сборника находится на сайте http://el-prog.narod2.ru/
Со
всеми вопросами и комментариями обращаться на E-mail: danildushistov@gmail.com
Аннотация
Этот сборник содержит подробные
решения 50 практических задач, данных в рамках учеб- ного курса «Введение в
информатику и программирование», который читается в Адыгейском гос-
ударственном университете. Он может быть интересен школьникам, студентам и всем, кто изу- чает основы программирования на языке Pascal.
В качестве дополнительного материала прилагаются
тексты решений всех задач для сред PascalABC.NET и Borland Delphi 7.
Предисловие от автора
Этот сборник не может быть использован в качестве учебного пособия. В
нем практически отсутствует теория, к тому же предполагается, что его читатель
уже знает некоторые базисные по- нятия в программировании, умеет объявлять
переменные и может самостоятельно скомпилировать
«пустую» программу. Единственное
исключение отводится для элементов синтаксиса – при первом упоминании их смысл
раскрывается довольно подробно.
На самом деле, во всем этом нет какой-то особой необходимости. В наше
время в Интернете можно найти массу интересных теоретических материалов по
программированию на языке Pascal, и по мере надобности читатель, если ему
что-то непонятно, может к ним обращаться.
Все, что можно найти в сборнике – это последовательные, максимально
подробные разборы задач. Они представлены в достаточно свободном стиле: сначала
задача анализируется, затем со- ставляется алгоритм, и для каждого его шага
дается детальное описание. В конце разбора каждой задачи для наглядности
приводится код всей программы. В некоторых случаях приводится алго- ритм на естественном языке,
блок-схема какой-то части программы или описание работы
алгоритма для определенного варианта исходных данных.
Уровень сложности повышается при увеличении номеров
задач, если не сказано обратное.
По- этому если читатель не может понять решение какой-то задачи, то ему
стоит подняться выше и попробовать понять более простые задачи.
Стоит учесть, что автор сборника – студент Адыгейского государственного
университета, пе- решедший на 2-ой курс и практически не имеющий педагогического
опыта, поэтому он будет при- знателен за любое указание на присутствующие в
сборнике ошибки, недостатки в изложении мате- риала и т. п., как и за любые
другие комментарии.
Глава 1. Линейные алгоритмы
Задача
№ 1. Вывести на экран сообщение «Hello World!»
Формулировка.
Вывести на экран сообщение «Hello
World!».
Некоторые учебные курсы по программированию рассматривают эту задачу
как самую первую при изучении конкретного языка или основ программирования.
Решение. Эта задача включает в себя лишь демонстрацию
использования оператора вывода write (или writeln), который будет
единственным в теле нашей маленькой программы. С помощью него мы будем
осуществлять вывод на экран константы ‘Hello
World!’ типа string (или, как допускается говорить, строковой
константы). В данном случае будем использовать оператор writeln.
Напомню, что при использовании оператора write курсор останется в той же строке, в которой
осуществлялся вывод, и будет находиться на одну позицию
правее восклицательного знака во фразе
«Hello World!», а при
использовании оператора writeln – на первой позиции слева в следующей
строке.
 |
Код:
Задача
№ 2. Вывести на экран три числа в порядке, обратном вводу
Формулировка. Вывести на экран три введенных с клавиатуры числа в порядке,
обратном их вводу.
Другими словами, мы ввели с клавиатуры три числа (сначала первое, потом
второе и третье), и после этого единственное, что нам нужно сделать – это
вывести третье, затем второе и первое.
Решение. Так как с клавиатуры вводится три числа,
необходимо завести три переменные. Обо- значим их как a, b и c. Ввиду того, что нам ничего не сказано
о том, в каком отрезке
могут распола- гаться
введенные числа, мы возьмем тип integer, так как он охватывает и
положительные, и отри- цательные числа в некотором диапазоне (от –2147483648 до 2147483647). Затем нам нужно исполь-
зовать оператор вывода write (writeln), в списке аргументов
которого (напомним, что список аргу- ментов write (writeln) может
содержать не только переменные, но и константы и арифметические выражения) эти переменные будут находиться в обратном порядке.
В данном случае
будем исполь- зовать оператор
writeln, который после
вывода результата переведет курсор на следующую строку:
writeln(c, b, a); Однако если мы оставим
его в таком виде, то увидим, что при выводе
между переменными не будет
никакого пробела, и они будут
слеплены и визуально смотреться как одно число. Это связано с тем,
что при вводе мы использовали пробелы для разделения чисел, а сами пробелы никаким
образом не влияют на
содержимое переменных, которые будут последовательно выведены оператором writeln
без каких-либо дополнений. Чтобы избежать этого,
нам нужно добавить
в список аргументов
writeln две
текстовые константы-пробелы. Проще говоря, пробельная константа – это символ
про- бела, заключенный в одиночные апострофы (апостроф – символ «’»). Первая
константа будет раз- делять переменные a и b, вторая – b и
c. В результате наш оператор вывода будет таким:
writeln(c, ‘ ‘, b, ‘ ‘, a); Теперь он работает так: выводит
переменную c, затем одиночный символ пробела, затем перемен- ную b, потом еще один символ
пробела и, наконец, переменную a.
 |
Код:
Задача № 3. Вывести на экран квадрат введенного числа
Формулировка.
Дано натуральное число меньше 256. Сформировать число, представляющее собой
его квадрат.
Решение. Для ввода числа
нам необходима одна переменная. Обозначим эту переменную как
a.
Так как нам ничего
не сообщается о необходимости сохранить исходное число, то для получения квадрата мы можем использовать
ту же самую переменную, в которую считывали число с клавиа- туры.
В условии задачи дается ограничитель величины вводимого числа – фраза «меньше 256». Это
означает, что оно может быть охвачено типом byte. Но что произойдет,
если в переменную a будет введено число 255, и затем мы попытаемся
присвоить ей его квадрат, равный 65025? Естественно, это вызовет переполнение
типа данных, так как используемой для переменной a ячейки памяти не
хватит для того, чтобы вместить число 65025. Значит, для ее описания мы должны
использовать более емкий числовой тип. При этом типом минимальной размерности,
охватывающим данный от- резок (от 1 (это 12) до 65025), является тип word.
Его мы и будем использовать при описании a.
Далее нужно сформировать в переменной a квадрат. Для этого присвоим
ей ее прежнее значе- ние,
умноженное само на себя:
a := a * a;
Теперь остается
вывести результат на экран. Для этого будем использовать оператор writeln.
 |
Код:
Задача № 4. Получить реверсную запись трехзначного числа
Формулировка. Сформировать число, представляющее собой реверсную
(обратную в по- рядке следования разрядов) запись заданного трехзначного числа.
Например, для числа 341 таким будет 143.
Давайте разберемся с условием. В нашем случае с клавиатуры вводится
некоторое трехзнач- ное число (трехзначными называются числа, в записи которых
три разряда (то есть три цифры), например: 115, 263, 749 и т. д.). Нам
необходимо получить в некоторой переменной число, которое будет представлять
собой реверсную запись введенного числа. Другими словами, нам нужно пере-
вернуть введенное число «задом наперед», представить результат в некоторой
переменной и выве- сти его на экран.
Решение. Определимся с выбором переменных и их количеством. Ясно,
что одна переменная нужна для
записи введенного числа с клавиатуры, мы обозначим ее как n. Так как нам
нужно пере- ставить разряды числа n в некотором порядке, следует для
каждого из них также предусмотреть отдельные
переменные. Обозначим их как a (для разряда
единиц), b (для
разряда десятков) и c (для разряда сотен).
Теперь можно начать запись самого
алгоритма. Будем разбирать его поэтапно:
1)
Вводим число n;
2)
Работаем с разрядами числа n. Как известно, последний разряд любого числа в десятичной системе счисления – это остаток от деления этого числа на 10. В терминах языка Pascal это означает, что для получения
разряда единиц нам необходимо присвоить переменной a остаток от деления
числа n на 10. Этому шагу соответствует следующий оператор:
a := n mod 10; Получив разряд единиц, мы должны отбросить
его, чтобы иметь возможность продолжить работу с разрядом десятков. Для этого разделим число n на
10. В терминах Pascal, опять же, это означает: присвоить переменной n
результат от деления без остатка числа n на 10. Это мы сделаем с
помощью оператора
n := n div 10;
3)
Очевидно, что после выполнения п. 2 в переменной n будет храниться двухзначное число,
состоящее из разряда сотен и разряда десятков исходного. Теперь, выполнив те же
самые действия еще раз, мы получим
разряд десятков исходного числа, но его уже нужно присва-
ивать переменной b.
4)
В
результате в переменной n будет храниться однозначное число – разряд сотен
исходного числа. Мы можем без дополнительных действий присвоить его
переменной c.
5)
Все полученные в переменных числа
– однозначные. Теперь переменная n нам больше не нужна, и в ней нужно
сформировать число-результат, в котором a будет находиться в раз- ряде
сотен, b – десятков, c – единиц. Легко понять, что для этого нам
следует умножить a на 100, прибавить к полученному числу
b, умноженное на 10 и c без
изменения, и весь этот
результат присвоить переменной c. Это можно записать так:
n := 100 * a + 10 * b + c;
6)
Далее остается только вывести
полученное число на экран.
 |
Код:
Проверим работу программы на произвольном варианте
введенных данных. Для этого выпол- ним ее «ручную прокрутку», проделав с введенным числом те же действия, которые
должен выпол- нить алгоритм.
Пусть пользователем введено
число 514. Покажем
в таблице, какие значения будут принимать
переменные после выполнения соответствующих строк. При этом прочерк
означает, что значение переменных на данном шаге не определено, а красным цветом
выделены переменные, которые из- меняются:
|
№ строки |
n |
a |
b |
c |
|
7 |
514 |
— |
— |
— |
|
8 |
514 |
4 |
— |
— |
|
9 |
51 |
4 |
— |
— |
|
10 |
51 |
4 |
1 |
— |
|
11 |
5 |
4 |
1 |
— |
|
12 |
5 |
4 |
1 |
5 |
|
13 |
415 |
4 |
1 |
5 |
Нетрудно понять, что написанная программа будет выводить правильный
ответ для любого заданного трехзначного числа, так как в соответствии с
алгоритмом заполнение данной таблицы возможно лишь единственным образом. Это
значит, что мы можем представить число в виде аб- страктного трехзначного числа xyz, (в нем каждая
буква должна быть заменена на любое число от 0 до 9, конечно, за исключением тех
случаев, когда оно перестает быть трехзначным), и работая с разрядами этого
числа, показать, что в результате работы ответом будет число zyx.
Задача № 5. Посчитать количество единичных битов числа
Формулировка. Дано натуральное число меньше
16. Посчитать количество его единичных битов. Например, если дано число 9,
запись которого в двоичной системе счисления равна 10012 (подстрочная цифра 2 справа от числа
означает, что оно записано в двоичной системе счисления), то количество его
единичных битов равно 2.
Решение. Нам необходима переменная для ввода с клавиатуры.
Обозначим ее как n. Так как мы должны накапливать количество найденных битов, то возникает потребность в еще одной пере- менной. Обозначим ее как count («count»
в переводе с англ. означает «считать», «подсчет» и т. д.). Переменные возьмем
типа byte (они
могут принимать значения
от 0 до 255), и пусть в данном случае такой объем избыточен, но это не
принципиально важно.
Как же сосчитать количество битов во введенном числе? Ведь число
же вводится в десятичной
системе счисления, и его нужно переводить в
двоичную?
На самом деле все
гораздо проще. Здесь нам поможет одно интересное правило:
То есть, деля некоторое десятичное число, например, на 10, в остатке мы
получаем разряд единиц этого числа в системе
счисления с основанием 10. Возьмем, например,
число 3468. Остаток от деления его на 10 равен 8, то
есть разряду единиц этого числа.
Понятно, что такие же правила господствуют и в арифметике в других
системах счисления, и в том числе в двоичной
системе. Предлагаю поэкспериментировать: запишите
на бумаге десятичное число, затем, используя любой
калькулятор с функцией перевода из одной системы счисления в другую, переведите
это число в двоичную систему счисления и также запишите результат. Затем
разделите исходное число на 2 и снова переведите в двоичную систему. Как оно
изменилось в ре- зультате? Вполне очевидно, что у него пропал крайний разряд
справа, или, как мы уже говорили ранее, разряд
единиц.
Но как это использовать для решения задачи?
Воспользуемся тем, что в двоичной
записи числа нет цифр, кроме 0 и 1. Легко убедиться
в том, что сложив все разряды двоичного
числа, мы получаем как раз таки количество его
единичных битов. Это значит, что вместо проверки значений разрядов двоичного представления числа мы можем прибавлять к счетчику сами эти разряды
– если в разряде был 0,
значение счетчика не изменится, а если 1, то повысится на единицу.
Теперь, резюмируя вышеприведенный
итог, можно поэтапно сформировать сам алгоритм:
1)
Вводим число n;
2)
Обнуляем счетчик разрядов count.
Это делается потому, что значения всех переменных при запуске программы считаются неопределенными, и хотя в большинстве компиляторов Pascal они обнуляются при запуске, все же
считается признаком «хорошего тона» в про- граммировании обнулить значение
переменной, которая будет изменяться в процессе ра- боты без предварительного
присваивания ей какого-либо значения.
3)
Прибавляем к count разряд
единиц в двоичной записи числа n, то есть остаток от деления
n на 2:
count := count + n mod 2; Строго говоря, мы могли бы не
прибавлять предыдущее значение переменной count к остатку от деления, так как оно все
равно было нулевым. Но мы поступили так для того, чтобы сделать код более
однородным, далее это будет видно.
Учтя разряд единиц
в двоич- ной записи n,
мы должны отбросить его, чтобы исследовать число далее. Для этого разде- лим n
на 2. На языке Pascal это будет выглядеть так:
n := n div 2;
4)
Теперь нам нужно еще два раза
повторить п. 3 , после чего останется единственный дво- ичный разряд
числа n, который
можно просто прибавить
к счетчику без каких-либо допол- нений:
count := count + n;
5)
В результате в переменной count
будет храниться количество единичных разрядов в дво- ичной записи исходного
числа. Осталось лишь вывести ее на экран.
 |
Код:
Программа работает правильно на всех вариантах правильных исходных
данных, в чем не- сложно убедиться с помощью простой проверки.
Глава 2.
Условные операторы
Задача
№ 6. Вывести на экран наибольшее из двух чисел
Формулировка. Даны два
числа. Вывести на экран то из них, которое больше.
Решение. Собственно, это самая простая
задача, с помощью
которой можно продемонстриро- вать использование
условного оператора if. Напомним, как нужно использовать этот оператор.
Мы вводим с клавиатуры числа в переменные a и b типа integer,
затем в операторе if проверяем булев- ское выражение «a > b»: если оно истинно,
то выполняется then-блок оператора, если ложно – else– блок. Соответственно, если a больше b (условие в заголовке истинно), то в then-блоке мы выводим a,
а если a не больше b (условие в заголовке ложно), то выводим b
(хотя сюда попадает и случай, когда a = b, что, впрочем, не
нарушает решения).
На языке Pascal мы можем записать весь оператор с if– и then-блоками
в одну строчку следу- ющим образом:
if a > b then writeln(a) else writeln(b); Данная строка легко понятна и читаема
по причине того, что мы выполняем столь простой набор операторов в обоих блоках ветвления
оператора if. Однако в более сложных примерах мы будем с первых же
написанных строчек следовать принципу аккуратного оформления кода, чтобы
не появ- лялось привычки «вытягивать» операторы ветвлений и другие конструкции
в одну строчку, так как в будущем это может сильно
сказаться на удобочитаемости и простоте понимания написанного про-
граммного кода, особенно при увеличении количества вложенных в блок операторов
(которые, например, тоже могут быть операторами ветвления). Не стоит забывать о том, что при вложенности в тело какого-либо оператора
хотя бы одного составного оператора или другой сложной конструк- ции требуется
равномерный отступ для подчиненной конструкции с адекватной расстановкой опе-
раторных скобок! Например, для оператора if это распределение
конструкций по мнемонической модели if-end, else-end, согласно
которой эти ключевые слова должны стоять на одном уровне по вертикали, а их
содержимое должно быть немного смещено вправо.
Конечно, для простейшей конструкции с условным оператором это вовсе не
самоцель, и можно разместить ее в одной строке, если оби ветви оператора (и if-блок,
и else-блок) не содержат составного оператора. В нашем же примере
«аккуратное оформление» показывается лишь в каче- стве введения.
 |
Код:
При таком оформлении хорошо видно, какой код выполняется при истинности
условия, а ка- кой – при его ложности.
Задача № 7. Вывести на экран наибольшее из трех чисел
Формулировка. Даны три
числа. Вывести на экран то из них, которое больше.
 |
Решение. Даная задача обобщает предыдущую. В ее решении также нужно
использовать условный оператор if, однако в данном случае для нахождения
максимального числа нам нужно выполнить минимум два сравнения. Сам механизм
выбора в виде условного оператора с вложен- ными в него двумя другими условными
операторами можно легко пояснить следующей блок-схе- мой:
Несмотря на то, что выполняется всего одна инструкция вывода, при
написании кода мы все ветвления будем помещать
в отдельный составной
оператор. Напомним: это значит, что при движе- нии от более общего уровня к
частному все конструкции нужно смещать на два пробела относи- тельно
родительского блока/оператора.
 |
Код:
Задача № 8. Вывести название дня недели по его номеру
Формулировка.
Вывести название дня недели по его
номеру.
Решение. Задача простейшим образом решается с помощью оператора
выбора case. Напом- ним, что этот оператор позволяет
организовать ветвления в зависимости от значений некоторой пе- ременной, для каждого
из которых можно
предусмотреть выполнение различных
действий. Причем если
значению переменной не соответствует ни один вариант, выполняется else-блок
(если он при- сутствует). Кстати, не стоит забывать,
что после перечисления всех вариантов оператора case необ- ходимо
написать ключевое слово end (выходит, ключевое слово case является еще и
открывающей операторной скобкой).
Для того чтобы воспользоваться оператором case, нам необходимо
произвести ввод номера дня недели в некоторую переменную i типа byte
и по этому номеру вывести
название текущего дня недели. Кстати, благодаря else-блоку
в этой программке мы впервые предусмотрим сообщение об ошибке, связанной с
некорректно введенным номером, которому не соответствует ни один из дней
недели.
 |
Код:
Кстати, в каждом из вариантов ветвлений может быть помещен составной
оператор, но при описании вариантов мы не стали
использовать операторные скобки,
так как на этот раз они наоборот испортили бы все оформление
кода, которое сейчас является достаточно гармоничным.
Задача
№ 9. Проверить, является ли четырехзначное число палиндромом
Формулировка. Дано
четырехзначное число. Проверить, является ли оно палиндромом.
Примечание: палиндромом называется число, слово или текст, которые
одинакового читаются слева
направо и справа налево. Например, в нашем случае это числа 1441, 5555, 7117 и
т. д.
Примеры других чисел-палиндромов произвольной десятичной разрядности, не
относящиеся к решаемой задаче: 3, 787, 11, 91519 и т. д.
Решение. Для ввода числа с клавиатуры будем использовать
переменную n. Вводимое число принадлежит множеству натуральных чисел и
четырехзначно, поэтому оно заведомо больше 255, так что тип byte для ее
описания нам не подходит. Тогда будем использовать тип word.
Какими же свойствами обладают числа-палиндромы? Из указанных примеров
легко увидеть, что в силу своей одинаковой «читаемости» с двух сторон в них
равны первый и последний разряд, второй и предпоследний и т. д. вплоть до
середины. Причем если в числе нечетное количество раз- рядов, то серединную цифру можно не учитывать при проверке, так как при выполнении названного правила число является
палиндромом вне зависимости от ее значения.
В нашей же задаче все даже несколько
проще, так как на вход подается четырехзначное число. А это означает, что для решения задачи нам нужно лишь
сравнить 1-ю цифру числа с 4-й и 2-ю цифру с 3-ей. Если выполняются оба эти
равенства, то число – палиндром. Остается только полу- чить соответствующие
разряды числа в отдельных переменных, а затем, используя условный опе- ратор,
проверить выполнение обоих равенств с помощью булевского (логического) выражения.
Однако не стоит спешить с решением. Может быть, мы сможем упростить выведенную схему?
Возьмем, например, уже упомянутое выше число 1441. Что будет, если разделить
его на два числа двузначных числа, первое из которых будет содержать разряд
тысяч и сотен исходного, а второе – разряд десятков и единиц исходного. Мы
получим числа 14 и 41. Теперь, если второе число заме- нить на его реверсную
запись (это мы делали в задаче 4),
то мы получим два равных
числа 14 и 14!
Это преобразование вполне очевидно, так в силу того, что палиндром читается
одинаково в обоих направлениях, он состоит
из дважды раза повторяющейся комбинации цифр, и одна из копий просто
повернута задом-наперед.
Отсюда вывод: нужно
разбить исходное число
на два двузначных, одно из них реверсировать, а затем выполнить
сравнение полученных чисел с помощью условного оператора if. Кстати, для
получения реверсной записи второй половины числа нам необходимо завести еще две
переменные для сохранения используемых разрядов. Обозначим их как a и b,
и будут они типа byte.
Теперь опишем сам алгоритм:
1)
Вводим число n;
2)
 |
Присваиваем разряд единиц числа n переменной
a, затем отбрасываем его. После присва- иваем разряд десятков n переменной
b и также отбрасываем его:
3)
Присваиваем переменной a число, представляющее собой реверсную запись хранящейся в переменных a и b второй
части исходного числа n по уже известной формуле:
a := 10 * a + b;
4)
Теперь мы можем использовать
проверку булевского выражения равенства полученных чисел n и a помощью
оператора if и организовать вывод ответа с помощью ветвлений:
if n = a then writeln(‘Yes’) else writeln(‘No’);
Так как в
условии задачи явно не сказано, в какой форме необходимо выводить ответ, мы
будем считать логичным вывести его на интуитивно понятном пользователю уровне,
до- ступном в средствах самого языка Pascal. Напомним, что с помощью
оператора write (writeln) можно выводить результат выражения булевского
типа, причем при истинности этого выражения будет выведено слово ‘TRUE’ («true» в пер. с англ. означает
«истин- ный»), при ложности – слово ‘FALSE’
(«false» в пер. с англ. означает «ложный»). Тогда предыдущая конструкция
с if может быть заменена на
writeln(n = a);
 |
Код:
Задача № 10. Проверить, является ли четырехзначное число
счастливым билетом
том».
Формулировка.
Дано четырехзначное число. Проверить, является ли оно «счастливым биле-
Примечание: счастливым билетом
называется число, в котором: а) при четном количестве
цифр в числе
сумма цифр его левой половины равна сумме цифр его правой половины; б) при не-
четном количестве цифр – то же самое,
но с отбрасыванием серединной цифры.
Например, рассмот- рим число 1322. Его левая половина
равна 13, а правая – 22, и оно является
счастливым билетом (т. к. 1 + 3 = 2 + 2). Аналогично: 1735
(1 + 7 = 3 + 5), 1111 (1 + 1 = 1 + 1) и т. д.
Примеры других счастливых билетов за рамками
условия текущей задачи:
7 (отбросили един- ственную цифру), 39466 (3 + 9 = 6 +
6, а 4 отбросили), 11 (1 = 1), и т. д.
Решение. Для ввода
достаточно одной переменной n типа word. Все, что необходимо сделать для решения – это последовательно получить все разряды
исходного числа, причем из двух млад- ших разрядов (единиц и десятков)
сформировать первую сумму, а из двух старших разрядов – вто- рую, после чего
вывести на экран результат булевского выражения равенства полученных сумм.
Первую сумму будем хранить в переменной right, а вторую – в переменной left (выбрано по распо-
ложению цифр в записи числа).
Значение обоих из них не может превосходить 18 (т. к. для наиболь- шего допустимого числа 9999 обе
суммы равны 9 + 9 = 18), поэтому для их описания используем тип byte.
Более детальный разбор
алгоритма:
1)
Вводим число n;
2)
 |
Присваиваем переменной right
значение последней цифры числа n, потом отбрасываем эту цифру, затем повторяем то же самое,
но на этот раз уже прибавляем добытую цифру к прежнему значению right:
3)
Присваиваем переменной left
последнюю цифру n, отбрасываем ее и прибавляем к right
 |
единственную оставшуюся в переменной n цифру:
4)
Выводим на экран результат
сравнения накопленных сумм:
writeln(left = right);
 |
Код:
Задача
№ 11. Проверить, является ли двоичное представление числа палиндромом
Формулировка. Дано число типа byte. Проверить, является
ли палиндромом его двоичное представление с учетом того, что сохранены старшие
нули. Пример таких чисел: 102 (т. к. 102 = 0110 01102, а это палиндром), 129 (129 = 1000
00012) и т. д.
Решение. Данная задача частично повторяет задачу 9.
Сходство состоит в том, что и там, и здесь у проверяемых чисел фиксированная
разрядность (длина), ведь здесь нам уже задан тип и получено указание
сохранить старшие нули,
так что в данном случае
двоичные представления всех подаваемых на вход программе чисел
будут восьмизначными.
Но как же упростить решение, чтобы не
делать сравнение всех разрядов «в лоб»? Для этого нам нужно вспомнить правило,
упомянутое в задаче 5, на этот раз несколько уточненное и допол- ненное:
 |
Для примера возьмем число 158 в десятичной системе счисления. Мы можем
получить его крайнюю цифру справа, которая равна 8, если возьмем остаток от
деления 158 на число 10, являю- щееся в данном случае основанием системы
счисления. С другой стороны, если мы умножим 158 на 10, то появляется новый
разряд справа, и в результате мы получаем число 1580.
Согласно правилу те же самые арифметические законы актуальны и для
двоичной системы счисления. А это в свою очередь означает, что мы можем
разработать алгоритм наподобие того, который использовался в задаче 9 для
формирования числа, представляющего собой правую поло- вину исходного числа,
которая записана в реверсном порядке. Для этого нам нужно использовать четыре
переменных для хранения двоичных разрядов правой половины двоичной записи
введен- ного числа, добыть
эти самые разряды
с удалением их в исходном
числе, сформировать из них дво- ичную реверсную запись и выполнить
сравнение. Обозначим эти переменные типа byte как a, b, c,
и d.
Опишем сам алгоритм:
1)
Вводим число n;
2)
 |
Последовательно получаем 4 крайних справа
разряда двоичной записи числа n: присваи- ваем их значение соответствующей
переменной, а затем отбрасываем в исходном
числе:
3)
Теперь нужно подумать, как
видоизменится формула, с помощью которой мы получали реверсную запись числа в задаче
4 и задаче 9. Очевидно, что в десятичной системе счис- ления
реверсную запись четырехзначного числа, разряд единиц которого находится в пе-
ременной k, разряд десятков – в переменной l, сотен – в m и
тысяч – в n мы можем найти по следующей формуле (x в данной
случае – любая переменная типа word):
x := 1000 * k + 100 * l + 10 * m + n; Можно представить, что мы формируем
четыре числа, которые затем складываем. Первое число 1000 * k – это разряд единиц
исходного числа, к которому справа приписано три разряда (три нуля), то есть,
трижды произведено умножение на основание системы счис- ления 10, проще говоря,
число k умножено на 103. Аналогично, к l нужно приписать
два нуля, к m – один ноль, а n оставить без изменения, так как
эта цифра будет находиться в разряде единиц формируемого «перевертыша».
Вспомнив правило, высказанное немного выше, преобразуем предыдущую формулу для
двоичной системы счисления (будем умно- жать цифры на двойку в соответствующих
степенях). Она получится такой (для формиро- вания числа используется
переменная a):
a := 8 * a + 4 * b + 2 * c + d;
4)
После применения вышеприведенной
строки останется лишь вывести на экран результат сравнения полученных чисел:
writeln(n = a);
 |
Код:
Выполним «ручную прокрутку» программы при вводе числа 102. Покажем в
таблице, какие значения будут принимать переменные после выполнения
соответствующих строк (операторов) кода. Значения переменных для наглядности
представлены как в десятичной, так и в двоичной си- стеме счисления (при этом дописаны
старшие нули до заполнения тетрады). При этом прочерк
озна- чает, что значение переменных на данном шаге не определено, а
красным цветом выделены пере- менные, которые
изменяются:
|
№ строки |
Десятичная система |
Двоичная система |
||||||||
|
n |
a |
b |
c |
d |
n |
a |
b |
c |
d |
|
|
7 |
102 |
— |
— |
— |
— |
0110 0110 |
— |
— |
— |
— |
|
8 |
102 |
0 |
— |
— |
— |
0110 0110 |
0000 |
— |
— |
— |
|
9 |
51 |
0 |
— |
— |
— |
0011 0011 |
0000 |
— |
— |
— |
|
10 |
51 |
0 |
1 |
— |
— |
0011 0011 |
0000 |
0001 |
— |
— |
|
11 |
25 |
0 |
1 |
— |
— |
0001 1001 |
0000 |
0001 |
— |
— |
|
12 |
25 |
0 |
1 |
1 |
— |
0001 1001 |
0000 |
0001 |
0001 |
— |
|
13 |
12 |
0 |
1 |
1 |
— |
0000 1100 |
0000 |
0001 |
0001 |
— |
|
14 |
12 |
0 |
1 |
1 |
0 |
0000 1100 |
0000 |
0001 |
0001 |
0000 |
|
15 |
6 |
0 |
1 |
1 |
0 |
0000 0110 |
0000 |
0001 |
0001 |
0000 |
|
16 |
6 |
6 |
1 |
1 |
0 |
0000 0110 |
0110 |
0001 |
0001 |
0000 |
Задача
№ 12. Решить квадратное уравнение
Формулировка. Даны вещественные числа a, b и c, причем a отлично от 0. Решить квадратное
уравнение ax2
+ bx + c = 0 или сообщить о том, что действительных
решений нет.
Решение.
Из алгебры известно, что:
Следовательно, нам
необходимо вычислить дискриминант (заведем для него вещественную переменную d
типа real) и в зависимости от его значения организовать ветвления.
Сначала нужно проверить, имеет ли уравнение действительные решения (для решений
заведем переменные x1 и x2 типа real). Если да, и
если дискриминант не равен нулю, то вычисляем оба решения по формулам, а если
дискриминант равен нулю, то вычисляем единственное решение. Если же
действительных решений нет, выводим текстовое сообщение об этом. Основной
алгоритм можно проиллюстриро- вать следующей
блок-схемой:
 |
Три нерасшифрованных блока представляют собой стандартные операторы
вывода. Разберем их подробнее:
1)
 |
При выводе двух корней выражение будет выглядеть
следующим образом:
При этом выводимое выражение будет выглядеть так: ‘x1 = m, x2 = n‘,
где синим цветом выделены однозначные текстовые константы, которые берутся из
списка аргумен- тов writeln, красным – вычисленные значения x1 и x2.
Причем корни выведены в форма- тированном виде: число после первого
двоеточия задает ширину
поля вывода для перемен-
ной вместе с точкой (при нехватке поля она будет расширено программой), а число
после второго двоеточия – количество выводимых дробных знаков (его при работе
программы изменить нельзя);
2)
При выводе одного корня – все то же самое,
только выводится один корень:
3)
При отсутствии действительных
корней выводим сообщение:
writeln(‘No
real solutions!’);
 |
В итоге внутренний условный оператор с телом включительно будет выглядеть так:
Код:
1.

2.
3.
var
4.
a, b, c,
d, x1, x2: real; 5.
6. begin
7.
readln(a,
b, c);
8. d
:= b * b – 4 * a * c;
9.
if d
>= 0 then begin
10.
if d
<> 0 then begin
11. x1
:= (-b + sqrt(d)) / 2 * a;
12. x2
:= (-b – sqrt(d)) / 2 * a;
13. writeln(‘x1
= ‘, x1:4:2, ‘, x2 = ‘, x2:4:2)
14.
end
15.
else begin
16. x1
:= -(b / 2 * a);
17. writeln(‘x
= ‘, x1:4:2)
18.
end
19.
end
20.
else begin
21.
writeln(‘No
real solutions!’);
22.
end
23. end.
Глава
3. Циклы
Задача
№ 13. Вывести на экран все натуральные числа до заданного
Формулировка. Дано натуральное число. Вывести на экран все
натуральные числа до задан- ного включительно.
Решение. Данная задача решается с использованием оператора цикла
for. Напомним, что с помощью цикла for можно совершить заданное
количество итераций (повторений) некоторых опе- раторов, которые синтаксически
заключены в содержимое его тела (так называемого тела цикла). При этом
некоторая целочисленная переменная изменяется от некоторого стартового значения
до некоторого конечного (оба значения включительно), увеличиваясь на единицу с
каждым повторе- нием тела цикла.
Так как нам необходимо выводить
натуральные числа, это означает, что вывод должен
всегда начинаться с единицы, и при этом выводятся все следующие за ней
натуральные числа до тех пор, пока значение переменной цикла (обычно используют
переменную i) не достигнет конечного n (на последнем шаге
значение переменной цикла будет равно n). После этого цикл завершится, и
будут выполнены те операторы, которые следуют непосредственно за ним. Кстати,
не стоит забывать,
что после выхода из цикла for его переменная цикла считается неопределенной!
 |
Код:
Пусть введено число
5, например. При входе i станет равно 1 и будет проверено
существование отрезка в заданных границах. Так как 1 меньше 5, то
произойдет вход в цикл, и будут выполняться следующие команды, пока i не
превысит n:
1)
Выполнение команд в теле цикла;
2)
Увеличение i на 1;
3)
Возвращение на шаг 1.
Нетрудно понять,
что в нашем случае i будет принимать значения 1, 2, 3, 4, 5 и будет выведена на экран строка ‘1 2
3 4 5 ‘. Здесь красным цветом выделены изменяющиеся значения
пере- менной цикла, а синим – выводящаяся неизменной пробельная константа.
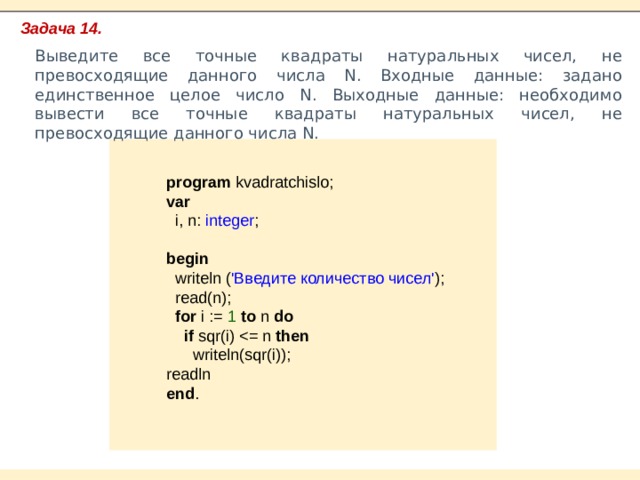
Задача № 14. Найти наибольший нетривиальный делитель
натурального числа
Формулировка. Дано натуральное число. Найти его наибольший
нетривиальный делитель или вывести единицу, если такового нет.
Примечание 1: делителем
натурального числа a называется натуральное число b, на которое a делится без остатка. То есть выражение
«b – делитель
a» означает: a / b = k,
причем k – натуральное
число.
Примечание: нетривиальным делителем называется делитель, который
отличен от 1 и от са- мого числа (так как на единицу и само на себя делится
любое натуральное число).
Решение. Пусть ввод с клавиатуры осуществляется в переменную n.
Попробуем решить за- дачу перебором чисел. Для этого возьмем число на единицу
меньшее n и проверим, делится
ли n на него. Если да, то выводим результат
и выходим из цикла с помощью оператора break. Если нет, то снова
уменьшаем число на 1 и продолжаем проверку. Если у числа нет нетривиальных
делителей, то на каком-то шаге проверка дойдет до единицы, на которую число гарантированно
поделится, после чего будет выдан соответствующий условию ответ.
Хотя, если говорить точнее, следовало бы начать проверку с числа,
равного n div 2 (чтобы отбросить дробную часть
при делении, если n нечетно), так как ни одно натуральное число не имеет делителей больших, чем половина
это этого числа. В противном случае частное от деления должно быть натуральным числом между 1 и
2, которого просто не существует.
Данная задача также решается через for, но через другую
его разновидность, и теперь счетчик будет убывать от n div 2 до
1. Для этого do заменится на downto, при позиции начального и
конеч- ного значений остаются теми же.
Алгоритм на естественном языке:
1)
Ввод n;
2)
Запуск цикла, при котором i изменяется
от n div 2 до 1. В цикле:
1.
Если n делится на i (то
есть, остаток от деления числа n на i равен 0), то выводим i на
экран и выходим из цикла с помощью break.
 |
Код:
Кстати, у оператора ветвления if в цикле отсутствует else-блок.
Такой условный оператор называется оператором ветвления с одной ветвью.
Задача
№ 15. Найти наименьший нетривиальный делитель натурального числа
Формулировка. Дано натуральное число. Найти его наименьший
нетривиальный делитель или вывести само это число, если такового нет.
Решение. Задача решается аналогично предыдущей. При этом
необходимо начать обычный цикл с увеличением, при котором переменная цикла i
изменяется от 2 до n (такая верхняя граница нужна для того, чтобы цикл всегда
заканчивался, так как когда i будет равно n, выполнится условие n mod i = 0). Весь остальной код при этом не отличается.
 |
Код:
Задача
№ 16. Подсчитать общее число делителей натурального числа
Формулировка. Дано
натуральное число. Подсчитать общее количество его делителей.
Решение. Задача достаточно похожа на две предыдущие. В ней также
необходимо провести перебор в цикле некоторого количества натуральных чисел на
предмет обнаружения делителей n, но при этом необходимо найти не первый
из них с какого-либо конца отрезка [1, n] (это отрезок, содержащий все
числа от 1 до n включительно), а посчитать их. Это можно сделать с
помощью
счетчика count,
который нужно обнулить непосредственно перед входом в цикл. Затем в условном
операторе if в случае истинности условия делимости числа
n (n mod i = 0) нужно увеличивать счет- чик count на единицу (это
удобно делать с помощью оператора inc).
Алгоритм на естественном языке:
1)
Ввод n;
2)
Обнуление переменной count (в
силу необходимости работать с ее значением без предва- рительного присваивания
ей какого-либо числа)
3)
Запуск цикла, при котором i изменяется
от 1 до n. В цикле:
1.
Если n делится на i (то
есть, остаток от деления числа n на i равен 0), то увеличиваем
значение переменной count на 1;
4)
Вывод на экран значения переменной count.
 |
Код:
Задача
№ 17. Проверить, является ли заданное натуральное число простым
Формулировка. Дано
натуральное число. Проверить, является ли оно простым.
Примечание:
простым называется натуральное число, которое имеет ровно два различных
натуральных делителя: единицу и само это число.
Решение. Задача отличается от предыдущей только тем, что вместо
вывода на экран числа делителей, содержащегося в переменной count,
необходимо выполнить проверку равенства счет- чика числу 2. Если у числа
найдено всего два делителя, то оно простое и нужно вывести положи- тельный
ответ, в противном случае – отрицательный ответ. А проверку через условный
оператор, как мы уже знаем, можно заменить на вывод результата самого
булевского выражения с помощью оператора write (writeln).
 |
Код:
Задача № 18. Вывести на экран все простые числа до
заданного
Формулировка.
Дано натуральное число. Вывести на экран все простые числа до заданного
включительно.
Решение. В решении данной
задачи используется решение предыдущей.
 |
Нам необходимо произвести тест простоты числа, который был описан в решении
предыду- щей задачи следующим кодом (обозначим его как код 1):
Здесь n – проверяемое на простоту число. Напомним, что данный
фрагмент кода в цикле про- веряет,
делится ли n на каждое i в отрезке от 1 до самого n, и
если n делится на i, то увеличивает счетчик count на 1.
Когда цикл заканчивается, на экран выводится результат проверки равенства
счетчика числу 2.
В нашем же случае нужно провести проверку на простоту всех натуральных
чисел от 1 до заданного числа (обозначим его как n). Следовательно, мы должны
поместить код 1 в цикл по всем k от 1 до n. Также в
связи с этим необходимо заменить в коде 1 идентификатор n на k,
так как в данном решении проверяются на простоту все числа k. Кроме
того, теперь вместо вывода ответа о подтверждении/опровержении простоты k необходимо
вывести само это число в случае простоты:
if count = 2
then write(k, ‘ ‘);
Обобщая вышесказанное, приведем
алгоритм на естественном языке:
1)
Ввод n;
2)
Запуск цикла, при котором k изменяется
от 1 до n. В цикле:
1.
Обнуление переменной count;
2.
Запуск цикла, при котором i изменяется
от 1 до k. В цикле:
a.
Если k делится на i,
то увеличиваем значение переменной count на 1;
3.
Если count = 2, выводим на
экран число k и символ пробела.
 |
Код:
Вычислительная сложность. В данной задаче мы впервые
столкнулись с вложенным
циклом (когда один цикл запускается внутри другого). Это означает, что
наш алгоритм имеет нелинейную сложность (при которой количество выполненных
операций равно размерности исходных данных (в нашем случае это n –
количество чисел) плюс некоторое количество обязательных операторов).
Давайте посчитаем количество выполненных операций в частном случае.
Итак, пусть необхо- димо вывести все натуральные
простые числа до числа 5. Очевидно, что проверка числа 1 пройдет в 1 + 2 шага,
числа 2 – в 2 + 2 шага, числа 3 – в 3 + 2 шага и т. д. (прибавленная двойка к
каждому числу – два обязательных оператора вне внутреннего цикла), так как мы
проверяем делители во всем отрезке от 1 до проверяемого числа.
В итоге количество проведенных операций
(выполненных операторов на низшем уровне) представляет собой сумму: 3 +
4 + 5 + 6 + 7 (также опущен обяза- тельный оператор ввода вне главного
(внешнего) цикла). Очевидно, что при выводе всех простых чисел от 1 до n приведенная
ранее сумма будет такой:
1
+ 3 + 5 + 6 + … + (n – 1) + n + (n + 1) + (n +
2),
где вместо многоточия нужно
дописать все недостающие члены суммы. Очевидно, что это сумма первых (n +
2) членов арифметической прогрессии с вычтенным из нее числом 2.
Как
известно, сумма k первых членов арифметической прогрессии выражена
формулой:
S = a1 + ak k ,
k 2
где a1 – первый член
прогрессии, ak – последний.
Подставляя в
эту формулу наши исходные данные и учитывая недостающее до полной суммы число
2, получаем следующее выражение:
1+ (n + 2) (n + 2) + (n + 2)
S = (n + 2) – 2 =
2 4 n + 2 + n2 + 4n + 4 – 4 n2 + 5n + 2 1 5
– = = = n2 + n +1
n 2 2 2 2 2 2 2
Чтобы найти асимптотическую
сложность алгоритма, отбросим коэффициенты при перемен-
ных и слагаемые
с низшими степенями (оставив, соответственно, слагаемое с самой высокой степе-
нью). При этом у нас остается член n2, значит, асимптотическая
сложность алгоритма – O(n2).
Конечно, в дальнейшем мы не будем так подробно находить асимптотическую
сложность ал- горитмов, а тем более, вычислять количество требуемых операций,
что интересно только теорети- чески. На самом деле, конечно, нас интересует
лишь порядок роста времени работы алгоритма (ко- личества необходимых операций), который можно выявить из анализа вложенности циклов и неко- торых других характеристик.
Задача № 19. Вывести на экран первых n простых чисел
Формулировка. Дано натуральное число n. Вывести
на экран n первых простых
чисел.
Например, при вводе числа 10
программа должна вывести ответ: 2 3 5 7 11 13 17 19 23 29
Решение. Эта задача похожа на предыдущую тем, что здесь нам тоже
необходимо проверить все натуральные числа на некотором отрезке, на этот раз
используя еще один счетчик для подсчета найденных простых. Однако на этот раз
мы не можем узнать, сколько придется проверить чисел, пока не насчитается n простых.
Следовательно, здесь нам не подходит цикл for, так как мы не мо- жем
посчитать необходимое количество итераций.
Здесь нам поможет цикл while. Напомним, что тело цикла while повторяется
до тех пор, пока остается истинным булевское
выражение в его заголовке (поэтому
его еще называют циклом с пред-
условием). Так как while не имеет переменной цикла, которая
увеличивается на 1 с каждым следу- ющим шагом, то при его использовании необходимо обеспечить изменение некоторых переменных в теле цикла, от которых зависит условие в его заголовке,
таким образом, чтобы при достижении требуемого результата оно стало ложным.
Так как мы должны найти и вывести n первых простых чисел,
подсчитывая их, и с каждый найденным простым числом некоторый счетчик (пусть
это будет primes с начальным значением 0) увеличивается на 1, то
условием в заголовке while будет выражение primes < n. Иными
словами, цикл продолжается, пока число найденных чисел меньше требуемого. На
последнем же шаге будет выведено последнее число, primes станет равным n и следующего шага цикла уже не будет,
так как условие в его
заголовке станет ложным. На этом работа программы будет закончена.
Проверяться на простоту будет некоторое число k, которое с каждой
итерацией цикла обяза- тельно будет увеличиваться на 1 (таким образом, мы
будем двигаться по отрезку натуральных чи- сел, пока не выберем из него
заданное количество простых).
Алгоритм на естественном языке:
1)
Ввод n;
2)
Обнуление переменной primes;
3)
Присваивание переменной k значения 1;
4)
Запуск цикла с предусловием primes
< n. В цикле:
1.
Обнуление переменной count;
2.
Запуск цикла, при котором i изменяется
от 1 до k. В цикле:
a.
Если k делится на i,
то увеличиваем значение переменной count на 1;
3.
Если count = 2, выводим на
экран число k, символ пробела и увеличиваем значение счетчика primes на 1;
4.
Увеличиваем значение k на 1.
 |
Код:
Выполним ручную прокрутку алгоритма, взяв в качестве n число 2.
При этом будем уже по привычке красным цветом обозначать переменные,
изменившиеся после выполнения данной строки, а прочерком те, которые на данном
шаге не определены, так как алгоритм до них еще «не дошел». При повторении
шагов цикла итерации явно считать не будем (хотя легко увидеть, что их номерам
полностью соответствует изменяющаяся после каждого очередного выполнения тела
пе- ременная k), и в таблице будет указана лишь та строка, которая
выполняется. На тех шагах, на ко- торых переменные не изменяются, будем
пояснять смысл выполняющихся операторов.
Для наглядности все же отделим
друг от друга
четные и нечетные
шаги основного цикла while,
при этом его внутренний цикл будем считать самоочевидным и в строке 12-14 будем
фиксировать те значения переменных, которые будут получены по выходу из него.
|
№ строки |
n |
k |
primes |
i |
count |
|
7 |
2 |
— |
— |
— |
— |
|
8 |
2 |
1 |
— |
— |
— |
|
9 |
2 |
1 |
0 |
— |
— |
|
10 |
(primes < n) = true – входим в цикл |
||||
|
11 |
2 |
1 |
0 |
— |
0 |
|
12-14 |
2 |
1 |
0 |
от 1 до 1 |
1 |
|
15-18 |
(count = 2) = false |
||||
|
19 |
2 |
2 |
0 |
— |
1 |
|
10 |
(primes < n) = true – входим в цикл |
||||
|
11 |
2 |
2 |
0 |
— |
0 |
|
12-14 |
2 |
2 |
0 |
от 1 до 2 |
2 |
|
15 |
(count = 2) = true |
||||
|
16 |
Вывод числа k (то |
||||
|
17-18 |
2 |
2 |
1 |
— |
2 |
|
19 |
2 |
3 |
1 |
— |
2 |
|
10 |
(primes < n) = true – входим в цикл |
||||
|
11 |
2 |
3 |
1 |
— |
0 |
|
12-14 |
2 |
3 |
1 |
от 1 до 3 |
2 |
|
15 |
(count = 2) = true |
|
16 |
Вывод числа k (то |
||||
|
17-18 |
2 |
3 |
2 |
— |
2 |
|
19 |
2 |
4 |
2 |
— |
2 |
|
10 |
(primes < n) = false – программа завершена |
Как видим, описать действия даже такого
элементарного алгоритма и даже при столь малых исходных данных – достаточно
трудоемкая и трудно проверяемая задача, поэтому очень важно по- нимать логику
самой программы и уметь представлять себе целостную картину ее поведения
с ми- нимальными потребностями в моделировании.
Вычислительная
сложность. Так как в данной
задаче в главном
цикле присутствует вложен- ный, в котором происходит ровно k операций (сложность этой конструкции мы определили в задаче
18), то его сложность явно не меньше O(n2) и превышает ее, так как нам
явно необходимо выпол- нить более чем n шагов
главного цикла. При этом точность
расчета сложности зависит
от распреде- ления простых
чисел, которое описывается с помощью достаточно сложных математических прие-
мов и утверждений, так что мы не будем далее рассматривать эту задачу.
Задача № 20. Проверить, является ли заданное натуральное
число совершенным
Формулировка. Дано
натуральное число. Проверить, является ли оно совершенным.
Примечание: совершенным числом называется натуральное число, равное
сумме всех своих собственных делителей (то есть натуральных делителей, отличных от самого числа).
Например, 6 – совершенное число, оно имеет три
собственных делителя: 1, 2, 3, и их сумма равна 1 + 2 + 3 = 6.
 |
Решение. Эта задача напоминает задачу 16, в которой нужно было
найти количество всех натуральных делителей заданного числа. Напомним код ее
основной части (назовем его кодом 1):
Как видно, в этом цикле проверяется делимость числа n на все
числа от 1 до n, причем при каждом выполнении условия делимости
увеличивается на 1 значение счетчика count с помощью функции inc.
Чтобы переделать этот код под текущую задачу, нужно вместо инкрементации (уве-
личения значения) переменной-счетчика прибавлять числовые значения
самих делителей к некото-
рой переменной для хранения суммы (обычно ее мнемонически называют sum,
что в пер. с англ. означает «сумма»). В связи с этим оператор
if n mod i = 0 then inc(count);
в коде 1 теперь уже будет
выглядеть так:
if n mod i = 0 then sum := sum + i;
Кроме того, чтобы не учитывалось само число n при суммировании
его делителей (насколько мы помним,
этот делитель не учитывается в рамках определения совершенного числа), цикл должен
продолжаться не до n, а до n – 1. Правда, если говорить точнее,
то цикл следовало бы проводить
до n div 2 (также это обсуждалось в задаче 14), так как
любое число n не может иметь больших дели- телей, иначе частное от
деления должно быть несуществующим натуральным число между 1 и 2.
Единственное, что останется теперь сделать – это вывести ответ, сравнив
число n с суммой его делителей sum как результат булевского
выражения через writeln:
writeln(n =
sum);
Код:
Задача № 21. Проверить, являются ли два натуральных
числа дружественными
Формулировка.
Даны два натуральных числа. Проверить, являются ли они дружественными.
Примечание: дружественными числами называются два различных натуральных
числа, для которых сумма всех собственных делителей первого числа равна второму
числу и сумма всех соб- ственных делителей второго числа равна первому числу.
Например, 220 и 284 – пара
дружественных чисел, потому что:
Сумма собственных делителей 220:
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284
Сумма собственных делителей 284:
1 + 2 + 4 + 71 + 142 = 220
Решение. Эта задача
напоминает задачу 19,
так как в ней мы тоже считали
сумму собственных делителей введенного числа, а затем сравнивали эту сумму с самим числом,
проверяя его на предмет
совершенности. В данном
же случае нам нужно найти не только
сумму собственных делителей
пер- вого числа (обозначим число как n1, а сумму его делителей sum1),
но и второго числа (возьмем обозначения n2 и sum2 соответственно).
Тогда ответом в задаче послужит сравнение: (n1 = sum2) and (n2 = sum1).
Кстати, здесь впервые в нашем повествовании мы используем логические опера- ции
(напомним, что логическое выражение X1 and X2 принимает значение истины
тогда и только тогда, когда истинны булевские выражения X1 и X2,
а в остальных случаях оно принимает ложное значение).
Однако предложенную схему можно упростить. Покажем это на примере:
пусть даны числа 8 и 4. Считаем сумму
собственных делителей числа 8: 1 + 2 + 4 = 7. Это число отлично от 4, поэтому
пара уже не соответствует определению дружественных чисел. Можно сразу вывести
отрицатель- ный ответ, избежав подсчета суммы делителей второго числа. Если
были бы даны числа 8 и 7, то необходимо было бы вычислить сумму собственных
делителей числа 7, она равна 1 (так как оно простое). Теперь необходимо сравнить
сумму собственных делителей второго с первым
числом: так как 1 отлично от
8, числа не дружественные.
Покажем на блок-схеме, как можно разветвить программу (вычисление обоих
сумм не изоб- ражается):
Таким образом, без логических
операций можно и обойтись.
 |
Код:
Задача
№ 22. Найти наибольший общий делитель двух натуральных чисел
Формулировка.
Даны два натуральных числа. Найти их наибольший общий делитель. Примечание:
наибольшим общим делителем (сокращенно пишут НОД) двух натуральных чи-
сел m и n называется
наибольший из их общих делителей. Обозначение: НОД(m, n).
Примечание
2: общим делителем двух натуральных чисел называется натуральное число, на
которое натуральное число, которое является делителем обоих этих чисел.
Например, найдем НОД(12, 8):
Выпишем все делители числа 12:
1, 2, 3, 4, 6, 12;
Выпишем все делители числа 8: 1,
2, 4, 8;
Выпишем все
общие делители чисел 12 и 8: 1, 2, 4. Из них наибольшее число – 4. Это и есть
НОД чисел 12 и 8.
Решение. Конечно, при решении мы не будем выписывать делители и
выбирать нужный. В принципе, ее можно было бы решить как задачу 14,
начав цикл с наименьшего из двух заданных чисел (так как оно тоже может быть
НОД, например, НОД(12, 4) = 4). Но мы воспользуемся так
называемым
алгоритмом Евклида нахождения НОД, который выведен с помощью математических
методов. В самом простейшем случае для заданных чисел m и n он
выглядит так:
 |
шего.
Как видим, в шаге 2 большее из
двух текущих чисел заменяется разностью большего и мень-
Приведем пример для чисел 12 и 8:
a.
Так как 12 > 8, заменим 12 на
12 – 8 = 4;
b.
Так как 8 > 4, заменим 8 на 8 –
4 = 4;
c.
4 = 4, конец.
Не проводя каких-либо
рассуждений над алгоритмом и не доказывая его корректности, пере-
ведем его описание в более близкую для языка Pascal форму:
Алгоритм на естественном языке:
1)
Ввод m и n;
2)
Запуск цикла с предусловием m
< > n. В цикле:
1.
Если m > n, то
переменной m присвоить m – n, иначе переменной n присвоить
n – m;
3)
Вывод m:
 |
Код:
Задача № 23. Найти наименьшее общее кратное двух
натуральных чисел
Формулировка.
Даны два натуральных числа. Найти их наименьшее общее кратное. Примечание:
наименьшим общим кратным двух чисел m и n называется наименьшее
нату-
ральное число, которое делится на m
и n. Обозначение: НОК(m, n)
Решение. Из теории чисел
известно, что НОК(m, n) связан с НОД(m, n) следующим образом:
НОК (m, n) = m × n
НОД
(m, n)
 |
Следовательно, для нахождения ответа нам нужно лишь использовать предыдущую
задачу нахождения НОД двух чисел m и n:
Так как исходные переменные будут испорчены в процессе работы алгоритма
Евклида, нам нужно вычислить их произведение до входа в описанный выше цикл и присвоить это произведение
переменной prod (от англ. product – «произведение»):
prod := m * n;
После этого нам остается вывести на экран результат арифметического
выражения в правой части нашей формулы. В качестве самого НОД будет
использоваться переменная m:
writeln(prod div m);
Кстати, деление в формуле будет целочисленным (через div) именно
потому, что если два числа делятся на некоторое число, то и их произведение
также делится на него.
 |
Код:
Задача № 24.
Вычислить xn
Формулировка. Даны
натуральные числа x и n (которое также может быть равно 0).
Вычис- лить xn.
Решение. Для того чтобы решить эту задачу, вспомним определение
степени с натуральным показателем: запись xn означает,
что число x умножено само на себя n раз.
Сразу из
определения видно, что здесь заранее известно количество повторений при
вычисле- нии результата, так что задача легко решается через цикл for.
Выходит, мы копируем исходное
число x в некоторую
переменную res (от англ. result – «результат»), а затем просто
умножаем его на x n раз? Не стоит торопиться с ответом.
Рассмотрим пример: 34 = 3 * 3 * 3 * 3 = 81. Если посмотреть на эту запись, то мы
видим, что возведение в четвертую степень как выражение содержит четыре
слагаемых, но только три опера- ции, так как мы с первого шага домножаем число 3 на три тройки.
Тогда реализация идеи из абзаца выше будет давать число в степени
на 1 больше, чем требуется.
Какой можно придумать выход? Например, можно сократить цикл на одну
операцию, но что тогда будет при вычислении нулевой степени? Как известно,
любое число в нулевой степени дает 1, а здесь при вводе в качестве n нуля
приведет к тому, что не будет осуществлен вход в цикл (так как не существует целочисленного отрезка от 1 до 0) и в итоге на выход так и пойдет
исходное число x.
А что, если изменить схему
умножения так: 34 = 1 * 3 * 3 * 3 * 3 = 81? Так мы можем сравнять показатель степени и число
требуемых операций, да и с нулевой степенью все становится просто, так как при
вводе в качестве n нуля не будет осуществляться вход в цикл и на выход в
программе пойдет число 1!
Теперь алгоритм на естественном
языке:
1)
Ввод x и n;
2)
Присваивание переменной res числа 1;
3)
Запуск цикла, при котором i изменяется
от 1 до n. В цикле:
1.
Присваиваем переменной res значение
res * x;
4)
Вывод переменной res.
 |
Код:
Кстати, стоит понимать, что объявление переменной res
при использовании типа word доста- точно условно, так как этот тип
принимает значения от 0 до 65535, что на единицу меньше числа 2562 хотя вводить в программу можно числа, предполагающие возведение в более высокую степень. Так как в условии
задачи не сказано
ничего о том, в каком числовом промежутке по x и n она
должна выдавать корректный ответ, оставим это в таком виде, достаточном
для проверки приложения на работоспособность.
Задача № 25. Вычислить xn по алгоритму быстрого возведения в
степень
Формулировка. Даны натуральные числа x и n.
Вычислить xn, используя алгоритм быстрого возведения в степень:
ì( x2 )n div 2 , если n четно
í
ïx × ( x2 )n div 2 , если n нечетно
Решение. Разберем этот пока неясный алгоритм,
представленный в нашей задаче лишь един- ственной формулой. Легко понять, что
указанное равенство имеет место: например, 34 = 34 div 2 = (32)2 = 92 = 81. Другой пример: 45 = 4 * (42)5 div 2 = 4 * (42)2 = 4 * 162 = 4 * 256 = 1024. Причем если выражение со
степенью нельзя в один шаг преобразовать таким образом, то необходимо продол-
жить преобразование выражения вплоть до получения конечного ответа. Однако как
теперь реали- зовать эту схему?
Рассмотрим пример немного сложнее. Вычислим 47 = 4 * (42)3 = 4 * (16)3 = 4 * 16 * (162)1 = 4 * 16 * 256 = 16384. Стоит обратить
внимание на то, что на каждом шаге при вычислении изменяется только
единственное обрабатывающееся число, а остальные множители выносятся однократно
и необходимы только для получения ответа в последнем действии.
Чтобы исключить их из рассмотрения, при нечетном текущем числе n мы
будем домножать на них некоторую промежуточную переменную r, поначалу
равную 1 (кстати, нечетность числа в Pascal определяет функция odd),
затем (уже независимо от условий) возведем в квадрат текущее x и
разделим n на 2 с отбрасыванием остатка. При повторении этих действий на
некотором шаге n обязательно станет равным 1. Это происходит потому, что
деление любого нечетного числа a на 2 с
отбрасыванием остатка равносильно делению на двойку
числа (a – 1), которое
является четным, и при
делении, двигаясь по цепочке четных
чисел, мы всегда
придем к единице.
Условие n = 1 и
будет окончанием цикла с предусловием. По выходе из цикла необходимо будет в качестве
ответа вывести последнее
значение x, умноженное на r.
Теперь алгоритм на естественном
языке:
1)
Ввод x и n;
2)
Присваивание переменной r числа 1;
5)
Запуск цикла с предусловием n
< > 1. В цикле:
1.
Если n нечетно, домножаем r
на x;
2.
Переменной x присваиваем
значение x * x;
3.
Переменной n присваиваем
результат от деления этой переменной на 2 с отбрасыва- нием остатка;
3) Вывод выражения x * r.
 |
Код:
Из анализа данного алгоритма
известно, что его асимптотическая сложность порядка O(log2n).
Задача № 26. Решить квадратное уравнение заданного вида
с параметром
Формулировка.
Дано натуральное число n. Вывести
на экран решения
всех квадратных урав- нений вида x2 + 2ax –
3 = 0 для всех a от 1 до n.
Решение. Эта задача очень похожа на задачу 12. В
принципе, ее можно было бы решить, ис- пользуя
код этой задачи,
взяв первый и последний коэффициенты равными 1 и –3 соответственно и запустив цикл по всем a от 1 до n, умножив a на
2 во всех формулах.
Однако исследуем это уравнение
математически и попытаемся оптимизировать решение:
1)
Найдем дискриминант уравнения:
D = (2a) – 4 ×1×(–3) = 4a2 +12 = 4 (a2 + 3)
Очевидно, что найденная
величина неотрицательна, и, если быть точнее, то при a от 1 до n она
всегда принимает значение не меньше 16 (так как при a = 1 она равна 4 *
(1 + 3) = 4 * 4 = 16). Следовательно, наше уравнение всегда имеет решение,
причем их два.
2)
Найдем формулы корней уравнения:
x1 = = = = –a +
2 2 2
a2 + 3, x
= –a –
Итак, формулы корней уравнения получены, и теперь только осталось
вывести в цикле значе- ния корней
для всех a от 1 до n, не забыв сделать вывод форматированным (так
как решения будут вещественными).
 |
Код:
Задача № 27. Вычислить значение многочлена в точке
Формулировка. Дано натуральное число n, вещественное число x
и набор вещественных чи- сел an, an-1, …, a0.
Вычислить значение многочлена n-ной степени с коэффициентами an, an-1,
…, a0 от одной переменной в точке x.
Примечание:
многочленом n-ной степени от одной переменной x называется
выражение вида
anxn + an-1xn-1 + … + a1x + a0, где an, an-1,
…, a0 – коэффициенты.
Решение. Собственно, в этой задаче требуется возведение переменной x (точнее, конкретного ее значения) в некоторую степень
n – 1 раз, а также n операций умножения
и n операций сложения.
В принципе, для полноценного решения она не требует одновременного знания более
чем одного коэффициента, так как мы можем
в цикле ввести коэффициент an в переменную a, умножить его на
xn и прибавить полученное число к переменной результата res (которой перед входом в цикл должно быть присвоено значение 0) и
повторить этот шаг для всех коэффициентов. Тогда количество опе- раций: (1 + 2
+ … + n + 2n), что примерно соответствует асимптотической
сложности O(n2).
Не занимаясь реализацией этого алгоритма, давайте
оптимизируем его. Например, пусть нам дан многочлен третьей степени a3x3 + a2x2 + a1x + a0. Вынесем за
скобки общий множитель x при слагаемых,
в которых это возможно. Получим:
(a3x2 + a2x + a1)x + a0. Вынесем
за скобки x также и в
полученном выражении со скобками, в итоге получим: ((a3x + a2)x + a1)x + a0.
Полученную форму записи
называют схемой Горнера. Очевидно, что она существует для мно-
гочлена любой степени.
Итак, имея n = 3 и коэффициенты a3, a2, a1 и a0, мы можем посчитать его значение с помощью
n операций умножения
и n операций сложения, а это значит,
что для вычисления требуется порядка 2n операций и алгоритм имеет линейную асимптотическую сложность O(n), что демонстрирует оче- видное преимущество перед предыдущим решением.
Посмотрим, как может выглядеть цикл, в котором вычисляется значение
многочлена в точке. Для этого немного
изменим представление в виде схемы Горнера, не меняя при этом значения
мно- гочлена: (((0x + a3)x + a2)x + a1)x + a0.
Теперь
нам требуется n + 1 операций, однако заведя переменную res для
накопления резуль- тата, которая перед входом в цикл будет равна 0, мы можем,
вводя коэффициенты a3, a2, a1 и a0, посчитать значение многочлена в одном цикле:
Примечание: оператор read нужен нам для того, чтобы можно было
вводить коэффициенты через пробел, а не через Enter.
Теперь разберем сам цикл. На первом шаге мы получаем
в res значение выражения 0x + a3 = a3, на втором – a3x + a2, на третьем – (a3x + a2)x + a1, на четвертом – ((a3x + a2)x + a1)x + a0. Как
видно, формула полностью восстановилась, причем вычисление идет от
наиболее вложенных скобок к верхним уровням.
Код:
Задача № 28. Вычислить факториал
Формулировка. Дано натуральное число n (которое также
может быть равно нулю). Вычис- лить n!
Примечание: n! (факториал числа n, читается
«эн факториал») – произведение всех натураль-
ных чисел до n включительно.
Решение. Задача очень просто решается
через цикл for
по всем i от 1 до n,
в теле которого мы на каждом
шаге домножаем переменную-результат fact (которой до входа в цикл
присвоено значе- ние 1) на i. При этом сохраняется и правило 0! = 1,
так как при вводе нуля программа не войдет в цикл и на выход пойдет
неизмененное в переменной fact число
1.
Код:
Примечание: для накопления результата мы использовали переменную fact
типа integer. Как уже говорилось, этот тип охватывает диапазон целых чисел от –2147483648 до 2147483647 (Borland Delphi 7 и PascalABC). Данная
переменная позволит сформировать результаты вплоть до 12! (= 479001600) включительно.
Задача
№ 29. Вычислить число сочетаний из n по k
Формулировка. Даны натуральные числа
n и k (k не
превышает n). Вычислить
число сочета- ний из n по k.
Примечание: в комбинаторике сочетанием из n по k называется набор k элементов, выбранных из данных n элементов; при этом наборы,
отличающиеся только порядком следования элементов,
считаются одинаковыми. Обозначение числа сочетаний из n по
k элементов: Ck . При этом счита-
ется, что Cn = 1, C0 =
1 и C0 = 1 для любого натурального n.
n n 0
Например, найдем все 2-элементные сочетания 3-элементного множества {1,
2, 3}. Таковыми являются {1, 2}, {1, 3} и {2, 3}. То есть, таковых сочетаний 3.
При этом, например, {1, 2} и {2, 1} – одинаковые сочетания, так как они
отличаются только порядком следования элементов.
Решение.
Из комбинаторики известна формула:
Ck = n! = n (n –1) (n – 2) ×…× (n – k +1)
n k !(n – k )! k !
Не интересуясь вопросом ее вывода и корректности, мы будем использовать
тот ее вариант, который написан после
второго знака равенства (если смотреть слева направо), так как он наиболее
оптимален для вычислений и позволит обойтись двумя циклами (для числителя for
с downto, для знаменателя – просто
for). Для числителя
и знаменателя предусмотрим соответственно переменные
num (от англ. numerator – «числитель») и denom (от англ. denominator
– «знаменатель»), которым нужно поначалу присвоить значения 1, чтобы
осуществить контроль частных случаев (этот вопрос упомянут в предыдущей задаче):
1)
При k = 0 переменная num останется неизменной и будет равна 1, так как невозможен вход в цикл с уменьшением от n до (n + 1),
переменная denom будет равна 1 как 0!;
2) При n = k num и denom будут вычислены и
при делении дадут единицу;
3)
При n = k = 0 переменная denom
будет вычислена как 0!, а переменная num не изменится по
невозможности входа в цикл с уменьшением от 0 до 1.
Код:
Задача № 30. Вывести таблицу квадратов и кубов всех
натуральных чисел до n
Формулировка. Дано натуральное число n, меньшее
256. Используя псевдографику, вывести на экран таблицу квадратов и кубов всех натуральных
чисел от 1 до n включительно.
Примечание: псевдографика – это совокупность символов для формирования видимых графи- ческих
примитивов (линий, прямоугольников, рамок, таблиц и т. д.). Она была актуальна
в те дале- кие времена, когда
устройства вывода компьютеров не способны были работать с графикой, либо это
было проблематично.
Символы, использующиеся для псевдографики, должны быть включены в набор
используе- мого в терминале (консоли) компьютерного шрифта.
Решение. В этой задаче мы впервые займемся графическим
оформлением выходных данных программы. Для начала подумаем, как может выглядеть
таблица в простейшем случае (n = 3):
Несмотря на то, что кодовые страницы для DOS
имеют определенный набор символов для рисования графических примитивов, в
частности, таблиц, мы будем пользоваться лишь символами ‘-‘ и
‘|’
для построения линий таблицы, а также ‘/’ и ” для
формирования ее угловых эле- ментов.
Построим псевдографический эквивалент этой таблицы:
|
/———————– |
||||||
|
| |
x |
| |
x^2 |
| |
x^3 |
| |
|
|———————–| |
||||||
|
| |
1 |
| |
1 |
| |
1 |
| |
|
| |
2 |
| |
4 |
| |
8 |
| |
|
| |
3 |
| |
9 |
| |
27 |
| |
———————–/
Примечание: в случае
ограниченных возможностей вывода
для обозначения возведения выра- жения в степень используется постфикс «^k», где k
– показатель степени. Кстати, здесь мы вырав- ниваем значения в середине
столбцов, сдвигая к середине разряд единиц упорядоченных по правому краю столбцов.
Как же сформировать вывод на экран такой таблицы? Понятно, что это
нужно сделать по- строчно. Однако какой ширины сделать
таблицу и как организовать вывод строк со степенями? Так как максимальное число, которое может
быть подано на вход – 255, и его куб равен 16581375 (он состоит из 8 цифр), то нам нужно сделать
колонки ширины 1 + 8 + 8 + 1 = 18 (крайние единицы
для отступов) символов, чтобы таблица выглядела равномерно:
/——————————————————–
| x | x^2 | x^3 |
|——————————————————–|
|
| |
1 |
| |
1 |
| |
1 |
| |
|
| |
2 |
| |
4 |
| |
8 |
| |
|
| |
… |
| |
… |
| |
… |
| |
|
| |
255 |
| |
65025 |
| |
16581375 |
| |
——————————————————–/
Как видим, при постепенном увеличении числа будут «вырастать» справа
налево. Чтобы вы- вести такую строку,
нужно вывести константу ‘|’, затем вывести соответствующее число с шири- ной поля вывода 9, потом вывести
константу ‘|’ с шириной
поля вывода 10 и аналогично вывести оставшиеся колонки:
writeln(‘|’,
i:9, ‘|’:10, i * i:9, ‘|’:10, i * i * i:9, ‘|’:10);
Схематически с учетом
форматирования это будет выглядеть так:
‘
Изменение цветов соответствует
чередованию аргументов в операторе вывода.
Так как заголовок таблицы один и тот же для всех вариантов исходных данных, мы
можем сразу вывести его с помощью трех строковых констант через writeln:
После вывода всех строк нужно вывести
нижнюю границу таблицы:
writeln(‘——————————————————–/’);
Вообще, все
эти константы и правила не взялись «просто так» или из расчетов. Единственный
использованный факт – разрядность числа не более 8, поэтому мы и взяли ширину
колонок «по
максимуму». В остальном нужно
было экспериментировать, чтобы
найти наиболее легкое и нагляд- ное решение. Конечно,
псевдографика – это не алгоритмическое программирование, и в нем тести- рование
и эксперимент играют чуть ли не самую важную
роль.
Код:
Задача № 31. Сформировать реверсную запись заданного
числа
Формулировка. Дано натуральное число n заранее
неизвестной разрядности. Сформировать и вывести на экран число, представляющее
собой реверсную запись n.
Решение. Это более общий случай задачи 4, в которой при
случае трехзначного n отчетливо видны повторяющиеся фрагменты кода.
Попытаемся получить общий алгоритм решения через цикл.
Пусть дано число 25893. Возьмем его последнюю цифру как остаток от
деления на 10 – это 3. Очевидно, она должна быть первой. Отбросим ее у числа n
и возьмем последнюю цифру 9 – она должна быть второй. Чтобы сформировать
две цифры реверсного числа, умножим 3 на 10 и приба- вим 9, потом добавим
третью цифру и т. д.
Так как разрядность числа неизвестна, мы будем использовать цикл с предусловием. Его тело будет
выглядеть так:
Поначалу результат r должен быть равен 0, и тогда умножение нуля
на 10 в первом шаге не разрушает формирование реверсной записи, которое теперь
может быть заключено в один цикл.
Каким же будет условие продолжения? Нетрудно понять, что когда мы будем
добавлять по- следнюю оставшуюся цифру исходного числа n к реверсной
записи r, мы умножим r на 10, приба- вим к ней как n mod 10 (в
данном случае этот остаток равен n) и разделим n на 10. Тогда n
станет равно 0 и цикл должен закончиться, так что условие его продолжения –
n < > 0.
Код:
Задача
№ 32. Проверить монотонность последовательности цифр числа
Формулировка. Дано натуральное число n. Проверить, представляют его ли цифры его вось-
меричной записи строго монотонную последовательность. При этом
последовательность из одной цифры считать строго монотонной.
Примечание: в математике строго возрастающие и строго убывающие
последовательности называются строго монотонными. В строго возрастающей последовательности каждый следующий член больше предыдущего.
Например: 1, 3, 4 ,7, 11, 18. В строго убывающей последовательности
каждый следующий член меньше предыдущего.
Например: 9, 8, 5, 1.
Решение. Здесь нам нужно будет последовательно получить разряды
восьмеричной записи числа, двигаясь по записи числа справа налево. Как мы уже
знаем, последний разряд числа в вось- меричной системе счисления есть остаток
от деления этого числа на 8.
Попытаемся определить несколько общих свойств строго возрастающих
(обозначим пример как 1) и строго убывающих (обозначим как 2)
последовательностей (для наглядности будем сразу брать восьмеричные
последовательности):
1) 3, 4, 5, 8, 9, 11.
2) 8, 7, 3, 2, 0.
Для начала введем в рассмотрение
некоторую формулу, обозначим ее как (I):
deltai = ai – ai+1,
где ai – член заданной последовательности с
индексом i. Нетрудно понять, что эта формула определяет разность
между двумя соседними элементами: например, если i = 5 (то есть, мы рассмат-
риваем пятую разность), то формула
будет выглядеть так: delta5 = a5 – a6. При этом стоит учитывать
множество всех значений, которые может принимать
i. Например, для последовательности (1) i мо- жет принимать значения от 1 до 5
включительно, для последовательности (2) – от 1 до 4 включи- тельно. Легко
проверить, что для всех других i формула (I) не имеет смысла, так как в
ней должны участвовать несуществующие члены
последовательности.
Найдем все deltai для последовательности (1): delta1 = 3 – 4 = –1, delta2 = 4 – 5 = –1, delta3 = 5
– 8 = –3, delta4 = 8 – 9 = –1, delta5 = 9 – 11 = –2.
Как видим, они все отрицательны. Нетрудно догадаться, что это свойство
сохраняется для всех строго возрастающих последовательностей.
Выпишем все deltai для последовательности (2), не
расписывая при этом саму формулу: 1, 4, 1, 2. Видим, что все они положительны.
Кстати, весьма примечательно, что в математическом анализе определение монотонной функ- ции дается в терминах, подобных
используемым в нашей формуле (I), которая рассматривается там несколько более гибко, а deltai при этом
называется приращением и имеет несколько иное обозна- чение.
Можно обобщить сказанное тем, что последовательность приращений показывает,
на какую величину уменьшается каждый член исследуемой последовательности
чисел, начиная с первого. Понятно, что если каждый член числовой
последовательности уменьшается на положительную ве- личину, то эта
последовательность строго убывает и т. д.
Из всех этих рассуждений делаем вывод о
том, что числовая последовательность является строго
монотонной (то есть,
строго возрастающей или строго убывающей) тогда и только
тогда, когда deltai имеют один и тот же знак для всех i. Таким образом, мы вывели понятие,
которое можно проверить с помощью последовательности
однотипных действий, то есть, циклической обработки.
Теперь нам необходимо попробовать унифицировать
проверку знакопостоянства всех delta для последовательностей обоих видов.
Для этого рассмотрим произведение каких-либо двух delta в последовательностях (1) и (2).
Примечательно, что оно положительно как произведение чисел од- ного знака.
Таким образом, мы можем в любой последовательности взять delta1 и получить
произ- ведения его со всеми остальными delta (обозначим эту формулу как (II)):
p = delta1 * deltai
Если все p положительны, то последовательность строго
монотонна, а если же возникает
хотя бы одно отрицательное произведение p, то условие
монотонности нарушено.
Теперь перенесем эти рассуждения из математики в программирование и
конкретизируем их на последовательность цифр восьмеричной записи числа.
Обозначим идентификатором delta ре- зультат вычисления формулы (I) для
двух текущих соседних членов последовательности.
Каким же образом двигаться по
разрядам числа n и обрабатывать все delta?
Сначала
мы можем получить последнюю цифру числа n (назовем ее b),
отбросить ее и полу- чить предпоследнюю цифру n (назовем ее a),
отбросить ее тоже, а затем вычислить delta = a – b. Кстати, отметим,
что при таком подходе мы будем для всех i находить deltai, двигаясь по ним справа
налево. Начальному фрагменту этих действий соответствует следующий код:
Теперь мы можем войти в цикл с предусловием n < > 0. В каждом шаге
цикла мы должны присвоить переменной b число a, затем считать
следующий разряд в a и отбросить этот разряд в n. Таким способом
мы «сдвигаем» текущую пару: например, на 1-ом шаге в примере (2) мы до входа в
цикл использовали бы цифры 2 (в переменной a) и 0 (в переменной b),
затем при входе в цикл скопировали бы 2 в b и 3 в a – таким
образом, все было бы готово для исследования знака по про- изведению. В связи с
этим основной цикл будет выглядеть так:
На месте многоточия и будет проверка
знакопостоянства произведений. Воспользовавшись формулой (II), мы заменим
deltai в качестве
текущего на саму разность a – b, чтобы не задействовать
дополнительную переменную. В итоге, если теперь delta * (a – b) <= 0,
то выходим из цикла:
if delta * (a – b) <= 0 then break;
Теперь рассмотрим развитие
событий по завершении цикла:
1)
Если произойдет выход по завершению цикла,
то есть «закончится» число в связи с превра- щением его в 0 на некотором
шаге, то значения
a, b и delta будут содержать значения, подтвержда- ющие строгую монотонность
последовательности, что можно проверить с помощью вывода значе- ния булевского
выражения на экран.
2)
Если в теле цикла произошел выход
через условный оператор, то эти переменные будут содержать значения,
с помощью которых
выявлено условие нарушения строгой монотонности. Это значит, что по выходе из цикла ответ
можно выводить в формате:
writeln(delta
* (a – b) > 0);
Код:
Кстати, что будет при вводе числа
n, меньшего 8, ведь его восьмеричная запись однозначна?
Хотя наша цепочка делений еще до
входа в цикл требует двух цифр в записи числа!
Посмотрим, как поведет
себя программа при вводе числа
n из единственной цифры k: сначала k идет в b (строка
9), затем отбрасывается в n (строка 10), которое теперь равно 0, затем в
a идет число 0, так как 0 mod 8 = 0 (строка 11). При этом строка
12 уже ничего не дает, так как n, которое сейчас равно нулю,
присваивается значение 0 div 8 = 0. Далее вычисляется delta = –k (строка
13), затем игнорируется цикл, так как n = 0 (строки 14 – 19), затем
выводится на экран значение выра- жения –k * –k > 0 (строка
20), которое истинно для любого действительного k кроме нуля, который и
не входит в условие нашей задачи, так как n
натуральное.
Как видим, вырожденный случай прошел обработку «сам собой» и для него не
пришлось раз- ветвлять программу,
что выражает несомненный плюс.
Задача
№ 33. Получить каноническое разложение числа на простые сомножители
Формулировка. Дано натуральное число n (n > 1).
Получить его каноническое разложение на
простые сомножители, то есть представить в виде произведения простых
сомножителей. При этом в разложении допустимо
указывать множитель 1. Например, 264 = 2 * 2 * 2 * 3 * 11 (программе
допустимо выдать ответ 264 = 1 *
2 * 2 * 2 * 3 * 11).
Решение. Данная задача
имеет достаточно красивое решение.
Из основной теоремы арифметики известно, что для любого
натурального числа больше 1 существует его каноническое разложение на простые
сомножители, причем это разложение един- ственно с точностью до порядка
следования множителей. То есть, например, 12 = 2 * 2 * 2 и 12 = 3
* 2 * 2 – это одинаковые
разложения.
Рассмотрим каноническую форму любого числа на конкретном примере.
Например, 264 = 2 * 2 * 2 * 3 * 11. Каким образом
можно выявить эту структуру? Чтобы ответить на этот вопрос,
вспом- ним изложенные в любом школьном курсе алгебры правила деления
одночленов, представив, что числа в каноническом разложении являются
переменными. Как известно, если разделить выраже- ние на переменную в некоторой
степени, содержащуюся в этом выражении в той же степени, оно вычеркивается в ее записи.
То есть, если мы разделим 264 на 2, то в его каноническом разложении
уйдет одна двойка. Затем мы можем
проверить, делится ли снова получившееся частное на 2. Ответ будет положитель-
ным, но третий раз деление даст остаток. Тогда нужно брать для рассмотрения
следующее нату- ральное число 3 – на него частное разделится один раз. В итоге,
проходя числовую прямую в поло- жительном направлении, мы дойдем до числа 11, и
после деления на 11 n станет равно 1, что будет говорить о необходимости
закончить процедуру.
Почему при таком «вычеркивании» найденных сомножителей мы не получим
делимостей на составные числа? На самом деле,
здесь все просто
– любое составное число является
произведением простых сомножителей, меньших
его. В итоге получается, что мы вычеркнем
из n все
сомножители любого составного числа, пока дойдем до него самого в
цепочке делений. Например, при таком переборе n никогда не разделится на
4, так как «по пути» к этому числу мы вычеркнем из n все
сомножители-двойки.
Алгоритм на естественном языке:
1)
Ввод n;
2)
Присвоение переменной p числа 2;
3)
Вывод числа n, знака
равенства и единицы для оформления разложения;
4)
Запуск цикла с предусловием n
< > 1. В цикле:
1.
Если m mod p = 0, то
вывести на экран знак умножения и переменную p, затем разде- лить n на p,
иначе увеличить значение i на 1;
Код:
Задача № 34. Сформировать число из двух заданных
чередованием разрядов
Формулировка. Даны два натуральных числа одинаковой десятичной
разрядности. Сформи- ровать из них третье число так, чтобы цифры первого числа
стояли на нечетных местах третьего, а цифры
второго – на четных. При этом порядки
следования цифр сохраняются. Например, при вводе 1234 и 5678 программа
должна выдать ответ 15263748 (для
наглядности разряды обоих чисел вы- делены разными цветами).
Решение. Так как у чисел (обозначим их a и b)
одинаковая десятичная разрядность, крайняя справа цифра у третьего числа (c,
которое поначалу должно быть равно 0) всегда будет на четном месте, так как при
его формировании мы работаем с длинами a и b как с числами одной
четности, сумма которых всегда четна, и длина c как раз и есть позиция
крайней справа цифры.
Это значит, что формирование c нужно в любом случае
начинать с последнего разряда b. При этом
каждый взятый из a или
b разряд мы должны сместить
на необходимую позицию
влево, чтобы добавлять разряды
c, используя операцию сложения. Мы сделаем это с помощью вспомогательной
переменной z, которая перед входом в цикл будет равна 1. В цикле же она
будет умножаться на последний добытый разряд b (при этом выражение z
* b mod 10 нужно прибавить к c), затем умно- жить z на 10 и проделать то же самое с последним
разрядом a и снова умножить
z на 10. Кстати, при этом нужно не забыть своевременно
отбросить уже рассмотренные разряды чисел.
Так как разрядность чисел неизвестна, нам нужен цикл с предусловием. В
силу одинаковой десятичной разрядности a и b мы можем сделать
условие по обнулению любого из них, так как второе при этом также обнулится.
Возьмем условие a < > 0.
Таким будет основной цикл:
В итоге конечное число c будет сформировано в таком виде (все
направления справа налево): первая цифра b, первая цифра a,
вторая цифра b, вторая цифра a и так далее до самых последних
разрядов слева. Кстати, скобки в двух операторах нужны для правильного
понимания компилято- ром приоритета выполняемых арифметических операций. Без них z умножится на соответствующее
число, и остаток от деления именно этого числа прибавится к c, что неправильно.
Алгоритм на естественном языке:
1)
Ввод a и b;
2)
Обнуление переменной c;
3)
Присвоение переменной z числа 1;
4)
Запуск цикла с предусловием a
< > 0. В цикле:
1.
Прибавляем последний разряд b в
текущий разряд c, определяемый с помощью мно- жителя z;
2.
Умножаем z на 10;
3.
Избавляемся от последнего разряда
в b;
4.
Прибавляем последний разряд a в
текущий разряд c с помощью множителя
z;
5.
Умножаем z на 10;
6.
Избавляемся от последнего разряда
в a;
5)
Вывод c.
Код:
Задача № 35. Вывести на экран x, записанное в системе
счисления с основанием n
Формулировка.
Даны натуральные числа x и n (n <= 10). Вывести на
экран число x, записан- ное в системе счисления с основанием n.
Решение. Вспомним
правило из задачи 5:
Раньше мы принимали это правило без доказательства, однако сейчас мы
коснемся его, так как оно достаточно краткое.
Воспользуемся формулой записи
десятичного числа x в системе счисления с основанием p,
состоящего из r знаков:
x
= ar–1 * pr–1 + ar–2 * pr–2 +
… + a2 * p2 + a1 * p1 + a0 * p0,
где pr–1, pr–2, …, p2, p1, p0 – основание системы счисления, возведенное в соответствующие сте- пени, ar–1, ar–2, …, a2,a1, a0 – цифры в записи этого числа в системе счисления с
основанием p.
Например, число 378 в десятичной системе
счисления выглядит так: 378 = 3 * 102 + 7 * 101 + 8 * 100. Если мы подряд выпишем
цифры a2 (= 3), a1 (= 7), a0 (= 8), то исходное число восстановится.
Запишем представление числа в 22 двоичной системе
счисления (переведем его с помощью калькулятора, оно равно 101102) по этой же
формуле: 22 = 1 * 24
+ 0 * 23 +
1 * 22 + 1 *
21 + 0 * 20. Понятно, что
если мы вычислим выражение в правой части равенства, то получим как раз 22.
Теперь покажем то, что если мы возьмем
остаток от деления
числа 22 на 2, затем разделим его на
2, отбросив остаток,
и будем повторять
эти действия до обнуления числа,
то в итоге получим все его разряды в порядке справа налево.
Возьмем его запись 1 * 24 + 0 * 23 + 1 * 22 + 1 * 21 + 0 * 20 и разделим ее на 2. Из алгебры известно, что если мы делим
сумму чисел на некоторое число, то на него делятся все слагаемые этой суммы. 1 * 24, 0 * 23, 1 * 22 и 1 * 21 делятся на 2, так как в них
присутствует множитель 2. 0 * 20 = 0 * 1 = 0 не делится на 2, соответственно, это число будет остат-
ком от деления на 2, и при этом по формуле оно является крайним
справа разрядом. Затем мы делим всю эту запись на 2 и отбрасываем
остаток, получаем: 1 * 23 + 0 * 22 + 1 * 21 + 1 * 20. Очевидно, что при следующем взятии остатка мы получим
цифру из крайнего справа слагаемого. Повторяя эту цепочку, мы постепенно
получим все цифры числа 22 в системе счисления с основанием 2.
Обобщая вышесказанное, приходим к выводу, что для формирования записи
числа нам необ- ходимо получить все остатки от деления x на основание n,
при этом деля x на n после каждого взятия остатка.
Каким образом мы запишем остатки
справа налево? Очень
просто: умножаем очередной оста- ток на некоторый множитель z, добавляющий
необходимое количество нулей, чтобы цифра оказа- лась в необходимой позиции, и
прибавляем к результату r. Поначалу z будет равен 1, так как мы
прибавляем цифру к разряду единиц, затем z в каждой итерации будет
умножаться на 10.
В итоге мы прибавляем к результату r первый остаток, умноженный на 1,
второй остаток, умноженный на 10, третий остаток, умноженный на 100 и так
далее, пока не будет сформировано искомое число:
Код:
Задача № 36. Найти наименьший нетривиальный делитель
двух заданных чисел
Формулировка.
Даны натуральные числа m и n. Вывести на экран их наименьший
нетриви- альный делитель или сообщить, что его нет.
Решение. Задача
похожа на задачу 15, в которой поиск минимального делителя осуществ-
лялся с помощью цикла:
Здесь все просто: проверяем все числа от 2 по возрастанию – если нашли
делитель, выводим его на экран
и выходим из цикла с помощью break. В нашем же случае нужно
проверять делимость двух
введенных чисел. При этом цикл должен проходить по всем i от 2 до минимального
из чисел m и n (назовем его min), так как оно может быть наименьшим нетривиальным делителем, когда оно простое. Например, для чисел 17 и 34
таковым является 17.
Найти наименьшее из двух чисел
можно так:
if n < m
then min := n else min := m;
Кстати, теперь в цикле мы должны не просто вывести на экран найденный
делитель, а сохра- нить его в некоторую переменную (mindiv), которая до
входа в цикл будет равна 1 (или 0), чтобы проверить, выполнилось ли условие
делимости в цикле. Если да, то необходимо вывести значение наименьшего общего
делителя, а если нет, и mindiv все еще равно 1 (или 0), то вывести
сообщение об отсутствии делителя.
Код:
Задача № 37. Проверить, является ли натуральное число
счастливым билетом
Формулировка.
Дано натуральное число n. Проверить, является ли оно счастливым
билетом.
Примечание: вообще, в математике обычно
рассматриваются счастливые билеты
с четным ко- личеством цифр, потому что у них
можно явно выделить левую и правую половины одинаковой длины, суммы цифр
которых и сравниваются. Однако мы несколько расширим это определение, полагая,
что если число имеет нечетную длину, его центральную цифру можно отбросить, так
как ее логично было бы прибавить к накапливаемым суммам обоих половин, что,
собственно, не изме- нит отношения между ними.
Например, число 14350 –
счастливый билет, так как 1 + 4 = 5 + 0, а центральную цифру мы отбросили.
Решение. Задача является
общим случаем задачи
10. Для ее решения необходимо знать длину числа (то
есть его разрядность), вследствие чего нам необходимо скопировать переменную n
в не- которую другую (например, a), чтобы на основе a посчитать
количество десятичных разрядов n и сохранить его в некоторой переменной digits
(digits в пер. с англ. означает «цифры»). Сделать это можно так:
Здесь мы в каждой итерации цикла отбрасываем одну цифру от a и
увеличиваем значение счетчика digits на 1. На некотором шаге число a будет
однозначно и станет равным нулю при деле-
нии на 10, и после
инкрементации счетчика, который
теперь уже будет
содержать количество цифр числа, произойдет выход из цикла.
Чтобы посчитать суммы левой и правой половины цифр числа (для
накопления которых мы предусмотрим переменные left и right), мы
должны запустить два последовательных цикла от 1 до digits div 2, в
которых прибавлять каждый полученный разряд к соответствующей переменной и
отбрасывать его. Если длина нечетная, нам необходимо отбросить серединную цифру
числа без прибавления к какой-либо сумме. Так как в первом цикле мы обработали
и отбросили правую по- ловину цифр числа, то по выходе из него серединная цифра
как раз будет находиться в разряде единиц. Поэтому необходим следующий шаг:
if odd(digits)
then n := n div 10;
Напомним, что функция
odd(n) возвращает значение
true, если n нечетно, и false, если n четно. То есть, написанный выше оператор проверяет счетчик digits (в
котором хранится длина исходного
числа) на нечетность, и если оно нечетно, отбрасывает последнюю его цифру.
Далее необходимо накопить сумму цифр левой половины числа и вывести на
экран результат сравнения сумм левой и правой половины.
Код:
Представим, как должен работать
алгоритм при вводе числа 14350:
1)
Считаем длину числа, она равна 5
(строки 11-14);
2)
В цикле из 5 div 2 = 2 повторений
прибавляем к right крайние справа цифры 0 и 5, после чего отбрасываем их
и имеем в n 143 (строки 17-20);
3)
Так как odd(digits) = odd(5) =
true, отбрасываем 3, после чего имеем в n 14 (строка 21);
4)
В цикле из 5 div 2 = 2 повторений
прибавляем к left оставшиеся цифры 1 и 4, после чего n
становится равно 0, что, впрочем,
нас уже не интересует (строки 22-25);
5)
Выводим на экран значение
выражения left = right – ответ положительный (строка 26).
Задача № 38. Проверить, является ли натуральное число
палиндромом
Формулировка.
Дано натуральное число n. Проверить, представляет ли собой палиндром
его десятичная запись.
Решение. Задача является общим случаем задачи 9. Чтобы
решить ее, необходимо разделить число n на
две половины одинаковой длины, отбросить серединную цифру в случае
нечетной длины n и
проверить равенство одной из частей реверсной записи другой части.
Так как нам
заранее неизвестна десятичная разрядность n, мы можем посчитать ее с
помощью следующего цикла (подробнее это описывалось в предыдущей задаче):
Теперь
рассмотрим варианты проверки числа на палиндром вместе с разбором на примере.
Пусть дано число нечетной длины, например, 79597. Мы можем отделить его
правую поло-
вину 97,
проведя ряд последовательных делений с взятием остатка в цикле из digits div
2 повторе-
ний. При этом необходимо сразу
сформировать ее реверс в переменную right (мы делали это в за- даче
31):
Так как число нечетно, нужно отбросить его центральную цифру 5, после
чего в переменной n (равной 79) будет содержаться левая половина числа,
а в переменной right (также равной 79) – его перевернутая правая
половина. Они равны, следовательно, ответ положительный.
Тот же порядок
действий применяется и для чисел четной длины,
однако теперь нам не нужно ничего
отбрасывать после накопления реверсной левой части числа в переменную right,
так как в числах четной длины нет серединной цифры. Например, дано число
1551: переворачиваем правую половину числа 51 (получим
15) и сравниваем ее с левой половиной: 15 = 15, ответ положительный.
Эти допущения
говорят о том, что необходима проверка длины числа n на нечетность и,
соот- ветственно, отбрасывание серединной цифры в случае нечетности:
if odd(digits) then n := n div 10;
Код:
1.
program CheckPalindrome; 2.
3.
var
4.
n, a,
right: longint;
5.
digits,
i: byte; 6.
7. begin
8.
readln(n);
9. a
:= n;
10.
digits
:= 0;
11.
while a
<> 0 do begin
12.
a := a
div 10;
13.
inc(digits)
14.
end;
15.
right := 0;
16.
for i :=
1 to digits div 2 do begin
17.
right :=
right * 10;
18.
right :=
right + n mod 10;
19.
n := n
div 10
20.
end;
21.
if
odd(digits) then n := n div 10;
22.
writeln(n
= right)
23. end.
Выполним «ручную прокрутку»
алгоритма на числе 147741:
1)
Считаем длину числа, она равна 6
(строки 11-14);
2)
В цикле из 6 div 2 = 3 повторений
прибавляем к right (формируя реверсную запись) по- следние три цифры числа n, после
чего отбрасываем их и имеем в n 147, в right 147
(строки 16-20);
3)
Так как odd(digits) = odd(6) =
false, ничего не делаем (строка 21);
4)
Выводим на экран значение
выражения n = right – ответ положительный (строка 22).
Задача № 39. Проверить, является ли натуральное число
степенью двойки
Формулировка.
Дано натуральное число n. Проверить, представляет ли оно собой
натураль- ную степень числа 2.
Решение. Проще говоря, нам нужно ответить на вопрос: можно ли
возвести число 2 в какую- либо натуральную степень (или в нулевую степень, так
как 20 = 1),
чтобы получилось число n?
Вообще, для решения этой задачи существует достаточно красивое
равенство, выполняюще- еся для всех натуральных степеней числа 2, позволяющее
получить ответ с помощью одной един- ственной логической побитовой операции:
n and (n – 1) = 0
Обозначим его как (1).
Дело в том, что натуральная степень числа 2 с
показателем p в двоичном виде всегда пред- ставляется как единица с p нулями справа. Это происходит потому, что двоичная
запись этого числа в десятичном виде представляется как
1 * 2p + 0 *
2p–1 + … +
0 * 21 + 0 *
20, где все
пропущенные слагаемые имеют коэффициент 0, и из этой записи легко восстановить
двоичное представление: 10…00, здесь нулей всего p. Поэтому если мы
отнимем от любой степени двойки 1, то получим число 1…11, где всего
p единиц (точнее
говоря, это будет число 01…11).
В итоге, если мы применим к этим двум числа побитовую
конъюнкцию, то всегда будем получать результирующее число, рав- ное 0.
Примечание: побитовая конъюнкция – это бинарная операция, которая
эквивалента обычной конъюнкции, примененной к двоичным разрядам операндов (двух
исходных чисел), стоящим на одинаковых позициях в двоичных представлениях этих
чисел. При этом результатом применения побитовой конъюнкции является некое
результирующее число, значение соответствующих битов которого зависит
от значений битов исходных чисел:
в соответствующем разряде
будет находиться 1 тогда и только
тогда, когда на этих позициях
в обоих исходных числах стояли
единичные биты, и 0, иначе.
Пример: выполним поразрядную конъюнкцию двоичных чисел 0110012 и 1010112 (при этом выпишем
их так, чтобы соответствующие двоичные разряды стояли друг под другом):
|
Первый операнд: |
0110012 |
|
Второй |
1010112 |
|
Результат: |
0010012 |
Биты, конъюнкция которых даст 0,
выделены красным цветом, а те, конъюнкция которых даст
1 – синим.
Так как 1-й разряд слева
у первого числа равен 0, а у второго – 1, то в соответствующий первый разряд результата идет бит 0. 2-е разряды,
соответственно, равны 1 и 0, и в результат снова
идет бит
0.
3-и разряды у обоих чисел равны 1
(выделены синим цветом), поэтому в 3-й разряд результата идет 1 и так далее.
Кстати, наша формула
(1) пропускает число 0 в качестве степени
двойки. Так как компиляторы
языка Pascal (гарантированно называются Borland Delphi
7 и PascalABC) реализуют числовые
типы данных в виде кольцевых отрезков
(то есть, например, в типе byte
после числа 255 следует число 0,
а перед числом 0 – число 255), то в любом таком типе выражение (0 – 1) имеет некоторое ненулевое битовое представление (так как нулевое битовое
представление имеет лишь число 0), а побитовая конъюнкция числа 0 и любого
другого числа дает в результате число 0.
Вообще, так как нам данное нам n является натуральным числом, число 0
вводиться не будет. Однако покажем,
как отсечь 0 при проверке числа по формуле (1): можно осуществить проверку
введенного числа на равенство нулю, и в случае равенства заменить его на какое-либо другое
число, заведомо не являющееся степенью двойки, чтобы условие формулы (1)
отработало правильно:
if n = 0 then
n := 3;
Вообще, формула (1) требует доказательства в обе стороны: мы лишь
доказали, что если n является степенью двойки, то есть n = 2p (где p –
любое натуральное число или 0), то выражение n and (n – 1) гарантированно
дает результат 0. Покажем это схематически еще раз:
|
Первый операнд: |
100…00 |
|
Второй |
011…11 |
|
Результат: |
000…00 |
Однако мы
также должны доказать, что никакое другое число n, кроме как степень
двойки, не может дать 0 в результате выполнения операции n and (n – 1).
Однако мы примем это утверждение
без доказательства. В итоге тело
программки может выглядеть так (для натурального n, которое также может
быть нулем):
Однако мы в качестве основного решения возьмем более
простую идею: пусть данное число n является степенью
двойки. Следовательно, его можно представить так: 2p = 1 * 2 * 2 * … * 2 (здесь ровно p двоек). Разделив
это выражение на 2 определенное количество раз, в результате мы получим
число 1.
Если же число n
не является степенью двойки, то на некотором шаге мы получим остаток при
делении на 2. В связи с этим возникает алгоритм:
1)
Вводим n;
2)
В цикле с предусловием n >
1 работаем с n:
1.
Если остаток от деления n на
2 равен 1 (n mod 2 = 1), то выходим из
цикла;
2.
Делим n на 2 (n := n div 2);
3)
Выводим на экран значение
выражения n = 1 (если цикл завершился, то это условие ис- тинно и n –
степень двойки, а если нет – то на каком-то шаге мы получили остаток при
делении на 2 и вышли через break);
Даже если
ввести n, равное 0, то программа выдаст правильный ответ, так как не
будет осу- ществлен вход в цикл (2) и на шаге (3) будет выведено значение
выражения 0 = 1, равное false.
Код:
Задача № 40. Вывести на
экран произведение четных элементов заданной последо- вательности натуральных
чисел
Формулировка. Дана последовательность натуральных чисел,
ограниченная вводом нуля. Вывести на экран
произведение четных элементов
этой последовательности. При этом ноль не счи- тается членом последовательности.
Примечание: задачи подобного
рода требуют выполнения каких-либо действий в зависимости
от некоторого характеристического свойства. Большинство из них математически неинтересны, од- нако
развивают способность совмещать отдельные приемы и методы программирования,
поэтому, в основном, способствуют наработке
опыта.
Решение. Так как нам заранее
неизвестна длина рассматриваемой последовательности, но мы знаем
о том, что она ограничивается вводом нуля, и поэтому можем сделать цикл с предусловием a
< > 0,
где a – текущий введенный член. Так как нет необходимости работать с несколькими членами одновременно, мы можем следовать данной схеме и в
конкретный момент времени работать лишь с одним элементом последовательности.
При всем этом перед циклом
нам необходимо считать
первый член a,
чтобы войти в цикл, если последовательность непустая
(а если пустая,
то есть состоит из одного
нуля, то и не нужно входить
в цикл и что-либо делать):
Кстати, мы используем оператор ввода read, чтобы можно было
вводить члены через пробел, а не через enter, как при использовании readln.
Внутри цикла вместо многоточия должна распола- гаться некоторая последовательность операторов, которые и будут выполнять обработку вводимых данных. После каждой итерации необходимо ввести
следующий член последовательности и про- должить обработку, если он не равен
нуля, и закончить в противном случае.
Примечательно, что лишь за некоторыми исключениями именно в цикле
такого вида будет располагаться основной блок обработки для всех задач на
последовательность, ограниченную вво- дом нуля.
Что же касается текущей задачи, то для ее решения мы в цикле должны
проверить каждый элемент на четность, и если он четный, домножить на него некоторую переменную prod для
накоп- ления результата (которую поначалу нужно сделать равной 1). При
этом если по завершении про- граммы переменная prod будет по-прежнему
равна 1, то это значит, что последовательность либо пуста, либо в ней нет
четных элементов, что побуждает сделать в этом случае соответствующую проверку
с выводом результата или сообщения об отсутствии элементов. В связи с
написанным возникает такой код:
|
read(a); |
||
|
prod := 1; |
||
|
while a <> |
0 |
do begin |
|
if a mod |
2 |
= 0 then prod := prod * a; |
|
read(a) |
||
|
end; |
||
|
if prod <> |
1 |
then writeln(prod) else writeln(‘ No such elements!’); |
При этом проверяется неравенство prod единице, так как хотелось
бы поместить в then-блоке
условного оператора вывод
«положительного» ответа (который
отвечает критерию задачи),
а в else– блоке – обработку «вырожденного случая». На самом
же деле такой порядок не должен быть само- целью и не считается «хорошим тоном»
в программировании, да и делается только по прихоти ав- тора, так что не было
бы никакой разницы, если бы в последней строчке было:
if prod = 1
then writeln(‘ No such elements!’)
else writeln(prod);
Код:
Задача № 41. Вывести на
экран произведение двузначных элементов последова- тельности натуральных чисел,
которые делятся на заданное число
Формулировка. Дано натуральное число n, а затем
последовательность натуральных чисел, ограниченная вводом нуля. Вывести
на экран произведение двузначных элементов этой последова-
тельности, которые делятся на n.
Решение. Задача очень похожа на предыдущую, только в этот раз
нам необходимо проверять делимость не на 2 (это было условие
четности), а на n. К тому же, мы должны рассматривать только двузначные члены. Для выявления
двузначного числа мы, однако, не будем считать
его разрядность и сравнивать
ее с двойкой, а воспользуемся тем, что любое двузначное число больше 9 и меньше
100.
В связи с этим условие
поиска члена последовательности, отвечающего заданным критериям, будет выглядеть так: (a >
9) and (a < 100) and (a mod n = 0).
Напомним, что and
– это конъюнкция, причем наше выражение
содержит три конъюнктивных члена, так как операция
применяется дважды. Оно истинно тогда и только
тогда, когда истинны
все три члена, и ложно во всех остальных случаях. При этом конъюнктивные
члены стоят в скобках, так как логические операции в языке Pascal имеют
больший приоритет, чем операции сравнения и арифметические операции. То есть,
если опустить скобки, то Pascal, вычисляя значение слева направо,
выполнит сначала операции 9 and a, 100 and a и т. д., что в корне неправильно.
Код:
Задача № 42. Найти количество простых членов
последовательности
Формулировка. Дана
последовательность натуральных чисел, ограниченная вводом нуля.
Вывести на количество простых
членов этой последовательности.
Решение. Принцип
решения этой задачи напоминает решения обеих предыдущих задач. При этом
алгоритм распознавания простых чисел можно взять из задачи 17, немного
изменив его:
Здесь мы предварительно поменяли названия переменных и вместо вывода
ответа о простоте числа работаем со счетчиком найденных простых чисел.
Напомним, что в цикле считается количе- ство
всех возможных натуральных делителей числа, и если их 2, то оно простое,
и необходимо уве- личить счетчик простых чисел count.
Когда вся числовая последовательность будет обработана, останется только
вывести на экран значение переменной count.
Код:
Задача № 43. Проверить,
начинается ли каждый из членов последовательности с десятичной цифры, на
которую оканчивается предыдущий
Формулировка. Дана последовательность натуральных чисел, ограниченная
вводом нуля. Проверить, начинается ли каждый из ее членов
(со второго) с десятичной цифры,
на которую окан- чивается предыдущий. Например,
таковой последовательностью будет являться 14 47 712 2179 9 9
93 0 (также
сохранен ограничивающий ноль).
Решение. Задача решается через цикл с предусловием, что
характерно для задач на последо- вательность
с ограничителем. При ее решении
мы могли бы не рассматривать «вырожденные вари-
анты», в которых на вход будет подаваться, например, пустая последовательность
(то есть состоя- щая из единственного нуля) или последовательность из одного
члена, так как на вопрос о том, удо-
влетворяют ли такие последовательности заданному критерию, ответить
теоретически достаточно трудно. Разумнее всего было бы считать выполнение
критерия для таких последовательностей не- определенным, что, однако, в формате
даваемого нами ответа не представляется возможным: под
«проверкой» характеристического свойства в данном случае понимается ответ на вопрос:
либо «да», и
последовательность отвечает заданным требованиям, либо «нет», и,
соответственно, не отвечает.
Следовательно, нам нужно вместо ответа о «неопределенности»
проверяемого свойства дать один из допустимых ответов. Наверное, разумно
было бы дать при обработке
вырожденных случаев
программой ответ «нет». Мы возьмем это на заметку и попытаемся сделать
контроль исключений, когда уже будет готово решение
задачи для общего
случая, чтобы заранее
не наделать ошибок.
Это необходимо потому, что мы попробуем инициализировать значения
переменных при запуске про- граммы таким образом, чтобы обработку вырожденных
случаев можно было выполнить с мини- мальным вложением дополнительного кода – мы
уже делали это в задаче 32.
Теперь о переменных. Так как нам необходимо проверять выполнение
критерия на двойках (парах) элементов, то и хранить
в памяти нужно сразу два элемента (a и b). Первый элемент не имеет
предшественника, поэтому после ввода мы не обрабатываем его и можем вводить
следующий эле- мент в одном операторе с ним:
read(a, b);
Имея два элемента, мы уже можем выполнить проверку нашего свойства. Однако уже на этом
этапе мы можем догадаться, что в силу необходимости выполнить проверку для всех пар элементов последовательности следует сразу
поместить ее в цикл. Мы будем считывать каждый очередной член
последовательности в переменную b, и так как последнее вводимое число по
условию – 0, то предусловием цикла будет b < > 0 (так как при b
= 0 цикл должен прекратиться):
На месте троеточия будет располагаться код проверки каждой пары,
полностью охватываю- щий определение нашего
свойства. Примечание: в
«шаблоне» основного цикла мы выделили
также оператор a := b, который обеспечивает движение по каждым
двум соседним элементам последова- тельности. Следует обратить внимание на то,
что мы должны проверять выполнение нашего свой- ства для 1-го и 2-го, 2-го и
3-го, 3-го и 4-го и т. д. элементов последовательности.
Когда мы уже выполнили проверку
для двух элементов, например, для 1-го (который хранится в переменной a) и 2-го (который
хранится в переменной b), то далее мы присваиваем переменной a значение
переменной b (в которой у нас хранился 2-ой элемент), затем считываем в b
3-й элемент, чтобы проверить свойство для 2-го и 3-го элементов и т. п.
При этом нужно четко понимать, что мы не можем считывать в цикле сразу
две переменные, так как при таком подходе проверка будет выполняться лишь для
1-го и 2-го, 3-го и 4-го и т. д. элементов, что неверно.
Разберем саму проверку. Так как на каждом
шаге цикла программе
требуется выяснить, начи- нается ли следующий член последовательности с десятичной цифры данного, то, имея данный
член в переменной a и следующий член в b,
мы должны сравнить
последнюю цифру a (обозначим ее как
last) с первой цифрой b (обозначим ее как first). Сделать
это можно так:
Здесь мы сначала
добыли последнюю цифру a (строка 1), затем скопировали в last значение b (переменную b нельзя изменять, так как ее значение
понадобится нам на следующем шаге цикла) и во вложенном цикле разделили last
на 10 столько
раз, чтобы в ней осталась
лишь одна цифра,
кото- рая является его первой цифрой.
Добыв нужные цифры, мы можем выполнить их сравнение и выйти из цикла в
том случае, когда они не равны, так как при этом нарушается наше характеристическое свойство, данное в усло- вии, и после этого дальнейшая
проверка бессмысленна:
if last
<> first then break;
Когда цикл завершится, нам останется лишь вывести на экран результат
сравнения перемен- ных last и first: если цикл завершился, то последовательность отвечает
заданному свойству (так как
не было выхода через break), они будут равны и будет выведен ответ true;
если же был совершен выход через break, то переменные неравны и ответ,
соответственно, false.
Теперь попробуем оптимизировать программу для обработки вырожденных
случаев для пу- стой последовательности (когда вводится единственный 0) и для
последовательности из одного члена (когда вводится некоторое число и 0): мы
договорились выводить для них ответ false.
Очевидно, в данный момент наша программа обрабатывает корректно
минимальный случай из двух членов: тогда проходит одно повторение тела цикла, в
котором переменные last и first по- лучают значения, затем может произойти выход
по break или
завершение цикла по вводу нуля, как
и должно быть.
Однако если мы введем последовательность из одного члена,
то при вводе a и b в
переменную a пойдет этот член, а в b окажется
ограничивающий ноль, что приведет к невыполнению входа в основной цикл и
программа перейдет к оператору вывода writeln(last = first), что
неверно, так как значение переменных last и first в данный момент
будет не определено и выражение в операторе вывода может дать любой результат.
Это значит, что для избегания подобного исхода нам нужно выполнить
инициализацию переменных last и first заведомо неравными
значениями, чтобы полу- чить гарантированный ответ false при вводе
последовательности из одного члена. Это можно сде- лать так:
Но что будет,
если ввести последовательность, состоящую из одного нуля? В нашей про- грамме это невозможно, так как оператор
ввода в начале содержит две переменные, и если мы сразу
введем 0, то программа «зависнет» в ожидании ввода второго числа. Чтобы
избежать этого, мы должны вводить одно число в переменную a, и если оно
не равно 0, нужно ввести b. Вместе с этим необходимо заранее присвоить
переменной b число 0, так как она была определена в случае после-
довательности из одного члена, чтобы не осуществился вход в основной цикл:
Эта конструкция заменит оператор read(a, b), который мы описывали в самом начале
решения задачи.
Код:
Задача
№ 44. Проверить, является ли последовательность пилообразной
Формулировка. Дана последовательность из трех и более натуральных
чисел, ограниченная вводом нуля. Проверить, является ли эта последовательность
пилообразной.
Примечание: пилообразной называется последовательность чисел, в которой
каждый член, имеющий соседние члены, меньше или больше их.
Пример такой последовательности: 14 12 18 7 10 2. Покажем, что данная
последовательность соответствует определению: ее 1-й член (14) мы не
рассматриваем, так как он имеет всего один соседний член; 2-й член (12) меньше
соседних: 1-го (14) и 3-го (18); 3-й член (18) больше 12 и 7, 7
меньше 18 и 10, 10 больше 7 и 2, а последний элемент 2 мы также не
рассматриваем. Эту запись можно формализовать, если между каждыми двумя
соседними членами последовательности поста-
вить знак отношения между их величинами («>» или «<»). В связи с этим
приведенный выше при- мер можно проиллюстрировать так: 14 > 12 < 18 >
7 < 10 > 2. При этом характерно направление значков, показывающее, что
каждый элемент либо меньше, либо больше соседних. При этом если мы выпишем сами
знаки сравнения, то получим символьное сочетание > < > < >. А
если выписать эти символы в столбик, становится понятно, почему такая
последовательность названа пилообраз- ной.
Решение. Исследуем свойства
пилообразной последовательности. В определении сказано,
что все ее элементы
(кроме двух крайних)
меньше либо больше
соседних. Конкретизируем это понятие:
любую тройку рядом стоящих элементов
(левый элемент, центральный элемент, правый элемент)
в данной последовательности мы будем называть «зубом».
Например, для указанного выше
примера зубьями будут являться тройки 14 12 18, 12 18 7, 18
7 10 и 7 10 2.
Каждый зуб удовлетворяет условию, данному в определении, следовательно, после-
довательность является пилообразной. Очевидно, что если все зубья в некоторой
последовательно- сти удовлетворяют данному условию, то эта последовательность
является пилообразной.
Найдем некоторые свойства
«правильных зубьев», то есть таких,
которые отвечают заданному определению. Для этого формализуем рассуждения над элементами зуба, обозначив их как L (левый
элемент, от англ. left – левый), M (средний элемент,
от англ. medium
– средний), R (правый элемент, от англ. right – правый).
Известно, что средний
элемент в зубе может быть либо меньше,
либо больше крайних,
в связи с чем для обоих
случаев возникает ряд следующих неравенств:
I
случай (средний элемент меньше крайних):
(1) (2)
M < L Ù M < R Þ M – L < 0 Ù M – R < 0
Здесь знак Ù обозначает
конъюнкцию (логическое «и»), а Þ
обозначает логическое следова- ние (то есть, из выражения, которое стоит левее
знака Þ , следует
выражение, стоящее правее
знака
Þ ).
II
случай (средний элемент больше крайних):
(1) (2)
M > L Ù M > R Þ M – L > 0 Ù M – R > 0
Итак, в обоих случаях мы
составили две разности, которые для удобства обозначили (1) и (2).
В I-ом случае (1) и (2) всегда
строго больше 0, а во II-ом случае – строго меньше 0.
Составим произведение выражений (1) и (2) и обозначим его как (3): (M
– L) * (M – R). В I-ом случае оно всегда положительно как
произведение отрицательных чисел, во II-ом случае – также всегда положительно
как произведение положительных чисел.
Что же следует из этого
выражения? А то, что если результат его вычисления – положительное
число, то тройка элементов L,
M, R образует «правильный зуб». И как мы помним, если все тройки соседних элементов последовательности образуют
«правильные зубья», то она является
пилообраз- ной.
Так как в
условии задачи на вход подается как минимум три элемента, мы можем прочитать их
в одном операторе:
read(L, M, R);
Затем мы входим в цикл с предусловием R < > 0. В этом цикле мы должны
исследовать каждую тройку L,
M, R по свойству (3):
На каждом шаге цикла мы сначала исследуем уже имеющуюся тройку
(оператор 1 в теле цикла), и если выражение (3) оказывается равно или меньше
нуля, то выходим из цикла, так как нашли «неправильный зуб», который нарушает
условие пилообразной последовательности, в силу чего дальнейшая проверка бессмысленна. Затем нам нужно «сдвинуть» последовательность: напри- мер, если в переменных L, M, R у
нас соответственно хранились 4-й, 5-й и 6-й элементы последо- вательности,
которые мы уже проверили, то с помощью оператора L := M мы переносим 5-й
эле- мент в L, а с помощью M := R переносим 6-й элемент в M. Далее мы вводим
7-й элемент в R, после чего в тройке L, M, R
у нас содержатся соответственно 5-й, 6-й и 7-й элементы, проверка которых
на соответствие условию будет произведена на следующем шаге цикла.
На последнем шаге цикла последовательность будет в очередной раз
«сдвинута» и в R будет введено число 0, после чего должен быть выведен результат. В связи с этим возможно
два варианта попадания на
этот этап:
a) в цикле был осуществлен выход через break. А
это значит, что в переменных L, M, и R в данном случае
как раз находится «неправильный зуб» и можно обойтись выводом
значения выражения (L – M) * (R – M) > 0, которое как раз даст
значение false:
writeln((L –
M) * (R – M) > 0);
b) последовательность была проверена до конца, и выход из
цикла был осуществлен по вводу в R нуля. Но здесь нужно учесть, что при этом в тройке
L, M, R теперь находится «несуще- ствующий зуб» (так как 0 не входит в саму
последовательность и не должен учитываться при проверке), который может и не
быть «правильным».
Самый простой
выход в этом случае – если переменная R равна 0, то заменить R на
L. Это приведет к тому, что в выводимом на экран выражении (3) мы
перемножаем не (1) и (2), а
(1)
и (1), что повлечет вывод true,
так как мы получаем произведение одинаковых ненуле- вых чисел, которое всегда положительно. Значит,
перед выводом выражения на экран необ- ходима следующая вставка:
if R = 0 then R := L;
Код:
К слову, данная задача может быть обобщена и на случай, когда длина
вводимой последова- тельности не имеет ограничений снизу, то есть,
последовательность может также быть пустой или содержать один член (для двух
членов она будет работать корректно – это легко проверить). Для этого можно
выполнить контроль ввода в зависимости от значений первых двух вводимых элемен-
тов и провести инициализацию значений для вывода необходимого для вырожденных
случаев от- вета.
Задача
№ 45. Проверить, является ли последовательность строго монотонной
Формулировка. Дана
последовательность натуральных чисел, ограниченная вводом нуля.
Проверить, является ли эта
последовательность строго монотонной.
Решение. Эта задача
– упрощенный вариант
задачи 32. Вообще,
эти две задачи
логично было бы в данном сборнике
поменять местами, однако она оказалась на этой позиции
из-за тематического
распределения задач.
Единственное отличие от задачи 32 состоит в том, что в нашем
случае члены последователь- ности вводятся с клавиатуры с помощью оператора
read() – их не нужно добывать как цифры неко- торого числа.
Воспользуемся
формулой (II) из задачи 32:
p = delta1 * deltai
Напомним,
что если произведение p отрицательно или равно нулю, то
последовательность не строго монотонна, так как нашлись
два delta разных знаков. Мы будем двигаться по последователь-
ности в порядке ввода, слева направо, исследуя при этом знаки всех произведений
p. Так как delta1 присутствует в формуле в качестве константы, его
значение необходимо вычислить заранее:
В цикле мы будем на каждом
шаге считывать один очередной член, поэтому необходимо
«сдвигать последовательность» и считывать его в освободившуюся переменную. Так как в перемен- ной a хранится левый член
каждой пары, а в переменной b – правый член, то очередное число мы будем считывать в переменную b. Так как ограничитель последовательности – ноль, то и цикл будет продолжаться до ввода в b нуля:
Здесь в первом
операторе тела цикла происходит проверка
произведения каждых двух delta по уже упомянутой формуле (II) из задачи 32. Далее идет «сдвиг» правого
члена текущей пары и ввод нового элемента вместо него.
Проще говоря, если,
например, у нас в a находился 1-й член последо- вательности, а в b – 2-й,
то данным способом мы переносим 2-й член в переменную a и считываем 3-й
член в переменную b, после чего можно проводить следующее сравнение.
Если введенный элемент – не ноль, то цикл
продолжается, и исследуется знак произведения delta1 и следующего вычисленного
delta. Если условие монотонности нарушается на каком-либо шаге, то
дальнейшая проверка бессмысленна, и можно переходить к выводу результата.
Каким же будет развитие событий
после выхода из цикла?
1)
Если выход был осуществлен через break, то есть по условию нарушения строгой монотон-
ности, то можно вывести на экран значение выражения delta * (a – b) > 0,
что даст ответ false;
2) Если цикл завершился по вводу нуля, то
последовательность строго монотонна, и нужно, соответственно, выводить ответ true.
Однако здесь мы сталкиваемся с проблемой из за- дачи 45, связанной с
тем, что вводимый ноль не обрабатывается в основном цикле, так как не входит в последовательность,
однако он вводится в обрабатываемую переменную b, чтобы можно
было выйти из цикла. Однако из-за этого с помощью оператора writeln(delta
* (a – b)
> 0) мы можем получить неправильный ответ, так как в последовательность
обра- батывается с вводимым нулем включительно.
Например, последовательность 1 2 3 0 строго монотонна, хотя программа выдаст
ответ false, потому
что по выходе из цикла delta будет содержать число –1, a – число
3, b – число 0, и выражение –1 * (3 – 0) > 0 – неверно.
На этот раз мы справимся с проблемой по-другому. Легко понять, что если
после выхода из цикла b = 0, то последовательность строго монотонна, так как проверка
прошла по всем delta вплоть до ввода ограничителя. Если же
после выхода b отлично от 0, то был совершен выход по break в
теле цикла и последовательность не является строго
монотонной. Поэтому логично
оформить вывод ответа так:
writeln(b = 0);
Кстати, в такой форме можно осуществить вывод и в задачах 32, 43 и 44, с некоторым, однако, изменением инициализации входных
значений переменных.
Напоследок необходимо позаботиться о правильной обработке вырожденных
случаев. Будем считать последовательность из единственного нуля не строго
монотонной, в отличие от последова-
тельности из одного члена. Она, кстати, итак уже будет обрабатываться корректно:
в a вводится некоторое число, а в b вводится 0. При этом не
осуществляется вход в основной цикл, и программа переходит к выводу выражения b
= 0, которое верно.
Сделаем корректной обработку
пустой последовательности. Во-первых, необходимо дать воз- можность ввода таковой, так как в
нашем наброске требуется ввод минимум двух чисел. Для этого мы будем считывать
сначала a, и если оно отлично от нуля, то считывать b:
При этом если a = 0, то мы обязательно присваиваем значение 0 переменной b, чтобы она была определена, и гарантированно не было
входа в цикл. Однако в этом случае вывод выражения b = 0 повлечет вывод true.
Чтобы избежать этого, нужна еще одна проверка: если a = 0, то присвоить b
натуральное число, отличное от 0 (например, 1), что повлечет вывод false:
if a = 0 then
b := 1;
Код:
Стоит отметить, что на первом
шаге в основном цикле значение
a и b еще не изменено, и грубо
говоря, delta в строке 12 умножается само на себя. Это нужно для того,
чтобы обеспечить правиль- ную
обработку последовательности из двух одинаковых чисел, которая не является
строго моно- тонной. Например, если на вход подается последовательность k k 0,
k – некоторое натуральное число, то delta будет равно 0 (строка
10), и при входе в цикл будет осуществлен выход по break (строка 12),
что повлечет вывод false, так как b отлично от 0.
Если бы мы в цикле
сначала осуществили сдвиг
последовательности и ввод третьего члена
(то есть, переместили бы строки 13-14 на одну позицию вверх,
а строку 12 поместили бы после них), то
по выходе из цикла через break b уже было бы равно 0, что повлекло бы
вывод true, а это неверно.
Задача
№ 46. Вывести на экран n-ное число Фибоначчи
Формулировка. Дано
натуральное n (которое также может быть равно 0). Вывести на экран
n-ное число Фибоначчи.
Примечание: последовательность чисел Фибоначчи задается следующей
рекуррентной фор- мулой:
ì0,
если n = 0
ï
Fn = í1, если n = 1
ïFn–1 + Fn–2 , если n ³ 2
То есть, нулевой член последовательности – это число
0, 1-й член – число 1, а любой другой член, начиная со 2-го, является суммой
двух предыдущих. Например, F2 = F1 + F0 = 1 + 0 = 1, F3 = F2 + F1 = 1 + 1 = 2 и т. д.
Решение. Найдем
несколько первых чисел Фибоначчи:
F2 = F1 + F0 = 1 + 0 = 1; F3 = F2 + F1 = 1 + 1 = 2; F4 = F3 + F2 = 2 + 1 = 3; F5 = F4 + F3 = 3 + 2 = 5;
Легко заметить, что при их последовательном вычислении нам не нужно
«расписывать» сла- гаемые по определению, и чтобы получить
очередной член последовательности, достаточно на каж- дом шаге складывать два предыдущих
полученных результата.
Так как нулевой
и первый члены последовательности не вычисляются и даются как часть опре- деления, будем полагать их заранее
известными. Обозначим их идентификаторами fib0 и fib1. По примеру
нахождения первых членов последовательности посчитаем количество операций,
необхо- димое для вычисления каждого члена (считая, что предыдущие члены
неизвестны). Легко увидеть, что для вычисления 2-го члена (при известном 1-ом и
нулевом членах) необходима одна операция сложения, 3-го – две операции сложения
и т. д. Видно, что по этим же правилам для вычисления n– ного члена необходимо выполнить (n – 1) операций.
Теперь можно начать писать программу. Сначала нам необходимо ввести значение n и выпол- нить инициализацию значений нулевого
и первого чисел Фибоначчи, так как мы считаем их заранее
известными:
Далее нам необходимо организовать цикл, в котором на каждом шаге
переменные fib0 и fib1 будут получать следующие значения в
последовательности чисел Фибоначчи. То есть, например, если в fib0 и fib1
будут находиться значения, соответственно, (n – 2)-го и (n – 1)-го
членов после- довательности Фибоначчи, то после одного шага цикла они будут
содержать значения (n – 1)-го и n-го членов. Для этого можно
создать некую вспомогательную переменную fib, в которую поме- стить
результат сложения fib0 и fib1, после чего в fib0 у нас
будет значение (n – 2)-го члена, в fib1
– (n – 1)-го, а в fib – n-го. Теперь нужно только
скопировать значение fib1 в fib0 и fib в fib1,
после чего значение переменной fib на этом шаге уже не имеет значения. С
учетом того, что мы уже по- считали необходимое количество повторений для
получения необходимого результата, цикл будет выглядеть так:
Такой метод решения общей задачи, основанный на использовании в ней решений
задач с меньшей размерностью исходных
данных (в данном
случае под размерностью понимается величина n),
называется динамическим программированием.
Если говорить конкретнее, то мы применили метод восходящего динамического программиро- вания, основывающийся на решении задач сначала минимальной размерности с постепенным полу- чением решений более
обширных задач. Этот метод наиболее
оптимален в плане реализации, быст- родействия и используемой памяти.
Однако далеко не для всех задач, решаемых с помощью динамического
программирования, можно выяснить, решения
каких подзадач потребуются для решения данной.
Для этого существует метод нисходящего
динамического программирования, с которым мы познакомимся позже.
Другой пример нисходящего динамического программирования – вычисление факториала (за- дача 28). Чтобы вычислить n!, необходим
вычисленный (n – 1)! и т. д.
Итак, вернемся к текущей задаче. Ранее было сказано,
что по исчерпании n – 1 шагов цикла в переменной fib1, которая
пойдет на вывод в программе, будет храниться значение Fn. Проверим
корректность обработки граничных значений (в частности, когда n = 0, 1, 2):
1)
При n = 0 границы цикла
будут в отрезке [1, 0 – 1]. При этом значение правой границы зависит от типа переменной i, так как компилятор, дабы избежать ошибок,
при вычислении
«расширяет» тип
выражений, означающих границы цикла.
Если i будет объявлено типа byte, то выражение 0 – 1 даст
в результате 255 (так как все числовые типы в языке Pascal большинство компиляторов считает кольцевыми), что вызо-
вет длинную цепочку вычислений, а это неверно.
Конечно, можно объявить
i типа integer,
и тогда
границы цикла будут
в отрезке [1, –1] и вход не будет осуществлен, но мы поступим иначе, стараясь сохранить память
для переменных.
Так как при вычислении важно лишь количество повторений, мы можем
сдвинуть отрезок [1, n –
1] на одну позицию правее на числовой прямой, и тогда цикл будет проходить от 2
до n, что поможет отсеять вход в цикл при вводе 0 в качестве n,
так как невозможен цикл по всем i от 2 до 0.
Однако тогда
мы столкнемся с другой проблемой: при вводе 0 будет выведено значение fib1, которой
было присвоено число
1 при инициализации. Справиться с проблемой можно, присвоив fib1 значение 0,
если n = 0:
if n = 0 then fib1 := 0;
2)
При n = 1 (с учетом
принятых в предыдущем пункте изменений) входа в цикл не будет, и на экран
выведется неизменное значение fib1, равное 1;
3)
При n = 2 произойдет
вход в цикл, где i будет изменяться от 2 до 2 (то есть, в этом случае
будет выполнен единственный шаг), в котором будет вычислено значение fib =
fib1 + fib0
= 1 + 0 = 1,
которое будет скопировано в fib1 и выведено на экран. Нетрудно понять,
что дальнейшая подстановка значений не требуется, так как корректность
циклической кон- струкции мы уже доказали.
Верхние значения мы не проверяем, так как не существует наибольшего
номера в последова- тельности чисел Фибоначчи (хотя понятно, что корректность
вычислений ограничена «вместимо- стью» типа integer, и при его
превышении в вычислениях числа уже будут неправильными).
Код:
Задача № 47. Вывести на экран сумму чисел Фибоначчи до
n-ного включительно
Формулировка. Дано натуральное n (которое также может
быть равно 0). Вывести на экран сумму чисел Фибоначчи до n-ного
включительно. Например, при n = 3 нам необходимо получить сумму 0-го,
1-го, 2-го и 3-го членов последовательности.
Решение. Задача основана на предыдущей, так как здесь нам тоже
необходимо найти каждое число Фибоначчи до n включительно, однако теперь
мы должны прибавлять найденные числа к некоторой переменной суммы (sum),
которая потом будет выведена на экран.
Используем код предыдущей
задачи:
Чтобы переделать
этот код по текущему назначению, мы должны добавить в цикл прибавле- ние
найденного числа Фибоначчи к переменной sum. Например, так:
Кроме того, следует исправить вывод ответа, так как нам необходимо
вывести не последнее найденное число Фибоначчи, а сумму найденных чисел:
writeln(sum);
Очевидно, что вход в цикл не происходит при n = 0 и
n = 1. Следовательно, правильную обра- ботку этих случаев мы должны обеспечить инициализацией
значений переменной sum, как мы это делали в предыдущей задаче.
Так как сумма нулевого и 1-го чисел Фибоначчи равна 1, то sum можно
инициализировать значением 1. При входе в цикл первые два числа уже обработаны,
поэтому при вводе n >= 2 накоп-
ление суммы также будет верным. Но очевидно, что в случае n = 0 необходимо
инициализировать переменную sum значением 0. Реализовать эти два
варианта можно так:
if n = 0 then
sum := 0 else sum := 1;
Код:
Задача № 48. Вывести на экран все числа Фибоначчи до
n-ного включительно
Формулировка. Дано натуральное n (которое также может
быть равно 0). Вывести на экран все числа Фибоначчи до n-ного
включительно.
Решение. Задача основана на задаче 46. В данном случае
нам необходимо лишь выводить каждое найденное число Фибоначчи на экран. Мы
можем легко получить решение этой задачи из задачи 46 или задачи 47.
Опишем основные фрагменты программы. Так как нулевой член
последовательности выво- дится при любом возможном n, то его можно
вывести на экран сразу после ввода n (или до, что не имеет значения). Затем, если n отлично от нуля, выводим
на экран 1-ый член (так как вывод
в цикле остальных членов
происходит при n >= 2):
Далее необходимо добавить вывод текущего найденного
члена в цикл:
Так как мы выводим все результаты
в самом цикле, на этом программа заканчивается.
Код:
Задача № 49. Проверить баланс круглых скобок в
символьном выражении
Формулировка. Дана последовательность символов длины n (n >= 1). Проверить баланс круг- лых
скобок в этом выражении. Например, при вводе выражения (())() программа должна
сообщить о правильности расстановки скобок, а при вводе выражения ((()) – о неправильности.
Примечание: сбалансированной скобочной записью называется символьное
выражение, в ко- тором каждой открывающей скобке соответствует закрывающая
скобка правее и наоборот, каждой закрывающей скобке соответствует открывающая
скобка левее.
Так как мы вводим последовательность произвольных символов, в которой
учитываются только круглые скобки,
то между знаками
скобок может находиться любая символьная информация, в силу чего корректная
программа может проверять баланс скобок в арифметических выражениях, тексте и
т. д. Например, выражение (7y + 1)(17 – (x + 3)) – правильное, а
(146x + 18(y + 9) – непра- вильное, что сможет распознать программа.
Решение. Представим себе посимвольный ввод скобочного выражения
с клавиатуры (когда уже введено некоторое количество символов) и подумаем,
какие выводы можно сделать на данном этапе (для простоты восприятия будем
рассматривать выражения, состоящие только из скобок):
1) ((()
Сейчас «как бы» мы видим
начало скобочного выражения и не знаем,
какие символы следуют далее. Какие выводы можно сделать
на этом этапе? Имеющееся выражение содержит лишние от- крывающие скобки
и его можно как сбалансировать, если дописать две закрывающие скобки,
так и нарушить, если оставить в том же виде или применить множество
других комбинаций. Вывод: если имеются лишние открывающие скобки, то выражение еще может
быть сбалансировано.
2) (()))
Это выражение содержит явное нарушение баланса скобок, которое уже не
может быть ском- пенсировано добавлением любых скобочных комбинаций справа, так
как не всем закрывающим скобкам соответствует по одной открывающей скобке
левее. Отсюда вывод: если в выражении
по- явилась хотя бы одна лишняя закрывающая скобка, то выражение
«неправильное» и дальнейшая проверка бессмысленна.
Приступим к реализации этих рассуждений. Заведем счетчик count для
подсчета открываю- щих и закрывающих скобок: при вводе открывающей скобки будем
увеличивать его на 1, а при вводе закрывающей – уменьшать на 1.
Нам нужно создать переменную c символьного
типа char, в которую мы будем последова- тельно вводить все символы
нашего выражения. Стоит отметить, что в тип char также входит про- бел,
что влияет на значение длины вводимой последовательности. Например, длина n вводимого
выражения (7y + 1)(17 – (x + 3)) равна 22 (пробелы выделены
красным цветом).
После ввода n мы входим в цикл из n повторений, в котором вводим
в c очередной символ. Полагаясь на предыдущие рассуждения, мы
увеличиваем count на 1, если c = ‘(‘ и уменьшаем на 1, если c
= ‘)’:
Примечание: функция dec(x) уменьшает
значение переменной x числового типа на 1.
Кстати, так как любой любая переменная не может иметь сразу два
каких-либо значения, мы можем поместить второй условной оператор цикла в else-блок
первого, что будет выглядеть логич-
нее, но мы не будем этого делать, чтобы повысить читаемость кода.
Отметим, что ввод n осуществляется с помощью readln(),
так как он требует ввод enter’а в качестве ограничителя. При вводе n через read() далее следующий
пробел или enter
будет включен
непосредственно во вводимую последовательность, что повлечет ошибку. Кроме
того, нельзя раз- делять лишними пробелами или enter’ами символы
последовательности при вводе, так как они не
игнорируются при вводе в
переменные типа char и должны быть включены в последовательность (при
этом каждый пробел добавляет к длине 1, а каждый enter – 2).
Вернемся к разбору.
Как же быть, если некоторый
начальный фрагмент вводимого выражения станет заведомо неправильным, то есть, если в нем появятся лишние закрывающие скобки?
Но тогда при появлении
лишней («некомпенсируемой») закрывающей скобки переменная count
станет равна
–1, что можно оформить как
условие выхода из цикла и поместить после первых двух операторов сравнения:
if count = -1
then break;
Какие результаты мы получим по
завершении цикла?
1)
Цикл прошел по всем символам, но
были найдены лишние открывающие скобки (то есть, count > 0), компенсирования которых мы ожидали,
однако они так и не были скомпенсиро- ваны и скобочная
последовательность неправильная;
2)
Цикл прошел по всем символам (то есть, не было выхода),
причем количество скобок
обоих видов равно (то есть, count
= 0) и скобочная последовательность, соответственно, правиль-
ная;
3)
Был осуществлен выход из цикла (то
есть, нашли «некомпенсируемую» закрывающую скобку и count = –1) и
последовательность неправильная.
Выходит, правильный ответ даст вывод выражения count = 0 (оно
истинно во 2-ом случае и ложно в 1-ом и 3-ем):
writeln(count
= 0);
Код:
Задача № 50. Вычислить экспоненту с заданной точностью
Формулировка.
Дано действительное число x. Вычислить значение экспоненциальной
функ- ции (то есть, показательной функции ex, где e – математическая
константа, e » 2,
718281828459045
) в точке x с заданной
точностью eps с помощью ряда Тейлора:
2 3 ¥ n
ex = 1+ x + x + x +L = å x
Примечание 1: показательными называются функции вида ax, где a –
некоторое действитель- ное число, x – независимая переменная, являющаяся
показателем степени.
Примечание 2: ряд Тейлора – это представление функции в виде суммы (возможно, бесконеч- ной) некоторых других функций по особым правилам
(требующим детального математического обоснования, что в данном случае нам не нужно).
Решение. Не вникая в теоретическую часть и полагая
представленную формулу корректной, попробуем разобраться в том, что же нам необходимо
сделать для того, чтобы решить эту задачу:
1) Нам дана некоторая точка на оси Ox,
и мы должны вычислить значение функции ex в этой точке. Допустим, если x
= 4, то значение функции в этой точке будет равно e4 » 2, 718284 » 54, 598
;
2)
При этом вычисление необходимо реализовать с помощью
заданной бесконечной формулы, в которой прибавление каждого
очередного слагаемого увеличивает точность
результата;
3)
Точность должна составить
вещественное число eps, меньшее 1 – это означает, что когда очередное
прибавляемое к сумме слагаемое будет меньше eps, то необходимо завершить
вычисление и выдать результат на экран. Это условие обязательно выполнится, так как ма-
тематически доказано, что каждое следующее слагаемое в ряде Тейлора меньше
предыду- щего, следовательно, бесконечная последовательность слагаемых – это
бесконечно убыва- ющая последовательность.
Теперь разберемся с вычислением самого ряда. Очевидно, что любое его
слагаемое, начиная со 2-го, можно
получить из предыдущего, умножив его на x и разделив на натуральное число,
явля- ющееся номером текущего шага при последовательном вычислении
(примем во внимание то, что тогда шаги нужно нумеровать с нуля). Значение x нам
известно на любом шаге, а вот номер теку- щего шага (будем хранить его в
переменной n) придется фиксировать.
Создадим вещественную переменную expf (от англ. exponential
function – экспоненциальная функция) для накопления суммы слагаемых. Будем
считать нулевой шаг уже выполненным, так как первое
слагаемое в ряду – константа 1, и в связи с этим expf можно заранее проинициализировать
числом 1:
expf := 1;
Так как мы начинаем вычисления не с нулевого, а с первого шага, то также нужно
инициали- зировать значения n (числом 1, так как следующий шаг будет
первым) и p (в ней будет храниться значение последнего вычисленного
слагаемого):
Теперь можно приступить к разработке цикла. С учетом заданной точности eps
условием его продолжения будет abs(p) >= eps, где abs(p) –
модуль числа p (модуль нужен для того, чтобы не возникло ошибки, если
введено отрицательное x).
В цикле необходимо домножить p на x и доделить его на текущий
номер шага n, чтобы обес- печить реализацию факториала в знаменателе, после
чего прибавить новое слагаемое p к результату expf и увеличить n для
следующего шага:
После выхода из цикла нужно осуществить форматированный вывод результата expf
на экран с некоторым количеством цифр после точки, например,
пятью. Отметим, что если при этом введен- ное eps содержало меньше 5
цифр после точки, то сформированное значение expf будет, соответ-
ственно, неточным.
Код:
Содержание
Предисловие от автора…………………………………………………………………………………………………………….. 1
Глава 1. Линейные алгоритмы………………………………………………………………………………………………… 2
Задача № 1. Вывести на экран
сообщение «Hello World!»………………………………………………………… 2
Задача № 2. Вывести на экран три числа в порядке, обратном
вводу………………………………………… 2
Задача № 3. Вывести на экран квадрат введенного числа…………………………………………………………. 3
Задача № 4. Получить реверсную запись трехзначного числа………………………………………………….. 4
Задача № 5. Посчитать количество единичных битов числа…………………………………………………….. 5
Глава 2. Условные операторы…………………………………………………………………………………………………. 7
Задача № 6. Вывести на экран
наибольшее из двух чисел………………………………………………………… 7
Задача № 7. Вывести на экран наибольшее из трех чисел………………………………………………………… 8
Задача № 8. Вывести название дня недели по его номеру………………………………………………………… 9
Задача № 9. Проверить, является ли четырехзначное число палиндромом……………………………… 10
Задача № 10. Проверить, является ли четырехзначное число счастливым билетом…………………. 11
Задача № 11. Проверить, является ли двоичное
представление числа палиндромом……………….. 12
Задача № 12. Решить квадратное уравнение………………………………………………………………………….. 14
Глава 3. Циклы………………………………………………………………………………………………………………………. 16
Задача № 13. Вывести на экран все
натуральные числа до заданного……………………………………… 16
Задача № 14. Найти наибольший нетривиальный делитель натурального числа……………………… 17
Задача № 15. Найти наименьший нетривиальный делитель натурального числа…………………….. 18
Задача № 16. Подсчитать общее число делителей натурального числа…………………………………… 18
Задача № 17. Проверить, является ли заданное натуральное число
простым…………………………… 19
Задача № 18. Вывести на экран все простые числа до заданного……………………………………………. 20
Задача № 19. Вывести на экран первых n простых
чисел……………………………………………………….. 21
Задача № 20. Проверить, является ли заданное натуральное число совершенным…………………… 24
Задача № 21. Проверить, являются ли два натуральных числа дружественными……………………. 25
Задача № 22. Найти наибольший общий делитель двух натуральных чисел……………………………. 26
Задача № 23. Найти наименьшее
общее кратное двух натуральных чисел………………………………. 27
Задача № 24. Вычислить xn……………………………………………………………………………………………………. 28
Задача № 25. Вычислить xn по алгоритму быстрого возведения в степень………………………………. 29
Задача № 26. Решить квадратное уравнение заданного вида с параметром…………………………….. 31
Задача № 27. Вычислить значение
многочлена в точке………………………………………………………….. 31
Задача № 28. Вычислить факториал………………………………………………………………………………………. 33
Задача № 29. Вычислить число сочетаний из n по k……………………………………………………………….. 33
Задача № 30. Вывести таблицу
квадратов и кубов всех натуральных чисел до n…………………….. 34
Задача № 31. Сформировать
реверсную запись заданного числа……………………………………………. 36
Задача № 32. Проверить
монотонность последовательности цифр числа………………………………… 37
Задача № 33. Получить
каноническое разложение числа на простые сомножители………………… 39
Задача № 34. Сформировать число
из двух заданных чередованием разрядов………………………… 41
Задача № 35. Вывести на экран x,
записанное в системе счисления с основанием n………………… 42
Задача № 36. Найти наименьший
нетривиальный делитель двух заданных чисел…………………… 43
Задача № 37. Проверить, является
ли натуральное число счастливым билетом………………………. 44
Задача № 38. Проверить, является
ли натуральное число палиндромом………………………………….. 46
Задача № 39. Проверить, является
ли натуральное число степенью двойки…………………………….. 47
Задача № 40. Вывести на экран
произведение четных элементов последовательности……………. 49
Задача № 41. Вывести на экран
произведение двузначных элементов последовательности, которые
делятся на заданное число……………………………………………………………………………………….. 51
Задача № 42. Найти количество
простых членов последовательности……………………………………. 51
Задача № 43. Проверить,
начинается ли каждый из членов последовательности с цифры, на которую оканчивается предыдущий………………………………………………………………………………………. 52
Задача № 44. Проверить, является
ли последовательность пилообразной……………………………….. 55
Задача № 45. Проверить, является
ли последовательность строго монотонной……………………….. 57
Задача № 46. Вывести на экран
n-ное число Фибоначчи………………………………………………………… 59
Задача № 47. Вывести на экран
сумму чисел Фибоначчи до n-ного включительно…………………. 61
Задача № 48. Вывести на экран все
числа Фибоначчи до n-ного включительно………………………. 63
Задача № 49. Проверить баланс
круглых скобок в символьном выражении……………………………. 63
Задача № 50. Вычислить экспоненту
с заданной точностью…………………………………………………… 65
Задача 1.
Вычислить: y = sin1 + sin1.1 + sin1.2 + … + sin2.
Первый вариант решения данной задачи.
Анализируя данную формулу, видим, что аргумент функции sin очередного слагаемого отличается от предыдущего на 0.1. Поэтому для решения данной задачи можно составить следующий алгоритм:
Переменные:
с – очередное слагаемое;
i – аргумент функции;
y – сумма.
- Обнуляем начальное значение переменной y (строка 5), в которой будем накапливать сумму.
- Начальное значение аргумента функции i равно 1 (строка 6).
- Проверяем, значение i меньше или равно 2, т.к. по заданию аргумент функции изменяется от 1 до 2 (строка 7)?
- Если «да», то определяем очередное значение функции (строка 9). Сохраняем его в переменной с. Если «нет», то расчет суммы закончен – переходим на шаг 78.
- Добавляем это слагаемое в сумму (строка 10).
- Увеличиваем значение аргумента i на 0.1 (строка 11).
- Переходим на шаг 3.
- Выводим результат на экран (строка 13).
|
var y, c, i : real; begin writeln(‘Полученное значение расчета формулы ‘, ‘y=sin1+sin1.1+sin1.2+ … +sin2 = ‘); y:=0; i:=1; while i <=2 do Begin c := sin(i); y:=y+c; i:=i+0.1; end; writeln(y); end. |
Второй вариант решения данной задачи.
Анализируя данную формулу, видим, что каждое слагаемое данной суммы можно рассчитать по формуле sin(1 + 0.1 * i), где i изменяется от 0 до 10. Поэтому для решения данной задачи можно составить следующий алгоритм.
Переменные:
i – параметр цикла;
y – сумма.
- Обнуляем начальное значение переменной y (строка 6), в которой будем накапливать сумму.
- Организуем цикл для определения суммы (параметр дан-ного цикла должен измениться от 0 до 10) .
- В данном цикле определяем очередное слагаемое по фор-муле и добавляем это слагаемое в сумму (строка 7).
- Выводим результат на экран (строка 8).
|
var y : real; i : integer; Begin writeln(‘Полученное значение расчета формулы ‘, ‘y=sin1+sin1.1+sin1.2+ … +sin2 = ‘); y:=0; for i:=0 to 10 do y:=y+sin(1+0.1*i); writeln(y); end. |
Задача 2.
Вычислить: y = 1*3*5* … *(2n–1), n>0;
|
var y : real; i, n : integer; begin writeln(‘Введите количество чисел’); readln(n); y:=1; for i:=1 to n do y:=y*(2*i–1); writeln(‘Полученное значение y= ‘, y) end. |
Задача 3.
Дано натуральное число N. Разложить его на простые множители.
Переменные:
n – исследуемое число;
i, j – переменные циклов;
f – вспомогательный флаг.
Алгоритм решения задачи:
- Вводим значение переменной n. Т.к. пользователь может случайно ввести отрицательное число, то необходимо дать ему возможность для повторного ввода значения переменной n. По-этому организуем цикл (строки 3–6 текста программы). Лучше использовать цикл с пост проверкой условия (Repeat…Until). Тело цикла составляют два оператора: вывода на экран приглашения для ввода значения переменной n (строка 4) и оператор чтения с клавиатуры – для непосредственного ввода значения переменной n (строка 5). Данный цикл будет выполняться до тех пор, пока пользователь не введет любое положительное число (срока 6).
- Выводим на экран значение переменной n и начинаем формировать ответ. Ответ будет представлен в следующем виде (например, в качестве значения переменной n ввели 8): 8 = 1*2*2*2. Т.к. единица является простым множителем для любого числа, то выводим ее на экран (строка 7). В результате выполнения данной строки на экране появится: 8=1.
- Вспомогательной переменной f присваиваем значение false. Данная переменная нам будет необходима для определения, а были ли вообще найдены простые множители у заданного числа n. Запоминаем исходное значение переменной n в переменной j (строка 8).
- В цикле по переменной i начинаем порождение натуральных чисел, не превосходящих середины заданного числа n, для определения делителей данного числа n (строка 9). Данный цикл начали с 2, т.к. единицу мы уже учли (шаг 2 данного алгоритма). Т.к. в цикле For можно использовать только целые переменные, то воспользовались оператором целочисленного деления на 2 (n div 2). В данном цикле выполняем следующее. Определяем, является ли очередное i делителем числа n (в качестве n в данном цикле используем j). Для этого определяем остаток от деления j на i. Если остаток равен 0 (строка 10), т.е. число i является делителем j, то определяем, сколько таких делителей, уменьшая число n (строки 11–18). Переменной f присваиваем значение true (строка 12) – это означает, что у заданного числа n есть делители. Организуем цикл, пока остаток от деления j на i равен 0 (строка 13). В данном цикле выводим делитель на экран (строка 15) и уменьшаем заданное число, деля его целочисленно на делитель (строка 16). Повторяем цикл. После завершения этого цикла возвращаемся на цикл For (строка 9), изменяем i и повторяем те же действия для нового делителя.
- Если у числа нет делителей (оно является простым), то данное число можно разложить только на 1 и само себя. Вспомогательная переменная f и определяет, были ли делители у числа n. Если значение переменной f осталось false, то делителей не было, поэтому выводим само это число (строка 19).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
var i, n, j : integer; f: boolean; begin repeat write(‘Введите натуральное число N= ‘); readln(n); until n>0; write (N:6, ‘=1’); f:=false; j:=n; for i:=2 to n div 2 do if j mod i = 0 then begin f:=true; {цикл определят, сколько таких множителей i в нашем числе n} while j mod i=0 do begin write(‘*’, i); j:=j div i; end; end; {f определяет, были ли найдены простые множители, которые больше единицы} if not f then writeln(‘*’, n); writeln end. |
Задача 4.
Даны натуральное число n и последовательность a1, a2,…,an вещественных чисел. Найдите знакочередующую сумму S = a1 –a2 + a3 –…+ (–1)n+1 an.
Переменные:
n – количество чисел;
a – очередное число;
p – булевский признак знака слагаемого;
i – переменная цикла;
S – знакочередующая сумма чисел.
Алгоритм решения задачи:
- вводим длину последовательности n и устанавливаем начальное значение S;
- булевская переменная p первоначально истинна, она будет указывать на знак слагаемого в сумме;
- последовательно считываем числа, и если p = true, то прибавляем очередное число к сумме S, иначе – отнимаем;
- на каждом шаге цикла значение p меняем на противоположное;
- выводим результат.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
var n, i : integer; a, S : real; p: boolean; begin repeat write(‘Введите длину последовательности n=’); readln(n); until n>0; p:= true; S:=0; for i:=1 to n do begin write(‘Введите a=’); readln(a); if p then S:=S+a else S:=S–a; p:= not p end; writeln(‘Знакочередующая сумма чисел S= ‘, S); end. |
Задача 5.
Найти сумму первых n членов ряда y = 1 + x/2 + x2/3 + +x3/4+…, при |x|<1.
Переменные:
n – количество членов ряда;
x – переменная ряда;
z – вспомогательная переменная;
i – переменная цикла;
y – сумма ряда.
Алгоритм решения задачи:
- вводим количество членов ряда n и переменную X;
- в цикле порождаем очередной член ряда и прибавляем его к сумме y;
- выводим результат.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
var x, y, z : real; n, i : integer; begin repeat writeln(‘Введите переменную ряда x, |x|<1, x=’); readln(x); write(‘Введите число членов ряда n=’); readln(n); until (abs(x)<1) and (n>0); y:=1; z:=1; for i:=2 to n do begin z:=z*x; y:=y+z/i; end; writeln(‘Сумма первых n членов ряда y =’, y); end. |
Задача 6.
Вводится последовательность из N целых чисел. Найти сумму всех отрицательных чисел.
Переменные:
n – количество чисел;
x – очередное число;
i – переменная цикла;
sum – сумма отрицательных чисел.
Алгоритм решения задачи:
- вводим длину последовательности n и устанавливаем на-чальное значение sum;
- последовательно считываем числа и, если число отрица-тельное, то прибавляем его к сумме sum;
- в зависимости от значения sum выводим результат.
|
var n, x, sum, i : integer; begin repeat write(‘Введите длину последовательности n=’); readln(n); until n>0; sum:=0; for i:=1 to n do begin write(‘Введите x=’); readln(x); if x<0 then sum:=sum+x; end; if sum=0 then writeln(‘Отрицательных чисел нет’) else writeln(‘Сумма отрицательных чисел sum= ‘, sum); end. |
Задача 7.
Вводится последовательность из N целых чисел. Найти наибольшее число.
Переменные:
n – количество чисел;
x – очередное число;
i – переменная цикла;
max – наибольшее число.
Алгоритм решения задачи:
- вводим длину последовательности n и устанавливаем на-чальное значение max по первому числу;
- последовательно считываем числа и, если очередное чис-ло x больше max, то переприсваиваем значение max := x;
- выводим результат.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
var n, x, max, i : integer; begin repeat write(‘Введите длину последовательности n=’); readln(n); until n>0; write(‘Введите x=’); readln(x); max:=x; for i:=2 to n do begin write(‘Введите x=’); readln(x); if (x>max) then max:=x; end; writeln(‘Наибольшее из чисел max=’, max); end. |
Задача 8.
Вводится последовательность целых чисел, 0 – конец по-следовательности. Найти два наименьших числа.
Переменные:
x – очередное число;
min1 – первое наименьшее число;
min2 – второе наименьшее число (min2>=min1).
Алгоритм решения задачи:
- устанавливаем начальные значения min1 и min2 по двум первым числам;
- последовательно считываем числа и, если очередное чис-ло x меньше или равно min1 (min1<min2), то переприсваиваем значение min1 и min2;
- если x попадает в интервал от min1 до min2, то перепри-сваиваем только min2;
- выводим результат.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
var x,min1,min2:integer; begin write(‘Введите x=’); readln(x); min1:=x; write(‘Введите x=’); readln(x); min2:=x ; {min1<=min2} repeat if x<=min1 then begin min2:=min1; min1:=x; end else if (min1<x) and (x<min2) then min2:=x; write(‘Введите x=’); readln(x); until (x=0); writeln( ‘Два наименьших числа равны’, min1, ‘и’, min2); end. |
Задача 9.
Вводится последовательность ненулевых чисел, 0 – конец последовательности. Определить, является ли последователь-ность возрастающей.
Переменные:
old – предыдущее число;
new – рассматриваемое число;
f – флаг.
Решение данной задачи строится от противного. Математи-чески для того, чтобы последовательность была возрастающей, для каждого очередного элемента new и предыдущего old должно выполняться условие new > old. Любое нарушение данного усло-вия приводит к тому, что последовательность не может быть возрастающей.
Алгоритм решения задачи:
- вводим два первых числа как old и new, задаем начальное значение флага f;
- в цикле ищем нарушение свойства членов возрастающей последовательности;
- пере присваиваем значение old:=new и вводим новое – new;
- в зависимости от флага выводим результат.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
var old, new : real; f : boolean; begin write(‘Введите x=’); readln(old); write(‘Введите x=’); readln(new); f:=true; repeat if new<=old then f:=false; old:=new; write(‘Введите x=’); readln(new); until new=0; if f then writeln( ‘Последовательность возрастающая’) else writeln( ‘Последовательность не является возрастающей’); end. |
Задача 10.
Даны натуральное n и последовательность веществен-ных чисел a1, a2,…, an. Сколько отрицательных чисел в начале по-следовательности (до первого неотрицательного)?
Переменные:
k – счетчик;
i – переменная цикла;
n – количество членов последовательности;
a – очередной член последовательности;
p – признак отрицательного числа в начале последователь-ности.
Алгоритм решения задачи:
- вводим длину последовательности, задаем начальное значение счетчика k;
- устанавливаем признак отрицательного цисла p=true;
- в цикле вводим очередной член последовательности;
- если это отрицательное число и до этого неотрицательных чисел не было, то увеличиваем значение счетчика на единицу;
- в противном случае, если член последовательности неот-рицателен, то полагаем p=false;
- в зависимости от k выводим результат.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
var a: real; p: boolean; k,n : integer; begin repeat write(‘Введите длину последовательности n=’); readln(n); until n>0; k:=0; p:=true; for i:=1 to n do begin writeln(‘Введите число’); readln(a); if (a<0) and p then k:=k+1else if a>=0 then p :=false end; if k=0 then writeln(‘отрицательных чисел в начале нет’) else writeln(‘последовательность начинается с ‘, k, ‘ чисел’) end. |
Задача 11.
Дан прямоугольный бильярдный стол со сторонами А и В, где А, В – натуральные числа (бильярд Льюиса Кэролла). Из угловой лузы вылетает шар под углом 45 градусов к боковым стенкам, ударяется о борт, отскакивает, ударяется еще раз и т.д., пока не вылетит через одну из угловых луз. Рассчитать ко-личество отрезков в ломаной траектории шара. Считать угол падения равным углу отражения.
Данная задача решается с помощью стандартных функций выделения целой части от деления y на x (y div x) и выделения остатка y mod x. При прохождении шаром прямоугольного стола и отражении его от боковых сторон происходит увеличение числа отрезков траектории на два, а обратный путь вычисляется как y:=a–x+y mod x, где y – обратный путь для шара, a – длинная сторона стола, x – короткая сторона стола.
Переменные:
в функции bill:
x, y – два натуральных числа (формальные параметры);
k – вспомогательная переменная (локальная переменная);
a – длинная сторона стола (глобальная переменная);
в основной программе:
a, b – два натуральных числа (глобальные переменные).
Алгоритм решения задачи:
- создаем описание функции bill;
- вводим два натуральных числа a и b (не кратные друг другу);
- вызываем функцию bill для определения количества от-резков;
- завершаем работу программы.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
var a, b : integer; function bill(y,x:integer):integer; var k:integer; begin k:=0; while y mod x <>0 do begin k:=k+y div x+2; y:=a–x+y mod x; end; bill:=k; end; begin repeat writeln(‘Введите два натуральных числа A>B’); readln(a,b); until a>=b; writeln(‘Количество отрезков в траектории: ‘, bill(a,b)); end. |
Задача 12.
Пусть процедура maxmin(x,y) присваивает параметру x большее из вещественных чисел x и y, а параметру y – меньшее. Описать данную процедуру и использовать ее для перераспреде-ления значений вещественных переменных a, b и c так, чтобы стало a > = b > = c.
|
var a,b,c : real; procedure maxmin( var x,y:real); var r:real; begin if x<y then begin r:=x; x:=y; y:=r end end; begin writeln(‘Введите три числа a,b,c –’); readln(a,b,c); maxmin(a,b); maxmin(a,c); {a=max} maxmin(b,c); {c=min} writeln(a,b,c); end. |
Задача 13.
Если среди чисел sin(x n) (где степень n = 1, 2, … ,30) есть хотя бы одно отрицательное число, то логической переменной t присво-ить значение true, а иначе – значение false.
|
var y,x : real; n : integer; t : boolean; begin write(‘Введите значение x –’); readln(x); y:=1; n:=0; repeat n:=n+1; y:=x*y; t:=sin(y)<0 until t or (n=30); writeln(t); end. |
Задача 14.
Определить k – количество трехзначных натуральных чисел, сумма цифр которых равна n ( 1 < n < 27 ). Операции деления ( /, div и mod) не использовать.
|
var d1, d2, d3, k, n : integer; begin writeln(‘Введите число n, с которым будем сравнивать сумму цифр числа’); readln(n); k:=0; {d1 – левая, d2 – средняя, d3 – правая цифры числа} for d1:=1 to 9 do for d2:=0 to 9 do for d3:=0 to 9 do if d1+d2+d3=n then begin k:=k+1; write(d1,d2,d3, ‘ ‘); end; writeln(‘Количество искомых чисел равно –’, k); end. |
Решение задач на языке программирования Pascal
(Подготовка к ОГЭ)
Авторы проекта: Александрова З.В., учитель физики и информатики МБОУ СОШ №5 пгт Печенга, Мурманская область
Задача 1 .
Напишите программу для выведения на экран трёх чисел в порядке обратном вводу. Нужно ввести с клавиатуры три числа (первое, второе и третье), а компьютер должен вывести третье, затем первое и второе.
Решение:
program tri_сhisla;
var a, b, c: integer;
begin
writeln(‘Введите три числа через пробел’);
readln(a, b, c);
writeln(c,’ ‘, a, ‘ ‘,b);
read
end .

Задача 2.
Напишите программу, которая производит обмен значений переменных x и y , если x больше y .
program Obmen;
var x,y: integer;
begin
writeln(‘Введите значения x и y’);
readln(x,y);
if xy then
begin
x:=x+y;
y:=x-y;
x:=x-y;
writeln(‘x=’,x);
writeln(‘y=’,y);
readln
end ;
end .

Задача 3.
Напишите программу для вычисления наибольшего общего делителя двух целых чисел.
1 способ
2 способ
program nod2;
var
m, n: integer;
nod: integer;
begin
writeln (‘Введите первое число m=’);
readln (m);
writeln (‘Введите второе число n=’);
readln (n);
repeat
if mn then m:=m-n;
if mthen n:=n-m
until m=n;
nod:=m;
writeln(‘НОД = ‘, nod);
readln
end .
program nod1;
var
m, n: integer;
nod: integer;
begin
writeln (‘Введите первое число m=’);
readln (m);
writeln (‘Введите второе число n=’);
readln (n);
while mn do
if mn then m:=m-n
else n:=n-m;
nod:=m;
writeln(‘НОД = ‘, nod);
readln
end .

Задача 4.
Напишите программу, в которой осуществляется ввод целых чисел (ввод осуществляется до тех пор, пока не будет введен 0) и подсчет количества введенных положительных и отрицательных чисел.
program podschet_chisel_1;
var n, k1, k2: integer;
begin
k1:=0;
k2:=0;
repeat
writeln (‘Введите целое число’);
readln (n);
if n0 then k1:=k1+1;
if nthen k2:=k2+1;
until n=0;
writeln (‘Введено:’) ;
writeln (‘положительных чисел – ‘, k1);
writeln (‘отрицательных чисел – ‘, k2);
readln
end .
Задача 5.
Даны натуральные числа n и k. Составить программу вычисления выражения 1 k + 2 k + … + n k . Для решения задачи нужно организовать два цикла, один из которых поместим внутрь другого. Такие конструкции называют вложенными циклами.
program dvazikla;
var
n,k,sum,d,i,j : integer;
begin
writeln(‘Введите значения n и k через пробел’);
readln(n,k);
sum:=0;
for i:=1 to n do
begin
d:= 1;
for j:=1 to k do
d:=d*i;
sum:= sum+ d;
end ;
writeln(sum);
readln
end .
Задача 6.
Проверить, является ли четырехзначное число счастливым билетом. Дано четырехзначное число. Проверить, является ли оно «счастливым билетом».
Счастливым билетом называется число, в котором: а) при четном количестве цифр в числе сумма цифр его левой половины равна сумме цифр его правой половины; б) при нечетном количестве цифр – то же самое, но с отбрасыванием серединной цифры.
program Schastliviy_bilet;
var
n: integer ;
left, right: integer ;
begin
writeln( ‘Введите номер билета – четырёхзначное число’ );
readln(n);
right := n mod 10 ;
n := n div 10 ;
right := right + n mod 10 ;
n := n div 10 ;
left := n mod 10 ;
n := n div 10 ;
left := left + n;
writeln(left=right);
if left=right then writeln( ‘Билет является счастливым’ )
else writeln( ‘Билет не является счастливым’ );
readln
end .
Задача 7.
Напишите программу, которая в последовательности натуральных чисел определяет СУММУ чисел. Программа получает на вход количество чисел в последовательности, а затем сами числа. Количество чисел не превышает 1000. Введённые числа не превышают 30 000. Программа должна вывести одно число – СУММУ чисел.
Program Summa_ch;
Var a, i, sum, n: integer ;
Begin
Writeln( ‘Введите количество чисел n
Readln(n);
sum:= 0 ;
For i:= 1 to n do
Begin
Writeln(‘Введите число’);
Readln(a);
sum:= sum + a;
End ;
Writeln( ‘sum=’ , sum);
readln
End .
Задача 8.
Напишите программу, которая в последовательности натуральных чисел определяет СУММУ чисел, КРАТНЫХ 4. В последовательности всегда имеется число, кратное 4. Программа получает на вход количество чисел в последовательности, а затем сами числа. Количество чисел не превышает 1000. Введённые числа не превышают 30 000. Программа должна вывести одно число – СУММУ чисел, кратных 4.
Program Summa_ch1;
Var a, i, sum, n: integer ;
Begin
Writeln( ‘Введите количество чисел n
Readln(n);
sum:= 0 ;
For i:= 1 to n do
Begin
Writeln(‘Введите число’);
Readln(a);
if a mod 4 = 0
then sum:= sum + a;
End ;
Writeln( ‘sum=’ , sum);
readln
End .
Задача 9.
Напишите программу, которая в последовательности натуральных чисел определяет СУММУ чисел, ОКАНЧИВАЮЩИХСЯ на 2. В последовательности всегда имеется число, ОКАНЧИВАЮЩЕЕСЯ на 2. Программа получает на вход количество чисел в последовательности, а затем сами числа. Количество чисел не превышает 1000. Введённые числа не превышают 30 000. Программа должна вывести одно число – СУММУ чисел, ОКАНЧИВАЮЩИХСЯ на 2.
Program Summa_ch2;
Var a, i, sum, n: integer ;
Begin
Writeln( ‘Введите количество чисел n
Readln(n);
sum:= 0 ;
For i:= 1 to n do
Begin
Writeln(‘Введите число’);
Readln(a);
if a mod 10 = 2
then sum:= sum + a;
End ;
Writeln( ‘sum=’ , sum);
Readln
End .
Задача 10.
Напишите программу, которая в последовательности натуральных чисел определяет СУММУ чисел, чётных чисел. В последовательности всегда имеется чётное число. Программа получает на вход количество чисел в последовательности, а затем сами числа. Количество чисел не превышает 1000. Введённые числа не превышают 30 000. Программа должна вывести одно число – СУММУ чётных чисел.
Program Summa_ch3;
Var a, i, sum, n: integer ;
Begin
Writeln( ‘Введите количество чисел n
Readln(n);
sum:= 0 ;
For i:= 1 to n do
Begin
Writeln( ‘Введите число’ );
Readln(a);
if a mod 2 = 0
then sum:= sum + a;
End ;
Writeln( ‘sum=’ , sum);
Readln
End .

Задача 11.
Подсчитайте, сколько среди данных N чисел нулей, положительных чисел, отрицательных чисел.
program chisla;
var
n, a, i, k, l, m: integer ;
begin
k := 0 ;
l := 0 ;
m := 0 ;
writeln ( ‘Введите количество чисел’ );
read(n);
for i := 1 to n do
begin
writeln ( ‘Введите число’ );
read(a);
if (a = 0 ) then
k := k + 1 ;
if (a 0 ) then
l := l + 1 ;
if (a then
m := m + 1 ;
end ;
writeln(k, ‘ ‘ , l, ‘ ‘ , m, ‘ ‘ );
end .

Задача 12.
Дано натуральное число N. Определить наименьшую и наибольшую цифры данного числа
program chislo1;
var
a, b, c: integer ;
begin
writeln ( ‘Введите число’ );
read(a);
b := 10 ;
c := – 10 ;
while a 0 do
begin
if (a mod 10 c) then
c := a mod 10 ;
if (a mod 10 then
b := a mod 10 ;
a := a div 10 ;
end ;
writeln(b, ‘ ‘ , c);
read
end .
Задача 13.
Программа получает на вход последовательность целых неотрицательных чисел, каждое число записано в отдельной строке. Последовательность завершается числом 0, при считывании которого программа должна закончить свою работу и вывести количество членов последовательности (не считая завершающего числа 0).Числа, следующие за числом 0, считывать не нужно
program posledov;
var
a, s: integer ;
begin
s := 0 ;
writeln ( ‘Введите число’ );
read (a);
while a 0 do
begin
s := s + 1 ;
read(a);
end ;
writeln(s);
end .
Задача 14.
Выведите все точные квадраты натуральных чисел, не превосходящие данного числа N. Входные данные: задано единственное целое число N. Выходные данные: необходимо вывести все точные квадраты натуральных чисел, не превосходящие данного числа N.
program kvadratchislo;
var
i, n: integer ;
begin
writeln ( ‘Введите количество чисел’ );
read(n);
for i := 1 to n do
if sqr(i) then
writeln(sqr(i));
readln
end .
Задача 15.
Определите количество четных элементов в последовательности, завершающейся числом 0. Само число 0, и все, что следует за ним, учитывать не нужно.
program posvedchet;
var
a, k: integer ;
begin
k := 0 ;
writeln ( ‘Введите число’ );
read(a);
while a 0 do
begin
if (a mod 2 = 0 ) then
k := k + 1 ;
read(a);
end ;
writeln(k);
end .
В этой публикации приведем примеры задач с решениями на языке Паскаль по теме “Массив“.
Задачи:
- Дан массив из 10 целых чисел. Найти сумму элементов, кратных данному числу k.
- Дан массив из N элементов. Найти количество элементов, равных максимальному.
- Дан массив из N элементов. Найти среднее значение положительных элементов.
Задача 1. Дан массив из 10 целых чисел. Найти сумму элементов, кратных данному числу k.
Исходные данные: a – массив 10 целых чисел (тип array); k – целое число (тип integer)
Выходные данные: sum – сумма элементов, кратных числу k
Как будем решать задачу:
- Введем массив 10 целых чисел оператором цикла for с счетчиком от 1 до 10.
- Введем число k
- Обнулим сумму sum
- В цикле for будем проверять, делится ли число, хранящееся в ячейке (элемент массива) на число k, если да, то будем этот элемент добавлять в сумму sum.
- Выведем значение sum на экран.
Программа решения задачи на языке Паскаль:
var a:array[1..10] of integer;
k,sum,j:integer;
begin
writeln(‘Введите массив 10 целых чисел’);
for j:=1 to 10 do
begin
readln(a[j]);
end;
write(‘Введите число k=’);
readln(k);
sum:=0;
for j:=1 to 10 do
begin
if a[j] mod k = 0 then sum:=sum+a[j];
end;
writeln(‘Сумма элементов, кратных числу ‘,k,’: ‘,sum);
end.
Программа решения задачи на языке Паскаль
С использованием методов для последовательностей в PascalABC.NET (версия 3.8.2)
var a:array[1..10] of integer;
k,s,j,x:integer;
begin
writeln(‘Введите массив 10 целых чисел’);
for j:=1 to 10 do
begin
readln(a[j]);
end;
write(‘Введите число k=’);
readln(k);
s:=a.Where(x -> x mod k = 0).sum;
writeln(‘Сумма элементов, кратных числу ‘,k,’: ‘,s);
end.
Задача 2. Дан массив из N элементов. Найти количество элементов, равных максимальному.
Исходные данные: N – количество элементов массива (тип integer); a – массив N целых чисел (тип array)
Промежуточные данные: m – максимальное значение (тип integer)
Выходные данные: k – количество элементов, равных максимальному (тип integer)
Как будем решать задачу
- Введем число N
- Введем массив из N элементов
- Найдем максимальное значение
- Найдем количество элементов, равных максимальному значению.
Программа решения задачи на языке Паскаль:
var a:array[1..10] of integer;
k,m,j,N:integer;
begin
writeln(‘Введите количество элементов массива’);
readln(N);
writeln(‘Введите массив целых чисел’);
for j:=1 to N do
begin
readln(a[j]);
end;
m:=a[1];
for j:=2 to N do
begin
if a[j]>m then m:=a[j];
end;
k:=0;
for j:=1 to N do
begin
if a[j]=m then k:=k+1;
end;
writeln(‘Количество элементов, равных максимальному k=’,k);
end.
Программа решения задачи на языке Паскаль
С использованием методов для последовательностей в PascalABC.NET (версия 3.8.2)
var a:array of integer;
k,m,j,N:integer;
begin
writeln(‘Введите количество элементов массива’);
readln(N);
setlength(a,N);
writeln(‘Введите массив целых чисел’);
for j:=0 to N-1 do
begin
readln(a[j]);
end;
k:=a.countof(a.max);
writeln(‘Количество элементов, равных максимальному ‘,k);
end.
Задача 3. Дан массив из N элементов. Найти среднее значение положительных элементов.
Исходные данные: N – количество элементов массива (тип integer); a – массив N целых чисел (тип array)
Промежуточные данные: s – сумма положительных элементов (тип integer), k – количество положительных элементов (тип integer)
Выходные данные: r – среднее значение положительных элементов (тип real)
Как будем решать задачу
- Введем число N
- Введем массив из N элементов
- Найдем сумму и количество положительных элементов
- Вычислим среднее значение положительных элементов
Программа решения задачи на языке Паскаль
var a:array[1..10] of integer;
k,s,j,N:integer;
r:real;
begin
writeln(‘Введите количество элементов массива’);
readln(N);
writeln(‘Введите массив целых чисел’);
for j:=1 to N do
begin
readln(a[j]);
end;
s:=0; k:=0;
for j:=1 to N do
begin
if a[j]>0 then
begin
s:=s+a[j];
k:=k+1;
end;
end;
r:=s/k;
writeln(‘Среднее значение положительных элементов ‘,r);
end.
Программа решения задачи на языке Паскаль
С использованием методов для последовательностей в PascalABC.NET (версия 3.8.2)
var a:array of integer;
k,s,j,N:integer;
r:real;
begin
writeln(‘Введите количество элементов массива’);
readln(N);
setlength(a,N);
writeln(‘Введите массив целых чисел’);
for j:=0 to N-1 do
begin
readln(a[j]);
end;
s:=a.Where(x->x>0).sum;
k:=a.Count(x->x>0);
r:=s/k;
//либо так: r:=a.Where(x->x>0).Average;
writeln(‘Среднее значение положительных элементов ‘,r);
end.
Сформировать массив случайных чисел