Как найти решение задачи по условию

Универсальный способ решения: составить систему уравнений, подставить известные значения и вычислить неизвестные. Раз у нас 2 объекта, то 2 уравнения описывают движение этих объектов, а остальные уравнения берутся из условий задачи.

1. s₁ = v₁ ⋅ t, формула движения, где s₁ – длина пути автобуса №1, v₁ – скорость автобуса №1, t – время движения каждого объекта.
2. s₂ = v₂ ⋅ t, формула движения, где s₂ – длина пути автобуса №2, v₂ – скорость автобуса №2, t – время движения каждого объекта.

Отметим, что время движения у них одинаковое, поэтому мы его обозначили одинаково как t.
Базовыми единицами измерения возьмём км для пути, ч для времени и км/ч для скорости.
Итак, у нас в формулах есть 5 величин, из которых 3 известные (s₁=100, v₁=25, v₂=50) и 2 неизвестные (s₂, t), которые предстоит найти для получения результата.
Для успешного решения неизвестных должно быть столько же или меньше, чем уравнений. В нашем случае одинаково – 2, то есть скорее всего решение найдётся.

Рассмотрим план действий, который поможет понять как решать задачи.

• 1. Внимательно прочитай задачу.
• 2. Сделай краткую запись условия или чертёж.
• 3. Объясни, что означает каждое число.
• 4. Повтори вопрос задачи. Подумай, можно ли сразу на него ответить. Каких данных для решения тебе не хватает? Как их найти?
• 5. Составь план решения задачи.
• 6. Реши задачу.
• 7. Проверь решение. Запиши ответ.

🔴  А ТЕПЕРЬ БОЛЕЕ ПОДРОБНЕЕ:

Определите, к какому типу относится задача. Это арифметическая задача? Действия с дробями? Решение квадратных уравнений? Прежде чем приступить к решению, выясните, к какой области математики относится задача. Примеры и виды Залач. показаны ниже) Это важно, поскольку значительно упростит поиск способа решения.

Внимательно прочитайте условие задачи. Даже если задача кажется простой, внимательно изучите ее условие. Не следует приступать к решению задачи, лишь бегло ознакомившись с ее условием. Если задача сложна, вам, возможно, понадобится несколько раз перечитать ее условие, чтобы полностью понять его. Не жалейте времени на это и не приступайте к дальнейшим действиям до тех пор, пока не узнаете точно, что дано в условии и что необходимо найти.

Изложите условие задачи. Для лучшего понимания задачи полезно изложить ее условие своими словами. Можно просто пересказать условие, либо записать его в том случае, если вам неудобно говорить вслух (например, на экзамене). Сравните собственное изложение задачи с ее первоначальным условием, выяснив тем самым, правильно ли вы поняли задание.

Изобразите задачу графически. Если вы считаете, что это поможет, представьте задачу графически — возможно, так легче будет определить дальнейшие действия. Необязательно создавать подробную схему, достаточно набросать условие задачи в общих чертах, указав численные значения. При создании схемы справляйтесь с условием задачи, по окончании сравните готовое изображение с условием еще раз. Задайте самому себе вопрос: «Верно ли мой рисунок отображает задачу?» Если да, можно приступить к решению задачи. Если же ответ отрицателен, перечитайте условие еще раз.

• Постройте диаграмму Венна. Эта диаграмма изображает соотношения между величинами, фигурирующими в задаче. Диаграмма Венна особенно полезна при решении арифметических задач.
• Постройте график либо диаграмму.
• Расположите приведенные в условии величины вдоль прямой линии.
• Чтобы представить более сложные объекты, используйте простые геометрические фигуры.

Изучите структуру задачи. Внимательно прочитав условие, вы, возможно, вспомните похожие задачи, решенные вами ранее. Можно построить таблицу с внесенными в нее данными, которая поможет вам определить характер задачи. Отметьте выявленные характерные черты задачи — они помогут вам при ее решении. Не исключено даже, что вы вспомните схожие задачи и сразу получите ответ.

Изучите сделанные пометки. Еще раз проверьте свои записи, убедившись, что вы не ошиблись в числах и прочих данных. Не приступайте к составлению плана решения до тех пор, пока не будете уверены в том, что обладаете всей необходимой информацией и полностью понимаете задачу. Если вы не до конца поняли задачу, изучите схожие примеры в учебнике или в интернете. Ознакомление с похожими задачами, решенными другими людьми, поможет вам понять, что требуется сделать для решения задачи, которую решаете вы.

ПРОСТЫЕ И СОСТАВНЫЕ ЗАДАЧИ

Простые Математические Задачи состоят из 5 частей:

• Условие
• Вопрос
• Краткая Запись
• Решение Ответ

Обязательно в задаче нужно выявлять ОПОРНЫЕ СЛОВА, ОПОРНЫЕ СЛОВА — это основа краткой записи, их нужно уметь находить для определения главного в задаче.

Напимер:

В вазе 3 белых и 2 розовых гвоздики.

Сколько всего гвоздик в вазе?

В указанной задаче:

Первое опорное слово- белые, которое в 1 классе сокращаем 1 буквой Б., но начиная со 2 класса -Бел.

Второе опорное слово — розовые, которое в первом классе, сокращаем словом Р, но начиная со  2 класса- Роз.

Третье опороное слово всегда содержится в вопросе.

В данной задаче третье опорное слово — всего, которое в краткой записи заменяется фигурной скобкой с вопросом посередине

Решение:

3+2=5 ( гвоздик)

Ответ: 5 гвоздик всего в вазе.

✅ На заметку!

Простые задачи решаются одним действием.

Составные задачи решаются двумя и более действиями, разными способами.

У Иры 3 куклы, что в 2 раза меньше, чем у Светы. Сколько кукол у обеих девочек?

Решение:

• по действиям с пояснениями

1) 3 • 2 = б (к.) — у Светы

2) 3 + 6 = 9 (к.) — у обеих девочек

• по действиям с вопросами

1. Сколько кукол у Светы? 3-2 = б(к.)

2. Сколько кукол у обеих девочек? 3 + 6 = 9 (к.)

• выражением

3 + 3 −2 = 9 (к.)

Ответ: у обеих девочек 9 кукол.

ЗАДАЧИ НА НАХОЖДЕНИЕ СУММЫ

a          +         b          =        c

первое           второе         сумма

слагаемое    слагаемое

Чтобы найти сумму, надо сложить слагаемые

У балалайки 3 струны, а у контрабаса — 4. Сколько всего струн у этих музыкальных инструментов?

Решение: 3 + 4 = 7 (с.) Ответ: у этих музыкальных инструментов 7 струн.

У Кати 3 книги, что на 2 книги меньше, чем у Иры. Сколько всего книг у девочек?

Решение: 1)3 + 2 = 5 (к.)-у Иры 2) 3 + 5 = 8 (к.) — всего Ответ: всего у девочек 8 книг.

а          —                b             =        с

уменьшаемое     вычитаемое     разность

Чтобы найти разность, надо из уменьшаемого вычесть вычитаемое

У кошки родилось 6 котят. Четырёх котят отдали. Сколько котят осталось?

Решение: 6-4 = 2 (к.) Ответ: осталось 2 котёнка.

У Маши было 4 конфеты. Бабушка дала ей ещё 8 конфет. После обеда девочка съела 3 конфеты. Сколько конфет осталось у Маши?

Решение:

1) 4 + 8 = 12 (к.) — было у Маши до обеда

2) 12 — 3 = 9 (к.) — осталось после обеда Ответ: у Маши осталось 9 конфет.

ЗАДАЧИ НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО УМЕНЬШАЕМОГО

а          —             b            =           с

уменьшаемое    вычитаемое    разность

Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое

Когда Вася решил 15 примеров, ему осталось решить ещё 11 при меров. Сколько всего примеров нужно решить Васе?

Решение: 15+ 11 = 26 (п.) Ответ: Васе нужно решить 26 примеров.

Мама решила связать новый шарф. Каждый день в течение неде ли она вязала по 20 см. Какой длины должен получиться шарф, если ей осталось связать ещё 10 см?

Решение:

1. 20 • 7 = 140 (см) — мама связала за неделю

2. 140 + 10 = 150 (см) — длина шарфа Ответ: шарф должен получиться длиной 150 см.

ЗАДАЧИ НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО ВЫЧИТАЕМОГО И СЛАГАЕМОГО

Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность

Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое

В журнале 45 страниц, а в книге 155 страниц. На сколько страниц в книге больше, чем журнале?

Решение: 155-45 = 110 (стр.) Ответ: в книге на 110 страниц больше.

Катя собрала 12 больших ромашек и 7 маленьких. Несколько ромашек она подарила бабушке, и у девочки осталось 10. Сколько ромашек Катя подарила бабушке?

Решение:

1. 12 + 7 = 19 (ром.) — собрала Катя

2. 19 — 10 = 9 (ром.) — подарила бабушке Ответ: 9 ромашек Катя подарила бабушке.

ЗАДАЧИ НА УВЕЛИЧЕНИЕ И УИЕНЬШЕНИЕ ЧИСЛА НА НЕСКОЛЬКО ЕДИНИЦ

Увеличить на… значит прибавить к числу несколько единиц

5 увеличить на 2 = 5 + 2

Уменьшить на значит вычесть из числа несколько единиц

5 уменьшить на 2 = 5 — 2

Новорождённый котёнок весит 100 г, а трёхнедельный — на 200 г больше. Сколько весит трёхнедельный котёнок?

Решение: 100 + 200 = 300 (г) Ответ: трёхнедельный котёнок весит 300 г.

Петя купил 15 шоколадок, а Юра на 3 шоколадки меньше. Сколько шоколадок купил Юра?

Решение: 15-3 = 12 (ш.) Ответ: Юра купил 12 шоколадок

ЗАДАЧИ НА НАХОЖДЕНИЕ ПРОИЗВЕДЕНИЯ

a                 •                   b              =                   С

первый множитель    второй множитель      произведение

Чтобы найти произведение, надо перемножить множители

У котёнка 4 лапы. Сколько лап у пятерых котят?

Решение: 4 • 5 = 20 (л.) Ответ: у пятерых котят 20 лап.

С первого куста смородины собрали 3 кг ягод, со второго — 4 кг, а с третьего — в 2 раза больше, чем с первого и со второго вместе. Сколько килограммов смородины собрали с третьего куста?

Решение:

1. 3 + 4 = 7 (кг) — собрали с двух кустов

2. 7 • 2 = 14 (кг) —собрали с третьего куста Ответ: с третьего куста собрали 14 кг смородины.

ЗАДАЧИ НА НАХОЖДЕНИЕ ЧАСТНОГО

a         :      b         =    c

делимое делитель частное

Чтобы найти частное, надо делимое разделить на делитель

У мамы было 10 мандаринов. Она раздала двум дочкам мандарины поровну. Сколько мандаринов получила каждая девочка?

Решение: 10 : 2 = 5 (м.) Ответ: каждая девочка получила 5 мандаринов.

Бабушка сварила варенье: 9 литров малинового и б литров клубничного. Всё варенье она разлила в трёхлитровые банки. Сколько банок с вареньем получилось?

Решение:

1. 9 + б = 15 (л) — всего варенья сварила бабушка

2. 15 : 3 = 5 (б) — всего банок Ответ: получилось 5 банок с вареньем.

Задачи на нахождение неизвестного делимого

а      :         b       =       c

делимое  делитель  частное

Чтобы найти делимое, надо частное умножить на делитель

За 2 дня учительнице надо проверить тетради учеников. Она со бирается проверять по 14 тетрадей вдень. Сколько всего тетрадей надо проверить?

Решение: 14 • 2 = 28 (т.) Ответ: всего надо проверить 28 тетрадей.

Переводчик в течение недели переводил по 6 страниц в день. Ему осталось перевести ещё 4 страницы. Сколько всего страниц он перевёл?

Решение:

1. 6 * 7 = 42 (стр.) — перевёл за неделю

2. 42 + 4 = 46 (стр.) — всего

Ответ: 46 страниц перевёл переводчик.

ЗАДАЧИ НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО ДЕЛИТЕЛЯ И МНОЖИТЕЛЯ

Чтобы найти неизвестный делитель, надо делимое разделить на частное

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель

Витя собирает марки. Папа подарил ему 20 марок, а дедушка — 15 марок. Все марки Витя разложил в альбом, на 5 страниц поровну. Сколько марок на каждой странице?

Решение:

1. 20 + 15 = 35 (м.) — всего у Вити

2. 35 : 5 = 7 (м.) — на каждой странице Ответ: на каждой странице по 7 марок.

ЗАДАЧИ НА УВЕЛИЧЕНИЕ ЧИСЛА В НЕСКОЛЬКО РАЗ И МЕНЬШЕНИЕ

Увеличить в… раз значит умножить число

3 увеличить в 2 раза =3-2

Уменьшить в… раз значит разделить число

6 уменьшить в 2 раза = 6:2

Маме 30 лет, а бабушка — в 2 раза старше. Сколько лет бабушке?

Решение: 30 • 2 = 60 (л.) Ответ: бабушке 60 лет.

Масса белого медведя 900 кг, а масса медведицы — в 3 раза меньше. Какова масса медведицы?

Решение: 900 : 3 = 300 (кг) Ответ: масса медведицы 300 кг.

ЗАДАЧИ НА РАЗНОСТНОЕ СРАВНЕНИЕ

Чтобы узнать, на сколько одно число больше или меньше другого, надо из большего числа вычесть меньшее

* На сколько 10 больше, чем 5? 10 — 5 = 5; 10 больше, чем 5, на 5

* На сколько 10 меньше, чем 15? 15 — 10 = 5; 10 меньше, чем 15, на 5

В классе 15 мальчиков и 12 девочек. 22 человека посещают школу, а остальные болеют. На сколько меньше болеющих учеников, чем посещающих школу?

Решение:

1. 15 + 12 = 27 (чел.) — учатся в классе

2. 27 — 22 = 5 (чел.) — болеют

3. 22 — 5 = 17 (чел.) — на сколько меньше Ответ: болеющих учеников на 17 меньше, чем посещающих школу.

Чтобы узнать, во сколько раз одно число больше или меньше другого, надо большее число разделить на меньшее

• Во сколько раз 10 больше, чем 5? 10 : 5 = 2; 10 больше, чем 5, в 2 раза

• Во сколько раз 5 меньше, чем 15? 15 : 5 = 3; 5 меньше, чем 15, в 3 раза

Машинка стоит 90 рублей, а шоколадка — в 3 раза дешевле. Сколько стоят машинка и шоколадка вместе?

Решение:

1. 90 : 3 = 30 (руб.) — стоит шоколадка

2. 90 + 30 = 120 (руб.) — стоят вместе Ответ: машинка и шоколадка стоят 120 рублей.

ЗАДАЧИ НА ДЕЛЕНИЕ ПО СОДЕРЖАНИЮ

Фрукты разложили на тарелки, по 4 штуки на каждую. Сколько по надобилось тарелок?

Ответ :2

4:2=2

Понадобилось 2 тарелки

Бабушка раздала внукам 15 яблок, по 5 штук каждому. Сколько Внуков у бабушки?

Решение: 15 : 5 = 3 (внуков) Ответ: у бабушки 3 внука.

ЗАДАЧИ НА ДЕЛЕНИЕ НА РАВНЫЕ ЧАСТИ

Детям раздали конфеты поровну. Сколько детей получило конфеты?

Двое детей получили конфеты

Для подготовки школьного спектакля учительница разделила 30 учеников на 5 групп. Сколько учеников в каждой группе?

Решение: 30 : 5 = 6 (уч.) Ответ: в каждой группе по 6 учеников.

Решение задач с помощью «Х». 1.За «х» берем то, что требуется найти. Если неизвестных несколько, то за «х» берем меньшее. 2.Обязательно составляем краткое условие – так будет понятнее, которое неизвестное меньше и что брать за «х». 3.Составляем запись, которая называется математическая модель. « Пусть «х»-…., тогда…… По условию задачи……, то составим уравнение:…..» 4.Составление уравнения самый ответственный момент. Внимательно смотри в условие задачи, что делают неизвестные? Складываются? Вычитаются? Сравниваются? Известна их разница? На все у нас свой способ составления уравнения. 5.Решив уравнение – расшифруй что ты нашел, для этого посмотри, а что ты брал за «х». 6.Проверь нужно ли благодаря найденному «х» найти другие неизвестные. 7.Сделай анализ найденного решения. (Вспомни «деду 781 год»). 8.Корректно запиши ответ, не забыв про пояснение и единицы измерения.

Решение задач с помощью «Х». 1.За «х» берем то, что требуется найти. Если неизвестных несколько, то за «х» берем меньшее. 2.Обязательно составляем краткое условие – так будет понятнее, которое неизвестное меньше и что брать за «х». 3.Составляем запись, которая называется математическая модель. « Пусть «х»-…., тогда…… По условию задачи……, то составим уравнение:…..» 4.Составление уравнения самый ответственный момент. Внимательно смотри в условие задачи, что делают неизвестные? Складываются? Вычитаются? Сравниваются? Известна их разница? На все у нас свой способ составления уравнения. 5.Решив уравнение – расшифруй что ты нашел, для этого посмотри, а что ты брал за «х». 6.Проверь нужно ли благодаря найденному «х» найти другие неизвестные. 7.Сделай анализ найденного решения. (Вспомни «деду 781 год»). 8.Корректно запиши ответ, не забыв про пояснение и единицы измерения.

Решение задач с помощью «Х». 1.За «х» берем то, что требуется найти. Если неизвестных несколько, то за «х» берем меньшее. 2.Обязательно составляем краткое условие – так будет понятнее, которое неизвестное меньше и что брать за «х». 3.Составляем запись, которая называется математическая модель. « Пусть «х»-…., тогда…… По условию задачи……, то составим уравнение:…..» 4.Составление уравнения самый ответственный момент. Внимательно смотри в условие задачи, что делают неизвестные? Складываются? Вычитаются? Сравниваются? Известна их разница? На все у нас свой способ составления уравнения. 5.Решив уравнение – расшифруй что ты нашел, для этого посмотри, а что ты брал за «х». 6.Проверь нужно ли благодаря найденному «х» найти другие неизвестные. 7.Сделай анализ найденного решения. (Вспомни «деду 781 год»). 8.Корректно запиши ответ, не забыв про пояснение и единицы измерения.

Решение задач с помощью «Х». 1.За «х» берем то, что требуется найти. Если неизвестных несколько, то за «х» берем меньшее. 2.Обязательно составляем краткое условие – так будет понятнее, которое неизвестное меньше и что брать за «х». 3.Составляем запись, которая называется математическая модель. « Пусть «х»-…., тогда…… По условию задачи……, то составим уравнение:…..» 4.Составление уравнения самый ответственный момент. Внимательно смотри в условие задачи, что делают неизвестные? Складываются? Вычитаются? Сравниваются? Известна их разница? На все у нас свой способ составления уравнения. 5.Решив уравнение – расшифруй что ты нашел, для этого посмотри, а что ты брал за «х». 6.Проверь нужно ли благодаря найденному «х» найти другие неизвестные. 7.Сделай анализ найденного решения. (Вспомни «деду 781 год»). 8.Корректно запиши ответ, не забыв про пояснение и единицы измерения.

Математика – царица наук. Её язык одинаков во всех странах и континентах, и образование ребёнка начинается, прежде всего, с изучения языка и математики. Математика в тех или иных формах изучается во всех классах общеобразовательной школы, способствуя повышению умственных способностей и развитию математических навыков ученика. Учебный процесс непосредственно связан с решением различных математических задач, которые задаются ученикам как на уроках, так и в форме домашних заданий. Если вы столкнулись с трудностями в их решении, вам помогут специальные сетевые сервисы и мобильные приложения, позволяющие решить задачу по математическим дисциплинам. Ниже мы разберём их перечень, а также поясним, как ими пользоваться.

Math10 – универсальный сетевой ресурс для решения задач

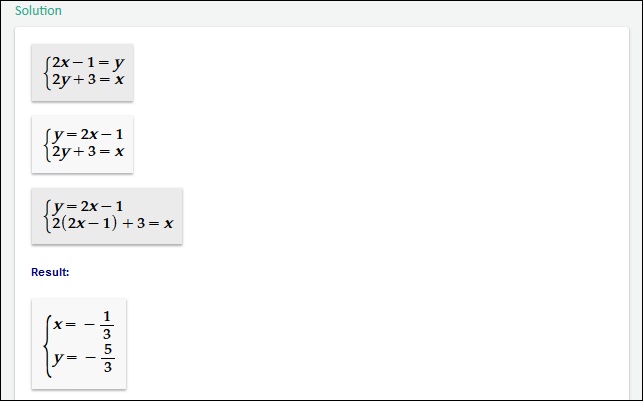
Сервис math10.com – универсальный сетевой ресурс для решения математических задач. Сервис позволяет решать задачи и примеры по базовой математики, алгебре, тригонометрии, статистике, линейной алгебре, химии и других точных науках. Ресурс является одним из лучших в данном плане, и может быть рекомендован всем желающим быстро решить ту или иную задачу онлайн.

Для работы с ресурсом выполните следующее:

Mateshka – поможет решить задачу с картинками

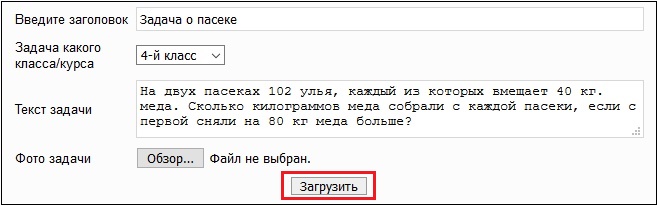
Сервис mateshka.ru представляет собой довольно универсальный решебник, позволяющий решать различные виды задач. Его функционал позволяет работать не только с отдельными примерами в полуавтоматическом режиме (как в случае предыдущего сервиса), но и загружать сфотографированные картинки с условием задачи, и получить через какое-то время готовый результат.

Для работы с сервисом выполните следующее:

1. Перейдите на http://mateshka.ru/reshenie_zadach/;
2. В изложенной форме на сайте укажите полный текст задачи. Введите её название, класс, текст задачи, сфотографируйте задачу и прикрепите её фото с помощью кнопки «Обзор»;
3. Нажмите на «Загрузить»;

   

   Введите условие задачи в соответствующую форму, а затем нажмите на «Загрузить»

4. Задача поступит на проверку администрации ресурса и через некоторое время станет доступна в поиске;
5. Когда она будет решена, вы увидите её на данной странице сайта.

Math-solution  — помощь в решении математики онлайн

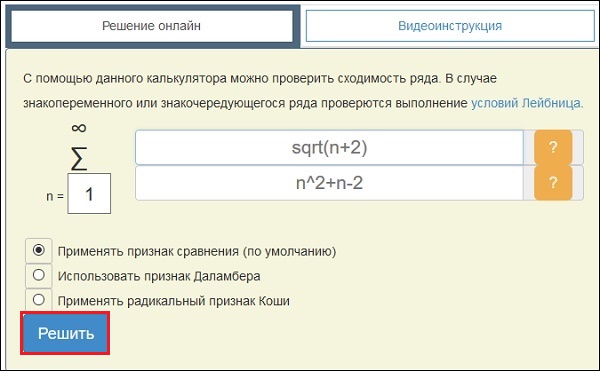
Ресурс math-solution.ru пригодится учащимся, которые в том или ином объёме изучают математику и геометрию, и поможет в решении соответствующих задач. В основу сайта положены математические программы (калькуляторы) для решения задач онлайн. Все необходимые вычисления выполняются на сайте, представлен поэтапный вариант получения ответа.

Для работы с сервисом выполните следующее:

1. Перейдите на math-solution.ru;
2. Сверху выберите один из аккаунтов для авторизации на ресурсе;
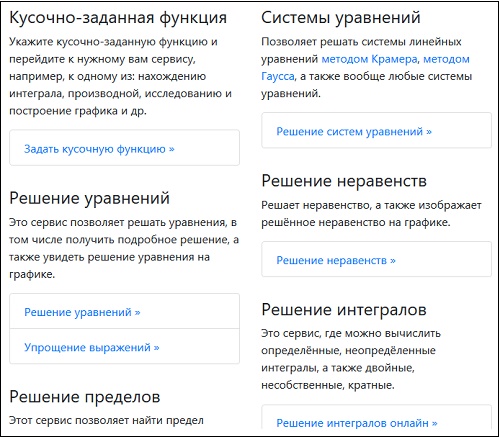
3. Справа снизу в разделе «Список задач» выберите тип задачи, который вам необходимо решить;
4. В открывшейся форме введите условие задачи, а затем нажмите внизу на кнопку запуска решения;
5. Просмотрите полученный результат.

Math.semestr.ru – онлайн-калькулятор

Сервис https://math.semestr.ru/example.php представляет собой различные калькуляторы по направлениям, включая высшую математику, аналитическую геометрию, вычислительную математику, статистику и другие дисциплины. Для решения имеющейся у вас задачи перейдите на данный ресурс, выберите интересующий вас калькулятор, тип задачи, вбейте данные, и нажмите на «Решить».

Кontrolnaya-rabota.ru – решение математических задач онлайн

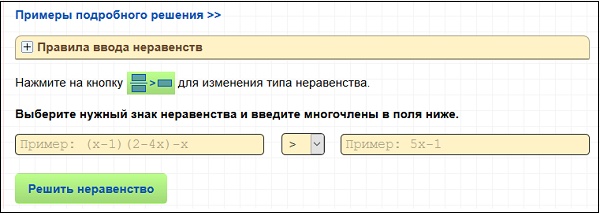
Еще одним ресурсом для решения математических задач является kontrolnaya-rabota.ru, позволяющее ввести автоматическое уравнение и получить его автоматическое решение. Интерфейс сервиса очень прост и интуитивно понятен, позволяя быстро получить нужный результат. Выполните следующее:

1. Перейдите на https://www.kontrolnaya-rabota.ru/s/#go;
2. Выберите тип необходимого для решения уравнения, имеющегося у вас в задаче;
3. Кликните на кнопке запуска решения.

Англоязычной альтернативой для решения различных типов математических задач является сервис webmath.com. Данный сайт генерирует ответы на определённые математические вопросы и задачи, вводимые пользователем. Ответы генерируются и отображаются в реальном времени. Помимо ответов, сервис показывает учащимся, как пройти к тому или иному ответу.

Для работы с сервисом выполните следующее:

1. Перейдите на https://www.webmath.com:443/;
2. Нажмите на стрелочку справа от «Math help item» и выберите тип нужной задачи для решения;
3. В открывшейся форме введите нужный тип задачи и просмотрите результат.

Альтернативным англоязычным ресурсом для поиска решения задач по математике является quickmath.com. Его функционал также позволяет в автоматическом режиме решать различные виды математических задач. Работа с ним не отличается от сервисов-аналогов. Перейдите на ресурс, введите в специальное поле задачу для решения, и нажмите внизу на «Solve».

Через несколько секунд вы получите результат с вариантами ответа.

Мобильные приложения для решения математических задач

Также отметим ряд специализированных математических приложений, позволяющих с помощью вашего телефона решить ту или иную задачу. Они следующие:

• «Photomath» (Андроид, iOS) – одно из ведущих мобильных, позволяющих ввести задачу и получить её решение по математике. Программа отлично пригодится для подготовки к предстоящим экзаменам по математике, она бесплатна и способна эффективно работать без Интернета. Просто запустите приложение, отсканируйте с помощью камеры телефона текст задачи, и вы получите необходимый ответ. Предоставляемое решение программа разбивает на простые шаги для лучшего понимания алгоритма ответа;

• «Mathway» (Андроид, iOS) – приложение позиционирует себя как мировой лидер среди решению различных типов математических задач. Программа быстро и эффективно решает сложные математические задачи, достаточно ввести условия задачи (или снять задачу на камеру), и вы получите ответ. Приложение удобное, имеет бесплатный характер, и охватывает множество математических дисциплин;
• «Malmath» (Андроид, iOS) – приложение для эффективного решения математических задач. Он хорошо справляется с интегралами, пределами, производными, логарифмами, уравнениями и другим. Как и в случае предыдущего приложения, программа подробно объясняет необходимые шаги по решению задачи;
• «Решение математики» — мобильный инструмент, созданный специально для решения математических задач. Хорошо понимает различные типы математических задач, справляется с полиноминальными уравнениями различных степеней, решает тригонометрические уравнения, системы уравнений и другое.

Читайте также: некоторый алгоритм из цепочки символов получает новую цепочку следующим образом.

Заключение

В статье рассмотрены сетевые сервисы и мобильные приложения, позволяющие написать условие задачи по математике и довольно быстро получить её решение. Каждый из перечисленных нами инструментов может оказаться полезным в решении вашей задачи, поскольку не только предоставляет конечное решение, но подробно описывает промежуточные шаги. Столкнувшись с трудной задачей, используйте данные сервисы и приложения, которые позволят вам быстро справиться с заданием, получив высокий оценочный бал.

Алгоритм решения задачи с помощью системы линейных уравнений

Например:

Задуманы два числа. Если от первого отнять второе, то получается 10. Если к первому прибавить удвоенное второе, то получается 91. Найдите задуманные числа.

Примеры

Пример 1. Периметр прямоугольника равен 48 см. Его длина больше ширины в 3 раза.

Найдите стороны прямоугольника.

Пусть a и b – длина и ширина прямоугольника.

По условию:

$$ {left{ begin{array}{c} P = 2(a+b) = 48 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} a+b = 24 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} 3b+b = 24 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} 4b = 24 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} a = 18 \ b = 6 end{array} right.} $$

Ответ: длина прямоугольника 18 см, ширина 6 см.

Пример 2. Два программиста из Бомбея, работающие в одном проекте, написали 100500 строк кода. Первый работал 70 дней, второй – 100 дней. Сколько строк писал каждый программист ежедневно, если за первые 30 дней первый написал на 5550 строк больше, чем второй?

Пусть x – ежедневное количество строк для 1-го программиста, y- для 2-го.

По условию:

$$ {left{ begin{array}{c} 70x+100y = 100500 |:10 \ 30x-30y = 5550 |:30 end{array} right.} (-) Rightarrow {left{ begin{array}{c} 7x+10y = 10050 \ x-y=185 | times 10 end{array} right.}$$

$$ Rightarrow (+) {left{ begin{array}{c} 7x+10y = 10050 \ 10x-10y = 1850 end{array} right.} Rightarrow {left{ begin{array}{c} 17x = 11900 \ y = x-185 end{array} right.} Rightarrow {left{ begin{array}{c} x = 700 \ y = 515 end{array} right.} $$

Ответ: 700 строк и 515 строк

Пример 3. За 2 кг конфет и 3 кг печенья заплатили 1540 руб. Сколько стоит 1 кг конфет и 1 кг печенья, если 2 кг печенья дороже 1 кг конфет на 210 руб.?

Пусть x – цена за 1 кг конфет, y – за 1 кг печенья.

По условию:

$$ {left{ begin{array}{c} 2x+3y = 1540 \ 2y-x = 210 | times 2 end{array} right.} Rightarrow (+) {left{ begin{array}{c} 2x+3y = 1540 \ -2x+4y = 420 end{array} right.} Rightarrow {left{ begin{array}{c} 7y = 1960 \ x = 2y-210 end{array} right.} Rightarrow {left{ begin{array}{c} x = 350 \ y = 280 end{array} right.} $$

Ответ: 1 кг конфет – 350 руб. и 1 кг печенья – 280 руб.

Пример 4. Катер за 3 ч движения против течения реки и 2 часа по течению проходит 73 км. Найдите собственную скорость катера и скорость течения, если за 4 ч движения по течению катер проходит на 29 км больше, чем за 3 ч движения против течения.

Пусть v – скорость катера (км/ч), u – скорость течения (км/ч).

По условию:

$$ {left{ begin{array}{c} 3(v-u)+2(v+u) = 73 \ 4(v+u)-3(v-u) = 29 end{array} right.} Rightarrow {left{ begin{array}{c} 3v-3u+2v+2u = 73 \ 4v+4u-3v+3u = 29 end{array} right.}$$

$$ Rightarrow {left{ begin{array}{c} 5v-u = 73 \ v+7u = 29 end{array} right.} Rightarrow {left{ begin{array}{c} 5(29-7u)-u = 73 \ v = 29-7u end{array} right.} Rightarrow {left{ begin{array}{c} 145-35u-u = 73 \ v = 29-7u end{array} right.} Rightarrow$$

$$ Rightarrow {left{ begin{array}{c} -36u = -72 \ v = 29-7u end{array} right.} Rightarrow {left{ begin{array}{c} v = 15 \ u = 2 end{array} right.} $$

Ответ: скорость катера 15 км/ч и скорость течения 2 км/ч

Пример 5. 5 карандашей и 3 тетрадки вместе стоили 170 руб. После того, как карандаши подешевели на 20%, а тетрадки подорожали на 30%, за 3 карандаша и 5 тетрадок заплатили 284 руб. Найдите первоначальную цену карандаша и тетрадки.

Пусть x – первоначальная цена карандаша, y – тетрадки.

По условию:

$$ {left{ begin{array}{c} 5x+3y = 170 \ 3cdot0,8x+5cdot1,3y = 284 end{array} right.} Rightarrow {left{ begin{array}{c} 5x+3y = 170 |times frac{2,4}{5} \ 2,4x+6,5y = 284 end{array} right.} Rightarrow (-) {left{ begin{array}{c} 2,4x+1,44y = 81,6 \ 2,4x+6,5y = 284 end{array} right.} $$

$$ Rightarrow {left{ begin{array}{c} (6,5-1,44)y = 284-81,6 \ x = frac{170-3y}{5} end{array} right.}Rightarrow {left{ begin{array}{c} y = 202,4:5,06 = 40 \ x = frac{170-120}{5} = 10 end{array} right.} $$

Ответ: карандаш сначала стоил 10 руб., тетрадка – 40 руб.

Пример 6*. Велосипедист планирует добраться из пункта А в пункт В. Если он будет ехать на 3 км/ч быстрее, чем обычно, он доберётся на 1 час раньше. А если он будет ехать на 2 км/ч медленней, чем обычно, то – на 1 час позже. Найдите обычную скорость велосипедиста и время поездки при этой скорости.

Пусть v – обычная скорость велосипедиста (км/ч), t – обычное время (ч).

Расстояние между А и В неизменно, и по условию равно:

$$ s_{AB} = vt = (v+3)(t-1) = (v-2)(t+1) $$

Получаем систему:

$$ {left{ begin{array}{c} vt = (v+3)(t-1) \ vt = (v-2)(t+1) end{array} right.} Rightarrow (-) {left{ begin{array}{c} vt = vt-v+3t-3 \ vt = vt+v-2t-2 end{array} right.} Rightarrow (+) {left{ begin{array}{c} v-3t = -3 \ -v+2t = -2 end{array} right.} Rightarrow $$

$$ Rightarrow {left{ begin{array}{c} -t = -5 \ v = 2t+2 end{array} right.} Rightarrow {left{ begin{array}{c} t = 5 \ v = 12 end{array} right.} $$

Ответ: обычная скорость 12 км/ч, время 5 ч

Пример 7*. В одной бочке налито 12 л, во второй – 32 л. Если первую бочку доверху наполнить водой из второй, то вторая бочка будет наполнена ровно наполовину своего объёма. Если вторую бочку доверху наполнить водой из первой, то первая бочка будет наполнена на 1/6 своего объёма. Найдите объём каждой бочки.

Пусть x – объём первой бочки (л), y – объём второй (л).

Пусть a л перелито из второй бочки, и первая наполнилась до краёв, а во второй воды осталось наполовину:

$$ (+) {left{ begin{array}{c} 12+a = x \ 32-a = frac{1}{2} y end{array} right.} Rightarrow x+ frac{1}{2} y = 44 $$

Теперь пусть b л перелито из первой бочки, и вторая наполнилась до краёв, а в первой воды осталось на 1/6:

$$ (+) {left{ begin{array}{c} 32+b = y \ 12-b = frac{1}{6} x end{array} right.} Rightarrow frac{1}{6}x+y = 44 $$

Получаем систему:

$$ {left{ begin{array}{c} x+ frac{1}{2} y = 44 | times 2 \ frac{1}{6} x+y = 44 end{array} right.} Rightarrow (-) {left{ begin{array}{c} 2x+y = 88 \ frac{1}{6} x+y = 44 end{array} right.} Rightarrow (+) {left{ begin{array}{c} 1frac{5}{6} x = 44 \ y = 88-2x end{array} right.} Rightarrow $$

$$ {left{ begin{array}{c} x = 44: frac{11}{6} = 44cdot frac{6}{11} = 24 \ y = 88-2cdot24 = 40 end{array} right.} $$

Ответ: первая бочка 24 л, вторая – 40 л

Пример 8*. Если школьник едет в школу на автобусе, а возвращается домой пешком, то он тратит на всю дорогу полтора часа. Если он едет туда и обратно на автобусе, то он тратит полчаса. Сколько времени потратит школьник, если он пойдёт туда и обратно пешком?

Пусть s – расстояние между домом и школой, v – скорость автобуса, u – скорость школьника, t – искомое время, потраченное на дорогу туда и обратно пешком.

По условию задачи:

$$ {left{ begin{array}{c} 1,5 = frac{s}{v} + frac{s}{u} \ 0,5 = frac{2s}{v} \ t = frac{2s}{u} end{array} right.} $$

Из второго уравнения $ frac{s}{v} = frac{0,5}{2} = 0,25 $. Подставляем в первое уравнение:

$$ frac{s}{u} = 1,5-frac{s}{v} = 1,5-0,25 = 1,25 $$

И тогда искомое время:

$$ t = frac{2s}{v} = 2cdot1,25 = 2,5 (ч) $$

Ответ: 2,5 ч