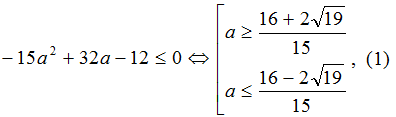Как найти решения параметра

Цель данной работы – изучение различных способов решения задач с параметрами.
Возможность и умение решать задачи с параметрами демонстрируют владение методами
решения уравнений и неравенств, осмысленное понимание теоретических сведений,
уровень логического мышления, стимулируют познавательную деятельность. Для
развития этих навыков необходимы длительнее усилия, именно поэтому в профильных
10-11 классах с углубленным изучением точных наук введен курс: “Математический
практикум”, частью которого является решение уравнений и неравенств с
параметрами. Курс входит в число дисциплин, включенных в компонент учебного
плана школы.

Успешному изучению методов решения задач с параметрами могут помочь
элективный или факультативный курсы, или компонент за сеткой по теме: “Задачи с
параметрами”.

Рассмотрим четыре больших класса задач с параметрами:

1. Уравнения, неравенства и их системы, которые необходимо решить для
   любого значения параметра, либо для значений параметра, принадлежащих
   определенному множеству.
2. Уравнения, неравенства и их системы, для которых требуется определить
   количество решений в зависимости от значения параметра.
3. Уравнения, неравенства и их системы, для которых требуется найти все те
   значения параметра, при которых указанные уравнения (системы, неравенства)
   имеют заданное число решений.
4. Уравнения, неравенства и их системы, для которых при искомых значениях
   параметра множество решений удовлетворяет заданным условиям в области
   определения.

Методы решений задач с параметрами.

1. Аналитический метод.

Это способ прямого решения, повторяющий стандартные процедуры нахождения
ответа в задачах без параметра.

Пример 1. Найдите все значения параметра
a, при которых уравнение:

(2a – 1)x² + ax + (2a – 3) =0  имеет не более
одного корня.

Решение:

При 2a
– 1 = 0 данное уравнение квадратным не является, поэтому случай
a =1/2 разбираем отдельно.

Если a = 1/2, то уравнение принимает вид
1/2x – 2 = 0, оно имеет один корень.

Если a ≠ 1/2,
то уравнение является квадратным; чтобы оно имело не более одного корня
необходимо и достаточно, чтобы дискриминант был неположителен:

D = a² – 4(2a – 1)(2a – 3) = -15a²
+ 32a  – 12;

Чтобы записать окончательный ответ, необходимо понять,

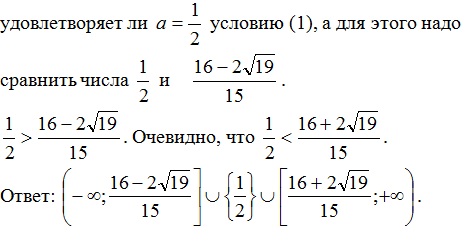
2. Графический метод.

В зависимости от задачи (с переменной x
и параметром a)
рассматриваются графики в координатной плоскости (x;y)
или в плоскости (x;a).

Пример 2. Для каждого значения параметра a
определите количество решений уравнения
.

Решение:

Заметим, что количество решений уравнения
 
равно количеству точек пересечения графиков функций

и y = a.

График функции

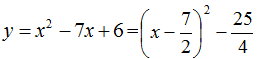
показан на рис.1.

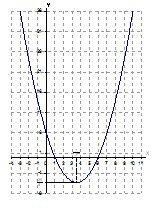
Рис.1

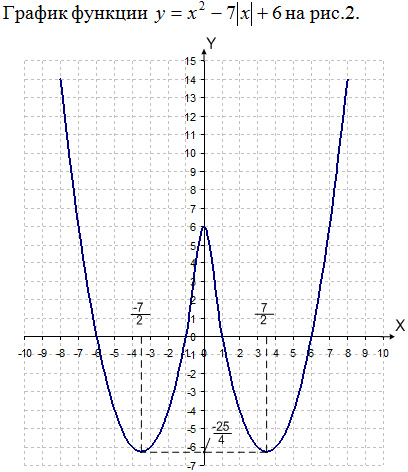
Рис. 2

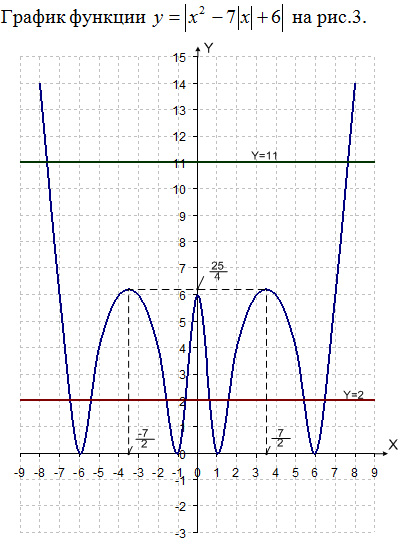
Рис. 3

y = a – это горизонтальная прямая. По графику несложно
установить количество точек пересечения в зависимости от a
(например, при  a =
11 – две точки пересечения; при a
= 2 – восемь точек пересечения).

Ответ: при a < 0 – решений нет; при a
= 0 и a = 25/4  – четыре решения; при
0 < a < 6  – восемь решений; при a
= 6 – семь решений; при

6 < a < 25/4 – шесть решений; при a >
25/4 – два решения.

3. Метод решения относительно параметра.

При решении этим способом переменные х и а принимаются
равноправными, и выбирается та переменная, относительно которой аналитическое
решение становится более простым. После упрощений нужно вернуться к исходному
смыслу переменных х и а и закончить решение.

Пример 3. Найти все значения параметра а , при каждом из которых
уравнение

= –ax +3a +2  имеет единственное решение.

Решение:

Будем решать это уравнение заменой переменных. Пусть

= t , t ≥ 0
, тогда x = t² + 8  и
уравнение примет вид at² + t + 5a – 2 = 0
 . Теперь задача состоит в том, чтобы найти все а,
при которых уравнение at² + t + 5a – 2 =
0  имеет единственное неотрицательное решение. Это имеет
место в следующих случаях.

1) Если а = 0, то уравнение имеет единственное решение t
= 2.

Решение некоторых типов уравнений и неравенств с параметрами.

Задачи с параметрами помогают в формировании логического мышления, в
приобретении навыков исследовательской деятельности.

Решение каждой задачи своеобразно и требует к себе индивидуального,
нестандартного подхода, поскольку не существует единого способа решения таких
задач.

Ⅰ. Линейные уравнения.

Задача № 1.
При каких значениях параметра b
уравнение

не имеет корней?

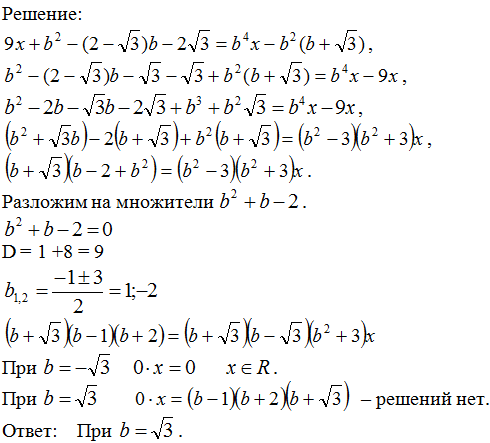
Ⅱ. Степенные уравнения, неравенства и их системы.

Задача №2. Найти все значения параметра a,
при которых множество решений неравенства:

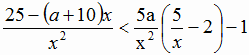
содержит число 6, а также содержит два отрезка длиной 6, не имеющие общих точек.

Решение:

.

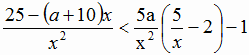Преобразуем обе части неравенства.

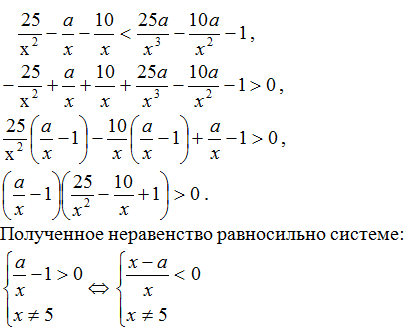
Для того, чтобы множество решений неравенства содержало число 6, необходимо и
достаточно выполнение условия:

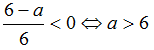
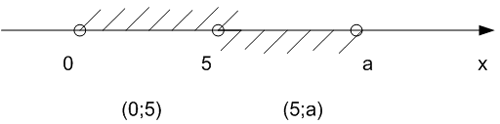Рис.4

При a > 6 множество
решений неравенства:
.

Интервал (0;5) не может содержать ни одного отрезка
длины 6. Значит, два непересекающихся отрезка длины 6 должны содержаться в
интервале (5; a).

Это

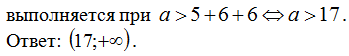
Ⅲ. Показательные уравнения, неравенства и системы.

Задача № 3. В области определения функции
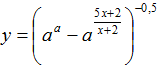взяли
все целые положительные числа и сложили их. Найти все значения, при которых
такая сумма будет больше 5, но меньше 10.

Решение:

1) Графиком дробно-линейной функции
   
является гипербола. По условию x > 0. При
неограниченном возрастании х дробь

монотонно убывает и приближается к нулю, а значения функции z возрастают
и приближаются к 5. Кроме того, z(0) = 1.

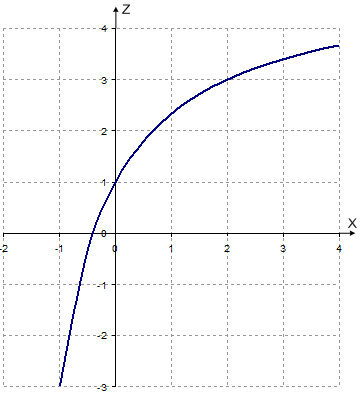
Рис. 5

2) По определению степени область определения D(y)
состоит из решений неравенства
.
При a = 1 получаем неравенство, у которого решений
нет. Поэтому функция у нигде не определена.

3) При 0 < a < 1 показательная функция с
основанием а убывает и неравенство
 
равносильно неравенству

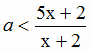
. Так как x > 0 , то z(x) >
z(0) = 1 . Значит, каждое положительное значение х
является решением неравенства

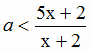
. Поэтому для таких а указанную в условии сумму нельзя найти.

4) При a > 1 показательная функция с основанием
а возрастает и неравенство
 
равносильно неравенству

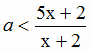
. Если a  ≥ 5,
то любое положительное число является его решением, и указанную в условии сумму
нельзя найти. Если 1 < a < 5, то множество
положительных решений – это интервал (0;x₀)
, где a = z(x₀) .

5) Целые числа расположены в этом интервале подряд, начиная с 1. Вычислим
суммы последовательно идущих натуральных чисел, начиная с 1 : 1; 1+2 = 3; 1+2+3
= 6; 1+2+3+4 = 10;… Поэтому указанная сумма будет больше 5 и меньше 10, только
если число 3 лежит в интервале (0;x₀),
а число 4 не лежит в этом интервале. Значит, 3 < x₀
≤ 4 . Так как

 
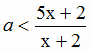
возрастает на
,
то z(3) < z(x₀)
≤ z(4) .

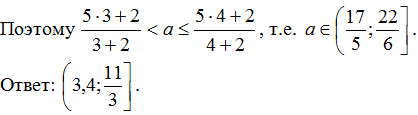
Решение иррациональных уравнений и неравенств, а также уравнений, неравенств
и систем, содержащих модули рассмотрены в Приложении 1.

Задачи с параметрами являются сложными потому, что не существует единого
алгоритма их решения. Спецификой подобных задач является то, что наряду с
неизвестными величинами в них фигурируют параметры, численные значения которых
не указаны конкретно, но считаются известными и заданными на некотором числовом
множестве. При этом значения параметров существенно влияют на логический и
технический ход решения задачи и форму ответа.

По статистике многие из выпускников не приступают к решению задач с
параметрами на ЕГЭ. По данным ФИПИ всего 10% выпускников приступают к решению
таких задач, и процент их верного решения невысок: 2–3%,
поэтому приобретение навыков решения трудных, нестандартных заданий, в том числе
задач с параметрами, учащимися школ по-прежнему остается актуальным.

На этой странице вы узнаете

• Игра в прятки: как значение одной переменной может помочь найти другую?
• Парадокс: как стоять на месте и бежать с любой скоростью одновременно? 
• Решаем параметры осторожно: как не совершить ошибку в квадратном уравнении с параметром? 

Мы привыкли, что в уравнении коэффициенты не меняются. Но возможно ли из одного уравнения составить бесконечное множество различных его вариантов? Узнаем об этом в статье. 

Что такое параметр 

Утром на термометре было некоторое количество градусов, которое мы обозначим за х. В обед температура воздуха изменилась в несколько раз. Во сколько раз должна была измениться температура воздуха, чтобы на термометре было 20 градусов? 

Такие задачи достаточно легко решаются. Если бы изначально было пять градусов, то искомое число было бы равно (frac{20}{5} = 4). А если было 10 градусов, то искомое число было бы равно (frac{20}{10} = 2). 

Но не все так просто. Мы не знаем, какой изначально была температура. Также мы не знаем, во сколько раз она изменилась. То есть мы получили уравнение с двумя неизвестными переменными. 

Обозначим вторую переменную a, у нас получится уравнение вида ax=20. Только что введенная нами переменная “a”  называется параметр. 

Параметр — это условная буква, вместо которой можно подставить число. 

То есть параметр — это еще одна переменная, которая может принять несколько значений. 

Как решать уравнения с параметром, если у нас целых две (а то и больше) неизвестных переменных? Нужен иной подход, чем при решении обычного уравнения.

Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется. 

Мы ищем не единственное значение параметра, а все возможные его значения для заданного условия.

Линейные уравнения с параметром

Вернемся к нашей погоде. У нас получилось уравнение ax = 20. Как найти, сколько градусов было изначально? Разделить все уравнение на число a. 

(x = frac{20}{a})

Какие значения может принимать параметр? Любые. Например, при a = 1 x = 20.
При a = 2 x = 10.
При a = 40 x = 0,5 

Что, если a=0? Мы получаем уравнение (x = frac{20}{0}), у которого нет решения, поскольку на 0 делить нельзя. 

Если мы не будем преобразовывать изначальное уравнение, то получится 0*x=20, то есть уравнение не будет выполняться: какое бы число мы ни умножили на 0, получится 0. 

Получается, решение есть при любых значениях a, кроме 0. Таким образом, мы и нашли ответ: при a = 0 решений нет, при a (neq) 0 — x = 20a. 

Добавим немного теории. Представим наше уравнение в виде ax = b, где a, b — действительные числа. Рассмотрим несколько случаев. 

1) b (neq) 0. 

Предположим, Пете необходимо в несколько раз увеличить скорость х, пробежать дистанцию и поставить рекорд. Чтобы поставить рекорд, он должен бежать со скоростью 15 км/ч — это и будет коэффициент b. 

Получаем уравнение ax = 15. Как найти начальную скорость Пети? (x = frac{15}{a}). 

Такое уравнение мы уже решали выше. Получаем два случая: 

• Если a = 0 — решений нет. 
• Если a (neq) 0, то изначальная скорость Пети была равна (x = frac{15}{a}). 

2) b = 0. 

Мы получаем уравнение ax = 0. Также разберем два случая значений параметра: 

• a = 0. Мы получаем уравнение 0 * x = 0. Какое значение х нужно подставить, чтобы уравнение выполнялось? 

Какое бы число мы ни умножили на 0, получим 0. Получаем бесконечное множество решений. 

• a (neq) 0. Здесь получается, что равен 0 уже х: (x = frac{0}{a} = 0). 

Подведем итог. Как можно решить уравнение вида ax = b?

• Если a = 0, b = 0 — бесконечное множество решений. 
• Если a = 0, b (neq) 0 — решений нет. 
• Если a (neq) 0, b (neq) 0 — решением будет (x = frac{b}{a}). 

Квадратные уравнения с параметром

Прежде чем приступать к изучению следующего материала, рекомендуем ознакомиться с понятием квадратного уравнения в статье «Линейные, квадратные и кубические уравнения». Также важно ориентироваться в графиках параболы из статьи «Основные элементарные функции». 

Квадратное уравнение имеет вид ax² + bx + c = 0, а графиком функции y = ax² + bx + c будет парабола. 

Как работать с такими уравнениями, если в них присутствует параметр? В первую очередь, важны рассуждения. Любое задание с параметром можно решить, проанализировав функцию.  

Решение квадратного уравнения опирается на понятие дискриминанта. В зависимости от его значений может получиться разное количество корней: 

• При D > 0 уравнение имеет два корня. 
• При D = 0 уравнение имеет один корень. 
• При D < 0 уравнение не имеет корней. 

Как это проверить на графике? Корни уравнения — это точки, в которых парабола пересекает ось абсцисс, то есть ось х. 

Рассмотрим три уравнения. 

1) x² — x — 2 = 0
Решим уравнение с помощью дискриминанта. 
D = 1² — 4 * 1 * (-2) = 1 + 8 = 9
Поскольку дискриминант больше 0, то уравнение имеет два корня. 

(x_1 = frac{1 + 3}{2} = 2)
(x_2 = frac{1 — 3}{2} = -1)

Проверим с помощью графика функции. Построим параболу и заметим, что она действительно дважды пересекает ось абсцисс, а координаты этих точек равны (−1; 0) и (2; 0) . 

2) x² -4x + 4 = 0
Решим уравнение с помощью дискриминанта. 
D = 16 — 4 * 1 * 4 = 16 — 16 = 0
Поскольку дискриминант равен 0, у уравнения всего один корень. 

(x = frac{4}{2} = 2)

Проверим на графике. И действительно, парабола касается оси х только один раз в вершине, координаты которой (2; 0). 

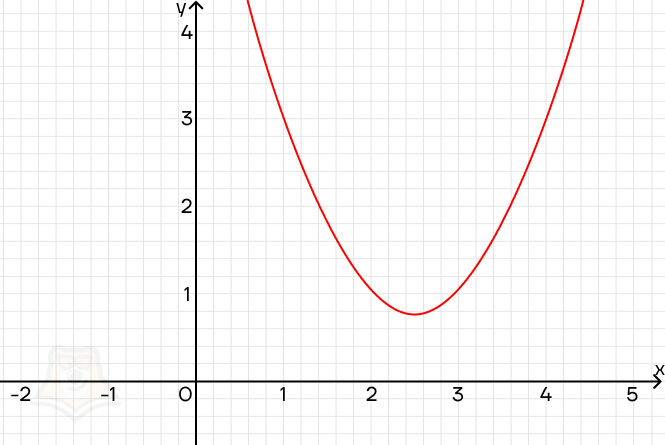
3) x² — 5x + 7 = 0
Решим уравнение с помощью дискриминанта. 
D = 25 — 4 * 1 * 7 = 25 — 28 = -3

Поскольку дискриминант отрицательный, у уравнения нет корней. И это отлично видно, если посмотреть на график функции: парабола лежит выше оси х и никогда ее не пересечет. 

Где можно применить эти знания, решая параметры? 

Пример 1. Найдите все значения параметра a, при которых уравнение x² + (3a + 11)x + 18,25 + a = 0 имеет два различных решения. 

Решение. Перед нами квадратное уравнение с коэффициентами b = 3a + 11, c = a + 18,25. В каких случаях это уравнение будет иметь два различных корня?

Квадратное уравнение имеет два корня, если D > 0. Нужно найти все значения параметра, при которых дискриминант будет положительным. 

1. Для начала найдем сам дискриминант. 

D = (3a + 11)² — 4 * 1 * (a + 18,25) = 9a² + 66a + 121 — 4a — 73 = 9a² + 62a + 48

2. Поскольку дискриминант должен быть больше 0, то получаем неравенство 9a² + 62a + 48 > 0

3. Решим его «Методом интервалов».

9a² + 62a + 48 = 0
D = 3844 — 1728 = 2116
(a_1 = frac{-62 + 46}{18} = -frac{16}{18} = -89)
(a_2 = frac{-62 — 46}{18} = -frac{108}{18} = -6)

4. Дискриминант будет положительным при (a in (-infty; -6) cup (-frac{8}{9}; +infty)). Это и будет ответ. 

Ответ: (a in (-infty; -6) cup (-frac{8}{9}; +infty)).

Важно: в уравнении мы указываем не сами решения уравнения, а значения параметра, при которых уравнение имеет два решения. 

Пример 2. При каких значениях параметра a уравнение (2a + 1)x² — ax + 3a + 1 = 0 имеет два различных решения? 

Решение. Этот пример похож на предыдущий, однако здесь есть одна важная особенность. Что произойдет с уравнением, если 2a+1 = 0? 

Мы получим уравнение 0,5x — 0,5 = 0, то есть линейное уравнение. У уравнения будет всего одно решение, что уже не подходит под условие задачи. 

1. Поскольку по условию должно быть 2 решения, мы получаем, что a (neq) -0,5. 

2. Найдем дискриминант уравнения. Он должен быть строго больше 0, чтобы у уравнения было два решения. 

D = a² — 4 * (2a + 1) * (3a + 1) = a² — 24a² — 20a -4 = -23a² — 20a — 4

3. Составим неравенство и решим его:

-23a² — 20a — 4 > 0
23a² + 20a + 4 < 0
23a² + 20a + 4 = 0
D = 400 — 4 * 23 * 4 = 400 — 368 = 32
(a_1 = frac{-20 + 4 sqrt{2}}{46} = frac{2sqrt{2} — 10}{23})
(a_2 = frac{-20 — 4sqrt{2}}{46} = frac{-2sqrt{2} — 10}{23})

4. Разложим уравнение на множители: 

(23a^2 + 20a + 4 = 23(a — frac{2sqrt{2} — 10}{23})(a — frac{-2sqrt{2} — 10}{23}))

5. Получаем неравенство:

(23(a — frac{2sqrt{2} — 10}{23})(a — frac{-2sqrt{2} — 10}{23} < 0)

6.Тогда  (a in (frac{-2sqrt{2} — 10}{23}; frac{2sqrt{2} — 10}{23})). Вспомним, что a (neq) -0,5, следовательно, мы получаем ответ (a in (frac{-2sqrt{2} — 10}{23}; -0,5) cup (-0,5; frac{2sqrt{2} — 10}{23})).

Ответ: (a in (frac{-2sqrt{2} — 10}{23}; -0,5) cup (-0,5; frac{2sqrt{2} — 10}{23}))

Теорема Виета 

Дискриминант — не единственный способ решить квадратное уравнение. Обратимся к теореме Виета. Если нам дано уравнение ax² + bx + c = 0, то его корни можно найти с помощью следующей системы: 

Теорему Виета удобно использовать, если на корни уравнения наложены дополнительные ограничения. 

Пример 3. При каких значениях параметра a корни уравнения x² — 3ax — a(a — 1) = 0 удовлетворяют условию x₁ = 5x₂. 

Решение. 1. Корни уравнения — это два различных числа. Значит, дискриминант должен быть строго больше 0: 

D = 9a² — 4 * 1 * (-a² + a) = 9a² + 4a² — 4a = 13a² — 4a = a(13a — 4)

Получаем неравенство a(13a — 4) > 0, следовательно, (a in (-infty; 0) cup (frac{4}{13}; +infty)). 

2. По теореме Виета найдем корни уравнения: 

3. По условию x₁ = 5x₂, тогда 5x₂ + x2 = 6x₂ = 3a, откуда получаем:
(x_2 = frac{3a}{6} = frac{a}{2})
(x_1 = 5 * a_2 = frac{5a}{2})

4. Подставим во второе уравнение системы:
(frac{a}{2} * frac{5a}{2} = a — a^2)
(frac{5a^2}{4} = a — a^2 | * 4)
5a² = 4a — 4a²
(9a^2 — 4a = 0 rightarrow a(9a — 4) = 0 rightarrow a = 0, a = frac{4}{9})

5. Мы нашли значения параметра, при которых выполняется условие. Осталось проверить, чтобы при этих значениях у уравнения было два корня. 

a = 0 не подходит, поскольку ограничение (a in (-infty; 0) cup (frac{4}{13}; +infty)) не включает точку 0. 

(a = frac{4}{9}) подходит, поскольку (frac{4}{9} > frac{4}{13}). 

Ответ: (a = frac{4}{9})

Условия на корни квадратного трехчлена 

Однако могут встретиться еще более сложные задания с параметрами. Рассмотрим каждый из этих случаев. 

1. Корни квадратного трехчлена меньше, чем число N. 

Построим параболу. Вспомним, что ветви параболы могут быть направлены или вверх, или вниз. 

Если ветви параболы направлены вверх. Отметим на оси х точку N так, чтобы она лежала правее обоих корней уравнения. Так мы зададим условие, что корни уравнения меньше, чем число N. 

Представим, что мы идем по холмистой местности, и у нас есть ее карта. Имея перед собой плоскую картинку, мы понимаем, как относительно друг друга располагаются точки в пространстве. Но посмотрев на рельеф сбоку, заметим, что точки имеют разную высоту. 

Пусть в точках, где парабола пересекает ось х, будут привалы на экскурсионном маршруте, а в точке N будет смотровая площадка. 

Что можно сказать про смотровую площадку на этой карте? Она находится выше, чем привалы, и лежит правее, чем самая низкая точка рельефа. 

Рассмотрим эти условия на графике. В точке N значение функции f(x) больше, чем в корнях уравнения. Более того, она лежит правее, чем вершина параболы, то есть ее абсцисса больше абсциссы параболы. 

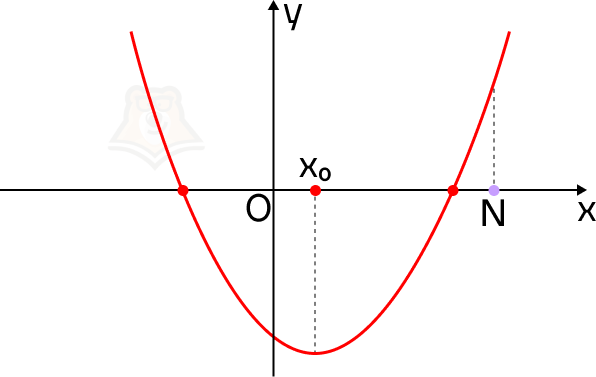
Почему эти условия так важны? Пусть точка N будет лежать левее вершины параболы. Тогда не выполняется условие, что корни меньше, чем N. 

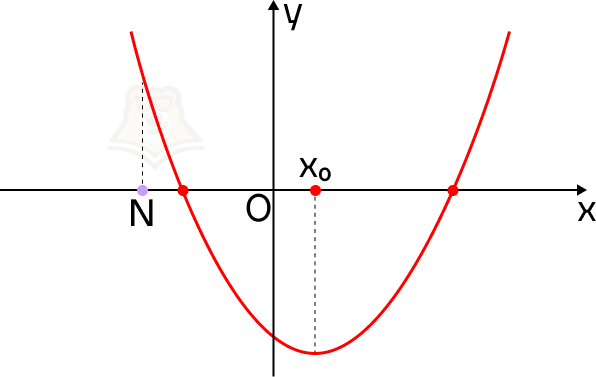
В этом случае на нашем экскурсионном маршруте смотровая площадка будет лежать до привалов. 

А если значение функции в точке N будет меньше, чем в корнях уравнения? Точка N будет лежать между ними. 

В этом случае смотровая площадка окажется между привалами. 

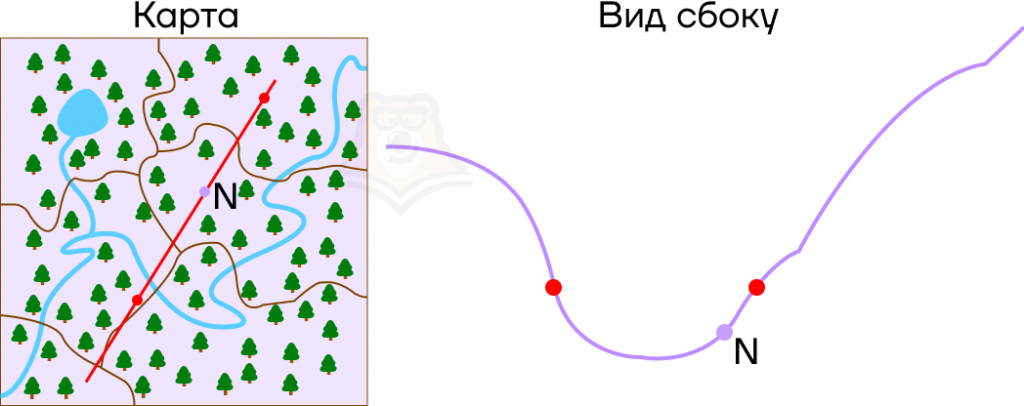
Аналогичным способом можно проследить изменение условий при любом положении точки N на графике. 

Для того чтобы оба корня квадратного трехчлена ax² + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий: 

Что произойдет, если ветви параболы будут направлены вниз? Наш экскурсионный маршрут немного поменяется: появится гора, а не овраг. 

Где теперь располагается смотровая площадка? Она будет ниже, чем привалы, и дальше, чем самая высокая точка горы. 

Мы можем сделать вывод, что точка N на графике будет лежать правее вершины параболы, а значение функции в ней будет меньше, чем значение функции в корнях уравнения. 

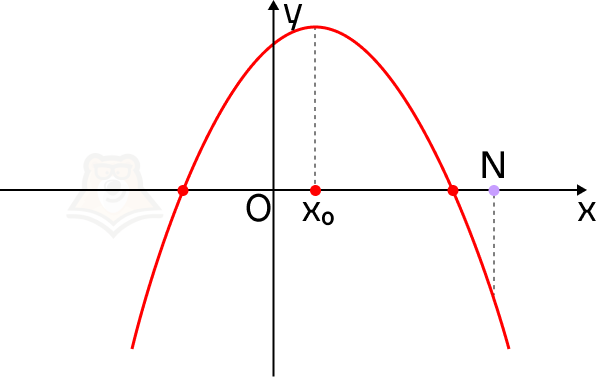
Для того чтобы оба корня квадратного трехчлена ax² + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий: 

2. Корни квадратного трехчлена больше, чем число N. 

Рассуждаем так же, как и в предыдущей функции, однако теперь точка N перемещается левее параболы. 

Если ветви параболы направлены вверх, то функция в точке N принимает большее значение, чем в корнях уравнения, а сама точка N будет лежать левее параболы. 

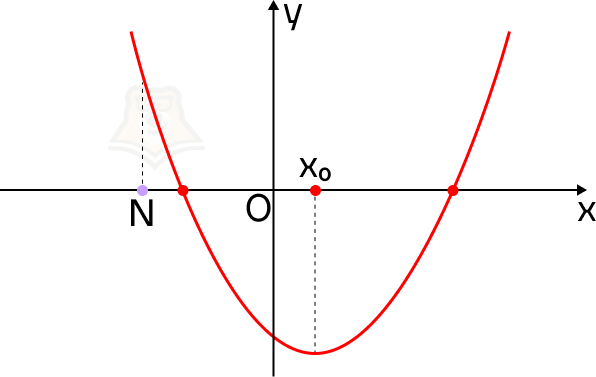
Для того чтобы оба корня квадратного трехчлена ax² + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий: 

Теперь направим ветви параболы вниз. Значение функции в точке N будет меньше, чем в корнях уравнения. 

Для того чтобы оба корня квадратного трехчлена ax² + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий: 

С помощью анализа расположения точек на графике функций можно задать условия для любой ситуации, даже если точек будет несколько. 

В итоге должна получиться система, с помощью которой можно решить задачу.

Фактчек

• Параметр — это буква a, вместо которой можно подставить число. Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется. 
• При решении линейного уравнения ax=b в зависимости от значения коэффициентов может получиться несколько вариантов решений. Если a = 0, b = 0 — бесконечное множество решений. Если a = 0, b (neq) 0 — решений нет. Если a (neq) 0, b (neq) 0 — решением будет (x = frac{b}{a}). 
• При решении квадратного уравнения обязательно проверять коэффициент перед x². Если коэффициент будет равен 0, то уравнение станет линейным.
• При решении квадратного уравнения важно учитывать значение дискриминанта: если он строго больше 0, то корней у уравнения два, если дискриминант равен 0, то у уравнения один корень, если дискриминант меньше 0, то у уравнения нет корней. 
• Решить квадратное уравнение можно и с помощью теоремы Виета. 
• Если в задаче даны дополнительные условия на корни уравнения (например, они должны быть больше или меньше определенного числа), то задать их можно с помощью системы. Неравенства в системе можно составить с помощью анализа примерного графика функций. 

Проверь себя

Задание 1. 
Что такое параметр?

1. Это буква a, вместо которой можно подставить число.
2. Это коэффициент перед x² в квадратном уравнении.
3. Это переменная х.
4. Это значение функции в определенной точке. 

Задание 2. 
Дано уравнение ax = b. Сколько решений оно имеет, если a = 0 и b = 0?

1. Решений нет.
2. Одно решение.
3. Бесконечное множество решений.
4. Невозможно определить количество решений. 

Задание 3. 
При каких значениях дискриминанта уравнение будет иметь корни?

1. D > 0
2. D = 0
3. D < 0
4. D (neq) 0

Задание 4. 
Корни квадратного уравнения меньше числа А. Где будет лежать вершина параболы относительно точки А?

1. Справа.
2. Слева.
3. Совпадать с точкой А.
4. Невозможно определить расположение вершины. 

Задание 5. 
Меньший корень квадратного уравнения больше числа А, но меньше числа В. Ветви параболы направлены вниз. Чему будет равно значение функции в точке В?

1. Значение функции в точке В будет меньше 0.
2. Значение функции в точке В будет равно 0.
3. Значение функции в точке В будет больше 0.
4. Невозможно определить значение функции. 

Ответы: 1. — 1 2. — 3 3. — 4 4. — 2 5. — 3.

Основы работы с параметром

Параметр – это буквенный коэффициент в уравнении.

Параметр – это всегда число, а не переменная, но мы не знаем, чему конкретно равен параметр. Например,

(y = kx + b)

это уравнение прямой, в котором (x) – переменная, (y) – зависимая от неё функция, а (k) и (b) – коэффициенты. Это значит, что (k) и (b) – какие-то числа, параметры. Когда мы видим конкретное уравнение прямой, например,

(y = – 5x + 8)

мы можем сказать, что в данном случае параметр (k = – 5), а параметр (b = 8). В зависимости от параметров функция может по-разному себя вести, но сам вид линейной функции не поменяется.

УРАВНЕНИЕ С ПАРАМЕТРОМ:

Существуют уравнения, где есть две неизвестных: (x) – корень уравнения и (a) (или любая другая буква) – параметр. Решение таких уравнений сводится не к поиску конкретных корней, а к анализу их количества. Для этого мы предполагаем, чему будут равны корни уравнения при определенных параметрах.

АЛГОРИТМ РЕШЕНИЯ УРАВНЕНИЙ С ПАРАМЕТРОМ

Рассмотрим примеры.

Пример №1:

Сколько корней имеет уравнение

(ax = 3a + 7)

1. Данное уравнение не имеет ограничений для (x), поэтому перейдем ко второму пункту.

2. Начнем рассуждать. В случае работы с параметром нужно предположить, как мы будем искать корень, если коэффициент при икс равен нулю и если не равен ему. В данном случае коэффициент при иксе и есть параметр. Допустим, (a = 0), тогда уравнение будет иметь вид:

(0 = 7)

Это невозможно, из чего делаем вывод, что при (a = 0) корней нет.

1. Теперь представим, что параметр не равен нулю, а равен любому другому числу (a neq 0), тогда выразим икс:

(x = frac{3a + 7}{a})

При условии, что (a neq 0), а равно обычному числу, (x) будет принимать одно единственное значение.

1. Так мы нашли, при каких параметрах уравнение будет иметь один корень, нужно проверить этот корень на ограничения. Этих ограничений из п.1 нет, значит мы полностью проанализировали уравнение и узнали, сколько корней оно будет иметь во всех возможных случаях изменения параметра:

({корней нет при a = 0 }{один корень frac{3a + 7}{a} при a neq 0 })

Ответ так и запишем.

Ответ: (корней нет при a = 0); (один корень frac{3a + 7}{a} при a neq 0).

При работе с линейными уравнениями нет ограничений для переменных и для параметра. Сейчас мы рассмотрим дробно-рациональное уравнение с параметром, где на каждом этапе нужно помнить об ограничениях в знаменателе.

Пример №2:

Сколько корней имеет уравнение

(frac{4}{x – 3} – frac{k}{2} = 2)

1. Для начала нужно выписать все ограничения для переменной. Знаменатель не может быть равен нулю, значит:

(x – 3 neq 0)

(x neq 3)

(frac{8}{2left( x – 3 right)} – frac{kleft( x – 3 right)}{2left( x – 3 right)} = frac{4left( x – 3 right)}{2(x – 3)})

(frac{8 – kx + k3}{2(x – 3)} = frac{4x – 12}{2(x – 3)})

Ограничение для переменной мы записали, поэтому смело можно убрать знаменатель и приравнять числители. Про ограничение не забывать!

(8 – kx + 3k = 4x – 12)

1. Вправо перенесем все с иксами, а влево перенесем все остальные числа:

(8 + 3k + 12 = 4x + kx)

(20 + 3k = xleft( 4 + k right))

1. Мы снова пришли к ситуации, когда (x) умножается на какое-то число ((4 + k)), значение которого мы не знаем, т. к. в нём есть параметр. Снова анализируем количество корней, если весь коэффициент перед (x) равен нулю, то есть:

(4 + k = 0)

(k = – 4)

тогда

(x = frac{20 + 3k}{0})

Чего не может быть, значит корней нет.

1. Рассмотрим случай, когда (4 + k neq 0):

(k neq – 4)

тогда

(x = frac{20 + 3k}{k})

Получается, что существует один единственный корень.

1. Мы не учли то, что единственным корнем может оказаться число 3, но в начале мы записали ограничение (x neq 3). Поэтому уравнение будет иметь один корень ( x = frac{20 + 3k}{k}) при (k neq – 4), если

(x = frac{20 + 3k}{k} neq 3)

Найдем такой параметр (k), при котором (x = 3). Нужно проверить, есть ли такой параметр, и если есть – исключить его:

(frac{20 + 3k}{k} = 3)

(20 + 3k = 3k)

(20 = 0)

Что невозможно, значит такого параметра не существует, и уравнение имеет ровно один корень без ограничений, кроме (k neq – 4). Запишем ответ.

Ответ: корней нет при (k = – 4); один корень (x = frac{20 + 3k}{k}) при (k neq – 4).

Поговорим немного о заданиях с параметром и графическом методе их решения.

Идея метода заключается в выражении функции параметра и поиск нужных промежутков на графиках.

Естественно, наглядность “решает”. Нарисовав график (или хотя бы схематичную картинку), можно либо сразу определить нужные промежутки, либо понять, что именно нужно просчитывать (например, точки пересечения каких графиков, или касательную к какой функции достаточно найти, чтобы успешно справиться с заданием).

Рассмотрим несколько параметрических задач и способы их решения