-
Короткое обучающее видео
Посмотрите Обучающее Видео, объясняющее
как вводить условие задачи. -
Как ввести условие задачи
Нажмите на кнопку “Ввести свою задачу”. После этого вводите условие либо с вашей
клавиатуры, либо с клавиатуры на экране. Для добавления специальных математических
конструкций, таких как интеграл или дробь, пользуйтесь клавиатурой на странице. По
условию можно перемещаться с помошью кнопок на вашей клавиатуре: влево, вправо, вверх,
вниз или с помощью мыши кликая в нужную область. Если вы хотите скопировать условие или
чсть условия, выделите ее(зажимаете кнопку shift и стрелочками влево или вправо
выделяете нужную область) и нажмите ctrl+c. Для вставки в необходимое место нажите
ctrl+v. При копировании происходит автоматическая трансформация в математический формат
латех, поэтому ваше условие вы можете скопировать как в свой текстовый редактор, так и в
другое окно ввода на сайте. За один раз можно решить только одну задачу. -
Как ввести систему уравнений
Если вы ввели несколько условий, они буду рассматриваться как система, например система
уравнений или неравенств. -
Как упростить выражение
Просто введите ваше выражение как условие и нажмите на кнопку “Решить”. Не нужно ставить
знак “=” в конце вашего выражения или выполнять какие-либо еще другие действия -
Переменные и параметры
По умолчанию при решении переменными являются x,y,z, a параметрами:a,b,c. Если у вас в
задаче указаны другие переменные или параметры, нажмите на кнопку “Настройки”, введите
ваши переменные и параметры через запятую в соответствующие поля и нажмите на кнопку
“ОК”. При решении следующей задачи не забудьте вернуть исходный вариант. Для этого
просто очистите поля и нажмите кнопку “ОК”. -
Как вводить геометрию
Старайтесь вводить геометрию точь в точь как в учебнике. Орфография очень важна.
Используйте перенос строки на клавиатуре. -
Как заполнять серые квадратики
Чтобы заполнить серый квадратик переведите в него курсор. Сделать это можно либо нажимая
стрелки <-,-> на клавиатуре, либо просто кликните мышкой в него. Далее введите
туда ваши данные и нажмите на пробел либо на стрелку ->. -
Как вводить начальные условия для дифференциальных уравнений
Начальные условия вводите как обычные условия. Порядок не важен. Например:
Условие
1: y’=y+x
Условие 2: y(0)=1 -
Сдвиг курсора на один символ влево: ←
Чтобы сдвинуть курсор влево от текущей позиции, нажмите на кнопку ←.
-
Сдвиг курсора на один символ вправо: →
Чтобы сдвинуть курсор вправо от текущей позиции, нажмите на кнопку →.
-
Удаление одного символа назад: ←
Чтобы удалить символ, поставьте курсор после символа и нажмите на кнопку ←. Передвинуть
курсор можно либо с помошью стрелок влево и вправо на клавиатуре либо кликнуть мышью в
область после символа. -
Удаление одного символа вперед: del
Чтобы удалить символ, поставьте курсор перед символом и нажмите на кнопку del. Передвинуть курсор можно либо с помошью стрелок влево
и вправо на клавиатуре либо кликнуть мышью в область перед символом. -
Цифра: 0
Чтобы ввести цифру 0, нажмите на кнопку 0.
-
Цифра: 1
Чтобы ввести цифру 1, нажмите на кнопку 1.
-
Цифра: 2
Чтобы ввести цифру 2, нажмите на кнопку 2.
-
Цифра: 3
Чтобы ввести цифру 3, нажмите на кнопку 3.
-
Цифра: 4
Чтобы ввести цифру 4, нажмите на кнопку 4.
-
Цифра: 5
Чтобы ввести цифру 5, нажмите на кнопку 5.
-
Цифра: 6
Чтобы ввести цифру 6, нажмите на кнопку 6.
-
Цифра: 7
Чтобы ввести цифру 7, нажмите на кнопку 7.
-
Цифра: 8
Чтобы ввести цифру 8, нажмите на кнопку 8.
-
Цифра: 9
Чтобы ввести цифру 9, нажмите на кнопку 9.
-
Точка для ввода нецелых чисел
Чтобы ввести точку для ввода нецелого числа(например 10.2), нажмите на кнопку .
-
Ввести переменную: x
Чтобы ввести переменную x, нажмите на кнопку x. Стандартными переменными являются: x,y,z.
Для ввода нестандартной переменной, нажмите на соответствующий символ на вашей
клавиатуре и добавьте данную переменную в настройках. См. подсказку “Переменные и параметры” -
Ввести переменную: y
Чтобы ввести переменную y, нажмите на кнопку y. Стандартными переменными являются: x,y,z.
Для ввода нестандартной переменной, нажмите на соответствующий символ на вашей
клавиатуре и добавьте данную переменную в настройках. См. подсказку “Переменные и параметры” -
Ввести переменную: z
Чтобы ввести переменную z, нажмите на кнопку z. Стандартными переменными являются: x,y,z.
Для ввода нестандартной переменной, нажмите на соответствующий символ на вашей
клавиатуре и добавьте данную переменную в настройках. См. подсказку “Переменные и параметры” -
Ввести корень
Чтобы ввести корень, установите курсор в место, куда необходимо ввести корень (сделать
это можно либо кликнув мышью в нужную область, либо используя стрелки влево, вправо на
клавиатуре). Далее нажмите на кнопку на клавиатуре. Появится корень. Курсор
автоматически окажется под корнем. Далее введите подкоренное выражение и после этого
нажмите на стрелку вправо. -
Ввести переменную в степени
Чтобы ввести переменную в степени, установите курсор в место, куда необходимо ввести
(сделать это можно либо кликнув мышью в нужную область, либо используя стрелки влево,
вправо на клавиатуре). Далее нажмите на кнопку на клавиатуре. Появится x в степени.
Курсор автоматически окажется в степени. Далее введите степень и после этого нажмите на
стрелку вправо. Если нужно изменить перемменную, кликнете на x мышью либо передвиньтесь
на него используя стрелки влево, вправо на клавиатуре. Далее удалите x с помошью красных
клавиш на клавиатуре(красная стрелка влево или del) и введите нужную вам переменную.
Чтобы продолжить ввод формулы справа, кликнете в самую правую часть мышью либо используя
стрелку вправо переведите курсор максимально в правую часть. -
Ввести выражение в степень
Чтобы ввести выражение в степень, установите курсор в место, куда необходимо ввести
(сделать это можно либо кликнув мышью в нужную область, либо используя стрелки влево,
вправо на клавиатуре). Далее нажмите на кнопку на клавиатуре. Появится () в степени.
Курсор автоматически окажется в степени. Далее введите степень и после этого перейдите
внутрь скобок(сделать это можно либо кликнув мышью в нужную область, либо используя
стрелки влево, вправо на клавиатуре). Далее введите нужное выражение в скобках. Чтобы
продолжить ввод формулы справа, кликнете в самую правую часть мышью либо используя
стрелку вправо переведите курсор максимально в правую часть. -
Корень n-ой степени
Чтобы ввести корень n-ой степени, установите курсор в место, куда необходимо ввести
корень (сделать это можно либо кликнув мышью в нужную область, либо используя стрелки
влево, вправо на клавиатуре). Далее нажмите на кнопку на клавиатуре. Появится корень.
Курсор автоматически окажется под корнем. Далее введите подкоренное выражение и после
этого нажмите на квадратик степени мышью, либо перейдите туда использую стрелки влево,
вправо на клавиатуре. Введите степень. -
Дробь
Чтобы ввести дробь, установите курсор в место, куда необходимо ввести дробь (сделать это
можно либо кликнув мышью в нужную область, либо используя стрелки влево, вправо на
клавиатуре). Далее нажмите на кнопку на клавиатуре. Появится дробь. Курсор автоматически
окажется в числителе. Далее введите числитель и после этого нажмите на квадратик
знаменателя мышью, либо перейдите туда использую стрелки влево, вправо на клавиатуре.
Введите знаменатель. -
+
Чтобы ввести +, нажмите на кнопку +
-
–
Чтобы ввести -, нажмите на кнопку –
-
Знак умножения
Чтобы ввести знак умножения, нажмите на кнопку $cdot$·
-
Знак деления
Чтобы ввести знак деления, нажмите на кнопку :
-
Модуль
Чтобы ввести модуль, нажмите на кнопку, курсор автоматически окажется внутри моддуля,
введите выражение, далее нажмите на стрелку вправо. -
Круглые скобки
Чтобы ввести круглые скобки, нажмите на кнопку, курсор автоматически окажется внутри
скобок, введите выражение, далее нажмите на стрелку вправо. -
cos
Чтобы ввести cos, нажмите на кнопку, введите выражение, далее нажмите на стрелку
вправо. -
sin
Чтобы ввести sin, нажмите на кнопку, введите выражение, далее нажмите на стрелку
вправо. -
tan
Чтобы ввести tan, нажмите на кнопку, введите выражение, далее нажмите на стрелку
вправо. -
cot
Чтобы ввести cot, нажмите на кнопку, введите выражение, далее нажмите на стрелку
вправо. -
ln
Чтобы ввести ln, нажмите на кнопку, введите выражение, далее нажмите на стрелку
вправо. -
lg
Чтобы ввести lg, нажмите на кнопку, введите выражение, далее нажмите на стрелку
вправо. -
log
Чтобы ввести log, нажмите на кнопку, введите выражение под логарифмом, далее нажмите на
квадратик для ввода основания(сделать это можно либо кликнув мышью в нужную область,
либо используя стрелки влево, вправо на клавиатуре), введите основание и перейдите
стрелками в нужную область для продолжения ввода. -
a
Параметр a. Стандартными параметрами являются: a,b,c. Для ввода нестандартного параметра,
добавьте данный параметр в настройках. См. подсказку “Переменные и параметры” -
b
Параметр b. Стандартными параметрами являются: a,b,c. Для ввода нестандартного параметра,
добавьте данный параметр в настройках. См. подсказку “Переменные и параметры” -
c
Параметр c. Стандартными параметрами являются: a,b,c. Для ввода нестандартного параметра,
добавьте данный параметр в настройках. См. подсказку “Переменные и параметры” -
arccos
Чтобы ввести arccos, нажмите на кнопку, введите выражение, нажмите на стрелку вправо.
-
arcsin
Чтобы ввести arcsin, нажмите на кнопку, введите выражение, далее нажмите на стрелку
вправо. -
arctan
Чтобы ввести arctan, нажмите на кнопку, введите выражение, далее нажмите на стрелку
вправо. -
arccot
Чтобы ввести arccot, нажмите на кнопку, введите выражение, далее нажмите на стрелку
вправо. -
‘
Чтобы ввести значок производной, нажмите на кнопку.
-
∫
Чтобы ввести неопределенный интеграл, нажмите на кнопку. Далее введите подинтегральное
выражение, после этого нажмите на кнопку d и введите переменную, по которой нужно
провести интегрирование. Серые квадратики оставьте незаполненными. Чтобы ввести
определенный интеграл, нажмите на кнопку. Далее введите подинтегральное выражение, после
этого нажмите на кнопку d(на своей клавиатуре или клавиатуре сайта) и введите
переменную, по которой нужно провести интегрирование. После этого кликните на нижний
серый квадратик и введите нижний пределе, кликните на верхний серый квадратик и введите
верхний предел.(перейти на серые квадраты можно либо кликнув на них, либо используя
кнопки влево, вправо) -
d
Знак дифференциала. Обозначение переменной, по которой нужно произвести
интегрирование. -
lim
Чтобы ввести предел нажмите на кнопку lim на клавиатуре. Курсор автоматически установится
в место, где нужно ввести функцию. Далее нажмите на серый квадратик ниже значка lim
мышью либо перейдите туда используя клавишы влево, вправо. Введите условие предела.
Далее нажмите на кнопку решить(писать знак равенства после предела не нужно). -
->(стремится)
Чтобы ввести значок ->(стремится), нажмите на кнопку.
-
Знак бесконечности
Чтобы ввести значок бесконечности, нажмите на соответствующую кнопку.
-
Знак суммы(ряда)
Чтобы ввести ряд, нажмите на кнопку суммы на клавиатуре. Курсор автоматически установится
в место, где нужно ввести ряд. Далее нажмите на серый квадратик ниже значка суммы мышью
либо перейдите туда используя клавишы влево, вправо. Введите нижнее условие. Далее
нажмите на серый квадратик выше значка суммы мышью либо перейдите туда используя клавишы
влево, вправо. Введите верхнее условие. Далее нажмите на кнопку Проверить
сходимость. -
Матрица
Чтобы ввести матрицу, нажмите на кнопку. Появится матрица 2 на 2. Каждая ячейка матрицы
должна быть в фигурных скобках {}. Чтобы ввести данные в ячейку, кликните мышью внутрь
фигурных скобок либо перейдите туда используя кнопки влево, вправо. Для того чтобы
добавить ячейку, установите курсор вне фигурных скобок с помошью мыши либо кнопок влево,
вправо и нажмите кнопку добавления элемента. Появятся фигурные скобки, введите туда
значение элемента. Для добавления строки нажмите кнопку добавления строки. -
Добавить элемент в матрицу
Для того чтобы добавить новый элемент(ячейку) в матрицу, установите курсор вне фигурных
скобок с помошью мыши либо кнопок влево, вправо и нажмите кнопку добавления
элемента. -
Добавить строку в матрицу
Для того чтобы добавить новую строку в матрицу, нажмите кнопку добавления строки.
-
Факториал(!)
Чтобы ввести факториал, нажмите на кнопку !
-
n
Чтобы ввести переменную n, нажмите на кнопку n
-
Разложить в ряд Фурье
Чтобы разложить в ряд Фурье, необходимо ввести задачу в виде двух условий, например:
1. y(x) = 5x
2. (-3,3)
-
Разложить в ряд Тэйлора
Чтобы разложить в ряд Тэйлора, необходимо ввести задачу в виде двух условий, например:
1. y(x) = sinx
2. x = 0
-
Провести анализ функции
Полное исследование функций:
– Промежутки возрастания, убывания
– Экстремумы
– Промежутки выпуклости, вогнутости
Задайте функцию в виде одного условия, например:
1. y(x) = x+5
Поиск значений выражений — основное математическое действие. Им сопровождается каждый пример, задача. Поэтому чтобы вам было проще работать с различными математическими выражениями, подробно разберем способы и правила их решения в данной статье. Правила представлены в порядке увеличения сложности: от простейших выражений до выражений с функциями. Для лучшего понимания каждый пункт сопровождается подробным пояснением и расписанными примерами.
Поиск значения числовых выражений
Числовые выражения представляют собой математические задачи, состоящие, преимущественно, из чисел. Они подразделяются на несколько групп в зависимости от своей сложности: простейшие, со скобками, корнями, дробями и т.д. Каждый тип выражений подразумевает свои правила нахождения значения, порядок действий. Рассмотрим каждый случай подробнее.
Простейшие числовые выражения. К простейшим числовым выражениям относятся примеры, состоящие из двух элементов:
- Числа (целые, дробные и т.д.);
- Знаки: «+», «—», «•» и «÷».
Чтобы найти значение выражения в данном случае, необходимо выполнить все арифметические действия (которые подразумевают конкретные знаки). В случае отсутствия скобок решение примера производится слева направо. Первыми выполняются действия деления и умножения. Вторыми — сложение и вычитание.
Пример 1. Решение числового выражения
Задача. Решить:
20 — 2 • 10 ÷ 5 — 4 = ?
Решение. Чтобы решить выражение, нам необходимо выполнить все арифметические действия в соответствии с установленными правилами. Поиск значения начинается с решения деления и умножения. В первую очередь находим произведение цифр 2 и 10 (если рассматривать с левой стороны, данное действие является первым по значимости). Получаем 20. Теперь это число делим на 5. Итог — 4. Когда известно значение основных действий, можем подставить его в наш пример:
20 — 4 — 4 = ?
Упрощенный пример также решаем слева направо: 20 — 4 = 16. Второе действие: 16 — 4 = 12. Ответ 12.
Решение без пояснений. 20 — 2 • 10 ÷ 5 — 4 = 20 — (2 • 10 ÷ 5) — 4 = 20 — 4 — 4 = 12.
Ответ. 12
Пример 2. Решение числового выражения
Задача. Решить:
0,2 — 5 • (— 4) + 1/2 • 5 • 4 = ?
Решение. Начинаем решение с умножения и деления. Умножая 5 на (— 4) получаем (— 20), т.к. производное сохраняет знак множителя. Далее умножаем 1/2 на 5. Для этого преобразуем дробь: 1/2 = 5/10 = 0,5. 0,5 умножаем на 5. Ответ — 2,5. Далее умножаем полученное число на 4. 2,5 • 4 = 10. Получаем следующее выражение:
0,2 — (— 20) + 10
Теперь нам остается решить сложение и вычитание. В первую очередь раскрываем скобку и получаем:
0,2 + 20 + 10 = 30,2
Решение без пояснений. 0,2 — 5 • (— 4) + 1/2 • 5 • 4 = 0,2 — (— 20) + 10 = 0,2 + 20 + 10 = 30,2
Ответ. 30,2
Находим значение выражения со скобками
Скобки определяют порядок действий при решении примера. Выражения, находящиеся внутри скобок «()» имеют первостепенную значимость, независимо от того, какое математическое действие в них выполняется.
Пример 3. Значение числового выражения со скобками
Задача. Решить:
5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = ?
Решение. Начинаем нахождение значения выражения с решения скобок. Порядок действий определяется слева направо. При этом не забываем, что после раскрытия скобок в первую очередь решаем умножение и деление и лишь потом — вычитание и сложение:
- 7 — 2 • 3 = 7 — 6 = 1
- 6 — 4 = 2
Когда скобки решены, подставляем полученные значения в наш пример:
5 + 1 • 2 ÷ 2
Снова решаем все по порядку, не забывая о том, что деление и умножение выполняется в первую очередь:
- 1 • 2 = 2
- 2 ÷ 2 = 1
Упрощенное выражение выглядит следующим образом:
5 + 1 = 6
Решение без пояснений. 5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = 5 + (7 — 6) • 2 ÷ 2 = 5+ 1 • 2 ÷ 2 = 5 + 1 = 6
Ответ. 6
Значение числового выражения со скобками
Задача. Решить:
4 + (3 + 1 + 4 • (2+3)) = ?
Решение. Подобные примеры решаются поэтапно. Помним, что поиск выражения со скобками начинается с решения скобок. Поэтому в первую очередь решаем:
3 + 1 + 4 • (2+3)
В уже упрощенном примере снова встречаются скобки. Их будем решать в первую очередь:
2 + 3 = 5
Теперь можем подставить определенное значение в общую скобку:
3 + 1 + 4 • 5
Начинаем решение с умножения и далее слева направо:
- 4 • 5 = 20
- 3 + 1 = 4
- 4 + 20 = 24
Далее подставляем полученный ответ вместо большой скобки и получаем:
4 + 24 = 28
Решение без пояснений. 4 + (3 + 1 + 4 • (2+3)) = 4 + (3 + 1 + 4 • 5) = 4 + (3 + 1 + 20) = 4 + 24 = 28
Ответ. 28
Важно: Чтобы правильно определить значение числового выражения с множественными скобками, необходимо выполнять все действия постепенно. Скобки читаются слева направо. Приоритет в решении внутри скобок остается за делением и умножением.
Поиск значения выражения с корнями
Часто алгебраические задания основываются на нахождении значений из-под корня. И если определить √4 несложно (напомним, это будет 2), то с примерами, которые полностью расположены под корнем, возникает ряд вопросов. На самом деле в таких заданиях нет ничего сложного. В данном случае порядок действий следующий:
- Решаем все выражение, которое находится под корнем (не забываем о правильной последовательности: сперва скобки, деление и умножение, а лишь потом — сложение и вычитание);
- Извлекаем корень из числа, которое получили в результате решения обычного примера.
Если же и под корнем имеется корень (например: √ 4 + 8 — √4), то начинаем решение примера с его извлечения (в нашем примере это будет: √ 4 + 8 — 2). Если подкоренные числа возведены во вторую степень, то их квадратный корень будет равняться модулю подкоренного выражения.
Значение числового выражения с корнями
Задача. Решить:
√ 2² • 2² • 3² = ?
Решение. Все действия под корнем одинаковы — умножение. Это дает нам право разделить выражение на множители. Получаем:
√2² • √2² • √3² = ?
Т.к. под квадратным корнем у нас числа, возведенные во вторую степень, получаем:
2 • 2 • 3 = 12
Решение без пояснений. √ 2² • 2² • 3² = √2² • √2² • √3² = 2 • 2 • 3 = 12
Ответ. 12
Нет времени решать самому?
Наши эксперты помогут!
Находим значение числовых выражений со степенями
Следующий математический знак, который имеет приоритет в процессе решения, — степени. Они представляют собой результат многократного умножения числа на себя. Само число является основанием степени. А количество операций умножения — ее показателем. Причем выражен он может быть не только целым числом, но и дробью, полноценным числовым выражением.
Начинается решение выражения со степенями с вычисления самих степеней. Если они представляют собой полноценное выражение (например: [3^{3 cdot 4-10}]), то его необходимо решить в нашем примере это будет: [3^{12-10}=3^{2}=9].
Задача. Решите:
[ 3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=? ]
Решение. Чтобы решить это выражение со степенями, воспользуемся равенством:
[(a cdot b)^{r}=a^{r} cdot b^{r}]
Рассматривая пример слева направо, видим, что у первых двух множителей одинаковые степени. Это позволяет нам упростить выражение:
[ (3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3} ]
Зная, что при умножении степени с одинаковыми показателями складываются, получаем следующее выражение:
[ 21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21 ]
Решение без пояснений: [3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=(3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21]
Ответ. 21
Интересно: Этот же пример можно решить и другим способом, преобразовав число 21 в степени ⅔ в два множителя. В данном случае решение будет выглядеть следующим образом:
[3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot(3 cdot 7)^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot 3^{2 / 3} cdot 7^{2 / 3}=3^{1 / 3+2 / 3} cdot 7^{1 / 3+2 / 3}=3^{1}+7^{1}=21]
Ответ. 21
Задача. Решить:
[ 2^{-2 sqrt{5}} cdot 4^{sqrt{5}-1}+left((sqrt{3})^{1 / 3}right)^{6} ]
Решение. В данном случает получить точные числовые значения показателей степеней не удастся. Поэтому искать значение выражения с дробями в виде степени будем снова через упрощение:

Ответ. 3,25
Выражения с дробями
Поиск значения выражения дробей начинается с их приведения к общему виду. В большинстве случаев проще представить все значения в виде обыкновенной дроби с числителем и знаменателем. После преобразования всех чисел необходимо привести все дроби к общему знаменателю.
Важно: Прежде чем найти выражение дробей, необходимо провести вычисления в их знаменателе и числителе отдельно. В данном случае действуют стандартные правила решения.
Когда дроби приведены к единому знаменателю можно переходить к решению. Вычисление значений верхней строки (числителя) и нижней (знаменателя) производятся параллельно.
Задача. Решить:
[ 6 frac{2}{13}+4 frac{1}{13}=? ]
Решение. Действуя по главному правилу, прежде чем найти значение числового выражения, преобразуем всего его части в простую дробь. Получаем:
[ frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13} ]
Теперь выполняем вычисления в знаменателе и числителе и находим ответ:
[ frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13}=frac{80}{13}+frac{53}{13}=frac{133}{13}=10 frac{3}{13} ]
Ответ. [10 frac{3}{13}]
Примеры(2):

Задача. Решить:
[ frac{2}{sqrt{5}-1}-frac{2 sqrt{5}-7}{4}-3=? ]
Решение. В данном примере мы не можем извлечь корень из пятерки. Но мы можем воспользоваться формулой разложения корней:
[ frac{2}{sqrt{5}-1}=frac{2(sqrt{5}+1)}{(sqrt{5}-1)(sqrt{5}+1)}=frac{2(sqrt{5}+1)}{5-1}=frac{2 sqrt{5}+2}{4} ]
Теперь можем придать нашему первоначальному выражению следующий вид:
[ frac{2 sqrt{5}+2}{4} frac{2 sqrt{5}-7}{4}-3=frac{2 sqrt{5}+2-2 sqrt{5}+7}{4}-3=frac{9}{4} 3=-frac{3}{4} ]
Ответ. [-frac{3}{4}].
Выражения с логарифмами
Как и степени, логарифмы (log), имеющиеся в выражении, вычисляются (если это возможно) в первую очередь. К примеру, зная, что [log _{2} 4=2] мы можем сразу упростить выражение [log _{2} 4+5 cdot 6] до простого и понятного 2 + 5*6 = 32.
Со степенями логарифмы объединяет и порядок выполнения действий. Прежде чем искать значение выражения логарифмов, необходимо вычислить его основание (если оно представлено математическим выражением).
В случаях, когда полное вычисление логарифма невозможно, производится упрощение примера.
Задача. Решить:
[log _{27} 81+log _{27} 9=?]
Решение. Чтобы найти логарифм выражения, воспользуемся свойствами логарифмов и представим значение логарифмов со степенями:
![]()
Это позволит нам решить пример следующим образом:

Ответ. 2
Решаем выражения с тригонометрической функцией
Часто в выражениях встречаются тригонометрические функции. Всего их в математике шесть:
- Синус;
- Косинус;
- Котангенс;
- Тангенс;
- Секанс;
- Косеканс.
Изучение тригонометрии начинается в 9-м классе, когда ученики уже подготовлены к сложным задачам. Большинство заданий представляются с sin и cos. Остальные функции встречаются значительно реже.
В математических примерах, которые содержат sin, cos, tg и др. функции, вычисление тригонометрической функции производится в первую очередь. Если это невозможно — осуществляется упрощение выражения до получения краткой формулы.
Задача. Решить:
[ frac{24}{sin ^{2} 127+1+sin ^{2} 217} ]
Решение. Разложим 217 на 90 и 127. Т.к. по формуле приведения sin(90 + a) = cosa, получаем:
sin217 — sin (90 + 127) = cos127
Теперь заменяем полученной формулой наше слагаемое в знаменателе дроби:
[ frac{24}{sin ^{2} 127+cos ^{2} 127+1} ]
Вспоминаем, что по тригонометрическому тождеству sin2a+ cos2 a= 1 (независимо от значения угла a). Поэтому одну часть слагаемого знаменателя (sin2127+ cos2127) преобразуем в единицу и получаем:
[ frac{24}{sin ^{2} 127+cos ^{2} 127+1}=frac{24}{1+1}=frac{24}{2}=2 ]
Ответ. 2

Важно: Не стоит бояться буквенных тригонометрических значений. Большинство примеров построено таким образом, чтобы функции можно было заменить более удобной для вычисления формулой. Поэтому вместо того, чтобы пытаться сразу решить пример, стоит обратить внимание на особенности функций и возможность их приведения к подходящей формуле.
Задача. Решить:
[ sqrt{4} 8-sqrt{1} 92 sin ^{2} frac{19 pi}{12}=? ]
Решение. Начинаем решение с разбора второй дроби. Обращаем внимание, что 192 = 48 • 2. А значит, корень этого числа можно представить в виде 2√48. Зная это и используя формулу косинуса двойного угла, преобразим наше выражение:

Теперь по формуле приведения решаем наш пример:
[ sqrt{4} 8 cos left(3 pi+frac{pi}{6}right)=sqrt{4} 8left(-cos frac{pi}{6}right)=-sqrt{4} 8 cdot frac{sqrt{3}}{2}=-4 sqrt{3} cdot frac{sqrt{3}}{2}=-6 ]
Ответ. — 6.
Общий случай: находим значения выражений с дробями, функциями, степенями и не только
Самым сложным считается поиск числовых выражений общих случаев. Они представляют собой тригонометрические примеры, которые могут содержать:
- Степени;
- Скобки;
- Корни;
- Функции и т.д.
Общие числовые выражения сложны только длительностью решения. В остальном же они ничуть не сложнее, чем решение каждого примера (со скобкой, степенями, функциями и т.д.) по отдельности.
Чтобы найти значение выражения с логарифмами, тригонометрическими функциями, скобками и/или другими действиями, необходимо помнить три основных правила:
- Упрощение. Прежде чем приступать к решению внимательно изучите выражение. Особенно — его степени, корни, логарифмы, функции. В большинстве случаев их можно сократить или заменить простым числовым значением еще до решения.
- Скобки. Независимо от типа выражения, действий, начинать решение всегда необходимо со скобок. Часто именно игнорирование этого правила приводит к получению неверного ответа или отсутствию решения в принципе.
- Общий вид. Старайтесь привести выражение к общему виду. Особенно это касается дробей. Смешанные и десятичные дроби преобразуйте в обычные.
- Последовательность. Действия в скобках и действия после их решения выполняются слева направо. В первую очередь необходимо совершать умножение и деление. Когда все произведения и частные найдены, можно переходить к сложению и вычитанию.
Для удобства решения и устранения возможных ошибок рекомендуем расставлять порядок действий непосредственно над математическими знаками.
Задача. Решить:
[ -frac{sqrt{2} sin left(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)right)+3}{operatorname{Ln} e^{2}}+left(1+3^{sqrt{9}}right)=? ]
Решение. Чтобы решить этот пример, сначала найдем значение выражения числителя дроби, а точнее — подкоренного выражения. Для этого необходимо вычислить значение sin и общего выражения. Начинаем с раскрытия скобок в числителе:

Полученное значение можем подставить в подкоренное выражение для вычисления числителя дроби:
[ sqrt{2} sin cdotleft(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)+3=sqrt{4}=2right. ]
Со знаменателем дела обстоят куда проще:
[ ln e^{2}=2 ]
Числитель и знаменатель у нас одинаковые, что позволяет нам их сократить:

Теперь остается решить следующее выражение:

Ответ. 27
Как видите, при последовательном решении примеров с большим количеством действий нет ничего сложного. Главное — верно обозначить последовательность шагов и четко ей следовать.
Как найти значение выражения числителя дроби, подкорневого значения рационально?
Независимо от типа выражения решать его необходимо последовательно, руководствуясь стандартными правилами (описаны ранее). Но не стоит забывать, что во многих случаях поиск ответа может быть значительно упрощен за счет рационального подхода к решению. Основывается он на нескольких правилах.
Правило 1. Когда произведение равно нулю
Производное равно нулю в том случае, если хотя бы один из его сомножителей равен нулю. Если вы решаете пример из нескольких сомножителей, одним из которых является «0», то проводить многочисленные вычислительные действия не стоит.
Например, выражение [3 cdotleft(451+4+frac{18}{3}right)left(1-sin left(frac{3 pi}{4}right)right) cdot 0] будет равняться нулю.
Правило 2. Группировка и вынесение чисел
Ускорить процесс поиска ответа можно за счет группировки множителей, слагаемых или вынесения единого множителя за скобки. Также не стоит забывать о возможности сокращения дроби.
Например, выражение [frac{left(451+4+frac{18}{3}right)}{4left(451+4+frac{18}{3}right)}] решать не надо. Достаточно сократить скобки, чтобы получить ответ [=frac{1}{4}]
Решение примеров с переменными
Примеры с переменными отличаются от числовых только формой предоставления. В данном случае значения предоставляются дополнительно к выражению.
Пример задания: Найдите значение выражения 2x — y, если x = 2,5, а y = 2. В данном случае решение будет выглядеть следующим образом:
2x — y = 2 • 2,5 — 2 = 3
При этом в таких примерах сохраняются все описанные выше правила. Касается это и советов по рациональному решению примеров. Так, решать дробь [frac{sqrt{y}}{sqrt{y}}] бессмысленно, т.к. при любых значениях «y» ответ будет одинаковым — 1.

Получите пошаговые объяснения
Узнайте, как решать задачи, и покажите свою работу, а также получите определения для математических понятий
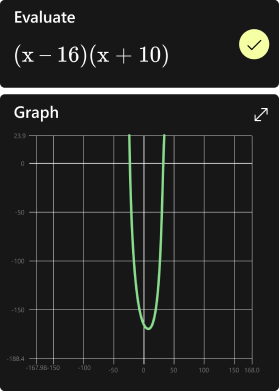
Создавайте графическое представление ваших математических задач
Мгновенно представьте любое уравнение в графическом виде, чтобы визуализировать вашу функцию и понять связь между переменными
Практика, практика и ещё раз практика
Ищите дополнительные учебные материалы, такие как связанные журналы и видеоуроки

Получите справку по математике на своем языке
Работает на испанском, хинди, немецком и других языках
Универсальный способ решения: составить систему уравнений, подставить известные значения и вычислить неизвестные. Раз у нас 2 объекта, то 2 уравнения описывают движение этих объектов, а остальные уравнения берутся из условий задачи.
- s1 = v1 ⋅ t, формула движения, где s1 – длина пути автобуса №1, v1 – скорость автобуса №1, t – время движения каждого объекта.
- s2 = v2 ⋅ t, формула движения, где s2 – длина пути автобуса №2, v2 – скорость автобуса №2, t – время движения каждого объекта.
Отметим, что время движения у них одинаковое, поэтому мы его обозначили одинаково как t.
Базовыми единицами измерения возьмём км для пути, ч для времени и км/ч для скорости.
Итак, у нас в формулах есть 5 величин, из которых 3 известные (s1=100, v1=25, v2=50) и 2 неизвестные (s2, t), которые предстоит найти для получения результата.
Для успешного решения неизвестных должно быть столько же или меньше, чем уравнений. В нашем случае одинаково – 2, то есть скорее всего решение найдётся.
В Интернете столько различных программ, что возникает вопрос: можно ли вычислять примеры для их решения в режиме онлайн. Такие приложение уже существуют. Они самостоятельно ищут ответ на ваши задачи и показывают на экране ответ. Это очень удобно и практично. О них и пойдёт речь далее.
Содержание
- «Математический сканер по фото» — поможет вычислить любой пример
- Порядок действий для проведения вычислений онлайн:
- Решение задач онлайн через камеру телефона
- Mathway — онлайн-сервис для вычисления примеров
- «Контрольная работа» — быстрое решение сложных задач онлайн
- Pocket Teacher — поможет вычислить уравнения по математике
- Видео-инструкция
«Математический сканер по фото» — поможет вычислить любой пример
Задание по разным предметам иногда заставляет нас с любой успеваемости зайти в тупик. Пример может сильно отличаться от тех, которые были рассмотрены в школе. Чтобы решить его, придется искать решение в Интернете вручную. Или просить более опытных людей помочь с этим заданием. Есть ещё один вариант выхода с этого положения — воспользоваться онлайн сканером «Математический сканер по фото» на Андроид.
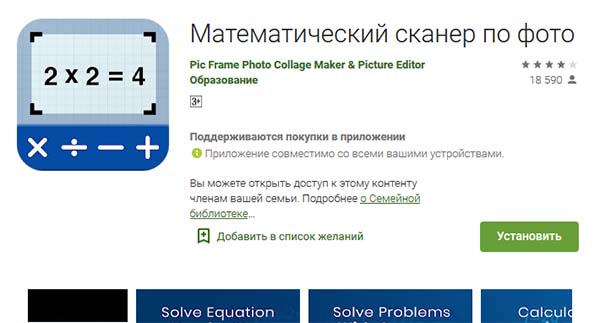
Он устанавливается на мобильный телефон в виде приложения и способен решать ваши задания при помощи фотографии.
Порядок действий для проведения вычислений онлайн:
- Работать сканер может в двух режимах: по фотографии и при вводе условий вручную;
- Чтобы сфотографировать пример, наведите камеру на условие и нажмите кнопку создания фото;

- На следующем экране появится решение этой задачи с несколькими действиями. Чтобы больше узнать о данном примере, просмотрите внимательно все его этапы решения. И попробуйте разобраться самостоятельно.
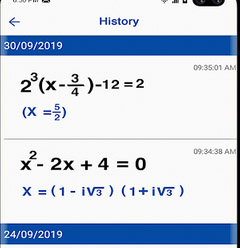
Если не выходит понять задачу, в меню приложение «Онлайн» сканер можно найти статьи по теме. В нём множество учебного материала на разные темы по математике и другим предметам. Для этой программы не требуется подключение к Интернету.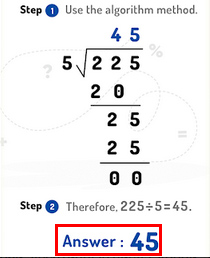 Она может решать любые примеры оффлайн без доступа к базе данным или поисковым системам. В приложение встроен умный калькулятор, который может быть вызван одной кнопкой на панели в меню.
Она может решать любые примеры оффлайн без доступа к базе данным или поисковым системам. В приложение встроен умный калькулятор, который может быть вызван одной кнопкой на панели в меню. 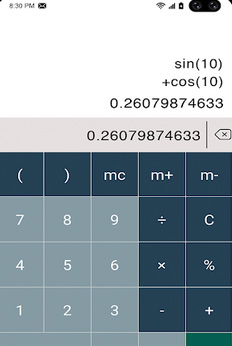 Сканер легко справляется с задачами по математике для начинающих и выпускных классов.
Сканер легко справляется с задачами по математике для начинающих и выпускных классов.
Это может быть полезным: решение задач по физике по фото.
Решение задач онлайн через камеру телефона
С каждым учебным годом математика усложняет задачи для учащихся. Становится всё труднее решать примеры быстро и практически не задумываясь. Появляются новые темы, функции, уравнения и прочее. Чтобы со всем этим справиться при вычислении примеров с верным решением, используйте «Камеру Калькулятор» на Андроид.
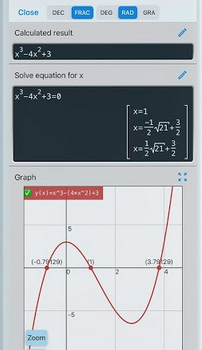
Это один из лучших способов решать примеры автоматически, применяя лишь камеру мобильного телефона. Пользователю нужно сфотографировать пример, чтобы решить его.
Возможности приложения:
- В приложении есть умный и удобный калькулятор для решения любых задач по предмету;
- Встроен научный калькулятор со всеми инструментами, которые есть в классической версии;
- Отдельно реализован калькулятор уравнений.

Мобильное приложение «Камера Калькулятор» способно справляться с решением интегралов, интеграций, производных, дифференцирования, пределов и многое другое. Для тех пользователей, которым необходимы простые функции, он является таковым. Более сложные инструменты находятся в меню и могут быть запущены при необходимости. Поэтому вычислить любой пример онлайн и получить его подробное решение не составим труда. Программа будет полезна школьникам старших классов, которые сталкиваются со сложными заданиями на самостоятельных работах и контрольных.
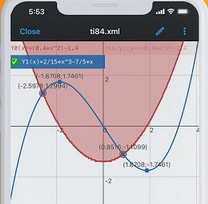
Также «Камера Калькулятор» станет незаменимым помощником для студентов разных профессий. Приложение не займёт много памяти в мобильном телефоне и может работать беззвучно.
Читайте также: решение задач по геометрии по фото.
Mathway — онлайн-сервис для вычисления примеров
С вычислением сложных примеров и их вычислением в Интернете поможет онлайн-приложение Mathway. Без надобности устанавливать какие-либо программы на телефон. Откройте в браузере ссылку на сайт Mathway.com.
При нажатии на кнопку с фотоаппаратом на экране появится виртуальная клавиатура со всеми подходящими символами для решения математических уравнений. Если к вашему устройству подключена веб-камера или вы используете сайт с мобильного устройства, то появится возможность сфотографировать условия задачи.

Также его можно записать в пустой строке, которая выше виртуальной клавиатуры приглашает: «Введите задачу».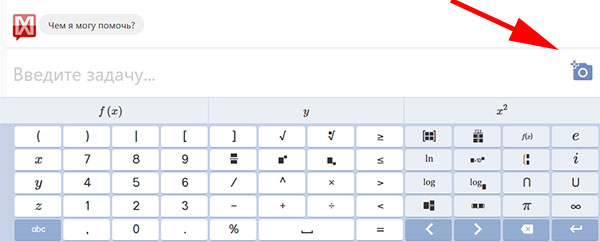 Чтобы выбрать другой предмет в онлайн-сервисе, нажмите на кнопку меню вверху.
Чтобы выбрать другой предмет в онлайн-сервисе, нажмите на кнопку меню вверху.
Среди них можно выбрать:
- Решение задач по элементарной математике;
- Тригонометрии;
- Статистике,
- Алгебре;
- Линейной алгебре;
- Химии;
- Создание графиков;
- Основа математического анализа.
В меню онлайн-программы доступны примеры по разным предметам. Чтобы их открыть, нажмите на кнопку с тремя точками вверху. И выберите пункт «Примеры».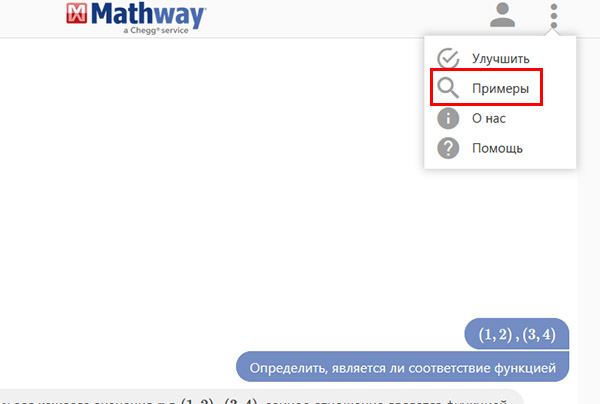 Появится новый раздел, где вы сможете выбрать примеры по алгебре. Для того, чтобы рассмотреть один из них, выберите его курсором мыши или тапом по экране мобильного. Когда пример будет выбран, его условия и решение развернется на экране.
Появится новый раздел, где вы сможете выбрать примеры по алгебре. Для того, чтобы рассмотреть один из них, выберите его курсором мыши или тапом по экране мобильного. Когда пример будет выбран, его условия и решение развернется на экране.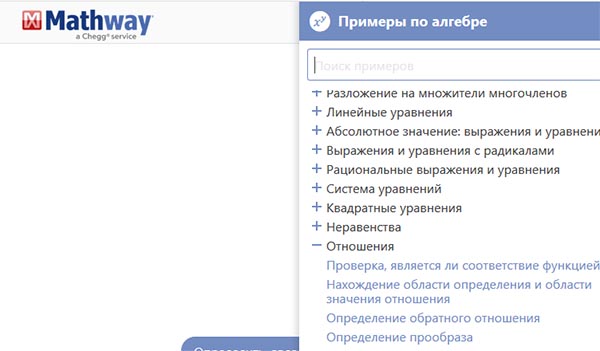 Дополнительно появится возможность открыть каждый шаг в решении. Или показать график из этого примера на экране. Ссылки для этого в конце примера.
Дополнительно появится возможность открыть каждый шаг в решении. Или показать график из этого примера на экране. Ссылки для этого в конце примера.
«Контрольная работа» — быстрое решение сложных задач онлайн
Быстро и точно примеры может решать сервис «Контрольная работа» www.kontrolnaya-rabota.ru/s. Всё что нужно пользователю — это ввести условие в пустую строку. Сервис удобно использовать на мобильном телефоне через браузер или на компьютере во время выполнения задания. Чтобы получить большой список калькуляторов для разных условий, на главной странице необходимо выбрать кнопку «Начать сейчас».
Чтобы получить большой список калькуляторов для разных условий, на главной странице необходимо выбрать кнопку «Начать сейчас».
Из перечня перед вами можно выбрать:
- Решение уравнений и упрощённых выражений онлайн с возможностью вводить условия;
- Калькулятор для решения неравенств с отображением графиков решения на экране;
- Поиск пределов в сервисе — найдите его для любой функции. Применяются решения по Лопиталю;
- На сайте есть производные функций, графики. Вы сможете построить свой график в пространстве;
- Калькулятор для решения неравенств;
- Доступны практически любые действия с неравенствами: умножение, возведение в степень, ранг матрицы, обратные матрицы и другое;
- На сайте есть возможность решить со своими условиями комплексные числа, геометрическую интерпретацию.

Кроме этого на сайте ещё множество возможностей, связанных с решением математических задач и условий по другим предметам. Можно найти таблицы интегралов, Брадиса, таблицы производных. Примеры из высшей математики и полезные и интересные калькуляторы. Если у вас возникнут трудности, в нижней части списка с возможностями находится подробная инструкция, как пользоваться тем или иным инструментом. Представлено множество текстов, описывающих не только работу калькуляторов и таблиц, но и с рассмотрением конкретных примеров.
Pocket Teacher — поможет вычислить уравнения по математике
Рассмотрим ещё один интересный онлайн-сервис с решениями для математики. Называется он Pocket Teacher.
Ссылка: https://www.pocketteacher.ru/solve-page. Сайт является большим и всесторонним инструментом, для решения практически любых математических условий заданий. На главной странице пользователю предлагается выбрать один из трёх основных разделов сайта: алгебра, геометрия, высшая математика и текстовая задача.
Сайт является большим и всесторонним инструментом, для решения практически любых математических условий заданий. На главной странице пользователю предлагается выбрать один из трёх основных разделов сайта: алгебра, геометрия, высшая математика и текстовая задача. На экране отображается клавиатура с математическими знаками.
На экране отображается клавиатура с математическими знаками.
- Начните вводить символы условия своей задачи;
- Возле примера находятся кнопки для управления вводом. Нажмите «Очистить» или «Удалить», если допустили ошибку при вводе;
- Чтобы пример решить, нажмите на соответствующую кнопку справа и выберите пункт «Решение».
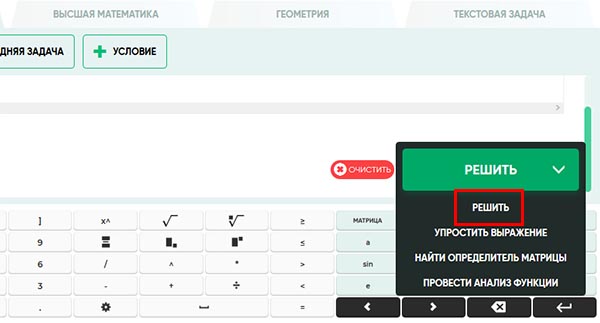
Каждое решение на время сохраняется на сайте. Его можно вернуть при помощи кнопок на панели. Это приложение можно скачать на мобильный телефон с Android или с IOS. Ссылки расположены на главной странице сайта.
Видео-инструкция
Рассмотренные инструменты помогут вычислить любой сложный пример в режиме онлайн с подробным решением. Посмотрите о дополнительных приложениях в видео.

