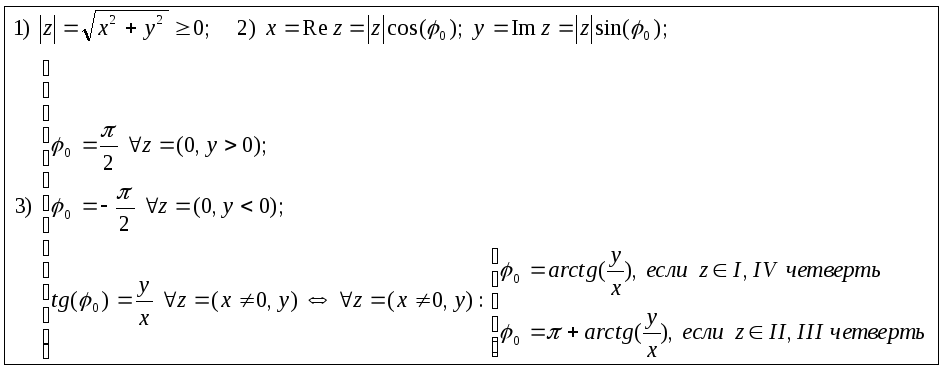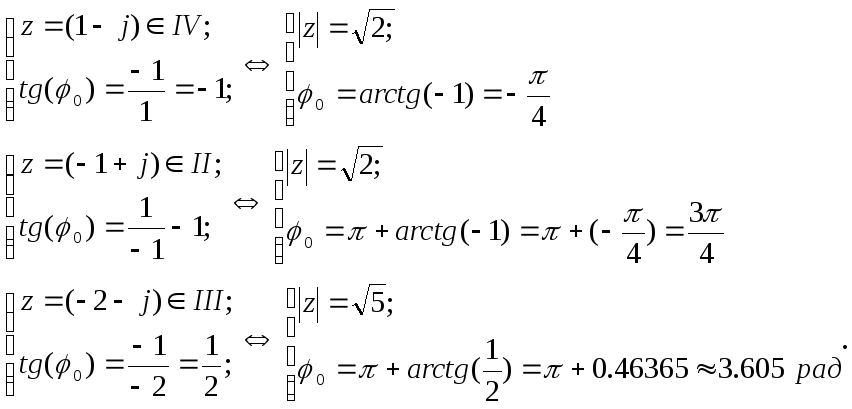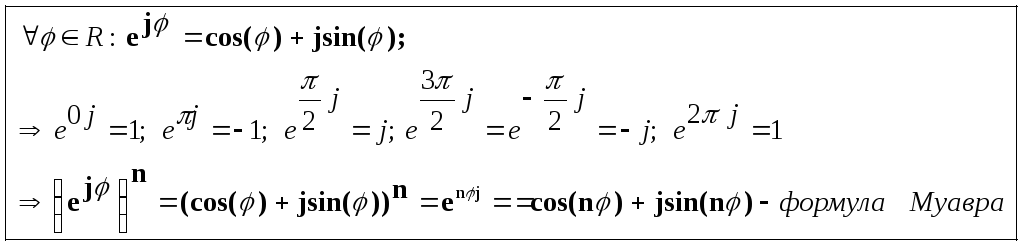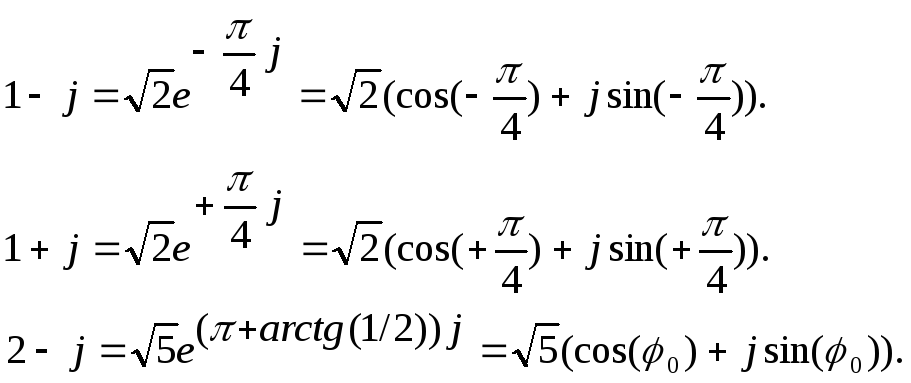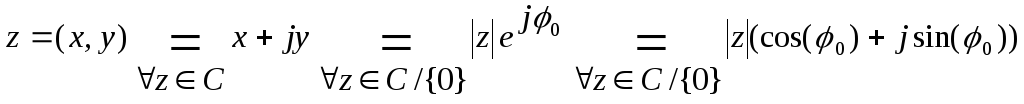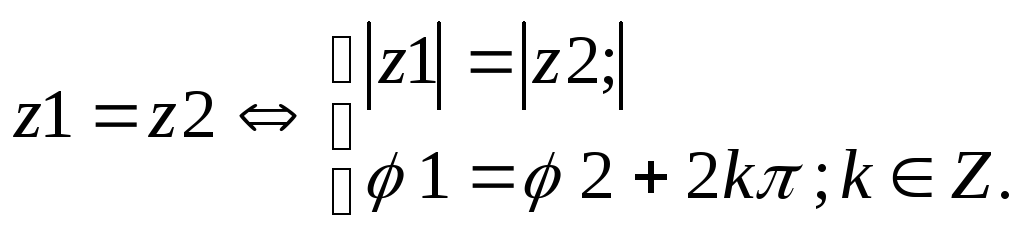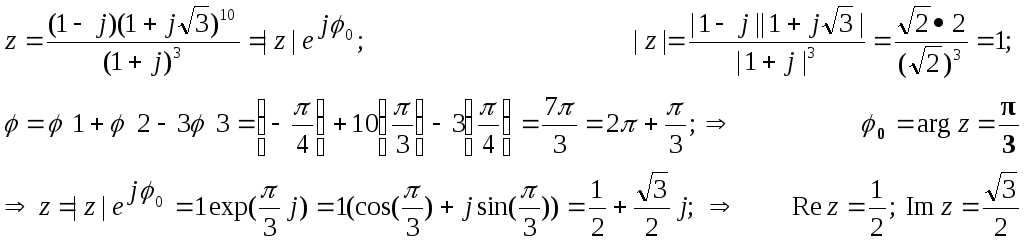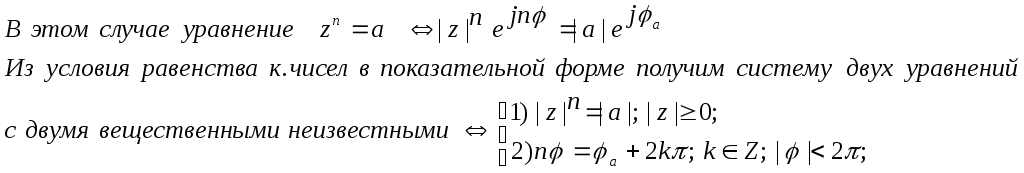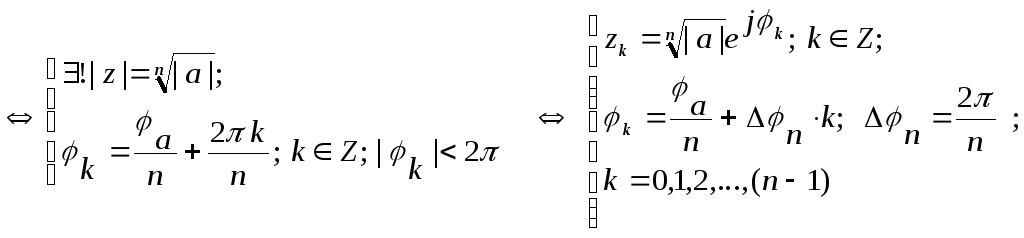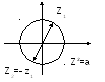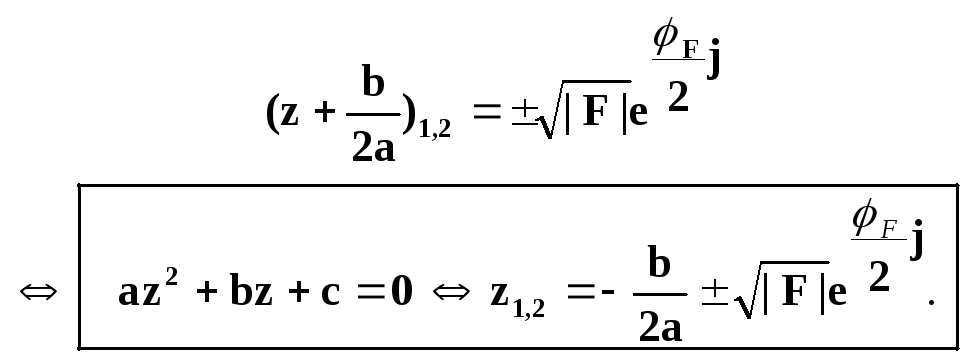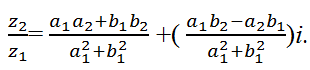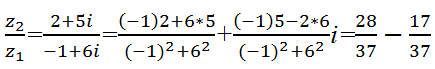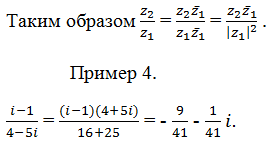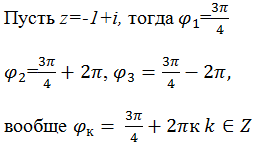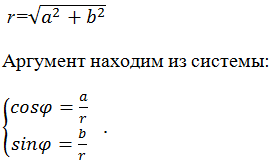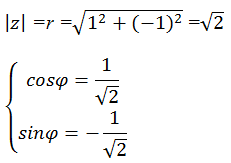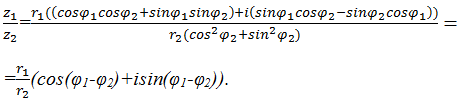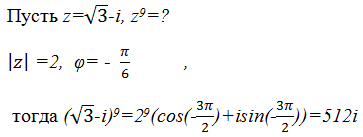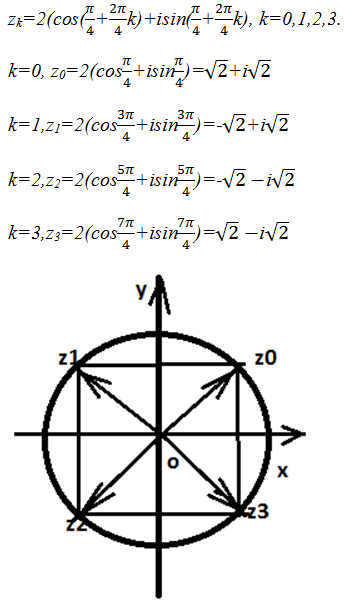Как найти rez imz

Определение. Число вида z = х + iy, где х,  , a i – так называе­мая мнимая единица, называется комплексным числом. Мни­мая единица определяется равенством:

                                                         (2.1)

Действительные числа x и y называются соответственно  действительной и мнимой частью комплексного числа z и обозначаются:

x = Rez;                        y = Imz                                                    (2.2)

Множество комплексных чисел обозначают буквой С.

Например,  – комплексное число, где Rez = 5 – действительная часть; Imz = 8 – мнимая часть.

Определение. Два комплексных числа считают равными тогда и только тогда, когда у них равны соответственно действительные и мнимые части. В частности, комплексное число z = х + iy рав­но нулю тогда и только тогда, когда х =0 и у =0 .

Определение. Числа z = х + iy и z = х – iy называются (комплексно) сопря­женными.

Пример 1

Записать сопряженное число для .

Решение

Сопряженное число: .

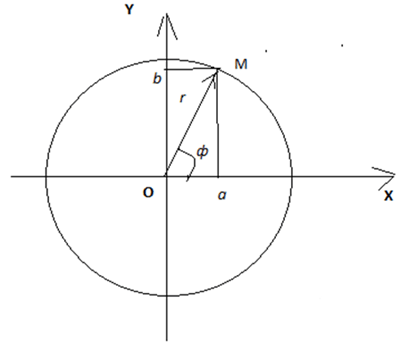
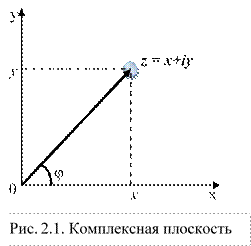
Выбираем на плоскости систему декартовых координат xОy (рис. 2.1) , тогда каждому z = х + iy будет соответствовать вектор  плоскости, начало которого совпадает с началом координат, и, наоборот, каждому вектору  плоскости xОy будет отвечать определённое комплексное число z = х + iy (последнее следует из основной формулы векторного исчисления), где x и y – компоненты (координаты) .

Таким образом, между множеством C и множеством векторов (и точек!) плоскости xOy устанавливается взаимно однозначное соответствие.

Определения. Плоскость xОy называется плоскостью комплексных чисел (или просто комплексной плоскостью), будем её обозначать   Z. Ось Ox – действительная ось; ось Oy – мнимая ось.

Поскольку  – вектор, то он имеет длину и характеризуется направлением.

Длину вектора называют модулем комплексного числа z = х + iy, а величину угла наклона вектора  по отношению к оси Ox – аргументом z. Их обозначают символами:

            и          .                                            (2.3)

Модуль комплексного числа есть однозначная функция:

.                                                        (*)

Из рисунка 2.1 видно, что:

, .                                              (2.4)

Аргумент  есть функция многозначная. Все значения аргумента  удовлетворяют соотношению:

                                                   (2.5)

При  аргумент не определен. Из множества значе­ний  (z0) выделяют одно, лежащее в интервале , которое обозначают argz и называют главным значением аргумента:

                                                       (2.6)

Очевидно, что

                                (2.7)

Из формул (2.5) и (2.6) следует:

                        (2.8)

Пример 2

Дано комплексное число .

Необходимо: найти модуль комплексного числа, изобразить число на комплексной плоскости, найти главное значение аргумента комплексного числа.

Решение

Используем формулу (*) и находим модуль комплексного числа:

Изобразим число на комплексной плоскости (рис. 2.2).

Определим главное значение аргумента комплексного числа , используя формулу (2.8), так как   т.е. , то

Известно, что между
точкой
комплексной
плоскости и соответствующим к. числом
существует взаимно-однозначное
соответствие M(x,y)z=(x,y)C.

В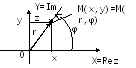ведем
на комплексной плоскости одновременно
две системы координат –прямоугольную
(оси абсцисс X=Rez
и ординат Y=Jmz)
и полярную
(полюс О и
полярная ось ОХ).

Точка на плоскости
определяется

либо
ее прямоугольными
координатами
– абсциссой и ординатой- M(x,y),

либо
ееполярными
координатами
– длиной радиус-вектора точки

и полярным
углом φ
-M(r,φ),
причем

Так как полярный
угол точки определен
не однозначно ₀+2к;
kZ;
|₀|<2,
для взаимно-однозначного соответствия
точки и ее полярных координат в качестве
полярного угла будем принимать ₀:
|₀|<2.

В дополнение к
обозначениям x=Rez;
y=Imz;

,введем
для комплексного
числа Z=C
еще два

определения:

Argz==₀+2к;kZ–
аргумент к.ч.;

argz=₀;
|argz|<2
–главное
значение аргумента к.ч.

Между Rez,
Imz,
|z|
и argz=₀
существуют
следующие соотношения:

“»Воспоминания»:
tg(-₀)=-
tg(₀)

0,рад	/2	/3	/4	/6	0
tg(0)	+	3	1	1/3	0

Например,z=1+j₀=
arg(1+j)=π/4;
=Arg(1+j)=
π/4+2kπ;
kZ.

Д/З: найти
значения argz
для множеств положительных и отрицательных
вещественных чисел.

Из
алгебраической формы к.ч и соотношений
2) следует тригонометрическая
форма к. числа:
zC/{0}:
z=(x,y)=|z|(cos(₀)+jsin(₀))

Кроме того, в третьем
семестре будет доказана формула
Эйлера

Из формулы Эйлера
и тригонометрической формы следует
показательная
форма к. числа:

Например,

—————————————————————————-

Замечания.

1)Условия
равенства к. чисел
:

(а)в
алгебраической форме –

(б)в
показательной и тригонометрической
формах

2)
Алгебраичесая форма предпочтительна
при сложении и вычитании к. чисел;

показательная
и тригонометрическая формы «удобны» в
операциях умножения, деления и возведения
к.чисел в натуральную степень, при этом:

(а)
модули, соответственно, перемножаются,
делятся или возводятся в степень –
;

(б)
аргументы, соответственно, складываются,
вычитаются
или умножаются на показатель степени
–

3)
Так как е^2kj=1,
в записи конечного
результата операций
в показательной (тригонометрической)
форме используется главное
значение аргумента ₀;
|₀|<2:
z=|z|exp[₀+2k)j]=|z|exp(₀j)=|z|(cos(₀)+jsin(₀)).

Экз.
задача. “Найти
Rez,
Imz,
|z|,
argz
и записать три формы к. числа.

§5.Решение двучленных
zⁿ=a
и квадратных z²+bz+c=0
уравнений в С; основная теорема
алгебры.

Пусть
задано в показательной форме к. число
a=|a|e^jφa.
Решение
уравнения zⁿ=a;

будем
искать так же в в показательной форме:

Первое
уравнение имеет единственное решение
-арифметическое значение корня степени
«n»
из неотрицательного числа: 1)
!

Второе
же уравнение системы имеет множество
решений:

Однако,
с учетом того, что e^2kj=1,
различным комплексным числам
соответствуют лишь “n”
значений аргумента:
так
как, например,

Таким
образом,

.

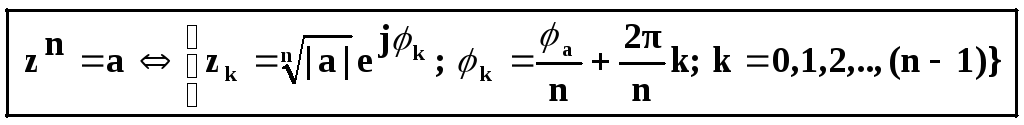
С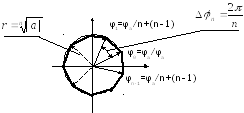ледовательно,
во множестве к. чисел двучленное уранениеzⁿ=a;

имеет
ровно «n»
различных решений.
Эти решения
имеют одинаковые модули, а их аргументы
отличаются на величину, кратную величине
.
На комплексной плоскости решения
уравнениярасполагаются
в вершинах правильного n-угольника,
вписанного в окружность радиуса r=.

Например,
–
решения двучленного квадратного
уравнения –противоположные
к. числа,

Основная
теорема алгебры.
«Полином степени «n”

имеет
ровно «n”
корней
,
считая совпадающие («кратные») корни,
и единственным образом представляется
в виде произведения

».

Например,
1)

2) z²+1=(z-j)(z+j).

Рассмотрим квадратное
уравнение az²+bz+c=0;
a#0.
Выделим по первым двум слагаемым «полный
квадрат»
и
приведем уравнение к двучленному
квадратному.

Обозначим
к. число

и запишем
решения
уравнения
(*) в
виде

Замечание.
Для квадратного
уравнения с
вещественными коэффициентами
имеют место следующие формулы:

1)
Если D>0
( φ_F=0),
получим известную формулу корней
квадратного уравнения с положительным
дискриминантом

Если D<0
(φ_F=π),

–
комплексно-сопряженные числа !!!;

например,

——————————————————————–

Экз.
задача. 1) Найти
и изобразить на к. плоскости все корни
уравнения z³+1=0.

(z1=-1;
z_2,3=0.5(1).
2) Решить уравнение z²+2z+5=0
и доказать, что полученные числа – корни
уравнения.

Экз.+1.
«Решив биквадратное уравнение z⁴+z²+1=0,
(а)записать
три формы всех его решений; (б)изобразить
решения на ;
(в) записать разложение на множители
полинома P₄(z)=
z⁴+z²+1.
(z{(1j3)/2}={exp(j/3)}={[cos(/3)+jsin(/3)]}

Соседние файлы в предмете Алгебра и геометрия

• #
• #
• #
• #
• #
• #

I. Введение.

Во многих разделах математики и ее приложениях невозможно ограничиться лишь
рассмотрением действительных чисел. Например, решение уравнений типа х²+х+1=0,
х²+1=0.

Для их решения надо расширить множество действительных чисел и таким
расширением являются комплексные числа.

Комплексные числа часто называют мнимыми. Это название объясняется тем, что,
хотя стали употребляться еще в XVI веке, они долго продолжали называться даже
выдающимися математиками чем-то реально не существующими, мнимыми в буквальном
смысле. Одному из создателей дифференциального и интегрального исчисления,
немецкому математику Г. Лейбницу (1646–1716) принадлежат,
например, такие слова:

“Комплексное число – это тонкое и поразительное средство божественного духа,
почти амфибия между бытием и небытием”.

Но уже во времена К. Гаусса (1777–1855) было дано геометрическое истолкование
комплексных чисел как точек плоскости. Трудами выдающихся математиков XIX века
О. Коши, Б. Римана, К. Вейерштрасса на базе комплексных чисел была построена
одна из самых красивых математических дисциплин – Теория функций комплексной
переменной.

II. Определение комплексного числа.

Комплексными числами называют выражения вида a +bi , где a и
b – действительные числа, i – некоторый символ и i²=-1,
для которых следующим образом вводятся понятия равенства и операции сложения и
умножения:

1. a₁+b₁i и a₂+b₂i
равны тогда и только тогда когда a₁=a₂ и
b₁=b_2.

2. Суммой a₁+b₁i и a₂+b₂i
есть число (a₁+a₂)+(b₁+b₂)i

3. Произведением чисел a₁+b₁i
и a₂+b₂i , есть число a₁a₂
-b₁b₂+ + (a₁b₂+a₂b₁)i

Комплексные числа часто обозначают одной буквой, причем обычно используют
буквы z и ω.

Равенство z=a+bi называют алгебраической формой записи числа z.

Под разностью z₁-z₂ понимают число (a₁-a₂)+(b₁-b₂)i.

Частное чисел z₂ и z₁ при условии z₁≠0
понимается следующее комплексное число:

Заметим что число 0+bi называют чисто мнимым и записывают bi,

Если b=0, то число a просто действительное.

Действительная часть числа z=a+bi обозначается Rez.

Мнимая часть числа z обозначается Imz.

Тогда z=Rez+Imzi

Пример 1.

Найти сумму и произведение чисел z₁=2+5i ,z₂=-1+7i.

z₁₊ z₂=(2+(-1))+(5+7)i=1+12i

z₁z₂=(2+5i)(-1+7i)=-2+14i-5i+35i²=-37+9i

Пример 2.

Найти разность и частное чисел z₂=2+5i , z₁=–
1+6i

z₂-z₁=3-i

Пример 3 i³=i*i*i=-i, i⁴=i*i*i*i=1.

III. Геометрическая интерпретация комплексных чисел. Модуль и аргументы
комплексного числа.

Рис.1

Хорошо известно, что между множеством действительных чисел и множеством точек
прямой можно установить взаимно однозначное соответствие. Геометрическую
интерпретацию можно использовать и при изучении комплексных чисел.

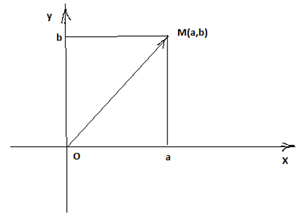
Каждому комплексному числу z=a+bi можно поставить в соответствие точку
M(a,b) координатной плоскости.

Причем: a=Rez, b=Imz

Сама координатная плоскость называется комплексной плоскостью. Ось абсцисс
называется действительной осью, а ось ординат мнимой осью.

Число z=a+bi есть вектор

, исходящий из начала координат О(0,0) и идущий в точку M(a,b).

При сложении z₁ и z₂ складываются их
действительные и мнимые части. При сложении

складываются их координаты.

Таким образом сумма (разность) комплексных чисел геометрически ,векторов,
соответствующих слагаемым комплексных чисел.

Модулем комплексного числа называется длина вектора соответствующего этому
числу и обозначается │Z│.

называется
комплексно сопряженным числу z=a+bi. Тогда имеем:
.
Произведение сопряженных чисел равно квадрату модуля.

Аргументы комплексного числа.

Комплексные числа имеющие один и тот же модуль  │Z│=
r, соответствуют, очевидно, точкам плоскости расположенными на окружности
радиуса r с центром в точке z=0.

Рис. 2

Определение. Аргументом комплексного числа z≠0 называется величина
угла между положительным направлением действительной оси и вектором

, причем величина угла считается положительной, если отчет ведется против
часовой стрелки и отрицательным, если отчет ведется по часовой стрелке. Для
обозначения аргументов комплексного числа z=a+bi используют обозначения
arg(a+bi) или argz. Аргумент комплексного числа z
определяется не однозначно.

Любые два аргумента комплексного числа отличаются друг от друга слагаемым
кратным 2π.

IV. Тригонометрическая форма записи комплексного числа. Операции над
комплексными числами.

Помимо алгебраической формы используются и другие формы записи комплексных
чисел – тригонометрическая форма и показательная форма записи комплексных чисел.

Рассмотрим тригонометрическую форму записи.

Действительная и мнимая части комплексного числа z=a+bi выражаются
через его модуль │Z│=r
и аргумент φ
следующим образом (рис.2).

Поэтому комплексное число z может быть записано в следующем виде:
z= r(cosφ
+ isinφ)

Такая запись называется тригонометрической формой записи.

Для того чтобы перейти от алгебраической формы z=a+bi к
тригонометрической форме записи числа, достаточно найти его модуль и один из
аргументов. Модуль определяется по формуле:

Пример 5.

Записать число z=1-I в тригонометрической форме.

Одним из решений этой системы будет:

но эти записи будут являться алгебраической, а не тригонометрической формой
записи комплексного числа.

Умножение и деление комплексных чисел записанных в тригонометрической форме.

z₁z₂ =r₁r₂(cosφ₁cosφ₂–sinφ₁sinφ₂+i(cosφ₂sinφ₁+cosφ₁sinφ₂)
)= =r₁r₂(cos(φ₁+φ₂₎+isin(φ₁+φ₂)).

Таким образом: модуль произведения двух комплексных чисел равен произведению
модулей, сумма аргументов есть аргумент произведения.

Следовательно, модуль частного двух комплексных чисел равен частному этих
модулей, разность аргументов делимого и делителя является аргументом частного.

Модуль произведения n комплексных чисел равен произведению всех
сомножителей, сумма аргументов всех сомножителей является аргументом
произведения. Отсюда, как частный случай, получается формула, которая носит
название формулы Муавра.

(r(cosφ+isinφ))ⁿ =rⁿ(cosnφ+isinφn)

Пример 6/

Перейдем к операции извлечения корня из данной степени комплексного числа.

Число z является корнем степени n из числа ω, если zⁿ
=ω.

Из данного определения вытекает, что каждое решение уравнения zⁿ=ω
является корнем n из числа ω.

Пусть ω≠0, тогда z=r(cosφ+isinφ),
ω=s(cosψ+isinψ)

Уравнение zⁿ=ω запишем
в виде: rⁿ(cosnφ+isinφn)=s(cosψ+isinψ)

Два комплексных числа равны, когда равны их модули, а аргументы различаются
слагаемым кратным 2π, то есть rⁿ=s и
nφ=ψ+2πk

 как пара комплексных чисел i и –i.

Пример 7.

Найти все значения
.
Запишем число ω =-16 в тригонометрической форме ω=16(cosπ+isinπ).

Рис.3

Точки z₀,z_1,z_2,z₃ есть
вершины квадрата вписанного в окружность радиуса 2.

V. Квадратные уравнения.

Рассмотрим уравнение: ax²+bx+c=0, a≠0

a,b,c – действительные числа , тогда D=b²-4ac
дискриминант и решение задается по формуле: x=
,если
D˂0,то уравнение не имеет решение в действительных числах.

Решим это уравнение в комплексных числах, тогда, если D˂0, мы получаем
решение в комплексных числах:

: z=

Пример 7.

Над множеством комплексных чисел справедлива основная теорема алгебры :
алгебраическое уравнение n – степени имеет ровно n корней.

VI. Комплексная степень числа e. Показательная форма записи.

Возведем e в степень z, где z=x+iy.e^z=e^xe^iy=e^x(cosy+isiny).

Доказательство данной формулы основано на разложении элементарных функций в
ряд Тейлора в окрестности нуля.

Пример 8.

Литература:

1. А.В. Бицадзе “Основы теории аналитических функций”. М, “Наука”,
   1984 г.
2. Г.Н. Яковлев и др. “Алгебра и начала анализа”. М, “Наука”, 1981
   г.

Модуль и аргумент комплексного числа

Пусть задано комплексное число $ z = a+bi $.

Формула

Модуль комплексного числа равен корню квадратному из суммы квадратов мнимой и действительной части и находится по формуле: $$ |z| = sqrt{a^2 + b^2} $$

Если комплексное число состоит только из действительной части $ z = a $, то его модуль равен $ |z| = |a| $.

Стоит заметить, что модуль комплексных чисел всегда неотрицательный $ |z| ge 0 $ и равен нулю $ |z| = 0 $, только в случае $ z = 0 $.

Формула

Аргумент комплексного числа обозначается $ varphi = arg z $ и зависит от полуплоскости, в которой лежат числа $a,b$: $ a > 0 $, тогда $ varphi = arctg frac{b}{a} $ $ a < 0, b ge 0 $, тогда $ varphi = pi + arctg frac{b}{a} $ $ a < 0, b < 0 $, тогда $ varphi = -pi + arctg frac{b}{a} $ $ a = 0, b > 0 $, тогда $varphi = frac{pi}{2}$ $ a = 0, b < 0 $, тогда $varphi = -frac{pi}{2}$

Пример 1

Найти модуль и аргумент комплексного числа $ z = 3 – 4i $.

Решение

Комплексное число состоит из действительной и мнимой части: $$ a = Re z = 3 $$ $$ b = Im z = -4 $$ Применяя формулу вычисления модуля получаем: $$ |z| = sqrt{a^2 + b^2} = sqrt{3^2 + (-4)^2} = sqrt{9+16} = 5 $$ Теперь вычисляем аргумент. Так как $a = 3 > 0$, то получаем аргумент: $$varphi = arctg frac{b}{a} = arctg frac{-4}{3} = -arctg frac{4}{3}.$$

Ответ

$$ |z| = 5, varphi = -arctg frac{4}{3} $$

Пример 2

Найти модуль и аргумент комплексного числа $ z = 3i $

Решение

В данном случае отсутствует действительная часть, а вернее она равна нулю: $$ a = Re z = 0 $$ Мнимая часть комплексного числа равна: $$ b = Im z = 3 $$ Вычисляем модуль по уже известной формуле: $$ |z| = sqrt{a^2 + b^2} = sqrt{0^2 + 3^2} = sqrt{9} = 3 $$ А вот аргумент здесь попадает под правило при $a = 0, b>0$ и значит равен $$varphi = frac{pi}{2}.$$

Ответ

$$ |z| = 3, varphi = frac{pi}{2} $$

Пример 3

Найти модуль и аргумент комплексного числа $$ z = 1+sqrt{3}i $$

Решение

Выписываем действительную и мнимую часть: $$ a = 1 $$ $$ b = sqrt{3} $$ Так как $ a > 0 $, то аргумент равен $$ varphi = arctg frac{sqrt{3}}{1} = arctg sqrt{3} = frac{pi}{3} $$ Находим модуль извлекая квадратный корень из суммы квадратов действительной и мнимой части: $$|z| = sqrt{1^2 + (sqrt{3})^2} = sqrt{1+3}=2.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ varphi = frac{pi}{3}, |z| = 2 $$

Пример 4

Найти аргумент комплексного числа $$ z = -1 + sqrt{3}i $$

Решение

Действительная часть $$ a = Re z = -1 $$ Мнимая часть $$ b = Im z = sqrt{3} $$ Так как $ a < 0 $ и $ b > 0 $, то пользуемся второй формулой: $$ varphi = arg z = pi + arctg frac{sqrt{3}}{-1} = pi + arctg (-sqrt{3}) = $$ $$ = pi – arctg(sqrt{3}) = pi – frac{pi}{3} = frac{2pi}{3}. $$

Ответ

$$ varphi = frac{2pi}{3} $$

Определение 1

Выражение вида $z=a+bi$, где $a$ и $b$ – вещественные числа, а $i$ – «мнимая единица», называется комплексным числом $z$. Мнимая единица определяется равенством $i=sqrt{-1} $ или $i^{2} =-1$.

«Алгебраическая форма комплексного числа» 👇