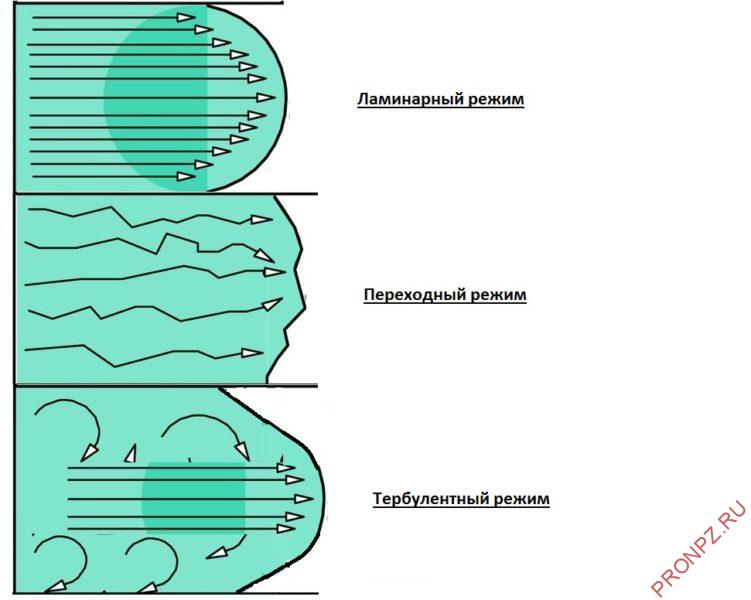
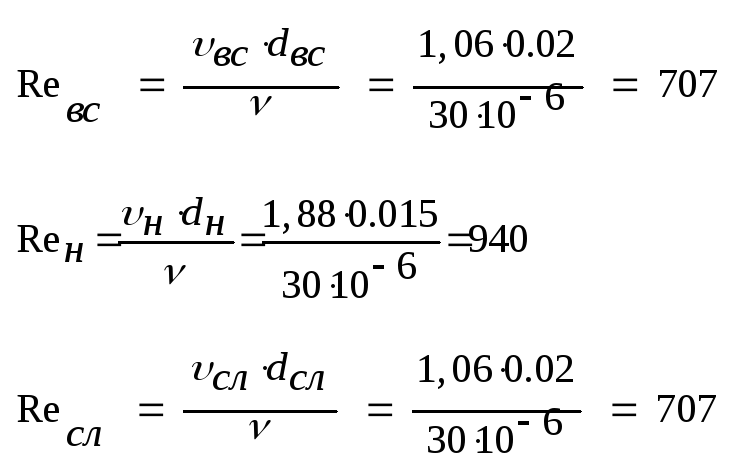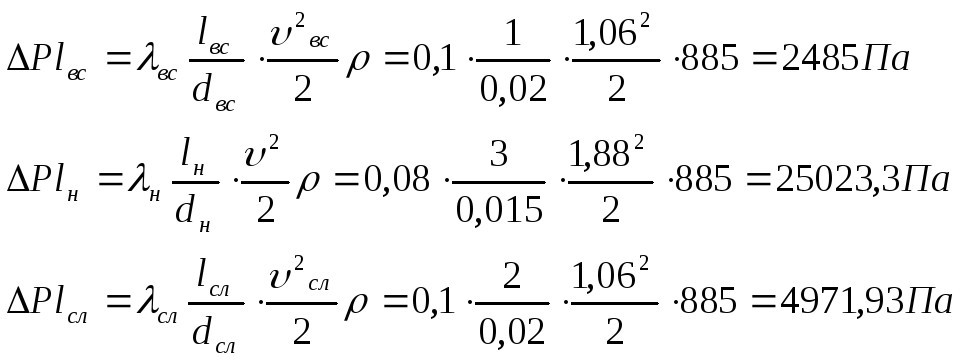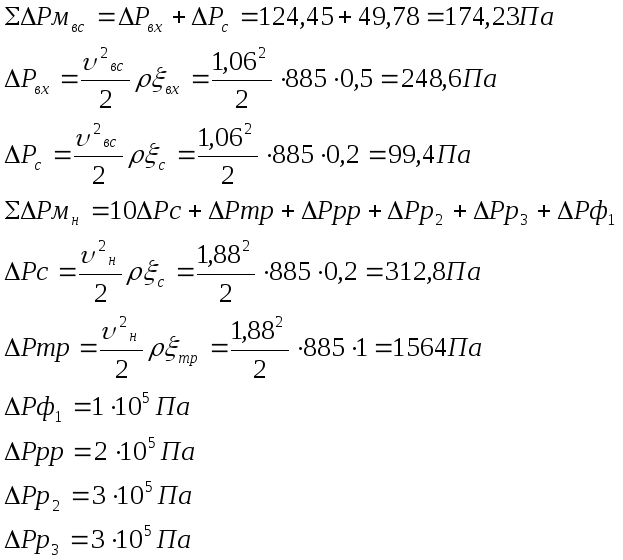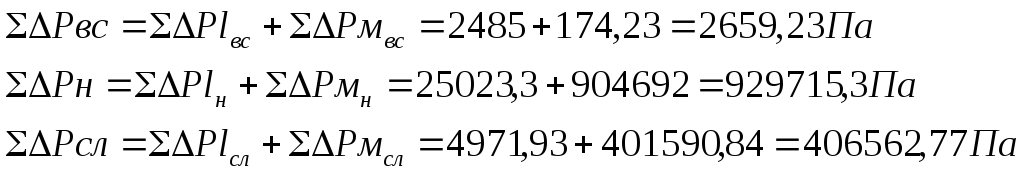Режимы движения реальных жидкостей
Наверняка каждому приходилось наблюдать за водным потоком в различных естественных и искусственных руслах – реках, каналах, протоках и т. п.
И любой наблюдатель, даже самый невнимательный, заметит, что в равнинных реках вода размеренно протекает словно единый жидкий массив со спокойной и ровной поверхностью, в горных реках с бешеным ревом несется бурлящим потоком, разбрасывая брызги с кипящей поверхности, взволнованной всплесками перемешивающихся струй.
Подвижная вода, словно живое существо, по-разному ведет себя с изменением условий, характеризующих ее путь. Таким же поведением характеризуется не только водный поток, но и поток любой другой жидкости.
Почему так происходит, и в какой момент в спокойном и ласковом потоке вдруг просыпается безумный бурлящий “демон”? Можно ли предсказать поведение потока в тех или иных условиях?
Давайте попробуем разобраться в этом вопросе с точки зрения современной науки.
Рассмотрим потоки, характеризуемые условием неразрывности – в любой момент времени расход жидкости постоянен во всех сечениях, т. е соблюдается соотношение:
v1S1 = v2S2 = v3S3 = … = vS,
где v1, v2, v3,…v – соответственно средние скорости потока в разных сечениях.
Наблюдения за такими потоками показывают, что в природе существуют два различных вида движения жидкости: во-первых, слоистое, упорядочное или ламинарное движение, при котором отдельные слои жидкости скользят друг относительно друга, не смешиваясь между собой, и, во-вторых, неупорядоченное, так называемое турбулентное движение, когда частицы жидкости движутся по сложным, все время изменяющимся траекториям и в жидкости происходит интенсивное перемешивание частиц и слоев.
Иногда выделяют третий режим движения жидкостей – переходный, при котором упорядоченное движение частиц очень неустойчиво, и при малейшем изменении условий перемещения потока может произойти переход от ламинарного режима к турбулентному, и наоборот.
***
Число Рейнольдса
Наблюдательными людьми давно подмечено, что вязкие жидкости (например, масла) движутся большей части упорядоченно, а маловязкие жидкости (вода, бензин, газообразные вещества) – почти всегда неупорядоченно.
Кроме того, на характер движения жидкости явно влияет скорость потока – медленно перемещающаяся по руслу жидкость ведет себя спокойно, но стоит увеличить ее скорость, и картина может измениться. Однако установить математическую зависимость между характером движения потока и его параметрами долгое время не удавалось никому.
Ясность в вопрос о том, как именно будет происходить движение жидкости в тех или иных условиях, была внесена в 1883 году в результате опытов английского физика О. Рейнольдса.
О. Рейнольдс определил общие условия, при которых возможны существование ламинарного и турбулентного режима движения жидкости и переход от одного режима к другому. Оказалось, что состояние (режим) потока жидкости в трубе зависит от величины некоторого безразмерного числа, учитывающего основные факторы, определяющие это движение: среднюю скорость, диаметр трубы (или другие линейные характеристики потока), плотность жидкости и ее вязкость.
Влияние всех этих величин на характер движения жидкости объединены в формуле, выражающей число Рейнольдса:
Re = ρvR/µ,
где: R – гидравлический радиус потока; v – скорость потока; µ – динамическая вязкость жидкости, ρ – плотность жидкости.
Число Рейнольдса (иногда его называют критерием Рейнольдса) является безразмерной величиной.
Осборн Рейнольдс (Osborne Reynolds, 1842-1912) – английский механик, физик и инженер, специалист в области гидромеханики и гидравлики. Член Лондонского королевского общества с 1877 г.
В 1883 г. он установил общий принцип прогнозирования режима движения жидкости при помощи упомянутого выше числа. Выводами и умозаключениями Рейнольдса потомки пользуются и в наши дни при гидравлических расчетах. Тем не менее, несмотря на то, что вопрос о неустойчивости ламинарного движения и его переходе в турбулентное, а также о величине критического числа Рейнольдса долгое время является предметом тщательных теоретических и опытно-экспериментальных исследований, до сих пор его полного решения так и не получено.
Поскольку динамическая вязкость жидкости связана с кинематической вязкостью соотношением µ = ρν, то критерий Рейнольдса можно записать в виде:
Re = vR/ν (1).
Число Рейнольдса определяет границы, между которыми режим движения жидкости может принимать ламинарный или турбулентный характер.
Эти границы характеризуются критическими значениями числа Рейнольдса: нижним Reкр и верхним Re’кр.
При Re < Reкр наблюдается устойчивый ламинарный режим течения жидкости, при Re > Re’кр – устойчивый турбулентный режим, а в интервале чисел Рейнольдса Re’кр> Re > Reкр режим течения жидкостей неустойчивый, т. е. ламинарный режим может легко переходить в турбулентный.
Формулу (1) применяют при определении числа Рейнольдса для потока любого сечения.
Для круглых цилиндрических труб с внутренним диаметром d:
Red = vd/ν.
Поскольку для таких труб гидравлический радиус R = 4d, то
Re = 4Red = 4vd/ν.
При проведении гидравлических расчетов цилиндрических труб обычно принимают Re = 250…500, Re’кр = 575. При этом Red будет равен: Redкр = 1000…2000, Red’кр = 2300.
Проведенные исследования показывают также, что критическое значение числа Рейнольдса увеличивается в сужающихся трубах и уменьшается в расширяющихся. Это можно объяснить тем, что при ускорении движения частиц жидкости в сужающихся трубах их тенденция к поперечному перемешиванию уменьшается, а при замедленном течении в расширяющихся трубах увеличивается.
По критическому значению числа Рейнольдса легко можно определить также критическую скорость, т. е. скорость, ниже которой будет иметь место ламинарное движение жидкости:
vкр = Reкрv/d = 2300v/d.
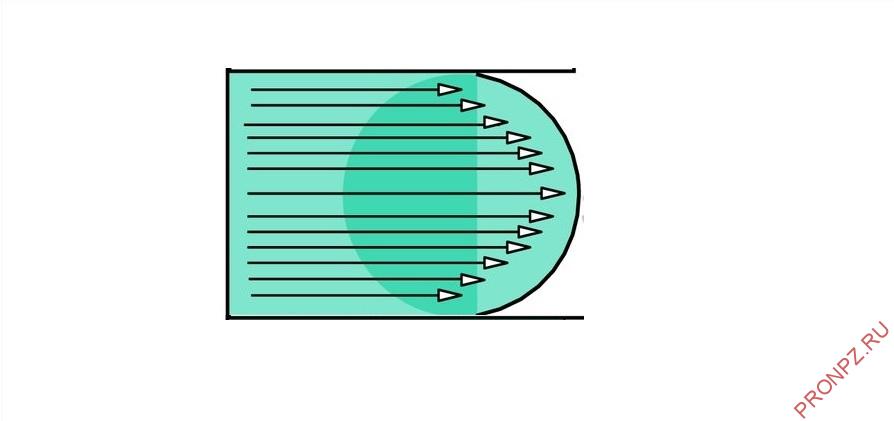
Ламинарному и турбулентному режимам движения жидкости соответствует и различное распределение скоростей частиц по живому сечению потока.
***
При ламинарном режиме течения жидкости по трубе (см. рис. 1) максимальная скорость наблюдается у частиц жидкости, движущихся по центральной оси трубы, а минимальная – у стенок трубы. Частицы подвижной жидкости, расположенные у стенок трубы буквально «прилипают» к стенкам благодаря силам трения и практически неподвижны.
По мере удаления от стенок трубы скорость частиц жидкости возрастает, поскольку на их движение влияет лишь трение между отдельными слоями (элементарными струйками) жидкости. Исследования показали, что при ламинарном режиме движения жидкости изменение скорости в поперечном сечении потока происходит по параболическому закону, т. е. эпюру скоростей частиц можно представить в виде параболы (см. рис. 1).
При турбулентном режиме течения жидкости распределение скоростей более равномерное по сечению потока, чем при ламинарном режиме. Это связано с перемешиванием частиц жидкости, имеющих разную скорость в слоях, и относительным выравниванием средней скорости на всей площади сечения потока. Т. е. отдельные частицы турбулентного потока могут иметь в одном и том же сечении весьма различные по величине и направлению скорости, однако эпюра (график) средней скорости всех частиц по сечению будет ровнее, чем при ламинарном режиме движения.
Лишь слои жидкости, прилегающие к стенкам трубы (поз. 1 на рисунке), движутся с малой скоростью, и режим движения здесь наблюдается ламинарный, несмотря на то, что весь поток характеризуется турбулентным режимом движения.
По этой причине можно утверждать, что «чистого турбулентного режима» движения жидкости не существует, поскольку граничные со стенками слои жидкости в любом случае имеют ламинарный характер движения. Однако толщина ламинарного слоя несравненно мала в сравнении с сечением потока, в котором частицы жидкости перемещаются хаотично (турбулентно), поэтому такой режим течения жидкости принято считать турбулентным.
***
Пример решения задачи с использованием числа Рейнольдса
Определить режим движения нефти в трубопроводе диаметром d = 400 мм при скорости движения v = 0,13 м/с.
Кинематическая вязкость нефти ν = 0,3×10-4 м2/с.
Решение:
Определим число Рейнольдса для данного режима движения жидкости (нефти):
Red = vd/ν = 0,13×0,4/0,3×10-4 = 1733.
Для круглых труб критические значения числа Рейнольдса имеют величину: Redкр = 1000…2000, Re’dкр = 2300.
Сравнив полученное расчетное значение с критическими значениями числа Рейнольдса, делаем вывод, что Red < Redкр, т. е. движение нефти в трубопроводе будет ламинарным.
Другие задачи на использование числа Рейнольдса для определения режимов движения жидкостей представлены здесь.
***
Уравнение Бернулли
Режим
течения на отдельных участках гидросистемы
определяется безразмерным числом
Рейнольдса Re.
Для трубопроводов (каналов) круглого
сечения
где
υм
–
скорость течения масла на рассматриваемом
участке гидросистемы при обеспечении
рабочей подачи выходного звена привода,
d
–
номинальный внутренний диаметр
трубопровода рассматриваемого
участка гидросистемы; ν – кинематическая
вязкость жидкости.
Различают
два режима течения жидкости: ламинарный,
при котором частицы жидкости движутся
параллельно стенкам трубопровода, и
турбулентный, когда движение частиц
приобретает беспорядочный характер.
Переход от ламинарного режима к
турбулентному происходит при
определенных условиях, характеризуемых
критическим числом Рейнольдса Reкр:
поток
ламинарный, если Re
<
Reкр,
поток турбулентной, если Re
>
Reкр.
Для круглых гладких труб Reкр
= 2100-2300, для гибких рукавов (шлангов) Reкр
= 1600.
Предпочтительным
является ламинарный режим течения
жидкости, при котором потери давления
минимальны. Следует избегать режимов
близких
к Reкр,
так
как при длительной работе оборудования
может возникнуть пульсация давления,
нарушение стабильности расходов на
отдельных участках системы, повышенный
нагрев жидкости и другие нежелательные
явления.
На
всех трех участках гидросистемы режим
течения жидкости является ламинарным,
т.к.
Re
< Reкр.
3.4 Определение потерь давления по длине трубопровода
Потери
давления по длине в трубах круглого
сечения, как при ламинарном, так и при
турбулентном режимах течения масла
определяют по общей формуле
где
λ
– коэффициент гидравлического трения;
l
и
d
–
длина и диаметр трубопровода
рассматриваемого участка гидросистемы;
υм
–
скорость
течения масла на рассматриваемом участке
гидросистем при ее работе в режиме
рабочей подачи; ρ
–
плотность масла.
Для ламинарного режима движения жидкости коэффициент гидравлического трения λ определяется по следующей зависимости
(к
= 75 – для жестких трубопроводов):
Длины
участков трубопроводов определяются
в каждом конкретном случае исходя из
габаритов проектируемого технологического
оборудования, места расположения
насосной станции и рабочих органов
машины, способов монтажа гидрооборудования
и других условий. Для технологического
оборудования малых и средних типоразмеров
можно принять длины участков в следующих
пределах:
3.5 Определение потерь на местных сопротивлениях
Криволинейные
участки трубопроводов, угловые,
Т-образные, концевые соединения,
гидроаппаратура создают местные
сопротивления течению жидкости.
Потери
давления в различных местных сопротивлениях
на участке гидросистемы определяют
по формуле
где
υм
–
скорость масла в местных сопротивлениях
рассматриваемого участка системы;
ξ – коэффициент сопротивления (значения
ξ см. табл. 3 [1]).
Виды
и количество местных сопротивлений
определяются по принципиальной
гидравлической схеме привода, при этом
учитываются влияние только тех
сопротивлений, через которые поток
жидкости проходит при обеспечении
рабочей подачи подвижного органа машины.
Величины
потерь давления ΔР
для нормализованной гидроаппаратуры
выбираются по табл.5 [1].

потери давления при движении жидкости
по участку гидросистемы складываются
из потерь давления по длине гидролинии
и потерь на местных сопротивлениях
Соседние файлы в папке Курсовая работа
- #
- #
- #
- #
- #
02.05.201456.18 Кб71Схема гидравлическая.cdw
- #
- #
Содержание
- 1 Калькулятор для расчета Re онлайн
- 1.1 Расчет по общей формуле
- 1.2 Расчет Re для воды
- 1.3 Расчет Re для воздуха
- 2 Формула
- 3 Физический смысл
- 4 Режимы течения
- 5 Критическое значение
- 6 Размерность
- 7 Течение в трубе
Калькулятор для расчета Re онлайн
Расчет по общей формуле
Расчет Re для воды
Расчет Re для воздуха
Формула
Расчетная формула числа Рейнольдса Re в общем виде:
- где
— плотность среды, кг/м3;
— характерная скорость, м/с;
— гидравлический диаметр, м;
— динамическая вязкость среды, Па·с или кг/(м·с);
— кинематическая вязкость среды (
), м2/с;
— объёмный расход потока, м3/с;
— площадь сечения канала, например, трубы, м2.
Для труб круглого сечения расчетная формула числа Рейнольдса Re будет:
Физический смысл
Физический смысл – число Рейнольдса Re характеризует смену режимов течения от ламинарного к турбулентному. Re является критерием подобия течения вязкой жидкости.
Критерий назван в честь выдающегося английского физика Осборна Рейнольдса (1842—1912).
В настоящее время не существует строгого научно доказанного объяснения этому явлению, однако наиболее достоверной гипотезой считается следующая: смена режимов движения жидкости определяется отношением сил инерции к силам вязкости в потоке жидкости. Если преобладают первые, то режим движения турбулентный, если вторые – ламинарный.
Режимы течения
Режим течения в динамическом пограничном слое зависит от числа Рейнольдса Re и может быть:
- Ламинарный режим – слоистое течение без перемешивания частиц жидкости и без пульсации скорости и давления, все линии тока направлены параллельно.
- Турбулентный режим – течение, сопровождающееся интенсивным перемешиванием жидкости с пульсациями скоростей и давлений, наряду с основным продольным перемещением жидкости наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости.
Критическое значение
Переход к турбулентному режиму течения жидкости в пограничном слое определяется критическим значением числа Рейнольдса. Это обусловлено тем, что при возрастании скорости, участвующей в расчете числа Re, его значение растет.
Таким образом, переход от ламинарного режима к турбулентному наблюдается при определенной скорости движения жидкости. Эта скорость называется критической Vкр.
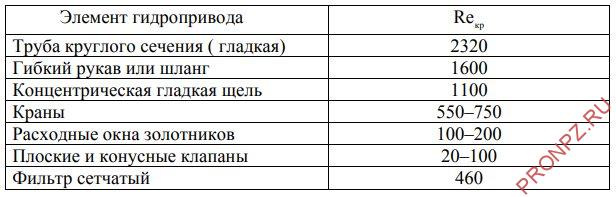
Значение критического числа Re для различных элементов гидропривода
Размерность
Числе Re не имеет единиц измерения. Re является безразмерным критерием подобия течения вязкой жидкости.
Течение в трубе
При ламинарном течении жидкости в прямой трубе или канале постоянного сечения все линии тока направлены параллельно оси трубы, при этом отсутствуют поперечные перемещения частиц жидкости.
При турбулентном течении в канале наряду с основным продольным перемещением жидкости в трубе наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости.
Зависимость режима течения от значения числа Re в гладких трубах:
- <2100 – Ламинарный режим
- 2100 – 2300 – Переходный режим
- >2300 – Турбулентный режим
Обычно предполагается, что при числе Re выше 2300 образуется турбулентный режим.
Тем не менее, при значениях Re выше критического и до определённого предела наблюдается переходной (смешанный) режим течения жидкости, когда турбулентное течение более вероятно, но ламинарное в некоторых конкретных случаях тоже наблюдается — так называемая неустойчивая турбулентность. В трубах такой переходный интервал может достигать вплоть до Re = 2300—10 000.
Число Рейнольдса

Движение жидкости, несмотря на кажущуюся на первый взгляд, беспорядочность движения имеет определенные закономерности.
Рейнольдс в своих опытах нашел определенные общие условия, при которых возможно существование того или иного режима течения и переход от одного режима к другому.
При проведении опытов Рейнольдс в 1883 г. подтвердил существование двух режимов течения жидкости. Ему удалось вычислить безразмерное число, описывающее характер потока вязкой жидкости
Содержание
- Опыты Рейнольдса
- Вывод формулы
- Число Рейнольдса и режимы течения.
- Видео по теме.
Опыты Рейнольдса
Эксперименты О.Рейнольдса показали, что при движении жидкости , последняя теряет определенное количество энергии. Эти потери зависят от особенностей движения частиц жидкости в потоке и от самого режима течения.
Опыты проводились на специальном лабораторном стенде, который представлял собой заполненный водой бак Б к которому в нижней части присоединена стеклянная трубка Т.
На конце трубки установлен кран К для регулирования расхода жидкости. Расход измеряется с помощью секундомера и мерного бочка М. Бак Б постоянно заполняется водой. Над баком Б расположена ёмкость с краской С. По тонкой трубочке Т1 краска попадает в жидкость, движущуюся в трубке Т. Подачу краски регулирует кран Р.
Опыт №1. Немного приоткрываем кран К. При этом в трубке Т начинается движение жидкости. Открываем кран Р и добавляем в жидкость краску. При небольшой скорости движения в трубке Т краска становится прямолинейной и резко выделяющейся в потоке воды цветной струйкой. Эта струйка не перемешивается с остальной жидкостью. Если ввести в жидкость краску несколькими струйками, то они так и будут двигаться не перемешиваясь с остальной водой.
Движение жидкости, наблюдаемое при малых скоростях, при котором отдельные струйки жидкости движутся параллельно друг другу и оси потока, называют ламинарным (от латинского ламина – слой) или струйчатым движением (режимом). Ламинарное движение может рассматриваться как движение отдельных слоев жидкости, происходящее без перемешивания частиц. Подробнее о ламинарном режиме здесь.
Опыт №2 При намного большем открытии крана струйка краски начинает искривляться и становится волнообразной. Открывая кран ещё больше и увеличивая скорость потока мы увидим, что струйка краски распадается на отдельные вихри и перемешивается с остальной массой воды
Движение жидкости, которое наблюдается при больших скоростях, называется турбулентным (по латински турбулентус – вихревой) движением (режимом). В этом случае в движении жидкости нет видимой закономерности. Отдельные частицы перемешиваются между собой и движутся по самым причудливым, все время меняющимся траекториям весьма сложной формы. Поэтому такое движение называется беспорядочным. Подробнее о турбулентном режиме здесь.
При этом чем больше размеры поперечного сечения и плотность жидкости и чем меньше её вязкость, тем легче при увеличении скорости осуществить турбулентный режим.
Для характеристики режима движения жидкости Рейнольдсом был выведен безразмерный параметр Re, учитывающий влияние перечисленных выше факторов, называемый число Рейнольдса. Таким образом формула
Re = υ×d× ρ / μ
Поскольку μ / ρ = ν ,
где ν – кинематическая вязкость жидкости, то формула меняет вид на
Re = υ×d / ν
Число Рейнольдса и режимы течения.
Границы существования того или иного режима движения жидкости определяются двумя критическими значениями числа Рейнольдса:
Значение скорости, соответствующее этим значениям Re называют критическими.
При значениях числа Рейнольдса Re < Reкр. н. возможен только ламинарный режим, а при значении Re > Reкр. в. – только турбулентный. При Reкр. н. < Re < Reкр. в. Наблюдается неустойчивое состояние потока. Таким образом, для определения характера режима необходимо в каждом отдельном случае вычислить число Рейнольдса и сопоставить его с критическими значениями этого числа.
В опытах самого известного физика значение числа Рейнольдса Reкр. было следующим:
Многие эксперименты, проведенные в последствии показали, что критические числа Рейнольдса не являются постоянными величинами и что в действительности при известных условиях неустойчивая зона может оказаться значительно шире.
В настоящее время при практических расчетах обычно принято исходить только из одного критического значения числа Рейнольдса, принимаемого Reкр =2300, считая, что при Re < 2300 всегда имеет место ламинарный, а при Re > 2300 – всегда турбулентный режимы.
При этом движении жидкости в неустойчивой зоне исключается из особого рассмотрения, это приводит к некоторому запасу и большей надежности в гидравлических расчетах в случае, если в этой зоне действительно имеет место ламинарный режим.
Без особого труда можно получить значения для Reкр для любой формы сечения, а не только круглой формы. Вспоминая, что при круглом сечении радиус
R = d / 4
подставляем в формулу для определения числа Рейнольдса
Re = υ×4×R / ν
Принимая для критического числа Рейнольдса независимо от формы живого сечения величину Reкр. = 2300, находим, что для сечения любой формы критериев для сужения о характере режима движения является величина, равная 2300 / 4 = 575.
Таким образом, режим ламинарный если значение числа Рейнольдса
И режим турбулентный, если

Видео по теме.
На практике в большинстве случаев (движение воды в трубах, каналах, реках) приходится иметь дело с турбулентным режимом. Ламинарный режим встречается реже. Он наблюдается, например, при движении в трубах очень вязких жидкостей, что иногда имеет место в нефтепроводах, при движении жидкости в очень узких трубках и порах естественных грунтов.
Вместе со статьей “Число Рейнольдса: опыты, формулы и режимы.” смотрят:

Как определить вязкость жидкости методом Стокса?

Гидростатическое давление: определение, формула и свойства.

Гидравлическое сопротивление
- Число Рейнольдса —
- безразмерная величина, характеризующая отношение инерционных сил к силам вязкого трения в вязких жидкостях и газах.
Число Рейнольдса также является критерием подобия течения вязкой жидкости.
Общие сведения
Число Рейнольдса обозначается в физике и инженерных расчетах — Re. Широко применяется при гидравлических и аэродинамических расчетах различных систем.
Число Рейнольдса служит для определения (является критериям) режима движения среды (жидкости или газа) в системе.
Различают несколько режимов движения жидкостей и газа:
-
- ламинарный;
- смешанный (иногда встречается, как критический);
- турбулентный.
Критерием перехода из одного режима в другой служит критическое значения числа Рейнольдса — Reкр. В расчетах обычно считается, что при Re<Reкр течение происходит в ламинарном режиме, а при Re>Reкр возможно возникновение турбулентности. Смешанный режим обычно относят к турбулентному режиму, как неустойчивая турбулентность.
Для систем трубопроводов с круглыми трубами с очень гладкими стенками критическое значения числа Рейнольдса обычно принимается Reкр≈ 2100÷2300.
Критическое значения числа Рейнольдса зависит от:
-
- от конкретного вида течения (например от формы сечения канала, обтекания шара и т. п.);
- различных возмущений потока (вызывающих изменение направления и модуля вектора скорости потока, например любые местные сопротивления, шероховатости стенок и т.п.).
На основании числа Рейнольдса и исходя из режима движения жидкости или газа при гидравлическом и аэродинамическом расчете определяется коэффициент гидравлических потерь λ (коэффициент путевых потерь).
Существуют методики расчета числа Рейнольдса, учитывающие в себе все выше указанным зависимости. Например расчет числа Рейнольдса при гидравлическом расчете газопроводов согласно методике СП 42-101-2003, разбивает турбулентный режим движения газа на несколько под режимов учитывающих:
-
- режим движения газа (включая смешанный/критический);
- шероховатость стенки трубы.
Примеры использования числа Рейнольдса в расчетах
-
- гидравлический расчет паропровода (калькулятор онлайн);
- гидравлический расчет трубопровода горячей воды (калькулятор онлайн);
- гидравлический расчет трубопровода СУГ (калькулятор онлайн);
- гидравлический расчет газопровода природного газа (методика).
Формулы расчет числа Рейнольдса. Калькуляторы числа Рейнольдса онлайн.
Классическая формула расчета числа Рейнольдса
Re=(u*D)/υ,
где u — характерная скорость, м/с; D — гидравлический диаметр, м; υ — кинематическая вязкость среды, м2/с.
Результат расчета числа Рейнольдса (Re1)
Формула расчета числа Рейнольдса:
Скачать результат расчета числа Рейнольдса:

Поделится ссылкой на расчет :
Формула расчета числа Рейнольдса через плотность
Re=(ρ*u*D)/η,
где ρ — плотность среды, кг/м3; u — характерная скорость, м/с; D — гидравлический диаметр, м; η — динамическая вязкость среды, Па·с или кг/(м·с).
Результат расчета числа Рейнольдса (Re2)
Формула расчета числа Рейнольдса:
Скачать результат расчета числа Рейнольдса:

Поделится ссылкой на расчет :
Формула расчета числа Рейнольдса через объемный расход жидкости или газа
Re=(Q*D)/(υ*S),
где Q — объёмный расход потока, м3/с; D — гидравлический диаметр, м; υ — кинематическая вязкость среды, м2/с; S — площадь сечения канала (например: трубы, воздуховода и т.п), м2.
Результат расчета числа Рейнольдса (Re3)
Формула расчета числа Рейнольдса:
Скачать результат расчета числа Рейнольдса:

Поделится ссылкой на расчет :
Формула расчета числа Рейнольдса природного газа согласно методике СП 42-101-2003 (п.3.28)
Re=(0.0354*Q)/(d*υ),
где Q — объёмный расход газа при нормальных условиях, м3/ч; d — внутренний диаметр газопровода, см; υ — кинематическая вязкость среды, м2/с.
Результат расчета числа Рейнольдса в газопроводе (Re4)
Формула расчета числа Рейнольдса в газопроводе:
Скачать результат расчета числа Рейнольдса в газопроводе:

Поделится ссылкой на расчет :
Справочные данные для расчета числа Рейнольдса (плотность и вязкость некоторых веществ)
В случае отсутствия нужного вещества или отсутствие данных по выбранному веществу (значение равно «0», «-«), можно указать в комментариях наименование вещества и рекомендуемый источник информации с физическими свойствами.
Видеоматериал по теме «Число Рейнольдса»
Историческая справка
Число названо в честь Осборна Рейнольдса. Экспериментально установил (1876—1883 гг.) критерий (число Рейнольдса) перехода ламинарного режима движения жидкости, текущей в цилиндрической трубе, в турбулентный режим.