Резонансные явления наблюдаются в колебательных системах, когда частота собственных колебаний элементов системы совпадает с частотой внешних (вынужденных) колебательных процессов. Данное утверждение справедливо и для цепей с циркулирующим переменным током. В таких электрических цепях при наличии определённых условий возникает резонанс напряжений, что влияет на параметры тока. Явление резонанса в электротехнике может быть полезным или вредным, в зависимости от ситуации, в которой происходит процесс.
Описание явления
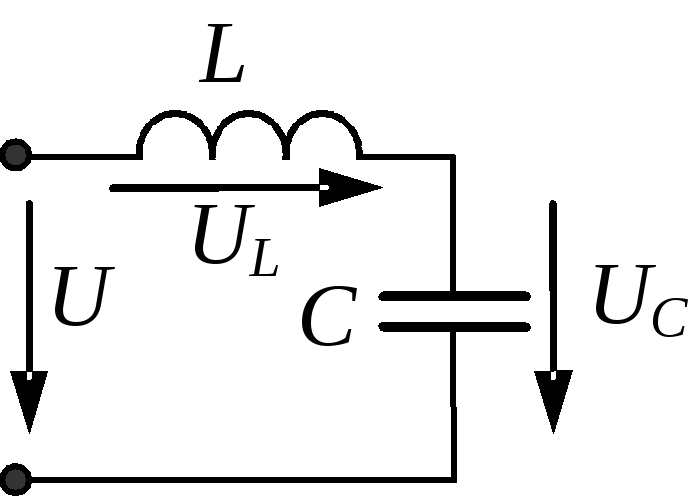
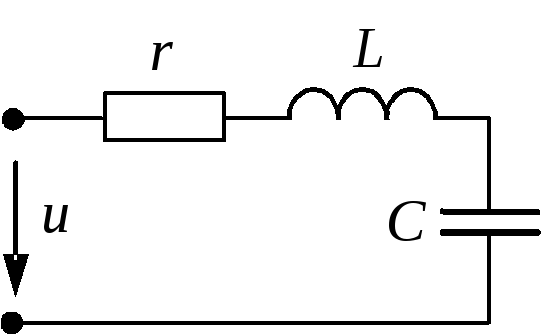
Если в некой электрической цепи (см. рис. 1) имеются ёмкостные и индуктивные элементы, которые обладают собственными резонансными частотами, то при совпадении этих частот амплитуда колебаний резко возрастёт. То есть происходит резкий всплеск напряжений на этих элементах. Это может вызвать разрушение элементов электрической цепи.
Давайте рассмотрим на этом примере, какие явления будут происходить при подключении генератора переменного тока к контактам схемы. Заметим, что катушки и конденсаторы обладают свойствами, которые можно сравнить с аналогом реактивного резистора. В частности, дроссель в электрической цепи создаёт индуктивное сопротивление. Конденсатор является причиной ёмкостного сопротивления.
Индуктивный элемент вызывает сдвиг фаз, характеризующийся отставанием тока от напряжения на ¼ периода. Под действием конденсатора ток, наоборот, на ¼ периода опережает напряжение.
Другими словами, действие индуктивности противоположно действию на сдвиг фаз ёмкостного сопротивления. То есть катушки индуктивности и ёмкостные элементы по-разному воздействуют на генератор и по-своему корректируют фазовые соотношения между электрическим током и напряжением.
Формула
Общее реактивное сопротивление рассматриваемых нами элементов равно сумме сопротивлений каждого из них. С учётом противоположности действий можно записать: Xобщ = XL — Xc , где XL = ωL — индуктивное реактивное сопротивление, выражение Xc = 1/ωC — это ёмкостное реактивное сопротивление.
На рисунке 2 изображены графики зависимости полного сопротивления цепи и связанной с ним силы тока, от реактивного сопротивления индуктивного элемента. Обратите внимание на то, как падает полное сопротивление при уменьшении реактивной сопротивляемости RL (график б) и как при этом возрастает ток (график в).
Электрические цепи, состоящие из последовательно соединённых конденсаторов, пассивный резисторов и катушек индуктивности называют последовательными резонансными (колебательными) контурами (см. рис. 2). Существуют также параллельные контуры, в которых R, L, C элементы подключены параллельно (рис. 3).
В режиме резонанса мощность источника питания будет рассеиваться только на активных сопротивлениях (в том числе на активном сопротивлении катушки). Для резонансных контуров характерны потери только активной мощности, которая израсходуется на поддержание колебательного процесса. Реактивная мощность на L C — элементах при этом не расходуется. Ток в резонансном режиме принимает максимальное значение:
Величину Q принято называть термином «Добротность контура». Данный параметр показывает, во сколько раз напряжение, возникшее на контактах реактивных элементов, превышает входное напряжение U электрической сети. Для описания соотношения выходного и входного напряжений часто применяют коэффициент K. При резонансе:
K = Uвых / Uвх = UC0 / U = Q
Формулировка
На основании вышеописанных явлений, сформулируем определение резонансного напряжения: «Если общее падение напряжения на ёмкостно-индуктивных элементах равно нулю, а амплитуда тока – максимальна, то такое особое состояние системы называется резонансом напряжений». Для лучшего понимания явления, немного перефразируем определение: резонансом напряжений является состояние, когда напряжение на CL — цепочке больше чем на входе электрической цепи.
Описанное явление довольно распространено в электротехнике. Иногда с ним борются, а иногда специально создают условия для образования резонанса. Основными характеристиками всякого резонансного контура являются параметры добротности и частоты [ 1 ].
В случае, если XL = Xc – справедливо равенство: ωL = 1/ωC , отсюда получаем:
Если ω = ω0 – возникает резонанс напряжений. Частоты совпадают в том случае, когда индуктивное сопротивление сравняется с ёмкостным сопротивлением конденсатора. В таких случаях в цепи будет действовать только активное сопротивление R. Наличие реактивных элементов в схеме приводит к увеличению полного сопротивления цепи (Z):
где R – общее активное сопротивление.
Учитывая, что по закону Ома U = I/Z, можно утверждать, что общее напряжение в цепи зависит, в том числе, и от слагаемых индуктивного и ёмкостного сопротивлений.
Если бы в рассматриваемой схеме (рис. 1) отсутствовало активное сопротивление R, то значение полного сопротивления Z стремилось бы к 0. Следовательно, напряжение на реактивных элементах при этом возрастает до критического уровня.
Поскольку XL и Xc зависят от частоты входного напряжения, то для возникновения резонанса следует подобрать соответствующую частоту сети, или изменять параметры катушки, либо конденсатора до тех пор, пока резонансные частоты не совпадут. Любое нарушение условий резонанса немедленно приводит к выходу системы из резонансного режима с последующим падением напряжения.
Условия наступления
Резонансные явления наступают только при наличии следующих условий:
- Наличие минимального активного сопротивления на участке электрической цепи.
- Равенство реактивных сопротивлений, возникших на цепочке LC.
- Совпадение входной частоты источника питания с резонансной частотой колебательного контура.
При резонансе в контуре напряжения на его элементах могут повышаться на порядок и больше.
Примеры применения на практике
Классическим примером применения резонанса колебательных контуров является настройка радиоприёмника на частоту соответствующей радиостанции. В качестве рабочего элемента настроечного узла используется конденсатор с регулируемой ёмкостью. Вращение ручки настройки изменяет ёмкость конденсатора, а значит и резонансную частоту контура.
В момент совпадения резонансной частоты с рабочей частотой какой-либо радиостанции возникает резонанс напряжений, в результате которого резко возрастает амплитуда колебаний принятой радиоприёмником частоты. Специальные фильтры отделяют эти колебания от несущих радиочастот, а усилители усиливают полученные сигналы. В динамике появляются звуки, генерируемые передатчиком радиостанции.
Колебательные контуры, построенные на принципе последовательного соединения LC-элементов, применяются в цепях питания высокоомных нагрузок, потребляющих токи повышенного напряжения. Такие же устройства применяют в полосовых фильтрах.
Последовательный резонанс применяют при пониженных напряжениях сети. В этом случае используют реактивную энергию обмоток трансформатора, соединённых последовательно.
Конденсаторы и различные катушки индуктивности (рис. 5) входят в конструкцию практически всех аналоговых устройств. Они используются для настройки фильтров или для управления токами в отдельных узлах.
Важно знать, что резонансные контуры не увеличивают количество электрической энергии в цепях. Они лишь могут повышать напряжения, иногда до опасных значений. Постоянный ток не причиной резонансных явлений.
Наряду с полезными свойствами резонансных явлений, в практической электротехнике часто возникают ситуации, когда резонанс напряжений приносит вред. В основном это связано с нежелательным повышением параметров тока на участках цепей. Примером могут служить опасное резонансные явления в кабельных линиях без нагрузки, что может привести к пробоям изоляции. Чтобы этого не случилось, на концевых участках таких линий устанавливают балластные нагрузочные элементы.
Режим
при котором в цепи, содержащей реактивные
элементы, ток и напряжение совпадают
по фазе, называется резонансным, т.е.
эквивалентное сопротивление цепи
является чисто активным.
2.10.3.1. Резонанс напряжений
Резонанс
напряжений возможен при (Рис.8)
последовательном соединении R,L,Cэлементов.
Условие
резонанса напряжений:
Угловая
резонансная частота
.
При
резонансе напряжений ток в контуре
.
Коэффициент
мощности
.
Напряжение
на емкости и на индуктивности одинаковы:
.
При
резонансе напряжений применяются
следующие соотношения и формулы:
характеристическое
сопротивление контура – сопротивление
каждого из реактивных элементов при
резонансе
;
-
добротность
контура
; -
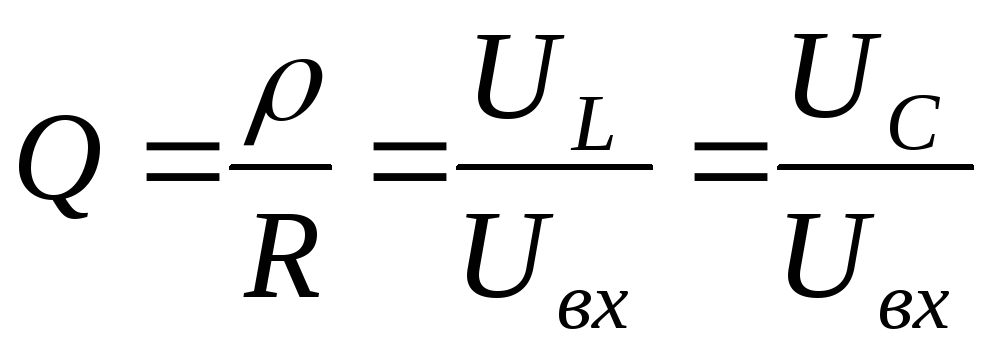затухание
контура
; -
абсолютная
расстройка
; -
относительная
расстройка
.
2.10.3.2. Резонанс токов
Резонанс
токов возможен в цепи, содержащей
параллельно соединенные индуктивности
и емкости (Рис. 9)
Условие
резонанса токов:
Угловая
резонансная частота:
,
где
характеристическое сопротивление
;
добротность
контура
;
сопротивление
контура при резонансе токов
;
ток
неразветвленной части цепи при резонансе
;
полоса
пропускания определяется из условия,
что ток на частотах f1иf2,
соответствующих границы полосы
пропускания, уменьшается в
;
абсолютное
значение полосы пропускания:
;
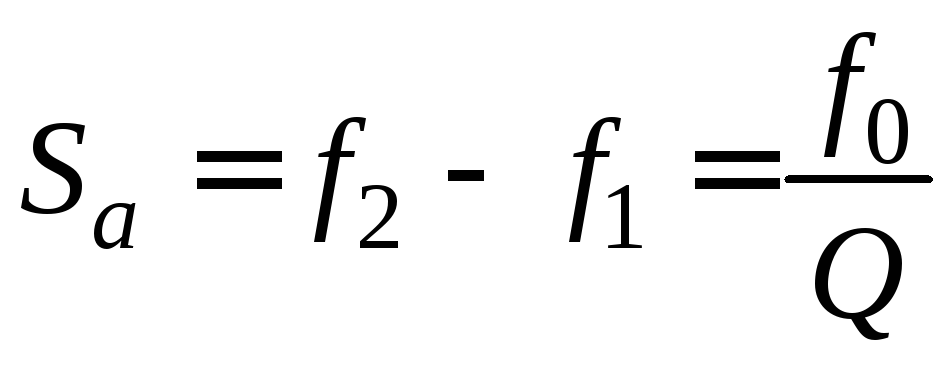относительное
значение полосы пропускания:
.
Пример
3.1
Электрическая
цепь состоит из последовательно
соединенных активного сопротивления
Ом,
катушки индуктивностью
мкГн
и конденсатора емкостью
пФ.
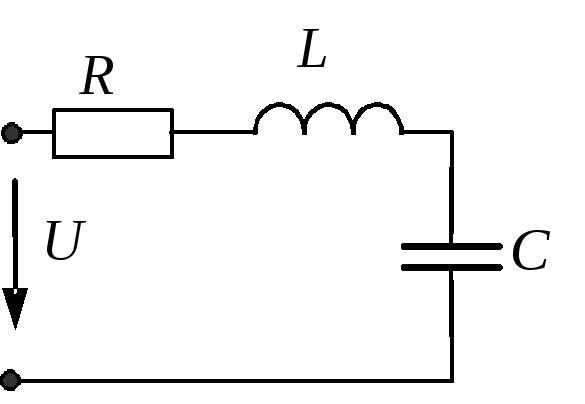
Определить
резонансную частоту
,
характеристическое сопротивление,
затухание и добротность контура. Чему
равны ток, расходуемая в цепи мощность,
напряжение на индуктивности и емкости,
если контур включен на напряжении 1 В?
Вычислить абсолютное значение полос
пропускания контура.
Решение:
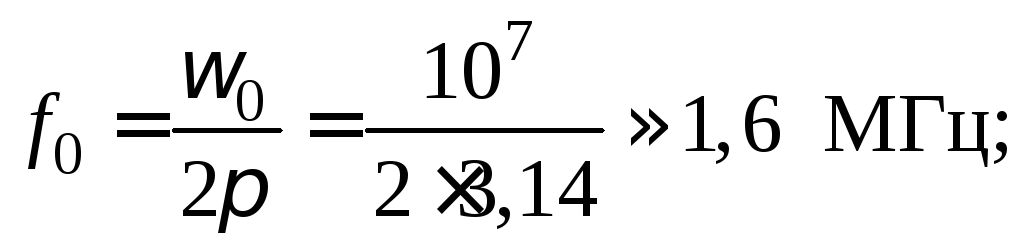
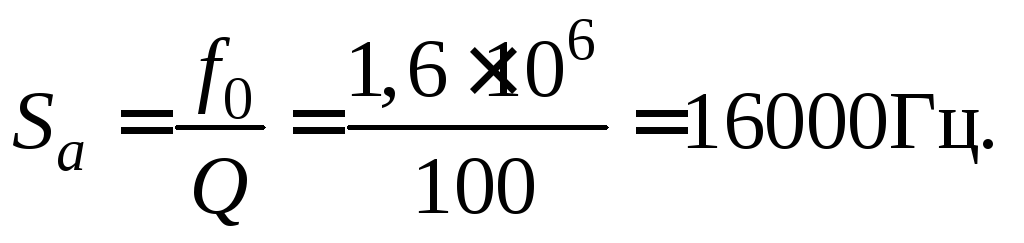
Пример 3.2
На
зажимах цепи поддерживается постоянное
по действующему значению напряжение
В,
Ом,
Ом,
Ом.
Определить
,
при котором цепь будет находиться в
резонансе.
Решение:
Условие
резонанса напряжений
,
;
Ток
при резонансе
Пример
3.3
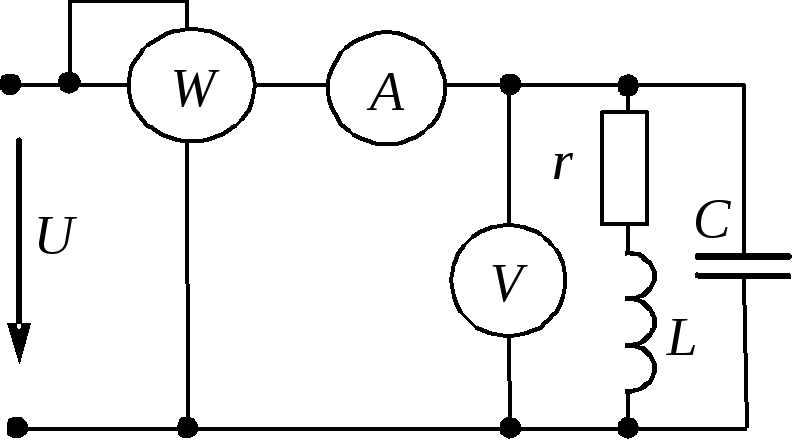
В схеме
без емкости приборы показывают
Вт,
А,
В,
Гц.
Определить
величину емкости, необходимую для
повышения коэффициента мощности (
)
до 1.
Решение:
Определим
параметры катушки по схеме без емкости
Ом;
при резонансе.
Условия
резонанса токов:
;
§2.11. Вопросы для самопроверки
1. Какой
ток называется переменным? Дайте
определение синусоидального тока.
2. Что
такое максимальное, действующее и
среднее значения синусоидальных величин
тока, напряжения, ЭДС. Запишите формулы,
связывающие действующие значения с
максимальными, средние значения с
максимальными?
3.
Назовите известные вам способы выражения
синусоидальных величин.
4. Дайте
определение векторной диаграмме.
5. Как
определяются знаки углов на векторной
диаграмме?
6. Дайте
определение индуктивности, емкости,
запишите выражения индуктивного,
емкостного сопротивления.
7. Чем
отличается реальная катушка индуктивности
от идеальной?
8.
Изобразите схему замещения реальной
катушки индуктивности и начертите для
нее векторную диаграмму.
9.
Начертите векторную диаграмму для цепи
с резистивным и емкостным элементом.
10.
Запишите закон Ома в комплексной форме
для резистивного, индуктивного и
емкостного элементов.
11. Как
определить угол сдвига фаз
по треугольнику напряжений, сопротивлений,
мощностей.
12. В
чем смысл символического метода расчета
цепей синусоидального тока?
13. В
каких электрических цепях и при каком
условии возникает резонанс напряжений?
14.
Запишите условие возникновения резонанса
токов.
Задачи
для самостоятельного решения:
Задачи
1.1. Ток
изменяется по синусоидальному закону.
Период
c,
амплитуда
A,начальная фаза
.
Ток
изменяется по синусоидальному закону
с той же частотой и амплитудой.
Записать
выражения
и
для случаев:
опережает ток
на угол
;
отстает от тока
на угол
;
находится в противофазе с током
;
совпадает по фазе с током
.
1.2. Ток
изменяется по синусоидальному закону.
Частота
Гц,
амплитуда
А,
начальная фаза
.
Ток
изменяется по синусоидальному закону
с той же частотой и амплитудой.
Записать
выражения
и
для случаев:
совпадает по фазе с током
;
отстает от тока
на угол
;
опережает ток
на угол
;
находится в противофазе с током
.
Построить
графики
.
1.3. Ток
изменяется по синусоидальному закону.
Период
мс,
амплитуда
A,
начальная фаза
.
Ток
изменяется по синусоидальному закону
с той же частотой, но амплитуда в два
раза больше.
Записать
выражения
и
для случаев:
опережает ток
а угол
;
отстает от тока
на угол
;
находится в противофазе с током
;
совпадает по фазе с током
.
Построить
графики
.
1.4. Ток
изменяется по синусоидальному закону.
Период
мс,
амплитудаIm1
= 2,8A,начальная фаза
.
Ток
изменяется по синусоидальному закону
с той же частотой и амплитудой.
Записать
выражения
и
для случаев:
опережает ток
на угол
;
отстает от тока
на угол
;
находится в противофазе с током
;
совпадает по фазе с током
.
Построить
графики
.
1.5.
Заданы мгновенные значения токов:
,
,
,
,
.
Записать
комплексные мгновенные, амплитудные и
действующие значения токов в алгебраической
и показательной формах.
Построить
векторы комплексных действующих значений
токов на комплексной плоскости.
1.6.
Заданы мгновенные значения токов:
,
,
,
,
.
Записать
комплексные мгновенные, амплитудные и
действующие значения токов в алгебраической
и показательной формах.
Построить
векторы комплексных действующих значений
токов на комплексной плоскости.
1.7.
Заданы мгновенные значения токов:
,
,
,
,
.
Записать
комплексные мгновенные, амплитудные и
действующие значения токов в алгебраической
и показательной формах.
Построить
векторы комплексных действующих значений
токов на комплексной плоскости.
1.8.
Заданы мгновенные значения токов:
,
,
,
,
.
Записать
комплексные мгновенные, амплитудные и
действующие значения токов в алгебраической
и показательной формах.
Построить
векторы комплексных действующих значений
токов на комплексной плоскости.
1.9.
Заданы комплексные действующие значения
токов и напряжений:
,
,
,
.
Построить
векторы токов и напряжений на комплексной
плоскости.
Записать
мгновенные значения
и
.
1.10.
Заданы комплексные действующие значения
токов и напряжений:
,
,
,
.
Построить
векторы токов и напряжений на комплексной
плоскости.
Записать
мгновенные значения
и
.
1.11.
Заданы комплексные действующие значения
токов и напряжений:
,
,
,
.
Построить
векторы токов и напряжений на комплексной
плоскости.
Записать
мгновенные значения
и
.
1.12.
Заданы комплексные действующие значения
токов и напряжений:
,
,
,
.
Построить
векторы токов и напряжений на комплексной
плоскости.
Записать
мгновенные значения
и
.
1.13.
Заданы комплексные действующие значения
токов и напряжений:
,
,
,
.
Построить
векторы токов и напряжений на комплексной
плоскости.
Записать
мгновенные значения
и
.
1.14.
Заданы комплексные действующие значения
токов и напряжений:
,
,
,
.
Построить
векторы токов и напряжений на комплексной
плоскости.
Записать
мгновенные значения
и
.
Задачи
|
2.1. |
|
|
Построить |
В,
В.
|
2.2. |
|
|
Построить |
,
В,
В.
|
2.3. |
|
|
Построить |
В,
В,
В.
|
2.4.
|
|
|
Определить |
Ом,
мГн,
Ом,
.
,
,
,
.|
2.5.
|
|
|
Определить |
Ом,
Ом,
мкФ,
В,
.
,
,
.|
2.6.
|
|
|
Определить |
мГн,
Ом,
мГн,
Ом,
В,
Гц.
,
,
,
.|
2.7.
|
|
|
Определить |
А,
Ом,
Ом,
Ом,
Ом.
.|
2.8. |
|
|
Определить |
Ом,
Ом,
Ом,
Ом,
В.
,
.|
2.9. |
|
|
Определить |
Ом,
мГн,
Ом,
мГн,
Ом,
В,
Гц.
,
и мощность, расходуемую в цепи. Построить|
2.10. |
|
|
Определить |
Ом,
МкФ,
Ом,
мкФ,
,
В.
.|
2.11.
|
|
|
Определить |
,
.
|
2.12. При
|
|
|
Определить |
и
.
|
2.13.
|
|
|
Вычислить, |
В,
Гц,
В,
В.
и
.|
2.14.
|
|
|
Определить Найти |
,
Ом,
Ом.
,
.|
2.15. При
а при
|
|
|
Вычислить |
Гц,
В,
А,
Гц,
В,
А.
,
.|
2.16.
При |
|
|
Определить |
Ом,
Ом,
мГн,
Гц.
цепи.|
2.17. |
|
|
Определить |
|
|
2.18. |
|
|
Определить |
Ом,
Ом,
Ом,
Ом,
Ом,
Ом,
В.
,
,
,
.
|
2.19. |
|
|
Найти |
,
,
Ом,
Ом.
методом эквивалентного генератора.|
2.20. |
|
|
Определить |
А,
А,
А.
|
2.21. |
|
|
Найти |
Ом,
Ом,
Ом,
Ом,
Ом.
В.
|
2.22.
|
|
|
Найти |
Ом,
Ом,
Ом,
Ом,
Ом,
Ом.
В.
|
2.23.
|
|
|
Определить |
,
Ом,
Ом,
Ом,
Ом.
и
.|
2.24.
|
|
|
Определить |
В,
Ом,
Ом,
Ом,
Ом.
|
2.25.
|
|
|
Определить |
Ом,
Ом,
Ом,
Ом,
Ом,
Ом,
А.
и
.|
2.26.
|
|
|
Определить |
Ом,
Ом,
Ом,
В.
|
2.27. |
|
|
Определить |
,
Гн,
мкФ,
Ом.
3.1. При
резонансе:
В,
В,
В,
А,
Гц.
Определить
.
3.2.
Ом,
Ом,
Ом,
Гц.
При
каком значении L наступит резонанс
.
3.3. При
резонансе:
В,
В,
Ом,
Гц.
Определить
показания приборов, значения L и С.
3.4.
Ом,
Ом,
Ом.
Определить значение
при котором наступает резонанс токов.
3.5.
,
Ом.
Определить показания приборов.
3.6. При
резонансе:
Вт,
В,
Ом.
Определить
r и
.
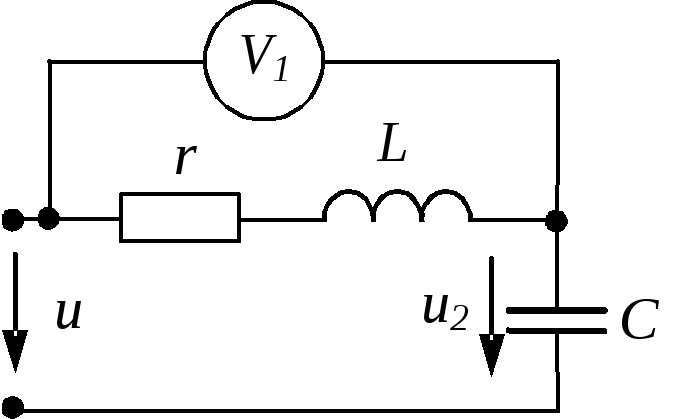
3.7. При
резонансе:
В,
Гц,
Ом,
В.
Определить
показания
,
и добротность цепи.
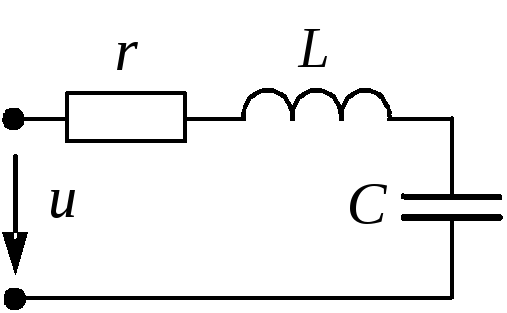
3.8.
В,
мкФ,
мГн,
Дж.
Определить
ток при резонансе, добротность цепи и
сопротивление.
3.9.
мкГн,
,
Ом,
пФ.
Определить
добротность контура и резонансную
частоту
и
.
3.10.
Ом,
Ом.
При
каком значении
в цепи наступит резонанс.
3.11.
Определить r и L контура, если при
резонансной частоте
кГц
отношение напряжения на конденсаторе
к напряжению на входе равно 50. Емкость
конденсатора
мкФ.
3.12.
Гн,
Ом,
мкФ.
Определить
частоту
при которой в цепи наступит резонанс
токов.
3.13.
Ом,
мГн,
мкФ,
.
Определить
резонансную частоту, волновое сопротивление
и затухание контура, напряжения
и
.
3.14.
Ом,
В,
Ом.
Определить
сопротивление
и все токи при резонансе.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Режим работы электрической цепи, при котором ток и напряжение на входе цепи совпадают по фазе, называют резонансом. При этом эквивалентное сопротивление всей цепи (в случае последовательного соединения RLC элементов) будет активным. В цепях, состоящих из резистора, катушки и конденсатора, различают резонанс напряжений и резонанс токов.
Продолжаем решать задачи по теории электрических цепей. Сегодня рассмотрим задачу на резонанс, а именно нужно определить резонансную частоту в цепи, изображенную на рисунке 1.
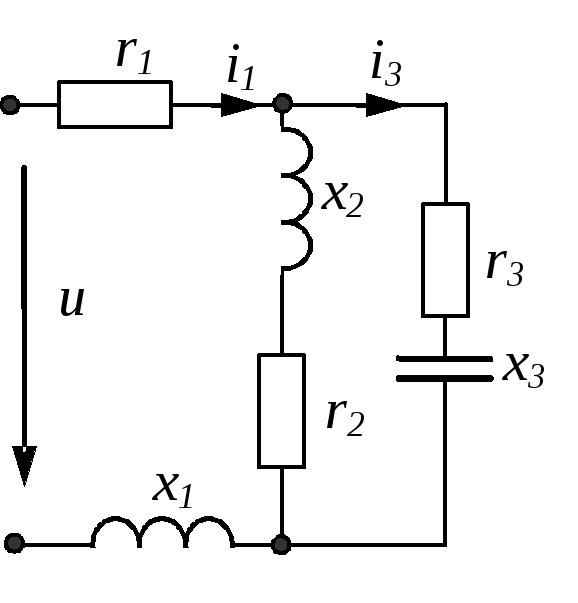
Вся сложность заключается в том, что тут не последовательное и не параллельное соединение RLC элементов(R – сопротивление резистора, L – индуктивность катушки и С – емкость конденсатора).
Для последовательной и параллельной RLC цепей существуют готовые формулы для нахождения резонансной частоты:
В цепях со смешанным соединением RLC элементов, эту частоту необходимо выводить. Делается это следующим образом. Записывается выражение для полной проводимости цепи (в случае, если в цепи катушка и конденсатор включены параллельно) или выражение для полного сопротивления (в случае, если катушка и конденсатор включены последовательно) в виде формулы.
Поскольку полная проводимость “У” цепи состоит из активной “G” и реактивной “B” проводимостей, то полученное выражение реактивной проводимости “B”, приравнивают к нулю и находят оттуда f0 (резонансную частоту).
Рассмотрим пример, как можно найти резонансную частоту в цепях со смешанным соединением RLC элементов более простым и быстрым способом. Переходим к решению задачи.
Имеется схема цепи со смешанным соединением. Даны сопротивления резисторов, ЭДС, индуктивность и емкость. Требуется найти резонансную частоту f0.
Если бы в данной цепи не было резистора R2, то резонансную частоту f0 можно найти легко, поскольку мы бы имели цепь с последовательным соединением R1, R3, L и C.
R1 и R3 объединили бы в 1 резистор, и по готовой формуле, изображенной на рисунке 2, вывели бы резонансную частоту.
А сделать из этой цепи одноконтурную мы можем. Для этого достаточно уметь пользоваться методом эквивалентного источника (об этом методе я подробно рассказывал в своем раннем видеоуроке под названием: как упрощать схемы цепей, уменьшать количество контуров). Если кто не смотрел то видео, оставляем ссылку.
Этот метод позволяет нам объединить ветвь с сопротивлением, подключенную параллельно любой ветви с последовательным включением резистора и ЭДС (для нашей схемы подходит ветвь с резистором R2, которая подключена параллельно ветви с R1 и E.
Представим эту часть цепи отдельно.
Теперь мы имеем следующий участок цепи:
Представим всю схему:
Теперь схема одноконтурная. Найдем активное сопротивление двух последовательно включенных резисторов:
R=R3+Rэ=25+25=50 (Ом)
И в итоге получаем:
Так как цепь получилась с последовательным соединением RLC элементов, в такой цепи может возникнуть резонанс напряжений. При последовательном соединении полное сопротивление цепи имеет чисто активный характер, т. е.
Z=R+jX=R, X=0(условие резонанса),
где X – реактивное сопротивление цепи
А реактивное сопротивление цепи X при последовательном соединении катушки и конденсатора, находится как:
Вот таким образом можно решать задачи на резонанс.
Если понравилась статья, подписывайтесь на канал и не пропускайте новые публикации.
Читайте также:
1. Как электроэнергия передается от электростанций до наших домов;
2. Что такое электрический ток – простыми словами;
Последовательный колебательный контур обозначение на схеме
Последовательный колебательный контур — это цепь, состоящая их катушки индуктивности и конденсатора, которые соединяются последовательно.
Идеальный последовательный колебательный контур
На схемах идеальный последовательный колебательный контур обозначается вот так:
где
L — индуктивность, Гн
С — емкость, Ф
Реальный последовательный колебательный контур
Реальный колебательный контур имеет сопротивление потерь катушки и конденсатора. Это суммарное суммарное сопротивление потерь обозначается буквой R. В результате, реальный последовательный колебательный контур будет иметь такой вид:
R — это суммарное сопротивление потерь катушки и конденсатора
L — собственно сама индуктивность катушки
С — собственно сама емкость конденсатора
Принцип работы последовательного колебательного контура
Генератор частоты и последовательный колебательный контур
Давайте проведем классический эксперимент, который есть в каждом учебнике по электронике. Для этого соберем вот такую схему:
Генератор (Ген)у нас будет выдавать синус.
Для того, чтобы снять осциллограмму силы тока через последовательный колебательный контур, мы подключим в схему шунтовый резистор с малым сопротивлением в 0,5 Ом и с него уже будем снимать напряжение. То есть в данном случае мы шунт используем для наблюдения силы тока в цепи.
А вот и сама схема в реальности:
Слева-направо: шунтовый резистор, катушка индуктивности и конденсатор. Как вы уже поняли, сопротивление R — это суммарное сопротивление потерь катушки и конденсатора, так как нет идеальных радиоэлементов. Оно «прячется» внутри катушки и конденсатора, поэтому в реальной схеме отдельным радиоэлементом мы его не увидим.
Теперь нам осталось подцепить эту схему к генератору частоты и осциллографу, и прогнать по некоторым частотам, снимая осциллограмму с шунта Uш , а также снимая осциллограмму с самого генератора UГЕН .
С шунта мы будем снимать напряжение, которое у нас отображает поведение силы тока в цепи, а с генератора собственно сам сигнал генератора. Давайте прогоним нашу схемку по некоторым частотам и глянем что есть что.
Влияние частоты генератора на сопротивление колебательного контура
В схеме я взял конденсатор на 1мкФ и катушку индуктивности на 1 мГн. На генераторе настраиваю синус размахом в 4 Вольта. Вспоминаем правило: если в цепи соединение радиоэлементов идет последовательно друг за другом, значит, через них течет одинаковая сила тока.
Красная осциллограмма — это напряжение с генератора частоты, а желтая осциллограмма — отображение силы тока через напряжение на шунтовом резисторе.
Частота 200 Герц с копейками:
Как мы видим, при такой частоте ток в этой цепи есть, но очень слабый
Добавляем частоту. 600 Герц с копейками
Здесь мы уже отчетливо видим, что сила тока возросла, а также видим, что осциллограмма силы тока опережает напряжение. Попахивает реактивным сопротивлением конденсатора.
Добавляем частоту. 2 Килогерца
Сила тока стала еще больше.
3 Килогерца
Сила тока увеличилась. Заметьте также, что сдвиг фаз стал уменьшаться.
4,25 Килогерц
Осциллограммы почти уже сливаются в одну. Сдвиг фаз между напряжением и силой тока становится почти незаметным.
И вот на какой-то частоте у нас сила тока стала максимальной, а сдвиг фаз стал равен нулю. Запомните этот момент. Для нас он будет очень важен.
Ну а давайте далее будем увеличивать частоту. Смотрим, что получается в итоге.
Еще совсем недавно ток опережал напряжение, а сейчас уже стал запаздывать после того, как выровнялся с ним по фазе. Так как ток уже отстает от напряжения, здесь уже попахивает реактивным сопротивлением катушки индуктивности.
Увеличиваем частоту еще больше
Сила тока начинает падать, а сдвиг фаз увеличивается.
22 Килогерца
74 Килогерца
Как вы видите, с увеличением частоты, сдвиг приближается к 90 градусов, а сила тока становится все меньше и меньше.
Резонанс последовательного колебательного контура
Давайте подробнее рассмотрим тот самый момент, когда сдвиг фаз был равен нулю и сила тока, проходящая через последовательный колебательный, контур была максимальна:
Это явление носит название резонанса.
Не будем углубляться в теорию высшей математики и комплексных чисел. Дело в том, что в этот самый момент реактивное сопротивление катушки и конденсатора становятся равными, но противоположными по знаку. Поэтому, эти реактивные сопротивления как-бы вычитаются друг из друга, что в сумме дает ноль, и в цепи остается только активная составляющая сопротивления, то есть то самое паразитное сопротивление катушки и конденсатора, или иначе, сопротивление потерь R.
Как вы помните, если у нас сопротивление становится малым, а в данном случае сопротивления потерь катушки и конденсатора очень маленькие, то в цепи начинает течь большая сила тока согласно закону Ома: I=U/R. Если генератор мощный, то напряжение на нем не меняется, а сопротивление становится пренебрежимо малым и вуаля! Ток растет как грибы после дождя, что мы и увидели, посмотрев на желтую осциллограмму при резонансе.
Формула Томсона (резонанса) для последовательного колебательного контура
Если при резонансе у нас реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора XL=XC , то можно уравнять их реактивные сопротивления и уже отсюда вычислить частоту, на которой произошел резонанс. Итак, реактивное сопротивление катушки у нас выражается формулой:
Реактивное сопротивление конденсатора вычисляется по формуле:
Приравниваем обе части и вычисляем отсюда F:
В данном случае мы получили формулу резонансной частоты. Это формула по другому называется формулой Томсона, как вы поняли, в честь ученого, который ее вывел.
Давайте по формуле Томсона посчитаем резонансную частоту нашего последовательного колебательного контура. Для этого я буду использовать свой RLC-транзисторметр.
Замеряем индуктивность катушки:
И замеряем нашу емкость:
Высчитываем по формуле нашу резонансную частоту:
У меня получилось 5, 09 Килогерц.
С помощью регулировки частоты и осциллографа я поймал резонанс на частоте 4,78 Килогерц (написано в нижнем левом углу)
Спишем погрешность в 200 с копейками Герц на погрешность измерений приборов. Как вы видите, формула Томпсона работает.
Резонанс напряжений
Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:
и конденсатор в 1000 пФ
Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.
Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор — это не есть хорошо, но что не сделаешь ради науки!
Ну что же, приступим ;-). Давайте сначала посчитаем резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.
Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:
Размах амплитуды 4 Вольта
Хотя на генераторе частоты размах более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.
Теперь небольшой прикол 😉
Вот этот сигнал мы подаем на наш последовательный колебательный контур:
Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.
Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:
Смотрим напряжение на конденсаторе:
Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!
Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:
Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!
Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14, и цепляю поочередно к ним лампочку:
Как видите — полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока — увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!
Объяснение резонанса напряжения
При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.
При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение UL = IXL , а на конденсаторе UC = IXC . А так как при резонансе у нас XL = XC , то получаем что UL = UC , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.
Добротность последовательного колебательного контура
Ну раз уж мы начали задвигать тему колебательных контуров, поэтому мы не можем обойти стороной такой параметр, как добротность колебательного контура. Так как мы уже провели некоторые опыты, то нам будет проще определить добротность, исходя из амплитуды напряжений. Добротность обозначается буквой Q и вычисляется по первой простой формуле:
Давайте посчитаем добротность в нашем случае.
Так как цена деления одного квадратика по вертикали 2 Вольта, следовательно, амплитуда сигнала генератора частоты 2 Вольта.
А это то, что мы имеем на зажимах конденсатора или катушки. Здесь цена деления одного квадратика по вертикали 5 Вольт. Считаем квадратики и умножаем. 5х4=20 Вольт.
Считаем по формуле добротности:
Q=20/2=10. В принципе немного и не мало. Пойдет. Вот так вот на практике можно найти добротность.
Есть также вторая формула для вычисления добротности.
где
R — сопротивление потерь в контуре, Ом
L — индуктивность, Генри
С — емкость, Фарад
Зная добротность, можно легко найти сопротивление потерь R последовательного колебательного контура.
Также хочу добавить пару слов о добротности. Добротность контура — это качественный показатель колебательного контура. В основном его стараются всегда увеличить различными всевозможными способами. Если взглянуть на формулу выше, то можно понять, для того, чтобы увеличить добротность, нам надо как-то уменьшить сопротивление потерь колебательного контура. Львиная доля потерь относится к катушке индуктивности, так как она уже конструктивно имеет большие потери. Она намотана из провода и в большинстве случаев имеет сердечник. На высоких частотах в проводе начинает проявляться скин-эффект, который еще больше вносит потери в контур.
Видео на тему «Как работает колебательный контур. Резонанс»:
Резюме
Последовательный колебательный контур состоит из катушки индуктивности и конденсатора, соединенных последовательно.
Катушка и конденсатор имеют паразитные омические потери, так как не являются идеальными радиоэлементами. Сумма этих потерь называется сопротивлением потерь R последовательного колебательного контура.
На какой-то частоте реактивное сопротивление катушки становится равным реактивному сопротивлению конденсатора и в цепи последовательного колебательного контура наступает такое явление, как резонанс.
При резонансе реактивные сопротивления катушки и конденсатора хоть и равны по модулю, но противоположны по знаку, поэтому они вычитается и в сумме дают ноль. В цепи остается только активное сопротивление потерь R.
При резонансе сила тока в цепи становится максимальной, так как сопротивление потерь катушки и конденсатора R в сумме дают малое значение.
При резонансе напряжение на катушке равняется напряжению на конденсаторе и превышает напряжение на генераторе.
Коэффициент, показывающий во сколько раз напряжение на катушке либо на конденсаторе превышает напряжение на генераторе, называется добротностью Q последовательного колебательного контура и показывает качественную оценку колебательного контура. В основном стараются сделать Q как можно больше.
На низких частотах колебательный контур имеет емкостную составляющую тока до резонанса, а после резонанса — индуктивную составляющую тока.
Резонанс напряжений и резонанс токов
В физике резонансом называется явление, при котором в колебательном контуре частота свободных колебаний совпадает с частотой вынужденных колебаний. В электричестве аналогом колебательного контура служит цепь, состоящая из сопротивления, ёмкости и индуктивности. В зависимости от того как они соединены различают резонанс напряжений и резонанс токов.
Резонанс напряжений
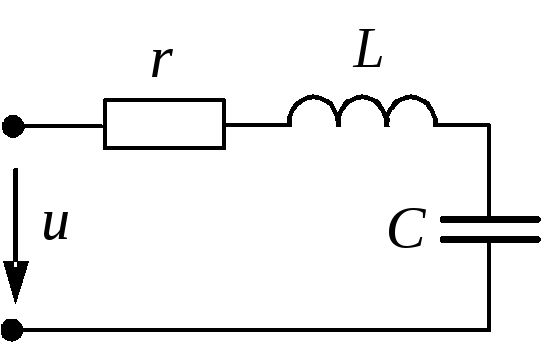
Резонанс напряжений возникает в последовательной RLC-цепи.
Условием возникновения резонанса является равенство частоты источника питания резонансной частоте w=wр, а следовательно и индуктивного и емкостного сопротивлений xL=xC. Так как они противоположны по знаку, то в результате реактивное сопротивление будет равно нулю. Напряжения на катушке UL и на конденсаторе UC будет противоположны по фазе и компенсировать друг друга. Полное сопротивление цепи при этом будет равно активному сопротивлению R, что в свою очередь вызывает увеличение тока в цепи, а следовательно и напряжение на элементах.
При резонансе напряжения UC и UL могут быть намного больше, чем напряжение источника, что опасно для цепи.
С увеличением частоты сопротивление катушки увеличивается, а конденсатора уменьшается. В момент времени, когда частота источника будет равна резонансной, они будут равны, а полное сопротивление цепи Z будет наименьшим. Следовательно, ток в цепи будет максимальным.
Из условия равенства индуктивного и емкостного сопротивлений найдем резонансную частоту
Исходя из записанного уравнения, можно сделать вывод, что резонанса в колебательном контуре можно добиться изменением частоты тока источника (частота вынужденных колебаний) или изменением параметров катушки L и конденсатора C.
Следует знать, что в последовательной RLC-цепи, обмен энергией между катушкой и конденсатором осуществляется через источник питания.
Резонанс токов
Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором.
Условием возникновения резонанса токов является равенство частоты источника резонансной частоте w=wр, следовательно проводимости BL=BC. То есть при резонансе токов, ёмкостная и индуктивная проводимости равны.
Для наглядности графика, на время отвлечёмся от проводимости и перейдём к сопротивлению. При увеличении частоты полное сопротивление цепи растёт, а ток уменьшается. В момент, когда частота равна резонансной, сопротивление Z максимально, следовательно, ток в цепи принимает наименьшее значение и равен активной составляющей.
Выразим резонансную частоту
Как видно из выражения, резонансная частота определяется, как и в случае с резонансом напряжений.
Явление резонанса может носить как положительный, так и отрицательный характер. Например, любой радиоприемник имеет в своей основе колебательный контур, который с помощью изменения индуктивности или емкости настраивают на нужную радиоволну. С другой стороны, явление резонанса может привести к скачкам напряжения или тока в цепи, что в свою очередь приводит к аварии.
