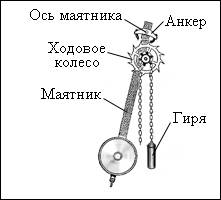
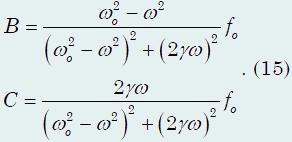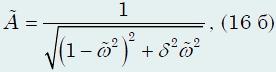Уравнение вынужденных колебаний и его решение. Резонанс.
Потери
механической энергии в любой колебательной
системе из-за
наличия сил трения неизбежны, поэтому
без «подкачки» энергии извне колебания
будут затухающими. Существует несколько
принципиально различных способов
создания колебательных систем незатухающих
колебаний. Остановимся более подробно
на рассмотрении незатухающих
колебаний под действием внешней
периодической силы.
Такие колебания называются
вынужденными.
Продолжим изучение
движения гармонического маятника (рис.
6.9 ).
рис.
6.9
Помимо
рассмотренных ранее сил упругости и
вязкого трения, на шарик действует
внешняя
вынуждающая
периодическая сила, изменяющаяся по
гармоническому закону
частота,
которой может отличаться от собственной
частоты колебаний маятника ωo.
Природа
этой сил в данном случае нам не существенна.
Создать такую силу можно различными
способами, например, сообщить шарику
электрический заряд и поместить его во
внешнее переменное электрическое
поле.
Уравнение движения шарика в
рассматриваемом случае имеет вид
Разделим
его на массу шарика и используем прежние
обозначения параметров системы. В
результате получим
уравнение
вынужденных колебаний:
где
fo
= Fo/m
− отношение амплитудного значения
внешней вынуждающей силы к массе
шарика.
Общее решение уравнения (3)
достаточно громоздко и, конечно, зависит
от
начальных условий. Характер движения
шарика, описываемого уравнением (3),
понятен: под действием вынуждающей силы
возникнуть колебания, амплитуда которых
будет возрастать. Этот переходный режим
достаточно сложен и зависит от начальных
условий. По прошествии некоторого
промежутка времени колебательный режим
установится, их амплитуда перестанет
изменяться. Именно установившийся
режим колебаний,
во многих случаях представляет основной
интерес. Мы не будем рассматривать
переход системы к установившемуся
режиму, а сконцентрируем внимание на
описании и изучении характеристик этого
режима.
При такой постановке задачи
нет необходимости задавать начальные
условия, так как интересующий нас
установившийся режим не зависит от
начальных условий, его характеристики
полностью определяются самим уравнением.
С
аналогичной ситуацией мы сталкивались
при изучении движения тела под действием
постоянной внешней силы и силы вязкого
трения
По
прошествии некоторого времени тело
движется с постоянной установившейся
скоростью
v
= Fo/β,
которая не зависит от начальных условий,
и полностью определяется уравнением
движения. Начальные условия определяют
режим, переходный к установившемуся
движению.
На основании здравого смысла
разумно предположить, что в установившемся
режиме колебаний шарик будет колебаться
с частотой внешней вынуждающей силы.
Поэтому решение уравнения (3) следует
искать в гармонической функции с частотой
вынуждающей силы.
Для начала решим
уравнение (3), пренебрегая силой
сопротивления
Попробуем
найти его решение в виде гармонической
функции
Для
этого вычислим зависимости скорости и
ускорения тела от времени, как производные
от закона движения
и
подставим их значения в уравнение (4)
Теперь
можно сократить на
cosωt.
Следовательно, это выражение обращается
в верное тождество в любой момент
времени, при выполнении условия
Таким
образом, наше предположение о решении
уравнения (4) в виде (5)
оправдалось: установившийся режим
колебаний описывается функцией
Отметим,
что коэффициент A
согласно полученному выражению (6) может
быть, как положительным (при ω
< ωo),
так и отрицательным (при ω
> ωo).
Изменение знака соответствует изменению
фазы колебаний на π
(причина такого изменение будет выяснена
чуть позже), поэтому амплитудой колебаний
является модуль этого коэффициента
|A|.
Амплитуда
установившихся колебаний, как и следовало
ожидать,
пропорциональна
величине вынуждающей силы. Кроме того,
эта амплитуда сложным образом зависит
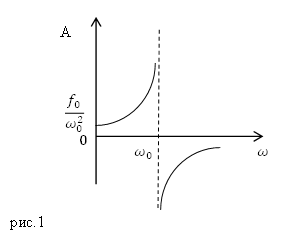
от частоты вынуждающей силы. Схематический
график этой зависимости показан на рис.
6.10
Рис.
6.10 Резонансная кривая
Как
следует из формулы (6) и хорошо видно на
графике, при приближении
частоты вынуждающей силы к собственной
частоте системы амплитуда резко
возрастает. Причина такого возрастания
амплитуды понятна: вынуждающая сила
«во время» подталкивает шарик, при
полном совпадении частот установившейся
режим отсутствует − амплитуда возрастает
до бесконечности. Конечно, на практике
такого бесконечного возрастания
наблюдать невозможно: во-первых,
это может привести к разрушению самой
колебательной системы, во-вторых,
при больших амплитудах колебаний нельзя
пренебрегать силами сопротивления
среды.
Резкое
возрастание амплитуды вынужденных
колебаний при приближении частоты
вынуждающей силы к собственной частоте
колебаний системы называется явлением
резонанса.
Приступим
теперь к поиску решения уравнения
вынужденных колебаний с учетом силы
сопротивления
Естественно,
что и в этом случае решение следует
искать в виде
гармонической функции с частотой
вынуждающей силы. Легко заметить, что
поиск решения в форме (5) в данном случае
не приведет к успеху. Действительно,
уравнение (8), в отличие от уравнения
(4), содержит скорость частицы, которая
описывается функцией синуса. Поэтому,
временная часть в уравнении (8) не
сократится. Следовательно, решение
уравнения (8) следует представить в общей
форме гармонической функции
в
которой два параметра Ao
и φ
необходимо найти с помощью уравнения
(8). Параметр Ao
является амплитудой вынужденных
колебаний, φ
− сдвиг фаз между изменяющейся координатой
и переменной вынуждающей силой. Используя
тригонометрическую формулу для косинуса
суммы, функцию (9) можно представить в
эквивалентной форме
которая
также содержит два параметра B
= Aocosφ
и C
= −Aosinφ,
подлежащих определению. Используя
функцию (10), запишем явные выражения для
зависимостей скорости и ускорения
частицы от времени
и
подставим в уравнение (8):
Перепишем
это выражение в виде
Для
того чтобы равенство (13) выполнялось в
любой момент времени
необходимо, чтобы коэффициенты при
косинусе и синусе были равны нулю. На
основании этого условия получаем два
линейных уравнения для определения
параметров функции (10):
Решение
этой системы уравнений имеет вид
На
основании формулы (10) определяем
характеристики вынужденных колебаний:
амплитуду
сдвиг
фаз
При
малом затухании эта зависимость имеет
резкий максимум при приближении частоты
вынуждающей силы ω
к собственной частоте системы ωo.
Таким образом, и в этом случае возможно
возникновения резонанса, поэтому
построенные зависимости часто называют
резонансной кривой. Учет слабого
затухания показывает, что амплитуда не
возрастает до бесконечности, ее
максимальное значение зависит от
коэффициента затухания − с возрастанием
последнего максимальная амплитуда
быстро убывает.
Полученная зависимость
амплитуды колебаний от частоты вынуждающей
силы (16) содержит слишком много независимых
параметров ( fo,
ωo,
γ)
для того, чтобы построить полное семейство
резонансных кривых. Как и во многих
случаях, эту зависимость можно существенно
упростить, перейдя к «безразмерным»
переменным. Преобразуем формулу (16) к
следующему виду
и
обозначим
− относительная
частота (отношение частоты вынуждающей
силы к собственной частоте колебаний
системы);
− относительная
амплитуда (отношение амплитуды колебаний
к величине отклонения Ao
= f/ωo2
при нулевой частоте);
−
безразмерный параметр,
определяющий величину затухания.
Используя эти обозначения, функция (16)
существенно упрощается
так
как содержит всего один параметр −
δ.
Однопараметрическое
семейство резонансных кривых, описываемых
функцией
(16 б) может быть построено, особенно
легко с помощью компьютера. Результат
такого построения показан на рис. 629.
рис.
6.11
Отметим,
что переход к «обычным» единицам
измерения может быть проведен элементарным
изменением масштаба осей координат.
Следует
отметить, что частота вынуждающей силы,
при которой амплитуда
вынужденных колебаний максимальна,
также зависит от коэффициента затухания,
слегка убывая с ростом последнего.
Наконец, подчеркнем, что увеличение
коэффициента затухания приводит к
существенному увеличению ширины
резонансной кривой.
Возникающий сдвиг
фаз между колебаниями точки и вынуждающей
силой также
зависит от частоты колебаний и коэффициента
их затухания. Более подробно с ролью
этого сдвига фаз мы познакомимся при
рассмотрении преобразования энергии
в процессе вынужденных колебаний.
частота
свободных незатухающих колебаний
совпадает с собственной частотой,
частота затухающих колебаний немного
меньше собственной, а частота вынужденных
колебаний совпадает с частотой вынуждающей
силы, а не собственной частотой.
Вынужденные
электромагнитные колебания
Вынужденными
называются
такие колебания, которые происходят в
колебательной системе под влиянием
внешнего периодического воздействия.
Рис.6.12.
Контур с вынужденными электрическими
колебаниями
Рассмотрим
процессы, протекающие в электрическом
колебательном контуре (рис.6.12),
присоединенном к внешнему источнику,
ЭДС которого изменяется по гармоническому
закону
,
г
– амплитуда внешней ЭДС,
– циклическая
частота ЭДС.
Обозначим
через UC
напряжение на конденсаторе, а через i
–
силу тока в контуре. В этом контуре кроме
переменной ЭДС (t)
действует еще ЭДС самоиндукции L
в катушке индуктивности.
ЭДС
самоиндукции прямо пропорциональна
скорости изменения силы тока в контуре
.
Для
вывода дифференциального
уравнения вынужденных колебаний
возникающих
в таком контуре используем второе
правило Кирхгофа
.
Напряжение
на активном сопротивлении R
найдем по закону Ома
.
Cила
электрического тока равна заряду
протекающему за единицу времени через
поперечное сечение проводника
.
Следовательно
.
Напряжение
UC
на конденсаторе прямо пропорционально
заряду на обкладках конденсатора
.
ЭДС
самоиндукции можно представить через
вторую производную от заряда по времени
.
Подставляя
напряжения и ЭДС во второе правило
Кирхгофа
.
Разделив
обе части этого выражения на L
и распределив слагаемые по степени
убывания порядка производной, получим
дифференциальное уравнение второго
порядка
.
Введем
следующие обозначения и получим
–коэффициент
затухания,
–циклическая
частота собственных колебаний контура.
.
(1)
Уравнение
(1) является неоднородным
линейным дифференциальным уравнением
второго порядка. Такого типа уравнения
описывают поведение широкого класса
колебательных систем (электрических,
механических) под влиянием внешнего
периодического воздействия (внешней
ЭДС или внешней силы).
Общее
решение уравнения (1) складывается из
общего решения q1
однородного
дифференциального уравнения (2)
(2)
и
любого частного решения q2
неоднородного
уравнения (1)
.
Вид
общего решения однородного
уравнения
(2) зависит от величины коэффициента
затухания .
Нас будет интересовать случай слабого
затухания
<< 0.
При этом общее решение уравнения (2)
имеет вид
,
(3)
где
B
и 0
– постоянные, задаваемые начальными
условиями.
Решение
(3) описывает затухающие колебания в
контуре. Входящие в (3) величины:
–циклическая
частота затухающих колебаний;
–амплитуда
затухающих колебаний;
–фаза
затухающих колебаний.
Частное
решение уравнения (1) ищем в виде
гармонического колебания, происходящего
с частотой, равной частоте
внешнего периодического воздействия
– ЭДС, и отстающего по фазе на
от него
,
(4)
где
– амплитуда вынужденных колебаний,
зависящая от частоты.
Подставим
(4) в (1) и получим тождество
Чтобы
сравнить фазы колебаний, используем
тригонометрические формулы приведения
,
.
Тогда
наше уравнение перепишется в виде
Представим
колебания в левой части полученного
тождества в виде векторной
диаграммы
(рис.6.13)..
Третье
слагаемое, соответствующее колебаниям
на емкости С,
имеющее фазу (t
– )
и амплитуду
,
изобразим горизонтальным вектором,
направленным вправо.
Рис.6.13.
Векторная диаграмма
Первое
слагаемое левой части, соответствующие
колебаниям на индуктивности L,
изобразится на векторной диаграмме
вектором, направленным горизонтально
влево (его амплитуда
).
Второе
слагаемое, соответствующие колебаниям
на сопротивлении R,
изобразим вектором, направленным
вертикально вверх (его амплитуда
),
т. к. его фаза на/2
отстает от фазы первого слагаемого.
Так
как сумма трех колебаний слева от знака
равно дает гармоническое колебание
,
то векторная сумма на диаграмме (диагональ
прямоугольника) изображает колебание
с амплитудойи фазойt,
которая на
опережает фазу колебаний третьего
слагаемого.
Из
прямоугольного треугольника по теореме
Пифагора можно найти амплитуду A()
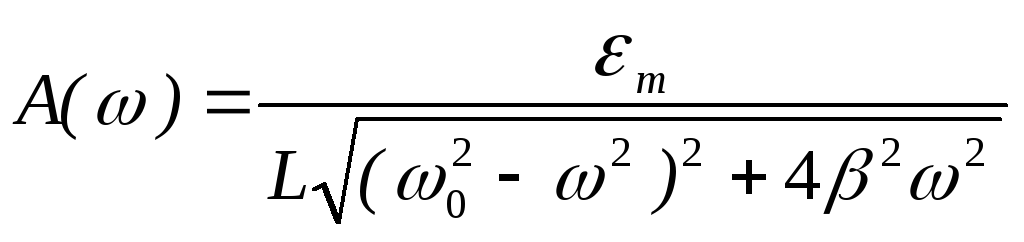
и
tg
как отношение противолежащего катета
к прилежащему катету.
.
(6)
Следовательно,
решение (4) с учетом (5) и (6) примет вид

(7)
Общее
решение дифференциального уравнения
(1) является суммой q1
и q2

(8)
Формула
(8) показывает, что при воздействии на
контур периодической внешней ЭДС в нем
возникают колебания двух частот, т.е.
незатухающие колебания с частотой
внешней ЭДС
и затухающие колебания с частотой
.
Амплитуда затухающих колебанийсо временем становится пренебрежимо
малой, и в контуре остаются только
вынужденные колебания, амплитуда которых
не зависит от времени. Следовательно,
установившиеся вынужденные колебания
описываются функцией (4). То есть в контуре
возникают вынужденные гармонические
колебания, с частотой, равной частоте
внешнего воздействия, и амплитудой,
зависящей от этой частоты (рис.3а)
по закону (5). При этом по фазе вынужденное
колебание отстает на
от вынуждающего воздействия.
Продифференцировав
выражение (4) по времени, найдем силу
тока в контуре
,
где
– амплитуда силы тока.
Запишем
это выражение для силы тока в виде
,
(9)
где
–сдвиг
по фазе между током и внешней ЭДС.
В
соответствии с (6) и рис.2
.
(10)
Из
этой формулы следует, что сдвиг по фазе
между током и внешней ЭДС зависит, при
постоянном сопротивлении R,
от соотношения между частотой вынуждающей
ЭДС
и собственной частотой контура 0.
Если
< 0,
то сдвиг по фазе между током и внешней
ЭДС
< 0. Колебания силы тока опережают
колебания ЭДС по фазе на угол .
Если
> 0,
тогда
> 0. Колебания силы тока отстают от
колебаний ЭДС по фазе на угол .
Если
= 0
(резонансная
частота),
то
= 0, т. е. сила тока и ЭДС колеблются в
одинаковой фазе.
Резонанс
– это
явление резкого возрастания амплитуды
колебаний при совпадении частоты
внешней, вынуждающей силы с собственной
частотой колебательной системы.
При
резонансе
= 0
и период колебаний
.
Учитывая,
что коэффициент затухания
,
получим
выражения для добротности при резонансе
Т
= Т0
,
с
другой стороны
.
Амплитуды
напряжений на индуктивности и емкости
при резонансе можно выразить через
добротность контура
,
(15)
.
(16)
Из
(15) и (16) видно, что при
= 0,
амплитуда напряжения на конденсаторе
и индуктивности в Q
раз больше амплитуды внешней ЭДС. Это
свойство последовательного RLC
контура используется для выделения
радиосигнала определенной частоты
из спектра радиочастот при перестройке
радиоприемника.
На
практике RLC
контура связаны с другими контурами,
измерительными приборами или усилительными
устройствами, вносящими дополнительное
затухание в RLC
контур. Поэтому реальная величина
добротности нагруженного RLC
контура оказывается ниже величины
добротности, оцениваемой по формуле
.
Реальная
величина добротности может быть оценена
как
Рис.6.14.
Определение добротности по резонансной
кривой
,
где
f
– ширина полосы частот, в которых
амплитуда составляет 0,7 от максимального
значения (рис.4).
Напряжения
на конденсаторе UC,
на активном сопротивлении UR
и на катушке индуктивности UL
достигают максимума при различных
частотах, соответственно
,
,

Если
затухание мало 0
>> ,
то все эти частоты практически совпадают
и можно считать что
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вынужденные колебания, резонанс, теория и онлайн калькуляторы
Вынужденные колебания, резонанс
Напомним, что собственные колебания – это колебания, которые происходят при отсутствии каких-либо внешних воздействий. Внешнее воздействие необходимо только для того, чтобы вывести колебательную систему из состояния равновесия, после чего она предоставляется самой себе. Дифференциальное уравнение, описывающее собственные колебания не имеет ни каких следов внешнего воздействия на систему. Внешнее воздействие отражается только в начальных условиях колебаний.
Однако, для того чтобы осуществлять незатухающие колебания в реальной действительности, необходимо компенсировать потери энергии колебательной системой, которые происходят в результате действия разного рода сил трения. Особенно важным и простым для изучения является случай, когда внешняя сила обладает периодическим характером. Общей характеристикой вынужденных колебаний, которые осуществляются при воздействии внешней периодической силы, является то, что через некоторое время после начала действия этой силы, колебательная система «забывает» свое начальное состояние, колебания носят стационарный характер и не зависят от начальных условий. Начальные условия играют существенную роль только при установлении колебаний, такой начальный период, обычно называют переходным процессом.
Определение вынужденных колебаний
Определение
Колебания, происходящие под воздействием периодически изменяющейся силы (периодически изменяющейся ЭДС),
называют вынужденными механическими (электромагнитными) колебаниями.
Гармоническое внешнее воздействие
Пусть на колебательную систему действует внешняя сила, которая изменяется по гармоническому закону:
[F=F_0{cos left(omega tright) }left(1right).]
Уравнение движения для системы, в которой на колебательную систему действуют возвращающая сила (например, сила упругости), сила сопротивления и вынуждающая сила может быть записано в виде:
[frac{d^2xi }{dt^2}+2дafrac{dxi }{dt}+{omega }^2_0xi =f_0{cos left(omega tright) }left(2right),]
где $xi $ – колеблющийся параметр, например, координата $x$, при колебаниях пружинного маятника вдоль оси X; $f_0=frac{F_0}{m}$ если колебания механические ($x_0=frac{U_m}{L}- в случае электрических колебаний$); $delta $ – коэффициент затухания; ${omega }_0$ – циклическая частота свободных незатухающих колебаний (если $delta $=0, то ${omega }_{0 }$называют собственной частотой колебаний).
Решение уравнения (2) – это сумма общего решения однородного уравнения:
[frac{d^2xi }{dt^2}+2delta frac{dxi }{dt}+{omega }^2_0xi =0 left(3right)]
и частного решения неоднородного уравнения.
Общее решение уравнения (3):
[{xi }_1=A_0e^{-delta t}{cos left({omega }_1t+{varphi }_1right)left(4right), }]
где $A_0$ – начальная амплитуда колебаний.
Частное решение уравнения (2) представляет выражение:
[xi =A{cos (omega t-varphi ) }left(5right),]
где $A=frac{f_0}{sqrt{{left({omega }^2_0-{omega }^2right)}^2+4{delta }^2{omega }^2}}(6)$; $varphi =arc tg frac{2delta omega }{{omega }^2_0-{omega }^2} (7)$.
Слагаемое ${xi }_1$ в решении уравнения (2) играет значительную роль в начальной стадии установления колебаний, пока амплитуда вынужденных колебаний не будет определяться выражением (6).
Установившиеся вынужденные колебания происходят с частотой $omega $ и являются гармоническими. Амплитуда и фаза этих колебаний определены формулами (6) и (7).
Резонанс при вынужденных колебаниях
При приближении частоты вынуждающей силы к собственной частоте колебаний, появляется резкий рост амплитуды колебаний. Это явление называют резонансом.
Формула (6) показывает, что амплитуда вынужденных колебаний имеет максимум. Найдем частоту при которой возникает резонанс. (частоты при которой $A=max$). Для этого необходимо отыскать максимум функции $A(omega )$. Вычислим производную $frac{dA}{domega }$ и приравняем ее к нулю имеем:
[-4left({omega }^2_0-{omega }^2right)omega +8{delta }^2omega =0 left(8right).]
Выражение (8) справедливо при:
[left{ begin{array}{c}
{omega }_1=0;; \
{omega }_2=sqrt{{omega }^2_0-2{delta }^2;;} \
{omega }_3=-sqrt{{omega }^2_0-2{delta }^2.} end{array}
right.]
Получаем, частота резонанса (${omega }_r$) равна:
[{omega }_r=sqrt{{omega }^2_0-2{delta }^2}left(9right).]
При ${delta }^2ll {omega }^2_0$ резонансная частота равна собственной частоте колебаний ${omega }_0.$ Подставив вместо частоты правую часть выражения (9) в формулу (6), амплитуда вынужденных колебаний равна:
[A_r=frac{f_0}{2delta sqrt{{omega }^2_0-{delta }^2}}left(10right).]
При малом затухании колебаний (${delta }^2ll {omega }^2_0$) амплитуда в состоянии резонанса:
[A_r=frac{f_0}{2delta {omega }_0}=Qfrac{f_0}{{omega }^2_0}left(11right),]
где $Q=frac{{omega }_0}{2delta }$ – добротность колебательной системы, величина, которая характеризует резонансные свойства колебательной системы. При увеличении добротности растет амплитуда резонанса.
Примеры задач с решением
Пример 1
Задание. Какова амплитуда установившихся вынужденных колебаний, если силой трения, действующей на колебательную систему можно пренебречь? Нарисуйте график зависимости амплитуды от частоты вынуждающей силы.
Решение. Запишем уравнение установившихся колебаний при воздействии на систему гармонической силы в отсутствии сил трения:
[frac{d^2xi }{dt^2}+{omega }^2_0xi =f_0{cos left(omega tright) }left(1.1right).]
Решение уравнения будем искать в виде:
[xi left(tright)=A{cos left(omega tright) }left(1.2right).]
Вычислим вторую производную от $xi left(tright)$ по времени:
[frac{dxi }{dt}=-Aomega {sin left(omega tright);; }frac{d^2xi }{dt^2}=-A{omega }^2{cos left(omega tright) left(1.3right). }]
Подставим результат (1.3) в уравнение (1.1), имеем:
[-A{omega }^2{cos left(omega tright) }+{omega }^2_0A{cos left(omega tright) }=f_0{cos left(omega tright) }to Aleft(-{omega }^2+{omega }^2_0right)=f_0to A=frac{f_0}{{omega }^2_0-{omega }^2}.]
Рассмотрим функцию
[A=frac{f_0}{{omega }^2_0-{omega }^2}(1.4).]
При $omega =0$ из выражения (1.4) получим:
[A=frac{f_0}{{omega }^2_0}left(1.5right).]
Из выражения (1.2) следует, что при $omega =0$:
[xi left(tright)=A=frac{f_0}{{omega }^2_0}=const]
Ответ. $A=frac{f_0}{{omega }^2_0-{omega }^2}$
Пример 2
Задание. Объясните, почему при описании вынужденных колебаний в состоянии резонанса следует учитывать силы трения?
Решение. При описании вынужденных колебаний около резонансных частот учет трения является принципиально необходимым. С учетом трения амплитуда колебаний становится конечной. Амплитуда вынужденных колебаний тем меньше, чем больше трение. Само понятие установившихся колебаний, строго говоря, применимо к системам при наличии в них трения. Если трение бы отсутствовало, то процесс установления колебаний был бы бесконечно долгим.
При малом трении установившиеся вынужденные колебания происходят в фазе с вынуждающей силой при $omega <{omega }_0$ и в противофазе при $omega >{omega }_0$, как и в отсутствии трения. Около резонанса фаза изменяется непрерывно. При точном совпадении $omega ={omega }_0$ смещение $xi (t)$ отстает от вынуждающей силы на четверть периода. При этом скорость $dot{xi }(t)$ софазна с вынуждающей силой, что создает максимально благоприятные условия для передачи энергии от источника внешней силы к колебательной системе.
Читать дальше: движение тела брошенного горизонтально.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Резонанс
При заданных возмущающей силе Fmax.возм
и коэффициенте трения β амплитуда Ym является функцией только угловой частоты возмущающей силы.
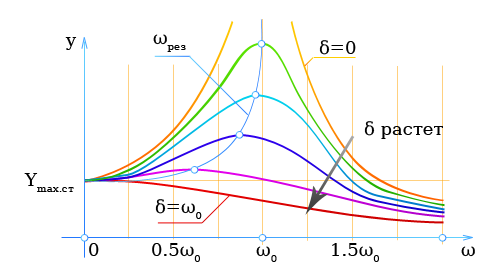
На рисунке показана зависимость Ym от ω (резонансная кривая).
Параметром служит коэффициент затухания δ.
При ω ≈ ω0 она достигает особенно большого значения (резонанс).
При самых малых значениях δ величина Ym резко возрастает.
Если δ > 0, то в случае резонанса ω < ω0; величина Ymax.ст представляет собой статическое отклонение системы под действием постоянной силы Ymax.возм (ω = 0).
Для определения резонансной частоты необходимо найти максимум функции Ym = Ym(ω) и приравнять первую производную нулю; тогда, если
| ωрез | резонансная частота, при которой амплитуда максимальна, | радиан/сек |
|---|---|---|
| ω0 | частота собственных незатухающих колебаний системы, | радиан/сек |
| m | масса колебательной системы, | кг |
| β | коэффициентом вязкого трения, | кг/сек |
| δ | коэффициентом затухания, | радиан/сек |
Частота резонанса
[
ω_{рез} = sqrt{ω_{0}^2 – frac{β^2}{2m^2}} = sqrt{ω_{0}^2 – 2δ^2}
]
Условие отсутствия резонанса
[
δ geqslant frac{ω_{0}}{sqrt{2}}
]
Амплитуда резонанса
Чтобы найти величину амплитуды в резонансном случае, нужно подставить формулу (1) в формулу отклонения при вынужденных колебаниях.
Если
| Ymax.рез | резонансная амплитуда колебаний системы, | метр |
|---|---|---|
| Fmax.возм | максимальное значение возмущающей силы, | Ньютон |
| m | масса колебательной системы, | кг |
| ωрез | резонансная частота, при которой амплитуда максимальна, | радиан/сек |
| ω0 | частота собственных незатухающих колебаний системы, | радиан/сек |
| ω | частота колебаний системы с затуханием, | радиан/сек |
| β | коэффициентом вязкого трения, | кг/сек |
| δ | коэффициентом затухания, | радиан/сек |
то имеем
[
Y_m = frac
{
F_{max.возм}
}
{
β sqrt{ ω_{0}^2 – frac{β^2}{4m^2} }
}
]
[
Y_m = frac{F_{max.возм}}{βω}
]
[
Y_m = frac{F_{max.возм}}{2δmω}
]
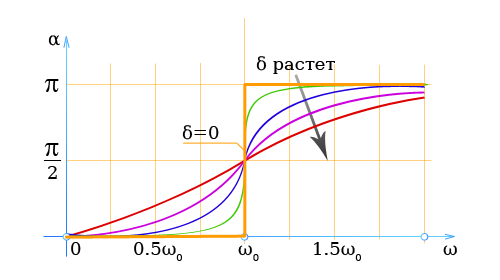
Согласно формуле, разность фаз α также зависит от частоты возмущающей силы.
Параметром служит коэффициент δ.
На рисунке представлена зависимость α от частоты.
Независимо от величины затухания при ω = ω0 разность фаз составляет
[
α = 90°
]
Резонанс играет большую роль в технике и в повседневной жизни. В большинстве механических устройств под действием внешних периодических сил могут возникать колебания. При резонансе происходит нарастание амплитуды колебаний, и это может привести к разрушениям («резонансная катастрофа»). В случае вращательного движения резонансную частоту называют критическим числом оборотов.
Резонанс |
стр. 558 |
|---|
Если колебания совершаются под воздействием внешней силы, они называются вынужденными. Работа внешней силы, которая обеспечивает колебательную систему энергией, при этом является положительной. Благодаря ей колебания не затухают и могут противодействовать силам трения.
Внешняя сила не обязательно должна быть постоянной. С течением времени она может изменяться по разным законам. Особый случай – воздействие на колебательную систему внешней силы, которая изменяется по гармоническому закону с частотой, равной ω, в то время как сама система совершает собственные колебания с той же самой частотой.
Установившиеся вынужденные колебания всегда происходят с частотой внешней силы. Частоту свободных колебаний определяют параметры системы.
Когда внешняя сила начинает воздействовать на колебательную систему, должно пройти некоторое время Δt , прежде чем вынужденные колебания установятся. Это время будет равно тому времени τ, за которое затухают свободные колебания в данной системе.
В момент начала воздействия в системе начинают происходить два процесса одновременно – свободные колебания с собственной частотой ω0 и вынужденные с частотой ω. Однако из-за сил трения свободные колебания в определенный момент затухают, поэтому по прошествии времени в системе сохраняются лишь стационарные колебания с той частотой, которая соответствует внешней (вынуждающей) силе.
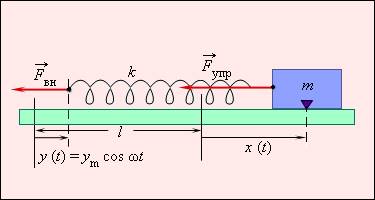
Разберем пример. У нас есть тело на пружине, совершающее вынужденные колебания (см. иллюстрацию ниже). Приложим внешнюю силу, обозначенную F→вн, к свободному концу пружины, после чего этот конец начнет перемещаться по закону, выражаемому формулой:
y=ymcos ωt.
Здесь буквой ω обозначена круговая частота, а ym – амплитуда колебаний.
Перемещения такого рода обеспечиваются шатунным механизмом, который преобразует круговые движения в возвратно-поступательные.
Рисунок 2.5.1. Груз на пружине, совершающий вынужденные колебания. Перемещение свободного конца выражено формулой y=ym cos ωt, где l означает длину недеформированной пружины, а k –ее жесткость.
При смещении левого конца пружины на некоторое расстояние y и правого – на x по сравнению с первоначальным положением недеформированной пружины будет происходить ее удлинение. Найти величину этого удлинения можно по следующей формуле:
∆l=x-y=x-ymcos ωt.
В таком случае мы можем переформулировать второй закон Ньютона для этого случая следующим образом:
ma=-k(x-y)=-kx+kymcos ωt.
Здесь сила, которая действует на тело, показана как сумма двух слагаемых, первым из которых является упругость, стремящаяся к равновесию тела, а вторым – внешнее воздействие, совершающееся с определенными интервалами. Внешнюю силу также называют вынуждающей.
Теперь выразим эту зависимость в строгой математической формуле, учитывающей связь между координатой тела a=x¨ и его ускорением. У нас получится следующее:
x¨+ω02x=A cos ωt.
Эта зависимость называется уравнением внешних колебаний. Здесь ω0=km является собственной круговой частотой свободного колебания, а ω – циклической частотой внешней (вынуждающей) силы.
Чтобы найти величину A для вынужденного колебания груза на пружине, нужно воспользоваться следующей формулой:
A=kmym-ω02ym.
То уравнение, что мы записали перед этим, не учитывает, что на тело действуют также и силы трения. В уравнении вынужденных колебаний, в отличие от уравнения свободных, учитываются сразу обе частоты – частота вынуждающей силы и частота свободных колебаний.
Вынужденные колебания груза на пружине, которые устанавливаются со временем, имеют частоту внешнего воздействия. Это определяется следующим законом:
x(t)=xmcos (ωt+θ).
Здесь xm обозначает амплитуду вынужденного колебания, а буква θ – его начальную фазу. Значения обоих этих показателей будут зависеть от амплитуды внешней силы и соотношения частот.
Если частоты очень низкие, т.е. ω≪ω0, то тело, прикрепленное к правому концу пружины, движется точно так же, как и левый конец этой пружины. Тогда получается, что x(t)=y(t). Сама пружина при этом практически не деформируется, а модуль внешней силы F→вн, приложенной к ее левому концу, стремится к нулю. Работа при этом не совершается.
Понятие резонанса
Резонанс – это резкое возрастание амплитуды вынужденных колебаний при сближении частоты внешней силы с собственной частотой колебания тела.
С помощью резонансной кривой (резонансной характеристики) можно описать зависимость, существующую между амплитудой внешних колебаний xm и частотой вынуждающей силы ω.
Когда происходит резонанс, амплитуда xm может оказаться значительно больше, чем амплитуда колебаний левого (свободного) конца пружины.. Если мы не будем учитывать силы трения, то получится, что при резонансной частоте амплитуда вынужденных колебаний будет возрастать неограниченно. В реальности она будет зависеть от следующего условия: работа внешней силы в течение всего времени колебаний должна совпадать с потерями механической энергии, происходящими из-за трения. При уменьшении трения (и, соответственно, повышении добротности Q колебательной системы) амплитуда вынужденных колебаний при резонансе возрастет.
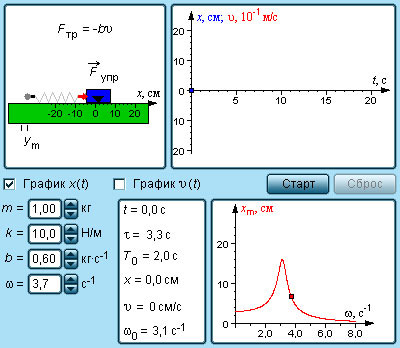
Рисунок 2.5.2. Моделирование вынужденных колебаний.
Если добротность колебательной системы невысока (менее 10), то частота резонанса будет находиться ближе к низким частотам. Это показано на иллюстрации 2.5.2.
Явление резонанса имеет большое практическое значение. Именно из-за него зачастую разрушаются здания, мосты и другие сооружения. Это происходит в тот момент, когда их собственные частоты совпадают с частотой внешней силы, например, колебаниями мотора.
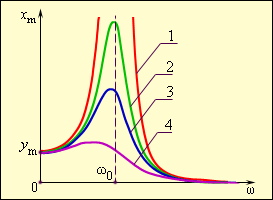
Рисунок 2.5.3. Изображение затухания различных колебаний при помощи резонансных кривых: 1 – условная система без учета трения (бесконечное возрастание амплитуды вынужденных колебаний), 2,3,4 – резонансные колебания в реальных условиях, происходящих в системах разной степени добротности (Q2>Q3>Q4). Если частоты низкие, то (ω≪ω0) xm≈ym, а если высокие, то (ω≫ω0) xm→0.
Вынужденные колебания являются незатухающими. При трении неизбежно теряется часть энергии, однако воздействие внешних периодически действующих сил компенсирует ее.
Что такое автоколебательные системы
Автоколебательные системы – это системы, в которых могут возникать незатухающие колебания безотносительно внешнего воздействия, а лишь за счет способности самостоятельно регулировать подвод энергии от внешнего источника. Процесс колебаний в таких системах называют автоколебаниями.
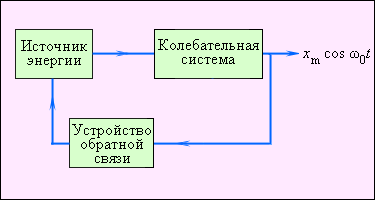
Внутри этой системы можно выделить три составляющих – саму систему, источник внешней постоянной энергии и обратную связь между ними. Первым элементом выступает любая механическая система, которая может совершать затухающие колебания, например, часовой маятник. В качестве источника можно использовать потенциальную энергию груза в поле тяжести или энергию деформации пружины. Система обратной связи – это, как правило, особый механизм, функцией которого является регулирование поступлений энергии. На иллюстрации показано, как эти компоненты взаимодействуют между собой.
Рисунок 2.5.4. Автоколебательная система со всеми основными составляющими.
Какие можно привести примеры таких систем? Ярким примером является часовой механизм с так называемым анкерным ходом. В нем есть ходовое колесо с косыми зубчиками, прочно сцепленное с зубчатым барабаном, через который перекинута цепочка с грузом. В верхней части маятника закреплен якорек (анкер), состоящий из двух твердых пластинок, дугообразно изогнутых по окружности с центром на основной оси. В механизме ручных часов вместо гири используется пружина, а вместо маятника – маховичок-балансир, соединенный со спиральной пружиной, который совершает круговые колебания вокруг своей оси. В качестве источника внешней энергии выступает заведенная пружина или поднятая гиря. Обратная связь осуществляется с помощью анкера: он позволяет ходовому колесу совершать поворот только на один зубец за полупериод. Когда анкер взаимодействует с ходовым колесом, происходит передача энергии. Когда маятник колеблется, зубец ходового колеса передает анкерной вилке энергию по направлению движения маятника, и именно этим компенсируются силы трения. Таким образом, энергия поднятой гири или заведенной пружины поступает маленькими порциями к маятнику.
Существует также много других автоколебательных систем, которые широко применяются в технике. Автоколебания происходят внутри двигателей внутреннего сгорания, паровых машин, электрических звонков, музыкальных инструментов, голосовых связок и т.д.
Рисунок 2.5.5. Схема маятникового часового механизма.