В прошлой статье мы с вами рассмотрели последовательный колебательный контур, так как все участвующие в нем радиоэлементы соединялись последовательно. В этой же статье мы рассмотрим параллельный колебательный контур, в котором катушка и конденсатор соединяются параллельно.
Параллельный колебательный контур
Идеальный колебательный контур
На схеме идеальный колебательный контур выглядит вот так:
где

L — индуктивность, Генри
С — емкость, Фарад
Реальный колебательный контур
В реальности у нас катушка обладает приличным сопротивлением потерь, так как намотана из провода, да и конденсатор тоже имеет некоторое сопротивление потерь. Потери в емкости очень малы и ими обычно пренебрегают. Поэтому оставим только одно сопротивление потерь катушки R. Тогда схема реального колебательного контура примет вот такой вид:
где
R — это сопротивление потерь контура, Ом
L — индуктивность, Генри
С — емкость, Фарад
Принцип работы параллельного колебательного контура
Давайте подцепим к генератору частоты реальный параллельный колебательный контур
Что будет, если мы подадим на контур ток с частотой в ноль Герц, то есть постоянный ток? Он спокойно побежит через катушку и будет ограничиваться лишь сопротивлением потерь R самой катушки. Через конденсатор ток не побежит, потому что конденсатор не пропускает постоянный ток. Об это я писал еще в статье конденсатор в цепи постоянного и переменного тока.
Давайте тогда будем добавлять частоту. Итак, с увеличением частоты у нас конденсатор и катушка начнут оказывать реактивное сопротивление электрическому току.
Реактивное сопротивление катушки выражается по формуле

а конденсатора по формуле

Более подробно про это можно прочитать в этой статье.
Если плавно увеличивать частоту, то можно понять из формул, что в самом начале при плавном увеличении частоты конденсатор будет оказывать бОльшее сопротивление, чем катушка индуктивности. На какой-то частоте реактивные сопротивления катушки XL и конденсатора XC уравняются. Если далее увеличивать частоту, то уже катушка уже будет оказывать большее сопротивление, чем конденсатор.
Резонанс параллельного колебательного контура
Очень интересное свойство параллельного колебательного контура заключается в том, что при ХL = ХС у нас колебательный контур войдет в резонанс. При резонансе колебательный контур начнет оказывать большее сопротивление переменному электрическому току. Еще часто это сопротивление называют резонансным сопротивлением контура и оно выражается формулой:

где
Rрез — это сопротивление контура на резонансной частоте
L — собственно сама индуктивность катушки
C — собственно сама емкость конденсатора
R — сопротивление потерь катушки
Формула резонанса
Для параллельного колебательного контура также работает формула Томсона для резонансной частоты как и для последовательного колебательного контура:

где
F — это резонансная частота контура, Герцы
L — индуктивность катушки, Генри
С — емкость конденсатора, Фарады
Как найти резонанс параллельного колебательного контура на практике
Ладно, ближе к делу. Берем паяльник в руки и спаиваем катушку и конденсатор параллельно. Катушка на 22 мкГн, а конденсатор на 1000пФ.
Итак, реальная схема этого контура будет вот такая:
Для того, чтобы все показать наглядно и понятно, давайте добавим к контуру последовательно резистор на 1 КОм и соберем вот такую схему:
На генераторе мы будет менять частоту, а с клемм X1 и X2 мы будем снимать напряжение и смотреть его на осциллографе.
Нетрудно догадаться, что у нас сопротивление параллельного колебательного контура будет зависеть от частоты генератора, так как в этом колебательном контуре мы видим два радиоэлемента, чьи реактивные сопротивления напрямую зависит от частоты, поэтому заменим колебательный контур эквивалентным сопротивлением контура Rкон.
Упрощенная схема будет выглядеть вот так:
Интересно, на что похожа эта схема? Не на делитель ли напряжения? Именно! Итак, вспоминаем правило делителя напряжения: на меньшем сопротивлении падает меньшее напряжение, на бОльшем сопротивлении падает бОльшее напряжение. Какой вывод можно сделать применительно к нашему колебательному контуру? Да все просто: на резонансной частоте сопротивление Rкон будет максимальным, вследствие чего у нас на этом сопротивлении «упадет» бОльшее напряжение.
У нас есть калькулятор резисторов по цветам. Самый крутой подборник.
Начинаем наш опыт. Поднимаем частоту на генераторе, начиная с самых маленьких частот.
200 Герц.

Как вы видите, на колебательном контуре «падает» малое напряжение, значит, по правилу делителя напряжения, можно сказать, что сейчас у контура малое сопротивление Rкон
Добавляем частоту. 11,4 Килогерца

Как вы видите, напряжение на контуре поднялось. Это значит, что сопротивление колебательного контура увеличилось.
Добавляем еще частоту. 50 Килогерц

Заметьте, напряжение на контуре повысилось еще больше. Значит его сопротивление еще больше увеличилось.
723 Килогерца

Обратите внимание на цену деления одного квадратика по вертикали, по сравнению с прошлым опытом. Там было 20мВ на один квадратик, а сейчас уже 500 мВ на один квадратик. Напряжение выросло, так как сопротивление колебательного контура стало еще больше.
И вот я поймал такую частоту, на которой получилось максимальное напряжение на колебательном контуре. Обратите внимание на цену деления по вертикали. Она равняется двум Вольтам.

Дальнейшее увеличение частоты приводит к тому, что напряжение начинает падать:

Снова добавляем частоту и видим, что напряжение стало еще меньше:

Что происходит на резонансной частоте в параллельном колебательном контуре
Давайте более подробно рассмотрим эту осциллограмму, когда у нас было максимальное напряжение с контура.

Что здесь у нас произошло?
Так как на этой частоте был всплеск напряжения, следовательно, на этой частоте параллельный колебательный контур имел самое высокое сопротивление Rкон. На этой частоте ХL = ХС. Потом с ростом частоты сопротивление контура снова упало. Это и есть то самое резонансное сопротивление контура, которое выражается формулой:

Резонанс токов
Итак, давайте допустим, мы вогнали наш колебательный контур в резонанс:
Чему будет равняться резонансный ток Iрез ? Считаем по закону Ома:
Iрез = Uген /Rрез , где Rрез = L/CR.
Но самый прикол в том, что у нас при резонансе в контуре появляется свой собственный контурный ток Iкон , который не выходит за пределы контура и остается только в самом контуре! Так как с математикой у меня туго, поэтому я не буду приводить различные математические выкладки с производными и комплексными числами и объяснять откуда берется контурный ток при резонансе. Именно поэтому резонанс параллельного колебательного контура называется резонансом токов.
Добротность параллельного колебательного контура
Кстати, этот контурный ток будет намного больше, чем ток, который проходит через контур. И знаете во сколько раз? Правильно, в Q раз. Q — это и есть добротность! В параллельном колебательном контуре она показывает во сколько раз сила тока в контуре Iкон больше сила тока в общей цепи Iрез
Или формулой:

Если сюда еще прилепить сопротивление потерь, то формула примет вот такой вид:
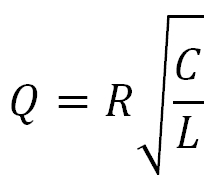
где
Q — добротность
R — сопротивление потерь на катушке, Ом
С — емкость, Ф
L — индуктивность, Гн
Применение параллельного колебательного контура
Параллельный колебательный контур применяется в радиоприемном оборудовании, где надо выделить частоту какой-либо станции. Также с помощью колебательного контура можно построить различные резонансные фильтры.
Также смотрите видео:
Колебательный контур LC
Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.
Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.
– Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
– Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.
Рассмотрим, как возникают и поддерживаются свободные электрические колебания в параллельном контуре LC.
Основные свойства индуктивности
– Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией  .
.
– Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.
Природа электромагнитных колебаний в контуре
Период свободных колебаний контура LC можно описать следующим образом:
Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит .
.
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток разряда конденсатора, создавая магнитное поле в катушке.

Внешний магнитный поток создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в каждом витке, поэтому конденсатор разрядится не мгновенно, а через время t1,
которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t1 =  .
.
По истечении времени t1, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит .
.
В идеальном рассмотрении, при полном отсутствии потерь в контуре, EC будет равна EL.
Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.

Далее изменение (уменьшение от максимума) магнитного потока накопленной энергии катушки будет создавать в ней ЭДС,
которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t2 = t1, он перезарядит конденсатор от нулевого до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.
Описанные интервалы t1 и t2 составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление.
Магнитная энергия вновь будет накапливаться в катушке в течении времени t3, сменив полярность полюсов.
В течении заключительного этапа колебания (t4),
накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U
(в случае отсутствия потерь) и процесс колебания повторится.
В реальности, при наличии потерь энергии на активном сопротивлении проводников,
фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t1 + t2 + t3 + t4 составит период колебаний  .
.
Частота свободных колебаний контура ƒ = 1 / T
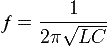
Частота свободных колебаний является частотой резонанса контура,
на которой реактивное сопротивление индуктивности XL=2πfL равно реактивному сопротивлению ёмкости XC=1/(2πfC).
Расчёт частоты резонанса LC-контура:
Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Расчёт частоты:
Частота резонанса колебательного контура LC.
ƒ = 1/(2π√(LC))
Расчёт ёмкости:
Ёмкость для колебательного контура LC
C = 1/(4𲃲L)
Расчёт индуктивности:
Индуктивность для колебательного контура LC
L = 1/(4𲃲C)
Похожие страницы с расчётами:
Рассчитать импеданс.
Рассчитать реактивное сопротивление.
Рассчитать реактивную мощность и компенсацию.
Замечания и предложения принимаются и приветствуются!
Колебательный контур — электрическая цепь, содержащая катушку индуктивности, конденсатор и источник электрической энергии. При последовательном соединении элементов цепи колебательный контур называется последовательным, при параллельном − параллельным.
Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания.
Резонансная частота контура определяется так называемой формулой Томсона:
ƒ = 1/(2π√(LC))
Для простоты расчета можно воспользоваться онлайн калькулятором расчета частоты резонанса колебательного контура – http://rcl-radio.ru/?p=28914
Также доступны онлайн калькуляторы для расчета ёмкости для колебательного контура и индуктивности для колебательного контура, расчет которых производится по следующим формулам:
C = 1/(4𲃲L) и L = 1/(4𲃲C)
Расчет резонансной частоты колебательного контура на сайте rcl-radio.ru
Выберите подписку для получения дополнительных возможностей Kalk.Pro
Любая активная подписка отключает
рекламу на сайте
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
![]()
Более 10 000 пользователей уже воспользовались расширенным доступом для успешного создания своего проекта. Подробные чертежи и смета проекта экономят до 70% времени на подготовку элементов конструкции, а также предотвращают лишний расход материалов.
Подробнее с подписками можно ознакомиться здесь.
Что такое резонансный контур
Содержание
- 1 Суть явления
- 2 Индуктивно-ёмкостной LC-контур
- 3 Что происходит в КК
- 4 Последовательный и параллельный КК
- 5 Радиосвязь и резонанс
- 6 Видео по теме
Физический эффект, получивший название резонанс (от французского resonanse — откликаться), наблюдается в системах, состояние которых носит колебательный (повторяющийся) характер. Колебания могут быть механическими, звуковыми, электромагнитными. Все эти процессы описываются схожими математическими уравнениями. Классическим примером является резонанс в колебательном контуре, возникающий при определённых условиях.

Суть явления
Резонанс может возникнуть только в системе, где происходит колебательный (повторяющийся с определённой частотой ω) процесс. Кроме частоты, основной характеристикой колебаний является амплитуда А.

Эффект резонанса возникает, когда на физическое тело или систему тел оказывается внешнее воздействие (механическое, акустическое или электрическое), но при условии, что частота внешнего фактора совпадает с собственной частотой системы. Если внутреннее трение или сопротивление невелико, то происходит резкий рост амплитуды вынужденных колебаний.

Резонансный эффект может иметь и негативный, катастрофический характер. На картинке ниже приведены два хрестоматийных примера, когда были разрушены мостовые конструкции.

В электроцепях также возможен вред от незапланированного резонанса. Например, если электроцепь предварительно не рассчитывалась на функционирование в условиях резонанса, то существует большая вероятность аварии: либо от скачка электронапряжения возникнет пробой изоляции, либо большой электроток нагреет электропровода до температуры воспламенения.
Индуктивно-ёмкостной LC-контур
На таком явлении, как резонанс основывается вся современная радиосвязь. Базовая двухэлементная схема состоит из индуктивности L и ёмкости C. Данная схема получила название колебательного контура (КК) или LC-контура. В такой электроцепи при пренебрежимо малом активном сопротивлении R возникают свободные электромагнитные колебания.

Формула для собственной резонансной частоты колебаний в контуре имеет следующий вид:

Данное уравнение является следствием формулы для периода колебаний в контуре, полученной английским физиком У. Томсоном в 1853 г.

Поскольку круговая частота ω0 связана соотношением с периодом Т:

то отсюда следует формула для определения резонансной частоты колебательного контура:

Величина электротока при вынужденных колебаниях достигает максимума, когда частота внешнего электронапряжения ωвн сравнивается с собственной частотой КК, то есть при выполнении условия ωвн=ω0.
Резонанс колебаний LC-контура проявляется в виде резкого скачка амплитуды электротока, когда частота внешнего переменного электронапряжения ωвн совпадает с собственной частотой колебательного контура ω0.
Передаваемая мощность будет максимальной при условии, что электронапряжение и сила электротока совпадают по фазе. В механических колебаниях (например, качели или маятник) эффект резонанса наступает при совпадении внешней силы (аналог электронапряжения) по фазе со скоростью (аналог электротока).
Что происходит в КК
Процессы, происходящие в КК можно рассмотреть на примере.

Изображенный на рисунке резонансный индуктивно-ёмкостной контур без внешнего воздействия работает следующим образом:
- Сначала происходит зарядка конденсатора С (фрагмент б).
- В электроцепи течёт синусоидальный электроток I (фрагмент в).
- Происходит разрядка конденсатора C через катушку индуктивности L.
- В катушке появляется ЭДС самоиндукции, направленная навстречу электротоку.
- После полной разрядки конденсатор начинает снова заряжаться от энергии, накопленной в катушке (фрагмент г). Но при этом полярность на обкладках конденсатора изменится на противоположную.
- Процесс повторятся заново, но происходит с постепенным затуханием, так как всегда имеются потери на излучение и нагрев активного сопротивления у катушки и проводов.
- Для поддержания постоянного колебательного процесса необходим внешний источник электроэнергии.

Существенным параметром LC-контура является добротность Q, от которой зависит амплитуда резонанса. Чем больше добротность КК, тем медленнее будет проходить процесс затухания.
Последовательный и параллельный КК
При использовании внешнего источника электроэнергии контур может быть подключён последовательно либо параллельно. Когда внешний источник, ёмкость и индуктивность соединены параллельно, возникает резонанс электротоков. Резонанс в последовательном варианте включения — это резонанс электронапряжений LC-контура.

Радиосвязь и резонанс
Резонансный эффект нашёл своё применение при создании радиосвязи. От антенн передающих радиостанций распространяется переменный радиосигнал, который воспринимают антенны радиоприёмников. Каждая станция работает на своей частоте, в связи с чем встаёт задача селекции — настройки приёмника на требуемую частоту. С приёмной антенной индуктивно связан КК.

Благодаря электромагнитной индукции в катушке контура возбуждается переменная ЭДС определённой частоты и электротоки такой же частоты. Но ощутимого увеличения электротока можно добиться лишь при условии возникновения резонанса.
Поиск — настройка на конкретную радиочастоту осуществляется с помощью переменного конденсатора, изменение ёмкости которого позволяет «найти» частоту нужной радиостанции.
Кроме использования в аппаратуре радиоприёмников резонанс применяется для стабилизации частоты в схемах, генерирующих сигналы переменного электротока, в полосовых и режекторных (заграждающих) фильтрах, усилителях и различных устройствах автоматики.
Видео по теме
