Как найти результат деления - Сайт, где вы сможете решить свои вопросы

Запрос «Деление» перенаправляется сюда; для просмотра других значений см. Деление.

Деление

Обозначение	обелюс
Противоположно	умножение
Медиафайлы на Викискладе

20:4=5

Деле́ние (операция деления) — действие, обратное умножению. Деление обозначается двоеточием , обелюсом div , косой чертой или записывается в виде дроби.

Для натуральных чисел деление обозначает нахождение, какое число (частное) надо взять столько-то (делитель) раз, чтобы получилось данное (делимое).

Другими словами, это нахождение максимально возможного количества повторений вычитания делителя из делимого; либо нахождение такой наибольшей величины, которая может быть отнята от делимого столько раз, сколько указано в делителе.

Рассмотрим, например деление на :

Сколько раз содержится в ?

Повторяя операцию вычитания из , мы находим, что содержится в четыре раза, и ещё «остаётся» число .

В этом случае число называется делимым, число — делителем, число — (неполным) частным и число — остатком (от деления).

Полным частным, отношением или соотношением чисел и называется такое число , что . В случае, когда и b=3 , их полное частное может быть записано в виде дроби ${displaystyle {frac {14}{3}}}$ или десятичной дроби .

Полное и неполное частные чисел и совпадают тогда и только тогда, когда делится нацело (делится) на . Соответствующее свойство данной пары чисел называется делимостью.

Формы записи и терминология[править | править код]

Деление записывается с использованием одного из «знаков деления» — «» между аргументами, такая форма записи называется инфиксной нотацией. В данном контексте знак деления является бинарным оператором. Знак деления не имеет специального названия, как например знак сложения, который называется «плюс».

Самый старый из используемых символов видимо — косая черта (/). Впервые его использовал английский математик Уильям Отред в своём труде «Clavis Mathematicae» 1631 г.
Немецкий математик Лейбниц предпочитал знак в виде двоеточия (:) Этот символ он использовал в своём труде Acta eruditorum 1684 г. До Лейбница этот знак был использован англичанином Джонсоном в 1633 году в своей книге, но как знак дроби, а не деления в узком смысле.
Йоханн Ран ввёл знак обелюс (÷) в качестве знака деления, она появилась в его книге «Teutsche Algebra» 1659 г. Знак Рана часто называют «английским знаком деления».

В русскоязычных учебниках математики в основном используется знак в виде двоеточия (:). Косая черта (/) используется в компьютерной нотации. Результат записывается с использованием знака равенства «», например:

;

(«шесть разделить на три равно два»);

(«шестьдесят пять разделить на пять равно тринадцать»).

Свойства[править | править код]

Операция деления на числовых множествах имеет следующие основные свойства:

Деление не перестановочно (не коммутативно) — от перемены мест аргументов частное изменяется:

Деление не ассоциативно — при последовательном выполнении деления трёх или более чисел последовательность выполнения операций имеет значение, результат изменится:

Деление дистрибутивно справа, это — свойство согласованности двух бинарных операций, определённых на одном и том же множестве, также известно, как распределительный закон^[1] :

Дистрибутивность:

{displaystyle (a+b):x=(a:x)+(b:x),~xneq 0;}

Нейтральный элемент справа:

Относительно деления в множестве существует единственный обратный элемент, получаемый делением единицы на число, что даёт число, обратное исходному:

Обратный элемент: ${displaystyle 1:x={frac {1}{x}}=x^{-1},~xneq 0;}$

Нулевой элемент слева:

{displaystyle 0:x=0,quad exists 0in A,~xneq 0;}

По правилам обычной арифметики деление на ноль (нулевой элемент) не определено;

Деление на ноль:

{displaystyle x:0=infty ,quad exists 0in A,~xneq 0;}

Деление на противоположный элемент даёт минус единицу:

{displaystyle x:(-x)=-1,quad exists !-xin A,~xneq 0.}

Результат деления не всегда является определённым для множеств натуральных чисел и целых чисел , чтобы получить натуральное или целое число в результате деления, делимое должно быть кратно делителю. Невозможно в рамках этих чисел получить дробный результат. В этом случае говорится о делении с остатком. То есть деление на этих множествах есть частичная бинарная операция.

Операция деления, определённая на множествах (в полях) рациональных , вещественных и комплексных чисел , даёт число (частное), принадлежащее этому же множеству, следовательно, множества ${displaystyle mathbb {Q_{-0}} ,mathbb {R_{-0}} ,mathbb {C_{-0}} }$ замкнуты относительно операции деления (в точке 0 имеется разрыв второго рода — следовательно кольца рациональных, вещественных и комплексных чисел разомкнуты относительно операции деления).

В математических выражениях операция деления имеет более высокий приоритет по отношению к операциям сложения и вычитания, то есть она выполняется перед ними.

Выполнение деления[править | править код]

Пример пошагового деления числа 8 на число 4 на числовой прямой.

Деление является гипероператором вычитания и сводится к последовательному вычитанию. :

${displaystyle a:b=operatorname {hyper-2} (a,b)=operatorname {hyper} (a,-2,b)=a^{(-2)}b=c.}$

${displaystyle a{^{(-2)}}b=a:b=aunderbrace {-b-b-dots -b} _{c}.}$

где: — последовательность операций вычитания, выполненная раз.

При практическом решении задачи деления двух чисел необходимо свести её к последовательности более простых операций: вычитание, сравнение, перенос и др. Для этого разработаны различные методы деления, например для чисел, дробей, векторов и др. В русскоязычных учебниках математики в настоящее время используется алгоритм деления столбиком. При этом следует рассматривать деление как процедуру (в отличие от операции).

Схема, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком:

Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места.

Примерный алгоритм процедуры деления натуральных чисел столбиком

Как видим, процедура достаточно сложная, состоит из относительно большого числа шагов и при делении больших чисел может занять продолжительное время. Данная процедура применима к делению натуральных и целых (с учётом знака) чисел. Для других чисел используются более сложные алгоритмы.

Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и в десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими многочленами^[2]. При этом нужно пользоваться таблицей вычитания соответствующей данному основанию системы счисления.

Пример деления натуральных чисел в двоичной, десятичной и шестнадцатеричной системах счисления:

     110010│101   │    0 — 0           50800│25    │    0 — 0           CD530│A8     │    0 — 0
     101   │1010  │ -101 — 1           50   │2032  │  -25 — 1           A8   │138E   │  -A8 — 1
       10                               08         │  -50 — 2           255          │ -150 — 2
        0                                0         │  -75 — 3           1F8          │ -1F8 — 3
       101                               80        │ -100 — 4            5D3         │ -2A0 — 4
       101                               75        │  ... — ...          540         │ -348 — 5
         00                               50                              930        │ -3F0 — 6
          0                               50                              930        │ -498 — 7
          0.                               0.                               0.       │ -540 — 8
                                                                                     │ -5E8 — 9
                                                                                     │ -690 — A
                                                                                     │ -738 — B
                                                                                     │ -7E0 — C
                                                                                     │ -888 — D
                                                                                     │ -930 — E

Деление чисел[править | править код]

Натуральные числа[править | править код]

Воспользуемся определением натуральных чисел как классов эквивалентности конечных множеств. Обозначим классы эквивалентности конечных множеств порождённых биекциями, с помощью скобок: . Тогда математическая операция «деление» определяется следующими образами:

— деление на равные части (отыскание числа элементов в каждом подмножестве разбиения), частным чисел и называется число элементов каждого подмножества разбиения;
— деление по содержанию (отыскание числа подмножеств разбиения), частным чисел и называется число (количество) подмножеств разбиения;

где: это — разбиение конечного множества на равночисленные попарно не пересекающиеся подмножества, такие что:

${displaystyle B_{alpha }=B_{beta },}$ ${displaystyle quad bigcup limits _{alpha in C}B_{alpha }+R=A,}$ ${displaystyle quad bigcap _{alpha ,beta in C}(B_{alpha },B_{beta },R)={emptyset },}$ для любых коэффициентов , таких что

— остаток (множество оставшихся элементов), ,

— нульарная операция “выделение элемента”.

В случае, если одно натуральное число не делится на другое без остатка, говорится о делении с остатком. На остаток накладываются следующее ограничение (чтобы он был корректно, то есть однозначно, определён): , ,

где: — делимое, — делитель, — частное, — остаток.

Данная операция на классах введена корректно, то есть не зависит от выбора элементов классов, и совпадает с индуктивным определением.

Арифметическая операция «деление» частична для множества натуральных чисел , (для полукольца натуральных чисел).

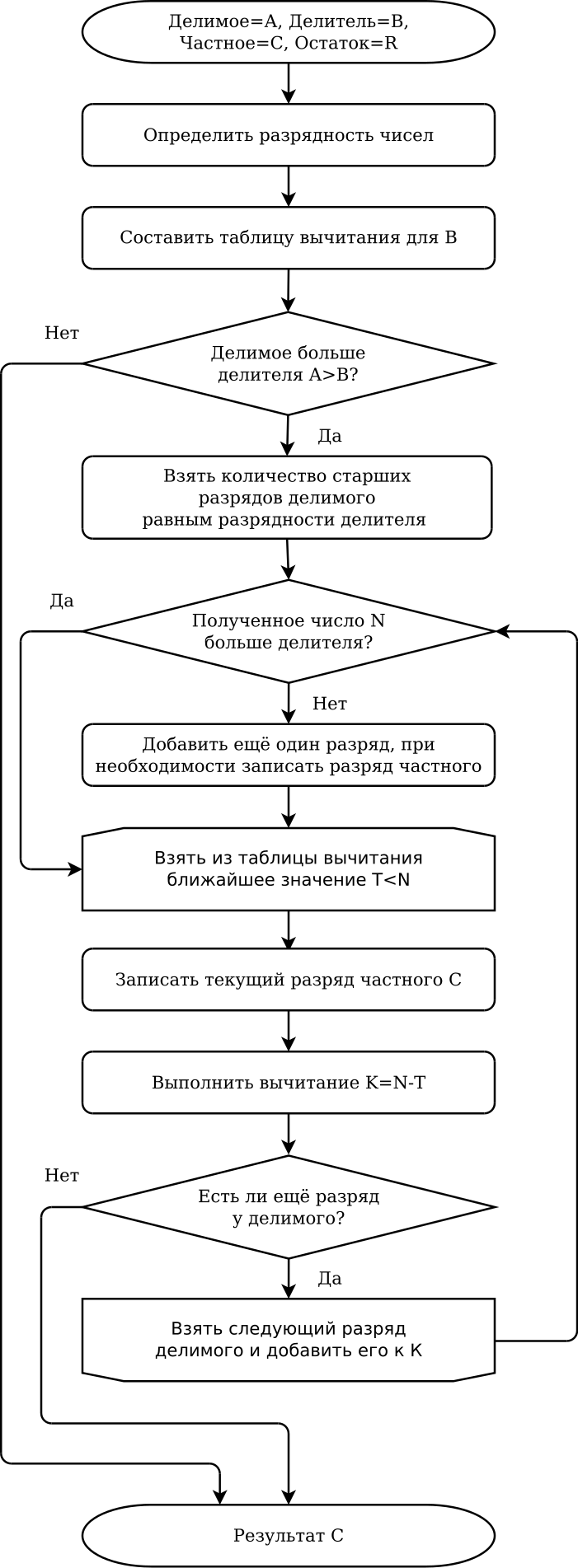
Примеры деления множества: верхний ряд — деление на равные части, нижний ряд — деление по содержанию.

Деление целых чисел[править | править код]

Деление произвольных целых чисел несущественно отличается от деления натуральных чисел — достаточно поделить их модули и учесть правило знаков.

Однако деление целых чисел с остатком определяется неоднозначно. В одном случае, (так же как и без остатка) рассматривают сначала модули и в результате остаток приобретает тот же знак, что делитель или делимое (например, с остатком (-1)); в другом случае понятие остатка напрямую обобщается и ограничения заимствуются из натуральных чисел:

Для устранения неоднозначности принято соглашение: остаток от деления всегда неотрицателен.

Деление рациональных чисел[править | править код]

Замыкание множества целых чисел по операции деления приводит к расширению его до множества рациональных чисел. Это приводит к тому, что результатом деления одного целого числа на другое всегда является рациональное число. Более того, полученные числа (рациональные) уже полностью поддерживают операцию деления (замкнуты относительно неё).

Правило деления обыкновенных дробей:
${frac {a}{b}}:{frac {c}{d}}={frac {acdot d}{bcdot c}}={frac {ad}{bc}}$

Деление вещественных чисел[править | править код]

Множество вещественных чисел — непрерывное упорядоченное поле, обозначается . Множество вещественных чисел не является счётным, его мощность называется мощностью континуума. Арифметические операции над вещественными числами представимых бесконечными десятичными дробями определяются как непрерывное продолжение^[3] соответствующих операций над рациональными числами.

Если даны два вещественных числа, представимые бесконечными десятичными дробями:

${displaystyle alpha =pm a_{0},a_{1}a_{2}ldots a_{n}ldots ={a_{n}},}$

${displaystyle beta =pm b_{0},b_{1}b_{2}ldots b_{n}ldots ={b_{n}},}$

определённые соответственно фундаментальными последовательностями рациональных чисел (удовлетворяющие условию Коши), обозначенные как: $alpha =[a_{n}]$ и $beta =[b_{n}]$ , то их частным называют число ${displaystyle gamma =[c_{n}]}$ , определённое частным последовательностей ${a_{n}}$ и ${b_{n}}$ :

${displaystyle gamma =alpha :beta {overset {text{def}}{=}}[a_{n}]:[b_{n}]=[a_{n}/b_{n}]}$

вещественное число , удовлетворяет следующему условию:

{displaystyle forall a',a'',b',b''in mathbb {Q} ;~~~~(a'leqslant alpha leqslant a'')land (b'leqslant beta leqslant b'')Rightarrow (a':b'leqslant alpha /beta leqslant a'':b'')Rightarrow (a':b'leqslant gamma leqslant a'':b'').}

Таким образом частное двух вещественных чисел alpha и beta является такое вещественное число gamma которое содержится между всеми частными вида с одной стороны и всеми частными вида с другой стороны^[4]. Дедекиндово сечение позволяет однозначно определить результат деления.

На практике для того, чтобы разделить два числа alpha и beta , необходимо заменить их с требуемой точностью приближёнными рациональными числами и . За приближенное значение частного чисел берут частное указанных рациональных чисел a:b . При этом не важно, с какой стороны (по недостатку или по избытку) взятые рациональные числа приближают alpha и beta . Деление производится по алгоритму деления столбиком.

Абсолютная погрешность частного приближённых чисел: ${displaystyle Delta left({frac {a}{b}}right)={frac {|b|cdot Delta a+|a|cdot Delta b}{b^{2}}}}$ , абсолютная погрешность числа принимается равной половине последней единицы разряда этого числа.

Относительная погрешность частного равна сумме относительных погрешностей аргументов: ${displaystyle delta left({frac {a}{b}}right)=delta a+delta b}$ . Полученный результат округляют до первой верной значащей цифры, значащая цифра приближенного числа является верной, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре.

Пример деления , с точностью до 3-го знака после запятой:

График[править | править код]

На множестве пар вещественных чисел $mathbb {R} ^{2}$ область значений функции деления графически имеет вид гиперболического параболоида — поверхности второго порядка^[5].

Так как , то и для этих множеств область значений функции деления будет принадлежать этой поверхности.

Деление комплексных чисел[править | править код]

Комплексное число z на комплексной плоскости.

Множество комплексных чисел с арифметическими операциями является полем и обычно обозначается символом .

Алгебраической форма[править | править код]

Частным двух комплексных чисел в алгебраической форме записи, называется комплексное число, равное:

${displaystyle z=c+fi={frac {z_{1}}{z_{2}}}={frac {a+di}{b+ei}}={frac {ab+de}{b^{2}+e^{2}}}+{frac {db-ae}{b^{2}+e^{2}}}i,}$

где: ${displaystyle z,z_{1},z_{2}}$ — комплексные числа, , — мнимая единица; ${displaystyle z_{2}neq 0,~~~b+eineq 0}$ .

На практике частное комплексных чисел находят умножением делимого и делителя на число, комплексно-сопряженное делителю:

${displaystyle z=c+fi={frac {z_{1}}{z_{2}}}={frac {a+di}{b+ei}}={frac {(a+di)(b-ei)}{(b+ei)(b-ei)}}={frac {ab+de}{b^{2}+e^{2}}}+{frac {db-ae}{b^{2}+e^{2}}}i,}$ ${displaystyle ~~z_{2}neq 0,~~~b+eineq 0;}$

делитель становится действительным числом, а в числителе умножаются два комплексных числа, затем полученная дробь почленно делится. Результат определён для всех

Тригонометрическая форма[править | править код]

Для того, чтобы разделить два комплексных числа в тригонометрической форме записи, нужно разделить модуль делимого на модуль делителя, а из аргумента делимого вычесть аргумент делителя:

${displaystyle z=c+fi={frac {z_{1}}{z_{2}}}={frac {a+di}{b+ei}}={frac {r_{1}(cos varphi _{1}+isin varphi _{1})}{r_{2}(cos varphi _{2}+isin varphi _{2})}}={frac {r_{1}}{r_{2}}}(cos(varphi _{1}-varphi _{2})+isin(varphi _{1}-varphi _{2}),}$

Деление комплексных чисел на комплексной плоскости.

где: ${displaystyle r_{n}=|z_{n}|=|x+yi|={sqrt {x^{2}+y^{2}}};~~~varphi _{n}=operatorname {Arg} (z_{n})=operatorname {arctg} {biggl (}{frac {x}{y}}{biggr )}}$ — модуль и аргумент комплексного числа; ${displaystyle z_{2}neq 0,~~~r_{2}neq 0}$ .

То есть модуль частного двух комплексных чисел равен частному модулей, а аргумент — разности аргументов делимого и делителя.

Показательная (экспоненциальная) форма[править | править код]

Деление комплексного числа ${displaystyle z_{1}=a+di=r_{1}e^{ivarphi _{1}}}$ в показательной форме, на комплексное число ${displaystyle z_{2}=b+ei=r_{2}e^{ivarphi _{2}}}$ сводится к повороту вектора, соответствующего числу $z_{1}$ , на угол ${displaystyle operatorname {Arg} (z_{2})}$ и изменению его длины на ${displaystyle |z_{2}|}$ раз. Для частного комплексных чисел в показательной форме верно равенство:

${displaystyle z=c+fi={frac {z_{1}}{z_{2}}}={frac {a+di}{b+ei}}={frac {r_{1}e^{ivarphi _{1}}}{r_{2}e^{ivarphi _{2}}}}={frac {r_{1}}{r_{2}}}e^{i(varphi _{1}-varphi _{2})};}$

где: — число e; ${displaystyle z_{2}neq 0,~~~r_{2}neq 0}$ .

Экспоненциальная запись[править | править код]

В экспоненциальной записи числа записываются в виде ${displaystyle a=pm xcdot P^{pm n}}$ , где — мантисса, ${displaystyle P^{n}}$ — характеристика числа, — основание системы счисления, . Для деления двух чисел, которые записаны в экспоненциальной форме необходимо разделить мантиссы и характеристики: ${displaystyle (acdot P^{n}):(bcdot P^{k})=(a:b)cdot (P^{n}:P^{k})={frac {a}{b}}cdot P^{n-k}.}$

Например:

${displaystyle (6{,}34cdot 10^{4}):~(2{,}16cdot 10^{-2})=(6{,}34:~2{,}16)cdot (10^{4}:10^{-2})approx 2{,}935cdot 10^{(4-(-2))}approx 2{,}94cdot 10^{4+2}approx 2{,}94cdot 10^{6}.}$

Деление физических величин[править | править код]

Единица измерения физической величины имеет определённое наименование (размерность): для длины (L) — метр (м), для времени (T) — секунда (с), для массы (M) — грамм (г) и так далее. Поэтому, результат измерения той или иной величины представляет собой не просто число, а число с наименованием^[6]. Наименование представляет собой самостоятельный объект, который равноправно участвует в операции деления. При производстве операции деления над физическими величинами, делятся как сами числовые составляющие, так и их наименования.

Помимо размерных физических величин существуют безразмерные (количественные) величины, которые формально являются элементами числовой оси, то есть числами, не имеющие привязки к определённым физическим явлениям (измеряются «штуками», «разами» и тому подобное). При делении чисел представляющих собой физические величины на безразмерную величину, делимое число изменяется по величине и сохраняет единицу измерения. Например если взять 15 гвоздей и разложить в 3 коробки, то в результате деления получим 5 гвоздей в каждой коробке:

{displaystyle 15~{text{гв}}:3=5~{text{гв}}.}

Деление разнородных физических величин надо рассматривать как нахождение новой физической величины, принципиально отличающейся от величин, которые мы делим. Если физически возможно создание такого частного, например, при нахождении работы, скорости или других величин, то эта величина образует множество, отличное от начальных. В этом случае композиции этих величин присваивается новое обозначение (новый термин), например: плотность, ускорение, мощность и прочее^[7].

Например, если разделить длину на время соответствующие одному физическому процессу, то получится именованное число (физическая величина) соответствующее этому же физическому процессу, которая называется «скорость» и измеряется в «метрах в секунду»:

{displaystyle V=L:T=8~{text{м}}:2~{text{с}}=4~~{text{(м : с)}}=4~{text{м/с}}.}

При описании математическими средствами физических процессов немаловажную роль играет понятие однородности, которое означает например, что «1 кг муки» и «1 кг меди» принадлежат разным множествам {мука} и {медь} соответственно и не могут быть непосредственно разделены. Также понятие однородности предполагает, что делимые величины принадлежат одному физическому процессу. Недопустимо делить, например скорость лошади на время собаки.

Деление в алгебре[править | править код]

В отличие от простейших арифметических случаев, на произвольных множествах и структурах деление может быть не только не определено, но и обладать множественностью результата.

Обычно в алгебре деление вводится через понятие единичного и обратного элементов. Если единичный элемент вводится однозначным образом (обычно аксиоматически или по определению), то обратный элемент часто может быть как левым ( $x^{{-1}}*x=e$ ), так и правым ( $x*x^{{-1}}=e$ ). Эти два обратных элемента могут по отдельности существовать или не существовать, равняться или не равняться друг другу.

К примеру, отношение матриц определяется через обратную матрицу, при этом даже для квадратных матриц может быть:

$B^{{-1}}cdot Aneq Acdot B^{{-1}}$

Отношение тензоров в общем случае не определено.

Деление многочленов[править | править код]

В общих чертах оно повторяет идеи деления натуральных чисел, ибо натуральное число есть не что иное, как значения многочлена, у которого коэффициенты — цифры, а вместо переменной стоит основание системы счисления:

$5334_{8}=5cdot 8^{3}+3cdot 8^{2}+3cdot 8^{1}+4cdot 8^{0}=left.(5x^{3}+3x^{2}+3x+4)right|_{{x=8}}$

Поэтому аналогично определяются: частное, делитель, делимое и остаток (с той лишь разницей, что ограничение накладывается на степень остатка). Поэтому к делению многочленов также применимо деление столбиком.

Отличие же заключается в том, что при делении многочленов основной упор делается на степени делимого и делителя, а не на коэффициенты. Поэтому обычно считается, что частное и делитель (а следовательно и остаток) определены с точностью до постоянного множителя.

Деление на ноль[править | править код]

По определению числовых множеств деление на число 0 не определено. Частное от деления какого-либо числа, отличного от нуля, на нуль не существует, так как в этом случае никакое число не может удовлетворять определению частного^[8]. Для определения данной ситуации полагают, что результат этой операции считается «бесконечно большим» или «равным бесконечности» (положительной или отрицательной, в зависимости от знака операндов). С геометрической точки зрения выполняется аффинное расширение числовой прямой. То есть привычная последовательность вещественных чисел «сжимается» так, чтобы можно было оперировать границами этой последовательности. В качестве границ (условных) введены две абстрактные бесконечно большие величины . С точки зрения общей топологии выполняется двухточечная компактификация числовой прямой путем добавления двух идеализированных точек (бесконечностей с противоположным знаком). Пишут:

Топологическая картинка проективного расширения числовой прямой и точки 0/0

, где aneq 0.

Если произвести проективное расширение множества вещественных чисел введением идеализированной точки ,которая соединяет оба конца вещественной прямой, тогда с точки зрения общей топологии будет выполнена одноточечная компактификация числовой прямой путем добавления бесконечности без знака. Дополним полученное множество чисел новым элементом , в результате получится ${displaystyle mathbb {R} _{perp }^{infty }=mathbb {R} cup {infty ,perp }}$ , на данной основе строится алгебраическая структура ${displaystyle {mathfrak {W}}=langle mathbb {R} _{perp }^{infty },0,1,+,cdot ,/rangle ~}$ называемая «Колесом^[en]» (Wheel)^[9]. Термин был взят из-за схожести с топологической картинкой проективного расширения числовой прямой и точки 0/0. Внесенные изменения превращают эту алгебраическую систему в моноид как по операции сложения (с нулем в качестве нейтрального элемента), так и по операции умножения (с единицей в качестве нейтрального элемента). Это тип алгебры, где деление всегда определено. В частности, деление на ноль имеет смысл.

Существуют и другие алгебраические системы с делением на ноль. Например, «общие луга» (common meadows)^[10]. Они чуть проще, так как не расширяют пространство, вводя новые элементы. Цель достигается как в колесах, трансформацией операций сложения и умножения, а также отказом от бинарного деления.

См. также[править | править код]

Признаки делимости
Наибольший общий делитель
Наименьшее общее кратное
Деление многочленов столбиком
Деление столбиком
Остаток от деления
Деление с остатком

Примечания[править | править код]

↑ Так эти свойства называются в учебниках для младших классов
↑ Системы счисления, 2006, p. 3.
↑ Поскольку на множестве вещественных чисел уже введено отношение линейного порядка, то мы можем определить топологию числовой прямой: в качестве открытых множеств возьмём всевозможные объединения интервалов вида
↑ Ильин, 1985, с. 46.
↑ Уравнение ${displaystyle z={frac {x}{y}}}$ заменой переменных легко свести к уравнению гиперболического параболоида ${displaystyle {frac {z^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}=2x}$ .
↑ Волинская Н. И. Интегрированный урок по физике и математике, Измерение физических величин и их единицы, СШ 7 г. Бреста. brestschool7.iatp.by. Дата обращения: 18 апреля 2016. Архивировано 7 августа 2016 года.
↑ Макаров Владимир Петрович. О «размерности» физических величин. lithology.ru, Литология.РФ. Дата обращения: 18 апреля 2016. Архивировано 6 мая 2016 года.
↑ М. Я. Выгодский Справочник по элементарной математике.
↑ Jesper Carlstrom. Wheels — On Division by Zero. — Stockholm: Department of Mathematics Stockholm University, 2001. — 48 с.
↑ Jan A. Bergstra and Alban Ponse. Division by Zero in Common Meadows. — The Netherlands: Section Theory of Computer Science
Informatics Institute, Faculty of Science
University of Amsterdam, 2014. — 16 с. Архивная копия от 26 марта 2018 на Wayback Machine

Литература[править | править код]

Ильин В.А. и др. Математический анализ. Начальный курс. (неопр.). — МГУ, 1985. — Т. 1. — 662 с.
Системы счисления. — Вологда: ГОУ СПО «Вологодский машиностроительный техникум», 2006. — С. 3. — 16 с.

Источник

В этой статье мы рассмотрим правила и алгоритмы деления натуральных чисел. Сразу отметим, что здесь мы смотрим только на деление нацело, то есть без остатка. О делении натуральных чисел с остатком читайте в нашем отдельном материале.

Перед тем, как формулировать правило деления натуральных чисел, нужно понять связь деления с умножением. После того, как мы установим эту связь, последовательно рассмотрим самые простые случаи: деление натурального числа на себя и на единицу. Далее разберем деление с помощью таблицы умножения, деление методом последовательного вычитания, деление на числа, кратные числу 10, различные степени числа 10.

Для каждого случая приведем и подробно рассмотрим примеры. В конце статьи покажем, как проводить проверку результата деления.

Связь деления с умножением

Чтобы проследить связь между делением и умножением, вспомним, что деление представляется, как разбиение исходного делимого множества на несколько одинаковых множеств. Умножение связано с объединением нескольких одинаковых множеств в одно.

Деление – действие, обратное умножению. Что это значит? Приведем аналогию. Представим, что у нас есть b множеств, в каждом из которых – по с предметов. Общее количество предметов во всех множествах равно a. Умножение – это объединение всех множеств в одно. Математически оно запишется так:

b·c=a.

Обратный процесс разбиения полученного общего множества на b множеств по с предметов в каждом соответствует делению:

a÷b=c.

На основе сказанного можно перейти к следующему утверждению:

Если произведение натуральных чисел c и b равно a, то частное чисел a и b равно c. Перепишем в буквенном виде.

Если b·c=a, то a÷b=c

Пользуясь переместительным свойством умножения, можно записать:

c·b=a

Отсюда также следует, что a÷с=b.

На основании сказанного можно сформулировать общий вывод. Если произведение чисел c и b равно a, то соответственно частные a÷b и a÷c равны c и b.

Подытожим все изложенное выше и дадим определение деления натуральных чисел.

Деление натуральных чисел

Деление – нахождение неизвестного множителя по известному произведению и другому известному множителю.

Это определение станет базой, на основе которой мы будем строить правила и методы деления натуральных чисел.

Деление методом последовательного вычитания

Только что мы говорили о делении в контексте умножения. На основе этого знания можно проводить операцию деления. Однако, существует еще один, достаточно простой и достойный внимания подход – деление методом последовательного вычитания. Этот способ понятен интуитивно, поэтому рассмотрим его на примере, не приводя теоретических выкладок.

Заголовок

Сколько будет 12 разделить на 4?

Иными словами данную задачу можно сформулировать так: имеется 12 предметов (например, апельсинов), и их нужно разделить на равные группы по 4 предмета (разложить в коробки по 4 штуки). Сколько будет таких групп или коробок по четыре апельсина в каждой?

Шаг за шагом будем отнимать от исходного количества по 4 апельсина и формировать группы по 4 до того момента, пока апельсины не закончатся. Количество шагов, которые нам придется сделать, и будет ответом на изначальный вопрос.

Из 12 апельсинов откладываем первую четверку в коробку. После этого в исходной куче апельсинов остается 12-4=8цитрусовых. Из этих восьми в другую коробку забираем еще 4. Теперь в исходной куче апельсинов осталось 8-4=4штуки. Из этих четырех штук как раз можно сформировать еще одну, отдельную третью коробку, после чего в исходной куче останется 4-4=0 апельсинов.

Итак, мы получили 3 коробки, по 4 предмета в каждой. Иными словами, мы разделили 12 на 4, и получили в результате 3.

Работая с числами, не нужно каждый раз проводить аналогию с предметами. Что мы делали с делимым и делителем? Последовательно вычитали делитель из делимого, пока не получили нуль в остатке.

Важно!

При делении методом последовательного вычитания количество операций вычитания до получения нулевого остатка и есть частное от деления.

Для закрепления рассмотрим еще один, более сложный пример.

Пример 1. Деление последовательным вычитанием

Вычислим результат деления числа 108 на 27 методом последовательного вычитания.

Первое действие: 108-27=81.

Второе действие: 81-27=54.

Третье действие: 54-27=27.

Четвертое действие: 27-27=0.

Более действий не требуется. Мы получили ответ:

108÷27=4

Отметим, что данный метод удобен только в случаях, когда необходимое количество последовательных вычитаний невелико. В остальных случаях целесообразно применять правила деления, которые мы рассмотрим ниже.

Деление равных натуральных чисел

Согласно свойствам натуральных чисел, сформулируем правило, как делить равные натуральные числа.

Деление равных натуральных чисел

Частное от деления натурального числа на равное ему натуральное число равно единице!

aa=1.

Например:

1÷1=1; 141÷141=1; 2589÷2589=1; 100000000÷100000000=1.

Деление на единицу

Основываясь на свойствах натуральных чисел, можно также сформулировать правило деление натурального числа на единицу.

Деление натурального числа на единицу

Частное от деления любого натурального числа на единицу равно самому делимому числу.

a1=a.

Например:

1÷1=1; 141÷1=141; 2589÷1=2589; 100000000÷1=100000000.

Деление с помощью таблицы умножения

Таблица умножения – удобный инструмент, который позволяет найти произведения однозначных натуральных чисел. Однако, ее можно использовать и для деления.

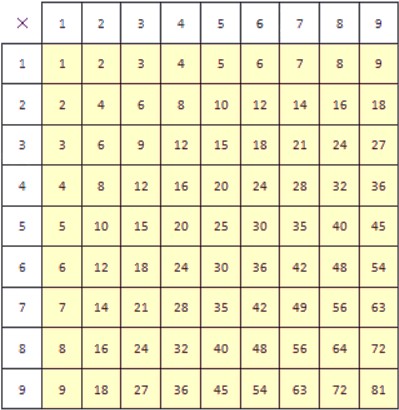
Таблица умножения позволяет находить не только результат произведения множителей, но и множитель по известному произведению и другому множителю. Как мы выяснили ранее, деление – это как раз и есть нахождение неизвестного множителя по известному произведению и еще одному множителю.

С помощью таблицы умножения можно проводить деление любого числа на желтом фоне на любое однозначное натуральное число. Покажем, как это делать. Есть два способа, применение которых мы будем рассматривать на примерах.

Разделим 48 на 6.

Способ первый.

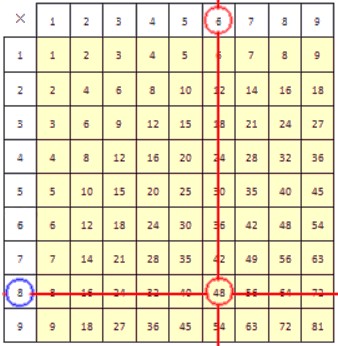
В столбце, верхняя ячейка которого содержит делитель 6, находим делимое 48. Результат деления при этом находится в крайней левой ячейке строки, содержащей делимое. Он обведен синей окружностью.

Способ второй.

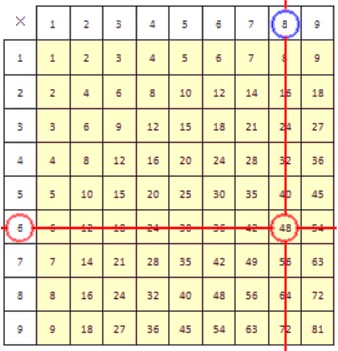
Сначала в строке с делителем 6 находим делимое 48. Результат деления при этом находится в крайней верхней ячейке столбца, содержащем делимое. Он обведен синей окружностью.

Итак, мы разделили 48 на 6 и получили 8. Результат был найден по таблице умножения двумя способами. Оба способа абсолютно идентичны.

Для закрепления рассмотрим еще один пример. Разделим 7 на 1. Приведем рисунки, иллюстрирующие процесс деления.

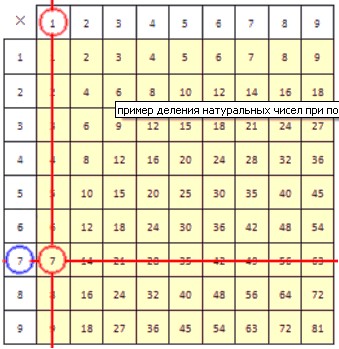
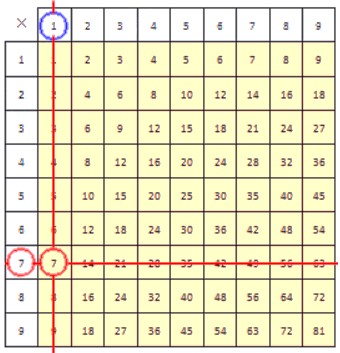
В результате деления числа 7 на 1, как вы уже догадались, получается число 7. В делении с помощью таблицы умножения очень важно знать эту таблицу наизусть, так как не всегда можно иметь ее под рукой.

Настоятельно рекомендуем выучить таблицу умножения!

Деление на 10, 100, 1000 и т.д.

Сразу сформулируем правило деления на натуральных чисел на 10, 100, 1000 и т.д. Сразу будем считать, что деление без остатка возможно.

Деление на 10, 100, 1000 и т.д.

Результатом деления натурального числа на 10, 100, 1000 и т.д. является такое натуральное число, запись которого получается из записи делимого если справа от него отбросить 1, 2, 3 и т.д. нулей.

Отбрасывается столько нулей, сколько из есть в записи делителя!

Например, 30÷10=3. От числа 30 мы отбросили один нуль.

Частное 120000÷1000 равно 120 – от числа 120000 отбрасываем справа три нуля, именно столько их содержится в делителе.

Обоснование правила строится на правиле умножения натурального числа на 10, 100, 1000 и т.д. Приведем пример. Пусть нужно разделить 10200 на 100.

10200=102·100

10200÷100=102·100100=102.

Представление делимого в виде произведения

При делении натуральных чисел не стоит забывать о свойстве деления произведения двух чисел на натуральное число. Иногда делимое можно представить в виде произведения, один из множителей в котором делится на делитель.

Рассмотрим типичные случаи.

Пример 2. Представление делимого в виде произведения

Разделим 30 на 3.

Делимое 30 можно представить в виде произведения30=3·10.

Имеем: 30÷3=3·10÷3

Воспользовавшись свойством деления произведения двух чисел, получаем:

3·10÷3=3÷3·10=1·10=10

30÷3=10

Приведем еще несколько аналогичных примеров.

Пример 3. Представление делимого в виде произведения

Вычислим частное 7200÷72.

Представляем делимое в виде 7200=72·100. При этом, результат деления будет следующим:

7200÷72=72·100÷72=72÷72÷100=100

Пример 4. Представление делимого в виде произведения

Вычислим частное: 1600000÷160.

1600000=160·10000

1600000÷160=160·10000÷160=160÷160·10000=10000

В более сложных примерах удобно пользоваться таблицей умножения. Проиллюстрируем это.

Пример 5. Представление делимого в виде произведения

Разделим 5400 на 9.

Таблица умножения подсказывает нам, что 54 делится на 9, поэтому делимое целесообразно представить в виде произведения:

5400=54·100.

Теперь закончим деление:

5400÷9=54·100÷9=54÷9·100=6·100=600

Для закрепления данного материала рассмотрим еще один пример, уже без подробных словесных пояснений.

Пример 6. Представление делимого в виде произведения

Посчитаем, сколько будет 120 разделить на 4.

120=12·10

120÷4=12·10÷4=12÷4·10=3·10=30

Деление натуральных чисел, оканчивающихся на нуль

При делении чисел, записи которых оканчиваются цифрой 0, полезно помнить свойство деления натурального числа на произведение двух чисел. При этом, делитель представляется в виде произведения двух множителей, после чего указанное свойство находит применение в совокупности с таблицей умножения.

Как всегда, поясним это на примерах.

Пример 7. Деление натуральных чисел, оканчивающихся на 0

Разделим 490 на 70.

Запишем 70 в виде:

70=7·10.

Используя свойство деления натурального числа на произведение, можно записать:

490÷70=490÷7·10=490÷10÷7.

Деление на 10 мы уже разобрали в предыдущем пункте.

490÷10÷7=49÷7=7

490÷70=7.

Для закрепления разберем еще один, более сложный пример.

Пример 8. Деление натуральных чисел, оканчивающихся на 0

Возьмем числа 54000 и 5400 и разделим их.

54000÷5400=?

Представим 5400 в виде 54·100 и запишем:

54000÷5400=54000÷54·100=54000÷100÷54=540÷54.

Теперь делимое 540 представляем в виде 54·10 и записываем:

540÷54=54·10÷54=54÷54·10=10

54000÷5400=10.

Подведем итог по изложенному в данном пункте.

Важно!

Если в записях делимого и делителя справа присутствуют нули, то нужно избавиться от одинакового количества нулей как в делимом, так и в делителе. После этого выполнить деление получившихся чисел.

Например, деление чисел 64000 и 8000 сведется к делению чисел 64 и 8.

Метод подбора частного

Прежде чем рассматривать этот способ деления, введем некоторые условия.

Пусть числа a и b делятся друг на друга, причем произведение b·10 дает число, большее, чем a. В таком случае частное a÷b является однозначным натуральным числом. Иными словами, это число от 1 до 9. Это типичная ситуация, когда метод подбора частного удобен и применим. Последовательно умножая делитель на 1, 2, 3, .. , 9 и сравнивая результат с делимым, можно найти частное.

Рассмотрим пример.

Пример 9. Подбор частного

Разделим 108 на 27.

Легко заметить, что 27·10=270; 270>108.

Начнем подбор частного.

27·1=2727·2=5427·3=8127·4=108

Бинго! Частное найдено методом подбора:

108÷27=4.

Отметим, что в случаях, когда b·10>a частное также удобно находить методом последовательного вычитания.

Представление делимого в виде суммы

Еще один способ, который может помочь найти частное – это представить делимое в виде суммы нескольких натуральных чисел, каждое из которых легко делится на делитель. После этого нам пригодится свойство деления суммы натуральных чисел на число. Вместе с примером рассмотрим алгоритм и ответим на вопрос: в виде каких слагаемых представлять делимое?

Пусть делимое равно 8551, а делитель равен 17.

Вычислим, на сколько в записи делимого больше знаков, чем в записи делителя. В нашем случае делитель содержит два знака, а делимое – четыре. Значит в записи делимого на два знака больше. Запоминаем число 2.
Справа в делителе дописываем два нуля. Почему два? В предыдущем пункте мы как раз и определили это число. Однако, если записанное в результате число окажется больше делителя, из числа, полученного в предыдущем пункте, нужно вычесть 1. В нашем примере, дописав нули к делителю, мы получили число 1700<8551. Таким образом, отнимать единицу из двойки, полученной в первом пункте, не нужно. В памяти так же оставляем число 2.
К числу 1 справа приписываем нули в количестве, определенном числом из предыдущего пункта. Тем самым мы получаем рабочую единицу разряда, с которым будем оперировать далее. В нашем случае, к единице приписываются два нуля. Рабочий разряд – сотни.
Проводим последовательное умножения делителя на 1, 2, 3 и т.д. единицы рабочего разряда до того момента, пока не получим число, большее, чем делимое. 17·100=1700; 17·200=3400; 17·300=5100; 17·400=6400; 17·500=8500; 17·600=10200Нас интересует предпоследний результат, так как следующий после него результат произведения больше делимого. Число 8500, которое получено на предпоследнем шаге при умножении, и является первым слагаемым. Запоминаем равенство, которое мы будем использовать далее: 8500=17·500.
Вычисляем разность между делимым и найденным слагаемым. Если она не равна нулю, возвращаемся к первому пункту и начинаем поиск второго слагаемого, используя вместо делимого уже полученную разность. Повторяем пункты до тех пор, пока в результате не получим нуль. В нашем примере разность равна 8551-8500=51. 51≠0, поэтому, переходим к пункту 1.

Повторяем алгоритм:

Сравниваем количество знаков в новом делимом 51 и делителе 17. В обоих записях по две цифры, разность количества знаков равно нулю. Запоминаем число 0.
Так как мы запомнили число 0, в записи делителя не нужно дописывать дополнительных нулей.
К единице также не будем добавлять нулей. Опять же, потому что в первом пункте мы запоминали число 0. Таким образом, нашим рабочим разрядом являются единицы
Последовательно умножаем 17 на 1, 2, 3,.. и т.д. Получаем: 17·1=17; 17·2=34; 17·3=51.
Очевидно, на третьем шаге мы получили число, равное делителю. Это и есть второе слагаемое. Так как 51-51=0, на этом этапе останавливаем поиск слагаемых – он завершен.

Теперь осталось найти частное. Делимое 8551 мы представили в виде суммы 8500+51. Запишем:

8500+51÷17=8500÷17+51÷17.

Результаты делений в скобках известны нам из проведенных ранее действий.

8500+51÷17=8500÷17+51÷17=500+3=503.

Результат деления: 8551÷17=503.

Рассмотрим еще несколько примеров, уже не комментируя каждое действие столь детально.

Пример 10. Деление натуральных чисел

Найдем частное: 64÷2.

1. В записи делимого на один знак больше, чем в записи делителя. Запоминаем цифру 1.

2. Справа у делителя приписываем один нуль.

3. К числу 1 приписываем один нуль и получаем единицу рабочего разряда – 10. Рабочий разряд, таким образом – десятки.

4. Начинаем последовательное умножение делителя на единицы рабочего разряда. 2·10=20; 2·20=40; 2·30=60; 2·40=80; 80>64.

Первое найденное слагаемое – число 60.

Равенство 60÷2=30 ещё пригодится нам в будущем.

5. Ищем второе слагаемое. Для этого вычисляем разность 64-60=4. Число 4 делится на 2 без остатка, очевидно, это и есть второе слагаемое.

Теперь находим частное:

64÷2=60+4÷2=60÷2+4÷2=30+2=32.

Пример 11. Деление натуральных чисел

Решим: 1178÷31=?

1. Видим, что в записи делимого на два знака больше, чем в делителе. Запоминаем число 2.

2. К делителю справа добавляем два нуля. Получаем число 3100.

3100>1178, поэтому запомненное число 2 из первого пункта нужно уменьшить на единицу.

2-1=1.

3. К единице справа добавляем один нуль и получаем рабочий разряд – десятки.

4. Умножаем 31 на 10, 20, 30, .. и т.д.

31·10=310; 31·20=620; 31·30=930; 31·40=1240

1240>1178, следовательно, первым слагаемым является число 930.

5. Вычисляем разность 1178-930=248. С числом 248 на месте делимого начинаем искать второе слагаемое.

1. В записи числа 248 на один знак больше, чем в числе 31. Запоминаем цифру 1.

2. К 31 прибавляем справа один нуль. Так как 310>248, уменьшаем полученную в предыдущем пункте единицу, и в итоге имеем число 0.

3. Так как мы запомнили число 0, то к единице не нужно приписывать дополнительных нулей, и разряд единиц – рабочий разряд.

4. Последовательно умножаем 31 на 1, 2, 3, .. и т.д., сравнивая результат c делимым.

31·1=31; 31·2=62; 31·3=93; 31·4=124; 31·5=155; 31·6=186; 31·7=217; 31·8=248

Таким образом, именно число 248 и является вторым слагаемым, которое делится на 31.

5. Разность 248-248 равна нулю. Заканчиваем поиск слагаемых, запоминаем соотношение 248÷31=8 и находим частное.

1178÷31=930+248÷31=930÷31+248÷31=30+8=38.

Постепенно увеличиваем сложность примеров.

Пример 12. Деление натуральных чисел

Разделим 13984 на 32.

В данном случае описанный выше алгоритм нужно будет применить три раза. Не будем приводить все выкладки, просто укажем, в виде каких слагаемых будет представлен делитель. Вы можете проверить себя, и провести вычисления самостоятельно.

Первое слагаемое равно 12800.

12800÷32=400.

Второе слагаемое равно 960.

960÷32=30.

Третье слагаемое равно 224.

224÷32=7.

Результат:

13984÷32=12800+960+224÷32=12800÷32+960÷32+224÷32=400+30+7=437.

Казалось бы, мы рассмотрели практически все возможные способы деления натуральных чисел. На этом, тему можно считать закрытой. Однако, есть способ, который в ряде случаев позволяет провести деление быстрее и рациональнее.

Рассмотрим его напоследок.

Представление делимого в виде разности натуральных чисел

Иногда делимое проще и удобнее представлять в виде разности, а не суммы. Это может значительно ускорить и облегчить процесс деления. Как именно? Покажем на примере.

Пример 13. Деление натуральных чисел

Разделим 594 на 6.

Если воспользоваться алгоритмом из предыдущего пункта, мы получим в результате:

594÷6=540+54÷6=540÷6+54÷6=90+9=99.

Однако, если число 594 представить в виде разности 600-6, все становится гораздо очевиднее. Оба числа 600 и 6) делятся на 6. По свойству деления разности натуральных чисел, мы получаем:

594÷6=600-6÷6=600÷6-6÷6=100-1=99

Результат тот же, но действия объективно легче и проще.

Решим еще один пример тем же методом. Отметим, что важно уметь правильно заметить, какую манипуляцию сделать с числами, чтобы провести деление легко. Скажем даже, что в этом присутствует некоторый элемент искусства.

Пример 14. Деление натуральных чисел

483÷7=?

Вспоминаем таблицу умножение и понимаем: число 483 удобно представить в виде 483=490-7.

490÷7=707÷7=1

Проводим деление:

483÷7=(490-7)÷7=490÷7-7÷7=70-1=69.

Проверка результата деления

Проверка никогда не бывает лишней, особенно, если мы делили большие числа. Как проверять, правильно ли выполнено деление натуральных чисел? При помощи умножения!

Проверка результата деления

Чтобы проверить правильно ли выполнено деление, нужно частное умножить на делитель. В результате должно получится делимое.

Если выходит иначе, можно сделать вывод о том, что где-то закралась ошибка.

Смысл этого действия очень прост. Например, у нас было a предметов, и эти a предметов мы разложили на b кучек. В каждой кучке оказалось по с предметов. Математически это выглядит так:

a÷b=c.

Теперь объединим обратно все b кучек по с предметов. В результате должно получится та же совокупность предметов a.

b·c=a.

Рассмотрим проведение проверки на двух примерах.

Пример 15. Проверка результата деления натуральных чисел

Число 475 разделили на 19. В результате получилось 25. Правильно ли выполнено деление?

Умножим частное 25 на делитель 19 и выясним, верно ли разделили числа.

25·19=475.

Число 475 равно делимому, значит, деление выполнено верно.

Пример 16. Проверка результата деления натуральных чисел

Разделите и проверьте результат:

1024÷32=?

Будем представлять делимое в виде суммы слагаемых и осуществлять деление.

1024÷32=960+64÷32=960÷32+64÷32=30+2=32.

Проверим результат:

32·32=1024.

Вывод: деление выполнено верно.

Проверка результата деления чисел делением

Рассмотренный выше способ проверки основан на умножении. Существует также проверка делением. Как ее проводить?

Проверка результата деления

Чтобы проверить верно ли найдено частное, нужно делимое разделить на полученное частное. В результате должен получится делитель.

Если выходит иначе, можно сделать вывод о том, что где-то закралась ошибка.

Правило основано на той же связи между делимым, делителем и частным, что и правило из предыдущего пункта.

Рассмотрим примеры.

Пример 17. Проверка результата деления натуральных чисел

Верно ли равенство:

104÷13=8.

Разделим делимое на частное:

104÷8=80+24÷8=80÷8+24÷8=10+3=13.

В результате получился делитель, значит, деление выполнено верно.

Пример 18. Проверка результата деления натуральных чисел

Вычислим и проверим: 240÷15=?

Представляя делимое в виде суммы, получаем:

240÷15=150+90÷15=150÷15+90÷15=10+6=16.

Проверяем результат:

240÷16=?

240÷16=160+80÷16=160÷16+80÷16=10+5=15.

Деление выполнено верно.

Источник

Частное чисел в математике: что это такое простыми словами для детей

Частное чисел в математике: что это такое? В школе учат действие деление, где есть делимое, делитель и частное. Что означают эти названия? Давайте разбираться!

Содержание статьи:

Частное чисел в математике: что это такое

Однажды клоун Бим решил выучить математическое действие деление и нашел для себя в интернете вот такое определение:

Определение. Говорят, что a делится на b, если существует натуральное число с, при умножении которого на b получается а: a=b*c. При этом записывают: a:b=с, — и называют а — делимым, b — делителем, с — частным.

Как мне это понять? — задумался Бим. — Но скоро представление, пойду ребят к нам приглашать.

Как найти частное чисел

Пришли в цирк трое ребят: Вася, Коля и Оля. На входе их встречал клоун Бим, который дарил детям шарики. У него в руках было 6 шариков, но дарил он их за отгадки. Клоун спросил у ребят:

— Мне надо подарить вам шарики, какое математическое действие я буду применять?

— Деление! — быстро ответил Коля. — Ты же будешь делить шарики между нами.

Клоун хитро прищурился:

— А как называются члены деления?

— Мы недавно это изучали! — воскликнула Оля. — Всё количество шариков, которое ты будешь делить, называется делимое. У тебя сейчас 6 шариков, значит здесь делимое — 6!

— А то, на сколько ребят ты их разделишь, называется делитель, — вмешался Вася. — Нас трое ребят, значит делитель — 3!

Коля продолжил:

— У каждого из нас будет часть шариков, и результат от деления называется частным.

— Какое же здесь будет частное? — спрашивает Бим.

— Два! — не сговариваясь, хором ответили ребята.

— Правильно, каждому из вас достанется по два шарика, это и есть частное.

Ребята ответили на все вопросы Бима, и каждый получил по два шарика — как результат деления:

6 (делимое) : 3 (делитель) = 2 (частное).

Запишем цифрами:

6:3=2

В этом выражении 6 (делимое) стоит самым первым, 3 (делитель) — на втором месте. А частное (2) — после знака равенства справа.

Итак, частное — это число, которое получается в результате деления делимого на делитель.

Полное и неполное частное

А потом было замечательное представление.

В антракте дети пошли в буфет. На подносе лежало семь пирожных. Как же их разделить поровну на трёх ребят?

Друзья задумались и взяли по 2 пирожных, а последним, которое было в остатке, угостили клоуна Бима.

— Теперь я понял! — воскликнул Бим. — Если нельзя всё число пирожных поделить между ребятами без остатка, то такой результат от деления называется неполным частным. А то, что осталось после деления, так и называется остатком и записывается это вот так:

7:3=2(1)

Здесь 7 (делимое) по-прежнему стоит в начале выражения, 3 (делитель) — в середине, 2 (неполное частное) — справа. Но после неполного частного ещё пишем в скобках остаток (1).

Полное частное — результат деления, когда делимое делится нацело на делитель (остаток равен 0, его и писать незачем).
Неполное частное — это результат деления с остатком (когда делимое не делится нацело на делитель).

Как найти делитель

Когда дети ушли занимать свои места, буфетчица подошла к Биму и спросила:

— Я забыла, сколько было ребят. Помню только, что каждый из них съел по два пирожных, а всего им досталось 6 штук. Сколько же посетителей было у меня?

Тут в буфет заглянул дрессировщик Бом и быстренько решил эту задачку. Он разделил 6 (делимое) на 2 (частное) и получил 3 (делитель).

— Всего было трое ребят, — ответил Бом.

— Верно! — вспомнил Бим.

Для того чтобы найти делитель, надо делимое разделить на частное.

6:2=3

Здесь 6 – делимое, 2 – частное, а 3 – делитель.

Как найти делимое

— А сколько ты подарил всего шариков трём ребятам? — спросил Бом.

— Забыл, — ответил Бим. — Помню только, что детей было трое, и каждому досталось по два шарика.

Бом и говорит:

— Тогда надо 3 (делитель) умножить на 2 (частное), получится 6.

Для того чтобы найти делимое, надо делитель умножить на частное.

Запишем это цифрами:

3*2=6.

3 — наш делитель, 2 — частное, а 6 — делимое.

Проверка деления умножением

— Я что-то не пойму. Это уже умножение, а не деление! — говорит Бим. — Выходит, что деление — действие обратное умножению. То есть, мы можем проверить деление умножением?

— Да, — ответил Бом.

Деление — действие, обратное умножению. Для того чтобы проверить деление, надо провести умножение.

Заключение

А клоун для себя сделал плакаты и теперь каждый день может сразу вспомнить, что:

Определение. Говорят, что а делится на b, если существует число с, при умножении которого на b получается а: a= b*c. При этом записывают: a:b=с, — и называют а — делимым, b — делителем, с — частным.

Деление — действие, обратное умножению;
умножение проверяет правильность математического действия — деления;
для того чтобы найти делимое, надо делитель умножить на частное;
для того чтобы найти делитель, надо делимое разделить на частное.

Итак, теперь мы знаем, что же такое частное в математике. Оказывается, оно бывает полным и неполным! Кроме того, нетрудно будет найти делитель, делимое и проверить деление умножением. И если учитель спросит в школе: «Частное чисел в математике: что это такое?» — сможем ответить сразу. И пусть любой пример или задача на эту тему будет вам по плечу!

Оригинальная идея подачи материала принадлежит Стуловой Лилии Валериевне (преподаватель математики от 5 лет и старше).

Источник

Математика, 2 класс

Урок № 55. Название чисел при делении

Перечень вопросов, рассматриваемых в теме:

1. Как называются числа при делении?

2. Как называется числовое выражение со знаком деление?

Глоссарий по теме:

Деление – это арифметическое действие, обратное умножению. С помощью деления по произведению и одному из множителей определяется второй множитель.

Делимое – это число стоящее слева от знака деления, которое делим.

Делитель – это число стоящее справа от знака деления, число на которое делим делимое. (какими частями делим, дробим)

Частное – это число стоящее после знака равно, результат деления, числовое выражение со знаком деление.

Обязательная литература и дополнительная литература:

Моро М. И., Бантова М. А. и др. Математика 2 класс. Учебник для общеобразовательных организаций. М.; Просвещение, 2017. – с. 62.
С. И. Волкова. Математика 2 класс. Тетрадь учебных достижений. Учебное пособие для общеобразовательных организаций. М.; Просвещение, 2018. – с. 44-47.

Теоретический материал для самостоятельного изучения

Запишем равенство, используя необходимое арифметическое действие:

10 яблок разложили на две тарелки поровну.

10 : 2 = 5

9 конфет раздали трём детям поровну.

9 : 3 = 3

8 тетрадей раздали четырём ученикам поровну.

8 : 4 = 2

Для того, чтобы выполнит задание, нам понадобилось действие деление.

Вы уже знаете, как называются числа при сложении и вычитании, недавно вы познакомились с названиями чисел при умножении.

Вы умеете называть выражения со знаками «плюс», «минус», со знаком умножения. Сегодня вы узнаете, как называются числа при делении. Выражение со знаком деления тоже имеет своё название. Хотите узнать? Вперёд!

Числа при делении имеют свои названия.

Рассмотрим рисунок.

8 листьев раздали детям, по 2 листа каждому.

8 : 2 = 4

4 человека получили листья.

Число, которое делят, называется делимым. 8 – это делимое. Число, на которое делят делимое, называется делитель. 2 – это делитель Результат действия деления называется частным. 4 – это частное. Выражение 8 разделить на 2 тоже называется частным.

Компоненты деления: делимое, делитель, частное.

Найдите частное, если делимое – 6, делитель – 3.

Проверьте: 6 : 3 = 2

Найдите частное чисел 12 и 6. Проверьте: 12 : 6 = 2

Решим задачу: 12 клубничек раздали 4 детям поровну. По сколько клубничек получил каждый ребёнок?

Для решения задачи выберем действие деление, так как надо узнать, сколько раз по 4 содержится в числе 12.

12 : 4 = 3 (кл.)

Ответ: по 3 клубнички получил каждый ребёнок.

Вспомним название чисел при делении. 12 – делимое, 4 – делитель. 3 – частное. 12 : 4 – это частное.

Вывод: компоненты действия деление – делимое, делитель, результат деления – частное.

Ответим на вопросы, поставленные в начале урока.

Число, которое делят, называется делимое.

Число, на которое делят делимое, называется делитель.

Результат деления – частное.

Числа, которые соединены знаком деления, тоже называются частное.

Выполним несколько тренировочных заданий.

1. По рисунку составьте задачи на деление. Запишите решение. Назовите компоненты действия деление.

а) 15 яблок разложили в 3 вазы, в каждую вазу поровну. Сколько яблок положили в одну вазу?

Проверьте: 15 : 3 = 5 (яб.).

Ответ: 5 яблок.

15 – делимое. 3 – делитель. 5 – частное. Выражение 15:3 – частное.

б) 15 яблок разложили в вазы, по 5 штук в каждую. Сколько ваз заняты яблоками?

15 : 5 = 3 (в.)

Ответ: 3 вазы.

15 – делимое. 5 – делитель. 3 – частное. Выражение 15:5 – частное.

2. Запишите выражение и найдите их значения:

Частное чисел 12 и 2.

Делитель 4, делимое 20.

Делимое 8, делитель 4.

Произведение 5 и 3.

Сумма чисел 6 и 4.

Проверьте.

12 : 2 = 6

20 : 4 = 5

8 : 4 = 2

5 ∙ 3 = 15

6 + 4 = 10

Источник

План урока:

Конкретный смысл действия деления

Название компонентов и результата деления

Приемы умножения и деления с числом 10

Здравствуйте, ребята. Сегодня мы отправимся с вами в дремучий лес. Страшно? Вовсе нет! Вместе с нами будет озорная, веселая, любознательная Маша. А приглашаем всех в гости к Мише.

К медведю Маша забрела.

Что за чудные дела?

Нет покоя Мишке:

Игры, шутки, книжки,

Уроки, перемены, чехарда.

Ну и Маша! Вот это да!

Конкретный смысл действия деления

Решение задач на деление по содержанию

Миша уже многому научил непоседливую ученицу Машу. Сейчас она решает задачи на деление. Давайте посмотрим, как девочка справляется с заданиями, и поможем, если ей будет трудно.

Задача

Мишка написал письма и запечатал их в конверты. Он дал девочке 6 марок. Маше нужно приклеить по 2 марки на каждый конверт. Сколько писем написал Миша?

Непростая задача! Давайте решим ее вместе.

Чтобы ответить на вопрос задачи, нужно узнать, сколько раз по 2 содержится в шести.

Сколько раз вы видите по 2 марки? Верно, 3. Шесть разделить на два, получится три.

Запишем решение.

6 : 2 = 3 (п.)

Ответ: 3 письма.

А теперь второе задание от медведя. Маше нужно раздать белочкам 10 орехов, каждой по 5. Сколько белочек получат орехи?

Проверьте, верно ли Маша решила.

10 : 5 = 2 (б.)

Ответ: 2 белки.

Маша – молодец! Все верно.

Перемена! Перемена! Можно попить чайку с вкусным пирогом. Тем более, что у Миши и Маши гости.

Ребята, помогите разделить пирог поровну на всех. Мишка разрезал на равные кусочки так:

По сколько кусочков пирога получит каждый? Прежде чем начать решать задачу, посчитайте, сколько желающих попить чайку с пирогом, на сколько частей разрезали пирог!

Проверь себя.

За столом собрались трое: Маша, Мишка и гостья. А вот пирог разрезан на 6 равных частей. Разделим количество кусков пирога (6) на троих.

6 : 3 = 2 (к.)

Ответ: 2 кусочка.

Звенит звонок вновь на урок:

Беремся за дело, решаем задачи смело!

Ребята, Маша неплохо научилась решать задачи. Она составила для вас несколько интересных заданий. Попробуйте их решить самостоятельно. Не волнуйтесь, будут маленькие подсказки!

Задание первое.

Как трем маленьким ежатам не поссориться и разделить поровну 9 яблочек? По сколько яблок достанется каждому ежу?

Подсказкой для вас будет рисунок!

Проверь себя.

9 : 3 =3 (я.)

Ответ: 3 яблока.

Задание второе.

Маша сделала схематический рисунок. Составьте по нему задачу на деление, запишите решение и ответ.

Проверь себя.

Составим задачу про Машу.

Маша угостила своих друзей конфетами: по 2 каждому. Скольким ребятам Маша раздала сладости, если всего было 8 конфет?

Решение.

8 : 2 = 4 (р.)

Ответ: 4 ребят.

Понравились вам задания, которые придумала Маша?

Название компонентов и результата деления

Ребята, как называются числа при делении? Должны же они как-то называться! Мы с вами знаем название чисел при сложении, вычитании, умножении. Давайте запомним и про деление тоже.

Примеры на деление можно прочитать по-разному. Маша умеет это делать тремя способами. Прочитайте на карточке, постарайтесь запомнить.

Маша записала для вас три примера на деление. Потренируйтесь каждый пример прочитать, ни разу не повторяясь!

А вот над следующим заданием Маша задумалась! Мишка записал в тетради математические предложения, которые нужно превратить в обычные примеры на деление и, конечно, записать результат деления. Помогите Маше справиться с заданием!

Проверь себя.

4 : 2 = 2

8 : 4 = 2

15 : 3 = 5

Совет от Миши!

Ребята, постарайтесь запомнить правило. Оно связано с новым действием делением. Это правило поможет нам правильно выполнять вычисления на умножение и деление.

Приемы умножения и деления с числом 10

Маша решает примеры. Давайте понаблюдаем, как она рассуждает.

2 ∙ 10 =

10 ∙ 2 =

20 : 10 =

20 : 2=

Ребята, у меня есть 2 коробки цветных карандашей. В каждой коробке по 10 штук. Сколько всего цветных карандашей в этих коробках?

Решение можно записать сложением 10 + 10 = 20. Мы видим, что по 10 взяли два раза. А это значит: 10 ∙ 2 = 20. Зная переместительное свойство умножения, запишем: 2 ∙ 10 =20.

Еще одно важное правило нужно вспомнить:

Пользуясь им, составим два примера на деление.

20 : 10 = 2

20 : 2= 10

Вот так Маша! Молодец! С заданием справилась на отлично. Попробуйте и вы, ребята, так же рассуждать. Решите примеры.

3 ∙ 10 =

10 ∙ 3 =

30 : 10 =

30 : 3=

Проверь себя.

3 ∙ 10 = 30

10 ∙ 3 = 30

30 : 10 = 3

30 : 3= 10

Мишка знает еще один способ решения примеров с числом 10.

Посмотрите внимательно на этот пример:

При умножении числа на 10 не забудь справа приписать к числу нуль.

Если же число делишь на 10, не забудь от этого числа отбросить нуль.

Какой способ вам понравился больше: тот, которым решала Маша или Мишин совет?

Выбирайте любой способ, будем соревноваться с Машей и Мишей решать примеры на время! Дается всего одна минута. Примеры записывать не нужно, пишите только ответы через запятую. Попросите друга напомнить, когда минута закончится.

Итак, начинаем!

Маша решила без ошибок, но времени на все примеры не хватило, осталось решить еще 2 примера. Миша решил все примеры без ошибок. Хороший результат! А как вы справились с заданием?

Напоследок Маша подготовила для вас, ребята, задачу на смекалку. Не торопитесь, хорошо подумайте!

Когда Мишка в своем домике находится без головы? Посмотрите на рисунок, думаю, он вам поможет дать правильный ответ

Правильный ответ: Миша будет находиться в своем домике без головы, если выглянет в окно. Голова-то будет на улице, а не в доме!

Нам еще многому предстоит научиться. А сегодняшний урок подошел к концу. Проверьте, как вы запомнили Мишины советы, все ли поняли.

Источник

Формы записи и терминология[править | править код]

Свойства[править | править код]

Выполнение деления[править | править код]

Деление чисел[править | править код]

Натуральные числа[править | править код]

Деление целых чисел[править | править код]

Деление рациональных чисел[править | править код]

Деление вещественных чисел[править | править код]

График[править | править код]

Деление комплексных чисел[править | править код]

Алгебраической форма[править | править код]

Тригонометрическая форма[править | править код]

Показательная (экспоненциальная) форма[править | править код]

Экспоненциальная запись[править | править код]

Деление физических величин[править | править код]

Деление в алгебре[править | править код]

Деление многочленов[править | править код]

Деление на ноль[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Связь деления с умножением

Деление методом последовательного вычитания

Деление равных натуральных чисел

Деление на единицу

Деление с помощью таблицы умножения

Деление на 10, 100, 1000 и т.д.

Представление делимого в виде произведения

Деление натуральных чисел, оканчивающихся на нуль

Метод подбора частного

Представление делимого в виде суммы

Представление делимого в виде разности натуральных чисел

Проверка результата деления

Проверка результата деления чисел делением

Частное чисел в математике: что это такое

Как найти частное чисел

Полное и неполное частное

Как найти делитель

Как найти делимое

Проверка деления умножением

Заключение

Конкретный смысл действия деления

Название компонентов и результата деления

Приемы умножения и деления с числом 10

Вам также может понравиться

Как найти нормальную маму

Как найти захороненных в братской могиле

Как найти приложение для фитнес браслета

Добавить комментарий Отменить ответ