Загрузить PDF
Загрузить PDF
Если вам необходимо найти напряжение на сопротивлении (резисторе), первым делом необходимо определить тип электрической цепи. Для лучшего понимания основных терминов, используемых в физике и электротехнике, начните с первого раздела. Если же вы знакомы с терминологией, пропустите его и перейдите к описанию типа электрической цепи.
-

1
Рассмотрим понятие электрического тока. Воспользуемся аналогией: представьте, что вы поместили несколько зерен кукурузы в воду, текущую по трубе. Поток эквивалентен электрическому току, а зерна служат аналогией электронов.[1]
Говоря о потоке, мы описываем его количеством зерен, пересекших поперечное сечение трубы за одну секунду. При рассмотрении электрического тока мы измеряем его в амперах, соответствующих определенному (очень большому) количеству электронов, пересекающих сечение провода за одну секунду. -

2
Рассмотрим понятие электрического заряда. Каждый электрон имеет “отрицательный” электрический заряд. Это означает, что электроны притягиваются, или движутся по направлению к положительному заряду и отталкиваются, или движутся от отрицательного заряда. Каждый электрон обладает отрицательным зарядом, поэтому они отталкиваются друг от друга, стремясь разойтись в стороны.
-

3
Ознакомьтесь с понятием напряжения. Напряжение между двумя точками соответствует разности электрических зарядов, размещенных в этих точках. Чем больше эта разница, тем сильнее данные точки притягиваются друг к другу. Рассмотрим понятие напряжения на примере обычной электрической батарейки:
- Внутри батарейки происходят химические реакции, в результате которых образуются свободные электроны. Эти электроны движутся к отрицательному полюсу батарейки, удаляясь от ее положительного полюса (эти полюса соответствуют отрицательной и положительной клеммам батарейки). Чем дольше длится данный процесс, тем большее напряжение возникает между полюсами.
- Если вы соедините проволокой отрицательный и положительный полюса, у скопившихся электронов появится возможность покинуть отрицательный полюс. Они начнут перетекать к положительному полюсу, создавая электрический ток. Чем выше напряжение, тем больше электронов переместится к положительному полюсу за единицу времени.
-

4
Рассмотрим понятие электрического сопротивления. Его название точно отображает смысл. Чем выше сопротивление какого-либо объекта, тем тяжелее электронам пройти через него. В результате уменьшается ток, поскольку за единицу времени через проводник проходит меньшее число электронов.
- Сопротивлением, или резистором называется что-либо, увеличивающее сопротивление электрической цепи. “Резистор” можно приобрести в магазине электротоваров, но в цепи его роль может выполнять и любой другой объект, обладающий сопротивлением, например, лампа накаливания.
-

5
Запомните закон Ома. Он представляет собой простое соотношение между током, напряжением и сопротивлением. Запишите или запомните это соотношение — оно пригодится вам при расчете электрических цепей:
- Ток равен напряжению, поделенному на сопротивление
- Это записывается следующим образом: I = V / R
- Подумайте о том, что происходит, если вы увеличиваете V (напряжение) или R (сопротивление). Соответствует ли это приведенным выше объяснениям?
Реклама
-

1
Ознакомьтесь с понятием последовательного соединения. Такое соединение легко определить — оно представляет собой набор расположенных в ряд сопротивлений. Ток течет по этим сопротивлениям, последовательно проходя через каждое из них.
- Величина тока одинакова в любой точке цепи.[2]
- При расчете напряжения неважно, где именно в цепи расположен тот или иной резистор. Можно поменять их местами, напряжение на каждом из них останется неизменным.
- В качестве примера рассмотрим цепь, состоящую из трех последовательно соединенных сопротивлений: R1, R2 и R3. Пусть цепь питается от 12-вольтовой батарейки. Найдем напряжение на каждом сопротивлении.
- Величина тока одинакова в любой точке цепи.[2]
-

2
Сначала рассчитаем общее сопротивление. Сложим все сопротивления, включенные в цепь. В результате получим общее сопротивление резисторов, соединенных последовательно.
- Пусть три резистора R1, R2 и R3 имеют сопротивления 2 Ома, 3 Ома и 5 Ом соответственно. Тогда общее сопротивление составит 2 + 3 + 5 = 10 Ом.
-

3
Найдем ток. Используем закон Ома для всей цепи. Как мы помним, при последовательном соединении ток одинаков в любой точке цепи. Поэтому достаточно один раз определить ток и использовать найденную величину во всех последующих расчетах.
- Согласно закону Ома, I = V / R. Напряжение в цепи составляет 12 вольт, а общее сопротивление – 10 Ом. Отсюда находим I = 12 / 10 = 1,2 ампера.
-

4
Применим закон Ома, чтобы найти напряжение на резисторах. При помощи простых преобразований можно выразить напряжение через ток и сопротивление, переписав закон Ома следующим образом:
- I = V / R
- IR = VR / R
- IR = V
- V = IR
-

5
Рассчитаем напряжение на каждом резисторе. Нам известны их сопротивления, протекающий через них ток, и в нашем распоряжении есть равенство, связывающее ток и сопротивление с напряжением. Подставляя в это равенство численные значения, находим ответ. Для нашего примера это выглядит следующим образом:
- Напряжение на резисторе R1 = V1 = (1,2A)(2Ома) = 2,4 вольта.
- Напряжение на резисторе R2 = V2 = (1,2A)(3Ома) = 3,6 вольта.
- Напряжение на резисторе R3 = V3 = (1,2A)(5Ом) = 6,0 вольт.
-

6
Проверим полученный ответ. При последовательном соединении сумма напряжений на каждом сопротивлении должна равняться общему напряжению в цепи.[3]
Сложите найденные напряжения, проверив, равна ли их сумма полному напряжению. Если нет, проверьте решение и найдите ошибку.- В нашем примере 2,4 + 3,6 + 6,0 = 12 вольт, что соответствует общему напряжению в цепи.
- Если ответ немного не совпадает с точным значением (например, 11,97 вместо 12), это, вероятно, вызвано тем, что вы на каком-то этапе округлили полученные величины. В этом случае ответ верен.
- Помните о том, что напряжение соответствует разности зарядов или количества электронов. Представьте себе, что вы подсчитываете число электронов, продвигаясь вдоль цепи. Если вы правильно сосчитаете их, то в результате получите разность зарядов между начальной и конечной точками цепи.
Реклама
-

1
Ознакомьтесь с понятием параллельного соединения. Представьте себе, что вы подсоединили провод к одному полюсу батарейки и расщепили его вдоль на две половины. Эти две части провода идут параллельно друг другу и затем вновь соединяются в один провод перед вторым полюсом батарейки. Если разместить на обеих ветках провода по резистору, они будут соединены «параллельно».[4]
- Параллельно можно соединить любое количество сопротивлений. Данное описание годится и для цепи, состоящей из сотни параллельных проводов.
-

2
Рассмотрим, как течет ток. При параллельном соединении он проходит через все ветки цепи. Ток будет течь через левый провод, пересекая расположенный на нем резистор; одновременно ток будет проходить и через правый провод с резистором. Пройдя через обе ветки, ток достигнет положительного полюса; ни на каком участке цепи ток не будет течь в обратном направлении.
-

3
Зная общее напряжение, найдем напряжение на каждом резисторе. Сделать это очень просто, если известно общее напряжение в цепи. При параллельном соединении напряжение на каждой ветке будет равно общему напряжению в цепи.[5]
Предположим, что наша цепь состоит из двух параллельно соединенных сопротивлений и питается 6-вольтовой батарейкой. В этом случае напряжение и на левом, и на правом сопротивлении составит 6 вольт. При этом каждая ветка может содержать любое число резисторов. Чтобы понять это, вернемся к последовательному соединению, рассмотренному выше:- Как мы помним, при последовательном соединении общее напряжение представляет собой сумму напряжений на каждом сопротивлении.
- Будем считать, что каждая ветка цепи представляет собой набор резисторов, соединенных последовательно. Таким образом, вычислив сумму напряжений на всех сопротивлениях одной из веток, мы найдем общее напряжение.
- Поскольку в нашем случае ток, текущий по каждой ветке, проходит через один резистор, напряжение на этом резисторе и будет общим напряжением в цепи.
-

4
Найдем общий ток в цепи. Если в условии задачи не указано общее напряжение, понадобятся некоторые дополнительные вычисления. Начнем с нахождения общего тока, протекающего по цепи. При параллельном соединении общий ток равен сумме токов, проходящих через каждую ветку цепи.[6]
- В математической записи это означает: Iобщий = I1 + I2 + I3…
- Для лучшего понимания представьте себе водопроводную трубу, разделенную на два рукава. Общее количество воды равно сумме воды, протекающей по каждому рукаву.
-

5
Найдем общее сопротивление цепи. При параллельном соединении резисторы не так сильно снижают ток через цепь, поскольку каждый из них вносит вклад в сопротивление лишь своей ветки цепи. Фактически чем больше ответвлений цепи, тем легче току пройти через нее. Чтобы найти общее сопротивление, необходимо решить относительно Rобщее следующее уравнение:
- 1 / Rобщее = 1 / R1 + 1 / R2 + 1 / R3 …
- Предположим, что цепь состоит из двух резисторов сопротивлением 2 Ома и 4 Ома, соединенных параллельно. Тогда 1 / Rобщее = 1/2 + 1/4 = 3/4 → 1 = (3/4)Rобщее → Rобщее = 1/(3/4) = 4/3 = ~1,33 Ома.
-

6
Вычислим напряжение. Как мы помним, общее напряжение в цепи равно напряжению на одной из ее веток. Воспользуемся законом Ома. Рассмотрим конкретный случай:
- Через цепь течет ток силой 5 ампер. Общее сопротивление цепи равно 1,33 Ома.
- Согласно закону Ома, I = V / R, откуда V = IR
- V = (5A)(1,33Ом) = 6,65 вольт.
Реклама
Советы
- Если вы имеете дело со сложной цепью, состоящей из последовательно и параллельно соединенных сопротивлений, рассмотрите сначала два соседних резистора. Найдите их общее сопротивление, пользуясь правилами для последовательного или параллельного соединения, в соответствии с тем, как соединены данные резисторы. После этого можно рассматривать два данных резистора как одно сопротивление. Продолжайте таким образом объединять резисторы до тех пор, пока у вас не получится простая цепь, состоящая из параллельно либо последовательно соединенных сопротивлений.[7]
- Напряжение на сопротивлении часто называют «падением напряжения».
- Усвойте терминологию:
- Цепь — набор элементов (например, резисторов, конденсаторов и катушек), соединенных проводами так, что через них может проходить электрический ток.
- Резисторы — элементы, оказывающие сопротивление протекающему через них току и понижающие его силу
- Ток — поток электрического заряда через проволоку и элементы цепи, измеряется в амперах (А)
- Напряжение — работа, затрачиваемая на перемещение единичного заряда, измеряется в вольтах (В)
- Сопротивление — мера сопротивления прохождению электрического тока, измеряется в омах (Ом)
Реклама
Об этой статье
Эту страницу просматривали 167 213 раз.
Была ли эта статья полезной?
Download Article
Download Article
Before you can calculate the voltage across a resistor, you’ll first have to determine what kind of circuit you are using. If you need a review of the basic terms or a little help understanding circuits, start with the first section. Otherwise, jump ahead to the type of circuit you have to solve.
-

1
Learn about current. Let’s think about current by using an analogy: imagine you pour a bag of corn kernels into a bowl. Each corn kernel is an electron, and the stream of kernels flowing into the bowl is the current.[1]
When talking about the flow, you describe it by saying how many kernels are flowing each second. When talking about a current, you measure it in amperes (amps), or a certain (very large) number of electrons flowing per second. -

2
Think about electrical charge. Electrons have a “negative” electrical charge. This means they attract (or flow toward) objects with a positive charge, and repel (or flow away from) objects with a negative charge. Since they’re all negative, electrons are always trying to push away from other electrons, spreading out wherever they can.
Advertisement
-

3
Understand voltage. Voltage measures the difference in electrical charge between two points. The greater the difference, the more energetically the two sides attract each other. Here’s an example with an everyday battery:
- Inside a battery, chemical reactions happen that produces a buildup of electrons. The electrons go to the negative end, while the positive end stays mostly empty. (These are called the negative and positive terminals.) The longer this goes on, the larger the voltage between the two ends.
- When you connect a wire between the negative and positive ends, the electrons at the negative end suddenly have somewhere to go. They shoot toward the positive end, creating a current. The larger the voltage, the more electrons move to the positive end each second.
-

4
Figure out resistance. Resistance is exactly what it sounds like. The more resistance something has, the harder it is for the electrons to push through. This slows the current, since fewer electrons can push through each second.
- A resistor is anything in the circuit that adds resistance. You can buy an actual “resistor” at an electronics store, but in a circuits problem it might represent a light bulb or anything else with resistance.
-

5
Memorize Ohm’s Law. There’s a very simple relationship between current, voltage, and resistance.[2]
Write this down or memorize it; you’ll use it often when solving circuit problems:- Current = voltage divided by resistance
- This is usually written: I = V / R
- Think about what happens when you increase V (voltage) or R (resistance). Does this match what you learned in the explanations above?
Advertisement
-

1
Understand a series circuit. A series circuit is easy to identify. It’s just one loop of wire, with everything arranged in a row. The current flows around the entire loop, going through each resistor or element in order.
- The current is always the same at any point along the circuit.[3]
- When calculating voltage, it doesn’t matter where the resistor is on the circuit. You can pick up the resistors and move them around, and you’ll still have the same voltage across each one.
- We’ll use an example circuit with three resistors in series: R1, R2, and R3. This is powered by a 12 volt battery. We’ll find the voltage across each one.
- The current is always the same at any point along the circuit.[3]
-

2
Calculate the total resistance. Add together all resistance values on the circuit. The answer is the total resistance of the series circuit.
- For example, the three resistors R1, R2, and R3 have resistances of 2 Ω (ohms), 3 Ω, and 5 Ω respectively. The total resistance is 2 + 3 + 5 = 10 ohms.
-

3
Find the current. Use Ohm’s Law to find the current of the entire circuit. Remember, the current is the same anywhere on a series circuit. Once we calculate the current this way, we can use it for all our calculations.
- Ohm’s Law says that the current I = V / R. The voltage across the whole circuit is 12 volts, and the total resistance is 10 ohms. The answer is I = 12 / 10 = 1.2 amperes.
-

4
Adjust Ohm’s Law to solve for voltage. With basic algebra, we can change Ohm’s Law to solve for voltage instead of current:[4]
- I = V / R
- IR = VR / R
- IR = V
- V = IR
-

5
Calculate the voltage across each resistor. We know the resistance, we know the current, and we have our equation. Plug in the numbers and solve. Here’s our example problem solved for all three resistors:
- Voltage across R1 = V1 = (1.2A)(2Ω) = 2.4 volts.
- Voltage across R2 = V2 = (1.2A)(3Ω) = 3.6 volts.
- Voltage across R3 = V3 = (1.2A)(5Ω) = 6.0 volts.
-

6
Check your answer. In a series circuit, the sum of all your answers must equal the total voltage.[5]
Add up every voltage you calculated and see if you get the voltage of the entire circuit. If you didn’t, go back and check for mistakes.- In our example, 2.4 + 3.6 + 6.0 = 12 volts, the voltage across the whole circuit.
- If your answer is slightly off (for instance, 11.97 instead of 12), you probably rounded a number at some point. Your answer is still correct.
- Remember, voltage measures the differences in charge, or numbers of electrons. Imagine counting the number of new electrons you see as you travel along the circuit. If you count them correctly, you’re going to end up with the total change in electrons from the beginning to the end.
Advertisement
-

1
Understand parallel circuits. Imagine a wire leaving one end of a battery, then splitting into two separate wires. These two wires run parallel to each other, then join up again before they reach the other end of the battery. If there’s a resistor on the left wire and a resistor on the right wire, those two resistors are connected “in parallel.”[6]
- You can have any number of wires in a parallel circuit. These instructions will still work for a circuit that splits into one hundred wires and comes back together.
-

2
Think about how the current flows. In a parallel circuit, the current flows across each path available to it. Current will flow through the wire on the left, cross the left resistor, and reach the other end. At the same time, current will flow through the wire on the right, cross the right resistor, and reach the end. No part of the current doubles back or flows through two parallel resistors.
-

3
Use the total voltage to find the voltage across each resistor. If you know the voltage across the whole circuit, the answer is surprisingly easy. Each parallel wire has the same voltage as the entire circuit.[7]
Let’s say a circuit with two parallel resistors is powered by a 6 volt battery. The voltage across the left resistor is 6 volts, and the voltage across the right resistor is 6 volts. It doesn’t even matter how much resistance there is. To understand why, think back to the series circuits described above:- Remember that adding voltage drops in a series circuit always results in the total voltage across the circuit.
- Think of each path the current takes as a series circuit. The same holds true for this: if you count up all the voltage drops, you’ll end up with the total voltage.
- Since the current through each of the two wires only passes through one resistor, the voltage across that resistor must equal the total voltage.
-

4
Calculate the total current of the circuit. If the problem doesn’t tell you what the total voltage of the circuit is, you’ll need to complete a few more steps. Start by finding the total current passing through the circuit. In a parallel circuit, the total current is equal to the sum of the current running through each parallel path.[9]
- In mathematical terms: Itotal = I1 + I2 + I3…
- If you’re having trouble understanding this, imagine a water pipe split into two paths. The total amount of water flow is just the amount of water flow in each pipe, added together.
-

5
Compute the total resistance of the circuit. Resistors are not as effective in a parallel circuit, because they only block the current going along one wire. In fact, the more wires there are, the easier it is for the current to find a way through. To find the total resistance, solve for Rtotal in this equation:[9]
- 1 / Rtotal = 1 / R1 + 1 / R2 + 1 / R3 …
- For example, a circuit has a 2 ohm and a 4 ohm resistor in parallel. 1 / Rtotal = 1/2 + 1/4 = 3/4 → 1 = (3/4)Rtotal → Rtotal = 1/(3/4) = 4/3 = ~1.33 ohms.
-

6
Find the voltage from your answers. Remember, once we find the total voltage of the circuit, we have found the voltage across any one of the parallel wires. Solve for the whole circuit using Ohm’s law.[10]
Here’s an example:- A circuit has 5 amperes of current running through it. The total resistance is 1.33 ohms.
- According to Ohm’s Law, I = V / R, therefore V = IR
- V = (5A)(1.33Ω) = 6.65 volts.
Advertisement
Add New Question
-
Question
What is the percentage of applied voltage that will be dropped across r3=70 if r1=80 and r2=50?

It would be 35%. The higher the resistance, the higher the voltage drop. The ratio of resistances here is 80:50:70. Solving for 70 ohms, we get 35%.
-
Question
What is the voltage of a 60 ohm resistor if the circuit voltage is 150 volts with two parallel 30 ohm resistors and one 60 ohm resister in the series?

Assuming you intend to ask what is the voltage drop across the 60 ohm resistor, the answer is 120v. The two parallel 30 ohm resistors have an equivalent resistance of 15 ohms. 1/(1/30 + 1/30) = 15. The total resistance appears as 75 ohms to the 150v source. Find the circuit current by I = E/R or I = 150/75 = 2 amps. Find the voltage drop for the 60 ohm resistor with E = I x R or E = 2 x 60 = 120V drop across the 60 Ohm resistor.
-
Question
What becomes the Voltage if we use 2 resistors of 4W in parallel?

As any other data is not provided, the voltage across two resistors of 4w in parallel is the same.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
If you have a complicated circuit that involves resistors in series and resistors in parallel, pick two nearby resistors. Find the total resistance across them using the rules for resistors in parallel or in series, as appropriate. Now you can treat them as a single resistor. Keep doing this until you have a simple circuit with resistors either in parallel or in series.[11]
-
The voltage across a resistor is often called a “voltage drop.”
-
Understand the terminology:
- Circuit – composed of elements (e.g. resistors, capacitors, and inductors) connected by wires and wherein current can pass through
- Resistors – elements that can reduce or resist current
- Current – flow of charge into wires; unit: Ampere, A
- Voltage – work done per unit charge; unit: Voltage, V
- Resistance – measurement of the opposition of an element to electric current; unit: Ohm, Ω
Advertisement
References
About This Article
Article SummaryX
To calculate voltage across a resistor in a series circuit, start by adding together all of the resistance values in the circuit. Then, divide the voltage across the circuit by the total resistance to find the current. Once you have the current, calculate voltage for the individual resistors by multiplying the current by the resistance. For example, in a series circuit with 3 resistors of 2, 3 and 5 Ohms, and a voltage of 12 volts, the current would be 12 divided by 10, or 1.2 amperes. For the 2 Ohm resistor, the voltage would be 1.2 times 2, or 2.4 volts. If you want to learn how to calculate voltage in a parallel circuit, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 914,725 times.
Reader Success Stories
-

Mohd Rodzi Mohamad
Aug 26, 2016
“This article is very neatly and clearly explained with illustrations of pictures for better comprehension. Very…” more
Did this article help you?
Что такое падение напряжения на резисторе
Электрический ток, проходя по цепи, испытывает сопротивление, которое может изменяться под воздействием разнообразных условий внешней среды (экстремально низкие температуры или нагрев) и может зависеть от характеристик конкретного проводника. Например, чем тоньше проводник или длиннее – тем оно выше.
На значение его величины влияют следующие факторы:
- сила тока;
- длина проводящих частей;
- напряжение;
- материал проводниковых элементов;
- нагрев (температура);
- площадь поперечного сечения.
Резисторы можно разделить на постоянные, переменные и подстроечные. Главное их отличие друг от друга – возможность изменения показателя сопротивления. Чаще всего встречаются постоянные резисторы – данный показатель в них нельзя изменить, поэтому они и получили такое название. Переменные отличаются тем, что величину сопротивления в них можно настраивать. В подстроечном резисторе её также можно изменять, но отличие данной разновидности в том, что он не рассчитан на частое изменение параметра. Подстроечные резисторы выполняются в более компактном корпусе по сравнению с переменными.
Чтобы вычислить падение напряжения на резисторе, нужно помнить, что снижение нагрузки, приложенной ко всей цепи (то есть, напряжения, подключённого к контуру) может быть получено как для всего контура, так и для любого элемента цепи. Напряжение понижается за счёт сопротивления, которым обладают проводники.
Падение напряжения на резисторе зависит от силы проходящего тока и характеристик проводников. Температура и показатели тока также имеют значение. Например, напряжение, измеренное вольтметром на лампочке, подключённой к сети 220 В, будет немного ниже за счёт сопротивления, которым обладает лампочка.
Источники питания имеют разную величину напряжения. Это значение может превышать то, которое бывает необходимо на выходе. Чтобы нагрузка, которую требуется запитать, не сгорела, часто возникает необходимость в понижении вольтажа, в том числе с помощью резисторов.
Сравнительная таблица напряжений
| Источник питания | Напряжение |
| NiCd аккумулятор | 1,2 В |
| Литий-железо-фосфатный аккумулятор | 3,3 В |
| Батарея типа «Крона» | 9 В |
| Автомобильный аккумулятор | 12 В |
| Аккумулятор для грузовых автомобилей | 24 В |
В этом случае резистор должен уменьшить протекающий по цепи ток. При этом ток не превращается в тепло, происходит именно его ограничение. То есть при включении резистора в цепь ток упадёт – в этом и состоит работа резистора, при совершении которой элемент нагревается.
В общем случае падения напряжения можно рассчитать, используя простую формулу, связывающее показатели между собой.
Но в ряде случаев, например, при параллельном подключении сопротивлений, посчитать необходимую величину уже сложнее. В этом случае по специальной формуле потребуется привести сопротивление параллельных веток к одному числу:
R = R1*R2 / (R1+R2)
При необходимости также учитываются другие сопротивления, суммирующиеся с этим значением (например, сопротивление провода и источника питания).
Физическое определение
Резистор — это элемент, использующийся в электрической цепи и не требующий для своей работы источника питания. Предназначен он для трансформирования силы тока в напряжение и обратно. Кроме этого, он может преобразовывать электрическую энергию в тепловую и ограничивать величину тока. Но перед расчётом падения напряжения на резисторе желательно разобраться в сути этого процесса.
Резистор — весьма распространённый элемент, характеризующийся рядом параметров. Основными из них являются:
- сопротивление;
- величина рассеиваемой энергии;
- рабочее напряжение;
- мощность;
- устойчивость к влиянию окружающей среды;
- паразитная составляющая.
Пассивный электрический элемент обозначается на схеме в виде прямоугольника с двумя выводами из середины его боковых сторон. В центре фигуры может указываться мощность римскими цифрами или чёрточками. Например, вертикальная полоска обозначает выдерживаемую мощность элемента, равную 1 Вт. Перечёркнутый прямоугольник в обозначениях на схеме указывает, что такой резистор является переменным.
Резисторы могут выпускаться с постоянным и переменным сопротивлением. Разновидностью вторых являются подстроечные элементы. Отличие их от переменных заключается лишь в способе установки нужного значения.
На схемах и в технической литературе устройство обозначается латинской буквой R, рядом с которой указывается порядковый номер и его номинал в соответствии с Международной системой единиц (СИ). Например, R12 5 кОм — резистор на пять килоом, расположенный в схеме под 12 номером.
При изготовлении элемента используется резистивный слой, который может быть плёночным или объёмным. Он наносится на диэлектрическое основание, а сверху покрывается защитной плёнкой.
Значение сопротивления
Сопротивление является фундаментальной величиной в электрических процессах. Его значение неизменно связано с током и напряжением. Их общая зависимость описывается с помощью закона Ома: сила тока, возникшая на участке цепи, прямо пропорциональна разности потенциалов между крайними точками этого участка и обратно пропорциональна его сопротивлению. Из этого закона находится сопротивление по следующей формуле:
R = U / I, где:
- R — сопротивление на участке цепи, Ом.
- I — сила тока, проходящая через этот участок, А.
- U — разность потенциалов на узлах части схемы, В.
Фактически же сопротивление элемента определяется его физической структурой и обусловлено колебаниями атомов в кристаллической решётке. Поэтому все материалы различаются на проводники, полупроводники и диэлектрики в зависимости от способности проводить электричество.
Ток — это направленное движение носителей заряда. Для его возникновения необходимо, чтобы вещество имело свободные электроны. Если к такому физическому телу приложить электрическое поле, то перемещаемые им заряды начнутся сталкиваться с неоднородностями структуры. Эти дефекты образуются из-за различных примесей, нарушения периодичности решётки, тепловых флуктуаций. Ударяясь о них, электрон расходует энергию, которая преобразовывается в тепловую. В результате заряд теряет импульс, а величина разности потенциалов уменьшается.
Но закон Ома можно применить не для всех веществ. В электролитах, диэлектриках и полупроводниках линейная зависимость между тремя величинами наблюдается не всегда. Сопротивление таких веществ зависит от физических параметров проводника, а именно — его длины и площади поперечного сечения, при этом оно чувствительно к изменению температуры.
Эта зависимость описывается с помощью формулы R = p * l / S. То есть сопротивление прямо пропорционально длине и обратно пропорционально площади проводника. Величина p называется удельным сопротивлением и определяется типом материала. Его значение берётся из справочника.
Импеданс резистора
Закон Ома применим для идеального резистора, не обладающего паразитными сопротивлениями. Полное сопротивление (импеданс) определяется исходя из эквивалентной схемы. Точный расчёт сопротивления для понижения напряжения необходимо проводить по другим формулам. Эквивалентная схема резистора, кроме активного импеданса, содержит также ёмкостное и индуктивное сопротивление.
Первое приводит к медленному накоплению заряда, который рассеивается при изменении направления тока. Чем больше паразитная ёмкость, тем дольше она заряжается. Соответственно, чем быстрее ток изменяет своё направление, тем меньше его ёмкостное сопротивление. Второе же характеризуется магнитным полем, чье появление мешает току изменять направление, поэтому, чем быстрее ток изменяет своё движение, тем больше становится индуктивное сопротивление.
Импеданс вычисляется по формуле: I = U/Z, где Z = (R2+(Xc-Xl)2)½. Где:
- R — активное значение, R = p*l/s.
- Xc — ёмкостная величина, Хс = 1/w*C.
- Xl — индуктивная величина, Хl = w*C.
- w- циклическая частота, w = 2πƒ.
Зная полное сопротивление резистора, можно точнее рассчитать падение напряжения в нём. Но для измерения паразитных составляющих понадобится использовать узкоспециализированные приборы. В обычных расчётах сопротивление вычисляют, учитывая только его активное значение, а паразитные величины принимают за ничтожно малые.
Характеристика мощности резистора
Мощность электрического тока на участке цепи можно узнать через произведение силы тока для него и напряжения на данном участке. Формула имеет следующий вид:
P= I * U (произведение силы тока и напряжения), где
P – значение мощности (Вт).
Резистор совершает работу по снижению силы тока, при этом он выделяет тепло в окружающее пространство. Но если работа по ограничению тока очень велика и тепло вырабатывается слишком быстро, то он перегреется и может сгореть, так как не будет успевать его рассеивать. Следует учитывать этот момент, подбирая мощность резистора
Важно! Мощность резистора – это очень важный параметр, который обязательно нужно учитывать при разработке электрических схем устройств Мощность резистора характеризуется максимальной величиной силы тока, которую он может выдерживать без перегрева и не выходя из строя.
Схема делителя напряжения на резисторах
Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал.
Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.
Как рассчитать сопротивление для понижения напряжения: формула падения на резисторе

Резистор является одним из самых распространённых элементов в электрической цепи. С его помощью ограничивается ток и изменяется напряжение. Конструируя схемы, часто может понадобится рассчитать сопротивление для понижения напряжения. Это актуально при построении делителей цифровых устройств или блоков питания, поэтому уметь выполнять такие вычисления должен каждый радиолюбитель.
Резистор — это элемент, использующийся в электрической цепи и не требующий для своей работы источника питания. Предназначен он для трансформирования силы тока в напряжение и обратно. Кроме этого, он может преобразовывать электрическую энергию в тепловую и ограничивать величину тока. Но перед расчётом падения напряжения на резисторе желательно разобраться в сути этого процесса.
Резистор — весьма распространённый элемент, характеризующийся рядом параметров. Основными из них являются:
- сопротивление;
- величина рассеиваемой энергии;
- рабочее напряжение;
- мощность;
- устойчивость к влиянию окружающей среды;
- паразитная составляющая.
Пассивный электрический элемент обозначается на схеме в виде прямоугольника с двумя выводами из середины его боковых сторон. В центре фигуры может указываться мощность римскими цифрами или чёрточками. Например, вертикальная полоска обозначает выдерживаемую мощность элемента, равную 1 Вт. Перечёркнутый прямоугольник в обозначениях на схеме указывает, что такой резистор является переменным.
Резисторы могут выпускаться с постоянным и переменным сопротивлением. Разновидностью вторых являются подстроечные элементы. Отличие их от переменных заключается лишь в способе установки нужного значения.
На схемах и в технической литературе устройство обозначается латинской буквой R, рядом с которой указывается порядковый номер и его номинал в соответствии с Международной системой единиц (СИ). Например, R12 5 кОм — резистор на пять килоом, расположенный в схеме под 12 номером.
При изготовлении элемента используется резистивный слой, который может быть плёночным или объёмным. Он наносится на диэлектрическое основание, а сверху покрывается защитной плёнкой.
Значение сопротивления
Сопротивление является фундаментальной величиной в электрических процессах. Его значение неизменно связано с током и напряжением. Их общая зависимость описывается с помощью закона Ома: сила тока, возникшая на участке цепи, прямо пропорциональна разности потенциалов между крайними точками этого участка и обратно пропорциональна его сопротивлению. Из этого закона находится сопротивление по следующей формуле:
R = U / I, где:
- R — сопротивление на участке цепи, Ом.
- I — сила тока, проходящая через этот участок, А.
- U — разность потенциалов на узлах части схемы, В.
Фактически же сопротивление элемента определяется его физической структурой и обусловлено колебаниями атомов в кристаллической решётке. Поэтому все материалы различаются на проводники, полупроводники и диэлектрики в зависимости от способности проводить электричество.
Ток — это направленное движение носителей заряда. Для его возникновения необходимо, чтобы вещество имело свободные электроны. Если к такому физическому телу приложить электрическое поле, то перемещаемые им заряды начнутся сталкиваться с неоднородностями структуры. Эти дефекты образуются из-за различных примесей, нарушения периодичности решётки, тепловых флуктуаций. Ударяясь о них, электрон расходует энергию, которая преобразовывается в тепловую. В результате заряд теряет импульс, а величина разности потенциалов уменьшается.
Но закон Ома можно применить не для всех веществ. В электролитах, диэлектриках и полупроводниках линейная зависимость между тремя величинами наблюдается не всегда. Сопротивление таких веществ зависит от физических параметров проводника, а именно — его длины и площади поперечного сечения, при этом оно чувствительно к изменению температуры.
Эта зависимость описывается с помощью формулы R = p * l / S. То есть сопротивление прямо пропорционально длине и обратно пропорционально площади проводника. Величина p называется удельным сопротивлением и определяется типом материала. Его значение берётся из справочника.
Импеданс резистора
Закон Ома применим для идеального резистора, не обладающего паразитными сопротивлениями. Полное сопротивление (импеданс) определяется исходя из эквивалентной схемы. Точный расчёт сопротивления для понижения напряжения необходимо проводить по другим формулам. Эквивалентная схема резистора, кроме активного импеданса, содержит также ёмкостное и индуктивное сопротивление.
Первое приводит к медленному накоплению заряда, который рассеивается при изменении направления тока. Чем больше паразитная ёмкость, тем дольше она заряжается. Соответственно, чем быстрее ток изменяет своё направление, тем меньше его ёмкостное сопротивление. Второе же характеризуется магнитным полем, чье появление мешает току изменять направление, поэтому, чем быстрее ток изменяет своё движение, тем больше становится индуктивное сопротивление.
Импеданс вычисляется по формуле: I = U/Z, где Z = (R2+(Xc-Xl)2)½. Где:
- R — активное значение, R = p*l/s.
- Xc — ёмкостная величина, Хс = 1/w*C.
- Xl — индуктивная величина, Хl = w*C.
- w- циклическая частота, w = 2πƒ.
Зная полное сопротивление резистора, можно точнее рассчитать падение напряжения в нём. Но для измерения паразитных составляющих понадобится использовать узкоспециализированные приборы. В обычных расчётах сопротивление вычисляют, учитывая только его активное значение, а паразитные величины принимают за ничтожно малые.
Параллельное соединение
В электрических схемах на участках цепи используется как параллельное, так и последовательное соединение. Первое представляет собой цепь, в которой каждый её элемент подключён к другому обоими контактами, но при этом между собственными его выводами нет прямой электрической связи. Т. е. существует две точки (электрические узлы), к которым присоединено несколько резисторов.
При таком включении ток, проходя через узел, начинает разделяться, и через каждый элемент потечёт разное его значение. Величина тока на каждом элементе будет прямо пропорциональна сопротивлению резистора, поэтому общая проводимость на этом участке увеличится, а её импеданс уменьшится.
Формула, с помощью которой можно рассчитать общую проводимость, выглядит так: G = 1/ Rобщ = 1/ R1 + 1/ R2 +…+ 1/ Rn, где n — обозначает порядковый номер резистора в цепи.
Преобразовав эту формулу, получится выражение вида: R общ = 1/G = (R1*R2*…* Rn) / (R1*R2 + R2*Rn +…+ R1*Rn. Проанализировав его, можно сделать вывод, что при параллельном соединении импеданс всегда будет меньше самого маленького значения отдельного резистора.
При таком соединении напряжение между узлами одновременно является общей разностью потенциалов для всего участка и на каждом отдельно взятом резисторе. Поэтому если рассчитать падение напряжения на одном приборе, то оно будет таким же на любом параллельно подключённом элементе: U общ = U 1 = U 2 =…= U n.
А вот электрический ток, проходящий через отдельный элемент, исходя из закона Ома будет равен: I Rn = U Rn / R n.
Последовательное включение
Так называется объединение в один участок цепи двух или более резисторов, в котором их соединение между собой происходит только в одной точке. Импеданс при последовательном включении определяется как сумма сопротивлений каждого отдельного элемента: Rобщ = R1+R2+…+Rn.
Следовательно, ток, протекающий через такую цепочку, будет становиться всё меньше после прохождения через последовательно включённый резистор. Чем будет больше элементов в цепи, тем труднее ему будет пройти их всех. Таким образом, его общее значение определяется как Iобщ = U / (R1+R2+…+Rn).
Поэтому можно утверждать, что в последовательном соединении существует только один путь для протекания тока. Чем будет больше количество резисторов в линии, тем меньше будет ток на этом участке.
Падение разности потенциалов при таком типе соединения на каждом элементе будет иметь своё значение. Оно определяется формулой URn = IRn*Rn, и чем больше будет импеданс элемента, тем больше энергии в нём начнёт выделяться.
Расчёт делителя напряжения
Резистивный делитель напряжения представляет элементарную схему для понижения напряжения. Состоять он может из двух или более элементов. Простейший делитель можно представить в виде двух участков цепи, которые называют плечами. Одно из них, которое располагается между положительной точкой потенциала и нулевой, — верхнее, а другое, между отрицательной и минусовой, — нижнее.
Такая схема используется для снижения напряжения как в постоянных, так и переменных цепях. Суть процесса заключается в следующем.
- На резистивную схему от источника питания подаётся напряжение U.
- Через резисторы последовательного участка цепи, образованного резисторами R1 и R2, начинает протекать ток.
- В результате на каждом из них выделяется какое-то количество энергии, т. е. возникает падение напряжения.
Сумма напряжений на всём размахе линии равняется значению разности потенциалов источника питания. В соответствии с формулой: U = I*R падение напряжения прямо пропорционально силе тока и величине сопротивления. Учитывая, что ток, протекающий через резисторы, одинаковый, справедливыми будут формулы U1 = I*R1 и U2= I*R2.
Тогда общее падение напряжение на участке будет равно U = I *(R1+ R2). Исходя из этого можно найти силу тока: I = U /(R1+ R2). Используя эти два выражения, можно получить окончательные формулы для расчёта падения напряжения на каждом элементе:
- U1 = R1*U/(R1+R2);
- U2 = R2*U/(R1+R2).
Практическое применение такого делителя очень распространено из-за несложности реализации понижения напряжения. Например, пусть источник питания выдаёт 12 В, а на нагрузку необходимо подать 6 В, при этом её сопротивление составляет 10 кОм. Для решения такой задачи рекомендуется использовать резисторы, сопротивление которых в десять раз меньше нагрузочного значения, поэтому, приняв R 1 = 1 кОм и подставив все известные значения в формулу напряжения на резисторе, получится, что 6 = R 2*12 (1000+ R 2) отсюда R 2 = 1 кОм.
Теперь, зная все величины, можно проверить верность расчёта. Падение разности потенциалов на первом элементе высчитывается как U 1 = 1000*12/(1000+1000) = 6 В, а общее напряжение — Uобщ = U 1+ U 2 = 12 В, что соответствует значению источника питания.
Следует отметить, что использование резисторов для понижения используется только при маломощных нагрузках, так как часть энергии превращается в тепло, а коэффициент полезного действия (КПД) очень низкий.
Определение силы тока на резисторе при разных типах соединения
Самым простым способом определить силу тока в резисторе можно воспользовавшись мультиметром. Измерение проводятся в разрыве цепи после резистора. На тестере выставляется максимальный диапазон величин, а щупы прибора подсоединяются к месту разъединения проводника. На дисплее мультиметра будут отображены результаты измерения силы тока в резисторе.
I = U/R, где у нас I – сила тока, U – напряжение, R – сопротивление.
В системе СИ эти величины измеряются в амперах (А), вольтах (В), омах (Ом) соответственно.
Подставляя необходимые значения в формулу можно определить сопротивление, напряжение и силу тока на резисторе или любом участке, или элементе электрической цепи.
Как понизить напряжение с помощью резистора
Чтобы нагрузка, которую требуется запитать, не сгорела, часто возникает необходимость снизить входное напряжение. Проще всего этого можно добиться, используя схему с двумя резисторами, более известную как делитель напряжения. Классическая схема выглядит так:

В этом случае напряжение подаётся на два резистора с использованием параллельного подключени, а на выходе его получают с одного. Подбор номиналов резисторов осуществляют по формуле так, чтобы напряжение, снимаемое на выходе, составляло какую-то часть от подаваемого. Расчет резистора для понижения напряжения можно воспользовавшись формулой, основанной на законе Ома:
Uвых= (Uвх*R2)/(R1+R2), где
Uвх – напряжение на входе, В;
Uвых – напряжение на выходе, В
R1 – показатель сопр. 1-ого резистора (Ом)
R2 – показатель сопр. 2-ого элемента, (Ом)
Подбор резистора для понижения напряжения
Для подбора нужного сопротивления резистора можно воспользоваться готовыми онлайн-калькуляторами или программами для моделирования работы электронных схем. Симуляторы электрических цепей способны не только рассчитать напряжение на выходе в зависимости от сопротивления элементов и способа их подключения, но и обладают функционалом, позволяющим визуализировать то, как падает ток и напряжение на резисторе. Например, приложение EveryCircuit позволяет изменять в схеме параметры элементов, выбирать скорость симуляции, получать данные в различных точках. При этом можно наблюдать за динамикой изменения значений, используя для ввода входных параметров вращающийся лимб в нижнем правом углу.

Существует ещё ряд бесплатных программ для эмуляции, позволяющие выполнить, в том числе, расчёт резистора при понижении напряжения, например:
- EasyEDA;
- Circuit Sims;
- DcAcLab;
и другие.
В статье мы ознакомились с понятием сопротивления, узнали о его единицах измерения, о маркировке резисторов, о программах эмулирующих работу цепи и облегчающих подбор нужного сопротивления, а также рассмотрели примеры расчёта падения напряжения на резисторе.
Какое напряжение после резистора

Есть другой способ снижения напряжения на нагрузке, но только для цепей постоянного тока. Про смотри здесь.
Вместо дополнительного резистора используют цепочку из последовательно включенных, в прямом направлении, диодов.
Весь смысл состоит в том, что при протекании тока через диод на нем падает «прямое напряжение» равное, в зависимости от типа диода, мощности и тока протекающего через него — от 0,5 до 1,2 Волта.
На германиевом диоде падает напряжение 0,5 — 0,7 В, на кремниевом от 0,6 до 1,2 Вольта. Исходя из того, на сколько вольт нужно понизить напряжение на нагрузке, включают соответствующее количество диодов.
Чтобы понизить напряжение на 6 В необходимо приблизительно включить: 6 В: 1,0 = 6 штук кремниевых диодов, 6 В: 0,6 = 10 штук германиевых диодов. Наиболее популярны и доступны кремниевые диоды.
Выше приведенная схема с диодами, более громоздка в исполнении, чем с простым резистором. Но, выходное напряжение, в схеме с диодами, более стабильно и слабо зависит от нагрузки. В чем разница между этими двумя способами снижения выходного напряжения?
У резистора (проволочного сопротивления) линейная зависимость между током, проходящем через него и падением напряжения на нем. Во сколько раз увеличится ток, во столько же раз увеличится и падение напряжения на резисторе.
Из примера 1: если мы к лампочке подключим параллельно еще одну, то ток в цепи увеличится, с учетом общего сопротивления двух лампочек до 0,66 А. Падение напряжения на добавочном резисторе будет: 12 Ом *0,66 А = 7,92 В. На лампочках останется: 12 В — 7,92 В = 4,08 В. Они будут гореть в пол накала.
Совсем другая картина будет если вместо резистора будет цепочка диодов.
Зависимость между током протекающем через диод и падающем на нем напряжении нелинейная. Ток может увеличиться в несколько раз, падение напряжения на диоде увеличится всего на несколько десятых вольта.
Т.е. чем больше ток диода, тем (сравнительно с резистором) меньше увеличивается его сопротивление. Падение напряжения на диодах мало зависит от тока в цепи.
Диоды в такой цепи выполняют роль стабилизатора напряжения. Диоды необходимо подбирать по максимальному току в цепи. Максимально допустимый ток диодов должен быть больше, чем ток в рассчитываемой цепи.
Падения напряжения на некоторых диодах при токе 0,5 А даны в таблице.
В цепях переменного тока, в качестве добавочного сопротивления можно использовать конденсатор, индуктивность, динистор или тиристор (с добавлением схемы управления).
Для человека, который знаком с электрооборудованием на уровне простого пользователя (знает, где и как включить/выключить), многие используемые электриками термины кажутся какой-то бессмыслицей. Например, чего только стоит «падение напряжения» или «сборка схемы». Куда и что падает? Кто разобрал схему на детали? На самом же деле, физический смысл происходящих процессов, скрывающийся за большинством этих слов, вполне доступен для понимания даже со школьными знаниями физики.
Чтобы объяснить, что такое падение напряжения, необходимо вспомнить, какие вообще напряжения бывают в (имеется в виду глобальная классификация). Их всего два вида. Первый — это напряжение который подключен к рассматриваемому контуру. Оно может также называться приложенным ко всей цепи. А второй вид — это именно падение напряжения. Может быть рассмотрено как в отношении всего контура, так и любого отдельно взятого элемента.
На практике это выглядит следующим образом. Например, если взять обычную вкрутить ее в патрон, а провода от него подключить в домашнюю сетевую розетку, то приложенное к цепи (источник питания — проводники — нагрузка) напряжение составит 220 Вольт. Но стоит нам с помощью вольтметра замерять его значение на лампе, как станет очевидно, что оно немного меньше, чем 220. Так произошло потому, что возникло падение напряжения на которым обладает лампа.
Пожалуй, нет человека, который не слышал бы о законе Ома. В общем случае формулировка его выглядит так:
где R — активное сопротивление цепи или ее элемента, измеряется в Омах; U — электрическое напряжение, в Вольтах; и, наконец, I — ток в Амперах. Как видно, все три величины непосредственно связаны между собой. Поэтому, зная любые две, можно довольно просто вычислить третью. Конечно, в каждом конкретном случае придется учесть род тока (переменный или постоянный) и некоторые другие уточняющие характеристики, но основа — вышеуказанная формула.
Электрическая энергия — это, фактически, движение по проводнику отрицательно заряженных частиц (электронов). В нашем примере спираль лампы обладает высоким сопротивлением, то есть замедляет перемещающиеся электроны.
Благодаря этому возникает видимое свечение, но общая энергия потока частиц снижается. Как видно из формулы, с уменьшением тока уменьшается и напряжение. Именно поэтому результаты замеров у розетки и на лампе различаются. Эта разница и является падением напряжения.
Данная величина всегда учитывается, чтобы предотвратить слишком большое снижение на элементах в конце схемы.
Падение напряжения на резисторе зависит от его и силы протекающего по нему тока. Также косвенное влияние оказывают температура и характеристики тока. Если в рассматриваемую цепь включить амперметр, то падение можно определить умножением значения тока на сопротивление лампы.
Но далеко не всегда удается вот так просто с помощью простейшей формулы и измерительного прибора выполнить расчет падения напряжения. В случае параллельно подключенных сопротивлений нахождение величины усложняется. На приходится дополнительно учитывать реактивную составляющую.
Рассмотрим пример с двумя параллельно включенными резисторами R1 и R2. Известно сопротивление провода R3 и источника питания R0. Также дано значение ЭДС — E.
Приводим параллельные ветки к одному числу. Для этой ситуации применяется формула:
R = (R1*R2) / (R1+R2)
Определяем сопротивление всей цепи через сумму R4 = R+R3.
Рассчитываем ток:
Остается узнать значение падение напряжения на выбраном элементе:
Здесь множитель «R5» может быть любым R — от 1 до 4, в зависимости от того, какой именно элемент схемы нужно рассчитать.
Итак, резистор… Базовый элемент построения электрической цепи.
Работа резистора заключается в ограничении тока, протекающего по цепи. НЕ в превращении тока в тепло, а именно в ограничении тока. То есть, без резистора по цепи течет большой ток, встроили резистор – ток уменьшился. В этом заключается его работа, совершая которую данный элемент электрической цепи выделяет тепло.
Пример с лампочкой
Рассмотрим работу резистора на примере лампочки на схеме ниже. Имеем источник питания, лампочку, амперметр, измеряющий ток, проходящий через цепь. И Резистор. Когда резистор в цепи отсутствует, через лампочку по цепи побежит большой ток, например, 0,75А.
Лампочка горит ярко. Встроили в цепь резистор — у тока появился труднопреодолимый барьер, протекающий по цепи ток снизился до 0,2А. Лампочка горит менее ярко. Стоит отметить, что яркость, с которой горит лампочка, зависит так же и от напряжения на ней. Чем выше напряжение — тем ярче.
Кроме того, на резисторе происходит падение напряжения. Барьер не только задерживает ток, но и «съедает» часть напряжения, приложенного источником питания к цепи. Рассмотрим это падение на рисунке ниже. Имеем источник питания на 12 вольт.
На всякий случай амперметр, два вольтметра про запас, лампочку и резистор. Включаем цепь без резистора(слева). Напряжение на лампочке 12 вольт. Подключаем резистор — часть напряжения упала на нем. Вольтметр(снизу на схеме справа) показывает 5В.
На лампочку остались остальные 12В-5В=7В. Вольтметр на лампочке показал 7В.
Разумеется, оба примера являются абстрактными, неточными в плане чисел и рассчитаны на объяснение сути процесса, происходящего в резисторе.
Единица измерения сопротивления резистора
Основная характеристика резистора — сопротивление. Единица измерения сопротивления — Ом (Ohm, Ω). Чем больше сопротивление, тем больший ток он способен ограничить, тем больше тепла он выделяет, тем больше напряжения падает на нем.
Закон Ома для электрической цепи
Основной закон всего электричества. Связывает между собой Напряжение(V), Силу тока(I) и Сопротивление(R).
Интерпретировать эти символы на человеческий язык можно по-разному. Главное — уметь применить для каждой конкретной цепи. Давайте используем Закон Ома для нашей цепи с резистором и лампочкой, рассмотренной выше, и рассчитаем сопротивление резистора, при котором ток от источника питания на 12В ограничится до 0,2. При этом считаем сопротивление лампочки равным 0.
V=I*R => R=V/I => R= 12В / 0,2А => R=60Ом
Итак. Если встроить в цепь с источником питания и лампочкой, сопротивление которой равно 0, резистор номиналом 60 Ом, тогда ток, протекающий по цепи, будет составлять 0,2А.
Характеристика мощности резистора
Микропрогер, знай и помни! Параметр мощности резистора является одним из наиболее важных при построении схем для реальных устройств.
Мощность электрического тока на каком-либо участке цепи равна произведению силы тока, протекающую по этому участку на напряжение на этом участке цепи. P=I*U. Единица измерения 1Вт.
При протекании тока через резистор совершается работа по ограничению электрического тока. При совершении работы выделяется тепло. Резистор рассеивает это тепло в окружающую среду. Но если резистор будет совершать слишком большую работу, выделять слишком много тепла — он перестанет успевать рассеивать вырабатывающееся внутри него тепло, очень сильно нагреется и сгорит. Что произойдет в результате этого казуса, зависит от твоего личного коэффициента удачи.
Характеристика мощности резистора — это максимальная мощность тока, которую он способен выдержать и не перегреться.
Расчет мощности резистора
Рассчитаем мощность резистора для нашей цепи с лампочкой. Итак. Имеем ток, проходящий по цепи(а значит и через резистор), равный 0,2А.
Падение напряжения на резисторе равно 5В (не 12В, не 7В, а именно 5 — те самые 5, которые вольтметр показывает на резисторе). Это значит, что мощностьтока через резистор равна P=I*V=0,2А*5В=1Вт.
Делаем вывод: резистор для нашей цепи должен иметь максимальную мощность не менее(а лучше более) 1Вт. Иначе он перегреется и выйдет из строя.
Соединение резисторов
Резисторы в цепях электрического тока имеют последовательное и параллельное соединение.
При последовательном соединении общее сопротивление резисторов является суммой сопротивлений каждого резистора в соединении:
При параллельном соединении общее сопротивление резисторов рассчитывается по формуле:
Источники
- https://math-nttt.ru/teoriya/raschet-padeniya-napryazheniya-na-rezistore.html
- https://ugstroialyans.ru/podbor-rezistora-dlya-ponizheniya-napryazheniya/
- https://strop-snab.ru/teoriya/ponizhenie-napryazheniya-rezistorom.html
- https://1000eletric.com/kak-rasschitat-padenie-napryazheniya-na-rezistore/
Как вам статья?

Павел
Бакалавр “210400 Радиотехника” – ТУСУР. Томский государственный университет систем управления и радиоэлектроники
Написать
Пишите свои рекомендации и задавайте вопросы
Задача
N10.2
Расчет
погрешности измерения в цепи переменного
тока
1.
Цель задачи.
Целью
данной задачи является научиться
рассчитывать методическую и инструментальную
погрешности измерения напряжения в
цепи переменного тока. Студенты должны
оценить влияние входного сопротивления
и входной емкости вольтметра на
методическую погрешность.
2.
Состав условия задачи
Имеется
делитель напряжения, состоящий из
последовательно включенных резисторов
R1 и R2, как это показано на рисунке 1

Рисунок 1. Электрическая схема делителя
напряжения
На
делитель напряжения подано переменное
напряжение с действующим значением U
и частотой f.
К резистору R2 подключен аналоговый
многопредельный вольтметр с внутренним
сопротивлением RV
на пределе измерения Uпр,
как показано на рисунке 2.

Рисунок 2. Электрическая схема делителя
напряжения с подключенным вольтметром
В
условии задачи приводятся также значения
входной емкости вольтметра и соединительных
проводов С, а также класса точности
вольтметра Кт.
Студенту
предлагается определить среднеквадратическую
относительную погрешность измерения
напряжения на резисторе R2,
обусловленную классом точности вольтметра
и методической погрешностью.
3. Порядок решения задачи
Решение задачи будет состоять из
следующих этапов:
1) расчет значения напряжения на резисторе
R2 для случая, когда к
делителю напряжения не подключен
вольтметр;
2) составление эквивалентной схемы
делителя напряжения с подключенным
вольтметром;
3) расчет эквивалентного сопротивления
нижней части делителя напряжения с
подключенным вольтметром;
4) расчет значения напряжения на резисторе
R2 для случая, когда к
делителю напряжения подключен вольтметр;
5) расчет методической погрешности
измерения напряжения на резисторе R2
для случая, когда к делителю напряжения
подключен вольтметр;
6) расчет погрешности измерения напряжения
на резисторе R2, обусловленной
классом точности вольтметра;
7)
расчет среднеквадратической относительной
погрешности измерения напряжения на
резисторе R2,
обусловленной классом точности вольтметра
и методической погрешностью.
Рассмотрим
указанные этапы более подробно.
3.1.1. Определим ток, протекающий по
резисторам R1 и R2,
когда к схеме не подключен вольтметр.
![]() , (1)
, (1)
где IR1nV
– ток, протекающий по резисторам R1
и R2, когда к схеме не
подключен вольтметр;
U
– напряжение, поданное на делитель
напряжения.
3.1.2. Определим падение напряжения на
резисторе R2, когда к схеме
делителя напряжения не подключен
вольтметр.
UR2nV=
IR1nV
·R2, (2)
где UR2nV
– падение напряжения на резисторе R2,
когда к схеме не подключен вольтметр.
Решая совместно уравнения (1) и (2), получим
![]() . (3)
. (3)
3.2. Составление эквивалентной схемы делителя напряжения с подключенным вольтметром;
Согласно условию задачи к резистору R2
подключен вольтметр. Электрическая
схема делителя напряжения с подключенным
вольтметром показана на рисунке 2.
Идеальный
вольтметр (вольтметр с бесконечно
большим входным сопротивлением и
бесконечно малой входной ёмкостью)
показал бы значение напряжения, равное
UR2nV.
Однако в данной задаче вольтметр имеет
входное сопротивление RV
и входную емкость С. В этом случае
параллельно резистору R2
подключаются активное и реактивное
сопротивления вольтметра, как показано
на рисунке 3.

Рисунок 3. Эквивалентная схема делителя
напряжения с подключенным вольтметром
Анализ схемы, представленной на рисунке
3, говорит о том, что в схеме присутствуют
активные сопротивления (резисторы R1,
R2 и входное сопротивление
вольтметра RV)
и реактивное сопротивление (входная
емкость вольтметра и емкость подводящих
проводов С). Это обстоятельство необходимо
учитывать в дальнейших расчетах.
3.3. Расчет эквивалентного сопротивления нижней части делителя напряжения с подключенным вольтметром
Для расчета полного сопротивления
нижней части делителя напряжения с
учетом того, что в сопротивлении
вольтметра присутствует реактивная
составляющая используем следующую
методику.
3.3.1. Определим эквивалентное активное
сопротивление параллельно включенных
резистора R2 и входного
активного сопротивления вольтметра RV
Rэ
= R2·RV/(R2+RV).
3.3.2. Определим круговую частоту источника
переменного напряжения
ω=2·π·f.
3.3.3. Определим эквивалентное полное
комплексное сопротивление нижней части
делителя напряжения с подключенным
вольтметром.
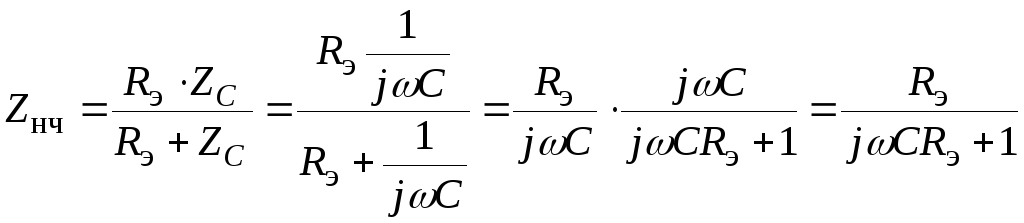 .
.
где ZC=1/(jωC)
– комплексное сопротивление конденсатора
С на частоте f.
Чтобы выделить действительную и мнимую
части полученного выражения, умножим
числитель и знаменатель на число,
сопряженное со знаменателем
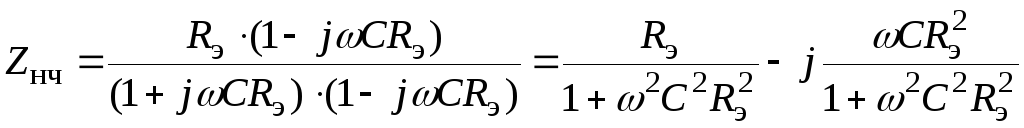 . (4)
. (4)
Чтобы упростить выражение (4), введем
вспомогательные коэффициенты:
![]() ,
,
 .
.
В результате эквивалентное полное
комплексное сопротивление нижней части
делителя напряжения с подключенным
вольтметром будет иметь вид
Zнч=F–jG.
3.4. Расчет значения напряжения на резисторе r2 для случая, когда к делителю напряжения подключен вольтметр
3.4.1. Определим эквивалентное полное
комплексное сопротивление делителя
напряжения с подключенным вольтметром.
Zдн=R1+Zнч=(R1+F)-jG.
Обозначим действительную часть
полученного выражения через коэффициент
А, т.е.
A=R1+F.
В результате эквивалентное полное
комплексное сопротивление делителя
напряжения с подключенным вольтметром
будет иметь вид
Zдн=А-jG.
3.4.2. Определим комплексное значение
тока, протекающего по делителю напряжения
с подключенным к нему вольтметром
![]() . (6)
. (6)
Чтобы упростить выражение (7), введем
вспомогательные коэффициенты:
![]() ,
,
![]() .
.
В результате комплексное значение тока,
протекающего по делителю напряжения с
подключенным к нему вольтметром, будет
иметь вид
Iдн=М+jN.
3.4.3 Определим падение напряжения на
резисторе R2, когда к схеме
делителя напряжения подключен вольтметр.
UR2V=
Iдн·Zнч=(M+jN)·(F–jG)=(FM+GN)+j(NF–GM).
3.4.4. Определим модуль напряжения на
резисторе R2, когда к схеме
делителя напряжения подключен вольтметр.
![]() .
.
Соседние файлы в папке задачи
- #
- #
- #
В этой статье обсуждалось, как легко найти напряжение на резисторе, например, в последовательной комбинации, параллельной комбинации и других комбинациях цепей.
Напряжение на любом резисторе можно определить:
- Различные законы или правила цепи, такие как закон Кирхгофа, правило деления тока или деления напряжения.
- Эквивалентное сопротивление требуемой части схемы.
- Путем определения характеристик или функций всей цепи или ее части.
Как найти напряжение на последовательном резисторе ?
Цепь последовательного резистора имеет только один путь или ветвь для протекания токов цепи. Все резисторы подключены к одному пути или ветви схемы в этом типе соединения схемы.
Падение напряжения на любом последовательное сочетание сопротивлений может варьироваться в зависимости от общего или отдельного номинала резистора.
Предполагая, что к последовательной комбинации подключено более одного резистора, вся комбинация сопротивлений может быть заменена одним резистором эквивалентного сопротивления. Предположим, резистор в последовательная схема имеет одинаковые значения. В этом случае падение напряжения (или падение электрического потенциала) на каждом резисторе можно определить, поскольку ток, протекающий через каждый резистор в цепи, одинаков.
Общее падение напряжения в любой цепи последовательного резистора равно сумме падений напряжения или потенциала на каждом отдельном резисторе в комбинации последовательных цепей.
В каком типе комбинации резисторов общее напряжение цепи делится между различными резисторами последовательная схема комбинация. Величина напряжения на каждом резисторе зависит от значения сопротивления соответствующего резистора, чтобы найти величину тока, протекающего через резистор.
Предположим, что имеется несколько резисторов, соединенных последовательно, и V1, V2, V3 … Вn человек падение напряжения на каждом резисторе в последовательной цепи комбинации, то общее падение напряжения в последовательной цепи можно обозначить как
В = В1 +V2 +V3 . . . +Вn
Чтобы определить общее или общее эквивалентное сопротивление последовательной комбинации n резисторов, используйте формулу:
Re = R1+ R2 + R3……+Рn
Где Re – эквивалентное или общее сопротивление комбинации последовательных сопротивлений
R1, R2, R3. . . . .Рn сопротивление отдельных резисторов, включенных в последовательную цепь из n резисторов.
Как найти напряжение на резисторе параллельно ?
Любая цепь может быть образована последовательно или параллельно комбинацией последовательного и параллельная цепь дизайн.
Компания падение напряжения (или электрического потенциала падение) на параллельном резисторе можно легко определить или рассчитать по формуле учитывая характеристики параллельной цепи сопротивления, поскольку падение напряжения или падение электрического потенциала на каждом пути или ветви в параллельной комбинации одинаково.
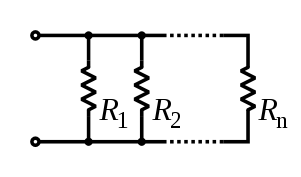
Ток, протекающий через каждую ветвь в комбинации параллельных цепей, можно определить по общему сопротивлению на пути или ветви цепи. Общий ток в цепи равен сумме мгновенных токов, протекающих через отдельные ветви в комбинации параллельных цепей. Если к параллельной цепи подключено более одного резистора, то эти резисторы можно заменить только одним резистором эквивалентной величины.
Цепь называется комбинацией параллельных цепей резистора, когда несколько сопротивлений соединяют два узла цепи, обеспечивая несколько путей для протекания тока.
Ток через каждое сопротивление также можно определить по формуле текущее правило делителя поскольку ток во всей цепи разделяется на все ветви в любой параллельной цепи резистора. Общая мощность, рассеиваемая в параллельной комбинации, пропорциональна сумме отдельных мгновенных мощностей, рассеиваемых любым регистром в параллельной комбинации цепей.
Как известно, общее напряжение в комбинации параллельных цепей сопротивления имеет ту же величину, что и постоянное падение электрического потенциала на каждом пути или ветви параллельной цепи сопротивления.
Предположим, что если имеется несколько ветвей в параллельном соединении сопротивлений, то V1, V2, V3, … являются индивидуальным падением напряжения на общем сопротивлении каждой ветви в параллельном соединении.
Затем V1 + V2…. = Вн
Например, предположим, что более одного резистора соединены параллельно. Значения сопротивления могут быть одинаковыми или разными в любом параллельная цепь комбинация. Предположим, что два резистора одинакового сопротивления соединены параллельно друг с другом. В этом случае токи, протекающие через них, будут одинаковыми по величине и с эквивалентным сопротивлением и правилом деления тока. Применив закон Ома, мы можем получить напряжение на каждом сопротивлении параллельно.
Предположим, что два резистора R1 и R2 имеют разные сопротивления, соединенные параллельно. Ток, протекающий через каждое сопротивление, может быть независим друг от друга.
После расчета тока через каждую ветвь по правилу деления тока и нахождения значения эквивалентного сопротивления всей цепи можно рассчитать с помощью закона Ома, можно определить напряжение на каждом сопротивлении.
Уравнение эквивалентного сопротивления в параллельная комбинация с резистором:
1 / Рe = 1 / R1 + 1 / R2 + 1 / R3 …+1/рn
Где Re Эквивалент сопротивление параллели Комбинация контуров.
R1, R2, R3… Различные резисторы, соединенные параллельно.
Когда два параллельно соединенных резистора (R) имеют одинаковое значение, эквивалентное сопротивление обоих резисторов составляет половину сопротивления одного резистора (R).
Как найти напряжение на резисторе в цепи RL?
Цепь RL содержит по крайней мере один резистор и катушку индуктивности в схеме параллельно или комбинация серий.
Падение напряжения на резисторе в цепи RL можно получить (или определить), применив закон Кирхгофа. Генерируется дифференциальное уравнение первого порядка, состоящее из падения напряжения на катушке индуктивности и резисторе.

Для любой RL-цепи падение напряжения на резисторе можно определить по протекающему через него току вместе с известным номиналом резистора с помощью закона Ома.
Для цепи серии RL
Vr = R/Rs + Ir
Для параллельной цепи RL
Ir = Vr (R/Rs)
Как найти максимальное напряжение на резисторе?
Каждый резистор имеет максимальную номинальную мощность, что означает, что это максимальная мощность, которую можно передать конкретному резистору без его повреждения.
Из текущего соотношения мощностей P = I2R, где R в этом случае считается постоянным), и путем обеспечения максимальной мощности резистора с учетом максимальной номинальной мощности этого конкретного резистора можно измерить максимальное напряжение на резисторе.
Как найти напряжение на резисторе в комбинированной цепи?
Комбинированная схема представляет собой комбинацию или смесь как последовательных, так и параллельных цепей вместе.

- Анализ комбинированной цепи возможен путем разрыва возможной комбинации параллельной и последовательной цепей.
- И после разбивки всей комбинации на разные части анализ или эквивалент этих конкретных частей можно рассчитать отдельно.
- Затем можно рассчитать общий эквивалент всей комбинации цепей после объединения эквивалентов всех частей (которые рассчитывались отдельно).
- Применяя закон Ома, закон Кирхгофа, можно определить падение напряжения на любом компоненте цепи.
Как найти среднеквадратичное напряжение на резисторе?
Среднеквадратичное значение напряжения означает среднеквадратичное напряжение Цепь переменного тока, где среднеквадратичное значение обозначает эквивалентную рассеиваемую мощность цепи постоянного тока.
В одном из AC цепи, среднеквадратичное напряжение может быть рассчитано по размаху напряжения цепи переменного тока. Закон Ома, закон Кирхгофа и другие законы цепи могут быть применены к цепи переменного тока для расчета мгновенного напряжения или тока через резистор.
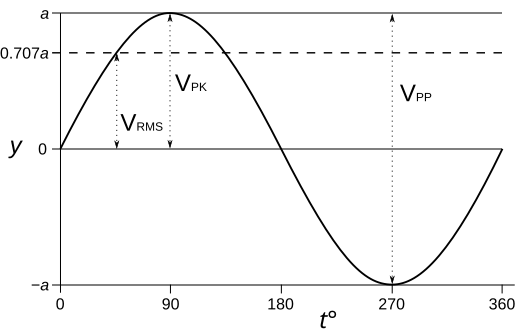
Пусть Vr — мгновенное напряжение на резисторе, тогда Vr = Vp sin ωt.
Ir — мгновенный ток через резистор, тогда Ir = Vr/R = Vr / Sin ωt
Таким образом, напряжение на резисторе можно определить как Vr = Ir sin ωt.
Как найти напряжение на нагрузочном резисторе?
Нагрузочный резистор представляет собой пассивный элемент схемы с двумя выводами, которые имеют некоторое значение сопротивления.
Падение напряжения на сопротивлении нагрузки можно определить, определив комбинацию цепей и применив требуемые законы цепи, такие как закон Ома, закон Кирхгофа и т. д. При необходимости эквивалентную цепь можно создать с помощью простых расчетов.
