Алгоритмизация и программирование
Алгоритмы, виды алгоритмов, описание алгоритмов. Формальное исполнение алгоритмов
Термин «алгоритм», впервые употребленный в современном значении. Лейбницем (1646–1716), является латинизированной формой имени великого персидского математика Мухаммеда бен Муссы аль-Хорезми (ок. 783 – ок. 850). Его книга «Об индийском счете» в XII в. была переведена на латинский язык и пользовалась широкой популярностью не одно столетие. Имя автора европейцы произносили как Алгоритми (Algorithmi), и со временем так стали называть в Европе всю систему десятичной арифметики.
Научное определение алгоритма дал А. Чёрч в 1930 году. В наше время понятие алгоритма является одним из основополагающих понятий вычислительной математики и информатики.
Алгоритм — это точное и полное описание последовательности действий над заданными объектами, позволяющее получить конечный результат.
Можно сказать, что алгоритм решения какой-либо задачи — это последовательность шагов реализации (или нахождения) этого решения, а процесс построения алгоритма (алгоритмизация) — разложение задачи на элементарные действия или операции.
Область математики, известная как теория алгоритмов, посвящена исследованию свойств, способов записи, области применения различных алгоритмов, а также созданию новых алгоритмов. Теория алгоритмов находит широкое применение в различных областях деятельности человека — в технике, производстве, медицине, образовании и т. д. Появление компьютера позволило решать чрезвычайно сложные, трудоемкие задачи.
Определение алгоритма для применения в области информатики нуждается в некотором уточнении. Во-первых, решение задач в информатике всегда связано с преобразованием информации, а значит, исходными данными и результатом работы алгоритма должна быть информация. Это может быть представлено в виде схемы.

Во-вторых, алгоритмы в информатике предназначены для реализации в виде компьютерных программ или для создания некоторой компьютерной технологии. Для выполнения алгоритма требуется конечный объем оперативной памяти и конечное время.
Основные требования, предъявляемые к алгоритмам:
Дискретность (прерывность): алгоритм должен представлять решение задачи в виде последовательности простых (или ранее определенных) этапов (шагов). Каждый шаг алгоритма формулируется в виде инструкций (команд).
Определенность (детерминированность; лат. determinate — определенность, точность): шаги (операции) алгоритма должны допускать однозначную трактовку и быть понятными для исполнителя алгоритма. Это свойство указывает на то, что любое действие в алгоритме должно быть строго определено и описано для каждого случая.
Массовость: алгоритм должен давать решение не только для конкретного набора значений, а для целого класса задач, который определяется диапазоном возможных исходных данных (область применимости алгоритма). Свойство массовости подразумевает использование переменных в качестве исходных данных алгоритма.
Результативность: алгоритм должен давать конкретный результат, т. е. должны быть рассмотрены все возможные ситуации и для каждой из них получен результат. Под результатом может пониматься и сообщение о том, что задача решения не имеет.
Конечность: количество шагов алгоритма должно быть конечным.
Эффективность: количество шагов и сами шаги алгоритма должны быть такими, чтобы решение могло быть найдено за конечное и, более того, приемлемое время.
Для оценки и сравнения алгоритмов существует много критериев. Чаще всего анализ алгоритма (или, как говорят, анализ сложности алгоритма) состоит в оценке временных затрат на решение задачи в зависимости от объема исходных данных. Используются также термины «временная сложность», «трудоемкость» алгоритма. Фактически эта оценка сводится к подсчету количества основных операций в алгоритме, поскольку каждая из них выполняется за заранее известное конечное время. Кроме временной сложности, должна оцениваться также емкостная сложность, т. е. увеличение затрат памяти в зависимости от размера исходных данных. Оценка сложности дает количественный критерий для сравнения алгоритмов, предназначенных для решения одной и той же задачи. Оптимальным (наилучшим) считается алгоритм, который невозможно значительно улучшить в плане временных и емкостных затрат.
Анализом сложности алгоритмов, исследованием классов задач, решаемых с помощью алгоритмов той или иной сложности, и многими другими теоретическими вопросами занимается специальная область информатики.
Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых элементов.
Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур:
- следование — образуется из последовательности действий, следующих одно за другим;
- ветвление (развилка) — обеспечивает в зависимости от результатов проверки условия (ДА или НЕТ) выбор одного из альтернативных путей алгоритма;
- цикл — обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла.
Для описания алгоритмов наиболее распространены следующие методы (языки):
Обычный язык. Изложение алгоритма ведется на обычном языке с разделением на последовательные шаги.
Блок-схемы. Графическое изображение алгоритма с помощью специальных значков-блоков.
Формальные алгоритмические языки (языки программирования). При записи алгоритмов используют строго определенный набор символов и составленных из них специальных зарезервированных слов. Имеют строгие правила построения языковых конструкций.
Псевдокод. Синтез алгоритмического и обычного языков. Элементы некоторого базового алгоритмического языка используются для строгой записи базовых структур алгоритма.
Словесный способ (запись на обычном языке) не имеет широкого распространения, т. к. таких описаний есть ряд недостатков:
- строго не формализуемы;
- достаточно многословны;
- могут допускать неоднозначность толкования отдельных предписаний;
- сложные задачи с анализом условий, с повторяющимися действиями трудно представляются в словесной или словесно-формульной форме.
Графический способ представления информации является более наглядным и компактным по сравнению со словесным. При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Такое графическое представление алгоритма называется блок-схемой. Определенному типу действия (ввод/вывод данных, проверка условия, вычисление выражения, начало и конец алгоритма и т. п.) соответствует определенная геометрическая фигура — блочный символ. Блоки соединяются между собой линиями переходов, которые определяют очередность выполнения действий.
| Название символа | Графическое изображение | Комментарии |
| Пуск/Останов (блоки начала и конца алгоритма) |  |
Указание на начало или конец алгоритма |
| Ввод/Вывод данных (блоки ввода, вывода |  |
Организация ввода/вывода в общем виде |
| Процесс (операторные блоки) |  |
Выполнение вычислительного действия или последовательности действий (можно объединять в один блок), которые изменяют значение, форму представления или размещение данных |
| Условие (условный блок) | 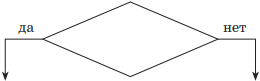 |
Выбор направления выполнения алгоритма. Если условие, записанное внутри ромба, выполняется, то управление передается по стрелке «да», в противном случае — по стрелке «нет». Таким образом, реализуется процесс изменения последовательности вычислений в зависимости от выполнения условия |
| Начало цикла с параметром |  |
Используется для организации циклических конструкций с известным количеством итераций (повторений) и известным шагом изменения параметра цикла. Внутри блока для параметра цикла указываются через запятую его начальное значение, конечное значение и шаг изменения. Цикл, для которого неизвестно количество повторений, записывается с помощью условного и операторных блоков |
| Предопределенный процесс |  |
Используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращения к библиотечным подпрограммам |
| Печать сообщений (документ) |  |
Вывод результатов на печать |
При составлении блок-схемы необходимо проверять выполнение следующих условий:
- из каждого прямоугольника и параллелограмма (кроме конца алгоритма) должна выходить только одна стрелка;
- в каждый прямоугольник и параллелограмм (кроме начала алгоритма) должна входить хотя бы одна стрелка;
- в каждый ромб должна входить хотя бы одна стрелка, а выходить из него — две стрелки, помеченные словами «ДА» и «НЕТ».
Псевдокод занимает промежуточное положение между естественным языком и языками программирования. В псевдокоде не приняты строгие синтаксические правила для записи команд, что отличает формальные языки программирования. Однако в псевдокоде есть некоторые конструкции, которые присущи формальным языкам, что облегчает переход от записи алгоритма на псевдокоде к записи алгоритма на языке программирования. Псевдокоды бывают разные. Рассмотрим учебный (школьный) алгоритмический язык АЯ.
Алфавит учебного алгоритмического языка является открытым. В него могут быть введены любые понятные всем символы: русские и латинские буквы, знаки математических операций, знаки отношений, специальные знаки и т. д. Кроме алфавита, в алгоритмической нотации определяются служебные слова, которые являются неделимыми. Служебные слова обычно выделяются жирным шрифтом или подчеркиванием. К служебным словам относятся:
| алг — заголовок алгоритма | нц — начало цикла | знач |
| нач — начало алгоритма | кц — конец цикла | и |
| кон — конец алгоритма | дано | или |
| арг — аргумент | надо | не |
| рез — результат | если | да |
| цел — целый | то | нет |
| сим — символьный | иначе | при |
| лит — литерный | всё | выбор |
| лог — логический | пока | утв |
| вещ — вещественный | для | ввод |
| таб — таблица | от | вывод |
| длин — длина | до |
Общий вид записи алгоритма на псевдокоде:
алг — название алгоритма (аргументы и результаты)
дано — условие применимости алгоритма
надо — цель выполнения алгоритма
нач — описание промежуточных величин
последовательность команд (тело алгоритма)
кон
Часть алгоритма от слова алг до слова нач называется заголовком, а часть, заключенная между словами нач и кон, — телом алгоритма (исполняемой частью алгоритма).
В предложении алг после названия алгоритма в круглых скобках указываются характеристики (арг, рез) и тип значения (цел, вещ, сим, лит или лог) всех входных (аргументы) и выходных (результаты) переменных. При описании массивов (таблиц) используется служебное слово таб, дополненное именем массива и граничными парами по каждому индексу элементов массива.
Команды учебного языка:
1. Оператор присваивания, который обозначается «:=» и служит для вычисления выражений, стоящих справа, и присваивания их значений переменным, указанным в левой части. Например, если переменная а имела значение 5, то после выполнения оператора присваивания а := а + 1, значение переменной а изменится на 6.
2. Операторы ввода/вывода:
ввод (список имен переменных)
вывод (список вывода)
Список вывода может содержать комментарии, которые заключаются в кавычки.
3. Оператор ветвления (с использованием команды если…то… иначе…всё; выбор);
4. Операторы цикла (с использованием команд для, пока, до).
Запись алгоритма на псевдокоде:

Здесь в предложениях дано и надо после знака «|» записаны комментарии. Комментарии можно помещать в конце любой строки, они существенно облегчают понимание алгоритма.
При записи алгоритма в словесной форме, в виде блок-схемы или на псевдокоде допускается произвольное изображение команд. Вместе с тем такая запись позволяет понять человеку суть дела и исполнить алгоритм. Однако алгоритм, предназначенный для исполнения на компьютере, должен быть записан на строго формализованном языке. Такой язык называется языком программирования, а запись алгоритма на этом языке — компьютерной программой.
Для решения одной и той же задачи можно предложить несколько алгоритмов. Алгоритмы составляются с ориентацией на определенного исполнителя алгоритма. У каждого исполнителя имеется свой конечный набор команд, которые для него понятны и исполняемы. Этот набор называется системой команд исполнителя. Пользуясь системой команд, исполнитель может выполнить алгоритм формально, не вникая в содержание поставленной задачи. От исполнителя требуется только строгое выполнение последовательности действий, предусмотренной алгоритмом. Таким образом, в общем случае алгоритм претерпевает изменения по стадиям:
- первая стадия — алгоритм должен быть представлен в форме, понятной человеку, который его разрабатывает;
- вторая стадия — алгоритм должен быть представлен в форме, понятной исполнителю алгоритма (вторая стадия может отсутствовать, если исполнять алгоритм будет сам разработчик).
Примеры решения задач
Пример 1. Исполнитель Утроитель может выполнить только две команды, которым присвоены номера:
1 — вычти 1;
3 — умножь на 3.
Первая команда уменьшает число на 1, вторая — увеличивает его втрое.
Написать набор команд (не более пяти) получения из числа 3 числа 16. В ответе указать только номера команд.
Решение.
1 (3 – 1 = 2)
3 (2 * 3 = 6)
3 (6 * 3 = 18)
1 (18 – 1 = 17)
1 (17 – 1 = 16)
Ответ: 13311
Пример 2. Имеется Исполнитель алгоритма, который может передвигаться по числовой оси.
Система команд Исполнителя алгоритма:
1. «Вперед N» (Исполнитель алгоритма делает шаг вперед на N единиц).
2. «Назад M» (Исполнитель алгоритма делает шаг назад на M единиц).
Переменные N и M могут принимать любые целые положительные значения. Известно, что Исполнитель алгоритма выполнил программу из 50 команд, в которой команд «Назад 2» на 12 больше, чем команд «Вперед 3». Других команд в программе не было. Какой одной командой можно заменить эту программу, чтобы Исполнитель алгоритма оказался в той же точке, что и после выполнения программы?
Решение.
1. Найдем, сколько было команд «Вперед», а сколько «Назад». Учитывая, что общее количество команд равно 50 и что команд «Назад» на 12 больше, чем команд «Вперед». Получим уравнение: x + (x + 12) = 50, где x — количество команд «Вперед». Тогда общее количество команд «Вперед»: x = 19, а количество команд «Назад»: 19 + 12 = 31.
2. Будем вести отсчет от начала числовой оси. Выполнив 19 раз команду «Вперед 3», Исполнитель алгоритма оказался бы на отметке числовой оси 57 (19 * 3 = 57). После выполнения 31 раз команды «Назад 2» (31 * 2 = 62) он оказался бы на отметке –5 (57 – 62 = –5).
3. Все эти команды можно заменить одной — «Назад 5».
Ответ: команда«Назад 5».
Пример 3. Черепашка является исполнителем для создания графических объектов на рабочем поле. При движении Черепашка оставляет след в виде линии. Черепашка может исполнять следующие команды:
| Название команды | Параметр | Действия исполнителя |
| вп | Число шагов | Продвигается в направлении головы на указанное число шагов |
| нд | Число шагов | Продвигается в направлении, противоположном направлению головы на указанное число шагов |
| пр | Число градусов | Поворачивается направо относительно направления, заданного головой черепашки |
| лв | Число градусов | Поворачивается налево относительно направления, заданного головой черепашки |
Для записи повторяющихся действий (цикла) используется команда Повтори. В этой команде два параметра: первый задает количество повторений (итераций), а второй — список команд которые должны повторяться (тело цикла); список заключается в квадратные скобки.
Записать для исполнителя Черепашка алгоритмы:
а) построения квадрата со стороной 100;
б) построения правильного шестиугольника со стороной 50.
в) построения изображения цифры 4, если голова Черепашки смотрит на север.
Ответ: а) Повтори 4 [вп 100 пр 90]; б) Повтори 6 [вп 50 пр 360/6]; в) вп 100; повтори [лв 135 вп 50].
Пример 4. Два игрока играют в следующую игру (это вариант восточной игры). Перед ними лежат три кучки камней, в первой из которых 2, во второй — 3, в третьей — 4 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или удваивает число камней в одной из кучек, или добавляет по два камня в каждую из них. Выигрывает игрок, после хода которого либо в одной из кучек становится не менее 15 камней, либо общее число камней в трех кучках становится не менее 25. Кто выиграет при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ следует обосновать.
Решение. Удобнее всего составить таблицу возможных ходов обоих игроков. Заметим, что в каждом случае возможны всего четыре варианта хода. В таблице курсивом выделены случаи, которые сразу же приносят поражение игроку, делающему этот ход (например, когда камней в какой-либо кучке становится больше или равно 8, другой игрок непременно выигрывает следующим ходом, удваивая количество камней в этой кучке). Из таблицы видно, что при безошибочной игре обоих игроков первый всегда выиграет, если первым ходом сделает 4, 5, 6. У второго игрока в этом случае все ходы проигрышные.
| 1-й ход | 2-й ход | |||
| Начало | 1-й игрок | 2-й игрок | 1-й игрок | 2-й игрок |
| 2,3,4 | 4,3,4 | 8,3,4 | выигрыш | |
| 4,6,4 | 8,6,4 | выигрыш | ||
| 4,12,4 | выигрыш | |||
| 4,6,8 | выигрыш | |||
| 6,8,6 | выигрыш | |||
| 4,3,8 | выигрыш | |||
| 6,5,6 | 12,5,6 | выигрыш | ||
| 6,10,6 | выигрыш | |||
| 6,5,12 | выигрыш | |||
| 8,7,8 | выигрыш | |||
| 2,6,4 | 4,6,4 | 8,6,4 | выигрыш | |
| 4,12,4 | выигрыш | |||
| 4,6,8 | выигрыш | |||
| 6,8,6 | выигрыш | |||
| 2,12,4 | выигрыш | |||
| 2,6,8 | выигрыш | |||
| 4,8,6 | выигрыш | |||
| 2,3,8 | выигрыш | |||
| 4,5,6 | 8,5,6 | выигрыш | ||
| 4,10,6 | выигрыш | |||
| 4,5,12 | выигрыш | |||
| 6,7,8 | выигрыш |
Пример 5. Записано 7 строк, каждая из которых имеет свой номер. В нулевой строке после номера записана цифра 001. Каждая последующая строка содержит два повторения предыдущей строки и добавленной в конец большой буквы латинского алфавита (первая строка — A, вторая строка — B и т. д.). Ниже приведены первые три строкиєтой записи (в скобках указан номер строки):
(0) 001
(1) 001001A
(2) 001001A001001AB
Какой символ находится в последней строке на 250-м месте (считая слева направо)?
Примечание. Первые семь букв латинского алфавита: A, B, C, D, E, F, G.
Решение. Найдем длину каждой строки. Длина каждой следующей строки в два раза больше длины предыдущей плюс один символ, длина строк составит:
(0) 3 символа;
(1) 32+1=7;
(2) 72+1=15;
(3) 152+1=31;
(4) 312+1=63;
(5) 632+1=127;
(6) 1272+1=255 символов.
Так как задано 7 строк, а нумерация начинается с нулевой строки, последняя строка имеет номер 6 и содержит 255 символов. Последний символ в строке — F. Предпоследний элемент — E, далее идут символы D, C, B, A, 1 (по правилу формирования строк). Таким образом, 250-й символ — это 1.
Ответ: 1.
Пример 6. Имеется фрагмент алгоритма, записанный на учебном алгоритмическом языке:
n := Длина(а)
k = 2
b := Извлечь(а, k)
нц для i от 7 до n – 1
с := Извлечь(а, i)
b := Склеить(b, с)
кц
Здесь переменные а, b, с — строкового типа; переменные n, i — целые.
В алгоритме используются следующие функции:
Длина(х) — возвращает количество символов в строке х. Имеет тип «целое».
Извлечь(х, i) — возвращает i-й символ слева в строке х. Имеет строковый тип.
Склеить(х, у) — возвращает строку, в которой находятся все символы строки х, а затем все символы строки у. Имеет строковый тип.
Какое значение примет переменная b после выполнения этого фрагмента алгоритма, если переменная а имела значение «ВОСКРЕСЕНЬЕ»?
Решение. Находим общее число символов в строке а, получим, что n = 11.
Выполняя команду b := Извлечь(а, k) при k = 2, получим, что b примет значение “О“.
В цикле последовательно, начиная с 7-го символа строки а и заканчивая предпоследним (n – 1), извлекаем символ из строки а и присоединяем к строке b.
В результате получим слово “ОСЕНЬ” (символы с номерами 2 + 7 + 8 + 9 + 10).
Ответ: “ОСЕНЬ“
Пример 7. Леонардо из Пизы, известный как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Числовой ряд, который называется его именем, получился в результате решения задачи о кроликах, которую Фибоначчи изложил в своей «Книге Абака», написанной в 1202 году. Он выглядит так:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,…
В этом ряду каждое следующее число, начиная с третьего, равно сумме двух предыдущих. Составить словесный алгоритм и блок-схему проверки принадлежности введенного числа n ряду Фибоначчи.
Решение. Словесный алгоритм:
- Ввести число n.
- Установить значение первых трех чисел Фибоначчи: 1, 1, 2 (сумма двух предыдущих чисел).
- Пока введенное число n больше очередного числа Фибоначчи, взять два последних числа Фибоначчи и получить из них новое число Фибоначчи.
- Если число Фибоначчи равно введенному n или было введено число n = 1, значит, что было введено число Фибоначчи, в противном случае — введенное число не является числом Фибоначчи.
Приведенный словесный алгоритм в пункте 1, 2 содержит начальные установки, в пункте 3 — цикл с условием, а пункт 4 — это вывод результата работы алгоритма.
Блок-схема алгоритма:
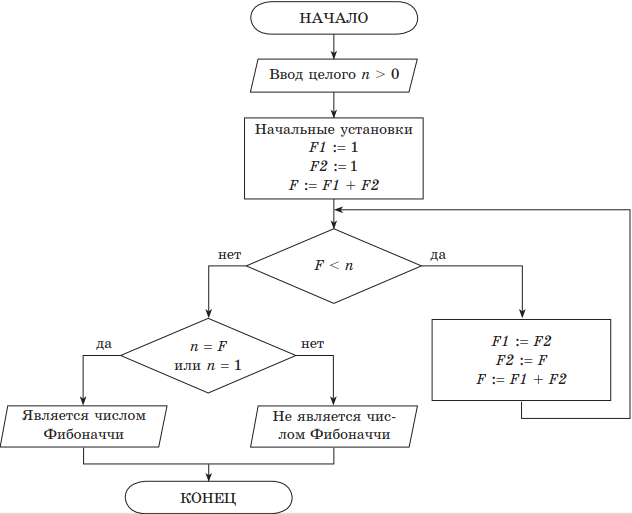
Обозначения:
F — текущее число ряда Фибоначчи;
F1 и F2 — два предыдущих числа ряда Фибоначчи для числа F;
n — число, для которого требуется определить, является ли оно числом из ряда Фибоначчи.
Использование основных алгоритмических конструкций: следование, ветвление, цикл
Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: следование, ветвление, цикл.
Базовая структура СЛЕДОВАНИЕ указывает на то, что управление передается последовательно от одного действия к другому.
| Учебный алгоритмический язык | Язык блок-схем |
| действие 1 действие 2 … действие n |
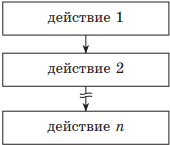 |
Использование исключительно этой структуры возможно лишь для достаточно простых задач, ход решения которых не меняется в зависимости от конкретных исходных данных и состоит в последовательном выполнении определенных операций.
В качестве примера рассмотрим решение простой задачи.
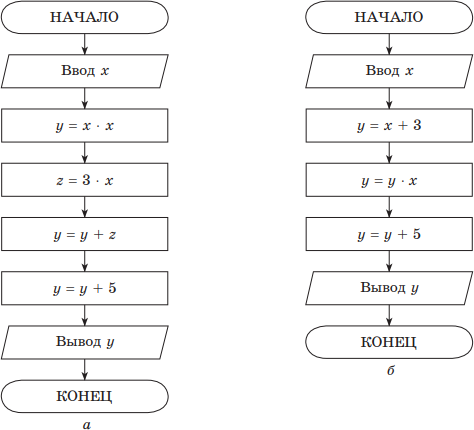
Пример. Найти y(x) = x2 + 3x + 5, используя только операции умножения и сложения.
Решение. На рис. приводятся два алгоритма, реализующие решение поставленной задачи.
Порядок вычисления y(x) в первом случае — обычный, а во втором — (x + 3) x + 5. Обе формулы эквивалентны, но в первом случае для вычисления необходимо 2 умножения, 2 сложения и 3 переменных (x, y, z), а во втором используются 1 умножение, 2 сложения и 2 переменные (x, y).
Приведенный пример показывает, что даже простые задачи могут решаться с помощью различных вариантов алгоритмов.
Обратите внимание, как в блоке следования используется оператор присваивания.
Операция присваивания — важнейшая операция во всех языках программирования. С помощью присваивания переменные получают новые значения: в левой части инструкции ставится идентификатор величины, а в правой части — выражение, значение которого можно определить.
В операторах присваивания используется либо привычный знак равенства, либо сочетание двоеточия и знака равенства «:=». Поскольку знак присваивания — это не знак равенства, возможны записи вида Х := Х + 1 или А := А – В. Нужно учитывать, что оператор присваивания будет выполняться только в том случае, если значения всех переменных правой части уже определены.
Базовая структура ВЕТВЛЕНИЕ (РАЗВИЛКА) используется в случае, когда выполнение программы может измениться в зависимости от результата проверки условия и пойти двумя разными (альтернативными) путями. Другими словами, условие является некоторым высказыванием (предикатом) и может быть истинным или ложным (принимать значение TRUE или FALSE). Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран.
Различают две структуры этого типа — полную и неполную. В случае полной структуры, если условие выполняется (является истинным), вслед за ним выполняется действие 1, иначе — действие 2. В случае неполной структуры, если условие выполняется (является истинным), то вслед за ним выполняется действие 1, иначе ничего не происходит.
Важную роль в операторах ветвления играют содержащиеся в них условия. В простейшем случае условиями служат отношения между величинами. Условия с одним отношением называют простыми условными выражениями, или простыми условиями. В некоторых задачах необходимы более сложные условия, состоящие из нескольких простых, например условие А < X < С, т. е. Х < А и (Х > C) (возможна запись (Х < А) and (Х > C)). Объединение нескольких простых условий в одно образует составное условное выражение, или составное условие. Составные условия образуются с помощью логических операторов not (отрицание), and (логическое И), or (логическое ИЛИ), хоr (исключающее ИЛИ).
Структура ВЕТВЛЕНИЕ существует в четырех основных вариантах:
если — то (неполная структура);
если — то — иначе (полная структура);
выбор (неполный);
выбор — иначе (полный).
| Учебный алгоритмический язык | Язык блок-схем |
| 1) если — то | |
|
если условие то действие 1 всё |
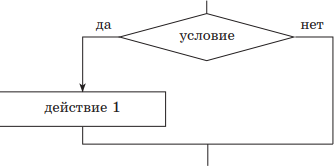 |
| 2) если — то — иначе | |
|
если условие то действие 1 иначедействие 2 всё |
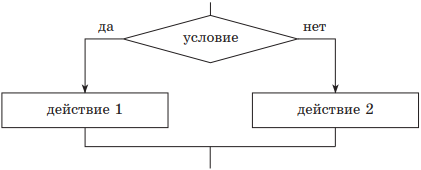 |
| 3) выбор | |
|
выбор при условие 1: действие 1 при условии 2: действие 2 … при условие N: действие N всё |
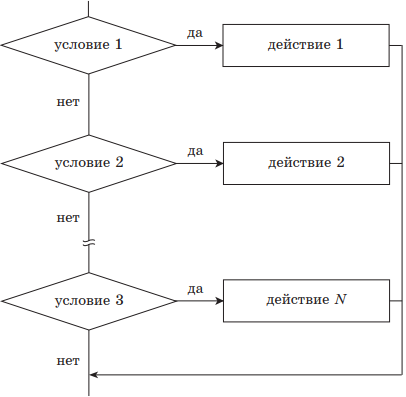 |
| 4) выбор — иначе | |
|
выбор при условие 1: действие 1 при условие 2: действие 2 … при условие N: действие N + 1 иначе действия N + 1 всё |
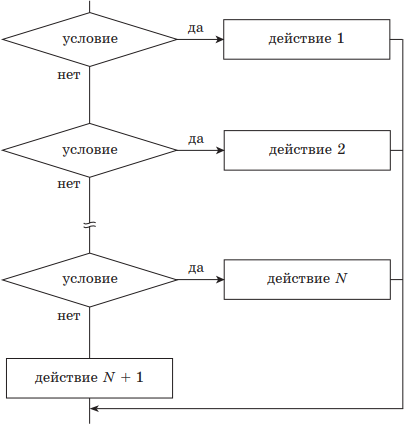 |
В качестве простого примера рассмотрим нахождение модуля числа y(x) = |x|. Решение приведено на рис. для случаев полной (а) и неполной (б) структур ветвления.
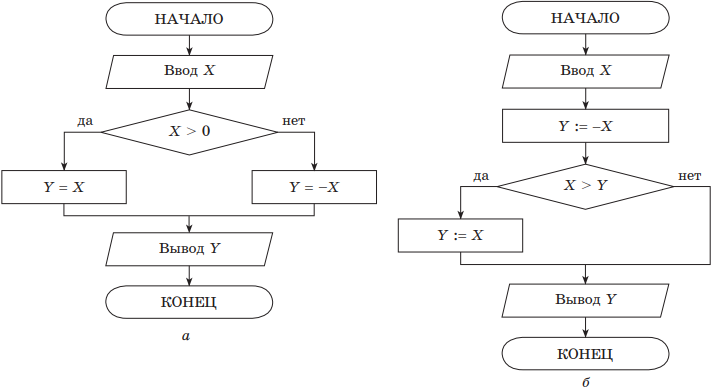
Базовая структура ЦИКЛ служит для записи алгоритмов, в которых некоторая часть алгоритма (тело цикла) должна повторяться несколько раз. Количество повторений цикла может определяться разными способами, в зависимости от которых различают три вида циклов.
1. Цикл с предусловием, или цикл «пока». При реализации этого цикла сначала проверяется условие его выполнения. Пока оно выполняется, будут происходить повторения тела цикла. Отсюда и другое его название — цикл «пока». Если условие не выполняется при первой проверке, то тело цикла не будет выполняться вообще. После выхода из цикла управление передается следующей структуре. Для того чтобы избежать зацикливания, т. е. бесконечного цикла, в теле цикла обязательно должны изменяться параметры, записанные в условии.
| Учебный алгоритмический язык | Язык блок-схем |
|
нц пока условие тело цикла (последовательность действий) кц |
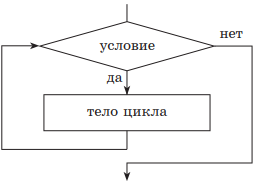 |
2. Цикл с параметром. Этот вид цикла удобно использовать в тех случаях, когда заранее извесно количество повторений цикла. Вводится понятие счетчика цикла, который по умолчанию считается равным либо 1, либо –1. В некоторых случаях изменение счетчика цикла (приращение) указывают явно. Для организации цикла необходимо задать верхнюю и нижнюю границы изменения счетчика цикла. В зависимости от значения верхней и нижней границы определяется шаг цикла (1 или −1), т. е. значение счетчика цикла.
| Учебный алгоритмический язык | Язык блок-схем |
|
нц для i от i1 до i2 тело цикла (последовательность действий) кц |
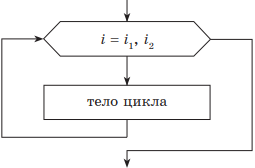 |
3. Цикл с постусловием, или цикл «до». При реализации этого цикла условие завершение цикла проверяется после тела цикла. В этом случае тело цикла всегда выполняется хотя бы один раз. Цикл будет выполняться до выполнения условия, отсюда и другое название — цикл «до». А пока условие не выполнено, будет повторяться тело цикла (выполнение условия, таким образом, является условием окончания цикла). В этом случае, как и в цикле «пока», необходимо предусмотреть в теле цикла изменение параметров условия цикла.
| Учебный алгоритмический язык | Язык блок-схем |
|
нц тело цикла (последовательность действий) до условие кц |
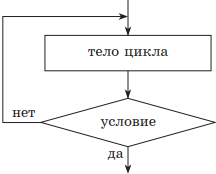 |
Для всех видов цикла предусмотрена возможность досрочного выхода, т. е. прерывание работы цикла.
Помимо трех рассмотренных видов цикла существует и так называемый интерационные циклы. Особенностью итерационного цикла является то, что число повторений операторов тела цикла заранее неизвестно. Для его организации используется цикл типа пока. Выход из итерационного цикла осуществляется в случае выполнения заданного условия. На каждом шаге вычислений происходит последовательное приближение и проверка условия достижения искомого результата. Классический пример — вычисление суммы ряда с заданной точностью.
Алгоритм, в состав которого входит итерационный цикл, называется итерационным алгоритмом. Итерационные алгоритмы используются при реализации итерационных численных методов. В итерационных алгоритмах необходимо обеспечить обязательное условие выхода из цикла (сходимость итерационного процесса). В противном случае произойдет зацикливание алгоритма, т. е. не будет выполняться основное свойство алгоритма — результативность.
Пример. Вычислить сумму знакопеременного ряда $S=x-{x^2}/{2}+{x^3}/{3}-{x^4}/{4}+…$ с заданной точностью $ε$.
Для данной знакочередующейся бесконечной суммы требуемая точность будет достигнута, когда очередное слагаемое станет по абсолютной величине меньше $ε$.
Решение. Запишем блок-схему алгоритма, где будем использовать следующие обозначения:
$S$ — частичная сумма ряда (стартовое значение равно 0);
$ε$ — точность вычисления;
$i$ — номер очередного слагаемого;
$m$ — значение очередного слагаемого;
$p$ — числитель очередного слагаемого.
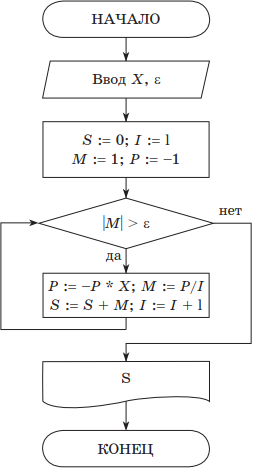
На псевдокоде алгоритм можно записать следующим образом:

Примечание. Следует отметить, что ряд будет сходящимся только при выполнении условия 0 < х < 1.
Возможны случаи, когда внутри тела цикла необходимо повторить некоторую последовательность операторов, т. е. организовать внутренний цикл. Такая структура получила название цикла в цикле, или вложенного цикла. Глубина вложения циклов (количество вложенных друг в друга циклов) может быть различной.
При использовании такой структуры для экономии времени выполнения необходимо выносить из внутреннего цикла во внешний все действия, результаты которых не зависят от параметра внутреннего цикла.
Пример. Вычислить сумму элементов для заданной матрицы (таблицы из 5 строк и 3 столбцов) А(5,3).
Решение. Алгоритм решения задачи на псевдокоде:

Основная часть блок-схемы нахождения суммы элементов матрицы будет иметь следующий вид:
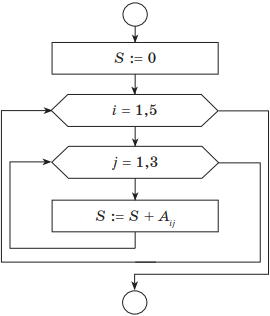
Здесь порядок выполнения вложенных циклов следующий: счетчик внутреннего цикла изменяется быстрее, т. е. для i = 1(внешний цикл), j пробегает значения 1, 2, 3 (внутренний цикл); далее i = 2, j опять пробегает значения 1, 2, 3 и т. д.
Примеры решения задач
Пример 1. Дан фрагмент блок-схемы некоторого алгоритма.
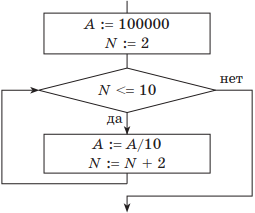
Определить значение переменной А после выполнения фрагмента алгоритма.
Какие исправления нужно внести, чтобы изменение значения переменной А происходило в обратном порядке?
Как записать исходный алгоритм с помощью двух других видов цикла?
Решение. Если представить пошаговое выполнение алгоритма в виде таблицы, получим:
| Начальные установки: | A = 100000; N = 2 |
| 1-я итерация | A = 10000; N = 4 |
| 2-я итерация | A = 1000; N = 6 |
| 3-я итерация | A = 100; N = 8 |
| 4-я итерация | A = 10; N = 10 |
| 5-я итерация, выполнилось условие выхода: N > 10 | Ответ: А = 1; N = 12 |
Таблица обратного хода изменения значения А будет иметь такой вид:
| Начальные установки: | A = 1; N = 2 |
| 1-я итерация | A = 10; N = 4 |
| 2-я итерация | A = 100; N = 6 |
| 3-я итерация | A = 1000; N = 8 |
| 4-я итерация | A = 10000; N = 10 |
| 5-я итерация, выполнилось условие выхода: N > 10 | А = 100000; N = 12 |
Блок-схема алгоритма примет такой вид:
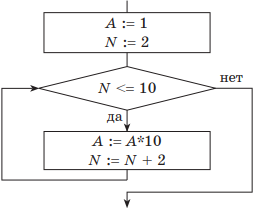
В алгоритме нужно изменить начальное значение А и операцию деления заменить операцией умножения. Счетчик N в данном случае изменять не нужно.
В приведенной в условии блок-схеме используется цикл с предусловием. Для цикла с параметром блок-схема алгоритма будет иметь такой вид:
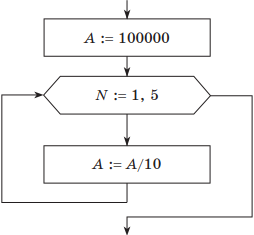
Понятно, что цикл должен выполниться пять раз. В заголовке цикла необходимо указать начальное и конечное значение счетчика цикла N (приращение по умолчанию равно 1).
Для цикла с постусловием блок-схема исходного алгоритма имеет такой вид:
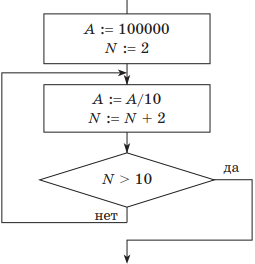
В данной схеме условие завершения цикла находится после тела цикла. Цикл, в отличие от цикла с предусловием, выполняется, пока значение условия ложно.
Пример 2. Сколько раз выполнится тело цикла в программе?
Q := 27; P := 36
нц пока (div(Q, 5) = div(P, 7))
Q := Q + 2
P := P + 3
кц
Примечание. Результат функции div(X, Y) — целая часть от деления X на Y.
Решение. Рассмотрим пошаговое выполнение алгоритма, оформив его в виде таблицы.
| Начальные установки | Q := 27; P := 36 |
| Проверка выполнения условия | div(27, 5) = 5; div(36, 7) = 5; 5 = 5 |
| 1-я итерация; выполнение тела цикла | Q := 29; P := 39 |
| Проверка выполнения условия | div(29, 5) = 5; div(39, 7) = 5; 5 = 5 |
| 2-я итерация; выполнение тела цикла | Q := 31; P := 42 |
| Проверка выполнения условия | div(31, 5) = 6; div(42, 7) = 6; 6 = 6 |
| 3-я итерация; выполнение тела цикла | Q := 33; P := 45 |
| Проверка выполнения условия | div(33, 5) = 6; div(45, 7) = 6 6 = 6 |
| 4-я итерация; выполнение тела цикла | Q := 35; P := 48 |
| Проверка выполнения условия. Условие не выполняется, цикл завершает работу | div(35, 5) = 7; div(48, 7) = 6; 7 ≠ 6 |
Ответ: цикл выполнится 4 раза.
Использование переменных. Объявление переменной (тип, имя, значение).
Локальные и глобальные переменные
Величины служат для описания объектов и процессов в материальном мире. Каждая величина имеет некоторые характеристики. В программировании понятие величины несколько отличается от понятия величины в естественных науках — оно является более формальным. Величиной называют объект — переменную, с которым связывается определенное множество значений. Такому объекту присваивается имя — идентификатор. Понятие переменной в программировании сходно с понятием переменной в математике. Например, в алгебраическом равенстве C = F + 2B – 5 значение переменной С зависит от значений переменных F и B, указанных в правой части равенства. Например, при F = 2 и B = 6, С = 9. Такое же равенство можно записать в программе, например на языке программирования Бейсик: C = F + 2B – 5. В терминах языка программирования C, F и B — это идентификаторы (имена) переменных.
Переменная — это объект программы, имеющий имя и изменяемое значение. Для хранения переменной в памяти компьютера выделено определенное место.
Переменные величины в отличие от постоянных величин (констант) могут со временем менять свое значение. Константой называется величина, которая в ходе выполнения программы не меняет своего значения.
Назначение программы состоит в обработке информации, при этом, конечно, основную роль играют переменные.
Переменная характеризуется:
- идентификатором;
- типом;
- значением.
Каждая переменная имеет свой идентификатор, т. е. свое уникальное имя. Имя переменной показывает, в каком месте памяти компьютера она хранится, значение переменной считывается из указанного ее именем места в памяти. Двух переменных с одним именем в одном программном модуле (блоке) быть не должно. Примерами идентификаторов величин могут быть, например, следующие последовательности символов: a1, SUMMA, X_1, Y_1, My_program.
Во многих языках программирования существуют некоторые ограничения на задания имен переменных. Имена составляются из букв и цифр; первой литерой должна быть буква. Знак подчеркивания «_» считается буквой, его удобно использовать, чтобы улучшить восприятие длинных имен переменных. Разумно давать переменным логически осмысленные имена, в соответствии с их назначением. Нельзя использовать в качестве имен зарезервированные (служебные) слова языка программирования.
Тип переменной — это диапазон (набор) всех значений, которые может принимать данная переменная. Тип переменной определяет, какие операции для нее допустимы. Другими словами, тип переменной — это характеристика, которая для величины определяет:
- необходимый размер памяти;
- диапазон значений, которые может принимать величина;
- возможные операции над величиной (подразумеваются действия относительно использования величин в выражениях);
- формы представления величин (или формат представления величин).
Стандартные типы — это числовые, литерные и логические типы.
Числовой тип, к которому относятся целые и вещественные величины, позволяет оперировать с числами. Целые числа, которые в учебном алгоритмическом языке составляют тип цел, сверху ограничены положительным числом Nmax, а снизу — отрицательным числом Nmin. Значения Nmax и Nmin определяются объемом ячеек памяти, в которые записываются целые числа. Обычно для целых чисел выделяется два байта памяти, соответственно границы диапазона равны [Nmin = –32768 и Nmax = 32767]. Считается, что все операции с величинами типа цел выполняются по обычным правилам арифметики, за одним исключением: возможны две операции деления div и mod.
Операция div обозначает целочисленное деление. При делении с точностью до целых чисел получается два результата — частное и остаток. Знак результата берется по обычным правилам, а полученный остаток игнорируется. Например:
23 div 5 = 4;
2 div 6 = 0;
(–13) div 5 = –2;
(–13) div (–5) = 2.
Операция mod определяет остаток при делении двух целых чисел.
Например:
23 mod 5 = 3;
2 mod 6 = 2;
(–13) mod 5 = –3;
(–13) mod (–5) = 3;
8 mod 2 = 0.
Целые числа чаще всего используются в простых арифметических выражениях и выступают в программах в качестве различных счетчиков и значений индексов.
К другому числовому типу относятся вещественные (вещ) величины. Значения вещественных величин могут изображаться в форме с фиксированной запятой (например, 0,3333; 2,0; –4,567 и т. д.) и с плавающей запятой (например, 7,0102, 5,173*10–3 и т. д.).
В отличие от целых чисел, действия с вещественными числами могут быть неточными — это связано с ошибками округлений. Объем памяти, который предоставляется для хранения значений вещественной переменной, — от 4 до 10 байтов (в зависимости от выбранного формата числа). Над числовыми величинами можно выполнять как арифметические операции, так и операции сравнения (>, <, >=, <=, =, ).
Литерный тип, включающий символы и строки, дает возможность работать с текстом. Литерные величины — это произвольные последовательности символов: букв, цифр, знаков препинания, пробела и других специальных знаков (возможными символами могут быть символы таблицы ASCII). Литерные величины обычно заключаются в кавычки: “а”, “В”, “СТРОКА”, “1_2_3”. В учебном алгоритмическом языке литерные величины обозначаются как лит. В других языках программирования (например, в Паскале) различают символьный (char) и строковый (string) типы. Величины символьного типа состоят из одного символа и занимают в памяти всего 1 байт. Величины строкового типа представляют собой различные последовательности символов, которые предусмотрены кодовой страницей, установленной в компьютере. Длина строки может составлять от 0 до 255 символов. Над всеми литерными величинами возможны операции сравнения. С помощью отношений типа “a” < “b”, “b” < “c”, “c” < “d”,… выполняется упорядочение литерных величин (сортировка по возрастанию или убыванию).
Еще одной операцией, характерной для символьных и строковых величин, является операция конкатенации (слияния): “a” + “b” = “ab”.
Логический тип позволяет определять логические переменные, которые могут принимать только два значения: истина (true) или ложь (false). Для представления логической величины достаточно одного бита, однако, поскольку место в памяти выделяется по байтам, логической величине отводится минимальная «порция» памяти — один байт. Над логическими величинами можно выполнять все стандартные логические операции.
Значение — это непосредственно то, чему равна переменная в конкретный момент времени. Это может быть число, символ, текст и т. д. Значение переменной в программе можно задать двумя способами: присваиванием и с помощью процедуры ввода.
Оператор присваивания
Во всех языках программирования оператор присваивания является одним из важнейших. С помощью присваивания переменные получают новые значения, например:
Д := 13;
D1 := C;
Х := Х + 1.
В операторах присваивания используется либо обычный знак равенства, либо сочетание двоеточия и знака равенства «:=». Поскольку знак присваивания — это не знак равенства, возможны записи вида Х := Х + 1 или А := А – В. Нужно учитывать, что оператор присваивания будет выполняться только в том случае, если значения всех переменных в правой части уже определены и выполняется соответствие типов для правой и левой части оператора присваивания. Например, С := А > B выполнится только в том случае, если для переменной С определен булевский (логический) тип. Операция присваивания может быть применена к большинству типов величин. Однако для каждого из типов предусмотрен свой набор операций.
Локальные, глобальные и общие переменные
Каждая переменная характеризуется областью действия или областью видимости. По зоне видимости в языках программирования различают локальные и глобальные переменные. Первые доступны только конкретному подалгоритму (вспомогательному алгоритму, подпрограмме, модулю), вторые — всему алгоритму (программе). С распространением модульного и объектного программирования появились еще и общие переменные, доступные для определенных уровней иерархии подпрограмм.
Ограничение зоны видимости придумали как для возможности использовать одинаковые имена переменных, так и для защиты от ошибок, связанных с неправомерным использованием переменных.
Имена локальных и глобальных переменных могут совпадать. При этом действует правило: локальные переменные на время работы подпрограмм, в которых они объявлены, экранируют, т. е. перекрывают глобальные переменные. Например, если в основной программе переменная с именем с определена как логическая, а в подпрограмме идентификатор с используется для задания вещественной переменной, то только на время работы подпрограммы с можно использовать как число — в остальных случаях идентификатор с определяет логическую переменную.
Примеры решения задач
Пример 1. Значения заданных переменных А, В перераспределить таким образом, чтобы А и В поменялись значениями.
Решение. Возможны два варианта решения:
| С использованием промежуточной переменной С | Без использования дополнительной переменной |
| C := A; A := B; B := C |
A := A + B; B := A – B; A := A – B |
Пример 2. Определить значение переменной A после выполнения фрагмента алгоритма:
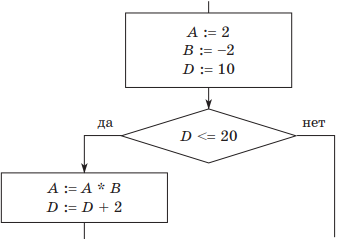
Решение. Оформим решение в виде таблицы.
| A | B | D | Условие |
| 2 | –2 | 10 | да |
| –4 | –2 | 12 | да |
| 8 | –2 | 14 | да |
| –16 | –2 | 16 | да |
| 32 | –2 | 18 | да |
| –64 | –2 | 20 | да |
| 128 | –2 | 22 | нет — окончание цикла |
Ответ: А = 128.
Пример 3. Определить значение переменной S:
A := –1; B := 1
нц пока A + B < 10
A := A + 1; B := B + A
кц
S := A * B
Решение. Оформим решение в виде таблицы.
| A | B | A + B | S |
| –1 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 2 | 3 | |
| 2 | 4 | 6 | |
| 3 | 7 | 10 — условие выхода из цикла | 21 |
Ответ: S = 21.
Пример 4. Записать последовательность операций присваивания (:=), которая позволит определить номера подъезда и этажа по номеру N квартиры девятиэтажного дома, считая, что на каждом этаже по 4 квартиры, а нумерация квартир начинается с первого подъезда.
Решение.
4 * 9 = 36 {количество квартир в подъезде}
Х := (N – 1) div 36 + 1 {номер подъезда}
N := N – (X – 1) * 36 { N ∊[1, 36] }
Y := (N – 1) div 4 + 1 {номер этажа}
Например, для квартиры с номером 150 получим:
Х = (150 – 1) div 36 + 1 = 4 + 1 = 5;
N = 150 – (5 – 1) * 36 = 6;
Y = (6 – 1) div 4 + 1 = 2.
Ответ: квартира с номером 150 находится в пятом подъезде, на втором этаже.
Решение
подобного рода задач основано на
пошаговом исполнении алгоритма, в
итоге делается вывод о том, какую задачу
выполняет этот алгоритм и что является
конечным результатом.
Предлагается
задача: в приведенном алгоритме при к
= 4
каким будет выведенное значение Р?
Это
задание можно сформулировать как
тестовое, где нужно выбрать правильный
ответ из нескольких предложенных и
обосновать его.
В
нашем случае варианты ответов (правильный
выделен жирным шрифтом).
1)
1; 3) 12;
5) 1944.
2)4;
4)81;
Кроме
того, можно предложить просто определить
ответ и сформулировать условие задачи,
решение которой приведено.
В
нашем примере задача формулируется
так:
найти произведение первых k
натуральных чисел, кратных 3; Р = 1944.
Этот
же алгоритм, в зависимости от того, как
преподавался курс алгоритмизации и
программирования, можно предложить
для исследования, записав его на одном
из алгоритмически
Язык
Бейсик
input
“Введите натуральное число: “, k
р
=: 1 t=: О
fог
i = 1 tо
k
t=t+3:
p=p*t
пехt
i
print
“Результат: “, р
епd.

Ввод
k
P
:=1
T:=0


начало
T:=T+3
I:=1,
k, 1



P:=P*T



Вывод
Р


Конец Билет №5
1. Операционная система компьютера (назначение, состав, способ организации диалога с пользователем). Загрузка компьютера.
2. Создание, преобразование, сохранение, распечатка рисунка в среде графического редактора.
1.
Операционная система компьютера
(назначение, состав, способ организации
диалога с пользователем). Загрузка
компьютера.
Операционная
система
— это важнейшая часть системного
программного обеспечения, которая
организует процесс выполнения задач
на ЭВМ, распределяя для этого ресурсы
машины, управляя работой всех ее
устройств и взаимодействием с
пользователем. Иными словами, это
своеобразный администратор компьютера,
распределяющий его ресурсы так, чтобы
пользователь мог решать свои задачи
максимально удобно.
Примечание.
Ресурсами компьютера являются
процессорное время, память всех
видов, устройства ввода/вывода, программы
и данные.

Роль
операционной системы можно наглядно
представить себе с помощью следующего
рисунка. В центре его изображен собственно
компьютер, т.е. все то оборудование,
которое стоит на вашем столе и которое
можно непосредственно “потрогать
руками” (в информатике эта часть
часто называется hardware).
Внешней оболочкой является разнообразное
программное обеспечение (software),
позволяющее многочисленным пользователям
решать свои прикладные задачи из всех
областей человеческой деятельности.
ОС организует их совместную работу
и служит своеобразным программным
расширением управляющего устройства
компьютера. Вы можете спросить: а так
ли нужен еще один дополнительный
слой? Очень
нужен,
учитывая тот факт, что невозможно
заложить в центральный блок информацию
обо всех устройствах, которые к нему
могут быть подсоединены. И, кроме
того, новое устройство может быть
изобретено уже после изготовления
компьютера! Отсюда очевидно, что
загружаемая (а следовательно, изменяемая)
программная часть, обеспечивающая
работу компьютерное аппаратуры,
совершенно необходима.
С
другой стороны, наличие операционной
системы очень существенно облегчает
разработку нового программного
обеспечения. Все наиболее часто
встречающиеся при работе компьютера
задачи сконцентрированы в ОС. Поэтому
программисту уже не требуется заботиться
о размещении своей программы в объеме
памяти каждого конкретного компьютера
или описывать отдельные технические
детали взаимодействия со всевозможными
внешними устройствами разнообразных
фирм-изготовителей — для этого достаточно
просто обратиться к соответствующей
функции операционной системы. Приведем
простой частный пример. Если бы об этом
не заботилась ОС, каждая программа
должна была бы самостоятельно проверять
наличие дискеты в дисководе при записи
информации или факт подключения
принтера перед печатью на бумагу. И
таких ситуаций существует великое
множество.
Но
наличие операционной системы удобно и
пользователю. Поскольку на современных
компьютерах диалог с ним ведется
именно средствами ОС, то интерфейс
(проще говоря, способы взаимодействия
с человеком) во
всех программах получается примерно
одинаковым. Так, освоив 2—3 программы в
системе Windows, пользователь может
довольно быстро научиться работать с
еще одной, даже совершенно новой для
него,
Таким
образом, мы видим, что операционная
система решает целый комплекс важных
задач управления компьютером. Сформулируем
их по возможности более полно. Итак, ОС
современного компьютера выполняет
следующие функции.
• Организация
согласованного выполнения всех процессов
в компьютере. Планирование работ,
распределение ресурсов.
• Организация
обмена с внешними устройствами. Хранение
информации и обеспечение доступа к ней,
предоставление справок.
• Запуск
и контроль прохождения задач пользователя.
• Реакция
на ошибки и аварийные ситуации. Контроль
за нормальным функционированием
оборудования.
• Обеспечение
возможности доступа к стандартным
системным средствам (программам,
драйверам, информации о конфигурации
и т.п.).
• Обеспечение
общения с пользователем.
• Сохранение
конфиденциальности информации в
многопользовательских системах.
Первые
операционные системы (СР/М, МS-DOS,Unix
) вели диалог с пользователем на экране
текстового дисплея. Это был в полном
смысле слова диалог, в ходе которого
человек и компьютер по очереди
обменивались сообщениями: человек
вводил очередную команду, а компьютер,
проверив ее, либо выполнял, либо отвергал
по причине ошибки. Такие системы в
литературе принято называть ОС
с интерфейсом командной строки.
Пользователь
последовательно набрал две команды
вывода каталога дисков, причем первую
компьютер выполнил нормально, и на
экране появился требуемый список
файлов, а вторую “отказался” делать,
поскольку оператор ошибочно указал
имя несуществующего диска. Очевидно,
что подобный способ общения не очень
удобен для человека, поскольку требует
постоянно держать в голове жесткий
синтаксис всех допустимых команд и
очень внимательно их вводить. Поэтому
почти сразу же стали появляться сервисные
системные программы, тем или иным
способом облегчающие работу с ОС.
Наиболее ярким примером таких
программ-оболочек может служить широко
известный Norton Commander,
который был настолько распространен,
что многие пользователи искренне
считали его частью операционной системы.
Развитие
графических возможностей дисплеев
привело к коренному изменению принципов
взаимодействия человека и компьютера.
Командная строка была безвозвратно
вытеснена
графическим интерфейсом,
когда объекты манипуляций в ОС изображаются
в виде небольших рисунков, а необходимые
действия тем или иным образом выбираются
из предлагаемого машиной списка — так
называемого меню. При подобном методе
диалога набор текста полностью отсутствует
и вполне достаточно всего нескольких
клавиш. Существенным дополнением к
графическому способу ведения диалога
явилось появление нового устройства
ввода информации в компьютер —
манипулятора “мышь”, без которого
сейчас просто невозможно представить
современный компьютер. Примерами
операционной системы с графическим
интерфейсом служат довольно похожие
ОС для компьютеров “Масintosh” (не
имеет специального названия и
обозначается просто System с номером
версии) и “IВМ РС” — 0S/2 и Windows.
Последняя система в нашей стране
распространена необычайно широко.
Перейдем
теперь к описанию состава операционных
систем. Он, конечно, может быть довольно
разным для различных систем. Так, для
“классических” ОС с командной
строкой довольно четко выделяются три
основные части:
• машинно-зависимая
часть для работы с конкретными видами
оборудования;
• базовая
часть (ядро), не зависящая от конкретных
деталей устройств: она работает с
абстрактными логическими устройствами
и при необходимости вызывает функции
из предыдущей части; отвечает за наиболее
общие принципы устройства ОС;
• программа
ведения диалога с пользователем (ее
часто называют
командным процессором).
Значительная
часть операционной системы находится
в памяти постоянно, что обеспечивает
ее эффективную работу. Программы для
некоторых редко используемых операций
типа форматирования дискет чаще всего
оформляются в виде самостоятельных
служебных программ и хранятся на внешних
носителях. Такие программы обычно
называют
утилитами.
Кроме того, в ОС, как правило, включают
небольшой стандартный набор самого
необходимого программного обеспечения,
например, простейший текстовый редактор.
Состав
операционных систем с графическим
интерфейсом типа Windows заметно шире,
но в целом имеет похожее строение.
В
момент включения компьютера в ОЗУ нет
осмысленной информации. Поэтому
особый интерес представляет вопрос о
том, как операционная система загружается.
Процесс этот в заметно упрощенном виде
выглядит так. При включении компьютера
(или при нажатии кнопки сброса) счетчик
процессора аппарате устанавливается
на начальный адрес ПЗУ, и стартует
выполнение программы начальной загрузки.
Прежде всею ищется и тестируется
установленное оборудование. Современные
компьютеры в основном используют внешние
устройства “plug
and р1ау” (переводится
— “включил и работай”), поэтому они
способны сообщить процессору свои
основные характеристики и условия
работы. Опрос внешних устройств и
проверка их работоспособности
занимают достаточно длительное время,
несмотря на высокое быстродействие
компьютера. В случае если все оборудование
функционирует нормально, происходит
переход к следующему этапу — поиску
начального загрузчика операционной
системы. Он может находиться на жестком
диске, на дискете, на СD-RОМ
и даже быть получен с помощью сетевой
платы. Поэтому компьютер опрашивает
перечисленные устройства по очереди,
в определенном порядке, до тех пор, пока
не обнаружит требуемую информацию (в
скобках заметим, что порядок поиска при
наличии достаточных навыков и знаний
может быть легко изменен). Итак, загрузчик,
представляющий собой не что иное,
как программу
дальнейшей загрузки,
обнаружен и прочитан в память. Дальнейшие
действия машины уже определяются тем,
что введено извне. Поскольку начальный
загрузчик очень мал, то он умеет очень
немного — найти и прочесть первый файл
ОС с фиксированным именем и передать
ему управление. И только после этого
будет загружена в ОЗУ остальная часть
операционной системы и машина сможет,
наконец, нормально общаться с
пользователем.
Примечание.
Несколько слов для тех, кого удивила
сложность описанного процесса. Почему
загрузка ОС такая многоступенчатая
• и почему, например, нельзя просто
записать начальный
загрузчик в то же самое ПЗУ? Технически
это не представляет никакого труда, но
все дело в том, что тогда мы сможем
пользоваться только
одной(!)
операционной системой, а именно той,
загрузчик для которой жестко “зашили”
в ПЗУ.
И
в заключение еще одно дополнительное
замечание. Может быть, не стоит
требовать этот материал с учеников, но
рассказать об этом, по-моему, стоит.
Всегда ли существовала ОС и может ли
компьютер работать без нее? Как ни
странно, ответ на оба вопроса отрицательный.
Операционная система существовала не
всегда,
а возникла на стыке второго и третьего
поколений.
Cсущественными
причинами возникновения ОС являются
появление сложных внешних устройств —
в первую очередь магнитных дисков, и
необходимость разделения ресурсов
между задачами и пользователями. Что
касается работы без ОС, то теоретически
можно написать такую программу, которая
будет сама загружаться и работать с
внешними устройствами без всякого
участия ОС. На практике это чересчур
сложно и никогда не делается. Даже если
компьютер целыми днями работает по
единственной программе (кассовый аппарат
в магазине или учет переводов в сберкассе),
в нем все равно обычно используется
операционная система.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Алгоритм. Свойства алгоритмов.
Блок-схемы. Алгоритмические языки
Код ОГЭ: 1.3.1. Алгоритм, свойства алгоритмов, способы записи алгоритмов.
Блок-схемы. Представление о программировании
Понятие алгоритма является одним из основных понятий вычислительной математики и информатики.
■ Алгоритм
— строго определенная последовательность действий для некоторого исполнителя, приводящая к поставленной цели или заданному результату за конечное число шагов.
Любой алгоритм составляется в расчете на конкретного исполнителя с учетом его возможностей. Исполнитель — субъект, способный исполнять некоторый набор команд. Совокупность команд, которые исполнитель может понять и выполнить, называется системой команд исполнителя.
Для выполнения алгоритма исполнителю недостаточно только самого алгоритма. Выполнить алгоритм — значит применить его к решению конкретной задачи, т. е. выполнить запланированные действия по отношению к определенным входным данным. Поэтому исполнителю необходимо иметь исходные (входные) данные — те, что задаются до начала алгоритма.

В результате выполнения алгоритма исполнитель должен получить искомый результат — выходные данные, которые исполнитель выдает как результат выполненной работы. В процессе работы исполнитель может создавать и использовать данные, не являющиеся выходными, — промежуточные данные.
Свойства алгоритмов
Алгоритм должен обладать определенными свойствами. Наиболее важные свойства алгоритмов:
- Дискретность. Процесс решения задачи должен быть разбит на последовательность отдельных шагов — простых действий, которые выполняются одно за другим в определенном порядке. Каждый шаг называется командой (инструкцией). Только после завершения одной команды можно перейти к выполнению следующей.
- Конечность. Исполнение алгоритма должно завершиться за конечное число шагов; при этом должен быть получен результат.
- Понятность. Каждая команда алгоритма должна быть понятна исполнителю. Алгоритм должен содержать только те команды, которые входят в систему команд его исполнителя.
- Определенность (детерминированность). Каждая команда алгоритма должна быть точно и однозначно определена. Также однозначно должно быть определено, какая команда будет выполняться на следующем шаге. Результат выполнения команды не должен зависеть ни от какой дополнительной информации. У исполнителя не должно быть возможности принять самостоятельное решение (т. е. он исполняет алгоритм формально, не вникая в его смысл). Благодаря этому любой исполнитель, имеющий необходимую систему команд, получит один и тот же результат на основании одних и тех же исходных данных, выполняя одну и ту же цепочку команд.
- Массовость. Алгоритм предназначен для решения не одной конкретной задачи, а целого класса задач, который определяется диапазоном возможных входных данных.
Способы представления алгоритмов:
- словесная запись (на естественном языке). Алгоритм записывается в виде последовательности пронумерованных команд, каждая из которых представляет собой произвольное изложение действия;
- блок–схема (графическое изображение). Алгоритм представляется с помощью специальных значков (геометрических фигур) — блоков;
- формальные алгоритмические языки. Для записи алгоритма используется специальная система обозначений (искусственный язык, называемый алгоритмическим);
- псевдокод. Запись алгоритма на основе синтеза алгоритмического и обычного языков. Базовые структуры алгоритма записываются строго с помощью элементов некоторого базового алгоритмического языка.
Словесная запись алгоритма
Произвольное изложение этапов алгоритма на естественном языке имеет свои недостатки. Словесные описания строго не формализуемы, поэтому может быть нарушено свойство определенности алгоритма: исполнитель может неточно понять описание этапа алгоритма. Словесная запись достаточно многословна. Сложные задачи трудно представить в словесной форме.
■ Пример 1. Записать в словесной форме правило деления обыкновенных дробей.
Решение.
Шаг 1. Числитель первой дроби умножить на знаменатель второй дроби.
Шаг 2. Знаменатель первой дроби умножить на числитель второй дроби.
Шаг 3. Записать дробь, числителем которой являет результат выполнения шага 1, знаменателем — результат выполнения шага 2.
Описанный алгоритм применим к любым двум обыкновенным дробям. В результате его выполнения будут получены выходные данные — результат деления двух дробей (исходных данных).
Формальные исполнители алгоритма
Формальный исполнитель — это исполнитель, который выполняет все команды алгоритма строго в предписанной последовательности, не вникая в его смысл, не внося ничего в алгоритм и ничего не отбрасывая. Обычно под формальным исполнителем понимают технические устройства, автоматы, роботов и т. п. Компьютер можно считать формальным исполнителем.
Программы на языке произвольного формального исполнителя могут состоять только из элементарных команд, которые входят в его систему (которые исполнитель «понимает»).
Исполнитель может иметь свою среду (например, систему координат, клеточное поле и др.). Среда исполнителя — это совокупность объектов, над которыми он может выполнять определенные действия (команды), и связей между этими объектами. Алгоритмы в этой среде выполняются исполнителем по шагам.
■ Пример 2. Исполнитель Крот имеет следующую систему команд:
- вперед k — продвижение на указанное число шагов вперед;
- поворот s — поворот на s градусов по часовой стрелке;
- повторить m [команда1 … командаN] — повторить m раз серию указанных команд.
Какой след оставит за собой исполнитель после выполнения следующей последовательности команд?
Повторить 5 [вперед 10 поворот 72]
Решение. Команда вынуждает исполнителя 5 раз повторить набор действий: пройти 10 шагов вперед и повернуть на 72° по часовой стрелке. Так как поворот происходит на один и тот же угол, то за весь путь исполнитель повернет на 5 х 72° = 360°. Поскольку все отрезки пути одинаковой длины и сумма внешних углов любого многоугольника составляет 360°, то в результате будет оставлен след в форме правильного пятиугольника со стороной в 10 шагов исполнителя.
Заметим, что если увеличить количество повторов серии команд, то исполнитель будет повторно передвигаться по тем же отрезкам (произойдет повторное движение по тому же пятиугольнику).
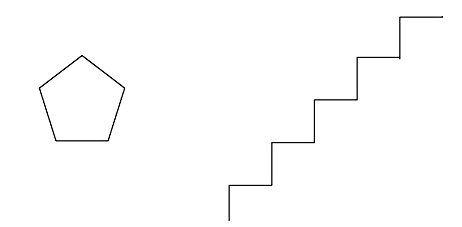
■ Пример 3. В системе команд предыдущего исполнителя Крот сформировать алгоритм вычерчивания пятиступенчатой лестницы (длина ступеньки — 10 шагов исполнителя).
Решение. За каждый шаг цикла должно происходить 4 действия: движение вперед на 10 шагов исполнителя, поворот на 90° по часовой стрелке, еще 10 шагов вперед и поворот на 90° против часовой стрелки (= 270° по часовой). В результате за один шаг цикла формируется ломаная из двух отрезков длиной 10 под прямым углом. За пять таких шагов сформируется 5–ступенчатая лестница (ломаная будет содержать 10 звеньев).
Повторить 5 [вперед 10 поворот 90 вперед 10 поворот 270]
Блок–схема
Блок–схема — наглядный способ представления алгоритма. Блок–схема отображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Определенному типу действия соответствует определенная геометрическая фигура блока. Линии, соединяющие блоки, определяют очередность выполнения действий. По умолчанию блоки соединяются сверху вниз и слева направо. Если последовательность выполнения блоков должна быть иной, используются направленные линии (стрелки).
Основные элементы блок–схемы алгоритма:

Общий вид блок–схемы алгоритма:
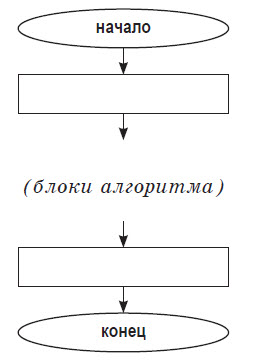
■ Пример 4. Алгоритм целочисленных преобразований представлен в виде фрагмента блок–схемы. Знаком := в нем обозначен оператор присваивания некоторого значения указанной переменной. Запись X := 1 означает, что переменная Х принимает значение 1.
Определить результат работы алгоритма для исходных данных Х = 7, Y = 12.
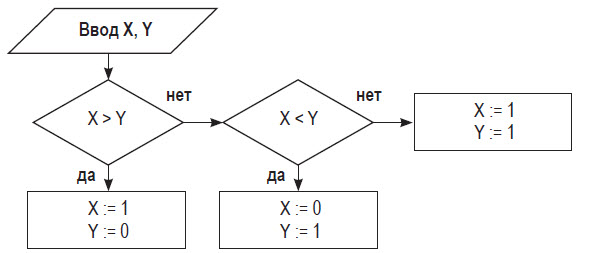
Решение.
- Блок ввода данных определит исходные значения переменных Х и Y (7 и 12 соответственно).
- В первом условном блоке осуществляется сравнение значений Х и Y. Поскольку условие, записанное в блоке, неверно (7 < 12), происходит переход по линии «нет».
- Во втором условном блоке выполняется второе сравнение, которое для исходных данных оказывается верным. Происходит переход по линии «да».
- Вычисляется результат выполнения алгоритма: X := 0, Y := 1.
Ответ: X := 0, Y := 1.
Алгоритмические языки
Алгоритмический язык — это искусственный язык (система обозначений), предназначенный для записи алгоритмов. Он позволяет представить алгоритм в виде текста, составленного по определенным правилам с использованием специальных служебных слов. Количество таких слов ограничено. Каждое служебное слово имеет точно определенный смысл, назначение и способ применения. При записи алгоритма служебные слова выделяют полужирным шрифтом или подчеркиванием.
В алгоритмическом языке используются формальные конструкции, но нет строгих синтаксических правил для записи команд. Различные алгоритмические языки различаются набором служебных слов и формой записи основных конструкций.
Алгоритмический язык, конструкции которого однозначно преобразуются в команды для компьютера, называется языком программирования. Текст алгоритма, записанный на языке программирования, называется программой.
Псевдокод
Псевдокод занимает промежуточное положение между естественным языком и языками программирования. Пример псевдокода — учебный алгоритмический язык. Алфавит учебного алгоритмического языка является открытым. Существенным достоинством этого языка является то, что его служебные слова, конструкции и правила записи алгоритма весьма схожи с теми, что применяются в распространенных языках программирования. Благодаря этому учебный алгоритмический язык позволяет легче освоить основы программирования.
Служебные слова учебного алгоритмического языка:
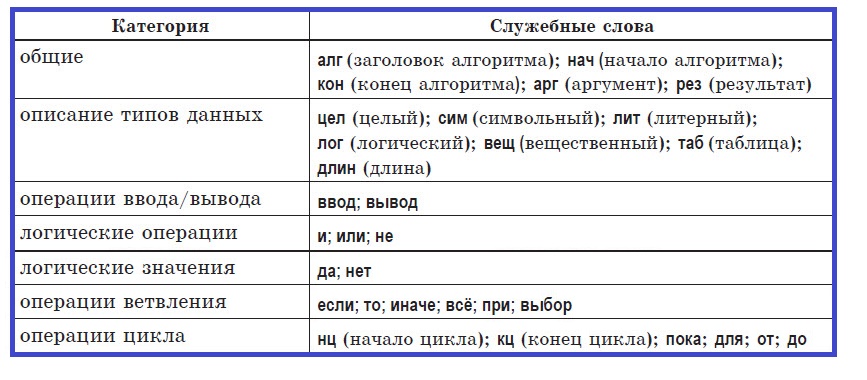
Стандартная структура алгоритма
Представление алгоритма на алгоритмическом языке (в том числе и языке программирования) состоит из двух частей. Первая часть — заголовок — задает название алгоритма и включает описание переменных, которые используются в нем. Вторая часть — тело алгоритма — содержит последовательность команд алгоритма.
Общий вид записи алгоритма на учебном алгоритмическом языке:

В начале заголовка записывается служебное слово алг, после чего указывается имя алгоритма. Описание переменных, являющихся аргументами алгоритма и его результатами, приводится после названия в круглых скобках.
В следующих строках конкретизируют, какие именно переменные являются аргументами алгоритма (входными данными), а какие — его результатами (выходными данными). Для этого после служебного слова арг приводится список имен переменных–аргументов; в следующей строке после служебного слова рез приводится список имен переменных–результатов.
Между служебными словами нач и кон размещается тело алгоритма — конечная последовательность команд, выполнение которых предписывает алгоритм. Команды алгоритма записывают одну за одной в отдельных строках. В случае необходимости можно записать две или более команд в одной строке, тогда соседние команды разделяют точкой с запятой. Если в алгоритме применяются промежуточные переменные, их описание приводят в начальной строке тела алгоритма рядом со словом нач.
Примеры заголовков алгоритмов:

В первом примере алгоритм имеет название Объем_шара, один вещественный аргумент Радиус и один вещественный результат Объем. Во втором примере алгоритм под названием Choice имеет три аргумента — целые M и N и логический b, а также два результата — вещественные Var1 и Var2.
Пример алгоритма вычисления гипотенузы прямоугольного треугольника:

На вход алгоритму даются два вещественных аргумента a и b (величины катетов), результатом является вещественная переменная с (гипотенуза). Для ее расчета используется функция вычисления квадратного корня sqrt.
Описание величин и действия над ними
При описании алгоритма необходимо указать названия (обозначения) всех величин, которые будут в нем найдены или использованы.
При представлении алгоритма решения в виде блок–схемы выбранные обозначения величин приводятся отдельно от блок–схемы (как объяснение к ней). Если алгоритм представлен на языке программирования, то характеристика обрабатываемых величин включается в программу. Учебный алгоритмический язык также предусматривает описание величин, используемых в алгоритме.
Все величины в алгоритме разделяют на постоянные (константы) и переменные. Константа не может изменять свои значения в процессе работы алгоритма. Переменная может приобретать различные значения, которые сохраняются до тех пор, пока она не получит новое значение. Переменным величинам назначают имена. Таким образом, переменная — это именуемая величина, которая в процессе выполнения алгоритма может приобретать и хранить различные значения.
В алгоритмическом языке не существует специальных правил именования переменных. Однако их названия не должны совпадать со служебными словами алгоритмического языка. Во многих языках программирования для имен можно использовать только латинские буквы, цифры, знак подчеркивания. Имена обязательно должны начинаться с буквы, при этом строчные и прописные буквы в именах не различаются. В одном алгоритме не могут существовать разные объекты с одинаковыми именами. Все имена являются уникальными. Имена переменных и констант стараются выбирать так, чтобы они напоминали их смысл. Например, имена переменных и констант: S, p12, result, итог.
При представлении алгоритма на алгоритмическом языке именуются не только величины, но и сам алгоритм, и другие объекты. Имя алгоритма выбирают так же, как и имена переменных.
Величина — переменная, с которой связывается определенное множество значений. Этой величине присваивается имя (в языках программирования его называют идентификатор).
Значение — то, чему равна переменная в конкретный момент. Значение переменной можно задать двумя способами: присваиванием и с помощью процедуры ввода.
Тип переменной определяет диапазон всех значений, которые может принимать данная переменная, и допустимые для нее операции. Существует несколько предопределенных типов переменных. К стандартным типам относятся числовые, литерные и логические типы.
Числовой тип предназначен для обработки числовых данных. Различают целый и вещественный числовые типы. Целый тип в учебном алгоритмическом языке обозначается служебным словом цел, к нему относятся целые числа некоторого определенного диапазона. Они не могут иметь дробной части, даже нулевой. Число 123,0 является не целым, а вещественным числом. Вещественные величины относятся к вещественному типу данных и обозначаются в учебном алгоритмическом языке служебным словом вещ. Такие величины могут отображаться двумя способами: в форме с фиксированной запятой (например, 0,0511 или –712,3456) и с плавающей запятой (те же примеры: 5,11*10-2 и –7,123456*102).
Над числовыми данными можно выполнять арифметические операции и операции сравнения.

Над целыми числами можно также выполнять две операции целочисленного деления div и mod. Операция div обозначает деление с точностью до целых чисел (остаток от деления игнорируется). Операция mod позволяет узнать остаток при делении с точностью до целых чисел. Например, результатом операции 100 div 9 будет число 11, а результатом 100 mod 9 — число 1.
Литерный тип представляет собой символы и строки, он дает возможность работать с текстом. Литерные величины — это произвольные последовательности символов. Эти последовательности заключаются в двойные кавычки: «результат», «sum_price». В качестве символов могут быть использованы буквы, цифры, знаки препинания, пробел и некоторые другие специальные знаки (возможными символами могут быть символы таблицы ASCII). В учебном алгоритмическом языке литерные величины обозначаются лит.
Над литерными величинами возможны операции сравнения и слияния. Сравнение литерных величин производится в соответствии с их упорядочением: «a» < «b», «b» < «с» и т. д. Слияние (конкатенация) литерных величин приводит к образованию новой величины: «пол» + «е» образует «поле».
Логический тип определяет логические переменные, которые могут принимать только два значения — истина (True) или ложь (False). Над логическими величинами можно выполнять все стандартные логические операции.
Команды учебного алгоритмического языка
Учебный алгоритмический язык использует следующие команды для реализации алгоритма:

ОПЕРАЦИЯ ПРИСВАИВАНИЯ
Ко всем типам величин может быть применена операция присваивания, которая обозначается знаком «:=» и служит для вычисления выражения, стоящего справа, и присваивания его значения переменной, указанной слева. Например, если переменная H имела значение 12, а переменная М — значение 3, то после выполнения оператора присваивания H := М + 10 значение переменной H изменится и станет равным 13.
Вычисления в операторе присваивания выполняются справа налево: сначала необходимо вычислить значение выражения справа от знака присваивания. Поэтому допустимы конструкции вида H := Н + 10. В этом случае сначала будет вычислено выражение в правой части (12 + 10), а его результат будет присвоен в качестве нового значения переменной Н (значение 22).
Для оператора присваивания обязательно должны быть определены значения всех переменных в его правой части. Кроме того, типы данных в левой и правой части должны соответствовать друг другу.
ВВОД И ВЫВОД ДАННЫХ
В процессе работы алгоритма происходит обработка исходных данных для получения выходных (результирующих) данных. В процессе этого преобразования могут быть найдены некоторые промежуточные результаты. Входные данные должны быть переданы алгоритму («введены»), а по окончании работы алгоритм должен вывести результат.
При записи алгоритма с помощью блок–схемы ввод и вывод данных отображаются с помощью блоков ввода/вывода (параллелограммов). При этом только указывается перечень данных для ввода или вывода, а сам процесс не детализируется.
Описание алгоритма средствами псевдокода может вовсе не предусматривать команды ввода или вывода данных. В заголовке алгоритма указывается, какие данные являются аргументами, какие — результатами работы алгоритма. Считается, что аргументы будут предоставлены до выполнения алгоритма, результаты будут выведены после его выполнения, и описывается лишь процесс превращения аргументов в результаты.
В записи алгоритма с помощью учебного алгоритмического языка для операций ввода/вывода используются команды ввод и вывод. После этих служебных слов указывается список ввода или вывода. Элементы этих списков перечисляются через запятую.
Список ввода может содержать только имена переменных. После выполнения команды ввод алгоритм получит значения перечисленных в списке переменных.
Список вывода может содержать имена переменных, константы и выражения. Если в списке вывода указано имя переменной, будет выведено ее значение. Если список вывода содержит выражение, будет выведен результат его вычисления. Текстовые константы следует записывать в списке вывода в кавычках (выводиться они будут без кавычек).

Если при выполнении алгоритма ввести значения 20 и 10, то переменная v примет значение 20, а переменная t — значение 10. По окончании работы алгоритма будет выведен результат:
Путь 200 м
Тот же результат был бы получен, если бы изменить строку вывода на
вывод «Путь «, v * t, » м»
Конспект по информатике «Алгоритм. Свойства алгоритмов. Блок-схемы. Алгоритмические языки».
Вернуться к Списку конспектов по информатике.
Билет № 4. 1. Понятие алгоритма: свойства алгоритмов, исполнители алгоритмов
1. Понятие алгоритма: свойства алгоритмов, исполнители алгоритмов. Автоматическое исполнение алгоритма. Способы описания алгоритмов. Основные алгоритмические структуры и их реализация на языке программирования. Оценка эффективности алгоритмов.
Алгоритм — это понятное и точное предписание исполнителю совершить последовательность действий, направленных на решение поставленной задачи или достижение указанной цели.
Термин имеет интересное историческое происхождение. В IX веке великий узбекский математик аль-Хорезми разработал правила арифметических действий над десятичными числами. Совокупность этих правил в Европе стали называть “алгоризм”. Впоследствии слово трансформировалось до известного нам сейчас вида и, кроме того, расширило свое значение: алгоритмом стали называть любую последовательность действий (не только арифметических), которая приводит к решению той или иной задачи. Можно сказать, что понятие вышло за рамки математики и стало применяться в самых различных областях.
Можно выделить три крупных разновидности алгоритмов: вычислительные, информационные и управляющие. Первые, как правило, работают с простыми видами данных (числа, вектора, матрицы), но зато процесс вычисления может быть длинным и сложным. Информационные алгоритмы, напротив, реализуют сравнительно небольшие процедуры обработки (например, поиск элементов, удовлетворяющих определенному признаку), но для больших объемов информации. Наконец, управляющие алгоритмы непрерывно анализируют информацию, поступающую от тех или иных источников, и выдают результирующие сигналы, управляющие работой тех или иных устройств. Для этого вида алгоритмов очень существенную роль играет их быстродействие, т.к. управляющие сигналы всегда должны появляться в нужный момент времени.
Каждый алгоритм — это правила, описывающие процесс преобразования исходных данных в необходимый результат. Заметим, что данное важное свойство в некоторых книгах приводят как определение алгоритма.
Для того чтобы произвольное описание последовательности действий было алгоритмом, оно должно обладать следующими свойствами.
· Дискретность
Процесс решения задачи должен быть разбит на последовательность отдельных шагов, каждый из которых называется командой. Примером команд могут служить пункты инструкции, нажатие на одну из кнопок пульта управления, рисование графического примитива (линии, дуги и т.п.), оператор языка программирования. Наиболее существенным здесь является тот факт, что алгоритм есть последовательность четко выделенных пунктов — такие “прерывные” объекты в науке принято называть дискретными.
· Понятность
Каждая команда алгоритма должна быть понятна тому, кто исполняет алгоритм; в противном случае эта команда и, следовательно, весь алгоритм в целом не могут быть выполнены. Данное требование можно сформулировать более просто и конкретно. Составим полный список команд, который умеет делать исполнитель алгоритма, и назовем его системой команд исполнителя (СКИ).
Требование использовать при составлении алгоритмов только те команды, которые входят в СКИ, связано с тем, что исполнение алгоритма осуществляется формально, без возможности вникнуть в суть команд и проанализировать их.
Одним из таких (вернее, основным из них) “бездушных” исполнителей является ЭВМ. Вообще ЭВМ является универсальным исполнителем алгоритмов. Это связано с тем, что любой алгоритм, составленный для ЭВМ, в конечном итоге транслируется в ее СКИ и, таким образом, становится доступным для исполнения.
· Определенность (детерминированность)
Команды, образующие алгоритм (или, можно сказать, входящие в СКИ), должны быть предельно четкими и однозначными. Их результат не может зависеть от какой-либо дополнительной информации извне алгоритма. Сколько бы раз вы не запускали программу, для одних и тех же исходных данных всегда будет получаться один и тот же результат.
При наличии ошибок в алгоритме последнее сформулированное свойство может иногда нарушаться. Например, если не было предусмотрено присвоение переменной начального значения, то результат в некоторых случаях может зависеть от случайного состояния той или иной ячейки памяти компьютера. Но это, скорее, не опровергает, а подтверждает правило: алгоритм должен быть определенным, в противном случае это не алгоритм.
Определенность также предполагает, что данные, необходимые для выполнения очередной команды алгоритма, получены на одном из предыдущих шагов алгоритма.
· Результативность (конечность)
Результат выполнения алгоритма должен быть обязательно получен, т.е. правильный алгоритм не может обрываться безрезультатно из-за какого-либо непреодолимого препятствия в ходе выполнения. Кроме того, любой алгоритм должен завершиться за конечное число шагов. Большинство алгоритмов данным требованиям удовлетворяют, но при наличии ошибок возможны нарушения результативности.
· Корректность
Любой алгоритм создан для решения той или иной задачи, поэтому нам необходима уверенность, что это решение будет правильным для любых допустимых исходных данных. Указанное свойство алгоритма принято называть его корректностью. В связи с обсуждаемым свойством большое значение имеет тщательное тестирование алгоритма перед его использованием. Как показывает опыт, грамотная и всесторонняя отладка для сложных алгоритмов часто требует значительно больших усилий, чем собственно разработка этих алгоритмов. При этом важно не столько количество проверенных сочетаний входных данных, сколько количество их типов. Например, можно сделать сколько угодно проверок для положительных значений аргумента алгоритма, но это никак не будет гарантировать корректную его работу в случае отрицательной величины аргумента.
· Массовость
Алгоритм имеет смысл разрабатывать только в том случае, когда он будет применяться многократно для различных наборов исходных данных. Например, если составляется алгоритм обработки текстов, то вряд ли целесообразно ограничивать его возможности только русскими буквами — стоит предусмотреть также латинский алфавит, цифры, знаки препинания и т.п. Тем более что такое обобщение особых трудностей не вызывает.
Таковы основные свойства алгоритмов. Если их внимательно проанализировать, то становится очевидным, что исполнитель алгоритма не нуждается в какой-либо фантазии и сообразительности. Более того, для выполнения алгоритма совсем не требуется его понимание, а правильный результат может быть получен путем формального и чисто механического следования содержанию алгоритма.
Из возможности формального исполнения алгоритма следует очень важное следствие: поскольку осознавать содержание алгоритма не требуется, его исполнение вполне можно доверить автомату или ЭВМ. Таким образом, составление алгоритма является обязательным этапом автоматизации любого процесса. Как только разработан алгоритм, машина может исполнять его лучше человека — быстрее и, что очень важно, не ошибаясь.
Основными способами записи алгоритмов являются:
· на алгоритмическом языке;
· на языке программирования высокого уровня.
Основными алгоритмическими структурами (ОАС) являются следование, развилка и цикл. В более сложных случаях используются суперпозиции (вложения) ОАС.
Источник
Правила построения алгоритма
Понятие алгоритма является центральным понятием информатики. Слово «алгоритм» произошло от имени узбекского математика аль-Хорезми, который еще в IX веке сформулировал правила выполнения арифметических действий. В современной математике и информатике термин алгоритм имеет следующие определения:
- — последовательность действий со строго определенными правилами выполнения;
- — предписание, определяющее содержание и последовательность операций, переводящих исходные данные в искомый результат;
- — точное описание некоторого вычислительного процесса или любой иной последовательности действий;
- — точное и полное предписание о последовательности выполнения конечного числа действий, необходимых для решения любой задачи данного типа.
Алгоритм может быть предназначен для выполнения его человеком или автоматическим устройством — формальным исполнителем. Задача исполнителя — точная реализация уже имеющегося алгоритма. Формальный исполнитель не обязан вникать в сущность алгоритма, а возможно, и неспособен его понять.
Примером формального исполнителя может служить стиральная машина-автомат, которая неукоснительно исполняет предписанные ей действия, даже если вы забыли положить в нее порошок. Человек тоже может выступать в роли формального исполнителя, но в первую очередь формальными исполнителями являются различные автоматические устройства, и компьютер в том числе. Каждый алгоритм создается в расчете па конкретного исполнителя.
Каждый исполнитель может выполнять команды только из некоторого строго заданного списка — системы команд исполнителя. Для каждой команды должны быть заданы условия применимости (в каких состояниях среды может быть выполнена команда) и описаны результаты выполнения команды. После вызова команды исполнитель совершает соответствующее элементарное действие.
В информатике универсальным исполнителем алгоритмов является компьютер.
Виды алгоритмов
Алгоритм применительно к вычислительной машине — точное предписание, т. е. набор операций н правил их чередования, при помощи которого, начиная с некоторых исходных данных, можно решить любую задачу фиксированного типа.
Алгоритмы в зависимости от цели, начальных условий задачи, путей ее решения, определения действий исполнителя подразделяются следующим образом:
- Вероятностный (стохастический) алгоритм дает программу решения задачи несколькими путями или способами, приводящими к вероятному достижению результата.
- Эвристический алгоритм (от греческого слова «эврика») — это такой алгоритм, в котором достижение конечного результата программы действий однозначно не предопределено, так же как не обозначена вся последовательность действий, не выявлены все действия исполнителя. К эвристическим алгоритмам относят, например, инструкции и предписания. В этих алгоритмах используются универсальные логические процедуры и способы принятия решений, основанные на аналогиях, ассоциациях и прошлом опыте решения схожих задач.
- Линейный алгоритм — набор команд (указаний), выполняемых последовательно друг за другом.
- Разветвляющийся алгоритм — алгоритм, содержащий хотя бы одно условие, в результате проверки которого ЭВМ обеспечивает переход на один из двух возможных шагов.
- Циклический алгоритм — алгоритм, предусматривающий многократное повторение одного и того же действия (одних и тех же операций) Над новыми исходными данными. К циклическим алгоритмам сводится большинство методов вычислений, перебора вариантов. Цикл программы — последовательность команд (серия, тело цикла), которая может выполняться многократно (для новых исходных данных) до удовлетворения некоторому условию.
- Вспомогательный (подчиненный) алгоритм (процедура) — алгоритм, ранее разработанный и целиком используемый при алгоритмизации конкретной задачи. В некоторых случаях при наличии одинаковых последовательностей указаний (команд) для различных данных с целью сокращения записи также выделяют вспомогательный алгоритм.
Алгоритм можно задать несколькими способами:
- — словесным, то есть записью последовательности действий на естественном языке;
- — графическим, с помощью специальных графических символов;
- — формульным, то есть с помощью математических формул, которые определяют порядок вычислений;
- — табличным, и виде таблицы, в которой фиксируются этапы исполнения алгоритма и результаты исполнения.
Блок-схема алгоритма
Задание алгоритмов с помощью блок-схем оказалось очень удобным средством изображения алгоритмов и получило широкое распространение.
Блок-схема алгоритма — графическое изображение алгоритма в виде связанных между собой с помощью стрелок (линий перехода) и блоков — графических символов, каждый из которых соответствует одному шагу алгоритма. Внутри блока дается описание соответствующего действия.
Источник
Как определить результат работы алгоритма
Понятие алгоритма является центральным понятием информатики. Слово «алгоритм» произошло от имени узбекского математика аль-Хорезми, который еще в IX веке сформулировал правила выполнения арифметических действий. В современной математике и информатике термин алгоритм имеет следующие определения:
- — последовательность действий со строго определенными правилами выполнения;
- — предписание, определяющее содержание и последовательность операций, переводящих исходные данные в искомый результат;
- — точное описание некоторого вычислительного процесса или любой иной последовательности действий;
- — точное и полное предписание о последовательности выполнения конечного числа действий, необходимых для решения любой задачи данного типа.
Алгоритм может быть предназначен для выполнения его человеком или автоматическим устройством — формальным исполнителем. Задача исполнителя — точная реализация уже имеющегося алгоритма. Формальный исполнитель не обязан вникать в сущность алгоритма, а возможно, и неспособен его понять.
Примером формального исполнителя может служить стиральная машина-автомат, которая неукоснительно исполняет предписанные ей действия, даже если вы забыли положить в нее порошок. Человек тоже может выступать в роли формального исполнителя, но в первую очередь формальными исполнителями являются различные автоматические устройства, и компьютер в том числе. Каждый алгоритм создается в расчете па конкретного исполнителя.
Каждый исполнитель может выполнять команды только из некоторого строго заданного списка — системы команд исполнителя. Для каждой команды должны быть заданы условия применимости (в каких состояниях среды может быть выполнена команда) и описаны результаты выполнения команды. После вызова команды исполнитель совершает соответствующее элементарное действие.
В информатике универсальным исполнителем алгоритмов является компьютер.
Виды алгоритмов
Алгоритм применительно к вычислительной машине — точное предписание, т. е. набор операций н правил их чередования, при помощи которого, начиная с некоторых исходных данных, можно решить любую задачу фиксированного типа.
Алгоритмы в зависимости от цели, начальных условий задачи, путей ее решения, определения действий исполнителя подразделяются следующим образом:
- Вероятностный (стохастический) алгоритм дает программу решения задачи несколькими путями или способами, приводящими к вероятному достижению результата.
- Эвристический алгоритм (от греческого слова «эврика») — это такой алгоритм, в котором достижение конечного результата программы действий однозначно не предопределено, так же как не обозначена вся последовательность действий, не выявлены все действия исполнителя. К эвристическим алгоритмам относят, например, инструкции и предписания. В этих алгоритмах используются универсальные логические процедуры и способы принятия решений, основанные на аналогиях, ассоциациях и прошлом опыте решения схожих задач.
- Линейный алгоритм — набор команд (указаний), выполняемых последовательно друг за другом.
- Разветвляющийся алгоритм — алгоритм, содержащий хотя бы одно условие, в результате проверки которого ЭВМ обеспечивает переход на один из двух возможных шагов.
- Циклический алгоритм — алгоритм, предусматривающий многократное повторение одного и того же действия (одних и тех же операций) Над новыми исходными данными. К циклическим алгоритмам сводится большинство методов вычислений, перебора вариантов. Цикл программы — последовательность команд (серия, тело цикла), которая может выполняться многократно (для новых исходных данных) до удовлетворения некоторому условию.
- Вспомогательный (подчиненный) алгоритм (процедура) — алгоритм, ранее разработанный и целиком используемый при алгоритмизации конкретной задачи. В некоторых случаях при наличии одинаковых последовательностей указаний (команд) для различных данных с целью сокращения записи также выделяют вспомогательный алгоритм.
Алгоритм можно задать несколькими способами:
- — словесным, то есть записью последовательности действий на естественном языке;
- — графическим, с помощью специальных графических символов;
- — формульным, то есть с помощью математических формул, которые определяют порядок вычислений;
- — табличным, и виде таблицы, в которой фиксируются этапы исполнения алгоритма и результаты исполнения.
Блок-схема алгоритма
Задание алгоритмов с помощью блок-схем оказалось очень удобным средством изображения алгоритмов и получило широкое распространение.
Блок-схема алгоритма — графическое изображение алгоритма в виде связанных между собой с помощью стрелок (линий перехода) и блоков — графических символов, каждый из которых соответствует одному шагу алгоритма. Внутри блока дается описание соответствующего действия.
Источник
Алгоритм. Свойства алгоритма
Теперь покажем, что конкретный алгоритм обладает этими свойствами. В качестве примера, возьмем алгоритм, изображенный на рис. 1 в виде блок-схемы [6].
Приведенный алгоритм проверяет правильность расстановки скобок, если скобки расставлены правильно – то каждой закрывающей скобке предшествует соответствующая открывающая, а каждой открывающей соответствует закрывающая.
Суть алгоритма заключается в подсчете глубины вложенности скобок друг в друга. Если в какой-то момент глубина получает значение меньше нуля – то скобки расставлены неправильно. Если просмотрены все символы строки, но счетчик не равен нулю – то в строке есть не закрытые скобки (расставлены неправильно). В противном случае скобки расставлены правильно.
Можно сказать, что алгоритм обладает свойством дискретности, так как весь алгоритм разбит на отдельные части (на блок-схеме это хорошо видно).
Доказать детерминированность алгоритма, достаточно сложно, например, когда алгоритм содержит части, которые выполняются параллельно, но не будем сейчас на этом останавливаться. Скажем, что в данном случае программа является детерминированной, т.к. не содержит фрагментов, зависящих от времени выполнения, т.е. сколько бы мы не тестировали алгоритм на одной и той же строке результат не изменится.
Чтобы показать результативность алгоритма, в данном случае достаточно заметить, что любой путь из начальной вершины в конечную содержит блок вывода результата. Перед блоком «конец» алгоритм содержит лишь 2 альтернативные ветви, каждая из которых выводит некоторый результат.
Алгоритм обладает свойством массовости, т.к. исходными данными для него может быть любая конечная последовательность символов. Алгоритм не обладал бы этим свойством, если бы работал лишь ограниченном наборе исходных данных, например на строках «()» и «())», но на остальных наборах не работал или работал не правильно.
Проверить свойство правильности алгоритма достаточно просто, для этого можно взять несколько примеров исходных данных, для которых результат очевиден и протестировать алгоритм на них, но доказать правильность алгоритма достаточно сложно. Доказательство правильности называется верификацией и явно выходит за рамки этой статьи.
В этой статье мы разобрались с тем, что такое алгоритм и какими основными свойствами он должен обладать. К теме алгоритмов я обязательно вернусь в будущих статьях.
Источник
На этой странице вы узнаете
- Почему Шерлок Холмс смог бы стать хорошим программистом?
- Как заставить одну программу анализировать другую?
- Как понять, с чем работал алгоритм?
Пройти из точки А в точку В по строгому алгоритму — одно дело. Но что, если мы повернем время вспять и попробуем угадать начальную точку, зная только конечную? Возможно ли это — узнаем в статье.
Анализ алгоритмов
В предыдущих выпусках мы с вами научились создавать:
- сами алгоритмы — в статье «Основы алгоритмов»;
- код на языке Python в статьях «Основы программирования. Часть 1», «Основы программирования. Часть 2».
Для полного понимания материала этой статьи нам понадобятся некоторые навыки составления алгоритмов, работы с циклами while и for, с условной конструкцией if. Если вы не уверены, что полностью изучили предыдущие темы, советуем «обновить» знания в статьях по ссылкам выше.

Одного лишь навыка написания алгоритмов может быть недостаточно. Имея на руках готовый алгоритм, иногда нам может потребоваться не выполнить его, а наоборот — по результату его работы найти исходные данные. Этим занимался и Шерлок Холмс — по картине места преступления восстанавливал изначальную ситуацию.

Сегодня мы разберем, как именно это делается — как анализируется алгоритм. За пример возьмем нашего старого знакомого — исполнителя Робота из статьи «Основы алгоритмов». Напомним: Робот умеет двигаться в 4 направлениях (вверх, вправо, вниз или влево) и может проверить, находится ли рядом с ним стена, в которую он не должен врезаться.
Допустим, мы знаем, что робот двигался согласно следующему алгоритму:
ПОКА снизу свободно ИЛИ справа свободно
ПОКА справа свободно
вправо
КОНЕЦ ПОКА
ЕСЛИ снизу свободно
ТО
вниз
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
По этому полю:
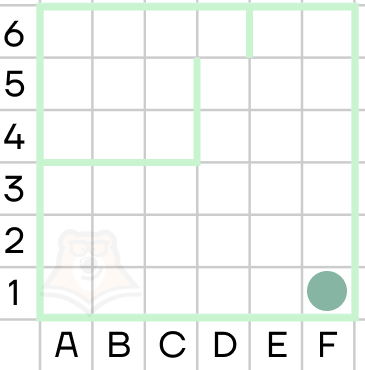
И по итогу Робот остановился в ячейке F1.
Наша задача: определить, из каких ячеек Робот мог начинать движение, чтобы по выполнении этого алгоритма он остановился именно в F1.
Для начала давайте подробнее изучим, как именно двигается робот по полю.
- В первую очередь Робот будет перемещаться вправо до тех пор, пока не упрется в стену. Если справа уже есть стена, он просто ничего не сделает.
- Далее Робот опустится на 1 ячейку вниз, если снизу нет стены. Если стена есть, ничего не произойдет.
- Шаги 1 и 2 будут повторяться до тех пор, пока стена не окажется и справа, и снизу.
Чтобы решить эту задачу, выберем несколько начальных позиций, из которых мы выполним данный алгоритм. Если по выполнении алгоритма Робот остановится в нужной ячейке — начальная позиция была подходящая.
- Начнем двигаться из А6. После первого шага цикла Робот попадет в ячейку D5, сдвинувшись максимально вправо до ячейки D6 и сделав 1 шаг вниз в D5.
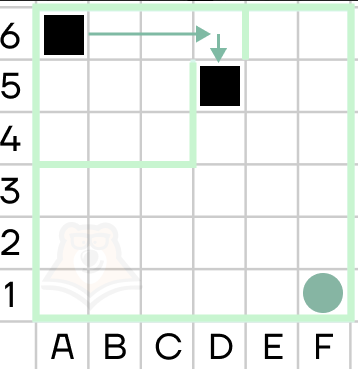
По условию эти же шаги продолжаются, пока и справа, и снизу не окажется стена. Этого пока не произошло, значит, Робот выполняет эти действия еще раз.
- Выполнив те же действия — максимально продвинувшись вправо и сделав 1 шаг вниз — Робот оказывается в ячейке F4.
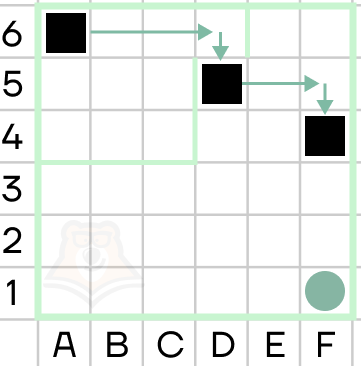
Условие остановки цикла еще не выполнилось, продолжаем двигать Робота.
- Теперь справа у него всегда будет стена, но не снизу. Поэтому первый шаг выполняться уже не будет, а второй — шаг вниз — будет, пока снизу не окажется стена. Так Робот и попадет в ячейку F6, где и прекратит свою работу.
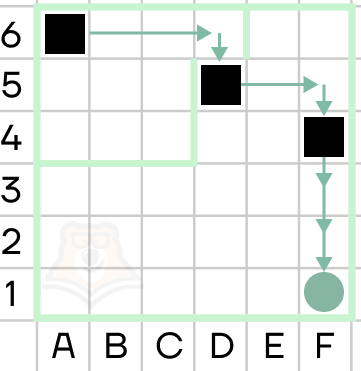
И вот мы знаем, что как минимум А6 подходит под ответ — оттуда можно попасть в F6.
Теперь попробуем начать движение из другой ячейки, например, из А5.
История будет максимально короткая: продвинувшись до конца вправо и сделав шаг вниз, мы попадем в угол. Дальше двигаться не сможем, так как цикл остановится — и справа, и снизу появилась стена.
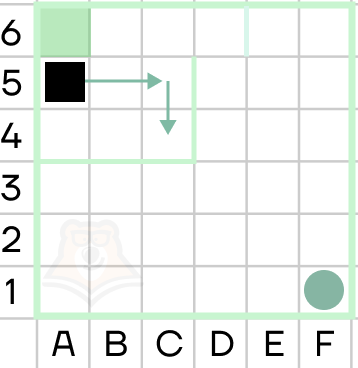
Так что ячейка А5 нам точно не подходит.

Проверив несколько ячеек таким образом, нам уже заметны некоторые закономерности, которые позволяют быстрее выяснить, подходит ячейка или нет. Например:
- Если мы дойдем до самой правой стены, мы спокойно спустимся вниз в нужную ячейку.
- Мы можем начать движение сразу из F1, тогда наш алгоритм моментально будет выполнен, и цель достигнута.
- Нам нельзя попадать в ячейку С4, из нее дальше дороги не будет.
И уже чисто логически, а при необходимости проверив еще пару ячеек, мы можем найти все ячейки, из которых Робот мог начать свою работу:
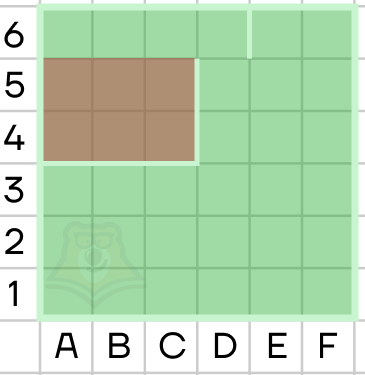
Задания на анализ алгоритма часто встречаются в номерах 15 ОГЭ и 12 ЕГЭ по информатике.
Разберем в качестве примера один из вариантов такого задания.
Сколько клеток лабиринта соответствуют требованию: выполнив предложенную программу, Робот уцелеет и окажется в клетке F6?
ПОКА снизу свободно ИЛИ справа свободно
ПОКА справа свободно
вправо
КОНЕЦ ПОКА
ЕСЛИ снизу свободно ТО
вниз
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
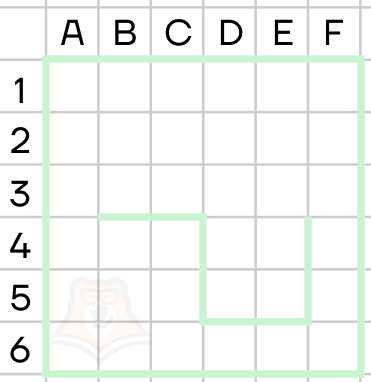
Решение.
Шаг 1. Как работает этот алгоритм? Если справа свободно, то Робот будет двигаться вправо, пока не упрется в стену. Если справа стена, то Робот будет проверять свободно ли снизу и будет двигаться вниз. Отсюда можно сделать вывод, что алгоритм будет работать, пока справа и снизу от Робота не окажутся стены.
Шаг 2. В каких клетках наш алгоритм закончится, не достигнув итоговой ячейки F6? Это клетки с координатами D4, E4, D5, E5. Здесь Робот «окажется в ловушке»: он упрется в стены, двигаясь или вниз, или вправо. Алгоритм будет завершен (так как есть стены справа и снизу), но Робот не достигнет точки F6.
Шаг 3. Что еще нужно учесть?
— В строках 1, 2, 3 Робот сначала будет идти вправо до стены. Затем, уперевшись в стену, он будет двигаться вниз до ячейки F6. Все клетки в столбце F имеют справа стену, а снизу свободны до F6, следовательно, они нам подходят.
— Из любой клетки в строке 6 Робот попадет в клетку F6, двигаясь направо.
— Ячейки А4, В4, С4 и А5, В5, С5 также нам подходят. Из этих клеток Робот будет двигаться направо до ближайшей стены, а далее пойдет вниз. Оказавшись на 6 строчке, Робот дойдет до точки F6.
Итого нам подходят 32 клетки из 36-ти возможных.
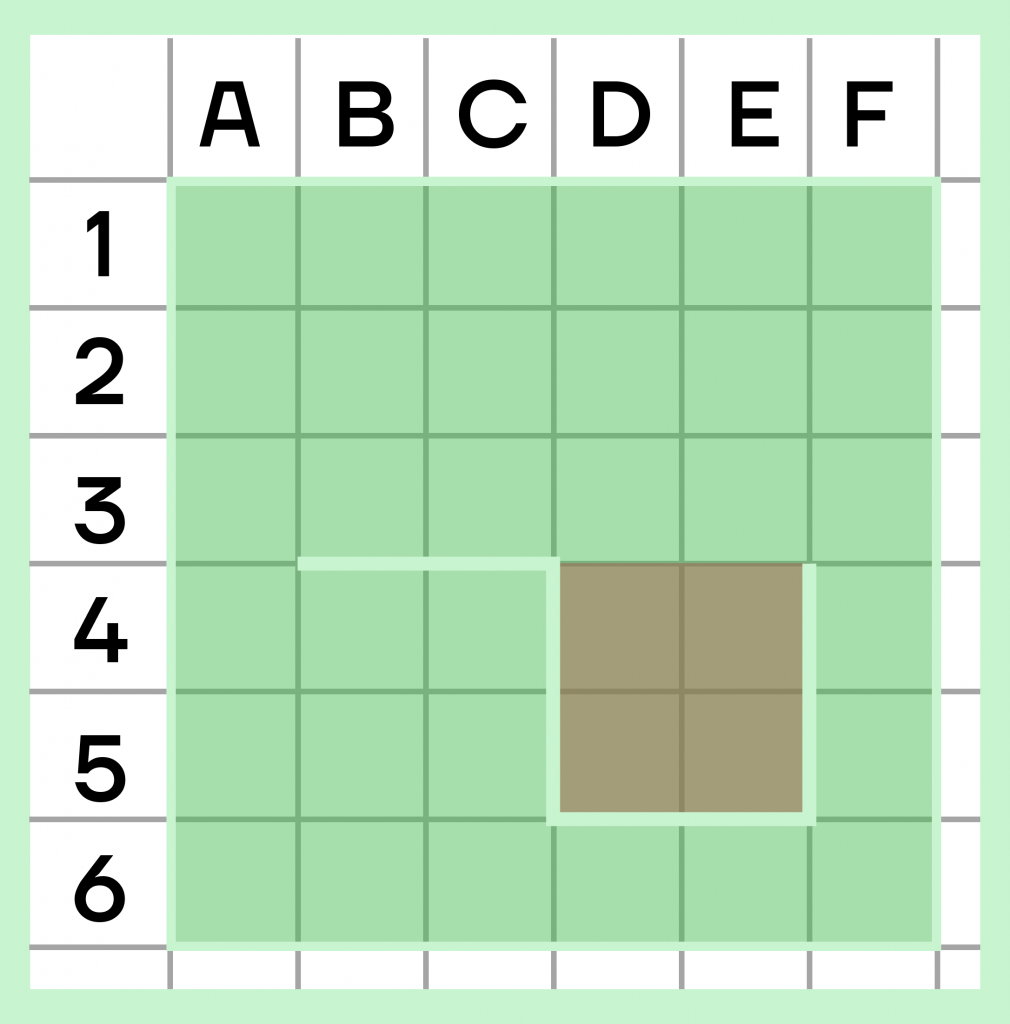
Ответ: 32
Анализ программного кода
Анализ кода может происходить по той же логике, что и анализ алгоритма. Берем несколько входных значений, ищем дополнительные закономерности и логически понимаем, какие еще значения могут быть начальными.
Или мы можем написать другую программу, которая сама будет перебирать возможные начальные значения, прогонять их по алгоритму и проверять, подходят ли они.
Разберем оба способа на примере такой задачи: необходимо найти наибольшее подходящее значение переменной s, при котором следующий код выведет на экран значение 77.
s = int(input())
n = 0
while s + n <= 400:
s = s — 7
n = n + 11
print(n)
Способ 1. Анализ кода
Давайте сразу переведем алгоритм в более понятный вид:
- Нам дано два числа — n и s.
- Пока их сумма не станет больше 400, s будет уменьшаться на 7, а n увеличиваться на 11.
- В конце программы на экран будет выведено значение n.
Отсюда можем уже увидеть интересный момент:
- n из 0 стала равна 77;
- за 1 раз к переменной n прибавлялось 11;
- значит, тело цикла while повторилось ровно 7 раз.
Так как здесь происходят циклические операции над числами, весь процесс можно обернуть в математическое выражение. Изменения обеих переменных происходили ровно 7 раз, а так как после этого цикл завершил работу, сумма их значений стала больше 400:
(s-(7 * 7)+n+(11 * 7)>400).
Решив это неравенство и подставив изначальное n = 0, находим, что s > 372:
(s-49+0+77>400)
(s > 372).
То есть s может принимать значения 373, 374… Но какое наибольшее?
Давайте составим еще одно неравенство. Цикл должен выполниться ровно 7 раз. Значит, если он выполнится 6 раз, цикл еще не остановится. Тогда сумма переменных s и n будет меньше или равна 400:
(s-(7 * 6)+n+(11 * 6) ≤ 400).
Отсюда получим (s ≤ 376):
(s-42+0+66 ≤ 400)
(s ≤ 376).
Итого: s лежит в диапазоне (372 < s ≤ 376).
Значит, наибольшее значение, которое может принять s — это 376.
Способ 2. Анализ с помощью программы
Используя метод решения программированием, мы можем не делать практически никакого анализа. Напишем программу, которая сама будет перебирать различные входящие значения, прогонять их по исходному алгоритму и, если начальное значение подошло, выводить его на экран.

Главный вопрос: какой диапазон начальных значений мы будем перебирать? Без анализа сложно быстро представить, каким примерно окажется правильный ответ.
Есть два, казалось бы, очевидных, но не таких простых варианта:
- Если ничего не мешает, перебираем по какому-нибудь максимально большому диапазону (чтобы он точно включал числа для полного решения задачи).
- Если что-то мешает, выбираем диапазон, в котором ничего не будет мешать.
Что именно нам может помешать, мы рассмотрим чуть позже. В данной задаче никаких помех у нас нет, так что пока не думаем об этом.
Что нам понадобится для реализации новой программы?
- Цикл for, который и будет перебирать различные начальные значения.
- Тело цикла, в котором будет реализован алгоритм из условия задачи.
- Условная конструкция if, которая проверит итоговое значение необходимой переменной.
В диапазоне цикла for, раз нам ничто не мешает, просто ставим достаточно большой диапазон, например, от -1000 до 1000.
Если мы получим ответ, очень близкий к границе диапазона, стоит увеличить его — возможно, мы взяли недостаточно большой.
Наша программа будет выглядеть так:
for i in range(-1000, 1000):
s = i
n = 0
while s + n <= 400:
s = s — 7
n = n + 11
if n == 77:
print(i)
Вывод:
373
374
375
376
Цикл for перебирает переданные ему значения и подставляет их к переменной s, после чего срабатывает код из условия задачи. Если по его выполнении значение переменной n стало равно 77, мы выводим изначальное значение переменной s на экран.
Нам вывелось несколько подходящих значений. По условию задачи нужно взять наибольшее, поэтому из всех значений выбираем максимальное.
И снова мы получили ответ — 376.
А теперь пара слов о том, что может испортить нам жизнь.
Как мы упомянули выше, при таком решении не нужен практически никакой анализ. Небольшие вычисления произвести все-таки придется, чтобы правильно выставить диапазон перебора.
Например, при том же условии (на экран выведено число 77, найти наибольшее возможное исходное значение s), но другом исходном коде наше решение уже не сработает:
s = int(input())
n = 0
while s <= 400:
s = s * 2
n = n + 11
print(n)
При использовании в решении того же диапазона начальных значений (от -1000 до 1000) начальных значений s мы попадаем в бесконечный цикл.
Почему это происходит? Мы берем начальное значение s отрицательным или равным 0 и умножаем его в цикле while на 2. Математика подсказывает нам, что значение операции никогда не станет больше 400. Оно даже выше 0 не поднимется, так как при умножении отрицательных чисел на положительные, получаются отрицательные числа (которые всегда меньше положительных). Также и с числом 0: любое число, умноженное на ноль, всегда будет меньше положительного.
Поэтому при решении этой задачи пользуемся тем же подходом, но не берем в качестве начальных значений отрицательные числа и 0:
for i in range(1, 1000):
s = i
n = 0
while s <= 400:
s = s * 2
n = n + 11
if n == 77:
print(i)
Вывод:
4
5
6
Ответом будет 6.
Задания на анализ кода, аналогичные разобранному выше, могут встретиться вам в номере 6 ОГЭ. Каким способом его решать — вручную (математическими вычислениями) или с помощью другой программы зависит от сложности самого алгоритма. При выборе способа решения мы советуем вам обратить внимание на структуры программы, если там присутствует большое количество ветвлений и циклов, то лучше поручить анализ другой программе.
Подведем итог.
По готовому алгоритму и результатам его работы можно определить, с чем именно работал алгоритм. Для этого у нас есть три варианта действий:
1. Записать исходную программу и, подставив в нее числа, посмотреть, как именно алгоритм их преобразует.
2. Написать дополнительную программу, с помощью которой алгоритм сам введет значения и выведет нам результат работы программы.
3. Посмотреть закономерности при вводе различных значений в наш алгоритм.
В этой статье мы проанализировали простейшие алгоритмы и разобрали несколько примеров на эту тему. Теперь подобные задачи не будут вызывать трудностей. Приглашаем вас продолжить изучение программирования и освоить новые решения для своих задач в статье «Работа со строками в Python».
Термины
Бесконечный цикл — ситуация, когда цикл while сам по себе никогда не сможет завершить свою работу, то есть значение его условия никогда не перестанет быть равным True.
Диапазон начальных значений — диапазон, из которого мы будем брать значения для нашей переменной при решении данной задачи.
Переменная — представляет собой ячейку в памяти компьютера, которая хранит имя и определенное значение.
Цикл (циклическая операция) — это многократное повторение определенной команды или набора команд. Для выделения тела цикла используется табуляция.
Фактчек
- При анализе алгоритма и поиске начальных значений по конечному имеет смысл представить сам алгоритм в более понятной формулировке.
- Мы можем проверить несколько начальных значений, взятых наугад, чтобы найти внутренние неочевидные закономерности. Так мы поймем принцип работы алгоритма и сможем найти начальные значения, пользуясь логикой.
- Один из способов найти исходные данные — записать действия алгоритма в виде математического выражения (если это возможно).
- Можно написать программу, которая сама будет подставлять начальные значения в исходный код и выбирать подходящие.
Проверь себя
Задание 1.
Сколько клеток лабиринта соответствуют требованию: выполнив предложенную программу, Робот уцелеет и окажется в клетке F6?
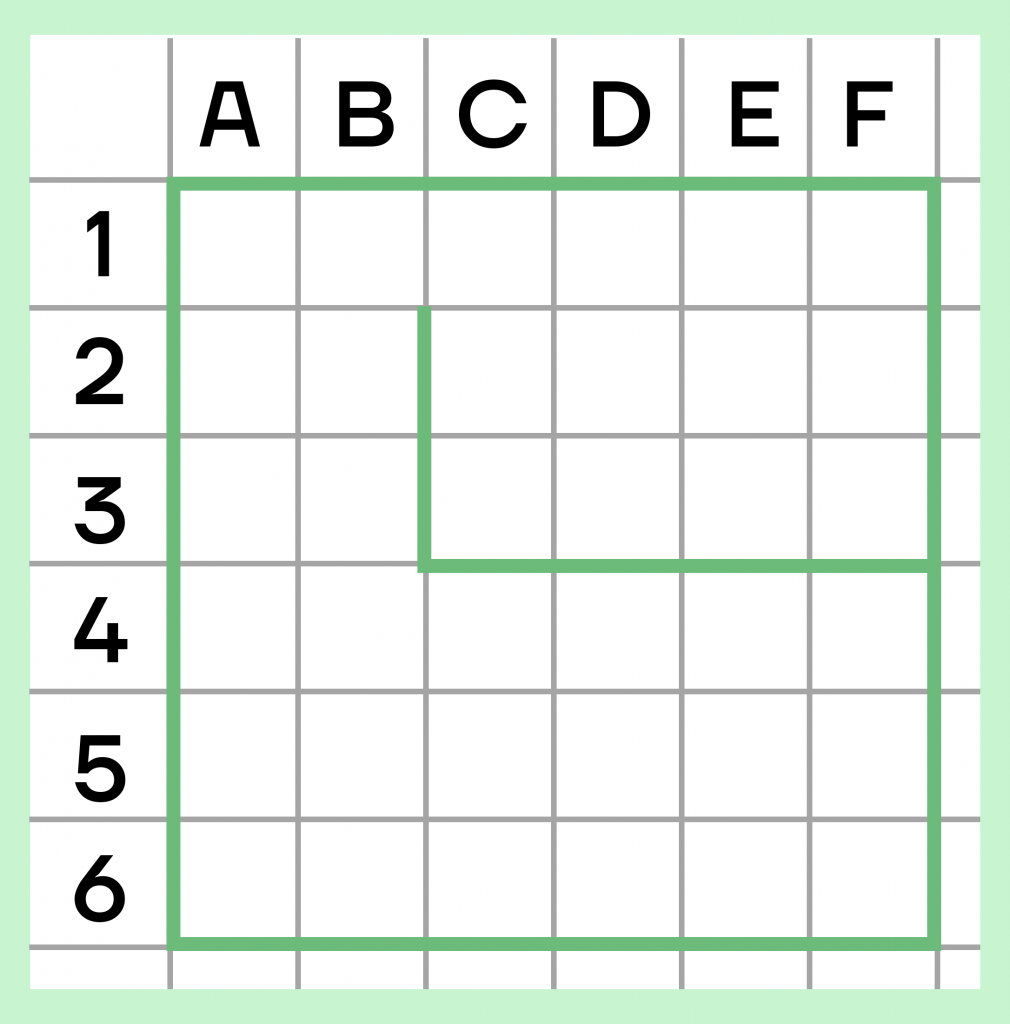
ПОКА снизу свободно ИЛИ справа свободно
ПОКА справа свободно
вправо
КОНЕЦ ПОКА
ЕСЛИ снизу свободно ТО
вниз
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
- 24
- 22
- 28
- 20
Задание 2.
В качестве ответа запишите наименьшее введенное значение s, при котором программа выведет число 1024 в результате своего выполнения.
s = int(input())
n = 1
while s < 75:
s = s + 6
n = n * 2
print(n)
- 15
- 20
- 25
- 30
Задание 3.
В качестве ответа запишите наибольшее введенное значение s, при котором программа выведет число 256 в результате своего выполнения.
s = int(input())
n = 1
while s < 10000:
s = s * 3
n = n * 2
print(n)
- 2
- 4
- 6
- 8
Ответы: 1. — 2; 2. — 1; 3. — 2.
