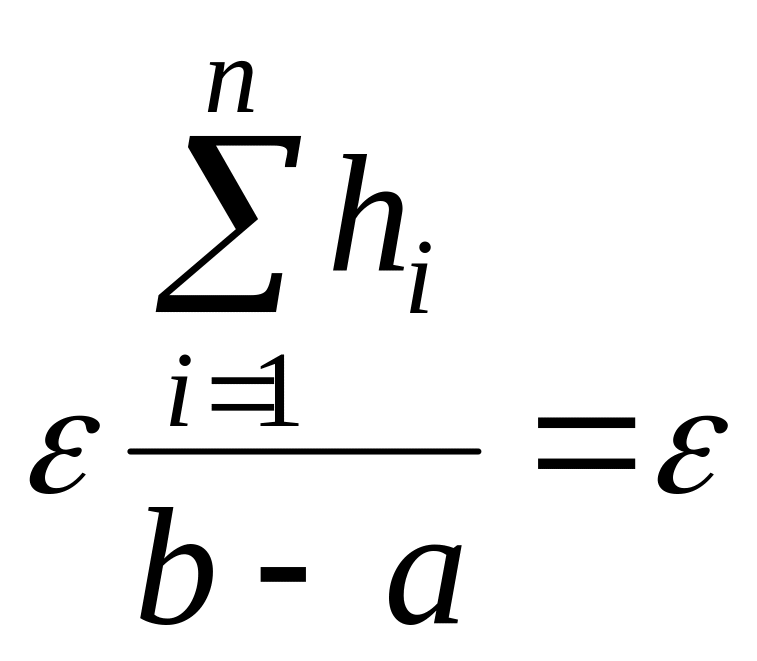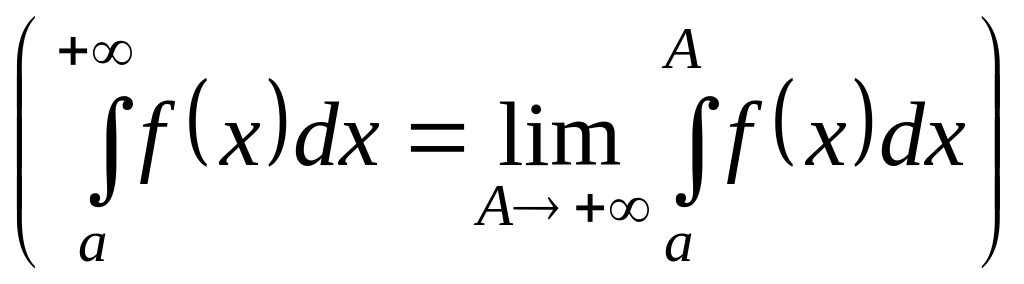Как найти результат с заданной точностью

РЕШЕНИЕ ВЫЧИСЛИТЕЛЬНЫХ ЗАДАЧ С ЗАДАННОЙ ТОЧНОСТЬЮ

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение

На языке алгебры формальные модели записываются с помощью уравнений, точное решение которых основывается на поиске равносильных преобразований алгебраических выражений, позволяющих выразить переменную величину с помощью формулы.

Точные решения существуют только для некоторых уравнений определённого вида (линейные, квадратные, тригонометрические и др.), поэтому для большинства уравнений приходится использовать методы приближённого решения с заданной точностью (графические или численные) [2].

Цель данной работы заключается в том, чтобы получить дополнительныезнания и навыки по этой теме.

Задача состоят в том, чтобы подобрать соответствующий материал с последующей систематизацией, обобщением и иллюстрацией текста, а также практического решения конкретной задачи на языке объектно-ориентированного программирования Python и в табличном процессоре MicrosoftExcel 2010 с использованием построения графика на основании составленной таблицы, языка VisualBasicforApplications (VBA) и надстройки Поиск решения.

Основная часть

Глава 1. Методы решения математических задач с заданной точностью

§ 1.Графические методы решения

Построение графиков функций может использоваться для грубо приближённого решения уравнений. Для уравнений вида f(x) = 0, где f(x) – некоторая непрерывная функция, корень или (корни) этого уравнения являются точкой или (точками) пересечения графика функции с осью X.

Графическое решение таких уравнений можно осуществить путём построения компьютерных моделей:

построением графика функции в системе объектно-ориентированного программирования Python.

в табличном процессоре Microsoft Excel 2010 путём построения диаграммы типа График [2].

§ 2.Численные методы

Для решения уравнений с заданной точностью можно применить разработанные в вычислительной математике численные методы решения уравнения путём последовательных приближений (итераций). Самый простой из них – метод половинного деления. Если мы определим числовой отрезок аргумента x, на котором существует корень, и функция на краях этого отрезка принимает значения разных знаков, то можно использовать метод половинного деления [2]. Можно использовать и другие методы, например дополнительные возможности приложения MS Excel 2010: встроенный язык программирования VisualBasicforApplications (VBA) и надстройку Поиск решения.

Практическая часть

Глава 2. Приближённое решение нелинейных уравнений

§ 3.Содержательная постановка задачи

Задача: Найти корень уравнения x³ – cosx = 0 приближёнными методами (графическим и численным методом деления пополам числового отрезка аргумента) на языках программирования Python и VisualBasicforApplications (VBA), а также надстройки Поиск решения в приложении MSExcel 2010.

§ 4.Формальная модель

Формальная модель задана уравнением x³ – cosx = 0.

Глава 3. Приближённое Решение уравнений с заданной точностью на языке Python

§ 5.Компьютерная модель

Для нахождения корня уравнения разработаем компьютерную модель (скрипты) на языке программирования Python с использование графического и численного методов решения (рис. 5.1, рис. 5.2).

5.1. Графический метод (рис. 5.1)

В начало программного кода ввести модули для работы с графикой matplotlip и функцией cos(x), установим пределы по оси x и y.

Программный код (скрипт):

#Графическое решение уравнения

import numpy as np #импортировать модули для работы с графикой

import matplotlib.pyplot as plt

#импортировать модуль для работы с функцией cos(x)

from math import cos

#построить график уравнения

plt.figure() #создать график

plt.xlim(-2, 2) #установить пределы графика по оси x

plt.ylim(-2, 2) #установить пределы графика по оси y

plt.title(“Графическое решение уравнения”) #установить имя графика

plt.xlabel(“Ось x”) #установить название оси x

plt.ylabel(“Ось y”) #установить название оси y

plt.grid() #добавить сетку на график

#Функция linspace() создает последовательность данных,

#равномерно расположенных на числовой прямой в заданном интервале

x = np.linspace(-2,2,100)

y1 = np.cos(x) #найти значение cos(x)

y = x**3 – y1 #найти значение уравнения

plt.plot(x,y,”b-“) #построение графика сплошной линией синего цвета

plt.show()

Запустить скрипт на выполнение, выполнив команду [Run – RunModule (F5)].

Рис. 5.1. Графическое решение уравнения на языке Python

График функции пересекает ось X один раз, следовательно, уравнение имеет один корень. По графику грубо приближённо можно определить, что  x 0,8 (рис. 5.1) [1].

5.2.Численный метод половинного деления (рис. 5.2)

Идея метода состоит в выборе точности решения и сведении первоначального числового отрезка [A; B], на котором существует корень уравнения, к отрезку заданной точности. Процесс заключается в последовательном делении отрезков пополам точкой C = (A + B) / 2 и отбрасыванию той половины отрезка [А; C] или [C; B], на котором корня нет.

Выбор нужной половины отрезка основывается на проверке знаков значений функции на его краях. Выбирается та половина, на которой произведение значений функции на краях отрицательно, т. е. когда функция имеет разные знаки – пересекает ось абсцисс.

Процесс продолжается до тех пор, пока длина числового отрезка не станет меньше заданной удвоенной точности. Деление этого отрезка пополам даёт значение корня с заданной точностью x (A + B) / 2.

Поместить на форму (рис. 5.2):

текстовые поля для ввода A и B;

текстовое поле для ввода точности вычислений P;

текстовое поле для вывода значений корня;

четыре надписи для вывода обозначений;

кнопку Button для запуска скрипта.

Ввести программный код, позволяющий вычислить корень уравнения методом половинного деления с использованием цикла с постусловием, который будет выполняться, пока выполняется условие (B – A) / 2 > P

В начало программного кода ввести модуль для работы с графикой Tkinter и функцией cos.

Программный код (скрипт):

#Численное решение уравнения

#Подключитьграфическуюбиблиотеку Tkinter

from tkinter import *

import tkinter

top=tkinter.Tk()

#Подключитьмодуль math

from math import cos

#Функция пользователя для командной кнопки

def process():

L2=Entry.get(E1)

L3=Entry.get(E2)

L4=Entry.get(E3)

#Ввод данных с преобразованием типа (float)

L2=float(L2)

L3=float(L3)

L4=float(L4)

while True:

L5 = (L2 + L3) / 2

if (L2*L2*L2 – cos(L2)) * (L5*L5*L5 – cos(L5)) < 0:

L3 = L5

else:

L2 = L5

if (L3 – L2) / 2 < L4: break

Entry.insert(E4,0,L5)

print(L5)

#Чтобы добавить текст, создать 4 компонента (виджет Label),

# ввести названия и установить их позиции

L1=Label(top,text=”Численныйметод“,).grid(row=0,column=1)

L2=Label(top,text=”A =”,).grid(row=1,column=0)

L3=Label(top,text=”B =”,).grid(row=2,column=0)

L4=Label(top,text=”P =”,).grid(row=3,column=0)

L5=Label(top,text=”X =”,).grid(row=4,column=0)

#Для ввода информации создать 4 компонента (текстовые поля – Entry)

E1=Entry(top,bd =5)

E1.grid(row=1,column=1)

E2=Entry(top,bd =5)

E2.grid(row=2,column=1)

E3=Entry(top,bd =5)

E3.grid(row=3,column=1)

E4=Entry(top,bd =5)

E4.grid(row=4,column=1)

#Создать командную кнопку (виджет – Button)

B=Button(top,text=”Выполнить“,command = process).grid(row=5,column=1)

top.mainloop()

Запустить скрипт на выполнение, выполнив команду [Run – RunModule (F5)].

Рис. 5.2. Приближённое решение уравнения на языке Python

с заданной точностью

Из графика функции видно, что корень находится на отрезке [0.5; 1]. Введём в текстовые поля значения концов числового отрезка, а также точность вычислений (например, 0.0001). На надпись будет выведено значение корня: x  0. 8653564453125 (рис. 5.2) [3].

Глава 4. Приближённое Решение уравнений с заданной точностью в приложении MSExcel 2010

§ 6.Компьютерная модель

Для нахождения корня уравнения разработаем компьютерную модель в приложении MS Excel. Представим функцию в табличной форме, построим её график, который позволит определить корень уравнения грубо приближённо.

6.1.Графический метод

Представить заданное уравнение в табличной форме.

В ячейку A1 ввести x;

В ячейку A2 ввести: y = x³ – cosx; поставить курсор после x; для степени выполнить команду[Вставка – Символ – Юникод (шестн.) – Найти в таблице нужное число], кликнуть по найденному числу или нажать на кнопку Вставить;

Выделить диапазон ячеек B1:I1 и B2:I2, щёлкнуть правой кнопкой; выполнить команду [Формат ячеек – Числовой – Число десятичных знаков – 3]<OK>;

В ячейку B1 ввести значение 0,000;

В ячейку C1 ввести формулу: =B1+0,200;

Выделить ячейку C1, щёлкнуть правой кнопкой, в меню выбрать [Копировать], выделить диапазон ячеек D2:I2, по выделенным ячейкам щёлкнуть правой кнопкой и выбрать команду [Вставить].

В ячейку B2 ввести формулу: =B1^3-COS(B1);

Выделить ячейку B2. Выполнить команды пункта 6;

Для изменения границ выделенных ячеек выполнить команду [Главная – Границы – Все границы] (рис. 6.1, рис. 6.2).

Рис. 6.1.Табличное представление уравнения

Выделить таблицу. Выполнить команду [Формулы – Показать формулы].

Рис. 6.2. Табличное представление уравнения с введёнными формулами

Выделить в таблице данные по Y (ячейки диапазона A2:I2) и построить График с маркерами, выполнив команду [Вставка – Диаграммы – График] (рис. 6.10).

Под маркерами ввести подписи данных: выделить построенный график и выполнить команду [Макет – Подписи данных – Справа] (рис. 6.3).

Рис. 6.3. Подписи данных

Для нанесения сетки выполнить команду [Главная – Макет – Сетка – Вертикальные линии – Основные линии сетки] (рис. 6.4).

Рис. 6.4. Основные линии сетки

Чтобы перенести подписи единичных отрезков по оси X вниз, необходимо Выделить график и выполнить команду[Макет – Оси – Основная горизонтальная – Дополнительные параметры основной горизонтальной оси… – Подписи оси – Внизу] (рис. 6.5).

Рис. 6.5. Подписи единичных отрезков

Для корректировки единичных отрезков по оси X согласно исходным данным (рис. 6.1) выполнить команды:

щелкните правой кнопкой мыши по осиXграфика, значения которого вы хотите изменить;

в появившемся меню нажмите Выбрать данные и далее на Изменить (рис. 6.6 – рис. 6.9);

Рис. 6.6. Окно для выбора данных

Рис. 6.7. Диалоговое окно “Выбор источника данных”

в исходной таблице (рис. 6.1) выделить ячейки по строке X, содержащие диапазон значений, на которые необходимо заменить текущие и нажать на кнопку <OK> (рис. 6.8, рис. 6.9).

Рис. 6.8. Ввести диапазон подписей оси x

Рис. 6.9. Диалоговое окно “Выбор источника данных” с заменой значений

Рис. 6.10. График функции

По графику приближённо можно определить, что x 0,800.

6.2. Численный метод половинного деления на языке VBA

Для создания графического интерфейса в MS Excel 2010 запустить систему объектно-ориентированного программирования Visual Basic for Applications (VBA) командой [Файл – Параметры – Настройка Ленты – Основные вкладки – Разработчик] <OK>. Для входа в систему выполнить команду [Разработчик – VisualBasic] или с помощью функциональных клавиш (Alt + F11 – войти в VBA; Alt + Q – закрыть VBA).

В окно интерфейса системы добавить форму командой [Insert –UserForm].

Поместить на форму (рис. 6.11):

кнопку CommandButton1 для запуска событийной процедуры;

два текстовых поля TextBox1 и TextBox2 для ввода числовых значений концов отрезка A и B;

текстовое поле TextBox3 для ввода точности вычислений P

надпись Label5 для вывода значений корня;

четыре надписи для вывода обозначений (Label1 – Label4).

Рис. 6.11. Графический интерфейс проекта

Ввести программный код, позволяющий вычислить корень уравнения методом половинного деления с использованием цикла с постусловием, который будет выполняться, пока выполняется условие (B – A) / 2 > P.

Программный код:

‘Численное решение уравнения

‘Объявить исходные данные типа Single

Dim A, B, C, P As Single

Private Sub CommandButton1_Click()

‘В текстовые окна ввести значения переменных

A = Val(TextBox1.Text)

B = Val(TextBox2.Text)

P = Val(TextBox3.Text)

‘Цикл с постусловием

Do

C = (A + B) / 2

If (A ^ 3 – Cos(A)) * (C ^ 3 – Cos(C)) < 0 Then

B = C

Else

A = C

End If

Loop While (B – A) / 2 > P

‘Полученный результат занести в Label5

Label5 = (A + B) / 2

End Sub

Запустить программу, выполнив команду [Run – RunSub/UserFormF5].

Рис.6.12. Выполнение программного кода

На надпись Label5 будет выведено значение корня: x 0,86541748046875.

Для сохранения программного кода выполнить команду [кнопка Файл – Сохранить как… – Выбрать папку для сохранения документа – Имя файла (Книга1) – Тип файла (Книга Excel с поддержкой макросов) – Сохранить].

Для повторного запуска программного кода выполнить команды:

Войти в приложение MS Excel 2010;

Выполнить команду [кнопка Файл – Параметры – Центр управления безопасностью – Параметры центра управления безопасностью – Параметры макросов – Включить все макросы (не рекомендуется)]<ОК>;

Выполнить команду [кнопка Файл – Открыть – Книга1 – Открыть];

Войти в среду программирования Visual Basic: [Разработчик – VisualBasic];

По окончании работы выполнить команду [Отключить все макросы без уведомления].

6.3.Надстройка – Поиск решения

Установим надстройку Поиск решения, войдя в приложение MSExcel 2010.

В появившемся диалоговом окне ввести команду [Файл – Параметры – Надстройки].В окне Параметры Excel щёлкнуть по кнопке Перейти и поставить галочку Поиск решения, нажать < OK > (рис. 6.13).

Рис. 6.13. Диалоговое окно Надстройки

В табличном процессоре Microsoft Excel 2010 ввести команду [Данные – Поиск решения] (рис. 6.14).

Рис. 6.14. Войти в диалоговое окно Поиск решения

В диалоговом окне Поиск решения установить:

Установить целевую ячейку, т.е. адрес целевой ячейки, предварительно выделив ячейку $F$2;

вариант оптимизации значения целевой ячейки (максимизация, минимизация или Значения – 0);

адрес ячейки, значения которой изменяются в процессе поиска решения (в которых хранятся значения параметров – $F$1).

Нажать на кнопку Найти решение (рис. 6.15, рис. 6.16).

Рис. 6.15. Диалоговое окно Поиск решения

Рис. 6.16. Результаты поиска решения

В ячейке аргумента F1 появится подобранное значение 0,865. Таким образом, корень уравнения x 0,865473833 найден с заданной точностью (рис. 6.17).

Рис. 6.17. Табличное и графическое представление уравнения

с заданной точностью (Надстройка – Поиск решения)

Глава 5. Анализ результатов компьютерного эксперимента

§ 7.Решение на языке Python

Графический метод решения (рис. 7.1)

Рис. 7.1. Графическое решение уравнения

График функции пересекает ось X один раз, следовательно, уравнение имеет один корень. По графику приближённо можно определить, что x 0.8.

Численный метод решения (рис. 7.2)

Рис. 7.2. Приближённое решение уравнения с заданной точностью

(метод половинного деления)

Использование численного метода решения задачи на языке Python даёт боле точный результат: корень уравнения x 0.8653564453125.

§ 8.Решение в приложении MSExcel 2010

Графический метод решения (рис. 8.1, рис. 8.2)

Рис. 8.1. Табличное представление уравнения (приближённые значения)

Рис. 8.2. Графическое представление уравнения

График функции пересекает ось X один раз, следовательно, уравнение имеет один корень. По графику приближённо можно определить, что x 0,8.

Численный метод решения на языке VBA(рис. 8.3)

Рис. 8.3. Выполнение программного кода (метод половинного деления)

Использование численного метода решения задачи в приложении MS Excel на языке объектно-ориентированного программирования Visual Basic  

for Applications (VBA) даёт боле точный результат: корень уравнения  

x 0,86541748046875.

Надстройка – Поиск решения (рис. 8.4)

Рис. 8.4. Табличное и графическое представление уравнения с заданной точностью (надстройка – Поиск решения)

По таблице приближённо можно определить, что x 0,865.

По графику приближённо можно определить, чтоx 0,865473833 .

Полученные результаты вычислений

№ п/п	Используемый метод решения задачи	Заданная точность	Полученный результат
1.	Графический метод решения на языке Python.	0.1	x 0.8
2.	Решение задачи на языке Python с использованием численного метода половинного деления.	0.0001	x 0.8653564453125
3.	Графический метод решения в приложении MS Excel на основании построенной таблицы исходных данных.	0,001	x 0,800
4.	Решение задачи на языке VBA (Visual Basic for Applications) в приложении MS Excel с использованием численного метода половинного деления.	0.0001	x 0,86541748046875
5.	Оптимизационное решение задачи в приложении MS Excel с заданными ограничениями и условиями оптимальности целевой функции с использованием надстройки Поиск решения.	0,001	x 0,865473833

Анализируя полученные данные, можно сделать вывод: численные методы решения уравнения (итерации) с заданной точностью дают более точные результаты по сравнению с графическими методами решения задачи (0,800  0,865); из трёх рассмотренных численных методов решения – наиболее точный результат получен при использовании надстройки Поиск решения в приложении MS Excel 2010: x 0,865473833.

Заключение

Поскольку рассмотренный в данной работе пример решения заданного нелинейного уравнения нельзя решить путём равносильных алгебраических преобразований, рассмотрены пять вариантов решения приближённо с заданной точностью (0,001 – 0.0001), используя языки объектно-ориентированного программирования Python, Visual Basic for Applications и табличный процессор MS Excel 2010 графическими и итерационными методами.

Для решения уравнения на языках программирования точность вычисления корня зависит не только от параметров используемого численного метода, но и от типа переменной.

Для решения уравнения в приложении MS Excel точность подбора зависит от заданной точности представления числа в ячейках таблицы.

Проведённый компьютерный эксперимент наглядно показывает практическую значимость проведённых исследований.

Таким образом, исследование компьютерной модели показало, что решение с заданной точностью даёт более точные результаты по сравнению с графическим методом решения задачи (0,800  0,865).

При использовании языков программирования Python и VisualBasicforApplications (VBA) для приложения MS Excel 2010, а также надстройки Поиск решения были получены следующие значения: x0.8653564453125, x 0.86541748046875, x 0,865473833; последний вариант (надстройка – Поиск решения) – наиболее точный.

Список использованных источников и литературы

Python рисует график функции синуса и косинуса [Электронный ресурс]. – Режим доступа: https://russianblogs.com/article/75031234547/

Исследование информационных моделей. Элективный курс: Учебное пособие / Н.Д. Угринович – М.: БИНОМ. Лаборатория знаний, 2004. – 183 с.

Создание графического интерфейса на Python [Электронный ресурс]. – Режим доступа: https://pythonru.com/uroki/obuchenie-python-gui-uroki-po-tkinter

Программное обеспечение

Операционная система Windows 10

Среда программирования Python – 3.8.0

Приложение Microsoft Office Excel 2010

Приложение Microsoft Office Word 2010

Просмотров работы: 257

Используя приведенные
в разд. 4.4 оценки погрешности вычисления
интегралов, можно априори определить
шаг интегрирования

,
при котором погрешность вычисленного
результата гарантированно не превысит
некоторую заданную погрешность

.
Однако на практике пользоваться
априорными оценками погрешности не
всегда удобно, в таких случаях контроль
за точностью получаемого результата
можно организовать следующим образом.
Пусть вычисления проводились с постоянным
шагом

и

– вычисленное с шагом

приближенное значение интеграла

.
Если затем вычислить приближенное
значение

с шагом

,
то в качестве оценки погрешности
последнего вычисленного значения можно
рассматривать величину

.

При необходимости
вычислить результат с заданной точностью

вычисления повторяют с последовательно
уменьшающимся (обычно вдвое) шагом

до тех пор, пока не выполнится условие

.

Можно применить
указанное правило для контроля за
погрешностью на каждом частичном отрезке

,

.
При этом длина очередного шага

,
посредством последовательного уменьшения
начальной длины вдвое, устанавливается
такой, чтобы выполнялось неравенство

.

Тогда, в худшем
случае, ошибка вычисления значения
интеграла на всем отрезке интегрирования
не будет превосходить сумму локальных
погрешностей

,

то есть не будет
превосходить заданного уровня погрешности.

Способ вычисления
интеграла с автоматическим выбором
шага имеет то преимущество, что он
«приспосабливается» к особенностям
подынтегральной функции: в областях
резкого изменения функции шаг уменьшается,
а там, где функция меняется слабо, –
увеличивается. Такого рода алгоритмы
называются адаптивными,
то есть приспосабливающимися, их
использование позволяет сократить
затраты вычислительных ресурсов без
потери точности вычисления.

Одним из подходов
к экономии вычислительных ресурсов ЭВМ
при необходимости сокращения шага
интегрирования вдвое является сохранение
в памяти ЭВМ результатов промежуточных
вычислений для исходного шага и дополнение
их результатами расчетов, связанных с
введением на отрезках интегрирования
дополнительных точек, располагающихся
в их середине.

4.6. Особые случаи численного интегрирования

Интегрирование
разрывных функций.
Если подынтегральная функция в некоторых
внутренних точках

(
)
отрезка интегрирования

имеет разрыв первого рода (скачок), то
интеграл следует вычислять для каждого
участка непрерывности отдельно, а
результаты складывать. Например, в
случае одной точки разрыва (рис. 4.9)

(
)
имеем

.

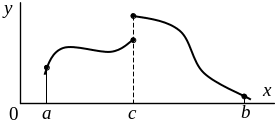
Рис. 4.9. Пример функции, имеющей разрыв
первого рода в точке

.

Для вычисления
каждого из интегралов в правой части
полученного равенства можно использовать
любой из рассмотренных в данной главе
методов.

Несобственные
интегралы.
К такому типу интегралов относятся
интегралы, которые имеют хотя бы один
бесконечный предел интегрирования или
подынтегральную функцию, имеющую разрыв
второго рода – обращающуюся в бесконечность
хотя бы в одной точке отрезка интегрирования.
Рассмотрим интеграл с бесконечной
границей интегрирования, например

.

Один из универсальных
способов вычисления подобных интегралов
заключается в их представлении в виде
суммы двух интегралов:

,

где

– некоторое большое положительное
число, рис. 4.10.

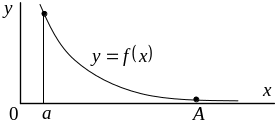
Рис. 4.10. Иллюстрация вычисления
интеграла с бесконечной границей
интегрирования.

Вычисление первого
интеграла на конечном отрезке

не вызывает затруднений. Выбор числа

производят таким образом, чтобы в
пределах допустимой погрешности вторым
интегралом можно было пренебречь.

В случае, когда
подынтегральная функция обращается в
бесконечность в некоторой точке

(
)
отрезка интегрирования

,
интеграл можно приближенно представить
в виде суммы двух интегралов

,

где

– некоторая достаточно малая положительная
величина, рис. 4.11.

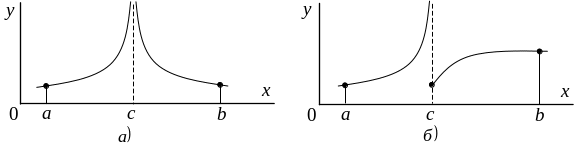
Рис. 4.11. Подынтегральная функция
обращается в бесконечность в некоторой
точке отрезка интегрирования: а) с двух
сторон от нее; б) с одной стороны от нее.

На отрезках

и

подынтегральная функция не имеет
особенностей и соответствующие интегралы
могут быть вычислены с помощью любого
из рассмотренных в данной главе методов.

Замечание. В
некоторых случаях при вычислении
несобственных интегралов подходящая
замена переменной интегрирования
позволяет вообще избавиться от
рассмотренных выше особенностей. Так,
например, при вычислении интеграла

имеется особенность
в точке

,
где подынтегральная функция обращается
в бесконечность. Заменой переменной

(
)
приходим к интегралу

,

который не имеет
особенностей и вычисляется с требуемой
точностью с применением любого из
рассмотренных в данной главе методов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

… метод применяется, если для получения результата требуется довольно ограниченное количество вычислений и если известен диапазон, в котором справедливо решение

Ответ: Аналитический

…dx – это отношение абсолютной погрешности Dx к модулю приближенного значения x¢

Ответ: Относительная погрешность

В методе Гаусса приведение системы линейных уравнений к треугольному виду это …

Ответ: прямой ход

В основе метода … лежит использование разложения функций в ряд Тейлора, причем члены, содержащие вторые и более высоких порядков производные, отбрасываются

Ответ: Ньютона–Рафсона

Во многих случаях, когда функция задана аналитически, определенный интервал вычисляется по формуле …

Ответ: Ньютона–Лейбница

Вычислительные методы делятся на прямые и …

Ответ: итерационные

Для приведенной ниже системы линейных алгебраических уравнений (СЛАУ) свободные члены системы – это …

Ответ: b1, b2 … bn

Для приведенной ниже системы линейных алгебраических уравнений (СЛАУ) a₁₁a₁₂ … aₙₙ – это …

Ответ: постоянные коэффициенты

Для решения систем линейных уравнений с трехдиагональной матрицей используется метод …

Ответ: прогонки

Если выразить относительную погрешность (x) через абсолютную погрешность x и модуль приближенного значения x, получим: …

Ответ: δx = Δx / |x’|

Если коэффициенты ai функции j(x) определяются из условия равенства f(xi) = j(xi), т.е. функции совпадают в заданных известных точках, то такой способ аппроксимации называется …

Ответ: интерполяцией

Если на всем интервале строится одна функция – это … интерполяция

Ответ: глобальная

Задача … функции заключается в том, чтобы для данной функции построить другую, отличную от нее функцию, значения которой достаточно близки к значениям данной функции

Ответ: приближения

Используя графические методы решения задач в математике, …

Ответ: в ряде случаев можно оценить порядок искомой величины, например, найти с определенной точностью корни алгебраического уравнения

Итерационным численным методом приближенного нахождения корня уравнения является метод …

Ответ: хорд

К группе прямых методов относят …

Ответ: метод простых итераций 2)метод хорд

Метод … это способ решения систем линейных алгебраических уравнений с числом уравнений, равным количеству неизвестных с ненулевым главным определителем матрицы коэффициентов системы

Ответ: Крамера

Метод … также известен как метод касательных

Ответ: Ньютона

Метод … является наиболее простым численным методом решения порядок точности (систем) обыкновенных дифференциальных уравнений и имеет первый порядок точности

Ответ: Эйлера

Метод бисекции – это другое название метода …

Ответ: половинного деления

Метод Гаусса и метод Крамера для систем линейных алгебраических уравнений относятся к … методам решения задач в математике

Ответ: аналитическим

Метод прогонки состоит из … этапов

Ответ: двух

Метод простых итераций является …

Ответ: популярным способом численного решения математических задач

Метод решения задачи называется итерационным, если …

Ответ: его смысл заключается в построении последовательных приближений к решению задачи

Метод решения задачи называется простым, если …

Ответ: он позволяет получить решение после выполнения конечного числа элементарных операций

Метод трапеций, метод прямоугольников и метод простых итераций относятся к … методам решения задач

Ответ: численным

Метод хорд является … численным методом приближенного нахождения корня уравнения

Ответ: итерационным

Многочисленные приближенные методы решения систем линейных алгебраических уравнений делятся на две большие группы – … методы и методы итераций

Ответ: прямые

На данный момент … решения систем нелинейных уравнений в общем виде

Ответ: не существует прямых методов

Наиболее эффективным методом решения нелинейных уравнений является метод …

Ответ: касательных

Найти с определенной точностью корни алгебраического уравнения можно с помощью … методов

Ответ: графических

Неверно, что к итерационным методам относится метод …

Ответ: половинного деления

Неверно, что к методам решения нелинейного уравнения относится метод …

Ответ: Крамера

Неверно, что к методам численного интегрирования относят метод …

Ответ: простой итерации

Неверно, что к прямым методам решения систем линейных алгебраических уравнений относят такие методы, как …

Ответ: метод Гаусса метод Крамера

Необходимым и достаточным условием существования единственного решения системы линейных уравнений является неравенство нулю определителя матрицы коэффициентов, а в случае если определитель матрицы равен нулю, …

Ответ: матрица называется вырожденной

Одним из основных численных методов является метод …, на принципах которого основаны остальные методы

Ответ: итераций

Определение аппроксимирующей функции представляет собой задание вида функций и нахождение …

Ответ: ее коэффициентов

При аппроксимации многочленами предварительно задаются степенью многочлена и находят его коэффициенты, при этом отклонение (x) от f(x) …

Ответ: должно быть наименьшим

При сложении или вычитании складываются … погрешности

Ответ: абсолютные

Приближение функции также называют … функции

Ответ: аппроксимацией

Приведенная ниже формула показывает, как получается полином любого порядка при интерполировании функций с помощью метода …

Ответ: Лагранжа

Процесс итераций сходится при условии …

Ответ: |j¢(c)| < 1

Решением дифференциального уравнения называется всякая функция y = (x), которая после ее подстановки в уравнение превращает его в …

Ответ: тождество

Согласно теореме …, если функция f(x) непрерывна на отрезке [a, b], то для любого e > 0 существует многочлен j(x) степени m = m(e), абсолютное отклонение которого от функции f(x) на отрезке [a, b] меньше e

Ответ: Вейерштрасса

Содержать некоторую погрешность (ошибку) может решение, получаемое … методом решения задач

Ответ: численным

Сущность методов конечных разностей состоит в том, что область непрерывного изменения аргумента и функции заменяется дискретным множеством точек, называемых …, которые составляют разностную сетку

Ответ: узлами

Условием существования корня непрерывной функции на интервале является …, что говорит о том, что на данном интервале функция изменяет знак, т.е. пересекает ось x

Ответ: f(a) + f(b) < 0 f(a) ∙ f(b) < 0

Уточнение корня – это вычисление приближенного значения корня с заданной точностью …

Ответ: e > 0

Формулы численного интегрирования называются …

Ответ: квадратурами+

9. Циклы while и repeat

Предыдущий раздел:

Следующий раздел:

При реализации многих численных методов точность вычислений зависит от числа шагов. Однако за какое именно число шагов будет достигнута приемлемая точность, заранее сказать трудно и желательно, чтобы программа сама определяла, когда следует остановиться.

Например, синус можно разложить в так называемый ряд Тейлора:

Чем большее количество членов ряда будет просуммировано, тем точнее будет вычислен синус. Пусть требуется вычислить до 5-го знака после запятой. То есть приемлемая погрешность . Для этого достаточно суммировать члены ряда до тех пор, пока очередной член ряда не окажется меньше 10^-5.

  eps:=1e-5;
  readln(x);
  p:=x;
  s:=x;
  n:=2;
  while abs(p)>eps do {Условие выхода: очередной член ряда по модулю меньше eps}
  begin
    p:=-p*x*x/(n*(n+1)); {Вычисление очередного члена ряда}
    s:=s+p;
    n:=n+2;
  end;
  writeln('sin(x) = ', s);

Если вычисления производятся в соответствии с рекуррентными соотношениями, то еще один способ поставить связанное с точностью условие прекращения вычислений заключается в следующем. Вычисления прекращаются, если изменение вычисляемой величины на очередном шаге меньше заданной величины:

Также условие можно наложить на относительное изменение:

Следующий раздел:

Предыдущий раздел:

Добавить комментарий