Как найти результативный вектор

Содержание

• Примеры
• Геометрические методы сложения двух векторов
• Метод параллелограмма
• Упражнения
• -Упражнение 1
• Решение
• Упражнение 2.
• Решение
• Вычисление декартовых компонент результирующего вектора
• Величина и направление результирующего вектора
• Ссылки

В результирующий вектор – это результат, полученный с помощью операции с векторами, результатом которой также является вектор. Обычно эта операция представляет собой сумму двух или более векторов, с помощью которой получается вектор с эквивалентным эффектом.

Таким образом получаются такие векторы, как результирующая скорость, ускорение или сила. Например, когда на тело действует несколько сил. F₁, F₂, F₃,…. векторная сумма всех этих сил равна чистой силе (равнодействующей), которая математически выражается следующим образом:

F₁ + F₂ + F₃ +… = F_р или F_N

Результирующий вектор, будь то силы или любая другая величина вектора, находится с применением правил сложения векторов. Поскольку векторы имеют направление и смысл, а также числовое значение, недостаточно добавить модули, чтобы получить результирующий вектор.

Это верно только в том случае, если задействованные векторы направлены в одном направлении (см. Примеры). В противном случае необходимо использовать методы векторной суммы, которые в зависимости от случая могут быть геометрическими или аналитическими.

Примеры

Геометрическими методами нахождения результирующего вектора являются метод траверса и метод параллелограмма.

Что касается аналитических методов, существует метод компонентов, с помощью которого можно найти вектор, полученный из любой системы векторов, при условии, что у нас есть его декартовы компоненты.

Геометрические методы сложения двух векторов

Предположим, что векторы или Y v (Мы обозначили их жирным шрифтом, чтобы отличить их от скаляров). На рисунке 2а) они расположены на плоскости. На рисунке 2 б) он переведен в вектор v таким образом, что его начало совпадает с концом или. Результирующий вектор идет от начала координат первого (или) до кончика последнего (v):

Результирующая фигура в этом случае представляет собой треугольник (треугольник – это 3-сторонний многоугольник). Если у нас есть два вектора в одном направлении, процедура такая же: поместите один из векторов за другим и нарисуйте тот, который идет от начала или хвоста первого до конца или конца последнего.

Обратите внимание, что порядок, в котором выполняется эта процедура, не имеет значения, поскольку сумма векторов коммутативна.

Также обратите внимание, что в этом случае модуль (длина или размер) результирующего вектора – это сумма модулей добавленных векторов, в отличие от предыдущего случая, когда модуль результирующего вектора меньше суммы модулей участников.

Метод параллелограмма

Этот метод очень подходит, когда вам нужно добавить два вектора, исходные точки которых совпадают, скажем, с началом системы координат x-y. Предположим, что это так для наших векторов или Y v (рисунок 3а):

На рисунке 3b) параллелограмм построен с помощью пунктирных линий, параллельных или уже v. Результирующий вектор имеет начало в точке O и конец в точке пересечения пунктирных линий. Эта процедура полностью эквивалентна описанной в предыдущем разделе.

Упражнения

-Упражнение 1

Учитывая следующие векторы, найдите результирующий вектор с помощью метода обхода.

Решение

Метод траверса – первый из известных. Помните, что сумма векторов коммутативна (порядок слагаемых не влияет на сумму), поэтому вы можете начать с любого из векторов, например или (рисунок 5а) или р (рисунок 5b):

Полученная фигура представляет собой многоугольник, а результирующий вектор (синий) называется р. Если вы начнете с другого вектора, сформированная форма может быть другой, как показано в примере, но результирующий вектор будет таким же.

Упражнение 2.

На следующем рисунке известно, что модули векторов или Y v соответственно они равны u = 3 условных единицы и v = 1,8 условных единиц. Угол, который или форма с положительной осью абсцисс составляет 45º, а v образует 60º с осью Y, как показано на рисунке. Найдите результирующий вектор, величину и направление.

Решение

В предыдущем разделе результирующий вектор был найден методом параллелограмма (на рисунке выделен бирюзовым цветом).

Простой способ найти результирующий вектор аналитически – выразить слагаемые векторы через их декартовы компоненты, что легко, когда известны модуль и угол, например векторы в этом примере:

или_Икс = u. cos 45º = 3 x cos 45º = 2,12; или_Y = u. грех 45º = 3x грех 45º = 2,12

v_Икс = v. sin 60º = 1,8 x sin 60º = 1,56; v_Y = -v. cos 60º = -1,8 x cos 60º = – 0,9

Векторы или Y v это векторы, принадлежащие плоскости, поэтому каждый из них имеет по две компоненты. Вектор u находится в первом квадранте, а его компоненты положительны, а вектор v – в четвертом квадранте; его компонент x положительный, но его проекция на вертикальную ось падает на отрицательную ось y.

Вычисление декартовых компонент результирующего вектора

Результирующий вектор находится путем алгебраического сложения соответствующих компонентов x и y, чтобы получить их декартовы компоненты:

р_Икс = 2.12 + 1.56 = 3.68

р_Y = 2.12 + (-0.9) = 1.22

Как только декартовы компоненты указаны, вектор становится полностью известным. Полученный вектор можно записать в квадратных скобках (подтяжки):

 R = <3,68; 1,22> условные единицы

Обозначение в квадратных скобках используется для отличия вектора от точки на плоскости (или в пространстве). Другой способ выразить полученный вектор аналитически – использовать единичные векторы я и j в плоскости (я, j Y k в пространстве):

р = 3.68 я + 1.22 j условные единицы

Поскольку обе компоненты результирующего вектора положительны, вектор р принадлежит к первому квадранту, который ранее уже был замечен графически.

Величина и направление результирующего вектора

Зная декартовы компоненты, величина R вычисляется по теореме Пифагора, так как полученный вектор рвместе со своими компонентами R_Икс и R_Y образуют прямоугольный треугольник:

Величина или модуль: R = (3.68² + 1.22²)^½ = 3.88

Направление q, взяв за основу положительную ось x: q = arctan (R_Y / Р_Икс) = arctg (1,22 / 3,68) = 18,3 º

Ссылки

1. Добавление векторов и правил. Получено с: newt.phys.unsw.edu.au
2. Фигероа, Д. Серия: Физика для науки и техники. Том 1. Кинематика. 31-68.
3. Физический. Модуль 8: Векторы. Получено с: frtl.utn.edu.ar
4. Хиббелер, Р. 2006. Механика для инженеров. Статический. 6-е издание. Континенталь Издательская Компания. 15-53.
5. Калькулятор сложения векторов. Получено с: www.1728.org

In mathematics, we often heard about the two terms scalar and vector. Scalar is a quantity which has only magnitude i.e. Scalar quantity describes the distance. On the other hand, Vector is a quantity which deals with both magnitude and direction. Vector quantity has both magnitude and direction.

Resultant vector formula gives the resultant value of two or more vectors. The result is obtained by computing the vectors with consideration of the direction of each vector with respect to others. This formula has various applications in Engineering & Physics. Based on the direction of a vector with respect to other vectors, the Resultant Vector formula is classified into three types.

Resultant vector 1st formula

If the vectors are in the same direction then the resultant of the vector can be calculated by adding the vectors which are in the same direction. Let “a” and “b” are the vectors with the same direction then the resultant vector “r” is given by-

r = a + b

Resultant vector 2nd formula

If the vectors are in different directions then the resultant of the vector can be calculated by subtracting the vectors from each other. Let “b” be a vector which is in opposite direction with respect to vector “a” then the resultant vector “r” is given by-

r = a – b

Resultant vector 3rd formula

If any vectors are inclined to each other at some angle then the resultant of these vectors can be calculated by this formula. Let “a”, and “b” are two vectors inclined to each other at an angle θ, then the resultant vector “r” is given by-

r = a² + b² + 2abcosθ

Here a², b² represents magnitude of the vector a, b.

Sample Problems

Question 1: Find the resultant vector for the vectors i+2j+3k and 4i+8j+12k

Solution:

Given two vectors are a=i+2j+3k and b=4i+8j+12k

The direction ratios of the two vectors are in equal proportion. So two vectors are in the same direction.

The resultant vector formula for the given vectors is given by-

r = a + b

= (i+2j+3k) + (4i+8j+12k)

= 5i+10j+15k

The resultant vector from the given vectors is 5i+10j+15k

Question 2: Find the resultant vector for the vectors i-2j+5k and 2i-4j+10k

Solution:

Given two vectors are a=i-2j+5k and b=2i-4j+10k

The direction ratios of the two vectors are in equal proportion. So two vectors are in the same direction.

The resultant vector formula for the given vectors is given by-

r = a + b

= (i-2j+5k) + (2i-4j+10k)

= 3i-6j+15k

The resultant vector from the given vectors is 3i-6j+15k

Question 3: Find the resultant vector for the vectors 2i-2j+k and 2i+7j+3k

Solution:

Given two vectors are a=2i-2j+k and b=2i+7j+3k

The direction ratios of the two vectors are not in equal proportions. So two vectors are in opposite direction.

The resultant vector formula for the given vectors is given by-

r = a – b

= (2i-2j+k) – (2i+7j+3k)

= 0i-9j-2k

The resultant vector from the given vectors is 0i-9j-2k

Question 4: Find the resultant vector for the vectors 9i+2j-3k and i-3j+2k

Solution:

Given two vectors are a=9i+2j-3k and b=i-3j+2k

The direction ratios of the two vectors are not in equal proportions. So two vectors are in opposite direction.

The resultant vector formula for the given vectors is given by-

r = a – b

= (9i+2j-3k) – (i-3j+2k)

= 8i+5j-5k

The resultant vector from the given vectors is 8i+5j-5k

Question 5: Find the resultant of the vectors 2i+2j+2k and i+2j+3k which are inclined at an angle 30° to each other.

Solution:

Given two vectors are a=2i+2j+2k and b=i+2j+3k

Also given that given two vectors are inclined at an angle θ=30°

So the resultant vector formula for the given vectors is given by-

r = a² + b² + 2abcosθ

Magnitude of vector a (a²) = sqrt{2^2+2^2+2^2}

= sqrt{4+4+4}

=√12

a²=2√3

Magnitude of vector b (b²) = sqrt{1^2+2^2+3^2}

= sqrt{1+4+9}

=√14

b²=√14

r = a² + b² + 2abcosθ

= 2√3 + √14 + 2(2√3)(√14)cos30°

= 2√3 + √14 + 4(√3)(√14)(√3/2)

= 29.65

The resultant vector from the given vectors is 29.65

Question 6: Find the resultant of the vector having magnitude 2, 4 which is inclined at 45°.

Answer:

Given,

Magnitude of vector a (a²)=2

Magnitude of vector b (b²)=4

θ = 45°

So the resultant vector formula for the given vectors is given by-

r = a² + b² + 2abcosθ

= 2+4+2(2)(4)cos45°

= 6+16×(1/√2)

= 17.31

The resultant vector from the given vectors is 17.31

Last Updated :
10 Jun, 2022

Like Article

Save Article

В механике существуют два типа величин:

• скалярные величины, задающие некоторое числовое значение – время, температура, масса и т.д.
• векторные величины, которые вместе с некоторым числовым значением задают направление – скорость, сила и т.д..

Рассмотрим сначала алгебраический подход к сложению векторов.

Покоординатное сложение векторов.

Пусть даны два вектора, заданные покоординатно ( чтобы вычислить координаты вектора, нужно вычесть из соответствующих координат его конца соответствующие координаты его начала, т.е. из первой координаты – первую, из второй – вторую и т.д.):

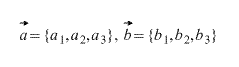
Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:

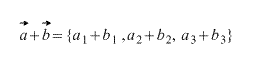
В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.

Теперь перейдем к геометрическому смыслу сложения двух векторов:

При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:

• правило параллелограмма
• правило треугольника
• тригонометрический способ

Правило параллелограмма. Сложение векторов по правилу параллелограмма.

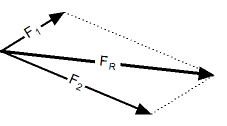Процедура сложения векторов по правилу параллелограмма заключается в следующем: нарисовать первый вектор, учитывая его величину и направление от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление дополнить рисунок до параллелограмма, считая, что два нарисованных вектора – это его стороны результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.

Правило треугольника. Сложение векторов по правилу треугольника.
	Сложение векторов по правилу треугольника заключается в следующем: нарисовать первый вектор, используя данные о его длине ( числовой величине) и направлении от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец – с концом второго.

Тригонометрический способ. Сложение векторов тригонометрическим способом.

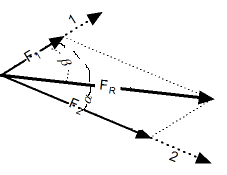Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов: Fрез. = [ F12 + F22 -2 F1 F2 cos(180о-α) ]1/2         (1) где F = числовое значение вектора α = угол между векторами 1 и 2 Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов: β = arcsin[ F2 *sin(180o-α) / FR ]         (2) где α = угол между исходными векторами

Пример – сложение векторов.

Сила 1 равна 5кН и воздействует на тело в направлении, на 80^o отличающемся от направления действия второй силы, равной 8 кН.

Результирующая сила вычисляется следующим образом:

F_рез = [ (5 кН)² + (8 кН)² – 2 (5 кН)(8 kН) cos(180^o – (80^o)) ]^1/2

    = 10,14кН

Угол между результирующей силой и первой силой равен:

β= arcsin[ (8кН) sin(180^o – (80^o)) / (10,14кН) ]

    = 51^o

А угол между второй и результирующей силой можно посчитать следующим образом: as

α = arcsin [ (5 кН) sin(180^o – (80^o)) / (10,2 кН) ]

    = 29^o

Он-лайн калькулятор сложения векторов.

Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.

В контексте физика , называется вектор к величина который определяется его адресом, точкой применения, количеством и значением. По его характеристикам можно говорить о разных видах векторов.

В латыни мы можем найти этимологическое происхождение этого термина, которое происходит именно от «vector-vectoris», что можно перевести как «тот, кто ведет».

Идея результирующий вектор может появиться, когда операция из сумма С векторами Используя звонок полигональный метод Вы должны поместить векторы, которые вы хотите добавить, рядом друг с другом на графике, чтобы начало каждого вектора совпадало с концом следующего вектора. Это называется результирующий вектор к вектору, который имеет начало, совпадающее с первым вектором и заканчивающееся в конце вектора, расположенного в последнем месте .

VR – это аббревиатура, используемая для обозначения результирующего вектора, который, как и остальные векторы, при анализе требует учета трех элементов, которые его формируют. Мы имеем в виду следующее:
-Модуль, который используется, чтобы упомянуть, какова интенсивность его величины и представлен, каков размер вектора.
Направление, которое относится к тому, что такое наклон линии.
-Смысл, который имеет особенность быть представленным тем, что является вершиной стрелки рассматриваемого вектора.

Добавление векторов через этот метод подразумевает движение векторы, заставляя их соединяться своими концами. Таким образом, мы возьмем вектор и поместим его рядом с другим, чтобы начало одного связывалось с концом другого. Результирующий вектор “Born” в начале первого вектора мы берем и «Окончание» В конце таблицы мы поместили в последний пробел.

Имейте в виду, что для добавления векторов с помощью полигонального метода важно не изменять свойства : векторы должны быть только перемещены.

Важно помнить, что, когда можно взять эту сумму, которая нас интересует, необходимо прибегнуть к некоторым фундаментальным элементам в математике и алгебре. Мы имеем в виду координатные оси X и Y. По сути, из этих и их соответствующих сумм мы получаем итоговый вектор.

Существует также разговор о результирующем векторе со ссылкой на тот, который в система , генерирует тот же эффект, что и векторы, составляющие его. Вектор, имеющий то же направление и величину, но в противоположном направлении, квалифицируется как уравновешивающий вектор.

Этот упомянутый уравновешивающий вектор, который также называется VE, как мы уже говорили, имеет противоположное направление, противоположен тому, что составляет 180º.
В дополнение к упомянутым есть много других типов векторов, таких как копланарные, параллельные, противоположные, параллельные, коллинеарные, фиксированные векторы …

Видео: Вектора и операции над векторами (May 2023).

Скользящие векторы, сходящиеся в одной точке. Результирующий вектор

• Учитывая вектор движения P2 hGF9, его линии действия пересекаются в определенной точке A. Каждый из этих векторов может двигаться вдоль своей линии действия. 11. Тогда результирующий вектор системы рассматриваемых векторов равен геометрической сумме, вектору Р, приложенному к точке А, или другому вектору, полученному в результате переноса вектора Р вдоль его линии action. Как показано на Рисунке результирующий вектор геометрически равен соответствующему заданному вектору AP , P ,… найденная путем построения непрерывно, точка А является начальным вектором. Результирующий вектор P соответствует A 2n. Проекция результирующего вектора.

Может, наконец, случиться, что изображаемая физическая величина такова, что два различных вектора изображают две различные физические величины, т.
Людмила Фирмаль

Мы уже указывали пункт 4.Проекции X, Y и 2 на координатные оси
результирующего вектора P соответственно равны сумме проекций
составляющих векторов X = Xx+ 2 + + н Г = Ык. 2 = 2К. Результирующий
вектор относительного момента Координатные оси. если он представлен x,
y, 2, то моменты вектора Pk Xk, Yk, 2k для осей имеют вид: = Г к 2 к МК =
rXk x2k, НК = значения ых И момент результирующего вектора для той же
оси будет равен: Д. = У2 ЗГ. М = ГХ Х2. Ч = ху ух. Координаты точки
А Исходя из значений X, K, 2 выше, b = b1 + b2 + … м =. = 2И к. Итак,
6 координат X, Y, 2, I, M, N в результирующем векторе будут равны сумме
соответствующих координат компонента вектора.

• Поскольку любую ось можно рассматривать как координату 1, то можно видеть, что проекция результирующего вектора заданной системы векторов, линии действия которых пересекаются в 1 точке на любой оси, равна сумме проекций этих векторов на одну и ту же ось. Момент результирующего вектора для оси равен сумме моментов составляющих вектора вокруг этой оси. Теорема валиньона. Отсюда это выглядит так: в момент результирующего вектора системы сходящихся векторов для определенной точки о равен геометрической сумме моментов компонент вектора.

Такого рода векторы, не имеющие ни определенной линии действия, ни определенной точки приложения, называются свободными.
Людмила Фирмаль

В самом деле, точки o, как происхождение, Я, м, х, точка О
результатах против вектора момента ОО осей проекции, Лк, Мк, Ик той же
точки относительно вектора Рк от 06к проекция будет. Однако предыдущие
равенства, 06 это вектор 06x, OO2,…. Это показывает, что это
геометрическая сумма 06г. Примечание иногда кажется необходимым
разложить данный вектор AP на другие векторы, применяемые в точке
A. Например, с помощью параллелограмма всегда можно разложить вектор AP
на 2 других с заданным направлением AB и AC, где плоскость содержит AP.

Смотрите также:

Предмет теоретическая механика