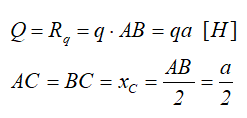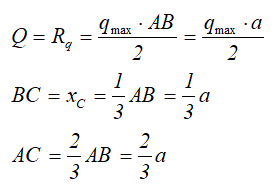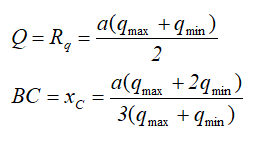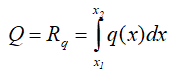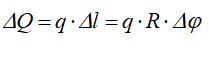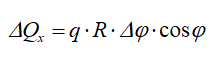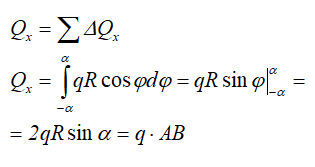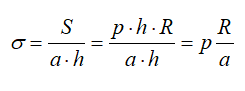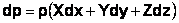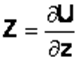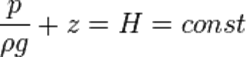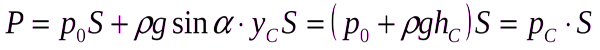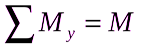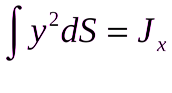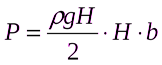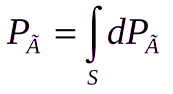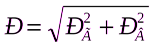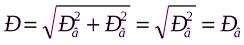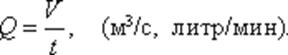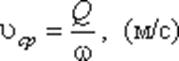Как найти результирующее давление

Результирующее давление

Cтраница 1

Результирующее давление на ось блоков Р проще всего определяется графическим путем, как показано на фиг.
 [1]

Результирующее давление получено посредством суммирования давлений, обусловленных стационарным движением и влиянием сил инерции.
 [2]

Результирующее давление взрыва в каждый момент времени определяется совместным решением обоих уравнений.
 [3]

Если результирующее давление окажется превосходящим критическое для данной пленки значение, происходит скачкообразное падение сопротивления на участке адсорбции агрессивных анионов.
 [4]

Если результирующее давление G pUI1T – – p, то выходное звено механизма МИМ ППХ будет перемещаться вниз, а если G – р – 1, то выходное звено перемещается вверх.
 [5]

Направление результирующего давления получается поворотом вектора скорости невозмущенного потока на пря: ой угол против циркуляции.
 [6]

Эпюра результирующих давлений гусениц с зоной отрицательных давлений недопустима, так как видно, что часть поверхности гусениц при принятых параметрах не работает.
 [7]

Подсчитаем теперь результирующее давление Р и результирующую силу вязкости на ту часть движущейся плоскости, которая находится непосредственно под пластинкой.
 [8]

Далее мы найдем результирующее давление, складывая давления, вызываемые данными источниками; поэтому слагающая результирующей скорости потока по данному направлению пропорциональна отрицательной производной от давления, взятой по этому направлению; та же слагающая пропорциональна слагающей результирующего действия электрических частиц по тому же направлению.
 [9]

При роР & результирующее давление на дне сосуда равно pgh, где h – глубина жидкости в сосуде.
 [10]

Это выражение количественно Определяет результирующее давление, действующее на диафраг-му.
 [11]

Поэтому молекулы воздуха создают результирующее давление на зачерненную поверхность крылышка, складывающееся с давлением света. Радиометрический эффект может привести к тому, что в опыте давление на зачерненное крылышко окажется больше давления на зеркальное крылышко тех же размеров.
 [12]

В обоих случаях эпюры результирующих давлений показывают, что в передаче нагрузки крана на грунт участвует вся площадь подошвы фундамента. Если при этом выполняется условие ртяк Рдоп, где рдоп – допускаемое давление для конкретного грунта см. табл. 50), то полученный результат проверки можно считать показателем правильности выбора размеров фундамента.
 [13]

Этот парадоксальный результат возникновения результирующего давления в составном потоке при отсутствии такового в составляющих его потоках – чисто поступательном и чисто циркуляционном, находит свое объяснение в асимметрии течения, получающегося при сложении этих потоков. Считая, например, циркуляцию положительной и взяв для сравнения две точки пересечения контура цилиндра с осью Оу, в которых векторы скоростей составляющих потоков коллинеарны, мы видим, что в верхней точке, где эти скорости противоположны по направлению, результирующая скорость окажется меньше по величине результирующей скорости в нижней точке контура, где величины составляющих скоростей складываются арифметически. Поэтому, как это следует из интеграла Бернулли, давление на цилиндр в верхней точке оказывается больше давления в нижней точке, что и объясняет возникновение результирующего давления, направленного вниз.
 [14]

Расчетной нагрузкой для нее является результирующее давление, как и в уголковых стенах, направленное сверху вниз.
 [15]

Страницы:  

   1

   2

   3

   4

В учебном курсе гидравлики (механики жидкости и газа) есть тема «сила давления на криволинейную поверхность». При поиске вертикальной составляющей силы давления воды на криволинейную поверхность (Fz = ρgW) необходимо правильно построить тело давления.

В данных задачах есть важнейшее правило: тело давления «строится» путем выделения определенных поверхностей в три шага. Правило звучит следующим образом >>>

“Тело давления” ограничено:

1)Криволинейной поверхностью

2)Её проекцией на поверхность жидкости (или на продолжение поверхности жидкости)

3)Вертикальными плоскостями, соединяющими границы криволинейной поверхности с соответствующими точками ее проекции

После построения телу давления присваивается знак:

(+): если тело давления заполнено жидкостью со стороны криволинейной поверхности

(-): если тело давления не заполнено жидкостью со стороны криволинейной поверхности

Этот знак определяет направление действия вертикальной составляющей силы давления воды: вертикально вверх, если (-) или вертикально вниз, если (+)

Также этот знак нужен, когда определяется равнодействующая вертикальных составляющих, у каждой из которых может быть тело давления со своим знаком.

Далее покажем построение тела давления на примере следующей задачи. Необходимо построить тело давления на данную криволинейную поверхность:

Построение ведем строго по правилу

Тело давления ограничено

1) криволинейной поверхностью

2) Ее проекцией на поверхность жидкости (или на продолжение поверхности жидкости)

Всегда проецируем наверх. В данном случае получается, что жидкости над криволинейной поверхностью нет, поэтому тогда продлеваем поверхность жидкости вправо пунктиром, и проецируем уже на этот пунктир

3) Вертикальными плоскостями, соединяющими границы криволинейной поверхности с соответствующими точками ее проекции. Выделяем границы и проводим через них вверх вертикальные линии до пересечения с проекцией. Замкнутое пространство и будет искомым телом давления.

Обратите внимание, что в данном случае левая граница и проекция и так совпадают, поэтому вертикальную плоскость слева не провести.

ИТОГ: вот такое тело давления, при этом знак у него минус (-), т.к. со стороны криволинейной поверхности нет жидкости:

Также необходимо отметить, что криволинейную поверхность всегда можно разделять на разные и находить тела давления для отдельных фрагментов криволинейной поверхности, а затем их складывать.

Возьмем ту же поверхность, с которой только что работали. Обозначим её за ABC, при этом точка B — крайняя слева. Построим по определению тела давления для AB (зеленое), и BC (красное). Тело давления для AB имеет знак (+), а тело давления для BC — знак (-). Их суммирование с учетом знака (т.е. вычитание из большего меньшее) и даст нам то же тело давления, что мы уже построили ранее. Его называют результирующим, т.е. для вертикальной составляющей силы давления на всю поверхность ABC.

Тело давления для AB находится внутри тела давления для BC, Результирующее тело давления — их разность.

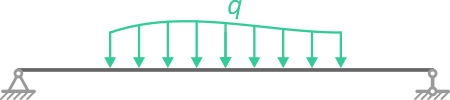
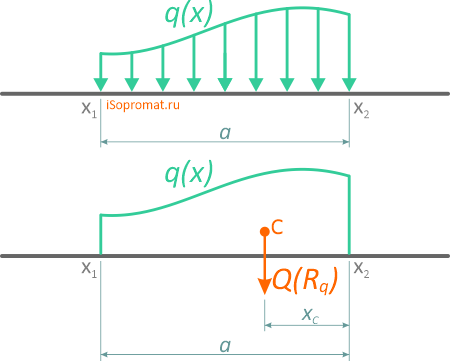
Распределенная нагрузка

Распределенной нагрузкой называют внешние или внутренние усилия, которые приложены не в одной точке твердого тела (т.е. не сосредоточены в одной точке), а равномерно, случайным образом или по заданному закону распределены по его определенной длине, площади (поверхности) или объему.

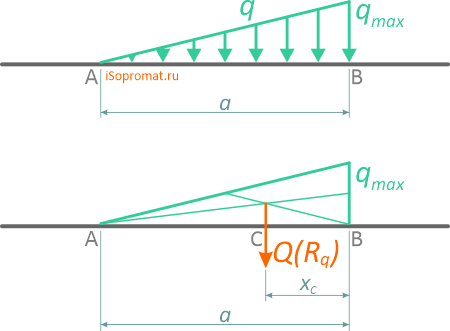
Рассмотрим виды распределенных нагрузок q: линейную, равномерную, треугольную (возрастающую или убывающую), трапециевидную, нелинейную, наклонную (направленную под углом) и замену их результирующей сосредоточенной силой — равнодействующей Q (R_q)

Воздействие на детали, конструкции, элементы механизмов может быть задано распределенными нагрузками: в плоской системе задается интенсивность действия по длине конструкции, в пространственной системе – по площади.

Это может быть собственный вес элемента конструкции, давление газа или воды, распределенный вес сыпучих материалов, ветровая нагрузка и тому подобное.

Обозначение распределенной нагрузки — q

Размерность:

• линейной нагрузки — Н/м,
• нагрузки распределенной по площади — Н/м²,
• объемной (например при учете собственного веса элементов конструкции) — Н/м³.

или кратные им, например кН/м.

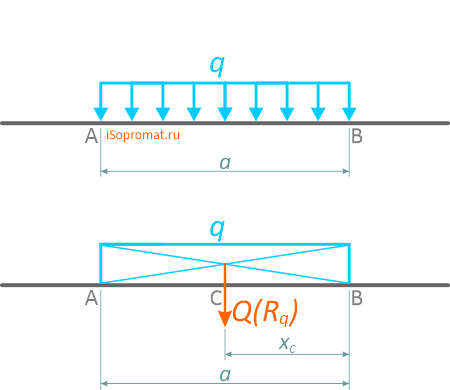
Равнодействующая распределенной нагрузки

При решении некоторых задач технической и теоретической механики, распределенную нагрузку удобно заменять её равнодействующей, обозначаемой Q или R_q, которая для линейного случая распределения, определяется произведением интенсивности нагрузки q на её длину AB.

Равнодействующая распределенной нагрузки действует в точке, расположенной в центре тяжести фигуры, ограниченной профилем её распределения.

Рассмотрим способы замены распределенных нагрузок их равнодействующей.

Равномерно распределенная нагрузка

Равномерно распределенная по длине AB нагрузка интенсивностью q, измеряемая в Н/м

может быть заменена сосредоточенной силой Q (R_q)

приложенной в центре (на пересечении диагоналей) прямоугольника, середине отрезка AB.

Линейно изменяющаяся (треугольная) нагрузка

Треугольная, линейно изменяющаяся убывающая (возрастающая) нагрузка

может быть заменена равнодействующей силой, приложенной в точке C

Отметим, что центр тяжести треугольника находится на пересечении его медиан, на расстоянии 1/3 высоты от основания или 2/3 высоты от его вершин.

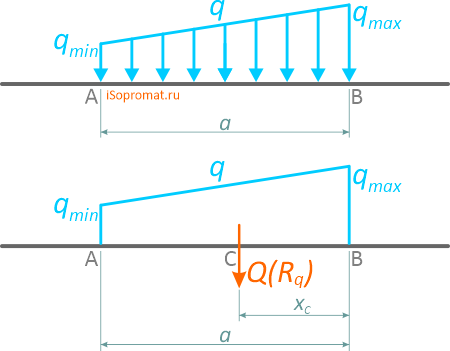
Трапециевидная распределенная нагрузка

Трапециевидная, равномерно убывающая или возрастающая нагрузка характеризуется длиной и двумя значениями интенсивности распределения нагрузки: минимальной q_min и максимальной q_max

Профиль такой нагрузки представляет собой трапецию.
Величина и положение равнодействующей Q в данном случае определяется по выражениям

Нелинейная распределенная нагрузка

В произвольном общем случае, интенсивность распределения нагрузки по её длине может описываться одной или несколькими функциями.

Зная функцию q(x), сосредоточенная эквивалентная (равнодействующая) сила рассчитывается по формуле

Эта сила также приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x).

Для расчета точки приложения равнодействующей нагрузки необходимо вычислить координату положения центра тяжести фигуры, образуемой нагрузкой.

Наклонная распределенная нагрузка

В случаях, когда распределенная нагрузка приложена под определенным углом, величина равнодействующей определяется аналогично ранее описанным способам.

При этом угол наклона самой силы будет равен углу наклона нагрузки q.

Например, линия действия равнодействующей наклонной равномерно распределенной нагрузки будет пересекать ось балки ровно посередине между крайними точками её приложения.

Величина равнодействующей будет равна площади параллелограмма, образованного профилем нагрузки.

Как рассчитывается момент распределенной нагрузки

Распределенная нагрузка от давления

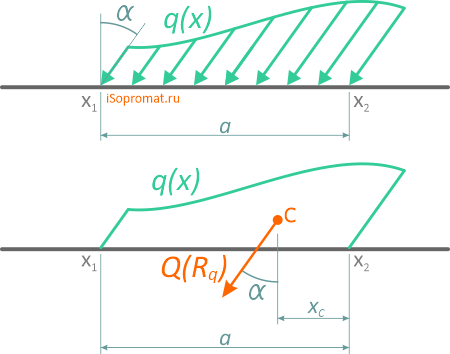
Примером распределенной нагрузки от давления может служить расчет усилий, разрывающих стенки баллона со сжатым газом.

Определим результирующую силу давления в секторе трубы при интенсивности q [Н/м];

где:
R – радиус трубы,
2α – центральный угол,
ось Ox – ось симметрии.

Выделим элемент сектора с углом ∆φ и определим силу ∆Q, действующую на плоский элемент дуги:

Проекция этой силы на ось Ox будет

В силу симметрии элемента трубы (с дугой AB) относительно оси Ox проекция результирующей силы на ось Oy:

Q_y = 0, т.е. Q = Q_x,

Тогда

где АВ – хорда, стягивающая концы дуги.

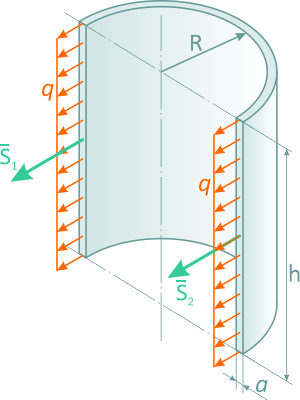
Для цилиндрической емкости высотой h и внутренним давлением P на стенки действует равномерно распределенная нагрузка интенсивностью q = p [Н/м²].

Если цилиндр рассечен по диаметру, то равнодействующая этих сил равна

F = q ∙ d ∙ h

где, d – внутренний диаметр, или

F = p ∙ 2R ∙ h.

Тогда, разрывающие баллон по диаметру усилия:

S₁ = S₂ = S;
2S = F;
S = p∙h∙R.

Если принять что a – толщина стенки, то (пренебрегая усилиями в крышке и дне цилиндра) растягивающее напряжение в стенке равно

Примеры решения задач >
Уравнения равновесия системы сил >

4-я лекция.

4. ГИДРОСТАТИКА-2

4.1. Сила давления жидкости па плоскую стенку.

4.2. Точка приложения силы давления.

4.3 Сила давления жидкости на криволинейную стенку.

4.4.Плавание тел.

4.5. Прямолинейное равноускоренное движение сосуда с жидкостью.

4.6. Равномерное вращение сосуда с жидкостью.

4.1. Сила давления жидкости па плоскую стенку

Рекомендуемые материалы

Давление жидкости на плоскую стенку, наклоненную к горизонту под произвольным углом  α, определяется по  основному уравнению гидростатики

Р=Р₀+hρg

Определим силу давления F, действующую со стороны жидкости, на участок рассматриваемой стенки, ограниченный произвольным контуром, имеющим площадь S.

Ось Ох направим перпендикулярно плоскости стенки от точки ее пересечения со свободной поверхностью жидкости, а ось Оу — перпендикулярно оси Ох в  плоскости стенки.

Выразим элементарную силу давления, приложенную к бесконечно малой площадке δS , для остальных площадок силы будут определяться таким же образом

δFж = P*δS =(P₀ + ρhg) δS = P₀*δS + ρhg*δS,

где Р₀ — давление на свободной поверхности, h — глубина расположения площадки  δS. 

Переходя к пределу при  стремлении  площадки δS→0, получим выражение для дифференциала силы давления:

dFж = P₀*dS + ρhg*dS,

Проинтегрировав этот дифференциал по площади S,  получим выражение для определения полной силы Fж

,

где у — координата площадки dS, h = у*Sinα .

Интеграл  представляет собой статический момент площади S относительно оси Ох , который  равен произведению  площади S на координату у_с ее центра тяжести – точки С:

Усилие давления жидкости на плоскую, наклоненную стенку равно

Fж = P₀S+ρg(y_c Sinα) S = P₀S+ρgh_cS,    (4.1)

здесь h_c = (y_c Sinα)— глубина расположения центра тяжести площади S.

Fж = ρg (H₀ +h_c)S = P_cS,                     (4. 2)

Сила давления жидкости Fж  = ρgh_cS – это вес объема V = h_cS жидкости.

Полная сила давления жидкости Fж на плоскую стенку равна произведению площади стенки S  на гидростатическое давление Р_с в центре тяжести этой площади.

1.В частном случае, когда давление Р₀ является атмосферным и действует также с другой стороны стенки, сила избыточного давления жидкости F_{изб ж}  на плоскую стенку равна лишь силе Fж давления от веса столба жидкости, т. е.

F_{изб ж} = P_cS= ρgh_cS.

2. В общем случае давление Р₀ может существенно отличаться от атмосферного, поэтому полную силу F давления жидкости на стенку можно  рассматривать как сумму двух сил: F₀ от внешнего давления Р₀ и силы Fж   от веса столба жидкости, т. е.

F= F₀ + Fж = (P₀+Pс)S.        (4.3.)

4.2. Точка приложения силы давления.

Внешнее давление Р₀ передается всем точкам площади S одинаково, и его равнодействующая сил внешнего давления F₀ будет приложена в центре тяжести площади S  с координатой  –  у_с.

Для нахождения точки D приложения силы давления Fж от веса жидкости применим теорему механики, согласно которой момент равнодействующей силы относительно оси Ох равен сумме моментов составляющих сил, в данном случае элементарных сил.

где у_D — координата точки приложения силы, h=y*Sinα.

Используя выражение для:

 F_ж = ρgh_c*S = ρg(y_cSinα)*S  – силы жидкости, действующей на плоскую стенку,

и для:

dF_ж= ρgh*dS= ρg(ySinα)*dS –  силы жидкости, действующей на элементарную площадку, получим 

        (4.4)

где  – момент инерции площади S относительно оси Оx.

Подставляя в формулу (4.4) значение:

 момента инерции и площади S – Jx  относительно оси х,  через момент инерции той же площади  – Jx₁  относительно центрально оси х₁ параллельной оси Ох, находим

Jx = Jx₁+y_C²S,                    (4.5)

у_D = у_C+ J_x1/(у_сS),              (4.6.)

Точка D  приложения силы F_ж расположена ниже центра тяжести площади стенки; расстояние между ними

Δу_D= у_D -Δу_C = J_x0/( у_сS),                 (4.7) .

Если давление Р₀ равно атмосферному, то точка D  будет центром давления.

При Р₀ > Pат  центр давления находят по правилам механики, как точку приложения равнодействующей двух сил F₀ и F_ж ,  чем больше первая сила по сравнению со второй  тем, очевидно, центр давления ближе к центру тяжести площади S.

Если стенка имеет форму прямоугольника размерами а × b (рис. 4.2) и с одной стороны  – атмосферное давление, центр давления D находится па расстоянии b/3 от нижней стороны.

4.3 Сила давления жидкости на криволинейную стенку.

Нахождение силы давления жидкости на поверхности произвольной формы в общем случае приводится к определению трех составляющих суммарной силы и трех моментов.

Рассмотрим действие жидкости на цилиндрические или сферические поверхности, имеющие вертикальную плоскость симметрии. Сила давления жидкости в этом случае сводится к равнодействующей силе, лежащей в плоскости симметрии.

Возьмем криволинейную поверхность АВ,  образующая которой  перпендикулярна к плоскости чертежа (рис.4.3а), определим силу давления жидкости на эту поверхность.

Выделим объем жидкости, ограниченный поверхностью АВ, вертикальными плоскостями, проведенными через границы этого участка ВС и AD,  свободной поверхностью жидкости. Рассмотрим  условия равновесия объема АВСD  в вертикальном и горизонтальном направлениях.

Сила давления  жидкости P действует на стенку АВ, стенка АВ удерживает действие  жидкости силой реакции стенки Rс = P, направленной в противоположную сторону. На рис. 4.3 сила реакции стенки и сила давления жидкости  разложены на горизонтальные и вертикальные составляющие.

Условие равновесия объема АВСD в вертикальном направлении имеет вид

Rс_в =Pжв= Р₀F_г + G = Р₀F_г + ρgV₀,                (4.8)

где Р₀  – давление на свободной поверхности жидкости; F_г – площадь горизонтальной проекции поверхности АВ; G – вес выделенного объема жидкостиV_0. Объем V₀  называют – объем тела давления..

Условие равновесия того же объема в горизонтальном направлении запишем с учетом того, что силы давления жидкости на поверхности ЕС и АD взаимно уравновешиваются и остается лишь сила давления на площадь ВЕ т. е. на вертикальную проекцию поверхности S_в = L_EB*B. Тогда

Rсг=Pжг= F_вρgh_c+ F_в Р₀ = F_в(ρgh_c+ Р₀).            (4.9)

Определив по формулам (4.8) и (4.9) вертикальную и горизонтальную составляющие полной силы Рж, найдем

 ,              (4.10).

Сила давления жидкости на криволинейную стенку будет равна сила реакции стенки Rж =  P и направлена в противоположную сторону.

Когда жидкость расположена снаружи (рис.4.3б), сила гидростатического давления на криволинейную поверхность АВ определяется также, но направление ее будет противоположным.

При этом под величиной G следует понимать так же, как и в первом случае вес жидкости в объеме АВСD, хотя этот объем и не заполнен жидкостью.

Положение центра давления на  цилиндрической стенке можно найти, если известны силы Fв и Fг и определены центр давления на вертикальной проекции h_D стенки и центр тяжести выделенного объема АВСD.

Задача значительно облегчается в том случае, когда рассматриваемая криволинейная  поверхность является круговой. Равнодействующая сила при этом пересекает ось поверхности, так как любая элементарная сила давления нормальна к поверхности, т. е. направлена по радиусу.

Изложенный способ определения силы давления на цилиндрические поверхности применим и к сферическим поверхностям, причем равнодействующая сила в этом случае также проходит через центр поверхности и лежит в вертикальной плоскости симметрии.

4.4. Плавание тел.

Описанный выше прием нахождения вертикальной составляющей силы давления жидкости па криволинейную стенку используют для доказательства закона Архимеда.

Пусть в жидкость погружено тело произвольной формы объемом V (рис.4.4).

Спроектируем его на свободную поверхность жидкости и проведем проек-тирующую цилиндрическую поверхность W, которая касается поверхности тела по замкнутой кривой. Эта кривая отделяет верхнюю часть поверхности тела АСВ от нижней ее части ADB.  Вертикальная составляющая F_в1 силы избыточного давления жидкости на верхнюю часть поверхности тела направлена вниз и равна весу жидкости в объеме АА’BВ’CA. Вертикальная составляющая F_в2 силы давления жидкости на нижнюю часть поверхности тела направлена вверх и равна весу жидкости в объеме АА’В’BDA. Отсюда следует, что вертикальная равнодействующая сил давления жидкости на тело будет направлена вверх и равна весу жидкости в объеме, равном разности указанных двух объемов, т. е.

F_А = F_в2  – F_в1  = G_ACBD =Vρg.                     (4.11)

Закон Архимеда: на тело, погруженное в жидкость, действует выталкивающая сила направленная вертикально вверх, численно равная весу жидкости вытесненной телом и приложенная в центре тяжести объема погруженной части тел.

Сила F_А называется архимедовой силой,  а точка ее приложения, т. е. центр тяжести объема V — центром водоизмещения.

В зависимости от соотношения веса G тела и архимедовой силы возможны три случая:

 1) G> F_А — отрицательная  плавучесть, тело тонет;

2) G<F_А — положительная плавучесть, тело всплывает и плавает на поверхности жидкости;

3) G = F_А нулевая плавучесть, тело плавает погруженным в жидкость полностью.

Для равновесия плавающего тела, кроме равенства G = F_А  должен быть равен нулю суммарный момент. Последнее условие соблюдается тогда, когда центр тяжести тела лежит на одной вертикали с центром водоизмещения. Условие устойчивого равновесия тела, плавающего в полностью погруженном состоянии,  заключается в следующем: центр тяжести тела должен находиться ниже центра водоизмещения.

4.5. Прямолинейное равноускоренное движение

сосуда с жидкостью.

Если при движении сосуда на частицы жидкости, кроме сил тяжести действуют еще силы инерции,  под действием этих сил жидкость принимает новое положение равновесия – положение  относительного покоя.

Относительным покоем называется равновесие жидкости, находящейся под действием сил тяжести и инерции в  движущемся сосуде.

При относительном покое положение свободной поверхности и поверхностей уровня,  отличается от их положения для жидкости в неподвижном сосуде.

При определении формы и положения этих поверхности учитывается основное свойство поверхности уровня. 

Основное свойство поверхностей уровня  –  равнодействующая массовых сил всегда нормальна  к этим поверхностям.

В полном дифференциале давления

dP=ρ(X*dх+У*dy+Z*dz),          (4.12)

Х,У,Z – алгебраическая сумма проекций на оси координат ускорений силы тяжести и сил инерции переносного движения.

Вдоль поверхности уровня  dР=0 , так как поверхности уровня  – это поверхности равного давления. Дифференциальное уравнение поверхности равного давления:

X*dх+У*dy+Z*dz = 0          (4.13),

Этот трехчлен (4.13) определяет элементарную работу массовых сил X,У,Z на перемещениях dх, dy, dz. В данном случае перемещение взято по поверхности равного давления, dР=0.

Из этого выражения следует, что  работа массовых сил вдоль поверхности равного давления равна нулю. Это значит, что в состоянии относительного покоя результирующее ускорение перпендикулярно к  соответствующему элементу поверхности равного давления.

Рассмотрим два случая относительного покоя.

Первый случай:   сосуд, движущийся прямолинейно и равноускоренно.

Второй случай: сосуд, вращающийся вокруг вертикальной оси с постоянной угловой скоростью.

На рис.4.5 изображен сосуд, движущийся вниз с ускорением а по плоскости наклонённой под углом  α   к горизонту. Оси координат оси координат связаны с движущимся телом. 

1. Пусть на жидкость действует  суммарная массовая сила F, проекции которой F_x, Fy, Fz , поделенные на  массу: Fx/m  являются проекциями единичной массовой силы на оси Ох, Оу, Oz:  Х, У и Z.

F = Fx+Fy+Fz = mа,  F/m = Fx/m +Fy/m +Fz/m = X +Y + Z = а.

Все выделенные составляющие являются векторными величинами.

 Проекции массовых сил, действующие на выделенный объем в направлении координатных осей, будут равны произведениям проекций единичных сил, умноженным на массу выделенного объема.

Fx = mX,               Fy = mY,                     Fz = mZ.

Результирующую единичную массовую силу, действующую на жидкость,  найдем как сумму единичных векторов силы инерции j  и силы тяжести g. Единичная сила инерции Fи = j = – a направлена в сторону  противоположную ускорению а (рис.4.5).

Проекции сумм массовых сил на оси:

          Ox: X = j – gSinα,   

         Oz : Z = –gCosα,

Оx: Y = 0.

При подстановке этих проекций в дифференциал давления, получим

(1/ρ)dp = [(j – gSinα)dx – (gCosα)dz].

Проинтегрировав дифференциал в проекциях, получим выражение для давления на поверхностях уровня

Р = ρ [(j – gSinα) x – (gCosα)z] + С.  (4.14)

На произвольной поверхности уровня давление постоянно Р = const и,  обозначив новую постоянную  С₁ – Р = const, где Р получим уравнение  изобарических поверхностей

ρ [(j – gSina) x – ρgCosa* z] +С₁ = 0                (4.15)

Это уравнение дает семейство плоскостей, параллельных оси Оу. Одной из них является свободная поверхность.

Обозначим через z₀ координату пересечения свободной поверхности с осью z. Подставив в формулу (4.15) х₀ = 0, z = z₀, находим С₁=ρg z₀Cosα для свободной поверхности. Уравнение этой поверхности имеет вид

ρ [(j – gSina) x – ρgCosa* z] + ρg z₀Cosα = 0

 (j – gSina) x –gCosa*( z + z₀) = 0

  

 где коэффициент в линейном уравнении равен тангенсу угла β .

Для определения положения свободной поверхности жидкости в сосуде, движущемся прямолинейно   и   равноускоренно к уравнению (4.16) нужно добавить уравнение объемов, т. е. нужно знать первоначальный объем жидкости в сосуде и выразить его через размеры сосуда В и Н и первоначальный уровень h.

Если сосуд движется только под действием силы тяжести, то j= gSinα β = 0, то свободная поверхность параллельна  плоскости движения.

 При нулевых условиях: х = 0, z = z₀, P = P₀  в  формуле (4.14),   получим C = P₀+ (ρgCosa)z₀:  

Р = ρ [(j – gSinα) x – (gCosα)z + С

Р = P₀+ρ(j-gSina)x+ρgCosa(z₀ – z).   (4.19)

Эта формула используется для определения давления в любой точке жидкости, находящейся в относительном покое при прямолинейном движении

Можно также использовать суммарную массовую единичную силу q для определения давления в любой точке.

Возьмем на рис.4.5 около точки М площадку dS, параллельную свободной поверхности, и на этой площадке построим цилиндрический  объем с осью, нормальной к  свободной поверхности. Условие равновесия указанного объема жидкости в направлении нормали к свободной поверхности будет иметь вид

РdS = P₀dS + q(ρldS),

где последний член представляет собой полную массовую силу,  q – суммарная единичная массовая сила, М = ρldS –   масса выделенного объема жидкости,  l — расстояние от точки М до свободной поверхности.

После сокращения на dS получим давление в точке

Р = P₀ + qρl,                          (4.20)

4.6. Равномерное вращение сосуда с жидкостью

Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему вращение с постоянной угловой скоростью ω  вокруг его вертикальной оси. Силы трения о стенки вращающегося сосуда будут увлекать за собой жидкость. Она постепенно приобретет ту же угловую скорость, что и сосуд, находясь по отношению к  сосуду в покое. Свободная поверхность жидкости  изменится.

В центральной части уровень жидкости опустится, у стенок  она поднимется, и вся свободная поверхность жидкости станет поверхностью вращения (рис.4.6).

На жидкость будут действовать силы давления, силы тяжести и силы инерции переносного движения. Частица жидкости будет находиться под действием ускорения силы тяжести и центростремительного ускорения, а  равное ему ускорение силы инерции будет центробежным. Единичная массовая сила тяжести F_g = g и единичная массовая центробежная сила F_цб = ω²r.

Проекции этих сил на оси координат дадут следующие выражения

X = (V²/r) Cos(r^x) = ω²r Cos(r^x)= ω²X

Y = (V²/r) Cos(r^y) = ω²r Cos(r^у)= ω²Y,  

                                      Z = -g

Подставляя эти проекции в дифференциальное уравнение поверхности   равного давления и интегрируя :                 

X*dх+У*dy+Z*dz = 0,

получим                                 ρ(ω²/2) (X²  + Y²) – ρgz + С = 0.

Уравнение  свободной поверхности, например, получим, при нулевых условиях:    Р₀ = const, х = у = 0, z= z₀,  где  координата вершины параболоида свободной поверхности. Тогда   С = ρgz₀.  

ρ(ω²/2) (X²  + Y²) – ρgz + ρgz₀  = 0,

(ω²/2) (X²  + Y²) =g(z – z₀)

и после деления на g   уравнение свободной поверхности получит вид

                      (4.22)

Таким образом, поверхности равного давления, в том числе и свободная поверхность, образуют семейство параболоидов, сдвинутых вдоль вертикальной оси. Каждому значению р соответствует свой параболоид, положение которого определяет константа С.

Эти поверхности  будут конгруэнтными параболоидами вращения  с осью Oz. Один из этих параболоидов – свободная поверхность жидкости, где Р₀= Ратм.

Две геометрические фигуры называются конгруэнтными, если их можно совместить одну с другой, изменив их положение в пространстве.

Подставляя проекции массовых сил в дифференциал давления

dp  = ρ(Xdx  +  Ydy + Zdz), 

получим                                  dp  = ρω² (Xdx  + Ydy) –ρ gdz,

вынесем знак дифференциала за скобки,

dp  = ρ d[(ω²/2) (X²  + Y²)] –ρ gdz,

и проинтегрировав,  получим выражение для определения давления в любой точке

 p  = ρ(ω²/2) (X²  + Y²) –ρ gz + С₁,    (4.21)

Значение константы для свободной поверхности Р = Р₀, x=y=0, z = z₀: С₁ = Р₀ + ρgz_0.

Получим уравнение для определения давления в любой точке:

             (4.22)

Пользуясь этими уравнениями  можно определить положение свободной поверхности и давление в сосуде.

Максимальная высота Н подъема жидкости в параболоиде со свободной поверхностью может быть определена, следующим образом.

 На практике часто рассматривается вращение сосуда с жидкостью, когда угловая скорость ω столь велика, что силой тяжести можно пренебречь по сравнению с центробежными силами. При этом закон изменения давления в жидкости легко получить из формулы (4.22),  в которой следует принять g(z₀ – z) = 0.

Поверхности уровня примут вид цилиндров с общей осью  –   осью вращения сосуда. Если сосуд не был заполнен перед началом вращения,  давление Р₀ будет действовать не в центре, а при r = r₀,  вместо выражения (4.22) будем иметь

Р = Р₀ + ρ ω² (r —r₀²)/2g,                          (4.23)

Часто бывает необходимо определить силу давления вращающейся вместе с сосудом жидкости на его стенку, нормальную к оси вращения (или на кольцевую часть этой стенки).

Для этого необходимо выразить сначала силу давления, приходящуюся на элементарную кольцевую площадку dS = 2πrdr радиусом r и шириной dr;

 

Уравнение, выражающее величину давления имеет вид

Ещё посмотрите лекцию “Лекция 11.1” по этой теме.

При определении давления на верхнюю крышку где Z=0,  Z₀ может быть больше нуля Z0>0, равно нулюи меньше нуля

В первом случае

а затем выполнить интегрирование в требуемых пределах.

При большой угловой скорости жидкости можно получить весьма значительную суммарную силу давления на стенку. Этот эффект используется в некоторых фрикционных муфтах, где для осуществления сцепления двух валов требуется создание больших сил нормального давления. Способ, указанный выше,  применяют для определения силы осевого давления жидкости на рабочие колеса центробежных насосов, а также на крышки центрифуг.

Давление на поверхность

Калькулятор рассчитывает давление в гравитационном поле тела заданной массы на поверхность заданной площади. Результат выводится в разных единицах давления.

Калькулятор рассчитывает давление оказываемое телом заданной массы на поверхность заданной площади в гравитационном поле.

Приведем определение давления из Википедии.
Давление — физическая величина, равная силе F, действующей на единицу площади поверхности S перпендикулярно этой поверхности. В данной точке давление определяется как отношение нормальной составляющей силы, действующей на малый элемент поверхности, к его площади:

Среднее давление по всей поверхности есть отношение силы к площади поверхности:

Для тела, находящегося в гравитационном поле, сила, действующая на площадь, известна — это его вес, или
, где g — ускорение свободного падения, метр, на секунду в квадрате.

Таким образом, итоговая формула давления тела на поверхность:

По умолчанию значение g в калькуляторе равно 9.80665, что примерно соответствует гравитационному полю Земли. Значение площади примерно соответствует площади подошв взрослого человека.
Ответ выдается в метрических единицах, паскалях, ну и для удобства в некоторых других единицах измерения давления, используемых в калькуляторе Конвертер единиц давления

Тревожный симптом: патологии у новорожденных

Несмотря на то, что новорожденный ребенок находится под тщательным наблюдением педиатра и других специалистов, именно от маминой внимательности и реакции часто зависит своевременное выявление тех или иных патологий у малыша.

О том, какие симптомы нельзя пропустить у крохи во избежание серьезных проблем со здоровьем в будущем, нам рассказала врач-педиатр клиники «9 месяцев» Авдеева Наталья Николаевна.

— Наталья Николаевна, какие патологии чаще всего встречаются у новорожденных?

— Почти 99 % новорожденных детей имеют неврологические отклонения, которые поначалу бывают минимальными и, при адекватном ведении ребенка, в большинстве случаев нивелируются к году.

— Что значит «адекватное ведение ребенка»?

— Имеется в виду вовремя проведенный массаж, вовремя начатая гимнастика. Причем, хочу заметить, что даже у абсолютно здорового ребенка до года желательно провести как минимум три курса гимнастики и массажа, с привлечением хорошего специалиста. Это необходимо для того, чтобы ребенок научился вовремя поворачиваться, садиться, вставать, ходить. Такие курсы нацелены на доразвитие нервной и, как следствие, скелетно-мышечной систем.

— Какие симптомы могут «подсказать» маме, что у малыша имеется то или иное неврологическое отклонение?

— Родителям следует обязательно обратить внимание на такой симптом, как подергивание подбородочка. Это может свидетельствовать о том, что идет недоразвитие нервной системы и отдельных структур головного мозга. Также должно вызвать опасения вставание ребенка на цыпочки. Как правило, на такое явление не обращают внимания. Но если малыш встает на цыпочки и при этом перекрещивает ножки, плохо опирается — это может быть слабовыраженным симптомом вялого нижнего парапареза, а в дальнейшем, к годику, может вылиться в ДЦП.
Дело в том, что обычно диагноз ДЦП до года не ставят, так как этот промежуток времени — большой реабилитационный период, когда у крохи есть хороший потенциал для восстановления. Первый год жизни вообще по своей восстановительной способности несоизмерим больше ни с одним промежутком в жизни человека. Здесь должна проходить очень большая работа самой мамы в совокупности с работой невропатолога, врача мануальной терапии, массажиста, врача ЛФК. В лечении применяются водотерапия, медикаментозная терапия, массаж, гимнастика и др.

Еще одним тревожным для мамы симптомом должен стать тремор рук. Обратите внимание, в каких ситуациях это возникает. Норма — если это реакция на яркий свет, сильный звук. Если же малыш старше месяца часто вскидывает руки в абсолютно спокойной обстановке, это может указывать на судороги. Здесь тоже необходимо полноценное обследование. Потребуется измерить внутричерепное давление у ребенка, сделать электроэнцефалограмму, проверить реакцию на световые и звуковые раздражители в спокойном состоянии, во сне и т. д.

Если же в сочетании со вздрагиваниями и испугами у малыша наблюдается также высовывание язычка — это может указывать на такую эндокринологическую патологию, как врожденный гипотиреоз. Изначально в роддоме проводится скрининг, когда берут кровь на 5 инфекций, и генетики это просматривают. Но необходима дальнейшая консультация эндокринолога. Раннее начало лечения предотвращает инвалидизацию ребенка. В связи с вышесказанным, хочу отметить, что крайне нежелательна ранняя выписка из роддома — на 3-4 сутки. Ведь многие такие моменты выявляются как раз на 4-5 сутки — то есть тогда, когда мама, выписавшаяся раньше, уже остается с ребенком и с возникшей проблемой наедине.

— Помимо неврологических, какие еще патологии родители могут самостоятельно заподозрить у ребенка?

— О многом говорит реакция малыша на внешние раздражители. Так, если ребенок в 2-3 месяца не реагирует на звуки (погремушки, голос), нужно срочно обратиться к отоларингологу. Первая проверка слуха проводится еще в роддоме, но в трехмесячном возрасте лор-врач обязательно должен осмотреть кроху. В Казани, например, довольно часто выявляются дети, которые сначала хорошо реагируют на проверки, но в конечном итоге у них обнаруживается кондуктивная тугоухость. Дело в том, что до этого ребенок мог реагировать чисто интуитивно, скажем, не на мамин голос, а на мимику. Бывает, что уже в 3 года таких детей начинают лечить как аутистов, хотя в действительности все дело в тугоухости.

Также должны возникнуть опасения, если ребенок не следит за предметами (на расстоянии 30 см — самое яркое зрение у новорожденных — кроха должен «поймать» мамино лицо и потянуться за ним, попытаться удержать его в своем поле зрения), к 3 месяцам не реагирует на свет, на цвета. Конечно, сами цвета малыш еще не идентифицирует, но смена цветов должна вызывать у него какие-то эмоции (радость или, наоборот, раздражение). Реакцию зрачка на свет мама тоже может отследить самостоятельно. Для этого нужно вынести малыша на яркий свет из темного помещения. Если при этом зрачки крохи не сузились, остались такими же широкими, как в темноте — значит, ребенок не видит свет, что говорит о патологии сетчатки глаз. В то же время, одинаковое сужение зрачка — это уже патология неврологическая. В любом случае, нужно срочно обратиться к специалистам.

На плановом осмотре у хирурга в месячном возрасте следует обязательно обратить внимание врача, если малыш часто и обильно срыгивает. По сути, ребенок должен срыгивать. Первые три месяца кроха дает отрыжку практически после каждого кормления. Но он не должен «фонтаном» выдавать всю еду наружу. Если так происходит, и ребенок за первые месяц-два плохо прибавил в весе, необходимо исключать пилороспазм — серьезную хирургическую патологию, требующую госпитализации.

Также мама должна внимательно следить за частотой и объемом мочеиспускания у ребенка. Считается, что до трехмесячного возраста ребенок должен мочиться понемногу, но каждый час. Если происходит задержка мочеиспускания, малыш выдает редко, но много мочи — это весьма тревожный симптом, который может указывать на такое серьезное заболевание мочевыводящей системы, как уретерогидронефроз, к сожалению, в последнее время встречающееся довольно часто. Выявить его можно уже на поздних сроках беременности при ультразвуковом обследовании. Для исключения этой же патологии проводится УЗИ в месячном возрасте. Здесь важно не упустить время, так как уже к 3 месяцам, при отсутствии лечения, происходит отмирание тканей почки.

Еще одним тревожным для мамы «звоночком» могут явиться бледность и синюшность носогубного треугольника у малыша, когда ребенок синеет при кормлении, плаче. Все это может быть вызвано низким гемоглобином, и в таком случае бывает достаточно назначить лечение кормящей маме. Однако важно не пропустить и кардиологическую патологию. Опять же, на последних сроках беременности при УЗИ-обследовании определяют грубые пороки сердца, но могут быть и малые аномалии, которые выявляются только после рождения малыша. Часто к трем годам малые аномалии нивелируются сами собой, но вполне возможно, что потребуется вмешательство. Поэтому если мама заметила, что ребенок регулярно синеет, у него одышка, он потлив (в норме грудные дети не потеют!), имеют место бледность и посинение ногтевых фаланг — это может говорить о скрытом пороке сердца. Нужно заострить на этом внимание педиатра, сделать кардиограмму, УЗИ сердца и записаться на прием к кардиологу.

В заключение хотелось бы обратиться ко всем молодым мамам: будьте внимательны к своим малышам, доверяйте интуиции и не стесняйтесь задавать вопросы врачу, рассказывайте обо всех своих подозрениях.
Вовремя забитая тревога — залог своевременного и успешного лечения, а значит, и здоровья вашего крохи!

Таблица тревожных симптомов

Патологии	Симптомы	Действия
Неврологические отклонения	Подергивание подбородочка. Вставание ребенка на цыпочки, при этом малыш перекрещивает ножки, плохо опирается. Это может быть симптомом вялого нижнего парапареза, в дальнейшем (к году) может вылиться в ДЦП. Тремор рук, надо обратить внимание в каких ситуациях это возникает. Норма — если это реакция на яркий свет, сильный звук и т. п. Если же малыш старше месяца часто вскидывает руки в абсолютно спокойной обстановке, это может указывать на судороги. Высовывание язычка. В сочетании со вздрагиваниями может говорить об эндокринологической патологии — врожденном гипотиреозе.	Необходимо обратиться к невропатологу. У многих детей неврологические отклонения минимальны и, при адекватном ведении ребенка, нивелируются к году. Применяются массаж, гимнастика, водотерапия, медикаментозная терапия и др. Могут потребоваться дополнительные обследования.
Тугоухость	Ребенок не реагирует на звуковые раздражители (погремушки, голос).	Обратиться к отоларингологу. Первый скрининг проводится еще в роддоме, но лор-врач обязательно должен осмотреть малыша в 3 месяца.
Патология сетчатки глаз	1. Ребенок не следит за предметами, к 3 месяцам не реагирует на свет, на цвета (смена цветов не вызывает никаких эмоций). 2. После того, как ребенка из темного помещения вынесли на яркий свет, его зрачки не сузились, остались широкими.	Обратиться к окулисту. Внимательно следите за реакцией ребенка. У новорожденного 30 см — самое яркое зрение. Кроха должен «поймать» на расстоянии 30 см мамино лицо и потянуться за ним, попытаться удержать его в своем поле зрения.
Хирургическая патология	Ребенок часто срыгивает «фонтаном», плохо набирает в весе при адекватном кормлении. Все это может свидетельствовать о пилороспазме.	На плановом осмотре у хирурга необходимо заострить внимание на имеющейся проблеме.
Патология мочевыводящей	Считается, что в норме ребенок до 3-месячного возраста должен мочиться понемногу, но каждый час. Если происходит задержка мочеиспускания, малыш выдает редко, но много мочи — это может свидетельствовать о серьезном заболевании — уретерогидронефрозе, которое, при отсутствии своевременного лечения, приводит к отмиранию тканей почек.	Уретерогидронефроз часто выявляют на поздних сроках беременности при ультразвуковом обследовании. Для исключения этой же патологии проводится УЗИ в месячном возрасте.
Пороки сердца	Бледность и синюшность носогубного треугольника. Ребенок синеет при кормлении, плаче. Все это может свидетельствовать о низком гемоглобине, и в этом случае часто достаточно назначить лечение кормящей маме. Однако если при этом у малыша наблюдается одышка, он потлив, имеются бледность и посинение ногтевых фаланг — это может говорить о скрытом пороке сердца.	Необходимо обратиться к педиатру, который назначит ребенку электрокардиограмму и УЗИ сердца. С результатами обратиться к кардиологу.

Даже у абсолютно здорового ребенка до года желательно провести как минимум три курса гимнастики и массажа, с привлечением хорошего специалиста.
Первый год жизни вообще по своей восстановительной способности несоизмерим больше ни с одним промежутком в жизни человека.
Крайне нежелательна ранняя выписка из роддома — на 3-4 сутки. Ведь многие такие моменты выявляются как раз на 4-5 сутки — то есть тогда, когда мама, выписавшаяся раньше, уже остается с ребенком и с возникшей проблемой наедине.
На расстоянии 30 см новорожденный должен «поймать» мамино лицо и потянуться за ним, попытаться удержать его в своем поле зрения.
До трехмесячного возраста ребенок должен мочиться понемногу, но каждый час.
Если мама заметила, что ребенок регулярно синеет, у него одышка, он потлив, имеют место бледность и посинение ногтевых фаланг — это может говорить о скрытом пороке сердца.

Хабибуллина Зульфия Кабировна

Врач педиатр, невролог, врач высшей категории. Наталья Авдеева, врач-педиатр высшей каиегории

Силы давления на плоские и криволинейные поверхности

Дифференциальное уравнение равновесия жидкости (уравнения Эйлера)

Система уравнений Эйлера (уравнения равновесия) определяет закон распределения давления в покоящейся жидкости вдоль соответствующей оси координат.

здесь X,Y,Z – напряжения массовых сил в проекциях на соответствующие оси координат x, y, z,

p – давление в соответствующей точке жидкости,

ρ – плотность жидкости.

Из уравнений Эйлера можно получить следующий вид основного дифференциального уравнения равновесия жидкости

Если ввести силовую (потенциальную) функцию U, такую, что

то для несжимаемой жидкости дифференциальное уравнение равновесия примет вид:

Основное уравнение гидростатики

В однородном поле силы тяжести при постоянстве плотности жидкости

dU=gdz,

dp= – ρgdz,

Проинтегрировав, получим основное уравнение гидростатики:

p=p0+ρgh,

h=(z0-z) – расстояние по вертикали между рассматриваемыми двумя точками (нулевой и точкой, в которой определяется давление)

Основным законом (уравнением) гидростатики называется уравнение:

р— гидростатическое давление (абсолютное или избыточное) в произвольной точке жидкости,

— плотность жидкости,

g — ускорение свободного падения,

z— высота точки над плоскостью сравнения (геометрический напор),

H— гидростатический напор.

Уравнение показывает, что гидростатический напор во всех точках покоящейся жидкости является постоянной величиной.

Иногда основным законом гидростатики называют принцип Паскаля.

Силы давления на плоские и криволинейные поверхности

Для определения силы давления жидкости на плоскую стенку, наклоненную к горизонту под углом α, используем основное уравнение гидростатики.

Расположим систему координат так, что стенка будет находиться в координатной плос-кости xOy, ось Oy пройдет вдоль стенки, начало координат О поместим в точку пересечения свободной поверхности и стенки (рис. 1.1). На схеме: dS — площадь элементарной площадки; h, z — глубина погружения и координата центра тяжести элементарной площадки; С — центр тяжести смоченной поверхности стенки; hC, yC — глубина погружения и координата центра тяжести смоченной поверхности стенки; р0 — давление на свободной поверхности; Р — сила давления на плоскую стенку; α — угол наклона стенки к горизонту.

Определим силу давления Р, действующую на стенку со стороны жидкости. Со строны жидкостина стенки действует сила, вызванная гидростатическим давлением. Для вычисления силы давления на стенку на ней выделяют элементарную площадку dS, малые размеры которой позволяют считать ее плоской, давление – равномерно распределенным по площадке. В таком случае силу давления dP на элементарную площадку dS определяет соотношение:

dP=(p0+ρgh)dS,

где р0 – давление на свободной поверхности; h – глубина погружения центра площадки, измеренная вдоль оси y от свободной поверхности. Заменяя h=y∙sinα для силы давления на площадку dS, будем иметь выражение

dP=(p0+ρgy∙sinα)dS,

а сила давления, действующая на плоскую стенку площадью, вычисляется интегрированием по площади стенки, соприкасающейся с жидкостью

Интергал представляет собой статический момент смоченной площади стенки S относительно оси Оx. Он равен =yC∙S. Таким образом, выражение для силы давления, действющей со стороны жидкости на плоскую стенку приобретает вид:

Из полученного выражения можно видеть, что значение силы давления равно произве-дению давления в центре тяжести смоченной поверхности pC на площадь смоченной поверхности.

Результирующая сила давления на стенку – это разность сил давления на стенку с двух сторон. Если с одной стороны на стенку действует давление на свободную поверхность р0 и давление жидкости pgh, а с другой – атмосферное давление ра, то результирующая сила:

R = (po + ρghC)S−paS = (p0 + pghC−pa)S

представляет собой силу избыточного давления, т.е.

R = ризбC∙S

ризбC = p0 + ρghC−рa

является избыточным давлением в центре тяжести смоченной поверхности.

Точку D, в которой приложена сила P, называют центром давления. Так как внешнее давле-ние р0 передаетсявсем точкам площади S одинаково, то равно-действующая этого давления будет приложена в центре тяжести площади S. Для нахождения точки приложения силы избыточного давления жидкости (точка D) используем теорему Вариньона: сумма моментов составляющих сил относительно какой-либо оси равна моменту равнодействующей относительно той же оси

Предположим, что центр избыточного давления находится в точке D с координатой yD. Тогда момент равнодействующей силы избыточного давления относительно оси у

M = RyD = pghСSyD,

где hC — расстояние от центра тяжести смоченной поверхности до оси Oy.

Момент составляющих силы избыточного давления относительно той же оси

h = y∙sina,

представляет собой момент инерции рассматриваемой смоченной поверхности относительно оси x. Таким образом:

∑My=pgJxsinα

Из равенства выражений

pghCSyD = pgJx sinα

yD = Jx sinα/(hCS) = Jx/(yСS),

где yС — координата центра тяжести смоченной поверхности.

Выражая момент инерции Jx через центральный момент инерции смоченной поверхности JC:

Jx = JC + y2С S,

определим координату центра избыточного давления

Из полученной формулы видно, что центр давления не совпадает с центром тяжести смоченной поверхности стенки (расположен ниже него).

Если давление ро равно атмосферному и оно действует с обеих сторон стенки, то точка D и будет центром давления. Когда же р0 является повышенным, то центр давления находится по правилам механики как точка приложения равнодействующей двух сил: R и р0S. При этом, чем больше вторая сила по сравнению с первой, тем очевидно ближе центр давления к центру тяжести площади S.

Выше было дано определение лишь одной координаты центра давления—yD. Для определения другой его координаты — xD следует составить уравнение моментов относительно оси оу.

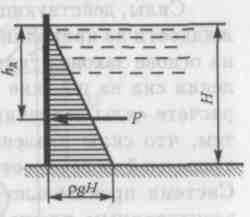
В том частном случае, когда стенка имеет прямоугольную форму, причем одна из сторон прямоугольника совпадает со свободной поверхностью жидкости, положение центра давления находится очень просто. Так как эпюра давления жидкости на стенку изображается прямоугольным треугольником (рис.1.2), центр тяжести которого находится на 1/3 высоты b треугольника, то и центр давления жидкости будет расположен на 1/3 b, считая снизу.

Силу давления и центр давления можно определить по эпюре давления. Построим эпюру давления на стенку (рис. 1.2), учитывая, что стенка имеет прямоугольную форму, причем одна из сторон совпадает со свободной поверхностью жидкости и что на свободной поверхности атмосферное давление ра, т.е. с одной стороны на стенку действует атмосферное давление и давление жидкости pgh, с другой — атмосферное давление.

Сила давления Р на стенку равна весу жидкости в объеме призмы:

P=Sэп a

где Sэп —площадь плоской эпюры; a — длина стенки.

В данном случае площадь эпюры – это площадь треугольника. Тогда сила давления на стенку

P = pgh∙b∙a/2,

где h — глубина жидкости; b — высота стенки.

Линия действия силы давления P будет проходить через центр тяжести пространственной эпюры давления и проектироваться на центр тяжести основания (в данном случае треугольника), который отстоит от вершины треугольника на 2/3 его высоты, т.е.

Определим силу давления и центр давления аналитически.

Сила избыточного давления равна

P = ризбС S = ρghC∙ba= ρgh∙b∙a/2,

где ризбС = ρghC =ρgh/2; S = b∙a.

Определим центр давления по формуле

Таким образом, результаты определения силы давления и центра давления по эпюре давления и аналитически совпадают.

В случае вертикальной стенки (рис.1.3а) эпюра распределения избыточного давления по высоте стенки имеет вид треугольника. Соответствующая этой эпюре сила давления на прямоугольную стенку равна

где b — ширина стенки.

Глубина hд погружения центра давления будет находиться в центре тяжести треугольника, который отстоит от вершины треугольника на 2/3 его высоты, или в соответствии с формулой

Как показывает формула , силы давления на горизонтальные стенки (днища сосудов), будут одинаковыми, если эти стенки имеют равные площади S и на них действуют одинаковые гидростатические давления. Форма сосуда не влияет на значение силы. На первый взгляд из-за различного количества одной и той же жидкости в показанных на рис. 1.3б сосудах силы давления на их днища будут разными. Такое неправильное суждение, противоречащее доказан-ному выше равенству сил давления, называют гидростатическим парадоксом.

Теперь определим силу давления на криволинейную поверхность АВ (рис.1.4а) при следу-ющих условиях. На свободную поверхность жидкости действует давление р0, которое больше ат-мосферного ра, а на поверхность АВ с одной строны действует полное гидростптическое давление р=р0+ρgh, а с другой стороны – атмосферное давление. Определить силу избыточного давления на цилиндрическую поверхностью.

Проекция силы давления на горизонтальную ось равна интегралу

где dPГ — проекция на горизонтальную ось элементарной силы dP, приложенной к выделенной на криволинейной стенке мощадке dS (рис. 1.4б) и равной

dP = (р0+ ρgh)dS

Здесь h — глубина погружения центра площадки, измеренная от свободной поверхности жидкости; ро — давление на этой поверхности. Обозначив через α угол наклона dP к горизонту, можно найти

dPГ = (ро + ρgh) cosαdS.

Произведение cosαdS соответствует проекции dSB элементарной площадки на вертикальную плоскость:

cosadS = dSB

dPГ = (р0 + pgh)dSB.

РГ = (р0 + ρghc) SВ

где hc — измеренная от свободной поверхности жидкости глубина погружения центра тяжести проекции криволинейной стенки на вертикальную плоскость; SB — площадь этой проекции.

Чтобы вычислить проекцию РВ на вертикальную ось, следует аналогичные операции выполнить с проекцией dPB элементарной силы давления. В этом случае

dPB = (p0 + pgh)dSГ,

где SГ – площадь проекции элементарной площадки на горизонтальную плоскость.

При интегрировании правой части этого уравнения получается два члена, первый из которых равен p0SГ, второй весу ρgV жидкости, занимающей объем 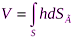между криволинейной поверхностью, свободным уровнем жидкости и вертикальными стенками 1,2,3:

Рв = р0SГ + ρgV

Объем V называют телом давления.

Полная сила гидростатического давления на криволинейную стенку составит

У стенок постоянной кривизны (цилиндрических, сферических) линия действия силы давления Р проходит через центр или ось кривизны. Точку приложения равнодействующей силы Р необходимо определять с помощью уравнения моментов.

Приведем другой вариант определения силы давления жидкости на криволинейную стенку.

Возьмем цилиндрическую поверхность АВ с образующей, перпендикулярной плоскости чертежа (рис.1.4), и рассмотрим определение силы давления жидкости на эту поверхность в двух случаях: а) жидкость расположена сверху (рис. 1.4б) и б) жидкость .расположена снизу (рис. 1.4в).

В случае «б» выделим объем жидкости, ограниченный рассматриваемой поверхностью АВ, вертикальными поверхностями, проведенными через границы этого участка, и свободной поверхностью жидкости, т. е. объем ABCD, и рассмотрим условия его равновесия в вертикальном и горизонтальном направлениях. Если. жидкость действует на поверхность АВ с силой Р, то поверхность АВ оказывает на жидкость такое же усилие Р, но направленное в обратную сторону. На рис. 1.4б показана эта сила реакции, разложенная на две составляющие: горизонтальную РГ, и вертикальную РВ.

Условие равновесия объема ABCD жидкости в вертикальном направлении имеет вид:

PB = p0SГ + G

где р0—давление на свободной поверхности жидкости;

SГ — площадь горизонтальной проекции поверхности АВ; G — вес выделенного объема жидкости, вес тела давления.

Условие равновесия того же объема жидкости в горизонтальном направлении запишем с учетом того, что силы давления жидкости на поверхности ЕС и AD взаимно уравновешиваются и остается лишь сила давления на площадь BE, т. е. на вертикальную проекцию поверхности АВ — SB. Будем иметь

PГ = SBρghc+paSb.

Определив вертикальную и горизонтальную составляющие полной силы давления Р, найдем эту последнюю:

В том случае, когда жидкость расположена снизу (случай «в», см. рис. 1.4), величина гидростатического давления во всех точках поверхности АВ будет иметь те же значения, что и в случае «б», но направление его будет противоположным, и суммарные силы РВ и РГ будут определяться теми же формулами, но с обратным знаком. При этом под величиной G следует понимать, так же как и в случае «б», вес жидкости в объеме ABCD, хотя этот объем и не заполнен жидкостью – вертикальная составляющая силы давления жидкости на твердую стенку направлена вверх. Положение центра давления на цилиндрической стенке легко может быть найдено, если силы РВ и РГ известны не только по величине, но и по направлению, т.е. если определены центр давления на вертикальной проекции стенки и центр тяжести выделенного объема ABCD. Задача значительно облегчается в том случае, когда рассматриваемая цилиндрическая поверхность является круговой, так как равнодействующая сила при этом пересекает ось поверхности. Это следует из того, что любая элементарная сила давления dP нормальна к поверхности, т. е, направлена по радиусу.

Изложенный способ определения силы давления на цилиндрические поверхности применим также и к сферическим поверхностям, причем равнодействующая сила в этом случае также проходит через центр поверхности и лежит в вертикальной плоскости симметрии.

Закон Архимеда

К рис. 1.6. r — радиус цилиндра; h — глубина погружения оси цилиндра; pg(h – r), pg(h + r) — давление на глубине h – r и h + r соответственно; Рг1 и Рг2 — горизонтальные составляющие силы давления на цилиндрическую поверхность; Рв1 и Рв2 — вертикальные составляющие силы давления на верхнюю и нижнюю части погруженного тела; Рв — вертикальная составляющая силы давления на погруженное тело.

Рассмотрим твердое тело, погруженное в покоящуюся жидкость (рис. 1.5). Оно находится в равновесии под действием двух сил, имеющих вертикальное направление: массовой силы G – веса тела, и поверхностной – результирующей силы давления жидкости P, окружающей тело. Результирующая сил давления в горизонтальном направлении равна нулю – силы давления, действующие на боковые поверхности справа и слева на тело, уравновешивают друг друга. Результирующую силу давления можно представить суммой двух составляющих P=Pверхн.+Pнижн

Составляющая Pверхн действует сверху на тело в направлении силы тяжести, погружая тело. Составляющая Pнижн действует на нижнюю поверхность тела, выталкивая его на поверхность, поскольку давления во всех точках нижней поверхности в соответствии с основным законом гидростатики больше давлений в точках верхней поверхности. Разность этих сил уравновешивается силой тяжести G тела: или . Если плотность тела равна плотности жидкости, то можно сформулировать условие равновесия тела как закон Архимеда: погруженное в покоящуюся жидкость тело испытывает со стороны жидкости вертикальное подъемное усилие, равное весу жидкости в объеме погруженного тела. Точка приложения результирующей силы давления, выталкивающей тело, называется центром давления.

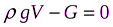
Закон Архимеда можно вывести и с точки зрения действия силы давления на криволинейную поверхность.

Определим силу давления жидкости на погруженное в нее тело (рис. 1.6), поверхность которого будем рассматривать как замкнутую криволинейную поверхность (например, цилиндр радиусом r, ось которого погружена на глубину h относительно пьезометрической плоскости).

Силу давления на данную криволинейную поверхность можно определить как геометрическую сумму вертикальной и горизонтальной составляющих.

Горизонтальная составляющая силы давления в рассматриваемом случае равна нулю, так как левая Рг1 и правая Рг2 составляющие численно равны и направлены в противоположные стороны:

Сила давления на поверхность погруженного тела равна вертикальной составляющей:

которая является результирующей двух сил:

Рв=Рв1+Рв2,

где Рв1 и Рв2 —- вертикальные составляющие, действующие соответственно на верхнюю и нижнюю части погруженного тела.

Определим разность сил Рв1 и Рв2. Рассечем погруженное тело горизонтальной плоскостью по диаметральной плоскости и построим тела давления на верхнюю и нижнюю части, а затем графически определим результирующее тело давления.

По рис. 1.6 видно, что результирующим телом давления является объем рассматриваемого цилиндра, и вертикальная составляющая силы давления равна весу жидкости в объеме, вытеснен-ном погруженным телом:

Рв=ρgV,

где V — объем тела.

Полученная формула выражает закон Архимеда: на погруженное в жидкость тело действует направленная вверх сила, численно равная весу вытесненной телом жидкости. Эта сила называется выталкивающей, или архимедовой, силой.

При выходе тела на свободную поверхность капельной жидкости выталкивающая сила уменьшается вследствие уменьшения объема погруженной части тела, и тело будет плавать на свободной поверхности. Условием плавания является выражение

G=ρgVП

где G — вес тела; VП— объем погруженной части тела.

С помощью этой формулы рассчитывается поплавковое устройство.

Подводное плавание тел. Рассмотрим остойчивость тела при подводном плавании. Тело будет плавать под водой, если сила тяжести тела под водой G равна силе Архимеда, т. е. G = Р. Тело будет тонуть, если G > Р и, наконец, тело всплывет,

если G G, то тело будет всплывать и часть тела при этом будет обсыхать. Тело будет всплывать до тех пор, пока сила Р не уменьшится настолько, что снова будет восстановлено равенство

P = G,

где Р равно весу жидкости в объеме погруженной части тела. Вес жидкости, вытесненный погруженной в нее частью тела, называется водоизмещением.

Плоскость сечения плавающего тела свободной поверхностью жидкости называется плос-костью плавания. Периметр плоскости плавания называется контуром плавания (ватерлинией).

При надводном плавании тело должно обладать остойчивостью, т. е. при малом крене (до 15—20°) тело должно возвращаться в первоначальное положение.

Тело обладает остойчивостью, если центр тяжести расположен ниже центра водоизмеще-ния. Но в плавающих судах это трудно бывает осуществить. Если центр тяжести расположен выше

центра водоизмещения, то плавающее над водой тело тоже может находиться в состоянии равновесия. В этом случае основное значение приобретает расположение точки М — метацентра. Метацентром называется точка пересечения оси плавания с линией действия силы Р (рис.1.9). Если метацентр расположен выше центра тяжести, то плавающее над водой тело остойчиво, так как возникающая при крене пара сил G — Р стремится возвратить его в состояние равновесия.

Расстояние вдоль оси плавания от центра тяжести тела до метацентра называется метацентрической высотой Нт. Метацентрическая высота положительна, если она от меряется вверх от центра тяжести. Если метацентрическая высота положительна, плавающее тело остойчиво.

Метацентрическая высота вычисляется по формуле:

Hm = I0 /V ± h = ρ±h

где I0—момент инерции площади ватерлинии (плоскости плавания) относительно продольной оси, проходящей через центр тяжести этой площади;

h — расстояние между центром тяжести тела и центром водоизмещения (рис.1.9);

ρ— метацентрический радиус.

На рис.1.9 показано остойчивое положение судна, а на рис. 1.10 – неостойчивое.

Закон Паскаля описывается формулой давления:

где р— это давление,

F — приложенная сила,

S — площадь сосуда.

Из формулы мы видим, что при увеличении силы воздействия при той же площади сосуда давление на его стенки будет увеличиваться. Измеряется давление в ньютонах на метр квадратный или в паскалях (Па), в честь учёного, открывшего закон, Паскаля.

На основе закона Паскаля работают различные гидравлические устройства: тормозные системы, гидравлические прессы и др.

Гидравлическая машина состоит из двух сообщающихся цилиндров разного диаметра, закрытых поршнями и заполненных жидкостью. Если на поршни действуют силы F1 и F2, то для равновесия системы необходимо, чтобы создаваемые этими силами давления были одинаковыми, так как согласно закону Паскаля давление передается жидкостью во все стороны одинаково. Следовательно, или

При равновесии силы, приложенные к поршням прямо пропорциональны площадям поршней. С помощью гидравлической машины можно малой силой уравновесить большую силу.

Гидродинамика – раздел гидравлики, в котором изучаются законы движения жидкости и ее взаимодействие с неподвижными и подвижными поверхностями.

Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.

Основные понятия о движении жидкости

Живым сечением ω (м²) называют площадь поперечного сечения потока, перпендикулярную к направлению течения. Например, живое сечение трубы – круг (рис. 1.11, б); живое сечение клапана – кольцо с изменяющимся внутренним диаметром (рис. 1.11, б).

Рис. 1.11. Живые сечения: а – трубы, б – клапана

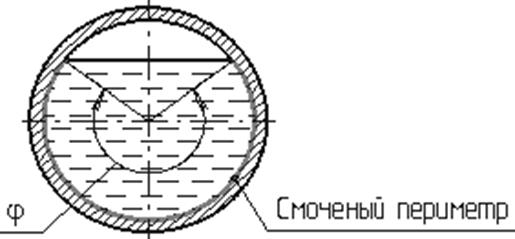
Смоченный периметр χ (“хи”) – часть периметра живого сечения, ограниченное твердыми стенками (рис. 1.12, выделен утолщенной линией).

Рис. 1.12. Смоченный периметр

Для круглой трубы

если угол в радианах, или

Расход потока Q – объем жидкости V, протекающей за единицу времени t через живое сечение ω.

Средняя скорость потока υ – скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω

Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.

Гидравлический радиус потока R – отношение живого сечения к смоченному периметру

Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени

υ = f(x, y, z)

P = φ f(x, y, z)

Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным

υ = f1(x, y, z, t)

P = φ f1(x, y, z, t)

Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.

Трубка тока – трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока называется элементарной струйкой.

Рис. 1.13. Линия тока и струйка

Течение жидкости может быть напорным и безнапорным. Напорное течение наблюдается в закрытых руслах без свободной поверхности. Напорное течение наблюдается в трубопроводах с повышенным (пониженным давлением). Безнапорное – течение со свободной поверхностью, которое наблюдается в открытых руслах (реки, открытые каналы, лотки и т.п.). В данном курсе будет рассматриваться только напорное течение.

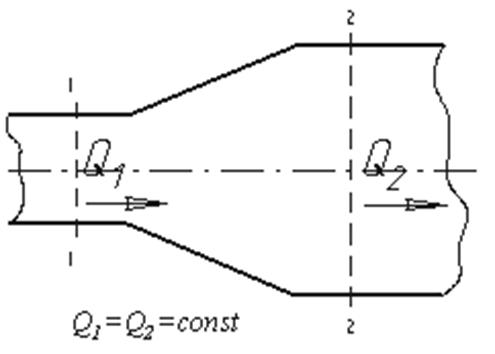
Рис. 1.14. Труба с переменным диаметром при постоянном расходе

Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений. Представим трубу с переменным живым сечением (рис.3.4). Расход жидкости через трубу в любом ее сечении постоянен, т.е. Q1=Q2= const, откуда

ω1υ1 = ω2υ2

Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:

[spoiler title=”источники:”]

http://c9m.ru/library/babies/trevozhnyy-simptom-patologii-u-novorozhdennykh/

http://lektsii.org/3-32254.html

[/spoiler]