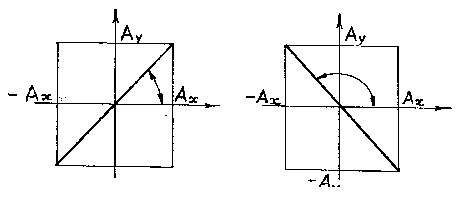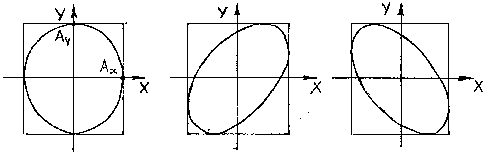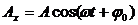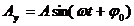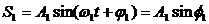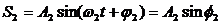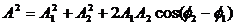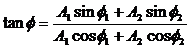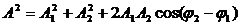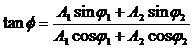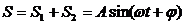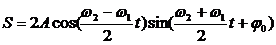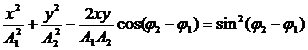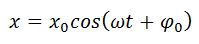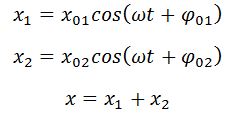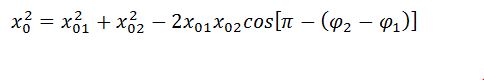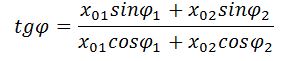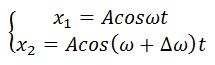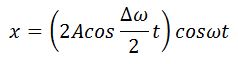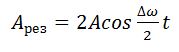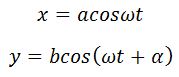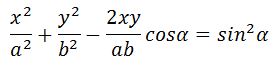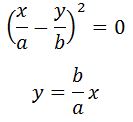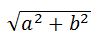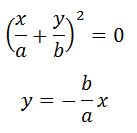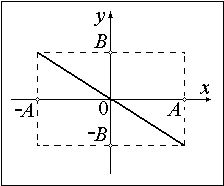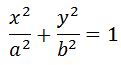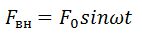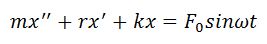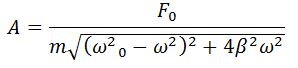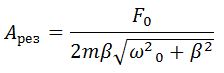Как найти результирующее уравнение колебаний

2.1. Сложение гармонических колебаний одного направления

2.2. Сложение взаимно перпендикулярных колебаний

Одно и то же тело может одновременно участвовать в двух и более движениях. Простым примером является движение шарика, брошенного под углом к горизонту. Можно считать, что шарик участвует в двух независимых взаимно перпендикулярных движениях: равномерном по горизонтали и равнопеременном по вертикали. Одно и то же тело (материальная точка) может участвовать в двух (и более) движениях колебательного типа.

Под сложением колебаний понимают определение закона результирующего колебания, если колебательная система одновременно участвует в нескольких колебательных процессах. Различают два предельных случая – сложение колебаний одного направления и сложение взаимно перпендикулярных колебаний.

2.1. Сложение гармонических колебаний одного направления

1. Сложение двух колебаний одного направления (сонаправленных колебаний)

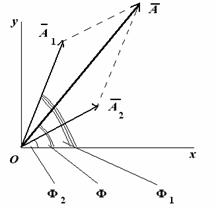
можно провести с помощью метода векторных диаграмм (Рисунок 9) вместо сложения двух уравнений.

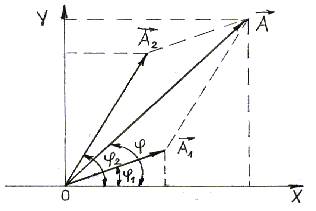
На Рисунке 2.1 показаны векторы амплитуд А₁(t) и А₂(t) складываемых колебаний в произвольный момент времени t, когда фазы этих колебаний соответственно равны и . Сложение колебаний сводится к определению . Воспользуемся тем фактом, что на векторной диаграмме сумма проекций складываемых векторов равна проекции векторной суммы этих векторов.

Результирующему колебанию соответствует на векторной диаграмме вектор амплитуды и фаза .

Рисунок 2.1 – Сложение сонаправленных колебаний.

Величина вектора А(t) может быть найдена по теореме косинусов:

.

Фаза результирующего колебания задается формулой:

.

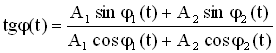
Если частоты складываемых колебаний ω₁ и ω₂ не равны, то и фаза φ(t), и амплитуда А(t) результирующего колебания будут изменяться с течением времени. Складываемые колебания называются некогерентными в этом случае.

2. Два гармонических колебания x₁ и x₂ называются когерентными, если разность их фаз не зависит от времени:

.

Но так как , то для выполнения условия когерентности двух этих колебаний должны быть равны их циклические частоты .

Амплитуда результирующего колебания, полученного при сложении сонаправленных колебаний с равными частотами (когерентных колебаний) равна:

.

Начальную фазу результирующего колебания легко найти, если спроектировать векторы А₁ и А₂ на координатные оси ОХ и ОУ (см. Рисунок 9):

.

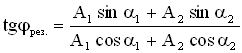
Итак, результирующее колебание, полученное при сложении двух гармонических сонаправленных колебаний с равными частотами, также является гармоническим колебанием .

3. Исследуем зависимость амплитуды результирующего колебания от разности начальных фаз складываемых колебаний.

Если , где n – любое целое неотрицательное число

(n = 0, 1, 2…), то , т.е. результирующая амплитуда будет минимальной. Складываемые колебания в момент сложения находились в противофазе. При результирующая амплитуда равна нулю .

Если , то , т.е. результирующая амплитуда будет максимальной. В момент сложения складываемые колебания находились в одной фазе, т.е. были синфазны. Если амплитуды складываемых колебаний одинаковы , то .

4. Сложение сонаправленных колебаний с неравными, но близкими частотами.

Частоты складываемых колебаний не равны , но разность частот много меньше и ω₁, и ω₂. Условие близости складываемых частот записывается соотношениями .

Примером сложения сонаправленных колебаний с близкими частотами является движение горизонтального пружинного маятника, жесткость пружин которого немного различна k₁ и k₂.

Пусть амплитуды складываемых колебаний одинаковы, а начальные фазы равны нулю . Тогда уравнения складываемых колебаний имеют вид: , .

Результирующее колебание описывается уравнением:

.

Получившееся уравнение колебаний зависит от произведения двух гармонических функций: одна – с частотой , другая – с частотой , где ω близка к частотам складываемых колебаний (ω₁ или ω₂). Результирующее колебание можно рассматривать как гармоническое колебание с изменяющейся по гармоническому закону амплитудой. Такой колебательный процесс называется биениями. Строго говоря, результирующее колебание в общем случае не является гармоническим колебанием.

Абсолютное значение косинуса взято потому, что амплитуда – величина положительная. Характер зависимости х_рез.при биениях показан на Рисунке 2.2.

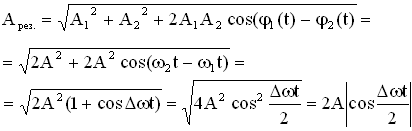
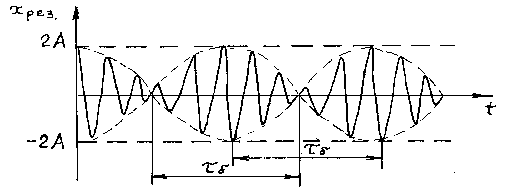
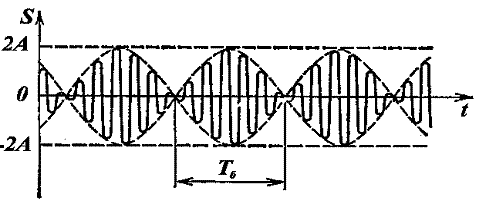
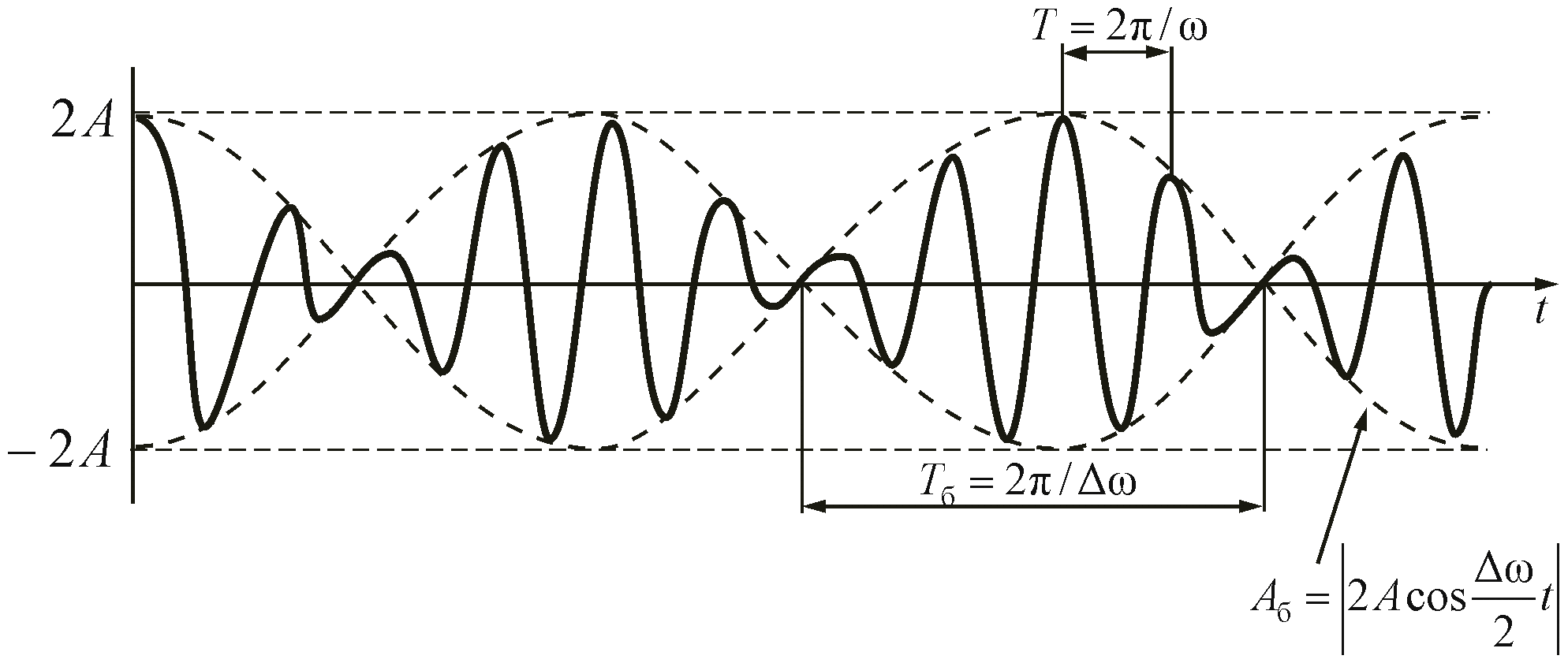
Рисунок 2.2 – Зависимость смещения от времени при биениях.

Амплитуда биений медленно меняется с частотой . Абсолютное значение косинуса повторяется, если его аргумент изменяется на π, значит и значение результирующей амплитуды повторится через промежуток времени τ_б, называемый периодом биений (см. Рисунок 12). Величину периода биений можно определить из следующего соотношения:

.

Величина – период биений.

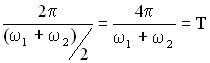
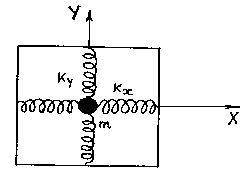
Величина есть период результирующего колебания (Рисунок 2.4).

1. Модель, на которой можно продемонстрировать сложение взаимно перпендикулярных колебаний, представлена на Рисунке 2.3. Маятник (материальная точка массой m) может совершать колебания по осям ОХ и ОУ под действием двух сил упругости, направленных взаимно перпендикулярно.

Рисунок 2.3

Складываемые колебания имеют вид:

.

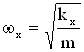
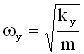
Частоты колебаний определяются как , , где , -коэффициенты жесткости пружин.

2. Рассмотрим случай сложения двух взаимно перпендикулярных колебаний с одинаковыми частотами , что соответствует условию (одинаковые пружины). Тогда уравнения складываемых колебаний примут вид:

Когда точка участвует одновременно в двух движениях, ее траектория может быть различной и достаточно сложной. Уравнение траектории результирующего колебаний на плоскости ОХУ при сложении двух взаимно перпендикулярных с равными частотами можно определить, исключив из исходных уравнений для х и y время t:

.

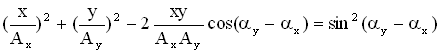
Вид траектории определяется разностью начальных фаз складываемых колебаний, которые зависят от начальных условий (см. § 1.1.2). Рассмотрим возможные варианты.

а) Если , где n = 0, 1, 2…, т.е. складываемые колебания синфазные, то уравнение траектории примет вид:

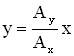
(Рисунок 2.3 а).

б) Если (n = 0, 1, 2 …), т.е. складываемые колебаний находятся в противофазе, то уравнение траектории записывается так:

(Рисунок 2.3б).

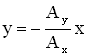
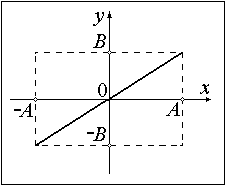
В обоих случаях ( а, б) результирующее движение точки будет колебание по прямой, проходящей через точку О. Частота результирующего колебания равна частоте складываемых колебаний ω₀, амплитуда определяется соотношением:

.

Угол, который прямая (траектория) составляет с осью ОХ, можно найти из уравнения:

(знак “плюс” – случай а, знак “минус” – случай б).

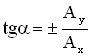
Результатом сложения взаимно перпендикулярных колебаний (случай а и б) является колебание, которое называется линейно поляризованным.

в) Если (n = 0, 1, 2 …), то уравнение траектории результирующего движения примет вид:

.

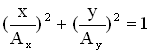
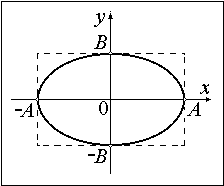
Это уравнение эллипса, его оси совпадают с осями координат ОХ и ОУ, а размеры его полуосей равны и (Рисунок 2.4 ).

Рисунок 2.4

Точка в результате участия в двух взаимно перпендикулярных колебаниях описывает эллипс за время, равное периоду складываемых колебаний .

3. Сложение взаимно перпендикулярных колебаний с кратными частотами.

Складываются взаимно перпендикулярные колебания, частоты которых не равны , но , , где a и b – целые числа.

Периоды колебаний вдоль осей ОХ и ОУ соответственно равны и . Отношение периодов .

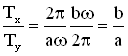
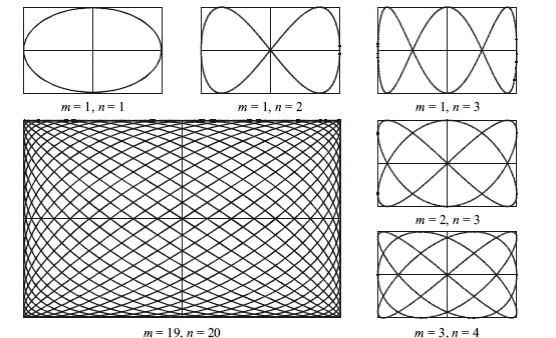
Траектория точки, участвующей во взаимно перпендикулярных колебаниях с кратными частотами, – замкнутая кривая, форма которой зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Такие замкнутые траектории называются фигурами Лиссажу.

Сложение гармонических колебаний

Если колебательная система одновременно участвует в двух (или более) независимых колебательных движениях, возникает задача — найти результирующее колебание. В случае однонаправленных колебаний под этим понимается нахождение уравнения результирующего колебания; в случае взаимно перпендикулярных колебаний — нахождение траектории результирующего колебания.

Метод векторных диаграмм

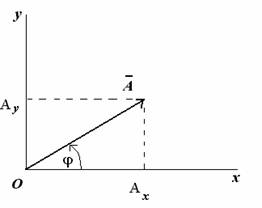
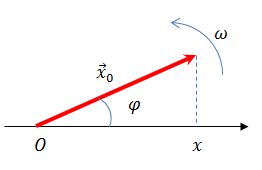
Рассмотрим вращающийся против часовой стрелки с постоянной угловой скоростью w вектор А. Очевидно, что угол j = w t + j₀ где j₀ — начальный угол.

Проекции вектора А на оси координат запишутся:

Видно, что проекции вращающегося вектора на оси координат по форме совпадают с уравнением гармонических колебаний, если угловой скорости вектора сопоставить угловую частоту колебаний, а начальному углу — начальную фазу.

Проводя аналогию дальше, можно сказать, что результат сложения двух однонаправленных колебаний можно получить следующим путем: необходимо сложить два вектора, а проекции суммарного вектора на оси координат будут являться уравнениями результирующего колебания. Рассмотрим этот метод на примере сложения двух колебаний с произвольными частотами. Пусть наше тело участвует в двух совпадающих по направлению колебаниях:

Сопоставим этим колебаниям два вектора А₁ и А₂, вращающихся с соответствующими угловыми скоростями.

Сопоставляем колебаниям проекции векторов на ось y. Задача сложения колебаний сводится к нахождению проекции вектора А на ось y (амплитуда результирующего колебания) и угла f (фаза результирующего колебания).

Из очевидных геометрических соображений находим:

Отметим, что в общем случае сложения колебаний с разными частотами амплитуда результирующего колебания будет зависеть от времени. Если же частоты одинаковы, то 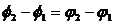, то есть зависимость от времени исчезает. На языке векторной диаграммы это означает, что складываемые векторы при своем вращении не меняют своего относительного положения. В этом случае формулы для амплитуды и фазы результирующего колебания запишутся так:

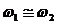
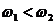
Рассмотрим сложение двух однонаправленных колебаний с неравными, но близкими частотами, то есть , и пусть для определенности . Для простоты пусть начальные фазы и амплитуды этих колебаний равны. В результате сложения двух колебаний

получим уравнение суммарного колебания:

Полученное результирующее колебание не является гармоническим (сравни с уравнением (1)); такого вида колебания носят название биений, название понятно, если посмотреть на график колебаний.

Величина, стоящая перед синусом, меняется со временем относительно медленно, так как разность частот мала. Эту величину условно называют амплитудой биений, а разность складываемых частот 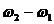— частотой биений (циклической).

При сложении взаимно перпендикулярных колебаний необходимо найти уравнение траектории тела, то есть из уравнений колебаний типа x = x(t), y = y(t) исключить t и получить зависимость типа y(x).

например, сложим два колебания с одинаковыми частотами:

исключив время, получим:

В общем случае это — уравнение эллипса. При A₁=A₂ — окружность, при 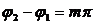(m — целое) — отрезок прямой.

Вид траектории при сложении взаимно перпендикулярных колебаний зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Получающиеся кривые носят название фигур Лиссажу.

Сложение колебаний

Тело, совершающее колебания, способно принимать участие в нескольких колебательных процессах одновременно. В таком случае возникает необходимость выяснить, каким будет результирующее колебание.

Сложение колебаний направленных по одной прямой

Рассмотрим сложение двух гармонических колебаний одинакового направления и равной частоты. Тогда смещение ($x$) совершающего колебания тела будет равно сумме смещений $x_1$ и $x_2$, которые представим в виде уравнений:

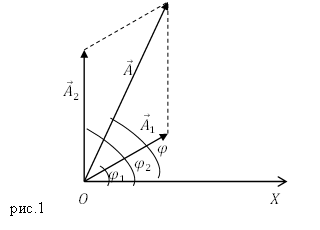
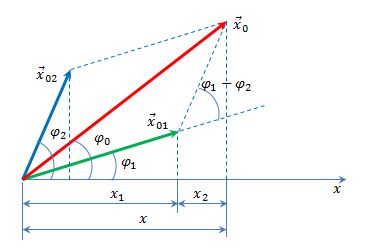
Колебания (1) и (2) представим на векторной диаграмме в виде векторов $<overline>_1$ и $<overline>_2$ (рис.1).

Из рис.1 видно, что амплитуду результирующего колебания можно найти как:

где $A_1$; $A_2$ — амплитуды сложенных колебаний; $<varphi >_2;;<varphi >_1$ — начальные фазы суммирующихся колебаний. При этом начальную фазу полученного колебания ($varphi $) вычисляют, применяя формулу:

Из выражения (4) видно, что если $<varphi >_2-<varphi >_1=0$, тогда получим колебание, амплитуда которого равна:

При разности фаз равной $<varphi >_2-<varphi >_1=pm pi $, что означает, что колебания находятся в противофазе, амплитуда сложенных колебания составляет:

Суперпозиция взаимно перпендикулярных колебаний

Пусть у нас происходят два взаимно перпендикулярные гармонические колебания с одной частотой $<omega >_0$. Колебания происходят вдоль осей X и Y. Пусть начало отсчета времени было таким, что начальная фаза первого колебания равнялась нулю. При этом уравнения колебаний предстанут в виде:

Уравнения (8) и (9) вместе представляют уравнение траектории движения точки в параметрическом виде. Исключаем время из уравнений, получаем уравнение траектории:

Уравнение траектории точки, которая принимает участие в перпендикулярных колебаниях с амплитудами $A_1$и $A_2$ и начальными фазами $<varphi >_2и<varphi >_1$:

Уравнение (10) — это уравнение эллипса.

В случае равенства начальных фаз составляющих колебаний уравнение траектории преобразуется к виду:

что говорит о движении точки по прямой линии. Точка, совершающая гармонические колебания движется по этой прямой, расстояние от начала координат до точки равно:

Если $Delta varphi =<varphi >_2-<varphi >_1=frac<pi ><2>,$ уравнением траектории становится выражение:

что означает, траектория движения эллипс.

Если частоты нормальных друг другу колебаний отличны на очень небольшую величину $Delta omega $, то их рассматривают как колебания с равными частотами, но переменной разностью фаз. При этом суммарное движение проходит по медленно изменяющей вид кривой.

Траектории движений суперпозиций взаимно нормальных колебаний с разными частотами представляют собой сложные кривые, которые называют фигурами Лиссажу.

Примеры задач на сложение колебаний

Задание. Какова разность фаз суммируемых колебаний, если складывались два колебания, направленных по одной прямой, обладающих одинаковыми амплитудами и периодами? Сложились они в колебание той же амплитуды.

Решение. В качестве основы для решения задачи используем выражение для вычисления амплитуды складывающихся колебаний, если они направлены вдоль одной прямой:

Учитывая условия задачи выражение (1.1) преобразуем к виду:

Выразим из (1.2) искомую разность фаз:

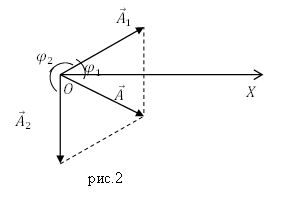
Изобразим векторную диаграмму колебаний (рис.2).

Ответ. $Delta varphi =frac<4pi ><3>илиfrac<2pi ><3>$

Задание. Материальная точка совершает одновременно два взаимно перпендикулярных колебания: $x=A<cos left(<omega >_0tright) >,y=B<cos left(<omega >_0tright) >,$ каким будет уравнение траектории движения точки?

Решение. Из уравнения:

Подставим правую часть выражения (2.2) вместо $<cos left(<omega >_0tright) >$ в формулу:

Уравнением движения точки будет прямая линия.

Ответ. $y=fracx$

Как найти результирующее уравнение колебаний

Сложение нескольких гармонических колебаний становится наглядней, если изображать колебания в виде векторов на плоскости. Полученная таким образом схема называется векторной диаграммой .

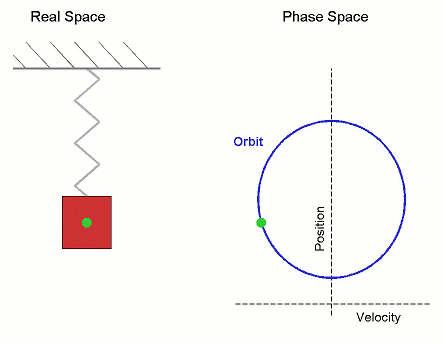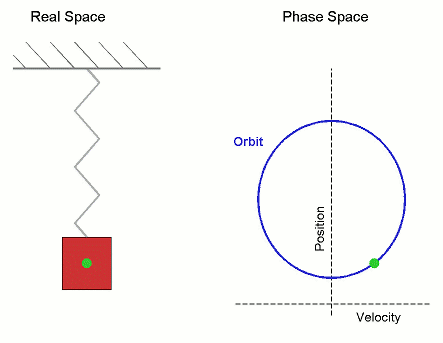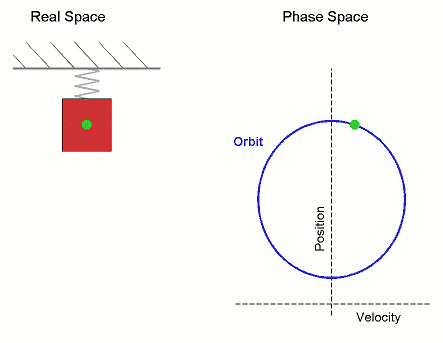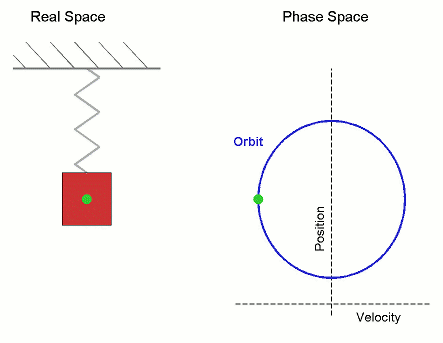
Тогда координата проекции вектора изменяется со временем по закону

Гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде колебаний, направление вектора образует с осью х угол, равный начальной фазе колебаний, а угловая скорость вращения вектора равна его циклической частоте.

Сложение двух гармонических колебаний одинакового направления и одинаковой частоты

Смещение х колеблющегося тела будет равно сумме смещений х₁ и х₂:

Вектор х₀ представляет собой результирующую амплитуду колебаний. Он вращается с той же угловой скоростью ω и начальной фазой φ₀.

Рассмотрим частные случаи.

Если разность фаз φ₁ — φ₂колебаний равна 0 (отличается на 2π), то амплитуда результирующего колебания равна сумме амплитуд: х = х₁ + х₂.

Если оба колебания находятся в противофазе (разность фаз равна ±π), то результирующая амплитуда х = |х₁ — х₂|.

Если частоты неодинаковы, то векторы будут вращаться с различной скоростью. Результирующий вектор пульсирует по величине и вращается с непостоянной скоростью.

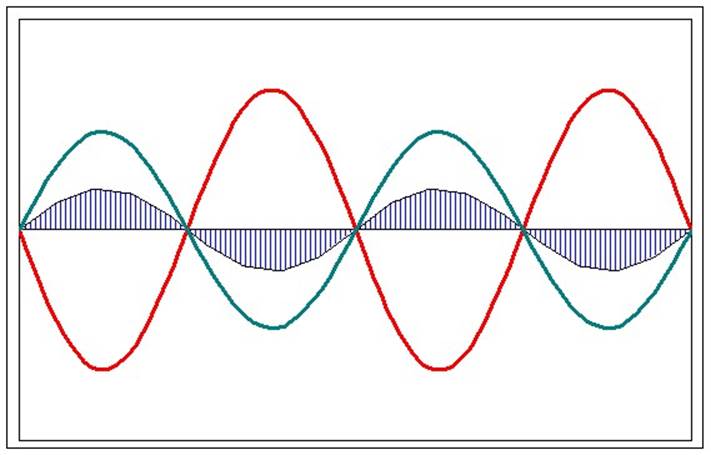
Биения

Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биением .

Пусть два колебания мало отличаются по частоте. Тогда амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω намного меньше ω. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:

Тогда результирующее колебание можно представить в виде:

Амплитуда результирующего колебания меняется со временем по закону

Сложение взаимно перпендикулярных колебаний

Допустим, что материальная точка может совершать колебания как вдоль оси х, так и вдоль перпендикулярной к ней оси у. Если возбудить оба колебания, материальная точка будет двигаться по некоторой, вообще говоря, криволинейной траектории, форма которой зависит от разности фаз обоих колебаний.

Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний запишутся следующим образом:

где α — разность фаз обоих колебаний.

После преобразования получим уравнение траектории, которое представляет собой параметрическое уравнение эллипса, оси которого повернуты относительно осей х и у.

Рассмотрим частные случаи.

1. Разность фаз равна нулю. В этом случае получается уравнение прямой.

Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и амплитудой

2. Разность фаз равна ±π. Уравнение имеет вид прямой.

3. При α = ±π/2 получается уравнение эллипса, приведенного к координатным осям. При равенстве амплитуд эллипс превращается в окружность.

При сложении взаимно перпендикулярных колебаний разных частот получаются различные траектории материальной точки, названные фигурами Лиссажу. Чем ближе отношение частот к единице, тем сложнее получается фигура Лиссажу.

Резонанс

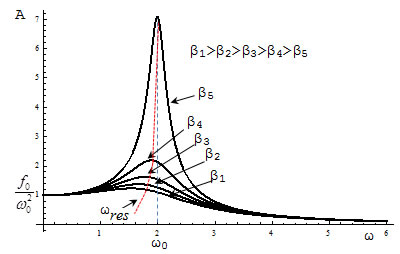
Резонанс — явление резкого возрастания амплитуды вынужденных колебаний при совпадении частот вынуждающей силы и собственных колебаний маятника. Вынужденные колебания происходят, если внешняя сила изменяется периодически:

Дифференциальное уравнение вынужденных колебаний

Амплитуда колебания определяется формулой

где коэффициент затухания β = r/2m.

Для определения резонансной частоты надо найти минимум знаменателя. Резонансная амплитуда

Автоколебания

При затухающих колебаниях энергия системы расходуется на преодоление сил сопротивления. Если восполнять эти потери, то колебания станут незатухающими. Если система сама управляет воздействием внешних сил, то такое колебательное движение называется автоколебанием.

В автоколебательной системе обязательно присутствуют элементы:

• сама колебательная ситема, ее параметры определяют частоту автоколебаний;
• источник энергии, поддерживающий автоколебания;
• клапан, регулирующий поступление энергии;
• механизм обратной связи, посредством которой система управляет клапаном так, чтобы поступающая энергия компенсировала потери за счет трения и сопротивления среды.

Для школьников.

Задача.

Даны уравнения одинаково направленных колебаний материальной точки:

Надо получить уравнение результирующего колебания точки.

Решение. Из уравнений видно, что складываемые колебания имеют одинаковую частоту, равную 5 рад/с.

Амплитуда результирующего колебания (см. рис 25):

Находим начальную фазу результирующего колебания точки:

отсюда

Тогда уравнение результирующего колебания имеет вид:

Таким образом, если материальная точка одновременно участвует в двух гармонических колебаниях одинаковой частоты и одного направления, то её результирующее колебание тоже будет гармоническим с той же частотой.

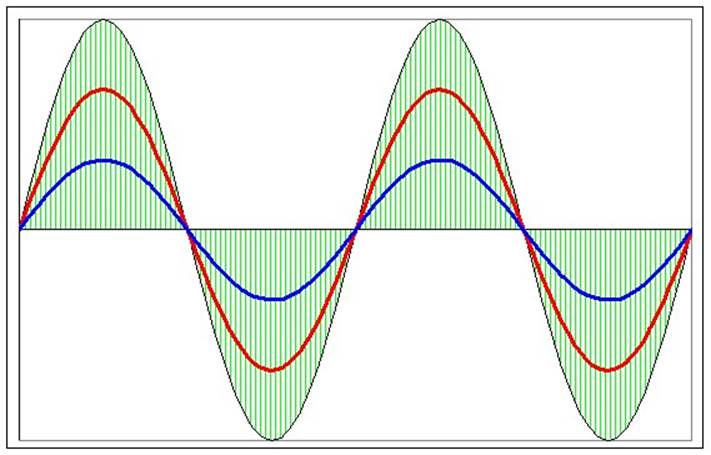
Если же материальная точка участвует одновременно в двух гармонических колебаниях одного направления, но частоты этих колебаний разные, то результирующее колебание уже не будет гармоническим (синусоидальным). Покажем это на рисунке.

Здесь пунктирными линиями показаны графики двух гармонических колебаний разных частот, в которых участвует материальная точка (горизонтальная линия соответствует её положению равновесия).

Алгебраическое сложение смещений в каждом из двух колебаний (в данный момент времени) даёт результирующее смещение материальной точки от её положения равновесия (АD = АВ + АС).

По полученным в результате сложения точкам построен график суммарного колебания материальной точки (сплошная линия), форма которой не является синусоидой.

Сплошная линия на рисунке есть график негармонического периодического суммарного колебания (его ещё называют формой периодического колебания или просто формой).

Период суммарного колебания (формы) равен периоду гармонического колебания с наиболее низкой частотой, называемой основной частотой (см. рисунок).

Определённой частоты у суммарного колебания нет.

Теперь рассудим наоборот. Пусть известна форма, т. е. график колебаний материальной точки (сплошная линия на рисунке).

Это сложное периодическое колебание (форму) можно разложить на набор гармонических колебаний (в рассматриваемом случае их два). В других случаях этот набор может включать в себя много гармонических колебаний (гармоник).

В этом заключается смысл теоремы Фурье: всякое периодическое колебание периода Т может быть представлено в виде суммы гармонических колебаний с периодами, равными T, Т/2, Т/3, Т/4 и т. д., т. е. с частотами, равными 1/Т, 2/Т, 3/Т, 4/Т и т. д.

Каждое из набора колебаний имеет определённую частоту.

Самая низкая (малая) частота называется основной частотой.

Частоты других гармонических колебаний (гармоник), на которые разложили периодическое сложное колебание (форму), в 2, 3, 4 и т. д. раз больше основной частоты.

Они называются второй, третьей, четвёртой и т. д. гармониками (высшими гармониками).

Такое действие – разложение сложного периодического колебания (формы) в гармонический ряд (на гармонические колебания) часто бывает нужно на практике и называется оно гармоническим анализом.

Гармонический анализ позволяет детально описать и проанализировать любой колебательный процесс.

С периодическими колебаниями (формами) мы встретимся ещё при рассмотрении звуковых колебаний.

Если частоты складываемых гармонических колебаний одного направления близки друг другу, то получается интересная картина.

Итак, нами рассмотрены примеры сложения гармонических колебаний. Говоря о сложении гармонических колебаний одного направления, но разных частот, приходим к выводу, что результирующее колебание (форма) уже не является гармоническим, но является периодическим. И ещё приходим к заключению, что любое сложное колебание можно разложить на совокупность гармонических колебаний (гармоник). Этим разложением, называемым гармоническим анализом, широко пользуются на практике.

https://yandex.ru/video/preview/?text=%D0%B4%D0%B5%D0%BC%D0%BE%D0%BD%D1%81%D1%82%D1%80%D0%B0%D1%86%D0%B8%D1%8F%20%D1%81%D0%BB%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5%20%D0%B3%D0%B0%D1%80%D0%BC%D0%BE%D0%BD%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D1%85%20%D0%BA%D0%BE%D0%BB%D0%B5%D0%B1%D0%B0%D0%BD%D0%B8%D0%B9&path=wizard&parent-reqid=1638617385109896-9444507951277324299-sas3-0841-245-sas-l7-balancer-8080-BAL-7543&wiz_type=vital&filmId=6200809953460406703

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.

Предыдущая запись: Пример нахождения характеристик гармонического колебания материальной точки.

Следующая запись: Затухающие колебания.

Ссылки на занятия до электростатики даны в Занятии 1 .

Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .

Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 5 8.

Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .

Часто
бывает так, что материальная точка
одновременно участвует в нескольких
колебательных движениях. Сложить два
или несколько колебаний – значит найти
закон, которому подчиняется результирующее
движение, найти траекторию этого
движения.

Сложение
колебаний в общем случае производится
аналитически, но в ряде случаев может
быть осуществлено геометрически, при
помо-

щи
так называемого вектора
амплитуды.

Вектор
амплитуды–
это вектор, модуль которого равен
амплитуде рассматриваемого колебания.

Если
вектор амплитуды привести во вращение
вокруг точки 0,
взятой на оси
,
с угловой скоростью(рис.48),
то проекция конца этого вектора на осьбудет совершать гармонические колебания
с цик-лической частотой:

,

где
–
угол, образованный вектором амплитуды
и осьюв
начальный момент времени.

Таким
образом, при помощи вектора амплитуды
можно построить геометрическую модель
гармонических колебаний, в которой
особые характеристики гармонического
движения
иполучают простой геометрический смысл.

1. Сложение двух гармонических колебаний одинаковой циклической частоты, происходящих вдоль одной прямой.

Пусть
;;.

Складываемые
колебания описываются уравнениями:

; (26.1)

. (26.2)

Так
как колебания происходят вдоль одной
прямой (вдоль оси
),
то результирующее смещение в любой
момент времени равно алгебраиче-

ской
сумме смещений
и:

(26.3)

Выполним
это сложение геометрически, с помощью
векторов амплитуды
и.
На рисунке 49 изображены положения
векторов амплитуды в начальный момент
времени. Вектор результирующей амплитудыравен геометрической сумме векторови.

Проекции
конца вектора
определяет результирующее смещение в
начальный момент времени. Так как оба
вектора,и,
вращаются в процессе колебаний с одной
и той же угловой скоростью,
с такой же скоростью будет вращаться и
вектор результирующей амплитуды.
Следовательно, результирующее колебание
представляет собой гармоническое
колебание той же частоты и происходит
вдоль той же прямой. Из рисунка 49 видно,
что

,

для
произвольного момента времени:

, (26.4)

где
и– амплитуда и начальная фаза результирующего
колебания. Изпо теореме косинусов получаем:

или

(26.5)

так
как

(26.6)

Амплитуда
результирующего колебания зависит от
разности фаз ()
слагаемых колебаний. Если (),
гдетои,
т.е. если разность фаз равна четному
числу,
колебания усиливают друг друга. Если,
тои,
т.е.

если
разность фаз равна нечетному числу
,
колебания максимально ослабляют друг
друга. В зависимости от разности фаз
амплитуда колебания может принимать
любые значения, лежащие в интервале:

.

2. Сложение двух гармонических колебаний со слегка

отличающимися
частотами, происходящих вдоль одной
прямой

Пусть

,
причем«(или),

и

.

Уравнения слагаемых
колебаний:

.

Как и в предыдущем
случае,

(26.7)

Так
как
векторы амплитуды складываемых колебаний
будут вращаться с неодинаковыми угловыми
скоростями. Это приведёт к тому, что
вектор результирующей амплитуды будет
пульсировать по величине. Последнее
видно из формулы (26.5), если в неё вместоподставить:
так как эта величина монотонно возрастает,
вектор амплитуды результирующего
колебания будет периодически изменяться.

Применив
формулы для суммы косинусов, преобразуем
(26.7):

(26.8)

Множитель,
выделенный вертикальными чертами,
изменяется с течением времени гораздо
медленнее, чем второй множитель. За
время,

в
течение которого второй множитель
совершит полное колебание, первый почти
не изменится (так как по условию
«).
Это позволяет рассматривать колебание
(26.8) как гармоническое колебание с
частотой,
амплитуда которого изменяется по
периодическому закону:

(26.9)

(взят
модуль этого выражения, так как амплитуда
– величина положительная). Гармонические
колебания с периодически изменяющейся
амплитудой называются биениями.

Найдём
частоту пульсаций амплитуды или частоту
биений, Так как период абсолютного
значения косинуса равен
,
то частота пульсаций определится из
соотношения:откуда

(26.10)

где
и–
частоты слагаемых колебаний. Мы видим,
что чем меньше отличаются частоты
слагаемых колебаний, тем меньше частота
биений. На рисунке 50 изображён график
биений.

Рис.50

3.
Сложение
взаимно перпендикулярных гармонических
колебаний

Пусть
материальная точка одновременно
участвует в двух колебаниях, происходящих
вдоль координатных осей
и,
причём

,
,:

(26.11)

Для
нахождения траектории результирующего
движения из этих уравнений нужно
исключить время. Разделив второе
уравнение на первое, получим

или(26.12)

Траектория
– прямая, проходящая через начало
координат и наклоненная к оси
под углом, тангенс которого равен(рис.51,а).

Точка
будет совершать гармоническое колебание
вдоль этой прямой:

,

где
– амплитуда колебания.

Рис.51

2.
Пусть теперь
;;

,:

,

Разделив
одно уравнение на другое, получим
уравнение прямой с отрицательным
тангенсом угла наклона (рис.51,б):

.
(26.13)

Пусть,
наконец,
;;;

Перепишем
эти уравнения в виде

возведём
в квадрат и почленно сложим:

(26.14)

Полученное
уравнение есть уравнение эллипса,
приведенное к координатным осям. Полуоси
этого эллипса равны соответствующим
амплитудам колебаний
и(рис.52). Приэллипс вырождается в окружность. Если
разность фаз слагаемых колебаний равнато движение точки по эллипсу (или по
окружности) будет происходить по часовой
стрелке.

Действительно,
в момент времени
точка имеет координаты:

(рис.52)

В
последующем
уменьшается, аy
становится
отрицательным. Это соответствует
движению по часовой стрелке. Нетрудно
убедиться в том, что если
(или,
что то же самое), движение происходит
против часовой стрелки.

При
всех других разностях фаз (но при
)
получаются эллипсы, не приведённые к
осями.

При
сложении взаимно перпендикулярных
гармонических колебаний с неодинаковыми
циклическими частотами результирующее
движение будет происходить по сложным
траекториям, называемым фигурами
Лиссажу. Форма фигур Лиссажу зависит
от соотношения частот складываемых
колебаний и разности их начальных фаз.

ПРИМЕРЫ РЕШЕНИЯ
ЗАДАЧ

Пример
1. Материальная
точка массой m
= 5 г
совершает гармонические колебания с
частотой
.
Амплитуда колебаний

А
= 3 см.
Определить:
1) скорость
в момент времени, когда смещениех
= 1,5 см;
2)
максимальную
силу
,
действующую на точку,

3) полную энергию
колеблющейся точки.

Решение.
1) Уравнение
гармонических колебаний имеет вид

где
х
– смещение колеблющейся точки от
положения равновесия, А
– амплитуда колебания,
– фаза колебания,– начальная фаза,

круговая
(циклическая) частота, t
– время.

Формулу скорости
получим, взяв первую производную по
времени от смещения,

Чтобы
выразить скорость через смещение, надо
исключить из этих выражений время. Для
этого возведём оба уравнения в квадрат,
разделим первое на
,
второе наи сложим:

или

Решив
последнее уравнение относительно
,
найдём

Подставив в это
выражение числовые значения величин,
получим

Знак
“плюс” соответствует случаю, когда
направление скорости совпадает с
положительным направлением оси х-ов.
Знак “минус” соответствует случаю,
когда направление скорости совпадает
с отрицательным направлением оси х-ов.

2)
Силу, действующую на точку, найдем по
второму закону Ньютона:
гдеа
– ускорение точки, которое получим,
если возьмём производную по времени от
скорости:

или

Получаем

.

Максимальное
значение силы

Подставив числовые
значения величин, найдем

3)
Полная энергия колеблющейся точки есть
сумма кинетической и потенциальной
энергий, вычисленных для любого момента
времени. В том числе она равна максимальной
кинетической энергии, когда потенциальная
равна нулю, т.е.

,

где

,
тогда

После подстановки
числовых значений получим

ВОПРОСЫ ДЛЯ
САМОПРОВЕРКИ

1.
Что такое колебания? Какие колебания
называются свободными, гармоническими?

2.
Дайте определение амплитуды колебаний,
фазы, периода, частоты, циклической
частоты колебаний.

3.
В чём заключается идея метода вращающегося
вектора амплитуды?

4. Выведите формулы
для скорости и ускорения гармонически
колеблющейся точки как функции времени.

5. От чего зависит
амплитуда и начальная фаза гармонических
механических колебаний?

6. Выведите и
прокомментируйте формулы для кинетической,
потенциальной и полной энергии при
гармонических колебаниях.

7.
Чему равно отношение полной энергии
гармонического колебания к максимальному
значению возвращающей силы, вызывающей
это колебание?

8.
Что называется гармоническим осциллятором,
пружинным маятником, физическим
маятником, математическим маятником?

9.
Выведите формулу для периодов колебаний
пружинного, физического и математического
маятников.

10.
Что такое приведённая длина физического
маятника?

11. Сформулируйте
и поясните теорему Штейнера.

12. Какова траектория
точки, участвующей одновременно в двух
взаимно перпендикулярных гармонических
колебаниях с одинаковыми периодами?
Когда получается окружность, прямая?

13. Что такое биения?
Чему равна частота биений, период?

14.
Запишите дифференциальное уравнение
затухающих колебаний и его решение.
Проанализируйте их.

15. Как изменяется
частота собственных колебаний с
увеличением массы колеблющегося тела?

16.
По какому закону изменяется амплитуда
затухающих колебаний? Являются ли
затухающие колебания периодическими?

17. Почему частота
затухающих колебаний должна быть меньше
частоты собственных колебаний системы?

18.
Что такое коэффициент затухания,
декремент затухания, логарифмический
декремент затухания?

19.
При каких условиях наблюдается
апериодическое движение?

20.
Что такое вынужденные колебания?
Запишите дифференциальное уравнение
вынужденных колебаний и его решение.

21.
От чего зависит амплитуда вынужденных
колебаний? Запишите выражение для
амплитуды и фазы при резонансе.

22.
Нарисуйте, проанализируйте резонансные
кривые для амплитуды смещения и скорости.
В чём их отличие?

23.
Чему равен сдвиг фазы между смещением
и вынуждающей силой при резонансе?

24. Что называется
резонансом? Какова его роль?

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Сложение колебаний, теория и онлайн калькуляторы

Сложение колебаний

Тело, совершающее колебания, способно принимать участие в нескольких колебательных процессах одновременно. В таком случае
возникает необходимость выяснить, каким будет результирующее колебание.

Сложение колебаний направленных по одной прямой

Рассмотрим сложение двух гармонических колебаний одинакового направления и равной частоты. Тогда смещение ($x$) совершающего колебания тела будет равно сумме смещений $x_1$ и $x_2$, которые представим в виде уравнений:

[x_1=A_1{cos left({omega }_0t+{varphi }_1right) }left(1right),]

[x_2=A_2{cos left({omega }_0t+{varphi }_2right) }left(2right).]

Колебания (1) и (2) представим на векторной диаграмме в виде векторов ${overline{A}}_1$ и ${overline{A}}_2$ (рис.1).

Результирующее колебание отображает вектор $overline{A}$, который вращается с той же скоростью (${omega }_0$),
что векторы его составляющие. Сложением колебание векторов ${overline{A}}_1$+${overline{A}}_2$=$overline{A}$ является гармоническим колебанием:

[x=A{cos {(omega }_0t+varphi ) (3) }.]

Из рис.1 видно, что амплитуду результирующего колебания можно найти как:

[A=sqrt{A^2_1+A^2_2+2A_1A_2{cos left({varphi }_2-{varphi }_1right) }left(4right),}]

где $A_1$; $A_2$ – амплитуды сложенных колебаний; ${varphi }_2;;{varphi }_1$ – начальные фазы суммирующихся колебаний. При этом начальную фазу полученного колебания ($varphi $) вычисляют, применяя формулу:

[tg varphi =frac{A_1{sin {varphi }_1+A_2{sin {varphi }_2 } }}{A_1{cos {varphi }_1+A_2{cos {varphi }_2 } }}left(5right).]

Из выражения (4) видно, что если ${varphi }_2-{varphi }_1=0$, тогда получим колебание, амплитуда которого равна:

[A=A_1+A_2left(6right).]

При разности фаз равной ${varphi }_2-{varphi }_1=pm pi $, что означает, что колебания находятся в противофазе, амплитуда сложенных колебания составляет:

[A=left|A_1-A_2right|left(7right).]

Если частоты сложенных гармонических колебаний не равны, то есть векторы ${overline{A}}_1$и ${overline{A}}_2$ вращаются с разной скоростью, результирующее колебание гармоническим не будет. Вектор $overline{A}$ будет пульсировать по величине, и вращаться с переменной скоростью.

Суперпозиция взаимно перпендикулярных колебаний

Пусть у нас происходят два взаимно перпендикулярные гармонические колебания с одной частотой ${omega }_0$. Колебания происходят вдоль осей X и Y. Пусть начало отсчета времени было таким, что начальная фаза первого колебания равнялась нулю. При этом уравнения колебаний предстанут в виде:

[x=A_1{cos left({omega }_0t{+varphi }_1right) }left(8right),]

[y=A_2{cos left({omega }_0t+{varphi }_2right) }left(9right),]

Уравнения (8) и (9) вместе представляют уравнение траектории движения точки в параметрическом виде. Исключаем время из уравнений, получаем уравнение траектории:

Уравнение траектории точки, которая принимает участие в перпендикулярных колебаниях с амплитудами $A_1$и $A_2$ и начальными фазами ${varphi }_2и{varphi }_1$:

[frac{x^2}{A^2_1}+frac{y^2}{A^2_2}-frac{2xy}{A_1A_2}{cos left({varphi }_2-{varphi }_1right) }={sin}^2left({varphi }_2-{varphi }_1right)left(10right).]

Уравнение (10) – это уравнение эллипса.

В случае равенства начальных фаз составляющих колебаний уравнение траектории преобразуется к виду:

[y=frac{A_2}{A_1}x или y=-frac{A_2}{A_1}x left(11right),]

что говорит о движении точки по прямой линии. Точка, совершающая гармонические колебания движется по этой прямой, расстояние от начала координат до точки равно:

[r=sqrt{x^2+y^2}.]

Если $Delta varphi ={varphi }_2-{varphi }_1=frac{pi }{2},$ уравнением траектории становится выражение:

[frac{x^2}{A^2_1}+frac{y^2}{A^2_2}=1left(12right),]

что означает, траектория движения эллипс.

Если частоты нормальных друг другу колебаний отличны на очень небольшую величину $Delta omega $, то их рассматривают как колебания с равными частотами, но переменной разностью фаз. При этом суммарное движение проходит по медленно изменяющей вид кривой.

Траектории движений суперпозиций взаимно нормальных колебаний с разными частотами представляют собой сложные кривые, которые называют фигурами Лиссажу.

Примеры задач на сложение колебаний

Читать дальше: тело, брошенное горизонтально.