Принцип суперпозиции сил
Определение
Результирующая, или равнодействующая, сила равна векторной сумме всех сил, действующих на тело:
−R=∑−Fi
Fi — сила, с которой электрическое поле зарядом q действует на пробный заряд qi, помещенный в это поле на расстоянии ri от этого заряда. Численно ее можно вычислить по формуле:
Fi=kqiqr2i
Алгоритм решения задач на определение равнодействующей силы (точечный заряд находится в поле, созданном другими точечными зарядами):
- Сделать чертеж. Указать расположение всех зарядов и их знаки.
- Выделить заряд, для которого определяют равнодействующую.
- Пронумеровать остальные заряды.
- Определить расстояния от выделенного заряда до всех остальных.
- Построить все силы, действующие на интересующий нас заряд. При этом необходимо учитывать знаки зарядов, их модули и расстояния между зарядами.
- Найти геометрическую (векторную) сумму всех сил, действующих на выделенный заряд.
- Пользуясь формулами геометрии и законом Кулона, определить модуль равнодействующей.
Пример №1. Как направлена (вправо, влево, вверх, вниз) кулоновская сила −FK, действующая на положительный точечный электрический заряд +2q, помещенный в центр квадрата, в вершинах которого находятся заряды +q, +q, –q, –q?
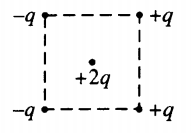
Известно, что одноименные заряды отталкиваются, а разноименные – притягиваются. Из рисунка видно, что заряд +2q, находящийся в центре квадрата, будет отталкиваться от зарядов +q, находящихся справа, и будет притягиваться к зарядам –q, находящимся слева.
Сила Кулона обратно пропорциональна квадрату расстояния между зарядами, то есть с увеличением расстояния r убывает по квадратическому закону. Так как заряд +q находится точно в центре квадрата, то расстояния от зарядов +q, +q, -q, -q будут равны, следовательно, равна по модулю и сила Кулона, действующая на заряд +2q. Суперпозиция сил, действующих на заряд +2q:
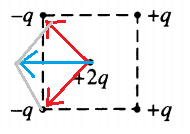
Из рисунка видно, что кулоновская сила −FK, действующая на положительный точечный электрический заряд +2q, направлена влево.
Принцип суперпозиции полей
Определение
Если в некоторой точке пространства складываются электрические поля от нескольких зарядов, то результирующая напряженность находится как векторная сумма напряженностей отдельных полей:
−E=∑−Ei
−Ei — напряженность, создаваемая зарядом qi в точке, находящейся на расстоянии ri:
−Ei=kqir2i
Векторное сложение напряженностей аналогично нахождению равнодействующей сил Кулона, только в интересующую нас точку пространства помещают положительный пробный заряд. Чтобы найти результирующий потенциал в точке, необходимо алгебраически сложить потенциалы всех полей. Нельзя забывать, что знак потенциала определяется знаком заряда, создающим электрическое поле:
φ=∑φi
φi — потенциал электростатического поля, создаваемого зарядом qi на расстоянии ri от него. Численно он равен:
φi=±kqiri
Для определения полной энергии надо сложить потенциальные энергии всех пар зарядов:
Wp=∑Wip
Wip — потенциальная энергия взаимодействия зарядов qi и qn, находящихся на расстоянии ri друг от друга. Численно она равна:
Wip=±kqiqnri
Примеры определения расстояний
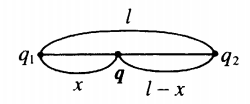 |
Два заряда лежат на одной прямой на расстоянии l друг от друга. Изучаемый заряд лежит между ними:
r1=x; r2=l−x |
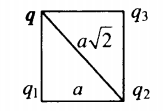 |
Изучаемый заряд лежит в вершине квадрата со стороной a:
r1=r3=a; r2=a√2 |
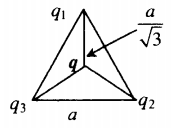 |
Изучаемый заряд лежит в центре равностороннего треугольника со стороной a:
r1=r2=r3=a√3 |
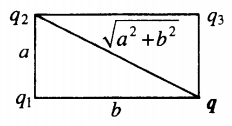 |
Изучаемый заряд лежит в вершине прямоугольника со сторонами a и b:
r1=b; r2=√a2+b2; r3=a |
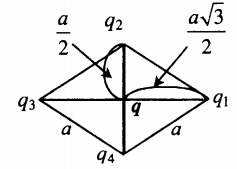 |
Изучаемый заряд лежит в точке пересечения диагоналей ромба со стороной a. Угол при вершине ромба 120о:
r1=r3=a√32; r2=r4=a2 |
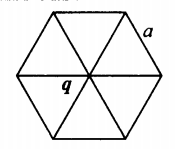 |
Изучаемый заряд лежит в центре правильного шестиугольника со стороной a:
r1=r2=r3=r4=r5=r6=a |
Пример №2. Маленький заряженный шарик массой m, имеющий заряд q, движется с высоты h по наклонной плоскости с углом наклона α. В вершине прямого угла, образованного высотой и горизонталью, находится неподвижный заряд Q. Какова скорость шарика у основания наклонной плоскости v, если его начальная скорость равна нулю? Трением пренебречь.
Построим чертеж:
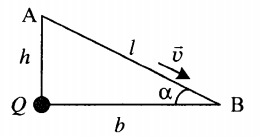
Применим закон сохранения энергии, согласно которому полная энергия шарика в точке А равна полной энергии шарика в точке В (трением пренебрегаем):
EA=EB
Полная энергия шарика с зарядом qв точке А равна сумме его механической потенциальной энергии и потенциальной энергии взаимодействия с зарядом Q:
EA=mgh+kqQh
В точке В механическая потенциальная энергия шарика равна нулю, но в этой точке максимальная его кинетическая энергия. Полная энергия шарика в точке В равна:
EB=mv22+kqQb
Расстояние между точкой В и местом, где находится заряд Q:
b=htanα
Приравняем правые части уравнений:
mgh+kqQh=mv22+kqQb
mgh+kqQh=mv22+kqQtanαh
mv22=mgh+kqQh−kqQtanαh=mgh+kqQh(1−tanα)
v=⎷2(mgh+kqQh(1−tanα))m=√2gh+2kQmh(1−tanα)
Задание EF17563
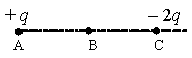 Точка В находится в середине отрезка АС. Неподвижные точечные заряды + q и −2q расположены в точках А и С соответственно (см. рисунок). Какой заряд надо поместить в точку С взамен заряда −2q, чтобы напряжённость электрического поля в точке В увеличилась в 2 раза?
Точка В находится в середине отрезка АС. Неподвижные точечные заряды + q и −2q расположены в точках А и С соответственно (см. рисунок). Какой заряд надо поместить в точку С взамен заряда −2q, чтобы напряжённость электрического поля в точке В увеличилась в 2 раза?
Ответ:
а) − 5q
б) − 4q
в) 4q
г) 5q
Алгоритм решения
1.Определить направление вектора напряженности для зарядов в точках А и С.
2.Определить напряженность поля в точке В, используя принцип суперпозиции.
3.Найти, какой заряд нужно поместить в точку С вместо имеющегося, чтобы напряженность электростатического поля в точке В увеличилась вдвое.
Решение
Вектор напряженности заряда в точке А направлен в направлении от этого заряда, так как он положительный. Это значит, что в точке В вектор напряженности EA направлен вправо. Вектор напряженности заряда в точке С направлен к этому заряду, так как он отрицательный. Поэтому в точке В вектор напряженности EC тоже направлен вправо. Следовательно, при векторном сложении модули напряженностей должны складываться:
E=EA+EC=k|q|r2+k|−2q|r2=3kqr2
Найдем, какой нужно поместить заряд в точку С, чтобы напряженность увеличилась вдвое:
k|q|r2+k|x|r2=2·3kqr2=6kqr2
Преобразуем выражение и получим:
|q|+|x|=6q
Отсюда:
|x|=5q
Этот заряд должен быть отрицательным, так как в этом случае линии напряженности поля, создаваемого зарядом в точке С, будут складываться с линиями напряженности поля, создаваемыми положительным зарядом в точке А. Следовательно, x = –5q.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17967
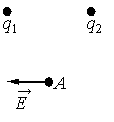 На рисунке показано направление вектора напряжённости электрического поля E в точке А, равноудалённой от равных по модулю точечных зарядов q1 и q2. Какие знаки имеют заряды?
На рисунке показано направление вектора напряжённости электрического поля E в точке А, равноудалённой от равных по модулю точечных зарядов q1 и q2. Какие знаки имеют заряды?
Ответ:
а) q1 > 0; q2 < 0
б) q1 < 0; q2 > 0
в) q1 > 0; q2 > 0
г) q1 < 0; q2 < 0
Алгоритм решения
1.Вспомнить, как направлены векторы напряженности полей, созданных положительным и отрицательным зарядами.
2.Построить параллелограмм, сторонами которого являются отрезки, равные длинам векторов напряженности полей, создаваемыми двумя точечными зарядами.
3.Определить, какое направление должны иметь векторы напряженности, чтобы результатом их вычитания/сложения был вектор −E.
4.Определить знаки зарядов с учетом направления векторов напряженности полей.
Решение
Векторы напряженности электростатического поля, создаваемого положительным точечным зарядом, направлены по радиусным линиям от заряда. Векторы напряженности электростатического поля, создаваемого отрицательным точечным зарядом, направлены по радиусным линиям к заряду.
Построим параллелограмм. Чтобы получить вектор −E, нужно вычесть из вектора −E1 вектор −E2. Причем первый должен быть направлен в сторону заряда, а второй — от заряда.
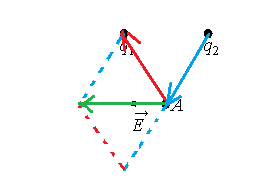
Следовательно, заряд q1 отрицательный (q1 < 0), а заряд q2 положительный (q2 > 0).
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18357
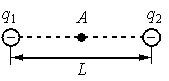 Два точечных отрицательных заряда: q1=−20 нКл и q2=−40 нКл находятся в вакууме на расстоянии L=1,5м друг от друга. Определите величину напряжённости электрического поля этих зарядов в точке А, расположенной на прямой, соединяющей заряды, на одинаковом расстоянии от обоих зарядов.
Два точечных отрицательных заряда: q1=−20 нКл и q2=−40 нКл находятся в вакууме на расстоянии L=1,5м друг от друга. Определите величину напряжённости электрического поля этих зарядов в точке А, расположенной на прямой, соединяющей заряды, на одинаковом расстоянии от обоих зарядов.
Ответ:
а) 160 Н/Кл
б) 320 Н/Кл
в) 125 Н/Кл
г) 640 Н/Кл
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Определить направление векторов напряженности в точке А.
3.Выполнить общее решение задачи, применив принцип суперпозиции полей.
4.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Величина первого заряда: q1 = –20 нКл.
• Величина второго заряда: q2 = –40 нКл.
• Расстояние между зарядами: L = 1,5 м.
–20 нКл = –20∙10–9 Кл
–40 нКл = –40∙10–9 Кл
Вектор напряженности поля, создаваемого первым зарядом в точке А, направлен влево (в сторону заряда), так как он отрицательный. Второй заряд тоже отрицательный, но он лежит по другую сторону от точки А. Поэтому в ней вектор напряженности поля, создаваемого вторым зарядом, будет направлен вправо. Так как модуль второго заряда больше модуля первого, результирующая напряженность будет направлена вправо. Напряженность в точке А в этом случае будет вычисляться как разность двух напряженности:
EA=E2−E1
Напряженность определяется формулой:
E=k|q|r2
Следовательно:
EA=k|q2|(0,5L)2−k|q1|(0,5L)2=k(0,5L)2(|q2|−|q1|)
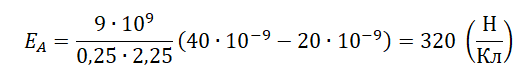
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 3.2k
Потенциал
поля точечного заряда q
равен потенциальной энергии единичного
точечного заряда q
в данной точке поля:
 .
.
(2.3.5)
Потенциал
электростатического поля системы
точечных неподвижных зарядов равен
алгебраической
сумме потенциалов поля каждого заряда
в отдельности:
 = 1
= 1
+ 2
+
3
+
…+
n.
(2.3.6)
Рассмотрим примеры
решения задач.
Пример
3. Имеются
два точечных заряда q1
=
2 нКл, q2
= 1 нКл, находящиеся на одной прямой на
расстоянии r
= 50 см друг от друга (по условию задачи
заряд q1
расположен
слева, заряд
q2
– справа). Найти потенциал электростатического
поля в точке О,
расположенной между зарядами на
расстоянии 10 см от заряда q2.
Дано: q1
= 2 нКл = 210–9
Кл,
q2
= 1 нКл = 110–9
Кл,
r
= 50 см = 0,5 м,
r2
= 10 см = 0,1 м.
Найти: рез.
Решение.
Делаем рисунок, на котором указываем
расположение зарядов и точку О,
в которой будем находить потенциал поля
данной системы зарядов:
q1
q2
![]()
А
О В
По
условию задачи и в соответствии с
рисунком, АВ
= r
= 0,5 м; ОВ
= r2
= 0,1 м; АО
= r1
= 0,4 м.
Исходные формулы
для расчета результирующего потенциала
в точке О
– формулы (2.3.5) и (2.3.6). В (2.3.5) подставим
числовые данные:
 =
=
45 В;
 =
=
90 В.
Используем
формулу (2.3.6) для расчета результирующего
потенциала:
 =
=
1
+ 2
= 135 В.
Ответ: рез
= 135 В.
Пример 4. Имеются
два точечных заряда q1
=
2 нКл,
q2
= – 1 нКл, находящиеся на одной прямой
на расстоянии r
= 50 см друг от друга (по условию задачи
заряд q1
расположен
слева, заряд
q2
– справа). Найти потенциал электростатического
поля в точке О,
расположенной между зарядами на
расстоянии 10 см от заряда q2.
Дано: q1
= 2 нКл = 210–9
Кл,
q2
= – 1 нКл = – 110–9
Кл,
r
= 50 см = 0,5 м,
r2
= 10 см = 0,1 м.
Найти: рез.
Решение.
Аналогично примеру 3, рассмотренному
выше, делаем рисунок, на котором указываем
расположение зарядов и точку О,
в которой будем находить результирующий
потенциал поля данной системы зарядов:
+
q1
– q2
![]()
А
О В
По
условию задачи и в соответствии с
рисунком, АВ
= r
= 0,5 м; ОВ
= r2
= 0,1 м; АО
= r1
= 0,4 м.
Подставим числовые
данные в формулу (2.3.5), а затем используем
формулу (2.3.6) для получения окончательного
ответа:
 =
=
45 В;
 =
=
– 90 В.
 =
=
1
+ 2
= – 45 В.
Ответ: рез
= – 45 В.
2.3.3. Работа силы Кулона
При
перемещении электрического заряда q
в
электрическом поле сила Кулона совершает
над ним работу:
Акул
= q(1
– 2),
(2.3.7)
где
1
и 2
– потенциалы начальной и конечной точек
поля соответственно.
В
силу того, что сила Кулона является
консервативной,
1)
ее работа не зависит от траекторий, по
которым перемещались заряды, а определяется
лишь начальным и конечным положением
этих зарядов;
2)
при перемещении заряда по замкнутой
траектории работа действующих на него
кулоновских сил равна нулю;
3)
работа кулоновских сил идет на изменение
потенциальной энергии системы зарядов.
Пример
5. Два шарика
с зарядами 6,7 и 13,3 нКл находятся на
расстоянии 40 см друг от друга. Какую
работу нужно совершить, чтобы сблизить
их до расстояния 25 см?
Дано: q1
=
6,7 нКл =
6,710–9Кл,
q2
= 13,3 нКл = 13,310–9Кл,
r1
= 40 см = 0,4 м,
r2
= 25 см = 0,25 м.
Найти:
Авн.
Решение.
В задачах такого типа удобно считать
один из шариков неподвижным, образующим
электрическое поле, а другой – движущимся
в поле первого шарика. Пусть шарик с
зарядом q1
создает электрическое поле, а шарик с
зарядом q2
движется в этом поле из точки, находящейся
на расстоянии r1
= 0,4 м от шарика q1,
в точку, находящуюся на расстоянии r2
= 0,25 м от него. Работа силы Кулона
определяется выражением (2.3.7):
Акул
= q2(1
– 2).
Поле
образовано точечным зарядом q1,
поэтому как исходную формулу для расчета
потенциала поля точечного заряда мы
используем формулу (2.3.5):
 .
.
Поскольку
в задаче надо найти не работу силы
Кулона, а работу внешней силы Авн,
которая совершает работу против силы
Кулона, то
Авн
= – Акул
= – q2(1
– 2)
= q2(2
– 1).
(2.3.8)
Теперь
используем вышеприведенные формулы
для нашего конкретного случая. Перепишем
формулу (2.3.5) для заряда, создающего поле
(это, как мы условились, заряд q1),
и найдем потенциалы в начальной и
конечной точках поля:
 ;
;
(2.3.9)
 .
.
(2.3.10)
Подставив
формулы (2.3.9) и (2.3.10) в формулу (2.3.8),
получим
для работы внешней силы:
А
 вн
вн
= q2(2
– 1)
= q2
 –
– .
.
(2.3.11)
После подстановки
числовых данных в (2.3.11), получим
окончательный ответ:
Авн
= 1,210–6Дж
= 1,2 мкДж
Ответ: 1,2 мкДж.
ВУЗ. Найти напряженность поля и потенциал (30.10.2011)
Чертов А. Г., Воробьев А. А. Задачник по физике: Учебное пособие для вузов. 7 изд., 2001 г.
- версия для печати
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Комментарии

В центре треугольника напряженность равна геометрической сумме напряженностей, создаваемых зарядами 1, 2 и 3.
Заряды по модулю равны, поэтому:
E1 = E2 = E3 = 3k|q| / a 2 , так как a(√3) / 3 — расстояние от вершины треугольника до центра треугольника О.
Напряженность поля в точке О: E = E3 + E1 cos 60° + E2 cos 60° = 2E1 = 6k|q| / a 2 .
Потенциал в точке O равен алгебраической сумме потенциалов, создаваемых зарядами 1, 2 и 3:
В двух вершинах равностороннего треугольника со стороной
Задача. В двух вершинах равностороннего треугольника со стороной длиной см находятся два заряда, модули которых нКл. Определите потенциал поля в третьей вершине треугольника, если: a) оба заряда положительные; b) оба заряда отрицательные; c) заряды противоположных знаков.
Дано:
Решение
Думаем: источником электростатического поля в задаче являются точечные заряды, тогда для потенциала точечного заряда:
Т.к. зарядов несколько,, то для поиска общих параметров системы будем использовать принцип суперпозиции для потенциала (полный потенциал, создаваемый в точке равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в этой точке):
Решаем: для визуализации системы нарисуем её (рис. 1).

Рис. 1. Система зарядов для поиска потенциала
Точка А — точка, где по нашему условию нужно найти потенциал. Каждый из зарядов создаёт свой потенциал в искомой точке, который мы можем найти из (1):
Тогда, исходя из (2), получим общий потенциал в точке A:
А теперь адаптируем получившееся соотношение (5) под условия задачи. Разница в условиях задачи по пунктам состоит в том, что значения зарядов различные.
a) в случае 0″ title=”displaystyle <_<1>>=<
_<2>>>0″ data-lazy-src=”https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%7B%7Bq%7D_%7B1%7D%7D%3D%7B%7Bq%7D_%7B2%7D%7D%3E0&is-pending-load=1#038;bg=ffffff&fg=000000&s=0″ srcset=”data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7″>:
Считаем: вспоминаем константы Н*м /Кл , И не забываем перевести все параметры (расстояния) в единицы СИ.
Принцип суперпозиции сил и полей
теория по физике 🧲 электростатика
Принцип суперпозиции сил
Результирующая, или равнодействующая, сила равна векторной сумме всех сил, действующих на тело:
Fi— сила, с которой электрическое поле зарядом q действует на пробный заряд qi, помещенный в это поле на расстоянии riот этого заряда. Численно ее можно вычислить по формуле:
F i = k q i q r 2 i . .
Алгоритм решения задач на определение равнодействующей силы (точечный заряд находится в поле, созданном другими точечными зарядами):
- Сделать чертеж. Указать расположение всех зарядов и их знаки.
- Выделить заряд, для которого определяют равнодействующую.
- Пронумеровать остальные заряды.
- Определить расстояния от выделенного заряда до всех остальных.
- Построить все силы, действующие на интересующий нас заряд. При этом необходимо учитывать знаки зарядов, их модули и расстояния между зарядами.
- Найти геометрическую (векторную) сумму всех сил, действующих на выделенный заряд.
- Пользуясь формулами геометрии и законом Кулона, определить модуль равнодействующей.
Пример №1. Как направлена (вправо, влево, вверх, вниз) кулоновская сила − F K , действующая на положительный точечный электрический заряд +2q, помещенный в центр квадрата, в вершинах которого находятся заряды +q, +q, –q, –q?

Известно, что одноименные заряды отталкиваются, а разноименные – притягиваются. Из рисунка видно, что заряд +2q, находящийся в центре квадрата, будет отталкиваться от зарядов +q, находящихся справа, и будет притягиваться к зарядам –q, находящимся слева.
Сила Кулона обратно пропорциональна квадрату расстояния между зарядами, то есть с увеличением расстояния r убывает по квадратическому закону. Так как заряд +q находится точно в центре квадрата, то расстояния от зарядов +q, +q, -q, -q будут равны, следовательно, равна по модулю и сила Кулона, действующая на заряд +2q. Суперпозиция сил, действующих на заряд +2q:

Из рисунка видно, что кулоновская сила − F K , действующая на положительный точечный электрический заряд +2q, направлена влево.
Принцип суперпозиции полей
Если в некоторой точке пространства складываются электрические поля от нескольких зарядов, то результирующая напряженность находится как векторная сумма напряженностей отдельных полей:
− E i — напряженность, создаваемая зарядом q i в точке, находящейся на расстоянии r i :
− E i = k q i r 2 i . .
Векторное сложение напряженностей аналогично нахождению равнодействующей сил Кулона, только в интересующую нас точку пространства помещают положительный пробный заряд. Чтобы найти результирующий потенциал в точке, необходимо алгебраически сложить потенциалы всех полей. Нельзя забывать, что знак потенциала определяется знаком заряда, создающим электрическое поле:
φ i — потенциал электростатического поля, создаваемого зарядом q i на расстоянии r i от него. Численно он равен:
φ i = ± k q i r i . .
Для определения полной энергии надо сложить потенциальные энергии всех пар зарядов:
W i p — потенциальная энергия взаимодействия зарядов q i и q n , находящихся на расстоянии r i друг от друга. Численно она равна:
W i p = ± k q i q n r i . .
Примеры определения расстояний
 |
Два заряда лежат на одной прямой на расстоянии l друг от друга. Изучаемый заряд лежит между ними: |
r 1 = x ; r 2 = l − x
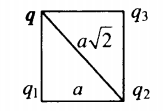
Изучаемый заряд лежит в вершине квадрата со стороной a:
r 1 = r 3 = a ; r 2 = a √ 2
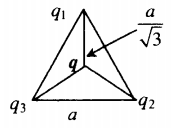
Изучаемый заряд лежит в центре равностороннего треугольника со стороной a:
r 1 = r 2 = r 3 = a √ 3 . .
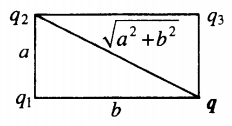
Изучаемый заряд лежит в вершине прямоугольника со сторонами a и b:
r 1 = b ; r 2 = √ a 2 + b 2 ; r 3 = a

Изучаемый заряд лежит в точке пересечения диагоналей ромба со стороной a. Угол при вершине ромба 120 о :
r 1 = r 3 = a √ 3 2 . . ; r 2 = r 4 = a 2 . .

Изучаемый заряд лежит в центре правильного шестиугольника со стороной a:
r 1 = r 2 = r 3 = r 4 = r 5 = r 6 = a
Пример №2. Маленький заряженный шарик массой m, имеющий заряд q, движется с высоты h по наклонной плоскости с углом наклона α. В вершине прямого угла, образованного высотой и горизонталью, находится неподвижный заряд Q. Какова скорость шарика у основания наклонной плоскости v, если его начальная скорость равна нулю? Трением пренебречь.

Применим закон сохранения энергии, согласно которому полная энергия шарика в точке А равна полной энергии шарика в точке В (трением пренебрегаем):
Полная энергия шарика с зарядом qв точке А равна сумме его механической потенциальной энергии и потенциальной энергии взаимодействия с зарядом Q:
E A = m g h + k q Q h . .
В точке В механическая потенциальная энергия шарика равна нулю, но в этой точке максимальная его кинетическая энергия. Полная энергия шарика в точке В равна:
E B = m v 2 2 . . + k q Q b . .
Расстояние между точкой В и местом, где находится заряд Q:
Приравняем правые части уравнений:
m g h + k q Q h . . = m v 2 2 . . + k q Q b . .
m g h + k q Q h . . = m v 2 2 . . + k q Q tan . α h . .
m v 2 2 . . = m g h + k q Q h . . − k q Q tan . α h . . = m g h + k q Q h . . ( 1 − tan . α )
v = . ⎷ 2 ( m g h + k q Q h . . ( 1 − tan . α ) ) m . . = √ 2 g h + 2 k Q m h . . ( 1 − tan . α )
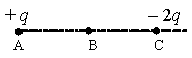 Точка В находится в середине отрезка АС. Неподвижные точечные заряды + q и −2q расположены в точках А и С соответственно (см. рисунок). Какой заряд надо поместить в точку С взамен заряда −2q, чтобы напряжённость электрического поля в точке В увеличилась в 2 раза?
Точка В находится в середине отрезка АС. Неподвижные точечные заряды + q и −2q расположены в точках А и С соответственно (см. рисунок). Какой заряд надо поместить в точку С взамен заряда −2q, чтобы напряжённость электрического поля в точке В увеличилась в 2 раза?
[spoiler title=”источники:”]
http://www.abitur.by/fizika/zadachi-po-fizike/potencial-elektrostaticheskogo-polya-zadachi/v-dvux-vershinax-ravnostoronnego-treugolnika-so-storonoj/
[/spoiler]
Условие задачи:
Найти потенциал электрического поля в точке, лежащей посредине между двумя зарядами по 50 нКл, расположенными на расстоянии 1 м в вакууме.
Задача №6.3.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(q=50) нКл, (r=frac{l}{2}), (l=1) м, (varphi-?)
Решение задачи:
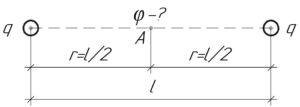 Так как заряды одинаковы, и они находятся на одинаковом расстоянии (r) от точки A, в которой нужно определить потенциал, значит потенциалы электрических полей в точке A, создаваемых каждым зарядом, также одинаковы. Это видно из формулы:
Так как заряды одинаковы, и они находятся на одинаковом расстоянии (r) от точки A, в которой нужно определить потенциал, значит потенциалы электрических полей в точке A, создаваемых каждым зарядом, также одинаковы. Это видно из формулы:
[{varphi _0} = frac{{kq}}{r}]
Здесь (k) – коэффициент пропорциональности, равный 9·109 Н·м2/Кл2.
Учитывая, что точка A находится посредине между двумя зарядами ((r=frac{l}{2})), то:
[{varphi _0} = frac{{2kq}}{l}]
Искомый потенциал (varphi) равен сумме потенциалов электрических полей в точке A, создаваемых каждым зарядом, поскольку потенциал – величина скалярная. Учитывая вышесказанное, имеем:
[varphi = {varphi _0} + {varphi _0}]
[varphi = 2{varphi _0}]
В итоге решение задачи в общем виде выглядит так:
[varphi = frac{{4kq}}{l}]
Произведём вычисления:
[varphi = frac{{4 cdot 9 cdot {{10}^9} cdot 50 cdot {{10}^{ – 9}}}}{1} = 1800;В = 1,8;кВ]
Ответ: 1,8 кВ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.8 На расстоянии 1 м от центра заряженного металлического шара радиусом 3 м
6.3.10 Сколько электронов следует передать металлическому шарику радиусом 7,2 см
6.3.11 Определить разность потенциалов (по модулю) между точками, отстоящими
Потенциал. Разность потенциалов.
Разность потенциалов (напряжение) между 2-мя точками поля равняется отношению работы поля по перемещению заряда из начальной точки в конечную к этому заряду:

,
Так как работа по перемещению заряда в потенциальном поле не зависит от формы траектории, то, зная напряжение между двумя точками, мы определим работу, которая совершается полем по перемещению единичного заряда.
Если есть несколько точечных зарядов, значит, потенциал поля в некоторой точке пространства определяется как алгебраическая сумма потенциалов электрических полей каждого заряда в данной точке:

.
Эквипотенциальной поверхностью, или поверхностью равного потенциала, является поверхность, для любых точек которой разность потенциалов равна нулю. Это означяет, что работа по перемещению заряда по такой поверхности равна нулю, следовательно, линии напряженности электрического поля перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности однородного поля представляют собой плоскости, а точечного заряда — концентрические сферы.
Вектор напряженности  (как и сила
(как и сила  ) перпендикулярен эквипотенциальным поверхностям. Эквипотенциальной является поверхность любого проводника в электростатическом поле, так как силовые линии перпендикулярны поверхности проводника. Внутри проводника разность потенциалов между любыми его точками равна нулю.
) перпендикулярен эквипотенциальным поверхностям. Эквипотенциальной является поверхность любого проводника в электростатическом поле, так как силовые линии перпендикулярны поверхности проводника. Внутри проводника разность потенциалов между любыми его точками равна нулю.
Напряжение и напряженность однородного поля .

В однородном электрическом поле напряженность E в каждой точке одинакова, и работа A по перемещению заряда q параллельно на расстояние d между двумя точками с потенциалами φ1, и φ2 равна:

,

.
Т.о., напряженность поля пропорциональна разности потенциалов и направлена в сторону уменьшения потенциала. Поэтому положительный заряд будет двигаться в сторону уменьшения потенциала, а отрицательный — в сторону его увеличения.
Единицей напряжения (разности потенциалов) является вольт. Исходя из формулы  ,
,  , разность потенциалов между двумя точками равна одному вольту, если при перемещении заряда в 1 Кл между этими точками поле совершает работу в 1 Дж.
, разность потенциалов между двумя точками равна одному вольту, если при перемещении заряда в 1 Кл между этими точками поле совершает работу в 1 Дж.
Электрический потенциал простыми словами: формулы, единица измерения
Электрический потенциал – это скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля.
Если вы хотите расширить свои знания об электрическом потенциале или сначала узнать, что такое электрический потенциал, то вы пришли по адресу.
Простое объяснение
В классической механике рассмотрение проблемы с точки зрения энергии может значительно упростить ситуацию по сравнению с рассмотрением ее с точки зрения сил, действующих на систему. В частности, в этом контексте существенную роль играет тот факт, что энергия является сохраняющейся переменной.
Также в классической электродинамике рассмотрение на энергетическом уровне оказывается очень полезным. Поэтому электрический потенциал φ (также называемый электростатическим потенциалом) определяется как отношение потенциальной энергии Eпот пробного электрического заряда и его величины электрического заряда q: φ = Eпот / q .
Возможность определения такого электрического потенциала обусловлена тем, что электрическое поле E распределения заряда и результирующая электростатическая сила Fc на пробном электрическом заряде является консервативной силой, подобной гравитационной силе.
Электрический потенциал имеет единицу измерения вольт В или также джоуль на кулон Дж / Кл .
Формулы
В этом разделе мы познакомим вас с двумя важными формулами для электрического потенциала определенных распределений электрических зарядов. Мы также кратко обсудим аналогию между электрическим потенциалом и гравитацией.
Пластинчатый конденсатор
Мы рассматриваем ситуацию, когда две плоские пластины расположены параллельно на расстоянии d друг от друга. Кроме того, пусть одна из двух пластин заряжена положительно, а другая – отрицательно. Такая комбинация также называется пластинчатым конденсатором. Обозначим точку на положительной пластине через A, а точку на отрицательной пластине через B. Тогда для разности потенциалов между этими двумя точками получим:
Здесь E – величина электрического поля между двумя пластинами, которое предполагается однородным. Такая разность потенциалов также называется электрическим напряжением, которое существует между этими двумя точками.
Из этого уравнения видно, что электрический потенциал на положительно заряженной пластине (пластина A) выше, чем потенциал на отрицательно заряженной пластине (пластина B). Поэтому положительный заряд в пластинчатом конденсаторе перемещается к отрицательной пластине. В общем случае электрическое поле – а значит, и направление движения положительного заряда – направлено в ту сторону, в которой электрический потенциал убывает быстрее всего.

Рис. 1. Пластинчатый конденсатор
Аналогия с гравитационным полем
Если умножить уравнение (приведенное выше в статье) на величину электрического заряда q пробного электрического заряда и предположить, что отрицательно заряженная пластина имеет электрический потенциал, равный нулю, то электрическая потенциальная энергия на расстоянии h от пластины равна:
Eпот. эл = q * φ = q * E * h
Здесь φ обозначает электрический потенциал в точке пробного электрического заряда.
Сравним это уравнение с потенциальной энергией в однородном гравитационном поле:
Eпот. гр = m * g * h .
Мы определяем, что количество заряда электрического q играет роль массы m, а величина электрического поля E играет роль гравитационного ускорения g. Масса, находящаяся на высоте h над землей, ускоряется по направлению к земле под действием земного притяжения.
Таким образом, масса движется в том направлении, в котором уменьшается ее потенциальная энергия. Аналогично, положительный электрический заряд движется в направлении, в котором его электрическая потенциальная энергия будет уменьшаться. Поскольку электрическая потенциальная энергия и электрический потенциал линейно связаны, это наблюдение аналогично тому, что положительно заряженная частица движется в направлении уменьшения электрического потенциала.

Рис. 2. Аналогия с гравитационным полем
Подобно потенциальной энергии, только разность потенциалов имеет физический смысл, поскольку при определении электрического потенциала необходимо произвольно определить точку отсчета, от которой затем можно обозначить другие точки в пространстве. В этом смысле электрический потенциал сам по себе не имеет реального физического смысла, поскольку для данной точки в пространстве его значение можно изменить, выбрав другую точку отсчета. Таким образом, электрический потенциал ведет себя подобно высоте, потому что вы не можете говорить о высоте, пока у вас нет точки отсчета.
На топографической карте – пути, вдоль которых высота не меняется, называются изолиниями. Аналогично, пути, вдоль которых электрический потенциал постоянен, называются эквипотенциальными линиями.
Заряженные частицы
Предположим, что частица с зарядом q находится в начале выбранной нами системы координат. Пусть положение другой точки равно r и пусть r – расстояние между двумя точками. Для электрического потенциала в точке r действует следующее соотношение:
φ (r) = q / 4 * π * ε0 * r ,
здесь ε0 – электрическая постоянная.
В этом уравнении предполагается, что под действием электрического поля положительный пробный электрический заряд переносится из бесконечности в положение r.
Примеры задач
Наконец, давайте вместе рассчитаем небольшой пример. Предположим, что электрон ускоряется от отрицательно заряженной пластины к положительно заряженной через разность потенциалов 2000 В. Как изменяется потенциальная энергия электрона?
Для разности электрических потенциалов между двумя пластинами: φB – φA = ΔEпот / q , преобразованной в искомое изменение потенциальной энергии, получаем:
Величина электрического заряда электрона равна qe = e = – 1,6 * 10 -19 Кл и поэтому получаем:
ΔEпот = e * ( φB – φA ) = – 1,6 * 10 -19 Кл * 2000 В = -3,2 * 10 -19 Дж.
Обратите внимание, что [ В ] = Дж / Кл. Кроме того, мы предположили, что пластина с точкой B заряжена положительно, поэтому перед 2000 В нет знака минус. Расчет показывает, что потенциальная энергия электрона уменьшается.
Найти потенциал электрического поля в точке, лежащей посредине между двумя
Найти потенциал электрического поля в точке, лежащей посредине между двумя зарядами по 50 нКл, расположенными на расстоянии 1 м в вакууме.
Задача №6.3.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Решение задачи:

Так как заряды одинаковы, и они находятся на одинаковом расстоянии (r) от точки A, в которой нужно определить потенциал, значит потенциалы электрических полей в точке A, создаваемых каждым зарядом, также одинаковы. Это видно из формулы:
Здесь (k) – коэффициент пропорциональности, равный 9·10 9 Н·м 2 /Кл 2 .
Учитывая, что точка A находится посредине между двумя зарядами ((r=frac)), то:
Искомый потенциал (varphi) равен сумме потенциалов электрических полей в точке A, создаваемых каждым зарядом, поскольку потенциал – величина скалярная. Учитывая вышесказанное, имеем:
В итоге решение задачи в общем виде выглядит так:
Ответ: 1,8 кВ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
