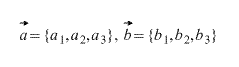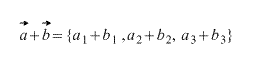Как найти результирующий вектор куба

Красивая математика или как представить 7-ми мерный куб

Однажды от своих родственников я услышал такую фразу: “Люди на МехМате МГУ не могут быть нормальными, ведь они могут представить себе 7-ми мерное пространство!”

И когда я это услышал, мне тоже показалось, что это – что-то нереальное, невозможное. Но вот прошли года, и когда я снова услышал эту фразу, меня повергло в шок – я тоже могу представить 7-ми мерное пространство и не сломаться. Или я уже не из тех, кто может спокойно гулять по улицам?

Ответ, казалось бы, так прост и так несложен, но многие просто не задумывались над этим вопросом, и поэтому это кажется чем-то странным и нереальным.

Так вот, в данной статье я хочу задуматься, ответить и рассказать, что же за простой ответ скрывается под таким странным вопросом: “Что такое 7-ми мерное пространство?”

В данной статье я попытаюсь рассказать свое понимание многомерного пространства, как я представляю его в своей голове. Возможно, что-то может показаться немного нестрогим – так оно и есть, понятное дело, я пропускаю некоторые детали и пытаюсь писать максимально научно-популярным языком. Надеюсь, Вам понравится мое видение многомерного пространства и Вы почувствуете ту же красоту математики, которую я вижу в данной иллюстрации чего-то непонятного.

Я постараюсь описать некоторые детали с самых азов, вкратце, чтобы любой желающий мог бы разобраться в моих словах.

Оглавление

Выражаю благодарность @AnnRemi за помощь в редактировании и опускании на землю моих амбиций по статье.

Начало начал, или что такое вектор

Вектор: наверняка каждый сталкивался с таким понятием в школе, это не сложно и очень понятно.

Вектором называется направленный отрезок или просто луч, имеющий конкретную длину.

То есть если луч, как и прямая – понятие бесконечное и простирается вправо и влево в бесконечность, то вектор – понятие ограниченное длиной. Обычная стрелочка, нарисованная на бумаге – вектор. Линейкой мы можем измерить длину этой стрелочки, а направление “этой длины” показывает сама стрелка. Важно понимать, что нам не важно, откуда отложен наш вектор, из какой точки. Нужно знать только длину и направление. Обычно мы изображаем наш вектор в осях координат – так удобно находить его параметры.

Вектор AB в осях координат

Для удобства мы отмечаем на оси Х и на оси У проекции наших точек. Теперь, чтобы посчитать длину нашего вектора достаточно воспользоваться Теоремой Пифагора

Направление, или угол наклона относительно оси Х легко посчитать, например, через тангенс, ведь мы знаем длины обоих катетов треугольника

Понятие радиус-вектора

Как мы уже увидели, в векторе нам важны только две вещи: длина и направление, так зачем его рисовать где-то в середине нашей координатной плоскости. Давайте сместим наш вектор к началу оси координат. Тогда нам надо будет хранить только координаты конца вектора – а координаты начала вектора у нас будут нулевыми.

Смещенная ось координат

Так теперь надо будет меньше мучаться – храним в векторе просто координаты его конца.

Такие вектора называются в школе радиус-векторами, но в дальнейшем мы будем все вектора брать радиус-векторами, ведь, как мы помним, все вектора имеющие одно направление и одну длину – одинаковые, один и тот же вектор, так почему бы нам не взять тот, который удобнее всего записывается.

Трехмерный вектор

Если мы уже разобрались, что такое вектор на плоскости – давайте перейдем к вектору в трехмерном пространстве – в объемном мире.

Достаточно просто представить себе стрелку в объеме – достаточно вспомнить, как Вы что-то измеряли рулеткой. Прислонили конец к шкафу, другой к полу, и померили его диагональ. Ну или не шкаф. каждому свое. Но точно можно сказать, что такое трехмерный вектор.

Но давайте немного формулизируем то, что мы поняли. Представим трехмерные координаты и в них наш радиус-вектор AB.

Трехмерный вектор AB

Понятно, что нам теперь совсем не хватит двух координат для описания вектора AB. Так что давайте добавим третью координату, просто дописав ее в конце.

Хммм. интересно, а по какому признаку мы можем вот так просто приписывать координаты? Может, можно просто так добить вектор до семимерного? Ну в принципе, нас никто остановить не может, и мы именно так и поступим, но сначала немного окунемся в линейную алгебру.

Базис в пространстве

Базис — упорядоченный набор векторов в векторном пространстве, такой, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого набора.

Линейная комбинация – это сумма некоторого набора элементов множества с допустимыми коэффициентами.

Также я собираюсь использовать в дальнейшем удобное следствие определения базиса: мы можем расширять наш базис с помощью векторов, линейно независимых с базисными.

Что значит расширить базис? Добавить еще один вектор, тем самым расширяя наше пространство еще в одном направлении.

Выше мы уже научились строить трехмерное пространство – просто объемный мир, в котором мы живем. Давайте попробуем расширить наш базис. Самым очевидным расширением базиса будет добавление времени, как еще одного параметра. То есть четырехмерное измерение – это объемная жизнь с привязкой ко времени. Ну разве это не похоже на обычную жизнь человека? То есть все это время мы жили в четырехмерном пространстве, а не трехмерном.

И, как не сложно заметить, время линейно независимо от объема, то есть наше расширение базиса вполне корректно.

7ми мерное пространство и почему только 7ми?

Как нам представить 5ти мерное пространство? Но мы же уже сказали, что на самом деле пространство – это то, что его задает – базис. То есть давайте теперь мыслить о пространстве, как о наборе параметров каждой его точки. Например для трехмерного объекта мы помним 3 координаты в пространстве – по x, y, z. И у нас это не вызывает диссонанса.

Давайте к координатам припишем еще и время, в которое у нас наблюдалась данное расположение тел. Например, у нас катится шар и мы следим за положением его центра. В момент времени 0 шар покоился. В 0,0. 01 он уже сместился. В момент времени 9. 9,0 он уже находится в совершенно другом месте. Но зачем нам так думать? Пусть эта точка шара существует одновременно везде, где проехался шар, только мы будем помнить, что в каждой точке мы еще приписываем время, когда шар был именно в данной позиции. Вот Вам и 4х мерное пространство – не сложно.

Казалось, так можно навесить еще какие-то параметры, такие как скорость ветра, влажность воздуха, сила трения и так далее, но давайте не будем извращаться и перейдем к более жизненному понятию.

Допустим у нас есть разные гаечки (прошу прощения, если я ошибусь в параметрах или названиях, я совсем не инженер). Для удобной фасовки и продажи гаек надо распределить их на группы одинаковых. Но как мы будем их отличать? Давайте запишем какой-то набор параметров (не претендующий на правильность):

Сплав метала гайки

Внутреннее сечение гайки

Внешняя форма гайки

Направление резьбы гайки

Максимальная нагрузка на гайку

Самозажимающаяся ли гайка?

Максимальная температура, при которой гайка выдерживает достаточную нагрузку

Понятно, что таких параметров может быть сколь угодно много. Но мы остановимся на 7ми – именно столько заявлено в заголовке статьи. Важно помнить! каждый параметр обязан быть независим от любого предыдущего. В нашем случае это условие выполняется: направление резьбы никак не зависит от сплава метала или от внутреннего сечения гайки. И так с каждым из параметров.

То есть только что мы создали свой, очень странный базис, где элементами нашего пространства выступают гайки, и мы их можем удобно расфасовать. Это и есть элементарное представление нашего 7ми и не только 7ми, но и большего, пространства.

Пространство – не куб!

В заголовке статьи я обещал куб, но пока говорил только о пространстве. Давайте определим, что же такое куб.

Например, в 2х мерном пространстве куб, очевидно,- это квадрат. То есть объект с точками вершинами:

В трехмерном пространстве куб – есть куб. С координатами:

Как мы заметили, в двумерном пространстве у куба 4 = 2^2 вершин, в трехмерном 8 = 2^3. Совпадение? Маловероятно. Ну и правильно, ведь из простейшей комбинаторики мы помним, что количество вершин равно 2^n для n-мерного куба. Ведь мы либо берем каждый из базисных n векторов, либо нет.

Тогда для построение 7ми или n-мерного куба нам достаточно взять точки с фиксированными координатами (0 или a) по каждой из осей.

Интересный факт

Именно из-за удобства понимания и описания n-мерного куба мы меряем любую n-мерную поверхность таким способом. Площадь квартиры с помощью квадратных метров, длину прямой в метрах, объем в кубических метрах. Это все кубы разной размерности. И в математике нам очень удобно оперировать именно такими понятиями. Примерно так мы определяем меру множества, которая очень важна для теории интегралов, теории вероятностей, теории меры и очень много где еще.

Послесловие

Как Вы, наверное, заметили, я привожу совсем иное понимание многомерного куба, в отличие от общепринятого.

Не то, чтобы красивые картинки многомерных кубов не вызывали у меня восхищения – совсем нет, но в этом есть что-то нереальное, непонятное и неприложимое. Я совсем не претендую на прикладное значение сортировки гаек, но мне кажется довольно захватывающим такое представление многомерности: как что-то такое далекое может быть таким емким.

4х мерный куб – Тессеракт

На самом деле я просто не имею настолько развитого пространственного воображения: я не понимаю, как можно визуализировать 4х, 5ти и более мерный куб на 2D картинке.

Также такая иллюстрация не позволяет представить, как увеличить пространство еще в одном направлении. Так что именно данная тема не рассматривается в моей статье, но, если Вас заинтересовал Тессеракт, есть огромная куча других, очень интересных, статей, описывающих его построение и даже расширение.

Сумма векторов в кубе

Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор.

Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор

В механике существуют два типа величин:

• скалярные величины, задающие некоторое числовое значение — время, температура, масса и т.д.
• векторные величины, которые вместе с некоторым числовым значением задают направление — скорость, сила и т.д..

Рассмотрим сначала алгебраический подход к сложению векторов.

Покоординатное сложение векторов.

Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:

В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.

Теперь перейдем к геометрическому смыслу сложения двух векторов:

При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:

Правило параллелограмма. Сложение векторов по правилу параллелограмма.

Процедура сложения векторов по правилу параллелограмма заключается в следующем:

• нарисовать первый вектор, учитывая его величину и направление
• от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление
• дополнить рисунок до параллелограмма, считая, что два нарисованных вектора — это его стороны
• результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.

Правило треугольника. Сложение векторов по правилу треугольника.

Сложение векторов по правилу треугольника заключается в следующем: нарисовать первый вектор, используя данные о его длине ( числовой величине) и направлении от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом второго.

Тригонометрический способ. Сложение векторов тригонометрическим способом.

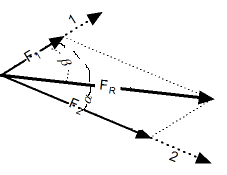Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов: Fрез. = [ F1 2 + F2 2 -2 F1 F2 cos(180 о -α) ] 1/2 (1) где F = числовое значение вектора α = угол между векторами 1 и 2 Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов: β = arcsin[ F2 *sin(180 o -α) / FR ] (2) где α = угол между исходными векторами

Пример — сложение векторов.

Сила 1 равна 5кН и воздействует на тело в направлении, на 80 o отличающемся от направления действия второй силы, равной 8 кН.

Результирующая сила вычисляется следующим образом:

F_рез = [ (5 кН) 2 + (8 кН) 2 — 2 (5 кН)(8 kН) cos(180 o — (80 o )) ] 1/2

Угол между результирующей силой и первой силой равен:

А угол между второй и результирующей силой можно посчитать следующим образом: as

α = arcsin [ (5 кН) sin(180 o — (80 o )) / (10,2 кН) ]

Он-лайн калькулятор сложения векторов.

Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.

Консультации и техническая
поддержка сайта: Zavarka Team

Сложение и вычитание векторов

Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .

Существование: Имеем два следующих случая:

Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .

Из данного выше построения сразу же будет следовать единственность данного вектора.

Сумма векторов. Сложение векторов. Правило треугольника

Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.

Такая операция выполняется по правилу многоугольника.

Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( + , + , + > right) )

Отметим несколько свойств сложения двух векторов:

Для произвольного вектора ( overrightarrow ) выполняется равенство

Для произвольных точек ( A, B и C ) справедливо следующее равенство

Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.

Разность векторов. Вычитание векторов

Разность двух одинаковых векторов равна нулевому вектору :
( vec — vec = vec )

Длина нулевого вектора равна нулю:
( left| vec right| = 0 )

Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec — vec = left( — , — , — > right) )

Умножение вектора на число

Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .

Длина вектора ( overrightarrow ) равна ( left|overrightarrow right|=left|kright||overrightarrow| ) ;

Обозначение: ( overrightarrow =koverrightarrow ) .

Геометрия. 10 класс

Сумма векторов

В кубе назовите вектор, равный сумме $overrightarrow+overrightarrow C_ >+overrightarrow > $

Вектор в пространстве

Установите соответствие между выражением и вектором $Х$

Длина вектора

Дано: АВ = 3 ВС = 4 СС₁ = 12

Длина вектора АС₁ =

Длина вектора

Диагонали параллелепипеда пересекаются в точке О.

Варианты ответа (введите порядковый номер):

Вектор в пространстве

Упростите выражение и выберите правильный результат преобразования:

Вектор в пространстве

В тетраэдре ABCD точка Е — середина АD.

Докажите, что $overrightarrow =frac (overrightarrow +overrightarrow )$

Сложим полученные равенства $overrightarrow +overrightarrow+overrightarrow +overrightarrow =2overrightarrow $

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму:

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

То есть A + C + D = 0.

Аналогично для точки K:

Получили систему из трех уравнений:

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

Выразим C и B через A и подставим в третье уравнение:

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать “параллелепипед”.

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

[spoiler title=”источники:”]

http://b4.cooksy.ru/articles/summa-vektorov-v-kube

http://ege-study.ru/ru/ege/materialy/matematika/vektory-v-prostranstve-i-metod-koordinat/

[/spoiler]

Содержание

• Примеры
• Геометрические методы сложения двух векторов
• Метод параллелограмма
• Упражнения
• -Упражнение 1
• Решение
• Упражнение 2.
• Решение
• Вычисление декартовых компонент результирующего вектора
• Величина и направление результирующего вектора
• Ссылки

В результирующий вектор – это результат, полученный с помощью операции с векторами, результатом которой также является вектор. Обычно эта операция представляет собой сумму двух или более векторов, с помощью которой получается вектор с эквивалентным эффектом.

Таким образом получаются такие векторы, как результирующая скорость, ускорение или сила. Например, когда на тело действует несколько сил. F₁, F₂, F₃,…. векторная сумма всех этих сил равна чистой силе (равнодействующей), которая математически выражается следующим образом:

F₁ + F₂ + F₃ +… = F_р или F_N

Результирующий вектор, будь то силы или любая другая величина вектора, находится с применением правил сложения векторов. Поскольку векторы имеют направление и смысл, а также числовое значение, недостаточно добавить модули, чтобы получить результирующий вектор.

Это верно только в том случае, если задействованные векторы направлены в одном направлении (см. Примеры). В противном случае необходимо использовать методы векторной суммы, которые в зависимости от случая могут быть геометрическими или аналитическими.

Примеры

Геометрическими методами нахождения результирующего вектора являются метод траверса и метод параллелограмма.

Что касается аналитических методов, существует метод компонентов, с помощью которого можно найти вектор, полученный из любой системы векторов, при условии, что у нас есть его декартовы компоненты.

Геометрические методы сложения двух векторов

Предположим, что векторы или Y v (Мы обозначили их жирным шрифтом, чтобы отличить их от скаляров). На рисунке 2а) они расположены на плоскости. На рисунке 2 б) он переведен в вектор v таким образом, что его начало совпадает с концом или. Результирующий вектор идет от начала координат первого (или) до кончика последнего (v):

Результирующая фигура в этом случае представляет собой треугольник (треугольник – это 3-сторонний многоугольник). Если у нас есть два вектора в одном направлении, процедура такая же: поместите один из векторов за другим и нарисуйте тот, который идет от начала или хвоста первого до конца или конца последнего.

Обратите внимание, что порядок, в котором выполняется эта процедура, не имеет значения, поскольку сумма векторов коммутативна.

Также обратите внимание, что в этом случае модуль (длина или размер) результирующего вектора – это сумма модулей добавленных векторов, в отличие от предыдущего случая, когда модуль результирующего вектора меньше суммы модулей участников.

Метод параллелограмма

Этот метод очень подходит, когда вам нужно добавить два вектора, исходные точки которых совпадают, скажем, с началом системы координат x-y. Предположим, что это так для наших векторов или Y v (рисунок 3а):

На рисунке 3b) параллелограмм построен с помощью пунктирных линий, параллельных или уже v. Результирующий вектор имеет начало в точке O и конец в точке пересечения пунктирных линий. Эта процедура полностью эквивалентна описанной в предыдущем разделе.

Упражнения

-Упражнение 1

Учитывая следующие векторы, найдите результирующий вектор с помощью метода обхода.

Решение

Метод траверса – первый из известных. Помните, что сумма векторов коммутативна (порядок слагаемых не влияет на сумму), поэтому вы можете начать с любого из векторов, например или (рисунок 5а) или р (рисунок 5b):

Полученная фигура представляет собой многоугольник, а результирующий вектор (синий) называется р. Если вы начнете с другого вектора, сформированная форма может быть другой, как показано в примере, но результирующий вектор будет таким же.

Упражнение 2.

На следующем рисунке известно, что модули векторов или Y v соответственно они равны u = 3 условных единицы и v = 1,8 условных единиц. Угол, который или форма с положительной осью абсцисс составляет 45º, а v образует 60º с осью Y, как показано на рисунке. Найдите результирующий вектор, величину и направление.

Решение

В предыдущем разделе результирующий вектор был найден методом параллелограмма (на рисунке выделен бирюзовым цветом).

Простой способ найти результирующий вектор аналитически – выразить слагаемые векторы через их декартовы компоненты, что легко, когда известны модуль и угол, например векторы в этом примере:

или_Икс = u. cos 45º = 3 x cos 45º = 2,12; или_Y = u. грех 45º = 3x грех 45º = 2,12

v_Икс = v. sin 60º = 1,8 x sin 60º = 1,56; v_Y = -v. cos 60º = -1,8 x cos 60º = – 0,9

Векторы или Y v это векторы, принадлежащие плоскости, поэтому каждый из них имеет по две компоненты. Вектор u находится в первом квадранте, а его компоненты положительны, а вектор v – в четвертом квадранте; его компонент x положительный, но его проекция на вертикальную ось падает на отрицательную ось y.

Вычисление декартовых компонент результирующего вектора

Результирующий вектор находится путем алгебраического сложения соответствующих компонентов x и y, чтобы получить их декартовы компоненты:

р_Икс = 2.12 + 1.56 = 3.68

р_Y = 2.12 + (-0.9) = 1.22

Как только декартовы компоненты указаны, вектор становится полностью известным. Полученный вектор можно записать в квадратных скобках (подтяжки):

 R = <3,68; 1,22> условные единицы

Обозначение в квадратных скобках используется для отличия вектора от точки на плоскости (или в пространстве). Другой способ выразить полученный вектор аналитически – использовать единичные векторы я и j в плоскости (я, j Y k в пространстве):

р = 3.68 я + 1.22 j условные единицы

Поскольку обе компоненты результирующего вектора положительны, вектор р принадлежит к первому квадранту, который ранее уже был замечен графически.

Величина и направление результирующего вектора

Зная декартовы компоненты, величина R вычисляется по теореме Пифагора, так как полученный вектор рвместе со своими компонентами R_Икс и R_Y образуют прямоугольный треугольник:

Величина или модуль: R = (3.68² + 1.22²)^½ = 3.88

Направление q, взяв за основу положительную ось x: q = arctan (R_Y / Р_Икс) = arctg (1,22 / 3,68) = 18,3 º

Ссылки

1. Добавление векторов и правил. Получено с: newt.phys.unsw.edu.au
2. Фигероа, Д. Серия: Физика для науки и техники. Том 1. Кинематика. 31-68.
3. Физический. Модуль 8: Векторы. Получено с: frtl.utn.edu.ar
4. Хиббелер, Р. 2006. Механика для инженеров. Статический. 6-е издание. Континенталь Издательская Компания. 15-53.
5. Калькулятор сложения векторов. Получено с: www.1728.org

В механике существуют два типа величин:

• скалярные величины, задающие некоторое числовое значение – время, температура, масса и т.д.
• векторные величины, которые вместе с некоторым числовым значением задают направление – скорость, сила и т.д..

Рассмотрим сначала алгебраический подход к сложению векторов.

Покоординатное сложение векторов.

Пусть даны два вектора, заданные покоординатно ( чтобы вычислить координаты вектора, нужно вычесть из соответствующих координат его конца соответствующие координаты его начала, т.е. из первой координаты – первую, из второй – вторую и т.д.):

Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:

В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.

Теперь перейдем к геометрическому смыслу сложения двух векторов:

При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:

• правило параллелограмма
• правило треугольника
• тригонометрический способ

Правило параллелограмма. Сложение векторов по правилу параллелограмма.

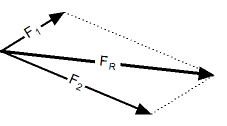Процедура сложения векторов по правилу параллелограмма заключается в следующем: нарисовать первый вектор, учитывая его величину и направление от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление дополнить рисунок до параллелограмма, считая, что два нарисованных вектора – это его стороны результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.

Правило треугольника. Сложение векторов по правилу треугольника.
	Сложение векторов по правилу треугольника заключается в следующем: нарисовать первый вектор, используя данные о его длине ( числовой величине) и направлении от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец – с концом второго.

Тригонометрический способ. Сложение векторов тригонометрическим способом.

Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов: Fрез. = [ F12 + F22 -2 F1 F2 cos(180о-α) ]1/2         (1) где F = числовое значение вектора α = угол между векторами 1 и 2 Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов: β = arcsin[ F2 *sin(180o-α) / FR ]         (2) где α = угол между исходными векторами

Пример – сложение векторов.

Сила 1 равна 5кН и воздействует на тело в направлении, на 80^o отличающемся от направления действия второй силы, равной 8 кН.

Результирующая сила вычисляется следующим образом:

F_рез = [ (5 кН)² + (8 кН)² – 2 (5 кН)(8 kН) cos(180^o – (80^o)) ]^1/2

    = 10,14кН

Угол между результирующей силой и первой силой равен:

β= arcsin[ (8кН) sin(180^o – (80^o)) / (10,14кН) ]

    = 51^o

А угол между второй и результирующей силой можно посчитать следующим образом: as

α = arcsin [ (5 кН) sin(180^o – (80^o)) / (10,2 кН) ]

    = 29^o

Он-лайн калькулятор сложения векторов.

Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.

In mathematics, we often heard about the two terms scalar and vector. Scalar is a quantity which has only magnitude i.e. Scalar quantity describes the distance. On the other hand, Vector is a quantity which deals with both magnitude and direction. Vector quantity has both magnitude and direction.

Resultant vector formula gives the resultant value of two or more vectors. The result is obtained by computing the vectors with consideration of the direction of each vector with respect to others. This formula has various applications in Engineering & Physics. Based on the direction of a vector with respect to other vectors, the Resultant Vector formula is classified into three types.

Resultant vector 1st formula

If the vectors are in the same direction then the resultant of the vector can be calculated by adding the vectors which are in the same direction. Let “a” and “b” are the vectors with the same direction then the resultant vector “r” is given by-

r = a + b

Resultant vector 2nd formula

If the vectors are in different directions then the resultant of the vector can be calculated by subtracting the vectors from each other. Let “b” be a vector which is in opposite direction with respect to vector “a” then the resultant vector “r” is given by-

r = a – b

Resultant vector 3rd formula

If any vectors are inclined to each other at some angle then the resultant of these vectors can be calculated by this formula. Let “a”, and “b” are two vectors inclined to each other at an angle θ, then the resultant vector “r” is given by-

r = a² + b² + 2abcosθ

Here a², b² represents magnitude of the vector a, b.

Sample Problems

Question 1: Find the resultant vector for the vectors i+2j+3k and 4i+8j+12k

Solution:

Given two vectors are a=i+2j+3k and b=4i+8j+12k

The direction ratios of the two vectors are in equal proportion. So two vectors are in the same direction.

The resultant vector formula for the given vectors is given by-

r = a + b

= (i+2j+3k) + (4i+8j+12k)

= 5i+10j+15k

The resultant vector from the given vectors is 5i+10j+15k

Question 2: Find the resultant vector for the vectors i-2j+5k and 2i-4j+10k

Solution:

Given two vectors are a=i-2j+5k and b=2i-4j+10k

The direction ratios of the two vectors are in equal proportion. So two vectors are in the same direction.

The resultant vector formula for the given vectors is given by-

r = a + b

= (i-2j+5k) + (2i-4j+10k)

= 3i-6j+15k

The resultant vector from the given vectors is 3i-6j+15k

Question 3: Find the resultant vector for the vectors 2i-2j+k and 2i+7j+3k

Solution:

Given two vectors are a=2i-2j+k and b=2i+7j+3k

The direction ratios of the two vectors are not in equal proportions. So two vectors are in opposite direction.

The resultant vector formula for the given vectors is given by-

r = a – b

= (2i-2j+k) – (2i+7j+3k)

= 0i-9j-2k

The resultant vector from the given vectors is 0i-9j-2k

Question 4: Find the resultant vector for the vectors 9i+2j-3k and i-3j+2k

Solution:

Given two vectors are a=9i+2j-3k and b=i-3j+2k

The direction ratios of the two vectors are not in equal proportions. So two vectors are in opposite direction.

The resultant vector formula for the given vectors is given by-

r = a – b

= (9i+2j-3k) – (i-3j+2k)

= 8i+5j-5k

The resultant vector from the given vectors is 8i+5j-5k

Question 5: Find the resultant of the vectors 2i+2j+2k and i+2j+3k which are inclined at an angle 30° to each other.

Solution:

Given two vectors are a=2i+2j+2k and b=i+2j+3k

Also given that given two vectors are inclined at an angle θ=30°

So the resultant vector formula for the given vectors is given by-

r = a² + b² + 2abcosθ

Magnitude of vector a (a²) = sqrt{2^2+2^2+2^2}

= sqrt{4+4+4}

=√12

a²=2√3

Magnitude of vector b (b²) = sqrt{1^2+2^2+3^2}

= sqrt{1+4+9}

=√14

b²=√14

r = a² + b² + 2abcosθ

= 2√3 + √14 + 2(2√3)(√14)cos30°

= 2√3 + √14 + 4(√3)(√14)(√3/2)

= 29.65

The resultant vector from the given vectors is 29.65

Question 6: Find the resultant of the vector having magnitude 2, 4 which is inclined at 45°.

Answer:

Given,

Magnitude of vector a (a²)=2

Magnitude of vector b (b²)=4

θ = 45°

So the resultant vector formula for the given vectors is given by-

r = a² + b² + 2abcosθ

= 2+4+2(2)(4)cos45°

= 6+16×(1/√2)

= 17.31

The resultant vector from the given vectors is 17.31

Last Updated :
10 Jun, 2022

Like Article

Save Article

0 Пользователей и 1 Гость просматривают эту тему.

---

---