В статье обсуждаются различные методы нахождения чистой силы с массой и скоростью, а также решенные проблемы.
Чистая сила, сумма всех сил, ускоряет любой объект, имеющий массу, изменяя его скорость. Эти концепции побуждают нас использовать различные подходы к тому, как найти результирующую силу с массой и скоростью, используя закон движения Ньютона, различные формулы силы и теорему работы-энергии.
В разделе Предыдущая статья, мы рассмотрели различные примеры чистой силы. Каждая сила, действующая на объект, задает его ускорение.. Следовательно, мы просто складываем все различные типы сил, действующих на объект, чтобы оценить одну результирующую силу, которая ускоряет объект в одном направлении, изменяя его движение.
Узнать больше оuт Чистая сила.
Как найти чистую силу с массой и скоростью по изменению импульса?
Второй закон движения Ньютона помогает нам определить результирующую силу в терминах массы и скорости.
Второй закон Ньютона гласит, что импульс P объекта изменяется, когда применяется чистая сила. Изменение количества движения означает, что объект, имеющий массу m в состоянии покоя или в движении, изменяет свою скорость v за единицу времени t, когда он перемещается из одного положения в другое.
Согласно Второй закон Ньютона,
Но Импульс Р = мв,
Fсеть =(мв-мв0)/(тт0)
Поскольку масса m не изменяется при действии чистой силы,
Fсеть =м*[(вв0)/(тт0)]
Изменение скорости объекта (v = v0) на единицу изменения времени (tt0) является объектом ускорение ‘а’ из-за чистой силы.
а=(вв0)/(тт0)=Δv/Δt
Следовательно, Fсеть = ма …………………. (*)
Узнать больше о Net Force Vs Force.
Самолет массой 40 кг движется по земле со скоростью 20 км / час за 10 мин. Если к тому же самолету применяется жизненная сила, он взлетает со скоростью 30 км / ч за 15 минут. Какая результирующая сила действует на самолет?
Данный:
m = 40 кг
v = 30 км / ч
v0 = 20 км / ч
t = 15мин
t0 = 10 мин.
Найти: Fсеть =?
Формула:
Fсеть ==м*[(вв0)/(тт0)]
И,
Fсеть = Ф1+F2+… FN
Решения:
Чистая сила, действующая на самолет, рассчитывается с использованием Второй закон движения Ньютона.
Fсеть =м*[(вв0)/(тт0)
Подставляя все значения,
Fсеть =40*[(30-20)/(15010)]
Fсеть = 80
Чистая сила на самолете массой 40 кг, летящем со скоростью 30 км / ч, составляет 80 Н.
Подробнее о том, как рассчитать массу по силе.
Как найти чистую силу с массой и скоростью, используя формулы силы?
Чистая сила с массой и скоростью оценивается по формулам различных типов сил.
Когда мы прикладываем силу к объекту вдоль земли, сила тяжести, которая всегда действует на объект, уравновешивается нормальной силой. Поверхность земли также оказывает силу трения, противоположную приложенной силе. Как равные, так и противоположные силы помогают нам оценить результирующую силу по массе и скорости.
Нормальная сила (мг) и гравитация (мг) компенсируют друг друга. Это означает, что FN + (-Фg) = мг – мг = o
Наблюдения и советы этой статьи мы подготовили на основании опыта команды формула приложенной силы является,
Fi = ма
Наблюдения и советы этой статьи мы подготовили на основании опыта команды формула силы трения является,
FФрич = мкФN = мкг
Наблюдения и советы этой статьи мы подготовили на основании опыта команды формула чистой силы дан кем-то,
Fсеть = Фi + (-ФФрич)
Fсеть = ma – мкмг
Fсеть = m (а – мкг)
Наблюдения и советы этой статьи мы подготовили на основании опыта команды формула чистой силы с массой и скоростью с использованием формул силы дан кем-то,
Fсеть =м*[(вв0)/(тт0)]-мкг
Узнать больше о Типах сил.
Сани имеют массу 5 кг и скользят по поверхности льда со скоростью 20 км / час за 5 минут. Поскольку ледяная поверхность имеет коэффициент трения около 1, она создает силу трения скольжения, снижая скорость саней до 15 км / ч за 2 мин. Рассчитайте чистую силу, действующую на салазки. (Дано: g = 9.8 м / с2)
Данный:
m = 5 кг
v = 15 км / ч
v0 = 20 км / ч
t = 10мин
t0 = 5 мин.
м = 1
g = 9.8 м / с2
Найти: Fсеть =?
Формула:
Fсеть =м*[(вв0)/(тт0)]-мкг
Решения:
Чистая сила на салазках рассчитывается как
Fсеть =м*[(вв0)/(тт0)]-мкг
Подставляя все значения,
Fсеть = 54
Чистая сила, действующая на салазки, составляет 5 кг, а скорость 15 км / ч составляет 54 Н.
Подробнее о том, как рассчитать силу.
Как найти чистую силу с массой, скоростью и расстоянием?
Чистая сила с массой, скоростью и расстоянием оценивается t по теореме работы-энергии.
Говорят, что объект, имеющий массу в состоянии покоя, совершает работу, когда он движется с определенной скорость из одного положения в другое. Ускорение возникает, когда на него действует результирующая сила, преобразующая его стационарную потенциальную энергию в кинетическую энергию для выполнения работы.
Наблюдения и советы этой статьи мы подготовили на основании опыта команды формула проделанной работы,
Вт = Фсетьd
Проделанная работа изменение кинетической энергии объекта. т.е. 1/2m(vv0)
(Кредит: Shutterstock)
Следовательно чистая сила с массой, скоростью и расстоянием с использованием формулы работы-энергии дан кем-то,
1/2м(вв0)=Fсетьd
Fсеть=[м(вв0)]2d
Узнать больше о выполненной работе.
Чистая сила действует на автомобиль массой 50 кг, который изменяет свою скорость с 30 км / ч за 15 минут до 40 км / ч за 20 минут.
● Рассчитайте пройденное расстояние на машине.
● Вычислите чистую силу, действующую на автомобиль, с учетом массы, скорости и расстояния.
Данный:
m = 50 кг
v = 40 км / ч
v0 = 30 км / ч
t = 20мин
t0 = 15 мин.
Найти:
- d =?
- Fсеть=?
Формула:
1) Кинематика уравнения движения
д=(в+в0) / 2
2) Жсеть=[м(вв0)]2d
Решения:
Расстояние, пройденное на машине, рассчитывается с использованием второго Кинематическое уравнение движения.
d = [(v+v0)/2]т
Подставляя все значения,
д=[(30+40)/2]*20
д=35*20
d = 70
Расстояние проехал на машине при действии чистой силы 70 м.
Посмотрите на график Формула работы-энергии, давайте рассчитаем чистую силу, действующую на автомобиль, с учетом массы, скорости и расстояния.
Fсеть=[м(вв0)]2d
Подставляя все значения,
Fсеть=[50(40-30)]/(2*70)
Fсеть=500140
Fсеть = 3.57
Чистая сила, действующая на автомобиль, составляет 3.57 Н.
Узнайте больше о том, как рассчитать выполненную работу.
Содержание
- – Что такое результирующая сила Выберите ответ?
- – Как найти равнодействующую сил под углом?
- – Что такое сложение сил в физике?
- – Что такое результирующий?
- – Как сложить две силы?
- – Как задать силу аналитически?
- – Как разложить силу на составляющие?
- – Как найти равнодействующую всех сил по графику?
- – Какие существуют виды сил?
- – Что такое сложение векторов?
ΣF = m·a – Результирующая (суммарная) сила равна произведению массы на ускорение.
Что такое результирующая сила Выберите ответ?
Если на тело одновременно действует несколько сил, тогда состояние тела или его движение определяет результирующая сила — сумма всех сил. Если силы действуют в одном направлении, результирующая сила равна сумме сил.
Как найти равнодействующую сил под углом?
Для нахождения равнодействующей совмещаем начало вектора F2 с концом вектора F1 (точка А) и соединяем начало вектора F1 с концом вектора F2. Полученный вектор F и есть равнодействующая. F ² = F1 ² +F2 ² – 2*F1*F2*cosA. Угол А равен 180-60 = 120 (градусов).
Что такое сложение сил в физике?
СЛОЖЕНИЕ СИЛ — нахождение геометрической суммы (т. н. главного вектора) данной системы сил путем последовательного применения правила параллелограмма сил или построения силового многоугольника.
Что такое результирующий?
РЕЗУЛЬТИРУЮЩИЙ — РЕЗУЛЬТИРУЮЩИЙ, результирующая, результирующее (научн., спец.). Имеющийся в результате, окончательный. Толковый словарь Ушакова.
Как сложить две силы?
Правило параллелограмма и правило многоугольника
Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ). 1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т. д.
Как задать силу аналитически?
Аналитический способ задания сил на плоскости
Силу F на плоскости Оxy можно задать через ее проекции Fх и Fу на оси прямоугольной системы координат по правилу сложения векторов, определив точку А (xA, yA) приложения силы: F = FхЧi + FуЧj, где i, j – единичные векторы.
Как разложить силу на составляющие?
Для разложения силы R на две составляющие, направление которых известно, эту силу принимают за диагональ параллелограмма сил, на которой строят параллелограмм или треугольник (в последнем случае сила будет являться третьей стороной треугольника).
Как найти равнодействующую всех сил по графику?
R = F 1 + F 2 , где R — равнодействующая сил. Если на тело действуют силы по одной прямой, но направленные в противоположные стороны, то равнодействующая этих сил направлена в сторону большей по модулю силы, а её модуль равен разности модулей составляющих сил. R = F 2 − F 1 , где R — равнодействующая сил.
Какие существуют виды сил?
Виды силы (классификация сил).
- слабое ;
- электромагнитное;
- сильное;
- и, возможно, гравитационное.
Что такое сложение векторов?
Суммой двух векторов u и v называется третий вектор w, проведенный из начала u к концу v, если начало вектора v совпадает с концом вектора u. Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.
Интересные материалы:
Гагарин сколько был в космосе?
Gpedit msc как запустить?
Грач какой род?
Hamachi через ретранслятор как исправить?
Horizon zero сколько часов геймплей?
Icloud почти заполнено как почистить?
Инициалы что такое?
Искусственное дыхание как делается?
Искусственное дыхание рот в рот сколько нажатий?
Искусственное дыхание сколько вдохов и нажатий?
Формула равнодействующей всех сил в физике
Формула равнодействующей всех сил
Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($overline{F}$) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $overline{F}$ – это векторная величина, то есть она обладает модулем (величиной) и направлением.
Определение и формула равнодействующей всех сил
В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:
[overline{F}=moverline{a} left(1right),]
где $m$ – масса тела, на которое действует сила $overline{F}$; $overline{a}$ – ускорение, которое сила $overline{F}$ сообщает рассматриваемому телу. Смысл второго закона Ньютона заключается в том, что силы, которые действуют на тело, определяют изменение скорости тела, а не просто его скорость. Следует знать, что второй закон Ньютона выполняется для инерциальных систем отсчета.
На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Силы, которые оказывают действие на тело, следует суммировать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline{F}$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
[overline{F}={overline{F}}_1+{overline{F}}_2+dots +{overline{F}}_N=sumlimits^N_{i=1}{{overline{F}}_i} left(2right).]
Формула (2) – это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена как вектор ускорения тела.
Основной закон динамики поступательного движения при наличии нескольких сил
Если на тело действуют несколько сил, тогда второй закон Ньютона записывают как:
[sumlimits^N_{i=1}{{overline{F}}_i}=moverline{a}left(3right).]
$overline{F}=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета скорость движения тела постоянна.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач на равнодействующую сил
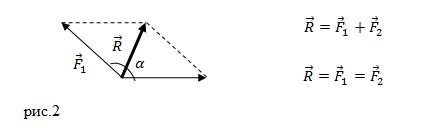
Пример 1
Задание. На материальную точку действуют две силы, направленные под углом $alpha =60{}^circ $ друг к другу. Чему равна равнодействующая этих сил, если $F_1=20 $Н; $F_2=10 $Н?
Решение. Сделаем рисунок.
Силы на рис. 1 складываем по правилу параллелограмма. Длину равнодействующей силы $overline{F}$ можно найти, используя теорему косинусов:
[F=sqrt{F^2_1+F^2_2+2F_1F_2{cos alpha }} left(1.1right).]
Вычислим модуль равнодействующей силы:
[F=sqrt{{20}^2+{10}^2+2cdot 20cdot 10{cos (60{}^circ ) }}approx 26,5 left(Нright).]
Ответ. $F=26,5$ Н
Пример 2
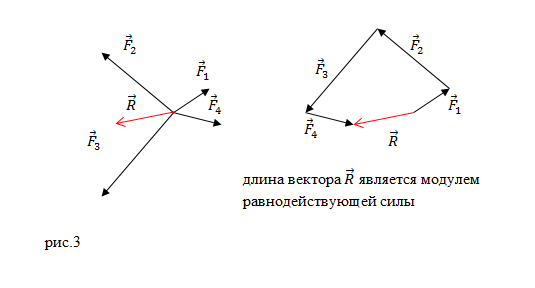
Задание. На материальную точку действуют силы (рис.2). Какова равнодействующая этих сил?
Решение. Равнодействующая сил, приложенных к точке (рис.2) равна:
[overline{F}={overline{F}}_1+{overline{F}}_2+{overline{F}}_3+{overline{F}}_4left(2.1right).]
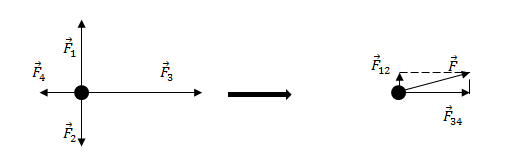
Найдем равнодействующую сил ${overline{F}}_1$ и ${overline{F}}_2$. Эти силы направлены вдоль одной прямой, но в противоположные стороны, следовательно:
[F_{12}=F_1-F_2=17-11=6 left(Hright).]
Так как $F_1>F_2$, то сила ${overline{F}}_{12}$ направлена в туже сторону, что и сила ${overline{F}}_1$.
Найдем равнодействующую сил ${overline{F}}_3$ и ${overline{F}}_4$. Данные силы направлены вдоль одной вертикальной прямой (рис.1), значит:
[F_{34}=F_3-F_4=18-10=8 left(Нright).]
Направление силы ${overline{F}}_{34}$ совпадает с направлением вектора ${overline{F}}_3$, так как ${overline{F}}_3>{overline{F}}_4$.
Равнодействующую, которая действует на материальную точку, найдем как:
[overline{F}={overline{F}}_{12}+{overline{F}}_{34}left(2.2right).]
Силы ${overline{F}}_{12}$ и ${overline{F}}_{34}$ взаимно перпендикулярны. Найдем длину вектора $overline{F}$ по теореме Пифагора:
[F=sqrt{F^2_{12}+F^2_{34}}=sqrt{6^2+8^2}=10 left(Нright).]
Ответ. $F$=10 Н
Читать дальше: формула равнодействующей силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Законы сложения сил в механике
При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.
Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:
R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .
Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.
Правило параллелограмма и правило многоугольника
Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).
Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма
Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:
R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α
При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.
Рисунок 2 . Сложение сил правилом многоугольника
Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.
Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.
Линией действия силы называют прямую, проходящую через вектор силы.
Рисунок 3 . Сложение сил, приложенных к различным точкам тела
Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.
Разложение вектора силы по направлениям
Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.
Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:
- направления 2 -х составляющих сил;
- модуль и направление одной из составляющих сил;
- модули 2 -х составляющих сил.
Пример 1
Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.
Рисунок 4 . Разложение вектора силы по направлениям
Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).
Рисунок 5 . Нахождение проекции вектора силы по заданным векторам
Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .
Итак, 2 -й способ решения: прибавим к силе силу, равную – F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .
Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.
Решение
Рисунок 6 . Нахождение равнодействующей силы по заданным векторам
Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β – F 3 cos γ = F x = 4 – 3 3 2 ≈ – 0 , 6 Н .
Точно также для проекций на ось O Y : – F 2 sin β + F 3 sin γ = F y = 3 – 2 3 2 ≈ – 0 , 2 Н .
Модуль равнодействующей определим с помощью теоремы Пифагора:
F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .
Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):
t g φ = F y F x = 3 – 2 3 4 – 3 3 ≈ 0 , 4 .
Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.
Решение
Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна
Дано:
F = 1 к Н = 1000 Н
Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что
F 1 → = F t g β ≈ 577 Н ;
F 2 → = F cos β ≈ 1155 Н .
Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .
Как найти равнодействующую трех векторов
Скорость автомобиля массой 1000 кг, движущегося вдоль оси Ox, изменяется со временем в соответствии с графиком (см. рисунок). Систему отсчета считать инерциальной. Чему равна равнодействующая всех сил, действующих на автомобиль? (Ответ дайте в ньютонах.)
Согласно второму закону Ньютона, равнодействующая всех сил, действующих на тело, связана с ускорением и массой тела соотношением Из графика определим ускорение, которое остается постоянным на протяжении всего интервала времени:
Таким образом, равнодействующая всех сил равна
а если бы ускорение было отрицательно, то и равнодействующая была бы отрицательной?
Скорость, сила, ускорение — все это векторные величины. Правильно говорить не про их знак, а про знак проекции этих векторов на некоторую ось. Если проекция скорости уменьшается, то ускорение направлено против оси, а значит, так же направлена и равнодействующая. Следовательно, проекции этих величин отрицательны. По графику модуля скорости о знаке проекций судить нельзя. Действительно, имея только график, приведенный в условии, мы не можем сказать, ускоряется тело вдоль оси или против. Проекция ускорения может быть тут как положительной, так и отрицательной.
“Систему отсчета считать инерциальной.” Возможно ошибаюсь, ребят, но, вроде, в ИСО равнодействующая всех сил равна нулю.
ИСО — это система отсчета, в которой тело, на которое не действует никаких внешних сил, двигается равномерно и прямолинейно или покоится.
Равнодействующая сил, конечно, же может и отличаться от нуля, это, согласно второму закону Ньютона, приведет к появлению ускорения.
т.е. в инерциальной системе отсчёта нет силы трения?
и ещё: вы говорите, что тело в ИСО движется равномерно, а в условии задачи дано равноускоренное движение. так бывает?
Я не так говорю, не вырывайте слова и контекста. Я даю определение ИСО: это система отсчета, в которой тело, НА КОТОРОЕ НЕ ДЕЙСТВУЮТ ВНЕШНИЕ СИЛЫ, двигается равномерно и прямолинейно, либо покоится. А вот если СИЛЫ ДЕЙСТВУЮТ, то это приводит к появлению ускорения, о чем нам и говорит второй закон Ньютона.
Наличие силы трения определяется свойством поверхностей, а не выбором системы отсчета. И в данной задаче, она, конечно, присутствует и направлена по скорости движения автомобиля, иначе бы он просто не мог бы разгоняться. Но чему она равна, мы найти из данного графика не можем, так как есть и другие силы, например, сила сопротивления воздуха. Что мы может тут определить, так это равнодействующую всех сил. Именно ей определяется ускорение.
Пыталась найти ускорение как тангенс угла наклона касательной, то есть производную от v по t. Тут угол – 45 град, тангенс = 1, ускорение, стало быть, так же 1 м/с^2.
Подскажите пожалуйста, где в моих рассуждениях ошибка?
Ошибка в том, что тангенс надо считать, учитывая масштаб графика по осям. То есть Вы должны определить катеты прямоугольного треугольника, используя числа на осях, а потом поделить один катет на другой.
Кстати, простое доказательство, почему Ваше решение не верно. Сожмем картинку с графиком по вертикали в два раза. Угол на рисунке изменится, а ускорение, конечно, же останется прежним.
а почему считают ускорение до 8с. а не до 18, если найдем ускорение по всей длине то получается 10-0/18=1,8 и получается другой ответ!
Делить нужно на 20. Масштаб по горизонтальной оси: в одной клеточке 4 с
На тело, находящееся на горизонтальной плоскости, действуют три горизонтальные силы (см. рисунок, вид сверху). Каков модуль равнодействующей этих сил, если (Ответ дайте в ньютонах и округлите до десятых.)
На рисунке обозначена равнодействующая векторов и
Поскольку модуль вектора силы равен 1 Н, заключаем, что масштаб рисунка такой, что сторона одного квадрата сетки соответствует модулю силы 1 Н. Таким образом, модуль равнодействующей равен по теореме Пифагора
А как определили эту равнодействующую трёх сил, я понять не могу?!
Чтобы найти равнодействующую, необходимо сложить вектора всех сил (например, по правилу треугольника или параллелограмма складываем вектора по два).
Если сложить вектор и вектор , получится вектор, направленный вверх длиной в одну клеточку. Теперь осталось прибавить к нему вектор . В результате и получается то, что показано красной стрелкой.
векторы F1 и F3 никак нельзя сложить правилом треугольника! дак как эту задачц решить тут решения совсем непонятные!
Когда Вы складываете параллельные вектора, у Вас просто получается “вырожденный треугольник”. Правила все те же, к концу первого вектора прикладываем начало второго. Сумма векторов — это вектор, который начинается в начале первого и заканчивается в конце второго. То есть в данном случае у Вас получится вектор, направленный вверх и длиной в одну клеточку.
Две силы 3 H и 4 H приложены к одной точке тела, угол между векторами сил равен 90°. Чему равен модуль равнодействующей сил? (Ответ дайте в ньютонах.)
Силы и их равнодействующая указаны на рисунке. По теореме Пифагора, модуль равнодействующей сил равен
Под действием одной силы F1 тело движется с ускорением 4 м/с 2 . Под действием другой силы F2, направленной противоположно силе F1, ускорение тела равно 3 м/с 2 . С каким ускорением тело будет двигаться при одновременном действии сил F1 и F2? Ответ дайте в метрах на секунду в квадрате.
Согласно второму закону Ньютона, ускорение тела пропорционально равнодействующей всех сил, действующих на него: Силы и по условию, направлены противоположно, поэтому при их одновременном действии тело будет двигаться с ускорением
Тело подвешено на двух нитях и находится в равновесии. Угол между нитями равен 90°, а силы натяжения нитей равны 3 H и 4 H. Чему равна сила тяжести, действующая на тело? (Ответ дайте в ньютонах.)
Всего на тело действует три силы: сила тяжести и силы натяжения двух нитей. Поскольку тело находится в равновесии, равнодействующая всех трех сил должна равняться нулю, а значит, модуль силы тяжести равен
в условии написано,что нужно найти вес тела.
а в решении модуль силы тяжести.
Как вес может измеряться в Ньютонах.
В условии ошибка(
Вы путаете понятия массы и веса. Весом тела называется сила (а потому вес измеряется в Ньютонах), с которой тело давит на опору или растягивает подвес. Как следует из определения, эта сила приложена даже не к телу, а к опоре. Невесомость — это состояние, когда у тела пропадает не масса, а вес, то есть тело перестает давить на другие тела.
Согласен, в решении была допущена некоторая вольность в определениях, сейчас она поправлена.
Понятие “вес тела” введен в учебную физику крайне неудачно. Если в бытовом понятии вес обозначает массу то в школьной физике, как вы правильно заметили весом тела называется сила (а потому вес измеряется в Ньютонах), с которой тело давит на опору или растягивает подвес. Заметим, что речь идет об одной опоре и об одной нити. Если опор или нитей несколько несколько, понятие веса исчезает.
Привожу пример. Пусть в жидкости на нити подвешено тело. Оно растягивает нить и давит на жидкость с силой равной минус сила Архимеда. Почему же, говоря о весе тела в жидкости, мы не складываем эти силы, как Вы делаете в своем решении?
Я зарегистрировался на Вашем сайте, но не заметил, что же изменилось в нашем общении. Прошу извинить мою тупость, но я, будучи человеком старым, недостаточно свободно ориентируюсь на сайте.
Действительно, понятие веса тела весьма расплывчато, когда тело имеет несколько опор. Обычно вес в этом случае определяют как сумму взаимодействий со всеми опорами. При этом воздействие на газообразные и жидкие среды, как правило, исключается. Это как раз подпадает под описанный Вами пример, с подвешенным в воде грузиком.
Здесь сразу вспоминается детская задачка: “Что весит больше: килограмм пуха или килограмм свинца?” Если решать эту задачу по-честному, то нужно несомненно учитывать силу Архимеда. А под весом скорее всего мы будем понимать то, что нам будут показывать весы, то есть силу, с которой пух и свинец давят, скажем, на чашку весов. То есть здесь сила взаимодействие с воздухом как бы из понятия веса исключается.
С другой стороны, если считать, что мы откачали весь воздух и кладем на весы тело, к которому привязана веревочка. То сила тяжести будет уравновешиваться суммой силы реакции опоры и силой натяжения нити. Если мы понимаем вес как силу действия на опоры, препятствующие падению, то вес тут будет равен этой сумме силы растяжения нити и силы давления на чашку весов, то есть совпадать по величине с силой тяжести. Опять возникает вопрос: чем нитка лучше или хуже силы Архимеда?
В целом тут можно договориться до того, что понятие веса имеет смысл только в пустом пространстве, где есть только одна опора и тело. Как тут быть, это вопрос терминологии, которая, к сожалению, у каждого здесь своя, поскольку не столь уж это и важный вопрос 🙂 И если силой Архимеда в воздухе во всех обычных случаях можно пренебречь, а значит, на величину веса она особо повлиять не может, то для тела в жидкости это уже критично.
Если уж быть совсем честным, то разделение сил на виды весьма условно. Представим себе ящик, который тащат по горизонтальной поверхности. Обычно говорят, что на ящик действуют две силы со стороны поверхности: сила реакции опоры, направленная вертикально, и сила трения, направленная горизонтально. Но ведь это две силы, действующие между одними и теми же телами, почему же мы просто не рисуем одну силу, являющуюся их векторной суммой (так, кстати, иногда и делается). Тут, это, наверное, вопрос удобства 🙂
Так что я немного в замешательстве, что делать с данной конкретной задачей. Проще всего, наверное, переформулировать ее и задавать вопрос про величину силы тяжести.
Не переживайте, все в порядке. При регистрации Вы должны были указать e-mail. Если теперь зайти на сайт под своим аккаунтом, то при попытке оставить комментарий в окне “Ваш e-mail” должен сразу появляться тот самый адрес. После этого система будет автоматически подписывать Ваши сообщения.
Формула модуля равнодействующей силы
На тело могут оказывать действие не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы.
Формула равнодействующей всех сил
Пусть на тело воздействуют в один и тот же момент времени N сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Сила является векторной величиной. Следовательно, силы, действующие на тело, нужно складывать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
Формула (1) – это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена также как вектор ускорения тела.
Складывают векторы, используя правило треугольника (рис.1)
правило параллелограмма (рис.2).
или многоугольника (рис.3):
Второй закон Ньютона и формула модуля равнодействующей
Основной закон динамики поступательного движения в механике можно считать формулой для нахождения модуля равнодействующей силы, приложенной к телу и вызывающей ускорение этого тела:
$overline=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета тело скорость движения тела.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач с решением
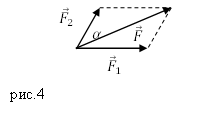
Задание. К материальной точке приложены силы, направленные под углом $alpha =60<>^circ $ друг к другу (рис.4). Чему равен модуль равнодействующей этих сил, если $F_1=40 $Н; $F_2=20 $Н?
Решение. Силы на рис. 1 сложим, используя правило параллелограмма. Длину равнодействующей силы $overline$ найдем, применяя теорему косинусов:
Вычислим модуль равнодействующей силы:
[F=sqrt<<40>^2+<20>^2+2cdot 40cdot 20<cos (60<>^circ ) >>approx 52,92 left(Нright).]
Ответ. $F=52,92$ Н
Задание. Как изменяется модуль равнодействующей силы со временем, если материальная точка массы $m$ перемещается в соответствии с законом: $s=A<cos (omega t)(м) >$, где $s$ – путь пройденный точкой; $A=const;; omega =const?$ Чему равна максимальная величина этой силы?
Решение. По второму закону Ньютона равнодействующая сил, действующих на материальную точку равна:
Следовательно, модуль силы можно найти как:
Ускорение точки будем искать, используя связь между ним и перемещением точки:
Первая производная от $s$ по времени равна:
Подставим полученный в (2.5) результат, в формулу модуля для равнодействующей силы (2.2) запишем как:
Так как косинус может быть меньше или равен единицы, то максимальное значение модуля силы, действующей на точку, составит:
[spoiler title=”источники:”]
http://phys-ege.sdamgia.ru/test?theme=206
http://www.webmath.ru/poleznoe/fizika/fizika_134_formula_modulja_ravnodejstvujushhej_sily.php
[/spoiler]
Второй закон Ньютона это закон который был выведен в результате проведения опытов Ньютоном.
В результате чего были выведена новая формула второго закона ньютона а = F /m,
Что такое второй закон Ньютона, масса и вес тела

Ньютон сформулировал второй закон динамики, количественно связывающий изменение движения тела с силами, вызывающими это изменение.
Чтобы исследовать зависимость между силой и ускорением количественно, рассмотрим некоторые опыты.
Ускорение от величины силы
I. Рассмотрим, как зависит ускорение одного и того же тела от величины силы, действующей на это тело. Предположим, что к тележке прикреплен динамометр, по показаниям которого измеряют силу.
Измерив длину пройденного тележкой пути за какой-нибудь промежуток времени t, по формуле s = (at2) : 2 определим ускорение a.
Изменяя величину силы, проделаем опыт несколько раз. Результаты измерения покажут, что ускорение прямо пропорционально силе, действующей на тележку
a1 : a2 = F1 : F2
ИЛИ
а ~ F.
Отношение силы, действующей на тело, к ускорению есть величина постоянная, которую обозначим m. Это отношение назовем массой тела.
Зависимость ускорения от массы
II. Установим зависимость ускорения тела от его массы. Для этого будем действовать на тележку какой-нибудь постоянной силой, изменяя массу (помещая различные грузы на тележку).
Ускорения тележки будем определять так же, как и в первом опыте. Опыт покажет, что ускорение тележки обратно пропорционально массе, то есть
(a1/a2) = (m2/m1), или а ~ (1/m)
Обобщая результаты опытов, можно заметить, что ускорение, приобретаемое телом, прямо пропорционально силе, действующей на тело, и обратно пропорционально массе данного тела (второй закон ньютона формулировка).
Этот вывод называется вторым законом Ньютона. Математически этот закон можно записать так (формула второго закона ньютона):
а = F /m
где а — ускорение, m—масса тела, F — результирующая всех сил, приложенных к телу. В частном случае на тело может действовать и одна сила.
Результирующая сила F равна векторной сумме всех сил, приложенных к телу;
F = mа.
Следовательно, сила равна произведению массы на ускорение.
Второй закон динамики можно записать в иной более удобной форме. Учитывая, что ускорение
а = (υ2 — υ1) / (t2 — t1)
подставим это выражение в уравнение второго закона Ньютона. Получим
F = ma = (mυ2 — mυ1) / (t2 — t1) = (∆(mυ))/∆t
Что такое импульс
Импульсом, или количеством движения, называется вектор, равный произведению массы тела на его скорость (тυ).
Тогда основной закон динамики можно сформулировать следующим образом: сила равна изменению импульса в единицу времени (второй закон ньютона в импульсной форме)
F = (∆(mυ))/∆t
Это и есть наиболее общая формулировка второго закона Ньютона. Массу тела Ньютон определил как количество вещества, содержащегося в данной теле. Это определение несовершенно.
Из второго закона Ньютона вытекает следующее определение массы. Из равенства
a1/a2= m2/m1
видно, что чем больше масса тела, тем меньше ускорение получает тело, то есть тем труднее изменить скорость этого тела и наоборот.
Следовательно, чем больше масса тела, тем в большей степени это тело способно сохранять скорость неизменной, то есть больше инертности. Тогда можно сказать, что масса есть мера инертности тела.
Эйнштейн доказал, что масса тела остается постоянной только при определенных условиях. В зависимости от скорости движения тела его масса изменяется по такому закону:
где m — масса тела, движущегося со скоростью υ; m0 — масса этого же тела, находящегося в покое; с = 3 • 108м/с скорость света в вакууме.
Проанализируем данное уравнение:
- Если υ«с, то величиной —, как очень малой, можно пренебречь и m = m0, то есть при скоростях движения, много меньших скорости света, масса тела не зависит от скорости движения;
- Если υ ≈ с, то υ2/с2 ≈ 1, тогда т = m0/0— отсюда вытекает, что m → ∞.
По мере увеличения скорости тела для его дальнейшего ускорения нужно будет прикладывать все увеличивающиеся силы.
Но бесконечно больших сил, которые потребовались бы для сообщения телу скорости, равной скорости света, в природе не существует.
Таким образом, заставить рассматриваемое тело двигаться со скоростью света принципиально невозможно.
Со скоростями, близкими к скорости света, современная физика встречается: так разгоняются, например, элементарные частицы в ускорителях.
Масса тела с ростом скорости
Масса тела с ростом скорости увеличивается, но количество вещества остается неизменным, возрастает инертность. Поэтому массу нельзя путать с количеством вещества.
Покажем связь между силой тяжести, массой тела и ускорением свободного падения. Любое тело, поднятое над Землей и ничем не поддерживаемое, падает снова на Землю.
Это происходит вследствие того, что между телом и Землей существует притяжение (этот вопрос более подробно рассмотрим позже).
Сила, с которой тело притягивается к Земле, называется силой тяжести. Падение тел в безвоздушном пространстве под действием силы тяжести (при υ0 = 0) называется свободным падением.
Отметим, что для тел, покоящихся в поле сил тяготения, сила тяжести равна весу тела Р.
Весом тела называется сила, с которой тело давит на горизонтальную подставку, неподвижную относительно Земли, или действует на подвес.
Если Р— сила тяжести, m — масса, g — ускорение силы тяжести (в данной точке Земли оно для всех тел одинаковой среднее его значение равно 9,8м/с2), то применяя второй закон динамики, получим
P = mg.
Выразим с помощью этой формулы веса двух различных тел. Тогда:
P1 = m1g и Р2 = m2g. Разделив почленно эти два равенства, будем иметь
P1/P2 = m1/m2
Следовательно, веса тел в данной точке земной поверхности прямо пропорциональны их массам.
Задачи на второй закон ньютона
1. Какая сила F действует на автомобиль массой кгm=1000 кг, если он движется с ускорением мсa=1 м/с2.
Дано:
m = 1000 кг
a = 1 м/с2
Найти: F — ?
Решение:
Запишем второй закон Ньютона :
F = mа.
F = 1000 кг • 1 м/с2 = 1000 Н
Ответ: 1000 Н.
2. На мяч действует сила F = 70Н, масса мяча m = 0,2 кг, найти его ускорение a.
Дано:
m = 0,2 кг,
F = 70Н
Найти:
a — ?
Решение:
Запишем второй закон Ньютона :
F = mа.
Следовательно а = F / m.
а = 70Н : 0,2 кг = 350 м/с.
Ответ: а = 350 м/с.
Статья на тему Второй закон Ньютона