Как найти ридберговскую поправку - Сайт, где вы сможете решить свои вопросы

Печатать эту главу

Задача №2.

Энергия для ионизации атома натрия E_i=5,12 эВ. Найти ридберговскую поправку σ(s) для этого атома.

Дано: E=5,12 эВ	Решение:
Найти: σ(s)=?

Дано:

E=5,12 эВ

Решение:

Найти:

σ(s)=?

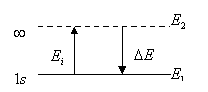
Энергия квантового перехода равна разности уровней энергии квантовых состояний, между которыми происходит переход

где E₂ – верхний уровень, E₁ – нижний уровень, то есть E₂>E₁. Энергией E_i ионизации атома называется энергия, необходимая для удаления из атома электрона, находящегося в основном состоянии 1s. Она равна

ΔE=E(∞)-E(1s)=-E(1s),

(2)

где E(∞) – уровень энергии удаленного электрона вне атома, принимается равной нулю, E(1s) – уровень энергии электрона в 1s состоянии. Спектральный терм T_n,i атома щелочного металла связан с соответствующим уровнем E_n,l энергии соотношением

Выражение для терма T_n,l определяется эмпирической формулой Ридберга

( T_{n,l}=frac{R}{{[n+sigma(s)]}^2} ).

(4)

Комбинируя формулы (2), (3) и (4) получаем

( E(1s)=+frac{chR}{{[n+sigma(s)]}^2} ).

(5)

Решая уравнение (5), находим

( sigma(1s)=sqrt{frac{chR}{E_i}}-n ).

(6)

Величина chR в энергетических единицах равна 13,6 эВ, для основного состояния атома натрия n=3.

Расчет:

( sigma(1s)=sqrt{frac{13,6}{5,12}}-3=-1,37 ).

(7)

Источник

Атомы щелочных металлов

В некотором смысле
атомы щелочных металлов являются
водородоподобными, однако не полностью.
Дело в том, что внешний электрон
деформирует электронный остов и тем
самым искажает поле, в котором движется.
В первом приближении поле остова можно
рассматривать как суперпозицию поля
точечного заряда +е, и поля точечного
диполя, расположенного в центре остова.
При этом ось диполя направлена все время
к внешнему электрону. Поэтому движение
последнего происходит так, как если бы
поле остова, несмотря на искажение,
сохранялось сферически симметричным.

Это позволяет
представить потенциальную энергию
внешнего электрона в поле такого остова
как:

U(r)
= -e²/r
– Ce²/r²,
(6.18)

где С – некоторая
постоянная.

Решение УШ для
электрона с потенциальной энергией
(6.18) приводит к тому, что теперь разрешенные
состояния энергии Е в области E
< 0 (для связных состояний внешнего
электрона) будет зависеть не только от
главного квантового числа n
(как в случае атома водорода), но и от
орбитального квантового числа l:

E_nl
= -ћR/(n
+ _l)²,
(6.19)

где _l)
– ридберговская поправка (или
квантовый дефект), зависящая от l
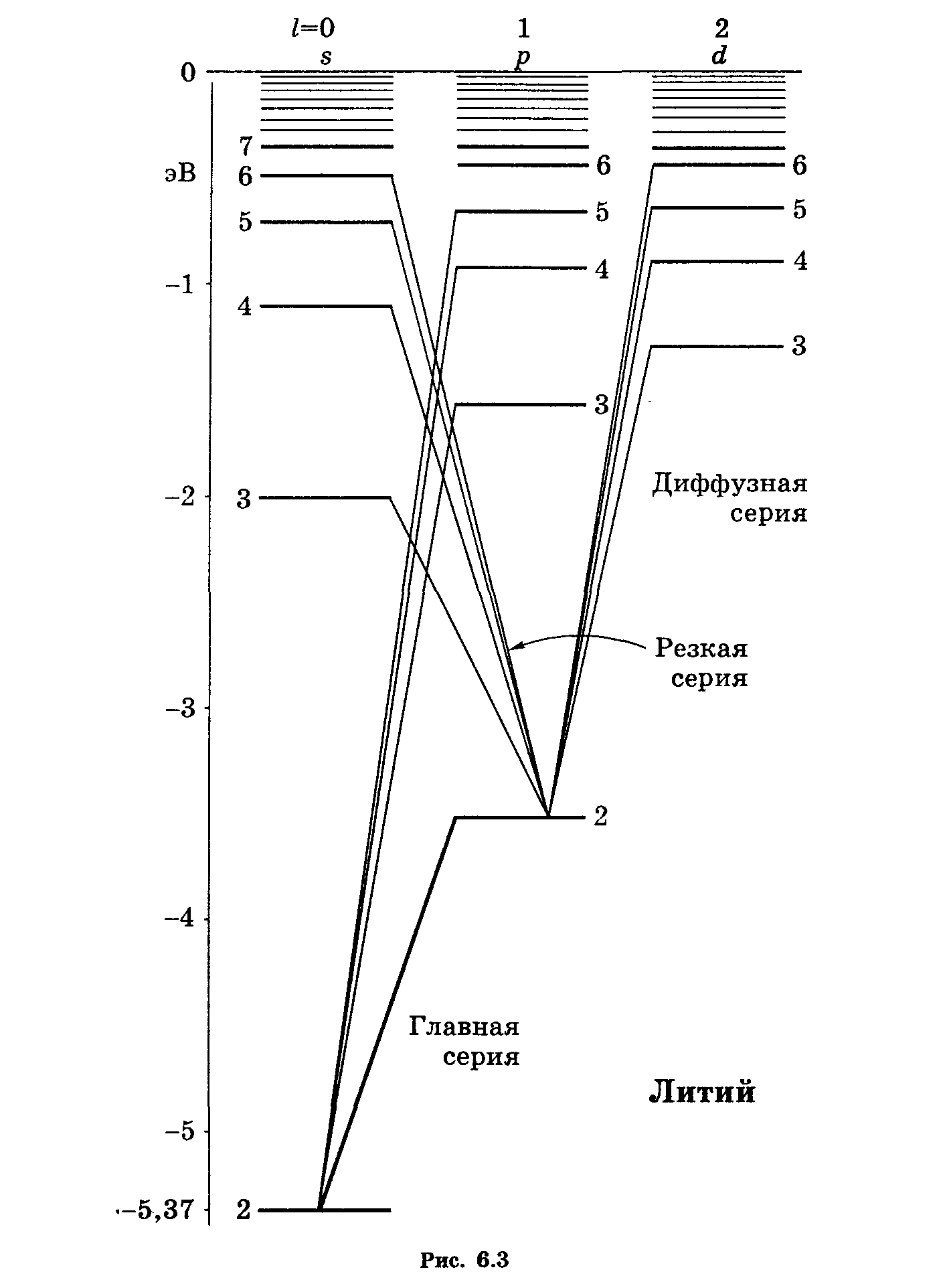
. Заметим, ц лития (см. рис. 6.3) основным
состоянием является 2s ,
так как состояние с n = 1
уже занято двумя электронами, входящими
в состав остова.

Энергетическому
уровню (6.19) соответствует терм, имеющий
согласно 2.30 вид:

T_nl
= R/(n + _l)²
(6.20).

Систематику
энергетических уровней атома принято
назвать системой термов. Терм T
– это величина, определяемая согласно
 =
R(1/n_o²
– 1/n²) (2.16) и E_n
= -me⁴Z²/2ћ²n² (2.25) как:

T_n
= R/n²
= |E_n|/ћ,

где R
– постоянная Ридберга. В отличие от
энергии E_n,
терм – величина положительная, и чем
выше уровень, тем больше его значение.
Терм имеет ту же размерность, что и
частота ,
т.е. с^-1. Соответствующая частота
фотона, испущенного при переходе атома
из состояния с квантовым числом n₁
в состояние с квантовым числом n₂,
определяется формулой:

₁₂
= T₂ –
T₁ =
R/n₂²
– R/n₁².
(2.31)

Все серии хххх
представляются в виде обобщенной формулы
Бальмера:

 = R(1/n_o²
– 1/n²) (2.16).

Энергия E_n
электрона на n-й стационарной
орбите определяется формулой

E_n
= -me⁴Z²/2ћ²n² (2.25).

1.4.х. Найти
ридберговскую поправку 3Р терма атома
Na , первый потенциал
возбуждения которого ₁
= 2,10 В, а энергия связи валентного
электрона в основном 3S-
состоянии Е_о = 5,14 эВ.

1.4.х. Используем
формулу E_nl
= -ħR/(n + _l)²
(6.19), которая содержит искомую
поправку _P.
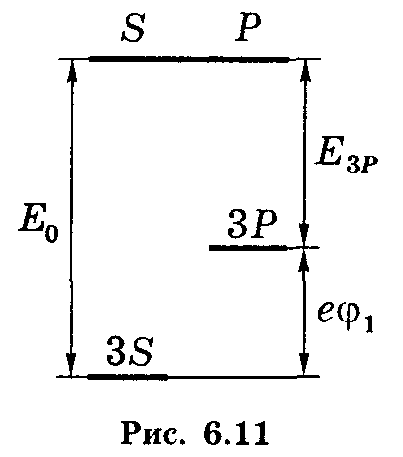
Согласно рис. 6.11. энергию 3Р – состояния
можно представить как:

E₃_P
= -(E_o
– e₁)
= -(5,14 – 2,19) эВ

(имея
в виду, что энергия уровня равна с
обратным знаком энергии связи на этом
уровне). Таким образом, имеем:



1.4.х. Найти
энергию связи валентного электрона в
основном состоянии атома лития, если
известно, что длины волн головной линии
резкой серии и ее коротковолновой
границы равны соответственно ₁
= 813 нм и _K
= 350 нм.

1.4.х. Согласно
формуле E_nl
= -ħR/(n + _l)²
энергия связи в 2s-
состоянии равна:

Задача сводится
к нахождению поправки _s.
Из рис. 6.3 и формулы 6.19 можно записать:

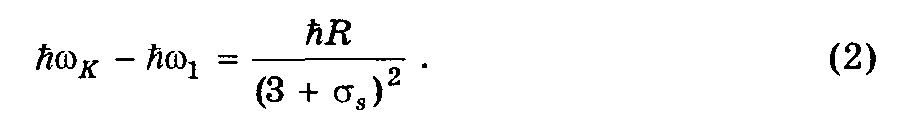
Т.к. 
= 2c//
перепишем (2) как:

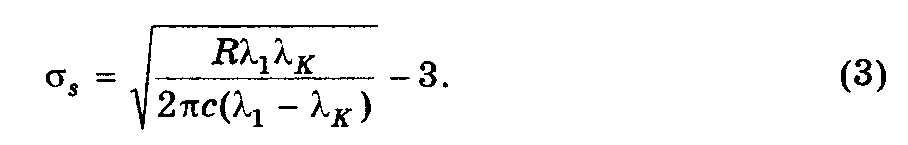
Подставив (3) в (1)
получим: E_св =
ћR/[(R₁_K/2c)^1/2
– 1]² = 5,3 эВ, где 
= ₁
–_K.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 мая 2021 года; проверки требуют 2 правки.

Формула Ридберга в том виде, в котором она была представлена в ноябре 1888 года

Фо́рмула Ри́дберга — эмпирическая формула, описывающая длины волн в спектрах излучения атомов химических элементов. Предложена шведским учёным Йоханнесом Ридбергом и представлена 5 ноября 1888 года.

Формула Ридберга для водородоподобных атомов выглядит следующим образом:

${displaystyle {frac {1}{lambda }}=RZ^{2}left({frac {1}{n_{1}^{2}}}-{frac {1}{n_{2}^{2}}}right),}$

где

— длина волны света в вакууме;

— постоянная Ридберга в общем случае различна для разных химических элементов;

— атомный номер, или число протонов в ядре атома данного элемента;

$n_{1}$

и $n_{2}$

— целые числа, такие что ${displaystyle n_{1}<n_{2}}$

История[править | править код]

В 1880-х годах, Ридберг работал над формулой, описывающей взаимосвязь между длинами волн в спектрах щелочных металлов. Он заметил, что линии образуют серии, и обнаружил, что может уменьшить трудоёмкость расчётов, введя спектроскопическое волновое число (величина, равная ${displaystyle {frac {1}{lambda }},}$ обратная длине волны, обозначается как ) в качестве единицы измерения. Он записал волновые числа () следующих друг за другом линий в каждой серии напротив расположенных параллельно в соответствующем порядке целых чисел, представляющих собой порядок линии в данной конкретной серии. Обнаружив, что получившиеся кривые имели похожие формы, он нашёл единую функцию, описывающую все эти кривые, при подстановке в неё соответствующих констант.

Сначала он проверил формулу ${displaystyle n=n_{0}-{frac {C_{0}}{m+m'}},}$ где — волновое число спектральной линии, $n_{0}$ — граница серии, — порядковый номер линии в серии (константа, различная для разных серий) и $C_{0}$ — универсальная константа. Эта формула не давала достаточно точных результатов.

Затем Ридберг проверил формулу ${displaystyle n=n_{0}-{frac {C_{0}}{(m+m')^{2}}},}$ когда ему стала известна формула Бальмера для спектра атома водорода ${displaystyle lambda ={hm^{2} over m^{2}-4}.}$ В этой формуле, ${displaystyle min mathbb {Z^{+}} ,h=const.}$

Ридберг переписал формулу Бальмера, используя обозначения волновых чисел, в следующем виде:

${displaystyle n=n_{0}-{4n_{0} over m^{2}}.}$

Это преобразование подсказало, что формула Бальмера для водорода может являться частным случаем при и ${displaystyle C_{0}=4n_{0},}$ где ${displaystyle n_{0}={frac {1}{h}}}$ — обратно константе Бальмера.

Величина ${displaystyle C_{0},}$ как было установлено позже, была универсальной константой, общей для всех элементов, равной Эта константа сейчас называют постоянной Ридберга, и величину называют квантовый дефект.

Как подчеркнул Нильс Бор^[1], выражение результатов через волновые числа, а не через длины волн, было ключом к открытию Ридберга. Фундаментальная роль волновых чисел была особо подчёркнута открытием комбинационного принципа Ридберга — Ритца в 1908 году. Фундаментальная причина важности волновых чисел лежит в области квантовой механики, так как энергия фотонов с разной длиной волны прямо пропорциональна волновым числам.

Волновые числа световых волн пропорциональны частоте ${displaystyle {frac {1}{lambda }}={frac {f}{c}},}$ и поэтому также пропорциональны энергии квантов света То есть, ${displaystyle {frac {1}{lambda }}={frac {E}{hc}}.}$ Современное понимание состоит в том, что графики Ридберга были упрощёнными (обладали невысокой степенью адекватности реальным зависимостям), так как отражали лишь простые свойства в поведении спектральных линий в условиях строго определённых (квантованных) разностей энергий между электронными орбиталями в атоме.

Классическое выражение Ридберга (в работе 1888 года) для длин волн спектральных серий не имело физическое объяснение. Пред-квантовое объяснение Ритца (1908 год) механизма «образования» спектральных серий состояло в том, что электроны в атоме ведут себя как постоянные магниты, и что эти магниты могут колебаться относительно атомного ядра (по крайней мере в течение некоторого времени), порождая электромагнитное излучение^[2]. Это явление впервые было понято Нильсом Бором в 1913 году так, как оно включено в описание Боровская модель атома.

В боровской модели атома целые числа Ридберга (и Бальмера) соответствуют электронным орбиталям на различных определённых расстояниях от ядра атома. Частота (или энергия), получается при переходе с уровня $n_{1}$ на уровень ${displaystyle n_{2},}$ поэтому представляет собой энергию фотона, излучённого или поглощённого, когда электрон «перепрыгивает» с орбитали (уровня) 1 на орбиталь 2.

Формула Ридберга для атома водорода[править | править код]

Схема энергетических уровней атома водорода и спектральные серии

${displaystyle {frac {1}{lambda }}=R_{infty }left({frac {1}{n^{2}}}-{frac {1}{m^{2}}}right),}$

где

— длина волны электромагнитного излучения в вакууме;

${displaystyle R_{infty }}$

— постоянная Ридберга;

— целые числа, причём

Принимая равным 1, и полагая, что может принимать целые значения от 2 до бесконечности, получаем спектральные линии, известные как серия Лаймана, коротковолновая граница длин волн которых стремится к 91 нм. При подстановке в формулу равным 2, 3, и т. д. аналогично получаются и другие спектральные серии:

n	m	Название серии	Коротковолновая граница серии
1	2 → ∞	Серия Лаймана	91,13 нм (Ультрафиолетовая часть спектра)
2	3 → ∞	Серия Бальмера	364,51 нм (Видимая часть спектра)
3	4 → ∞	Серия Пашена	820,14 нм (Инфракрасная часть спектра)
4	5 → ∞	Серия Брэккета	1458,03 нм (Инфракрасная часть спектра)
5	6 → ∞	Серия Пфунда	2278,17 нм (Инфракрасная часть спектра)
6	7 → ∞	Серия Хэмпфри	3280,56 нм (Инфракрасная часть спектра)

Формула Ридберга для любых водородоподобных атомов[править | править код]

Формула для атома водорода, приведённая выше, может быть дополнена для применения к любым водородоподобным атомам:

${displaystyle {frac {1}{lambda _{mathrm {vac} }}}=RZ^{2}left({frac {1}{n_{1}^{2}}}-{frac {1}{n_{2}^{2}}}right),}$

где ${displaystyle lambda _{mathrm {vac} }}$

— длина волны излучения в вакууме;

— постоянная Ридберга для данного химического элемента;

— порядковый номер элемента в периодической таблице, то есть, количество протонов в атомных ядрах данного элемента;

$n_{1}$

и $n_{2}$

— целые числа, причём ${displaystyle n_{1}<n_{2}.}$

Важно заметить, что эта формула применима только для водородоподобных атомов, то есть для таких атомов, которые содержат в электронной оболочке только один электрон. Такими атомами являются, например, ${displaystyle {ce {He^+, Li^{2+}, Be^{3+}}}}$ и любые другие многократно ионизированные атомы с одним электроном в электронной оболочке.

Формула Ридберга позволяет получать правильные значения длин волн для атомов, находящихся в высоких степенях возбуждения, когда эффективный заряд ядра можно считать таким же как и у водорода, когда все, кроме одного, заряды в ядре экранированы другими электронами, и центр атома имеет эффективный положительный заряд, равный +1.

Для других спектральных переходов в многоэлектронных атомах, формула Ридберга даёт некорректные результаты, поскольку величина экранирования внутренних электронов для переходов внешних электронов варьируется, и нет возможности сделать в формуле подобную простую «компенсирующую» «ослабление действия заряда ядра» поправку, как приведено выше.

Формула Ридберга для характеристического рентгеновского излучения[править | править код]

При определённом изменении (замене на и использовании целых чисел дающих численное значение ${displaystyle {frac {3}{4}}}$ для разности их обратных квадратов (в формуле выше)), формула Ридберга даёт корректные результаты в специальном случае K-альфа линий, подобные переходы являются K-альфа переходом электрона с орбитали на орбиталь называемом характеристическим рентгеновским излучением. Это аналогично переходу, соответствующего линии Лаймана-альфа, для водорода, и имеет тот же самый частотный множитель. Поскольку 2p-электрон не экранирован от ядра в атоме никакими другими электронами, то заряд ядра ослаблен единственным остающимся 1s-электроном, делая атом фактически водородоподобным атомом, но со сниженным зарядом ядра Частота излучения для этого перехода, таким образом, является частотой линии Лайман-альфа атома водорода, возрастая, благодаря величине ${displaystyle (Z-1)^{2}.}$ Эта формула ${displaystyle f={frac {c}{lambda }}=lambda [mathrm {La} _{alpha }](Z-1)^{2}}$ исторически известна как закон Мозли (добавляя скорость света в формулу для замены длины волны на частоту), и может быть использована для вычисления длин волн ${displaystyle K_{alpha }}$ (K-альфа) рентгеновских спектральных линий в рентгеновских спектрах излучения химических элементов от алюминия до золота. Об исторической важности этого закона можно узнать, ознакомившись с биографией Генри Мозли. Этот закон был эмпирически установлен примерно в то же время, когда была создана боровская модель атома.

Примечания[править | править код]

↑ Bohr, N. Rydberg’s discovery of the spectral laws // Collected works / Kalckar, J.. — Amsterdam: North-Holland Publ. Cy., 1985. — Т. 10. — С. 373—379.
↑ Ritz, W. Magnetische Atomfelder und Serienspektren (нем.) // Annalen der Physik : magazin. — 1908. — Bd. 330, Nr. 4. — S. 660—696. — doi:10.1002/andp.19083300403.

Ссылки[править | править код]

Sutton, Mike. Getting the numbers right: The lonely struggle of the 19th century physicist/chemist Johannes Rydberg (англ.) // Chemistry World (англ.) (рус. : magazine. — 2004. — July (vol. 1, no. 7). — P. 38—41. — ISSN 1473-7604.
Martinson, I.; Curtis, L.J. Janne Rydberg – his life and work (англ.) // Nuclear Instruments and Methods in Physics Research Section B (англ.) (рус.. — 2005. — Vol. 235, no. 1—4. — P. 17—22. — doi:10.1016/j.nimb.2005.03.137. — Bibcode: 2005NIMPB.235…17M.

Источник

Макеты страниц

Спектры испускания атомов щелочных металлов, подобно спектру водорода, состоят из нескольких серий линий. Наиболее интенсивные из них получили названия: главная, резкая, диффузная и основная (или серия Бергмана). Эти названия имеют следующее происхождение. Главная серия названа так потому, что наблюдается и при поглощении. Следовательно, она соответствует переходам атома в Основное состояние. Резкая и диффузная серии состоят соответственно из резких и размытых (диффузных) линий. Серия Бергмана была названа основной (фундаментальной) за свое сходство с сериями водорода.

Линии серий атома можно представить как переходы между энергетическими уровнями, изображенными на рис. 29.1. Эта схема отличается от схемы уровней водородного атома (см. рис. 28.1) тем, что аналогичные уровни в различных рядах лежат на неодинаковой высоте. Несмотря на это отличие, обе схемы обнаруживают большое сходство. Это сходство дает основание предположить, что спектры щелочных металлов испускаются при переходах самого внешнего (так называемого валентного или оптического) электрона с одного уровня на другой.

Из рис. 29.1 видно, что энергия состояния оказывается зависящей, кроме квантового числа , также от того, в какой ряд попадает данный терм, т. е. от номера ряда термов.

На схеме уровней атома водорода различные ряды термов (с совпадающими по высоте уровнями) отличаются значениями момента импульса электрона. Естественно предположить, что различные ряды термов щелочных металлов также отличаются значениями момента импульса валентного электрона.

Рис. 29.1,

Поскольку уровни различных рядов в этом случае лежат на неодинаковой высоте, следует принять, что энергия валентного электрона в атоме щелочного металла зависит от величины момента импульса электрона (чего мы не наблюдали для водорода).

Предположение о зависимости энергии валентного электрона щелочных атомов от квантового числа (т. е. от значения М) подтверждается квантовомеханическими расчетами. В более сложных, чем водород, атомах можно считать, что каждый из электронов движется в усредненном поле ядра и остальных электронов. Это поле уже не будет кулоновским (т. е. пропорциональным ), но обладает центральной симметрией (зависит только от ). В самом деле, в зависимости от степени проникновения электрона в глубь атома заряд ядра будет для данного электрона в большей или меньшей степени экранироваться другими электронами, так что эффективный заряд, воздействующий на рассматриваемый электрон, не будет постоянным. Вместе с тем, поскольку электроны движутся в атоме с огромными скоростями, усредненное по времени поле можно считать центрально-симметричным.

Решение уравнения Шрёдингера для электрона, движущегося в центрально-симметричном некулоновском поле, дает результат, аналогичный результату для водородного атома, с тем отличием, что энергетические уровни зависят не только от квантового числа , но и от квантового числа

Таким образом, в этом случае снимается вырождение по Отличие в энергии между состояниями с различными l и одинаковыми вообще не так велико, как между состояниями с различными . С увеличением l энергия уровней с одинаковыми возрастает.

Момент импульса атома в целом слагается из моментов всех электронов, входящих в состав атома. Значение результирующего момента определяется квантовым числом L (см. § 24). Каждому столбцу уровней на рис. 29.1 соответствует свое значение

Использованные на схеме рис. 29.1 обозначения S, Р, D, F являются первыми буквами английских названий серий: sharp — резкий, principal — главный, diffuse — размытый, fundamental — основной. Каждая из серий возникает за счет переходов с уровней, принадлежащих соответствующему ряду. После того, как было выяснено, что различные ряды уровней отличаются значением квантового числа L, обозначения S, Р, Д F (или s, р, d, f) были применены для обозначения состояний с соответствующими значениями L (или l).

Исследования оптических спектров ионов щелочных металлов показали, что момент импульса атомного остатка (т. е. ядра и остальных электронов, кроме наименее связанного валентного электрона, удаляющегося при ионизации) равен нулю. Следовательно, момент атома щелочного металла равен моменту его валентного электрона, и L атома совпадает с l этого электрона.

Для l валентного электрона атомов щелочных металлов действует такое же правило отбора, как и для l электрона водородного атома (см. формулу (28.5)).

При возбуждении атома щелочного металла и при испускании им света изменяется только состояние валентного электрона. Поэтому схему уровней щелочного атома можно считать тождественной схеме уровней валентного электрона.

Обозначим термы, отвечающие столбцам уровней, помеченным на рис. 29.1 буквами S, Р, D, F, символами . Согласно формуле (12.6) частота спектральной линии равна разности термов конечного и начального состояний. Следовательно, спектральные серии натрия могут быть представлены в следующем виде:

Еще в конце прошлого столетия Ридберг установил, что термы щелочных металлов с большой степенью точности можно представить с помощью эмпирической формулы

Здесь R — постоянная Ридберга (см. (12.3)), — главное квантовое число, а — дробное число, называемое ридберговской поправкой или квантовым дефектом. Эта поправка имеет постоянное значение для данного ряда термов. Ее принято обозначать той же буквой, какой обозначен соответствующий ряд термов, — буквой s для -термов, буквой — для Р-термов и т. д. Значения поправок определяются экспериментально. Для разных щелочных металлов они имеют различные значения. Для натрия эти значения равны

Заметим, что терм (29.2) отличается от терма водородного атома (см. (12.5)) только наличием поправки а. Для -термов эта поправка равна нулю. Поэтому основная серня (возникающая при переходах с F-уровней) оказывается водородоподобной.

Подставив эмпирические выражения в соотношения (29.1), получим формулы для частот спектральных серий натрия:

Поправки s, p, d, f в этих формулах имеют значения (29.3).

Оглавление

ПРЕДИСЛОВИЕ
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ЧАСТЬ 1. КВАНТОВАЯ ОПТИКА
§ 1. Тепловое излучение и люминесценция
§ 2. Закон Кирхгофа
§ 3. Равновесная плотность энергии излучения
§ 4. Закон Стефана — Больцмана и закон Вина
§ 5. Стоячие волны в пространстве трех измерений
§ 6. Формула Рэлея — Джинса
§ 7. Формула Планка
ГЛАВА II. ФОТОНЫ
§ 8. Тормозное рентгеновское излучение
§ 9. Фотоэффект
§ 10. Опыт Боте. Фотоны
§ 11. Эффект Комптона
ЧАСТЬ 2. АТОМНАЯ ФИЗИКА
§ 12. Закономерности в атомных спектрах
§ 13. Модель атома Томсона
§ 14. Опыты по рассеянию а-частиц. Ядерная модель атома
§ 15. Постулаты Бора. Опыт Франка и Герца
§ 16. Правило квантования круговых орбит
§ 17. Элементарная боровская теория водородного атома
ГЛАВА IV. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
§ 18. Гипотеза де-Бройля. Волновые свойства вещества
§ 19. Необычные свойства микрочастиц
§ 20. Принцип неопределенности
§ 21. Уравнение Шрёдингера
§ 22. Смысл пси-функции
§ 23. Квантование энергии
§ 24. Квантование момента импульса
§ 25. Принцип суперпозиции
§ 26. Прохождение частиц через потенциальный барьер
§ 27. Гармонический осциллятор
ГЛАВА V. ФИЗИКА АТОМОВ И МОЛЕКУЛ
§ 28. Атом водорода
§ 29. Спектры щелочных металлов
§ 30. Ширина спектральных линий
§ 31. Мультиплетность спектров и спин электрона
§ 32. Результирующий механический момент многоэлектронного атома
§ 33. Магнитный момент атома
§ 34. Эффект Зеемана
§ 35. Электронный парамагнитный резонанс
§ 36. Принцип Паули. Распределение электронов по энергетическим уровням атома
§ 37. Периодическая система элементов Менделеева
§ 38. Рентгеновские спектры
§ 39. Энергия молекулы
§ 40. Молекулярные спектры
§ 41. Комбинационное рассеяние света
§ 42. Вынужденное излучение
§ 43. Лазеры
§ 44. Нелинейная оптика
ЧАСТЬ 3. ФИЗИКА ТВЕРДОГО ТЕЛА
§ 45. Кристаллическая решетка. Индексы Миллера
§ 46. Теплоемкость кристаллов. Теория Эйнштейна
§ 47. Колебания систем с большим числом степеней свободы
§ 48. Теория Дебая
§ 49. Фононы
§ 50. Эффект Мёссбауэра
ГЛАВА VII. ЗОННАЯ ТЕОРИЯ ТВЕРДЫХ ТЕЛ
§ 51. Квантовая теория свободных электронов в металле
§ 52. Распределение Ферми — Дирака
§ 53. Энергетические зоны в кристаллах
§ 54. Динамика электронов в кристаллической решетке
ГЛАВА VIII. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ И ПОЛУПРОВОДНИКОВ
§ 55. Электропроводность металлов
§ 56. Сверхпроводимость
§ 57. Полупроводники
§ 58. Собственная проводимость полупроводников
§ 59. Примесная проводимость полупроводников
ГЛАВА IX. КОНТАКТНЫЕ И ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ
§ 60. Работа выхода
§ 61. Термоэлектронная эмиссия. Электронные лампы
§ 62. Контактная разность потенциалов
§ 63. Термоэлектрические явления
§ 64. Полупроводниковые диоды и триоды
§ 65. Внутренний фотоэффект
ЧАСТЬ 4. ФИЗИКА АТОМНОГО ЯДРА И ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
§ 66. Состав и характеристики атомного ядра
§ 67. Масса и энергия связи ядра
§ 68. Модели атомного ядра
§ 69. Ядерные силы
§ 70. Радиоактивность
§ 71. Ядерные реакции
§ 72. Деление ядер
§ 73. Термоядерные реакции
ГЛАВА XI. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
§ 74. Виды взаимодействий и классы элементарных частиц
§ 75. Методы регистрации элементарных частиц
§ 76. Космические лучи
§ 77. Частицы и античастицы
§ 78. Изотопический спин
§ 79. Странные частицы
§ 80. Несохранение четности в слабых взаимодействиях
§ 81. Нейтрино
§ 82. Систематика элементарных частиц
§ 83. Кварки
§ 84. Великое объединение
ПРИЛОЖЕНИЯ
I. ГРАВИТАЦИОННОЕ ВЗАИМОДЕЙСТВИЕ

Источник

Задача №2.

Атомы щелочных металлов

История[править | править код]

Формула Ридберга для атома водорода[править | править код]

Формула Ридберга для любых водородоподобных атомов[править | править код]

Формула Ридберга для характеристического рентгеновского излучения[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Вам также может понравиться

Как найти ветерана по военному билету

Как исправить перегоревшую лампочку

Как составить резюме или портфолио

Добавить комментарий Отменить ответ