В этой теме мы уже изучили много закономерностей: в § 9-в мы выяснили, как распределяются силы токов при последовательном и параллельном соединении проводников. В § 9-г мы узнали как рапределяются напряжения в этих же соединениях. Опираясь на эти знания, а также на закон Ома для участка цепи (см. § 9-д), выведем формулы для расчёта сопротивлений соединений проводников.
| Последовательное соединение проводников | | | |
Параллельное соединение проводников |
| Так как | ||
| U = U1 + U2 | | | I = I1 + I2 |
| и по закону Ома | ||
| U = I · R | | | I = U / R |
| то получим: | ||
| I · R = I1 · R1 + I2 · R2 | | | U / R = U1 / R1 + U2 / R1 |
| Учитывая, что | ||
| I = I1 = I2 | | | U = U1 = U2 |
| заменяя, получим: | ||
| I · R = I · R1 + I · R2 | | | U / R = U / R1 + U / R2 |
| Сократим общий множитель: | ||
| 1 · R = 1 · R1 + 1 · R1 | | | 1 / R = 1 / R1 + 1 / R2 |
| Обобщая, получим: | ||
|
Rоб = R1 + R2 + … |
и |
1/Rоб = 1/R1 + 1/R2 + … |
| Общее сопротивление последовательного соединения проводников равно сумме сопротивлений его отдельных участков. | | | | | | |
Величина, обратная общему сопротивлению параллельного соединения проводников, равна сумме величин, обратных сопротивлениям его участков. |
Рассмотрим формулу в левой рамке: общее сопротивление складывается (суммируется) из отдельных сопротивлений. Поскольку сумма всегда больше любого из слагаемых, при последовательном соединении проводников общее сопротивление соединения всегда больше сопротивления любого его участка. Например, соединение составлено из резисторов с сопротивлениями 4 Ом и 5 Ом, тогда общее сопротивление будет равно 9 Ом (общее сопротивление больше большего).
Перейдём к формуле в правой рамке: при параллельном соединении проводников общее сопротивление соединения всегда меньше сопротивления любого его участка. Проверим это на примере с теми же сопротивлениями: 4 Ом и 5 Ом. Сделав вычисления по формуле, мы найдём, что общее сопротивление этих же двух резисторов, соединённых параллельно, ≈ 2,2 Ом (общее сопротивление меньше меньшего).
Продолжим изучать физические закономерности математическими методами. Теперь выведем две дополнительные формулы, описывающие общее сопротивление одинаковых проводников.
Вообразим, к примеру, что пять одинаковых резисторов соединены последовательно. Тогда их общее сопротивление будет таково:
Rоб = R + R + R + R + R = 5·R .
Обобщая это на случай n проводников, получим, что их общее сопротивление увеличивается в n раз.
Вообразим теперь, что те же пять одинаковых резисторов соединены параллельно. Тогда их общее сопротивление вычислится так:
1 / Rоб = 1/R + 1/R + 1/R + 1/R + 1/R = 5/R .
Обобщая это на случай n проводников, получим, что их общее сопротивление уменьшается в n раз.
Примечание. При выводе последней формулы мы воспользовались правилом из алгебры: если две величины равны друг другу, то и величины, обратные им, также равны.
Загрузить PDF
Загрузить PDF
Элементы электрической цепи можно соединить двумя способами. Последовательное соединение подразумевает подключение элементов друг к другу, а при параллельном соединении элементы являются частью параллельных ветвей. Способ соединения резисторов определяет метод вычисления общего сопротивления цепи.
-

1
Определите, является ли цепь последовательной. Последовательное соединение представляет собой единую цепь без каких-либо разветвлений. Резисторы или другие элементы расположены друг за другом.
-

2
Сложите сопротивления отдельных элементов. Сопротивление последовательной цепи равно сумме сопротивлений всех элементов, входящих в эту цепь.[1]
Сила тока в любых частях последовательной цепи одна и та же, поэтому сопротивления просто складываются.- Например, последовательная цепь состоит из трех резисторов с сопротивлениями 2 Ом, 5 Ом и 7 Ом. Общее сопротивление цепи: 2 + 5 + 7 = 14 Ом.
-

3
Вычислите сопротивление по известной силе тока и напряжению. Если сопротивление каждого элемента цепи не известно, воспользуйтесь законом Ома: V = IR, где V – напряжение, I – сила тока, R – сопротивление. Сначала найдите силу тока и общее напряжение.
- Сила тока в любых частях последовательной цепи одна и та же.[2]
Поэтому можно использовать известное значение силы тока на любом участке последовательной цепи. - Общее напряжение равно напряжению источника тока. Оно не равно напряжению на каком-либо элементе цепи.[3]
- Сила тока в любых частях последовательной цепи одна и та же.[2]
-

4
Подставьте известные значения в формулу, описывающую закон Ома. Перепишите формулу V = IR так, чтобы обособить сопротивление: R = V/I. Подставьте известные значения в эту формулу, чтобы вычислить общее сопротивление.
- Например, напряжение источника тока равно 12 В, а сила тока равна 8 А. Общее сопротивление последовательной цепи: RO = 12 В / 8 А = 1,5 Ом.
Реклама
-

1
Определите, является ли цепь параллельной. Параллельная цепь на некотором участке разветвляется на несколько ветвей, которые затем снова соединяются. Ток течет по каждой ветви цепи.
- Если цепь включает элементы, расположенные до или после разветвления, или если на одной ветви два и более элементов, перейдите к третьему разделу этой статьи (такая цепь является комбинированной).
-

2
Вычислите общее сопротивление на основе сопротивления каждой ветви. Каждый резистор уменьшает силу тока, проходящего через одну ветвь, поэтому она оказывает небольшое влияние на общее сопротивление цепи. Формула для вычисления общего сопротивления:
, где R1 – сопротивление первой ветви, R2 – сопротивление второй ветви и так далее до последней ветви Rn.
-

3
Вычислите сопротивление по известной силе тока и напряжению. Сделайте это, если сопротивление каждого элемента цепи не известно.
- В параллельной цепи напряжение на одной ветви равно общему напряжению в цепи.[4]
Поэтому достаточно знать значение напряжение на любой ветви цепи. Общее напряжение также равно напряжению источника тока. - В параллельной цепи сила тока на каждой ветви разная. Поэтому необходимо знать значение общей силы тока, чтобы найти общее сопротивление.
- В параллельной цепи напряжение на одной ветви равно общему напряжению в цепи.[4]
-

4
Подставьте известные значения в формулу закона Ома. Если известны значения общей силы тока и напряжения в цепи, общее сопротивление вычисляется по закону Ома: R = V/I.
- Например, напряжение в параллельной цепи равно 9 В, а общая сила тока равна 3 А. Общее сопротивление: RO = 9 В / 3 А = 3 Ом.
-

5
Поищите ветви с нулевым сопротивлением. Если у ветви параллельной цепи вообще нет сопротивления, то весь ток будет течь через такую ветвь. В этом случае общее сопротивление цепи равно 0 Ом.
- В реальной жизни это означает, что резистор неисправен или шунтирован (замкнут); в этом случае большая сила тока может повредить другие элементы цепи.[5]
Реклама
- В реальной жизни это означает, что резистор неисправен или шунтирован (замкнут); в этом случае большая сила тока может повредить другие элементы цепи.[5]
-

1
Разбейте комбинированную цепь на последовательную и параллельную. Комбинированная цепь включает элементы, которые соединены как последовательно, так и параллельно. Посмотрите на схему цепи и подумайте, как разбить ее на участки с последовательным и параллельным соединением элементов. Обведите каждый участок, чтобы упростить задачу по вычислению общего сопротивления.
- Например, цепь включает резистор, сопротивление которого равно 1 Ом, и резистор, сопротивление которого равно 1,5 Ом. За вторым резистором схема разветвляется на две параллельные ветви – одна ветвь включает резистор с сопротивлением 5 Ом, а вторая – с сопротивлением 3 Ом. Обведите две параллельные ветви, чтобы выделить их на схеме цепи.
-

2
Найдите сопротивление параллельной цепи. Для этого воспользуйтесь формулой для вычисления общего сопротивления параллельной цепи:
.
-

3
Упростите цепь. После того как вы нашли общее сопротивление параллельной цепи, ее можно заменить одним элементом, сопротивление которого равно вычисленному значению.
- В нашем примере избавьтесь от двух параллельных ветвей и замените их одним резистором с сопротивлением 1,875 Ом.
-

4
Сложите сопротивления резисторов, соединенных последовательно. Заменив параллельную цепь одним элементом, вы получили последовательную цепь. Общее сопротивление последовательной цепи равно сумме сопротивлений всех элементов, которые включены в эту цепь.
- После упрощения цепи она состоит из трех резисторов со следующими сопротивлениями: 1 Ом, 1,5 Ом и 1,875 Ом. Все три резистора соединены последовательно:
Ом.
- После упрощения цепи она состоит из трех резисторов со следующими сопротивлениями: 1 Ом, 1,5 Ом и 1,875 Ом. Все три резистора соединены последовательно:
-

5
Воспользуйтесь законом Ома, чтобы найти неизвестные величины. Если сопротивление каждого элемента цепи не известно, попытайтесь вычислить его. Вычислить сопротивление по известной силе тока и напряжению можно по закону Ома: R = V/I.
Реклама
-

1
Запомните формулы, включающие мощность. Электрическая мощность – это величина, которая характеризует скорость преобразования электроэнергии и скорость ее передачи (например, к лампочке).[6]
Общая мощность цепи равна произведению общего напряжения на общую силу тока. Формула: P = VI.[7]
- Запомните: чтобы вычислить общее сопротивления, нужно знать общую мощность. Значение мощности на одном элементе цепи для этих целей не подходит.
-

2
Вычислите сопротивление по известным значениям мощности и силы тока. В этом случае можно объединить две формулы, чтобы найти сопротивление.
- P = VI (мощность = напряжение х сила тока)
- Закон Ома: V = IR.
- В первую формулу вместо V подставьте произведение IR: P = (IR)I = I2R.
- Обособьте переменную R: R = P / I2.
- Сила тока в любых частях последовательной цепи одна и та же. Это не так в параллельной цепи.
-

3
Вычислите сопротивление по известным значениям мощности и напряжения. В этом случае можно объединить две формулы, чтобы найти сопротивление. Учитывайте общее напряжение в цепи, которое равно напряжению источника тока.
- P = VI
- Перепишите закон Ома так: I = V/R
- В первой формуле замените I на V/R: P = V(V/R) = V2/R.
- Обособьте переменную R: R = V2/P.
- В параллельной цепи напряжение на одной ветви равно общему напряжению в цепи. Это не так в последовательной цепи, где общее напряжение не равно напряжению на одном элементе цепи.
Реклама
Советы
- Мощность измеряется в ваттах (Вт).
- Напряжение измеряется в вольтах (В).
- Сила тока измеряется в амперах (А) или в миллиамперах (мА). 1 мА =
A = 0,001 А.
- В приведенных формулах переменная Р – это мгновенная мощность, то есть мощность в определенный момент времени. Если цепь подключена к источнику переменного тока, мощность постоянно меняется. Поэтому для цепей с источником переменного тока специалисты вычисляют среднюю мощность; для этого используется формула: PСР = VIcosθ, где cosθ – это коэффициент мощности цепи.[8]
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 407 314 раз.
Была ли эта статья полезной?
Цели:
- Образовательная: систематизировать и
закрепить знания учащихся о различных
соединениях проводников, сформировать умения
применять законы последовательного и
параллельного соединений для расчёта
электрических цепей, объединить знания,
полученные на уроках физики и математики. - Развивающая: развить мышление учащихся,
активизировать познавательную деятельность
через решение задач на расчет электрических
цепей, развить умение рассчитывать параметры
электрических цепей и совершенствовать
полученные на уроке навыки. - Воспитательная: формирование интереса к
изучаемому предмету, продолжить формирование
коммуникативных умений.
Тип урока: урок проверки и закрепления новых
знаний по физике и математике.
Метод проведения урока: практический
Оборудование:
- Громов С.В. Учебник “Физики-9”;
- план урока;
- методика расчета участка электрической цепи
постоянного тока; - карточки-задания.
Приложение 1
Ход урока
Сегодня на уроке мы должны применить
полученные ранее знания о законах
последовательного и параллельного соединений
для расчёта участка электрической цепи, а также
определить степень усвоения изученного
материала с помощью карточек – заданий.
Прежде чем приступить к рассмотрению
электрических цепей, вспомним то, что мы уже
знаем и ответим на вопросы:
1) Какие виды соединений бывают и как они
изображаются на электрических схемах?
2) Назовите законы последовательного соединения?
3) Назовите законы параллельного соединения?
4) Какая отличительная особенность параллельного
соединения?
Рассмотрим расчёт участка электрической цепи
на примере следующих задач:
1. Рассчитайте общее электрическое
сопротивление участка цепи?
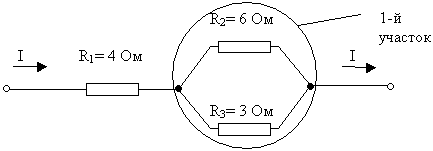
1) Наиболее удалённые от источника элементы –
это резисторы R2 и R3.
2) Объединяем эти два резистора в первый участок
и рассчитываем их общее сопротивление. Резисторы
R2 и R3 подключены параллельно, т.к
образуют в соединении два узла, следовательно:
Ом
3) Изображаем получившуюся в результате
свёртывания резисторы R2 и R3
электрическую схему:
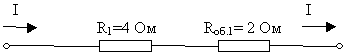
4) Полученные в результате объединения схему с
двумя резисторами группируем во второй участок и
рассчитываем их общее сопротивление. Так как
резисторы R1 и Rоб.1 соединены
последовательно, значит:
Rоб = R1 + Rоб.1 = 4 Ом + 2 Ом = 6 Ом
Ответ: общее сопротивление резисторов на
участке электрической цепи 6 Ом.
2. Рассчитайте общее электрическое
сопротивление участка цепи?
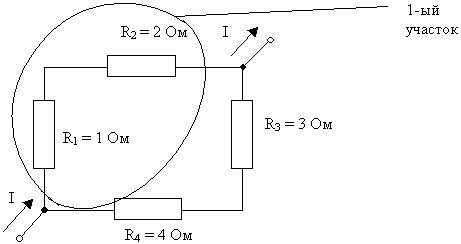
1) Резисторы R1 и R2 соединены между
собой последовательно:
Rоб.1 = R1 + R2 = 1 Ом + 2 Ом = 3 Ом
Изобразим полученный электрический участок
цепи:
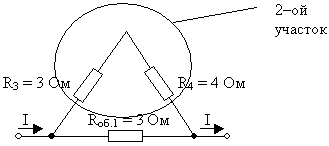
2) Резисторы R3 и R4 соединены между
собой последовательно:
Rоб.2 = R3 + R4 = 3 Ом + 4 Ом = 7 Ом
Изобразим полученный электрический участок
цепи:
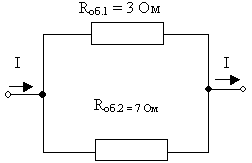
3) Полученные в результате объединения схему с
двумя резисторами группируем в третий участок и
рассчитываем их общее сопротивление. Так как
резисторы Rоб.1 и Rоб.2 соединены
параллельно, значит:
Ом
Ответ: общее сопротивление резисторов на
участке электрической цепи 2,1 Ом.
3. Выполните задания самостоятельно по
карточкам (дифференцированные),
воспользовавшись памяткой расчета участка
электрической цепи постоянного тока:
а) Рассчитайте общее электрическое
сопротивление участка цепи?
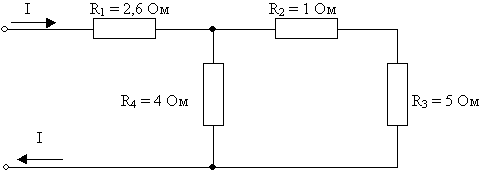
б) Рассчитайте общее электрическое
сопротивление участка цепи?
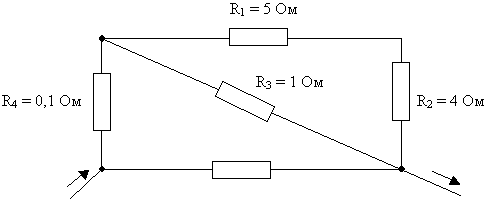
в) Рассчитайте общее электрическое
сопротивление участка цепи?
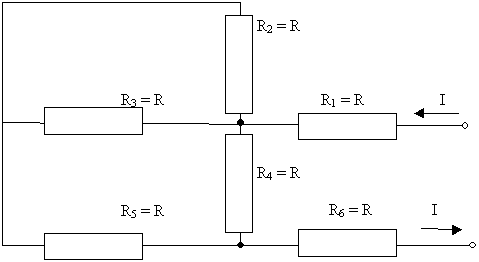
Сегодня на уроке мы рассмотрели различные
схемы участков электрических цепей, научились
рассчитывать цепи, применяя законы
последовательного и параллельного соединений, а
также закрепили полученные знания с помощью
карточек – заданий.
Последовательное и параллельное соединение резисторов
Последовательное соединение резисторов
Последовательное соединение – это соединение двух или более резисторов в форме цепи,
в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
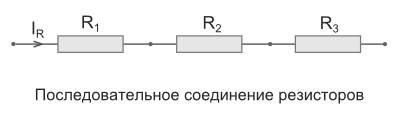
Общее сопротивление Rобщ
При таком соединении, через все резисторы проходит один и тот же электрический ток.
Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него.
Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается,
и оно равно сумме всех сопротивлений.
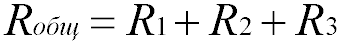
Напряжение при последовательном соединении
Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:
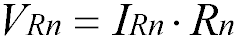
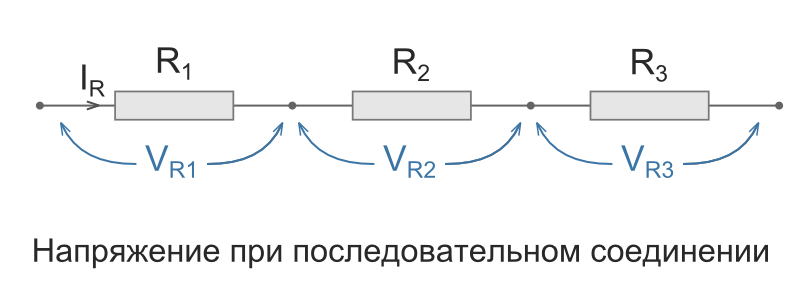
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.
Параллельное соединение резисторов
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами.
В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
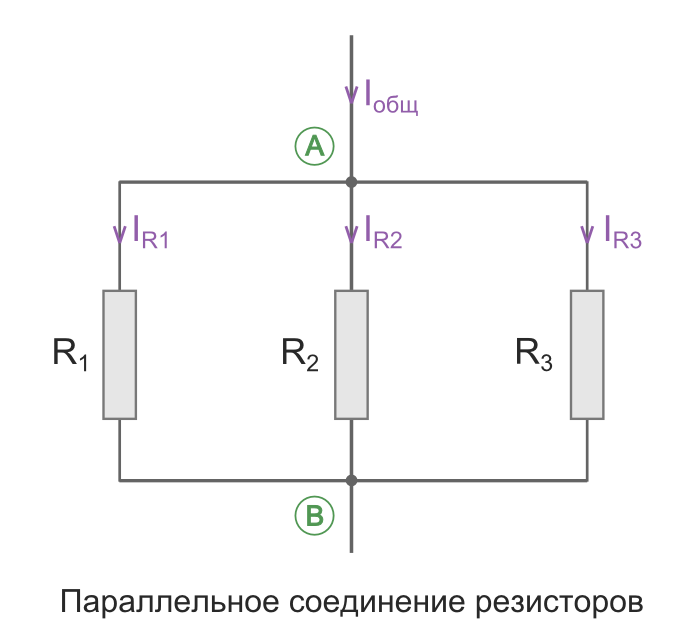
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток.
Сила данного тока будет обратно пропорциональна сопротивлению резистора.
В результате общая проводимость такого участка электрической цепи увеличивается,
а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением,
общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
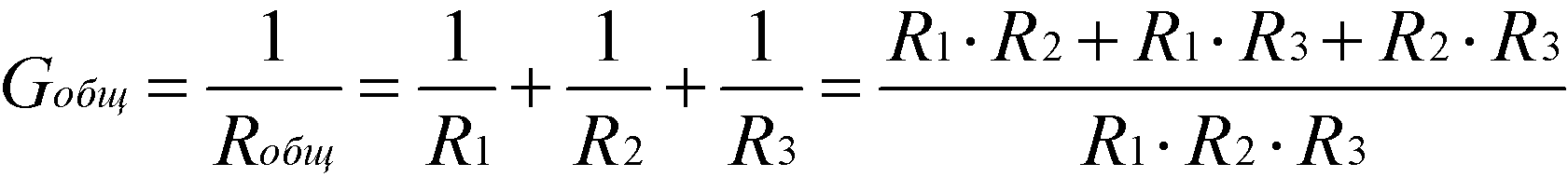
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
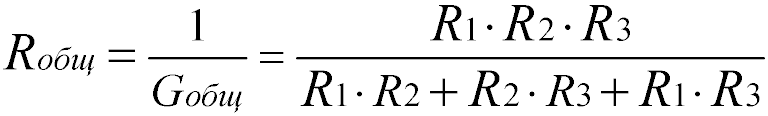
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
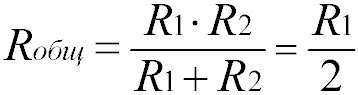
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
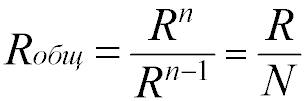
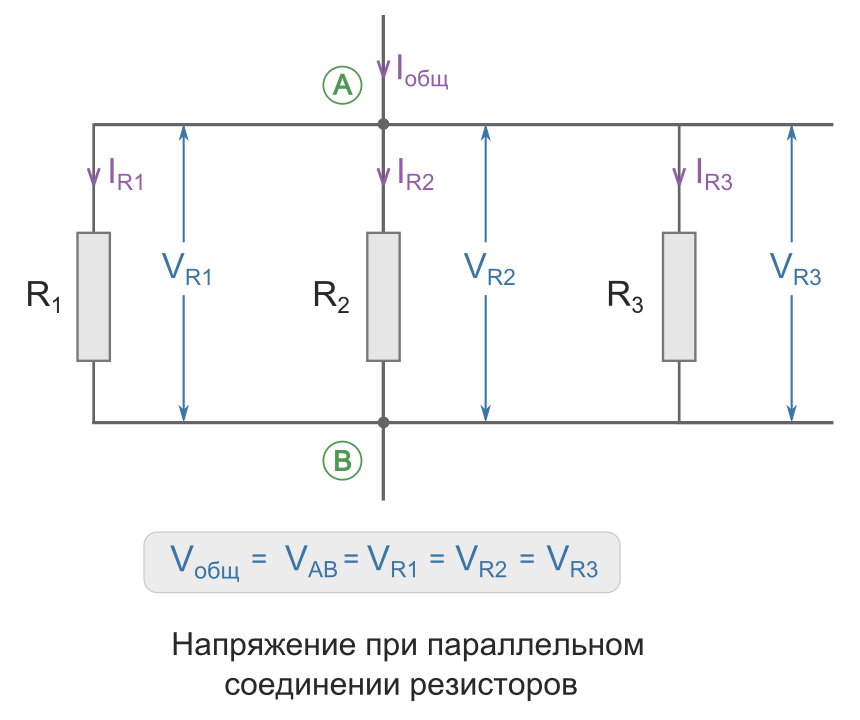
Напряжение при параллельном соединении
Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности.
Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.
Электрический ток при параллельном соединении
Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора.
Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:
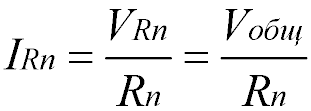
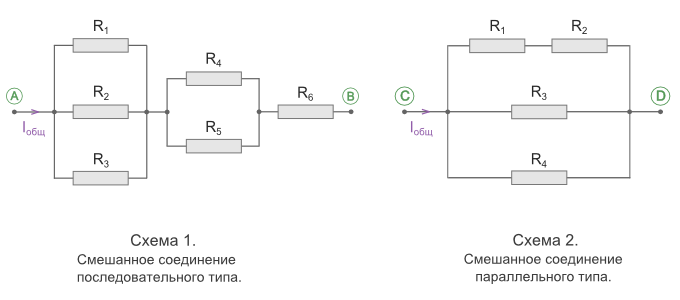
Смешанное соединение резисторов
Смешанным соединением называют участок цепи, где часть резисторов
соединяются между собой последовательно, а часть параллельно.
В свою очередь, смешанное соединение бывает последовательного и параллельного типов.
Общее сопротивление Rобщ
Для того чтобы посчитать общее сопротивление смешанного соединения:
- Цепь разбивают на участки с только пареллельным или только последовательным соединением.
- Вычисляют общее сопротивление для каждого отдельного участка.
- Вычисляют общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
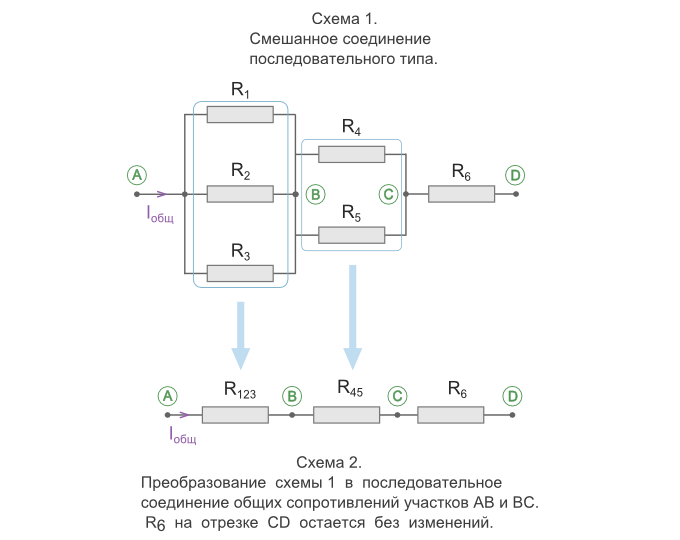
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения.
Можно, в соответствии схеме, сразу записывать формулу следующим образом:
- Если резисторы соединяются последоватеьно — складывать.
- Если резисторы соединяются параллельно — использовать условное обозначение «||».
- Подставлять формулу для параллельного соединения где стоит символ «||».
Так это будет выглядеть для схемы 1:

После подстановки формулы параллельного соединения вместо «||»:
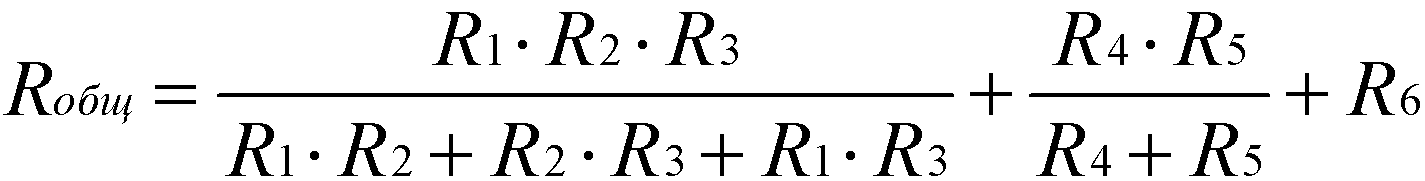

Закон Ома — эмпирический физический закон, определяющий связь электродвижущей силы источника (или электрического напряжения) с силой тока, протекающего в проводнике, и сопротивлением проводника. Установлен Георгом Омом в 1826 году (опубликован в 1827 году) и назван в его честь.
В данном обзоре приведены программы и калькуляторы закона Ома. Также дополнительно приведены основные формулы и методики расчетов.
Закон Ома для постоянного тока — расчет, формулы
Закон Ома для постоянного тока определяет зависимость между током (I), напряжением (U) и сопротивлением (R) в участке электрической цепи.
Закон Ома для полной цепи:
I = ε / (R + r), где:
- ε — ЭДС источника напряжения, В;
- I — сила тока в цепи, А;
- R — сопротивление всех внешних элементов цепи, Ом;
- r — внутреннее сопротивление источника напряжения, Ом.
Из закона Ома для полной цепи вытекают следующие следствия:
- При r < R сила тока в цепи обратно пропорциональна ее сопротивлению, а сам источник в ряде случаев может быть назван источником напряжения.
- При r > R сила тока не зависит от свойств внешней цепи (величины нагрузки), и источник может быть назван источником тока.
Часто выражение I = U / R тоже называют законом Ома. При этом формулировка следующая — сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи, где:
- I — сила тока, измеряемая в Амперах (A).
- U — напряжение, измеряемое в Вольтах (V).
- R — сопротивление, измеряемое в Омах (Ом, Ω).
Помимо закона Ома, важнейшим является понятие электрической мощности. Мощность постоянного тока (P) равна произведению силы тока (I) на напряжение (U):
P = I × U, где:
- P — электрическая мощность, измеряемая в Ваттах (W).
- I — сила тока, измеряемая в Амперах (A).
- U — напряжение, измеряемое в Вольтах (V).
Комбинируя две формулы можно получить зависимость между силой тока, напряжением, сопротивлением и мощностью, и создадим таблицу:
Множительные приставки в системе СИ примирительные к закону Ома:
- Сила тока, Амперы (A): 1 килоампер (1 kА) = 1000 А; 1 миллиампер (1 mA) = 0,001 A; 1 микроампер (1 µA) = 0,000001 A.
- Напряжение, Вольты (V): 1 киловольт (1kV) = 1000 V; 1 милливольт (1 mV) = 0,001 V; 1 микровольт (1 µV) = 0,000001 V.
- Сопротивление, Омы (Ом): 1 мегаом (1 MОм) = 1000000 Ом; 1 килоом (1 kОм) = 1000 Ом.
- Мощность, Ватты (W): 1 мегаватт (1 MW) = 1000000 W; 1 киловатт (1 kW) = 1000 W; 1 милливатт (1 mW) = 0,001 W.
Правила работы на калькуляторе
В быту нас интересуют, как правило, четыре взаимосвязанных характеристики электричества:
- напряжение;
- ток;
- сопротивление;
- или мощность.
Если тебе известны две величины, входящие в закон Ома (U, R, I), то вводи их в соответствующие строки, а оставшийся параметр и мощность будут вычислены автоматически.
Будь внимательным, чтобы не допустить ошибки.
Все значения надо заполнять в одной размерности: амперы, вольты, омы, ватты без использования обозначений дольности или кратности.
Осуществить переход к ним тебе поможет наглядная таблица.
Закон Ома для цепи переменного тока
В цепи переменного тока сопротивление кроме активной, может иметь как емкостную, так и индуктивную составляющие. Рассмотрим цепь переменного тока, состоящую из резистора сопротивлением R, конденсатора емкостью C и катушки индуктивностью L, соединенных последовательно.

Мгновенные значения силы тока на всех элементах этой цепи одинаковы, а мгновенное значение напряжения между концами цепи равно алгебраической сумме мгновенных значений напряжений на резисторе (UR), конденсаторе (UC) и катушке индуктивности (UL).
Для того чтобы определить амплитудные (или действующие) значения напряжения и силы тока, а также сдвиг фаз между ними удобно использовать метод векторных диаграмм. Здесь действующие значения всех напряжений и токов рассматриваются как векторы, вращающиеся с угловой скоростью ω, равной циклической частоте переменного тока, а их мгновенные значения определяются проекциями этих векторов на горизонтальную ось. Так как сила тока в цепи одинакова, то построение векторной диаграммы начинается с вектора I¯0, модуль которого равен амплитудному значению силы тока в цепи. Направление этого вектора может быть любым. Зададим угол α = ωt к горизонтали.

Колебания напряжения на активном сопротивлении совпадают по фазе с колебаниями силы тока, поэтому вектор U¯0R, модуль которого равен U0R = I0 × R, совпадает по направлению с вектором I¯0. Сдвиг фаз между колебаниями силы тока и колебаниями напряжения на индуктивном сопротивлении составляет π / 2, причем ток отстает по фазе от напряжения. Поэтому вектор U¯0L, модуль которого равен U0L = I0 × ωL, нужно повернуть относительно вектора I¯0 на угол π / 2 против часовой стрелки. Вектор U¯0C, модуль которого равен I0 / ωC, отстает по фазе от вектора I¯0 на π / 2, поэтому его нужно повернуть на этот угол по часовой стрелке.
Для того чтобы найти напряжение на зажимах цепи, необходимо сложить три вектора: U¯0 = U¯0R + U¯0L + U¯0C.
В первую очередь сложим векторы U¯0R и U¯0C. Модуль этой суммы U’0 = [U¯0R + U¯0C]. Пусть ωL > 1 / ωC, тогда: U’0 = I0 × (ωL — 1 / ωC).
Теперь сложим векторы U¯0R и U’¯0. Модуль вектора U¯0 определяется по теореме Пифагора: U0² = U0R² + (U0L — U0C)² = I0² × R² + I0² × (ωL — 1 / ωC)². Соответственно амплитудное (действующее) значение силы тока в цепи переменного тока равно отношению амплитудного (действующего) значения напряжения на концах этой цепи к его полному сопротивлению (закон Ома для цепи переменного тока):
I0 = U0 / √(R² + (ωL — 1 / ωC)²) = U0 / Z, где:
- Z — полное сопротивление (импеданс) цепи.
- R — его активное сопротивление.
- ωL — 1 / ωC — реактивное сопротивление цепи переменного тока.
- ω = 2 × π × γ — циклическая, угловая частота. γ — частота переменного тока.
Импеданс при параллельном подключении Z = 1 / √(1 / R² + 1 / (1 / ωL — ωC)²).
Сдвиг фаз между силой тока и напряжением равен углу φ между векторами U¯0 и I¯0. В соответствии с графиком выше ток отстает от напряжения на угол φ, причем tgφ = (ωL — 1 / ωC) / R.
Для того чтобы определить мгновенные значения напряжений на активном, емкостном и индуктивном сопротивлениях, необходимо спроектировать векторы U¯0R, U¯0L, U¯0C на прямую АВ.

Тогда:
- UR = I0 × R × sin × (ωt + φ).
- UL = I0 × ωL × sin × (ωt + φ + π / 2).
- UC = (I0 / ωС) × sin × (ωt + φ — π / 2).
Если 1 / ωС > ωL, то:
- U’0 = I0 × (1 / ωС — ωL).
- tgφ = (1 / ωC — ωL) / R, причем ток опережает напряжение по фазе на угол φ.
Последовательное включение
Такой вид включения подразумевает вид соединения, когда резисторы соединяются между собой только одним выводом, образовывая цепочку, при этом между её началом и концом отсутствует проводимость, соответствующая режиму короткого замыкания. При использовании последовательного соединения сила тока будет одинакова для любого проводника, а разность потенциалов на участке цепи составит значение равное сумме разностей потенциалов, на выводах каждого из проводников. Расчёт общего значения импеданса в этом случае совсем несложен, для этого просто суммируются все номинальные значения элементов входящих в состав цепочки: Rобщ=R1+R2+…+Rn.
Например, в схеме применяется цепочка сопротивлений, состоящая из пяти резисторов: R1=32 Ом, R2=16 Ом, R3=1 кОм, R4=4,7 кОм, R5=1 Ом. После приведения всех номиналов к международной системе, получится ответ, равный: Rобщ = 32+16+1000+4700+10=5758 Ом или 5,75 кОм, что соответствует стандартному значению 5,6 кОм.
Таблица удельных сопротивлений проводников
Электрическое сопротивление (ρ) 1 метра провода, сечением 1 мм², при температуре 20 С°:
| Материал проводника | Удельное сопротивление ρ, Ом |
| Серебро | 0.015 |
| Медь | 0.0175 |
| Золото | 0.023 |
| Латунь | 0,025. 0,108 |
| Хром | 0,027 |
| Алюминий | 0.028 |
| Натрий | 0.047 |
| Иридий | 0.0474 |
| Вольфрам | 0.05 |
| Цинк | 0.054 |
| Молибден | 0.059 |
| Никель | 0.087 |
| Бронза | 0,095. 0,1 |
| Железо | 0.1 |
| Сталь | 0,103. 0,137 |
| Олово | 0.12 |
| Свинец | 0.22 |
| Никелин (сплав меди, никеля и цинка) | 0.42 |
| Манганин (сплав меди, никеля и марганца) | 0,43. 0,51 |
| Константан (сплав меди, никеля и алюминия) | 0,44-0,52 |
| Копель (медно-никелевый сплав с 43% никеля и 0,5% марганца) | 0.5 |
| Титан | 0.6 |
| Ртуть | 0.94 |
| Хромель (хром 8,7 — 10 %; никель 89 — 91 %; кремний, медь, марганец, кобальт — примеси) | 1.01 |
| Нихром (сплав никеля, хрома, железа и марганца) | 1,05. 1,4 |
| Фехраль | 1,15. 1,35 |
| Висмут | 1.2 |
| Хромаль (Сплав 4,5 — 6% алюминия, 17 — 30% хрома, железа) | 1,3. 1,5 |
Сопротивление проводника определяется по формуле r = (ρ × l) / S, где:
- r — сопротивление проводника, Ом.
- ρ — удельное сопротивление проводника, Ом.
- l — длина проводника, м.
- S — сечение проводника, мм².
Смешанное подключение
В этом случае на участке схемы используется комбинация параллельного и последовательного включения элементов. Такое соединение часто называется параллельно-последовательным:
- При последовательном включении общий импеданс элементов прямо пропорционален сумме сопротивлений каждого из резисторов.
- При параллельном включении проводников значение, обратное сумме импеданса цепи, соответствует сумме значений, обратных сопротивлениям параллельно включённых элементов.

Используя эти правила, которые справедливы для любого числа соединённых проводников в схеме, определяется общее значение импеданса для любого вида подключения. Для того чтобы определить эквивалентное значение сопротивления параллельно-последовательного соединения, участок схемы делится на небольшие группы из параллельно или последовательно включённых резисторов. Затем используется алгоритм, помогающий оптимально посчитать значение эквивалента:
Определяется общее сопротивление всех узлов в схеме с параллельным подключением резисторов:
- При нахождении в этих узлах последовательно соединённых проводников первоначально считается их сопротивление.
- Как только значения эквивалентных значений вычислены, схема упрощается до последовательной цепочки из эквивалентных резисторов.
- Находится окончательное значение общего сопротивления.
Например, существует схема, в которой надо определить полное сопротивление цепи, при этом сопротивление резисторов R1=R3=R5=R6=3 Ом, а R2 =20 Ом и R4=24 Ом. Сопротивления R3, R4, и R5 включены последовательно, поэтому общий импеданс на этом участке цепи равен: Rоб1 = R3+R4+R5 = 30 Ом.
После замены R3, R4, R5 на Rоб1 резистор R3 окажется подключённым параллельно этому сопротивлению. Поэтому импеданс на этом участке будет равен:
Rоб2 = (R2* Rоб1) / (R3+Rоб1) = (20*30) / (20+30) = 12 Ом.
Резисторы R1 и R6 включены с Rоб2 последовательно, а это значит, что эквивалент всей схемы равен: Rэкв = Rоб1+Rоб2+ R6 = 3+12+3 = 18 Ом.
Так шаг за шагом вычисляется эквивалентное значение любой сложности схемы. При множестве проводников, входящих в электрическую цепь, нетрудно ошибиться при расчётах, поэтому все операции выполняются аккуратно или используются онлайн-калькуляторы.
Виды резисторов
Резистор – инертный (пассивный) элемент цепи, у которого сопротивление может быть как постоянным, так и переменным. Это зависит от его конструкции. Он применяется для регулирования силы тока и напряжения в цепях, рассеивания мощности и иных ограничений. Дословный перевод с английского слова «резистор» – сопротивляюсь.

Классификацию резисторов можно провести по следующим критериям:
- назначение элемента;
- тип изменения сопротивления;
- материал изготовления;
- вид проводника в элементе;
- ВАХ – вольт-амперная характеристика;
- способ монтажа.
Устройства делятся на элементы общего и специального назначения. У специальных деталей повышенные характеристики сопротивления, частоты, рабочего напряжения или особые требования к точности.
Тип изменения сопротивления делит их на постоянные и переменные. Переменные резисторы конструктивно отличаются не только от элементов, имеющих постоянное сопротивление, но и между собой. Они различны по конструкции: бывают регулировочные и подстроечные.
Регулировочные элементы переменного типа предназначены для частого изменения сопротивления. Это входит в процесс работы схемы устройства.
Подстроечный тип предназначен для того, чтобы выполнить подстройку и регулировку схемы при первичном запуске. После этого изменение положения регулятора не выполняют.
При изготовлении резистивных тел (рабочей поверхности) используются такие материалы, как:
- графитовые смеси;
- металлопленочные (окисные) ленты;
- проволока;
- композиционные компоненты.
Особое место занимают в этом ряду интегральные элементы. Это резисторы, выполненные в виде p-n перехода, который представляет собой зигзагообразный канал, интегрируемый в кристалл микросхемы.
Внимание! Интегральные элементы всегда отличаются повышенной нелинейностью своей ВАХ. Поэтому они применяются там, где использование других типов не представляется возможным.
Вид вольт-амперной характеристики делит рассматриваемые элементы на линейные и нелинейные. Особенность нелинейности заключается в том, что компонент меняет своё сопротивление в зависимости от следующих характеристик:
- напряжения (варисторы);
- температуры (терморезисторы);
- уровня магнитного поля (магниторезисторы);
- величины освещённости (фоторезисторы);
- коэффициента деформации (тензорезисторы).
Нелинейность вольт-амперной характеристики расширило возможности их применения.
Способ монтажа может быть:
- печатным;
- навесным;
- интегрированным.
При печатном монтаже выводы детали вставляются в отверстие на плате, после чего припаиваются к контактной дорожке панели. Такой способ установки автоматизирован, и пайка происходит путём погружения контактных площадок в ванну с припоем.
Навесной монтаж, в большинстве своём, ручной. Выводы соединяемых деталей сначала скручиваются между собой, потом спаиваются для улучшения контакта. Сама пайка не предназначена для выдерживания механических нагрузок.
Интегрированный монтаж проводится в процессе изготовления кристаллов микросхем.
Как рассчитать ток?
Наш расчет мощности также работает как калькулятор тока, поскольку он касается простой формулы тока. Когда указаны напряжение (В) и расчет сопротивления, вам следует использовать формулу для расчет тока по мощности. Вы можете рассчитать ток по данной формуле!
Текущая формула:
[Ток (I) = Напряжение (В) ÷ Сопротивление (R)] I (А) = В (В) ÷ R (Ом)
Например:
Найдите ток, протекающий через резистор 3 Ом, когда к нему приложена разность потенциалов 30 В.
Решение: Ток (I) = V ÷ R; I = 30 В ÷ 3 Ом; I = 10 А
Зависимость сопротивления от температуры
Использование резисторов, как термометров, обусловлено почти линейной зависимостью их сопротивления от температуры. Это касается тех резисторов, у которых в качестве резистивного материала используется проволока или металл. Формула зависимости:
R = R0+α(t-t0),
- α – температурный коэффициент, К-1;
- R0 – сопротивление проводника при 00К;
- t0 – температура проводника при 00К.
Речь идёт о значении температуры в Кельвинах. При температурах, приближающихся к нулю по Кельвину (-273°С), у множества металлов при охлаждении R скачком падает до нулевой отметки. В этом случае можно говорить о сверхпроводимости.
Интересно. Металлы, имеющие хорошую проводимость при нормальной температуре, могут не быть сверхпроводниками при критической отметки этой физической величины. Сверхпроводники в нормальном состоянии имеют сопротивление большее, чем традиционные тоководы: медные, серебряные или золотые.
При нагревании проводников изменение сопротивления происходит в основном за счёт изменения его удельного значения и имеет линейную зависимость.
как найти сопротивление?
расчет мощности также называют калькулятором сопротивления, поскольку он помогает рассчитать расчет сопротивления. Когда даны напряжение (В) и ток (I), вы можете определить сопротивление, используя простую формулу для сопротивления.
Формула сопротивления:
[Сопротивление (R) = Напряжение (В) ÷ Ток (I)] R (Ом) = В (вольты) ÷ I (амперы)
Например:
Найдите значение неизвестного резистора, которое падает на 5 В при протекании через него тока 20 мА.
Решение: Сопротивление (R) = Напряжение (В) ÷ Ток (I) в амперах; R = 5 В ÷ 20 мА; R = 250 Ом
Физика явления в электролитах и её применение
Сопротивление проводящих жидкостей — электролитов — определяется наличием и концентрацией ионов различных знаков — атомов или молекул, потерявших или присоединивших электроны. Такие ионы при недостатке электронов называются катионами, при избытке электронов — анионами. При приложении внешнего электрического поля (помещении в электролит электродов с разностью потенциалов) катионы и анионы приходят в движение; физика процесса заключается в разрядке или зарядке ионов на соответствующем электроде. При этом на аноде анионы отдают излишние электроны, а на катоде катионы получают недостающие.
Гальваническое покрытие хромом пластмассовой душевой головки. На внутренней стороне, не покрытой хромом, виден тонкий красный слой меди.
Существенным отличием электролитов от металлов, полупроводников и газов является перемещение вещества в электролитах. Это свойство широко используется в современной технике и медицине — от очистки металлов от примесей (рафинирование) до внедрения лекарственных средств в больную область (электрофорез). Сверкающей сантехнике наших ванн и кухонь мы обязаны процессам гальваностегии – никелированию и хромированию. Излишне вспоминать, что качество покрытия достигается именно благодаря управлению сопротивлением раствора и его температурой, а также многими другими параметрами процесса осаждения металла.
Поскольку человеческое тело с точки зрения физики представляет собой электролит, применительно к вопросам безопасности существенную роль играет знание о сопротивлении тела человека протеканию электрического тока. Хотя типичное значение сопротивления кожи составляет около 50 кОм (слабый электролит), оно может варьироваться в зависимости от психоэмоционального состояния конкретного человека и условий окружающей среды, а также площади контакта кожи с проводником электрического тока. При стрессе и волнении или при нахождении в некомфортных условиях оно может значительно снижаться, поэтому для расчётов сопротивления человека в технике безопасности принято значение 1 кОм.
Любопытно, что на основе измерения сопротивления различных участков кожи человека, основан метод работы полиграфа — «детектора» лжи, который, наряду с оценкой многих физиологических параметров, определяет, в частности, отклонение сопротивления от текущих значений при задавании испытуемому «неудобных» вопросов. Правда этот метод ограниченно применим: он даёт неадекватные результаты при применении к людям с неустойчивой психикой, к специально обученным агентам или к людям с аномально высоким сопротивлением кожи.
В известных пределах к току в электролитах применим закон Ома, однако, при превышении внешнего прилагаемого электрического поля некоторых характерных для данного электролита значений, его сопротивление также носит нелинейный характер.
Многие все еще предпочитают ламповые усилители за их теплый, так называемый «ламповый звук». Этот компактный ламповый усилитель для гитары Jolida Glass FX 10 выполнен на лампах 6Н2П и 6П14П российского производства.
Физика явления в диэлектриках и её применение
Сопротивление диэлектриков весьма высоко, и это качество широко используется в физике и технике при применении их в качестве изоляторов. Идеальным диэлектриком является вакуум и, казалось бы, о каком сопротивлении в вакууме может идти речь? Однако, благодаря одной из работ Альберта Эйнштейна о работе выхода электронов из металлов, которая незаслуженно обойдена вниманием журналистов, в отличие от его статей по теории относительности, человечество получило доступ к технической реализации огромного класса электронных приборов, ознаменовавших зарю радиоэлектроники, и по сей день исправно служащих людям.
Магнетрон 2М219J, установленный в бытовой микроволновой печи
Согласно Эйнштейну, любой проводящий материал окружён облаком электронов, и эти электроны, при приложении внешнего электрического поля, образуют электронный луч. Вакуумные двухэлектродные приборы обладают различным сопротивлением при смене полярности приложенного напряжения. Раньше они использовались для выпрямления переменного тока. Трёх- и более электродные лампы использовались для усиления сигналов. Теперь они вытеснены более выгодными с энергетической точки зрения транзисторами.
Однако осталась область применения, где приборы на основе электронного луча совершенно незаменимы — это рентгеновские трубки, применяемые в радиолокационных станциях магнетроны и другие электровакуумные приборы. Инженеры и по сей день всматриваются в экраны осциллографов с электронно-лучевыми трубками, определяя характер происходящих физических процессов, доктора не могут обойтись без рентгеновских снимков, и все мы ежедневно пользуемся микроволновыми печами, в которых стоят СВЧ-излучатели — магнетроны.
Поскольку характер проводимости в вакууме носит только электронный характер, сопротивление большинства электровакуумных приборов подчиняется закону Ома.
Резисторы поверхностного монтажа
как найти мощность?
Приведенный выше калькулятор поможет как найти мощность по простой формуле мощности. Если указаны напряжение и расчет тока по мощности, то можно легко рассчитать значение мощности.
Формула силы:
Мощность (P) = Напряжение (В) * Ток (I)
Например:
Если приложение падения напряжения 15 на резисторе приводит к протеканию через него тока 10 мА, то как оценить рассеиваемую на нем мощность.
Решение: P = V * I; P = 15 В * 10 мА; P = 0,15 Вт
Что ж, пора узнать об ограничениях закона Ома.
