Площадь ромба можно вычислить разными способами.
Например, через половину произведения двух диагоналей
друг на друга, через синус и сторону в квадрате…
Также, площадь ромба равна площади параллелограмма.
Как следствие, так, как ромб является параллелограммом, с
равными сторонами, поэтому площадь ромба
можно найти через площадь параллелограмма.
Для ромба истинны и верны все свойства параллелограмма.
Формула площади ромба и формула
площади параллелограмма одинаковая.
Ромб — параллелограмм, у которого
все четыре стороны равны.
Формулировка площади ромба через параллелограмм:
Площадь ромба равна произведению
высоты на основание.
Формула площади ромба через параллелограмм:
( S = ah )
a — основание; h — высота;
Площадь ромба, можно также найти другим способом. Для
этого мысленно разделим ромба на четыре треугольника,
так чтобы каждая вершина была соединена с противоположной
вершиной. Получившиеся линии называют диагоналями. Если
известны длины двух диагоналей ромба, то можно найти площадь.
Диагонали ромба являются биссектрисами его углов, кроме этого,
пересекаются под углом 90 градусов.
Формулировка площади ромба через две диагонали:
Площадь ромба равна половине произведения
одной диагонали на другую.
Формула площади ромба через две диагонали:
( S = frac{1}2d_1 d_2 )
d1 и d2 — диагонали;
В самых редких случаях, если известен синус и одна из сторон,
используют формулу площади ромба через синус и квадрат стороны.
Формулировка площади ромба через синус и сторону в квадрате:
Площадь ромба равна произведению квадрата стороны
на синус угла прилежащего к этой стороне.
Формула площади ромба через синус и сторону в квадрате:
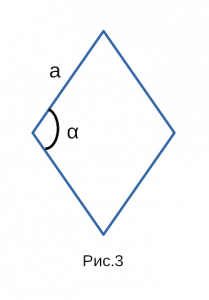
( S = a^2sinalpha )
a — сторона; sin α — синус угла;
Рис. 1 — площадь ромба через площадь параллелограмма / основание и высоту.
Рис. 2 — площадь ромба через две диагонали
Рис. 3 — площадь ромба через синус и сторону в квадрате
Также, вы можете прочитать про свойства и признаки ромба.
Приветствую Вас, уважаемые читатели!
В школьном курсе геометрии 7-9 класс, очень много формул площадей различных фигур, которые необходимо знать, для успешного прохождения итоговой аттестации и при обучении в 8-9 классе.
После прочтения, Вы поймете, как эти формулы зависят друг от друга, и какие нужно знать, а какие можно просто вывести из других.
В 8 классе учащиеся начинают знакомится с четырехугольниками (параллелограммом, ромбом, прямоугольником, квадратом, трапецией). Все формулы для этих фигур схожие. Нужно знать только три основные формулы, с помощью которые находят площадь параллелограмма.
Третья формула дается в курсе геометрии 9 класса, а вот вторая формула практически не используется в учебнике геометрии, хотя на нее есть задания в ОГЭ.
От всех формул, которые приведены выше, выводятся все остальные формулы, и легко понять, почему у той или иной фигуры такая формула, а не другая.
Рассмотрим фигуры подробней.
1) Ромб – это параллелограмм, у которого все стороны равны. Значит, все формулы, что есть в параллелограмме, используются для ромба.
Формула нахождения ромба через диагонали, в учебнике не выделена, ее нужно доказать из задачи. Но как вы видите. все формулы, которые есть в ромбе, это формулы параллелограмма.
2) Прямоугольник. Прямоугольник – это параллелограмм, у которого все углы равны. Именно поэтому прямоугольник, с которым дети знакомятся еще в младших классах, имеет формулу нахождения площади S=ab.
В 8 классе, учащиеся узнают, что Sin90=1 (синус 90 градусов равен 1), поэтому, взяв третью формулу, мы получаем, что площадь прямоугольника равна S=ab (площадь прямоугольника равна, произведению длин его смежных сторон).
Вторая формула для параллелограмма используется так же и для прямоугольника. Но в прямоугольнике, диагонали равны, поэтому формула упрощается, и мы получаем, что площадь прямоугольника равна половине произведения квадрата диагонали. Эту формулу покажу в квадрате.
3) Квадрат – это параллелограмм у которого все стороны и углы равны.
Если мы проведем диагональ в параллелограмме, прямоугольнике или ромбе, то получим два равных треугольника. Площадь любого треугольника будет равна половине площади параллелограмма, но мы сможем использовать только первую и третью формулу, поскольку диагоналей в треугольнике нет.
Следующая фигура – это трапеция. Трапеция – это четырехугольник, у которого две стороны параллельны (называются основания), а две другие не параллельны (боковые стороны).
Формулы нахождения площади для трапеции, состоит из двух формул площади треугольника, которые в свою очередь вывели из параллелограмма.
Так же площадь трапеции, можно найти с помощью второй формулы параллелограмма, через диагонали.
Эта формула, универсальная, для любого выпуклого четырехугольника (четырехугольник, все стороны которого лежат по одну сторону от прямой, соединяющий две его соседние вершины)
Это основные формулы, которые могут вам встретить на ОГЭ по математике в 17 и 18 задании.
Видео объяснение этого материала, можешь посмотреть ниже:
Спасибо, что прочитали. Вы меня очень поддержите, если поставите класс и подпишитесь на мой блог.
Формулы параллелограмма, трапеции, квадрата, прямоугольника и ромба
Анна Кирпиченкова
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Понятие четырехугольника
Введем для начала понятие многоугольника вообще.
Определение 1
Многоугольником называется геометрическая фигура в плоскости, которая состоит из попарно соединенных между собой отрезков, соседние из которых не лежат на одной прямой.
При этом отрезки называются сторонами многоугольника, а их концы — вершинами многоугольника.
Определение 2
Четырехугольником называется многоугольник, у которого $4$ вершины.
Четырехугольники могут быть выпуклыми и невыпуклыми.
Определение 3
Если четырехугольник всегда будет лежать по одну сторону от любой прямой, проходящей через его стороны, то он называется выпуклым (рис. 1).
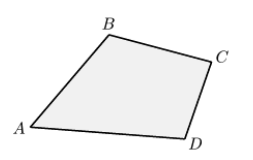
Рисунок 1. Выпуклый четырехугольник
Определение 4
Если четырехугольник лежит по разные стороны хотя бы одной прямой, проходящей через его стороны, то он называется невыпуклым (рис. 2).
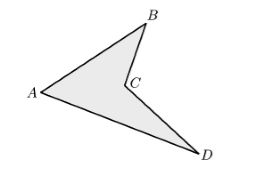
Рисунок 2. Невыпуклый четырехугольник
Классическими примерами выпуклых четырехугольников являются квадрат, прямоугольник, трапеция, ромб, параллелограмм. Рассмотрим далее эти фигуры по отдельности.
Параллелограмм
Определение 5
Параллелограмм — это четырехугольник, в котором противоположные стороны параллельны между собой (рис. 3).
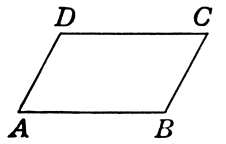
Рисунок 3. Параллелограмм
[P=2(a+b)] [S=ah] [S=absinalpha ]
Трапеция
Определение 6
Трапеция — это четырехугольник, в котором две противоположные стороны параллельны между собой, а другие две противоположные стороны не параллельны между собой (рис. 4).
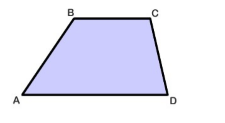
Рисунок 4. Трапеция
[S=frac{1}{2}(a+b)h]
«Формулы параллелограмма, трапеции, квадрата, прямоугольника и ромба» 👇
Квадрат
Определение 7
Прямоугольник, у которого все его четыре стороны равны между собой, называется квадратом (рис. 5).
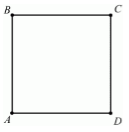
Рисунок 5. Квадрат
[P=4a] [S=a^2]
Прямоугольник
Определение 8
Параллелограмм, у которого есть прямой угол, называется прямоугольником (рис. 6).

Рисунок 6. Прямоугольник
[P=2(a+b)] [S=ab]
Ромб
Определение 9
Параллелограмм, у которого все его четыре стороны равны между собой, называется ромбом (рис. 7).
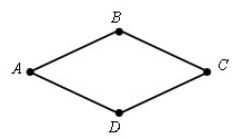
Рисунок 7. Ромб
[P=4a] [S=ah] [S=a^2sinalpha ]
Пример задачи
Пример 1
Найти площадь ромба, диагонали которого равняются $8$ см и $6$ см.
Решение.
Рассмотрим ромб $ABCD$, диагонали которого пересекаются в точке $O$ (рис. 8).
Найдем его площадь по следующей формуле $S=a^2sinalpha $.
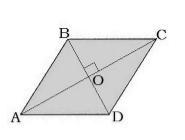
Рисунок 8.
Так как диагонали ромб делятся пополам их точкой пересечения и перпендикулярны друг другу и являются биссектриссами, то $triangle ABO$ — прямоугольный с катетами, равными $3$ см и $4$ см. По теореме Пифагора
[a^2=9+16] [a^2=25] [a=5]
По определениям синуса и косинуса, имеем
[sinBAO=frac{BO}{AB}=frac{3}{5}=0,6, cosBAO=frac{AO}{AB}=frac{4}{5}=0,8 ]
Тогда
[sinalpha =2sinBAOcosBAO=2cdot 0,6cdot 0,8=0,96] [S=5^2cdot 0,96=24]
Ответ: $24.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 12.05.2023
Ромб. Формулы, признаки и свойства ромба
Определение.
Ромб — это параллелограмм, который имеет равные стороны. Если у ромба все углы прямые, тогда он называется квадратом.
Ромбы отличаются между собой размером стороны и размером углов.
Признаки ромба
Параллелограмм ABCD будет ромбом, если выполняется хотя бы одно из следующих условий:
1. Две его смежные стороны равны (отсюда следует, что все стороны равны):
АВ = ВС = СD = AD
2. Его диагонали пересекаются под прямым углом:
AC┴BD
3. Одна из диагоналей (биссектриса) делит содержащие её углы пополам:
∠BAC = ∠CAD или ∠BDA = ∠BDC
4. Если все высоты равны:
BN = DL = BM = DK
5. Если диагонали делят параллелограмм на четыре равных прямоугольных треугольника:
Δ ABO = Δ BCO = Δ CDO = Δ ADO
6. Если в параллелограмм можно вписать круг.
Основные свойства ромба
2. Диагонали перпендикулярны:
AC┴BD
3. Диагонали являются биссектрисами его углов:
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре:
AC2 + BD2 = 4AB2
5. Точка пересечения диагоналей называется центром симметрии ромба.
6. В любой ромб можно вписать окружность.
7. Центром окружности вписанной в ромб будет точка пересечения его диагоналей.
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
2. Формула стороны ромба через площадь и синус угла:
3. Формула стороны ромба через площадь и радиус вписанной окружности:
4. Формула стороны ромба через две диагонали:
5. Формула стороны ромба через диагональ и косинус острого угла (cos α) или косинус тупого угла (cos β):
6. Формула стороны ромба через большую диагональ и половинный угол:
7. Формула стороны ромба через малую диагональ и половинный угол:
8. Формула стороны ромба через периметр:
Диагонали ромба
Определение.
Диагональю ромба называется любой отрезок соединяющий две вершины противоположных углов ромба.
Ромб имеет две диагонали – длинную d1, и короткую – d2
Формулы определения длины диагонали ромба:
1. Формулы большой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d1 = a√2 + 2 · cosα
d1 = a√2 – 2 · cosβ
2. Формулы малой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d2 = a√2 + 2 · cosβ
d2 = a√2 – 2 · cosα
3. Формулы большой диагонали ромба через сторону и половинный угол:
d1 = 2a · cos(α/2)
d1 = 2a · sin(β/2)
4. Формулы малой диагонали ромба через сторону и половинный угол:
d2 = 2a · sin(α/2)
d2 = 2a · cos(β/2)
5. Формулы диагоналей ромба через сторону и другую диагональ:
d1 = √4a2 – d22
d2 = √4a2 – d12
6. Формулы диагоналей через тангенс острого tgα или тупого tgβ угла и другую диагональ:
d1 = d2 · tg(β/2)
d2 = d1 · tg(α/2)
7. Формулы диагоналей через площадь и другую диагональ:
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
Периметр ромба
Определение.
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Формула периметра ромба через сторону ромба:
P = 4a
Площадь ромба
Определение.
Площадью ромба называется пространство ограниченное сторонами ромба, т.е. в пределах периметра ромба.
Формулы определения площади ромба:
1. Формула площади ромба через сторону и высоту:
S = a · ha
2. Формула площади ромба через сторону и синус любого угла:
S = a2 · sinα
3. Формула площади ромба через сторону и радиус:
S = 2a · r
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла (tgα) или малую диагональ и тангенс тупого угла (tgβ):
Окружность вписанная в ромб
Определение.
Кругом вписанным в ромб называется круг, который примыкает ко всем сторонам ромба и имеет центр на пересечении диагоналей ромба.
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
6. Формула радиуса круга вписанного в ромб через две диагонали:
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Формулы площади. Площадь треугольника, квадрата, прямоугольника, ромба, параллелограмма, трапеции, круга, эллипса.
Формулы площади. Площадь треугольника, квадрата, прямоугольника, ромба, параллелограмма, трапеции, круга, эллипса.
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Онлайн калькуляторы для вычисления площадей плоских фигур
Формулы площади треугольника
-
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты -
Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p — a)(p — b)(p — c)
-
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. -
Формула площади треугольника по трем сторонам и радиусу описанной окружности
-
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.где S — площадь треугольника,
a, b, c — длины сторон треугольника,
h — высота треугольника,
γ — угол между сторонами a и b,
r — радиус вписанной окружности,
R — радиус описанной окружности,p = a + b + c — полупериметр треугольника. 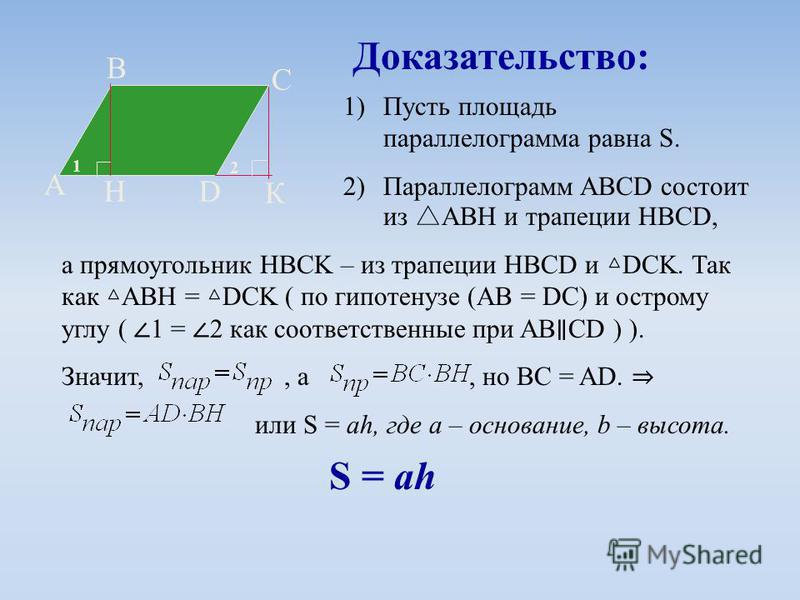
2
Вы можете воспользоваться онлайн калькулятором для расчета площади треугольника.
Формулы площади квадрата
-
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.S = a2
-
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.где S — площадь квадрата,
a — длина стороны квадрата,
d — длина диагонали квадрата.
Вы можете воспользоваться онлайн калькулятором для расчета площади квадрата.
Формулы площади параллелограмма
-
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
S = a · h
-
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
S = a · b · sin α
-
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.где S — Площадь параллелограмма,
a, b — длины сторон параллелограмма,
h — длина высоты параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма.
Вы можете воспользоваться онлайн калькулятором для расчета площади параллелограмма.
Формулы площади ромба
-
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.S = a2 · sin α
-
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.где S — Площадь ромба,
a — длина стороны ромба,h — длина высоты ромба,
α — угол между сторонами ромба,
d1, d2 — длины диагоналей.
Вы можете воспользоваться онлайн калькулятором для расчета площади ромба.
Формулы площади трапеции
-
Формула Герона для трапеции
S = a + b √(p-a)(p-b)(p-a-c)(p-a-d) |a — b| -
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высотугде S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,p = a + b + c + d — полупериметр трапеции. 2
Вы можете воспользоваться онлайн калькулятором для расчета площади трапеции.
Формулы площади выпуклого четырехугольника
-
Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
где S — площадь четырехугольника,
d1, d2 — длины диагоналей четырехугольника,
α — угол между диагоналями четырехугольника. -
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
S = p · r
-
Формула площади четырехугольника по длине сторон и значению противоположных углов
S = √(p — a)(p — b)(p — c)(p — d) — abcd cos2θ
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d2 — полупериметр четырехугольника,
θ = α + β2 — полусумма двух противоположных углов четырехугольника.
-
Формула площади четырехугольника, вокруг которого можно описать окружность
S = √(p — a)(p — b)(p — c)(p — d)
Вы можете воспользоваться онлайн калькулятором для расчета площади четырехугольника.
Формулы площади круга
-
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.S = π r2
-
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.где S — Площадь круга,
r — длина радиуса круга,
d — длина диаметра круга.
Вы можете воспользоваться онлайн калькулятором для расчета площади круга.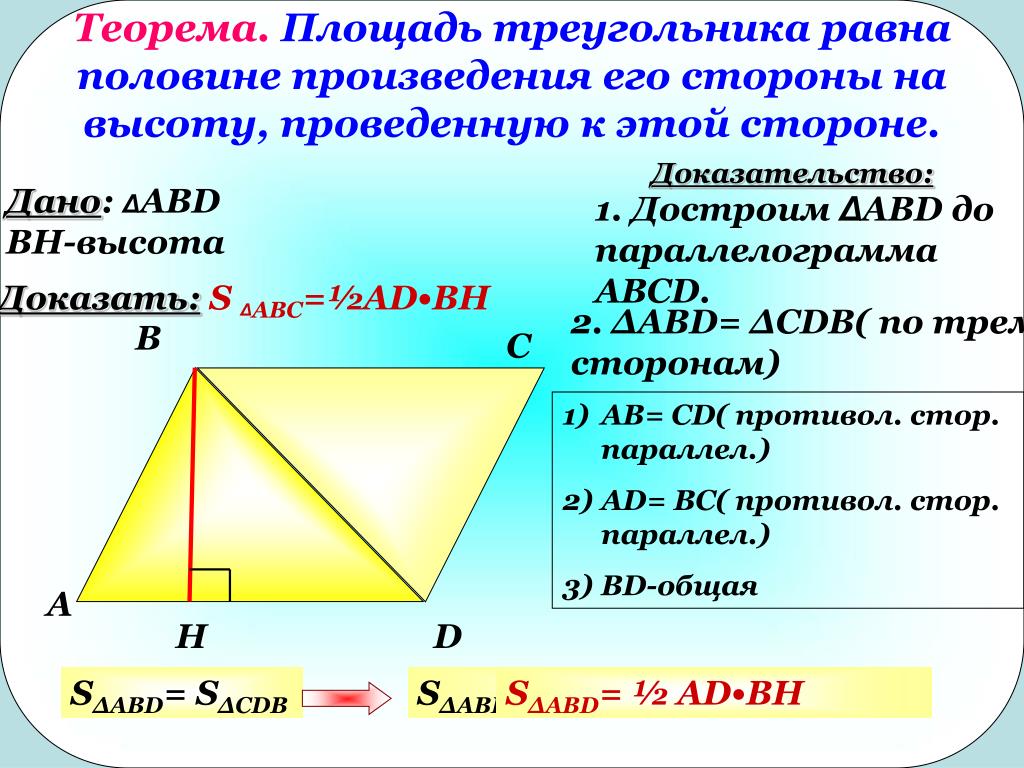
Все таблицы и формулы
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Справочник по математике | Геометрия (Планиметрия) | Четырехугольники |
| Формулы для площадей четырехугольников |
| Вывод формул для площадей четырехугольников |
| Вывод формулы Брахмагупты для площади вписанного четырехугольника |
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
S = ab,
которая позволяет найти площадь прямоугольникапрямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
| Четырехугольник | Рисунок | Формула площади | Обозначения |
| Прямоугольник | S = ab |
a и b – смежные стороны |
|
|
Посмотреть вывод формулы |
d – диагональ, |
||
|
S = 2R2 sin φ Получается из верхней формулы подстановкой d=2R |
R – радиус описанной окружности, |
||
| Параллелограмм |
S = a ha Посмотреть вывод формулы |
a – сторона, |
|
|
S = absin φ Посмотреть вывод формулы |
a и b – смежные стороны, |
||
|
Посмотреть вывод формулы |
d1, d2 – диагонали, φ – любой из четырёх углов между ними |
||
| Квадрат | S = a2 |
a – сторона квадрата |
|
| S = 4r2 |
r – радиус вписанной окружности |
||
|
Посмотреть вывод формулы |
d – диагональ квадрата |
||
|
S = 2R2 Получается из верхней формулы подстановкой d = 2R |
R – радиус описанной окружности |
||
| Ромб |
S = a ha Посмотреть вывод формулы |
a – сторона, |
|
|
S = a2 sin φ Посмотреть вывод формулы |
a – сторона, |
||
|
Посмотреть вывод формулы |
d1, d2 – диагонали |
||
|
S = 2ar Посмотреть вывод формулы |
a – сторона, |
||
|
Посмотреть вывод формулы |
r – радиус вписанной окружности, |
||
| Трапеция |
Посмотреть вывод формулы |
a и b – основания, |
|
| S = m h |
m – средняя линия, |
||
|
Посмотреть вывод формулы |
d1, d2 – диагонали, φ – любой из четырёх углов между ними |
||
|
Посмотреть вывод формулы |
a и b – основания, |
||
| Дельтоид | S = ab sin φ |
a и b – неравные стороны, |
|
|
a и b – неравные стороны, |
|||
|
S = (a + b) r Посмотреть вывод формулы |
a и b – неравные стороны, |
||
|
Посмотреть вывод формулы |
d1, d2 – диагонали |
||
| Произвольный выпуклый четырёхугольник |
Посмотреть вывод формулы |
d1, d2 – диагонали, φ – любой из четырёх углов между ними |
|
| Вписанный четырёхугольник |
, Посмотреть вывод формулы Брахмагупты |
a, b, c, d – длины сторон четырёхугольника, Формулу называют «Формула Брахмагупты» |
| Прямоугольник | |
|
S = ab где |
|
|
где Посмотреть вывод формулы |
|
|
S = 2R2 sin φ где Формула получается из верхней формулы подстановкой d = 2R |
|
| Параллелограмм | |
|
S = a ha где Посмотреть вывод формулы |
|
|
S = absin φ где Посмотреть вывод формулы |
|
|
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
|
| Квадрат | |
| S = a2
где |
|
| S = 4r2
где |
|
|
где Посмотреть вывод формулы |
|
|
S = 2R2 где Получается из верхней формулы подстановкой d = 2R |
|
| Ромб | |
|
S = a ha где Посмотреть вывод формулы |
|
|
S = a2 sin φ где Посмотреть вывод формулы |
|
|
где Посмотреть вывод формулы |
|
|
S = 2ar где Посмотреть вывод формулы |
|
|
где Посмотреть вывод формулы |
|
| Трапеция | |
|
где Посмотреть вывод формулы |
|
|
S = m h где |
|
|
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
|
|
где Посмотреть вывод формулы |
|
| Дельтоид | |
|
S = ab sin φ где |
|
|
где |
|
|
S = (a + b) r где Посмотреть вывод формулы |
|
|
где Посмотреть вывод формулы |
|
| Произвольный выпуклый четырёхугольник | |
|
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
|
| Вписанный четырёхугольник | |
|
, где Формулу называют «Формула Брахмагупты» Посмотреть вывод формулы Брахмагупты |
| Прямоугольник |
|
S = ab где |
|
где Посмотреть вывод формулы |
|
S = 2R2 sin φ где Формула получается из верхней формулы подстановкой d = 2R |
| Параллелограмм |
|
S = a ha где Посмотреть вывод формулы |
|
S = absin φ где Посмотреть вывод формулы |
|
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Квадрат |
|
S = a2 где |
|
S = 4r2 где |
|
где Посмотреть вывод формулы |
|
S = 2R2 где Получается из верхней формулы подстановкой d = 2R |
| Ромб |
|
S = a ha где Посмотреть вывод формулы |
|
S = a2 sin φ где Посмотреть вывод формулы |
|
где Посмотреть вывод формулы |
|
S = 2ar где Посмотреть вывод формулы |
|
где Посмотреть вывод формулы |
| Трапеция |
|
где Посмотреть вывод формулы |
|
S = m h где |
|
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
|
где Посмотреть вывод формулы |
| Дельтоид |
|
S = ab sin φ где |
|
где |
|
S = (a + b) r где Посмотреть вывод формулы |
|
где Посмотреть вывод формулы |
| Произвольный выпуклый четырёхугольник |
|
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Вписанный четырёхугольник |
|
где Формулу называют «Формула Брахмагупты» Посмотреть вывод формулы Брахмагупты |
Вывод формул для площадей четырехугольников
Утверждение 1.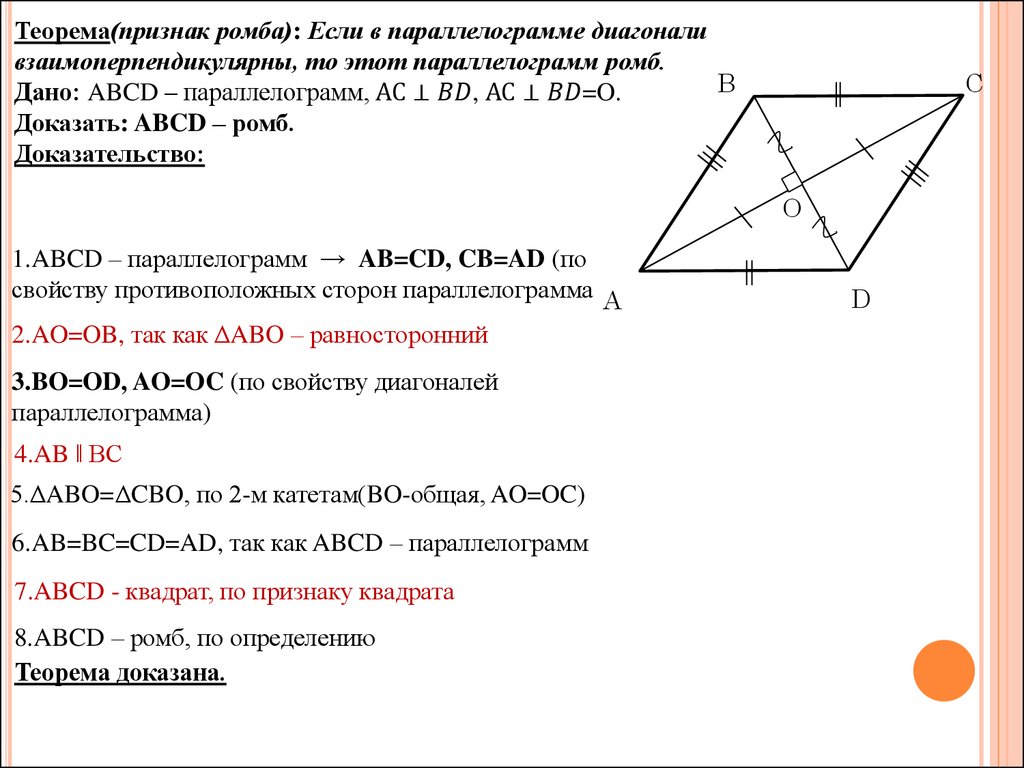 Площадь выпуклого четырёхугольника можно найти по формуле
Площадь выпуклого четырёхугольника можно найти по формуле
где d1 и d2 – диагонали четырёхугольника, а φ – любой из четырёх углов между ними (рис. 1).
Рис. 1
Доказательство. В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2. Площадь параллелограммапараллелограмма можно найти по формуле
S = a ha ,
где a – сторона параллелограмма, а ha – высотавысотавысота, опущенная на эту сторону (рис. 2).
Рис. 2
Доказательство. Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
SABCD = SAEFD = a ha ,
что и требовалось доказать.
Утверждение 3.Площадь параллелограмма параллелограмма можно найти по формуле
S = ab sin φ,
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
Рис. 3
Доказательство. Поскольку
ha = b sin φ,
то, в силу утверждения 2, справедлива формула
S = a ha = ab sin φ,
что и требовалось доказать.
Утверждение 4. Площадь ромбаромба можно найти по формуле
,
где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
Рис. 4
Доказательство. Поскольку каждая из диагоналей ромба является биссектрисой угла, а каждая точка биссектрисы угла равноудалена от сторон угла, то точка пересечения диагоналей ромба равноудалена от всех сторон ромба и является центром вписанной в ромб окружности.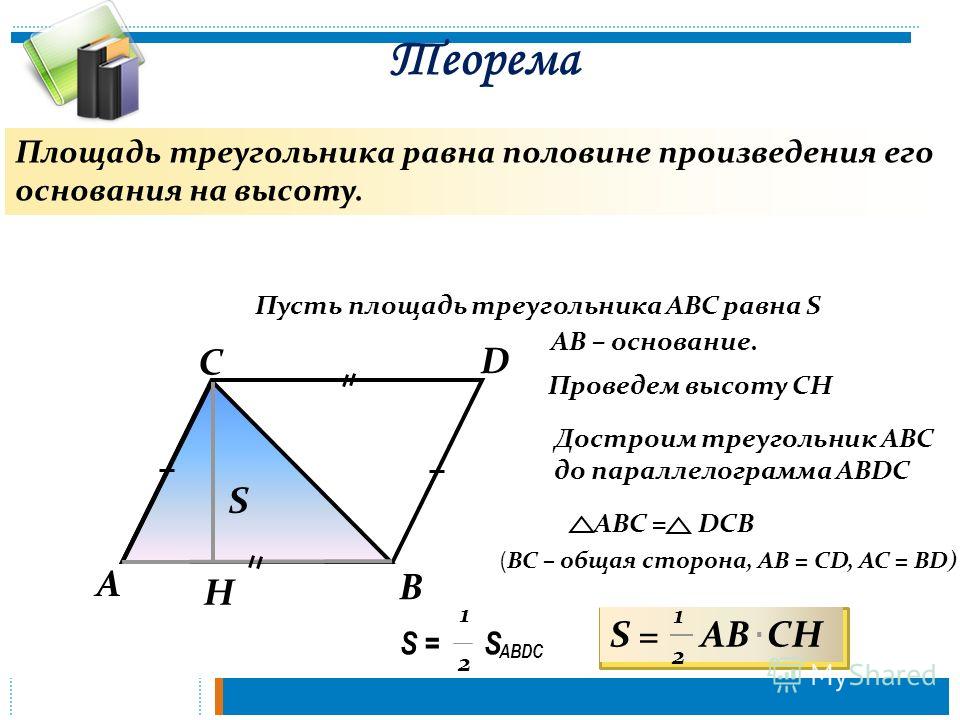 Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому
Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому
что и требовалось доказать.
Утверждение 5. Площадь трапеции можно найти по формуле
,
где a и b – основания трапеции, а h – высотавысотавысота (рис.5).
Рис. 5
Доказательство. Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD. Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF. Поэтому
что и требовалось доказать.
Утверждение 6. Площадь трапеции трапеции можно найти по формуле
,
где a и b – основания, а c и d – боковые стороны трапеции,
(рис. 6).
6).
Рис. 6
Доказательство. Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):
Следовательно,
где
,
что и требовалось доказать.
Утверждение 7. Площадь дельтоида, дельтоида, можно найти по формуле:
S = (a + b) r,
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Рис. 7
Доказательство. Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D, а биссектрисы углов A и C пересекаются в некоторой точке O, лежащей на диагонали BD. Точка O и является центром вписанной в дельтоид окружности.
Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
что и требовалось доказать.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
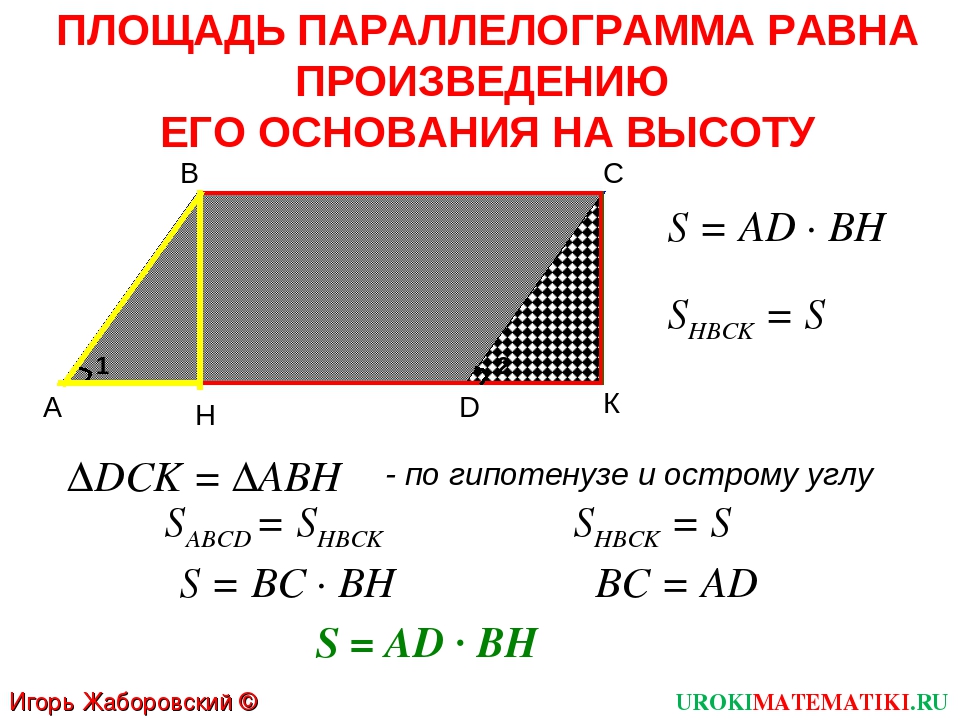
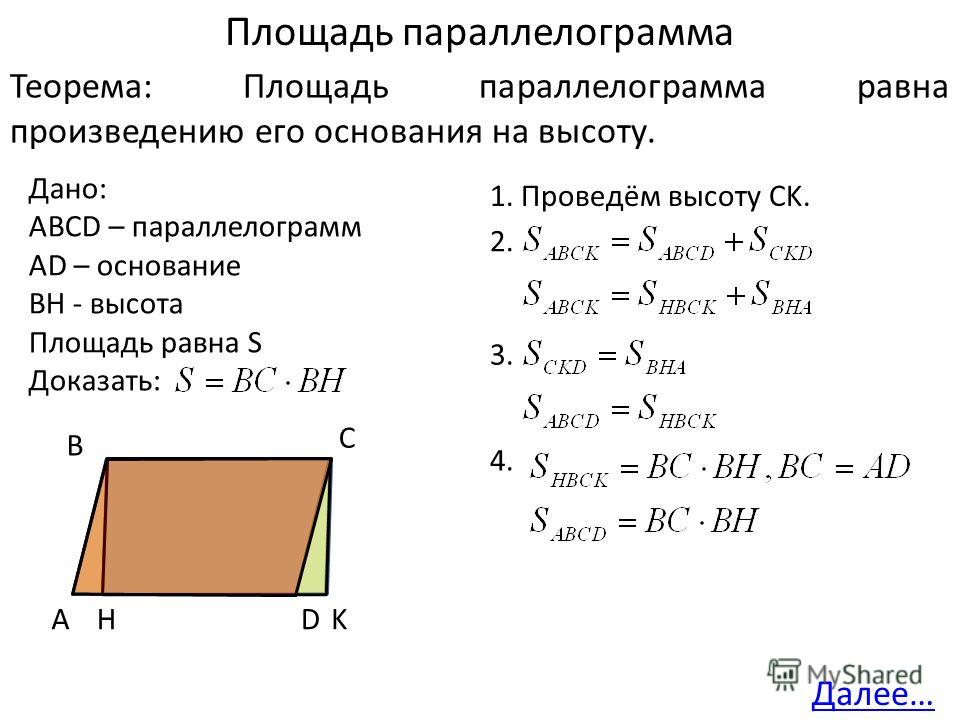
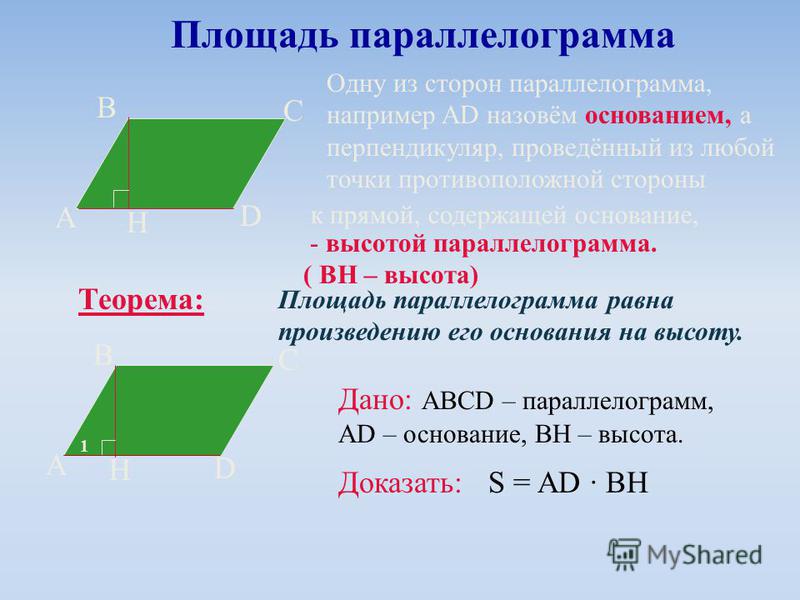
2.3 Площадь параллелограмма
Вывод
формулы площади параллелограмма сводится
к построению прямоугольника, равного
данному параллелограмму по площади.
Примем одну сторону параллелограмма
за основание, а перпендикуляр, проведенный
из любой точки противолежащей стороны
на прямую, содержащую основание будем
называть высотой параллелограмма. Тогда
площадь параллелограмма будет равна
произведению его основания на высоту.
[4, c.
254]
Теорема.
Площадь
параллелограмма равна произведению
его основания на высоту.
Доказательство.
Рассмотрим параллелограмм
с площадью.
Примем сторонуза
основание и проведем высотыи(рисунок 2. 3.1). Требуется доказать, что.
3.1). Требуется доказать, что.
Рисунок
2.3.1
Докажем
сначала, что площадь прямоугольника
также равна.
Трапециясоставлена из параллелограммаи треугольника.
С другой стороны, она составлена из
прямоугольника НВСК и треугольника.
Но прямоугольные треугольникии
равны
по гипотенузе и острому углу (их
гипотенузыиравны как противоположные стороны
параллелограмма, а углы 1 и 2 равны как
соответственные углы при пересечении
параллельных прямыхисекущей),
поэтому их площади равны. Следовательно,
площади параллелограммаи прямоугольникатакже равны, то есть площадь прямоугольникаравна.
По теореме о площади прямоугольника,
но так как,
то.
Теорема
доказана.
Пример
2.3.1.
В
ромб со стороной
и острым углом
вписана окружность. Определить площадь
четырёхугольника, вершинами которого
являются точки касания окружности со
сторонами ромба.[5, c.
150]
Решение:
Радиус
вписанной в ромб
окружности (рисунок 2. 3.2),
3.2),
поскольку
Четырёхугольникявляется прямоугольником, так как его
углы опираются на диаметр окружности.
Его площадь,
где(катет, лежащий против угла),.
Рисунок
2.3.2
Итак,
Ответ:
Пример
2.3.2.
Дан
ромб
,
диагонали которого равны 3 см и 4 см. Из
вершины тупого угла
проведены высотыиВычислить площадь четырёхугольника
Решение:
Площадь
ромба
(рисунок 2.3.3).
Рисунок
2.3.3
Далее,
из
находим(см) и, следовательно,(см). Тогда изполучим:
(см).
Итак,
Ответ:
Пример
2.3.3.
Площадь
четырёхугольника равна
Найти площадь параллелограмма, стороны
которого равны и параллельны диагоналям
четырёхугольника.
Решение:
Так
как
и(рисунок 2. 3.4), то– параллелограмм и, значит,.
3.4), то– параллелограмм и, значит,.
Рисунок
2.3.4
Аналогично
получаем
откуда следует, что.
Ответ:
.
Существует
несколько формул для вычисления площади
треугольника. Рассмотрим те, что изучаются
в школе.
Первая
формула вытекает из формулы площади
параллелограмма и предлагается учащимся
в виде теоремы. [4, c.
254]
Теорема.
Площадь треугольника равна половине
произведения его основания на высоту.
Доказательство.
Пусть
– площадь треугольника.
Примем сторонуза основание треугольника и проведем
высоту.
Докажем что:
Рисунок
2.4.1
Достроим
треугольник
до параллелограмматак, как показано на рисунке. Треугольникииравны по трем сторонам (– их общая сторона,икак противоположные стороны параллелограма),
поэтому их площади равны. Следовательно,
Следовательно,
площадь S треугольника АВС равна половине
площади параллелограмма,
т.е.
Теорема
доказана.
Важно
обратить внимание учащихся на два
следствия, вытекающих из данной теоремы.
А именно:
-
площадь
прямоугольного треугольника равна
половине произведения его катетов. -
если
высоты двух треугольников равны, то их
площади относятся как основания.
Эти
два следствия играют важную роль в
решении разного рода задач. С опорой на
данную доказывается еще одна теорема,
имеющая широкое применение при решении
задач.
Теорема.
Если
угол одного треугольника равен углу
другого треугольника, то их площади
относятся как произведения сторон,
заключающих равные углы.
Доказательство.
Пусть
и– площади треугольникови,
у которых углыиравны.
Рисунок
2. 4.2
4.2
Докажем,
что:
.
Наложим
треугольник
.
на треугольниктак, чтобы вершинасовместилась с вершиной,
а стороныиналожились соответственно на лучии.
Рисунок
2.4.3
Треугольники
иимеют общую высоту,
поэтому,.
Треугольникиитакже имеют общую высоту –,
поэтому,.
Перемножая полученные равенства, получим.
Теорема
доказана.
Вторая
формула. Площадь
треугольника равна половине произведения
двух его сторон на синус угла между
ними.
Существует несколько способов
доказательства этой формулы, и я
воспользуюсь одним из них.
Доказательство.
Из
геометрии известна теорема о том, что
площадь треугольника равна половине
произведения основания на высоту,
опущенную на это основание:
.
В
случае остроугольного треугольника
.
В случае тупого угла.
Ho,
а поэтому.
Итак, в обоих случаях.
Подставив вместов геометрической формуле площади
треугольника,
получим тригонометрическую формулу
площади треугольника:
Теорема
доказана.
Третья
формула
для площади треугольника – формула
Герона
,
названа так в честь древнегреческого
ученого Герона Александрийского, жившего
в первом веке нашей эры. Эта формула
позволяет находить площадь треугольника,
зная его стороны. Она удобна тем, что
позволяет не делать никаких дополнительных
построений и не измерять углов. Ее вывод
основывается на второй из рассмотренных
нами формул площади треугольника и
теореме косинусов:
и
.
Далее
мы должны из второй формулы (теоремы
косинусов) выразить через
сначала,
а затем ии подставить в формулу для площади.
Прежде
чем перейти к реализации этого плана,
заметим, что
Точно
так же имеем:
Теперь
выразим косинус через
и:
Так
как любой угол в треугольнике больше
и меньше,
то. Значит,.
Теперь
отдельно преобразуем каждый из
сомножителей в подкоренном выражении.
Имеем:
Значит,
Подставляя
это выражение в формулу для площади,
получаем:
Тема
«Площадь треугольника» имеет большое
значение в школьном курсе математики.
Треугольник – простейшая из геометрических
фигур. Он является «структурным элементом»
школьной геометрии. Подавляющее
большинство геометрических задач
сводятся к решению треугольников. Не
исключение и задача о нахождении площади
правильного и произвольного
n-угольника.[6,c.238]
Пример
2.4.1.
Чему
равна площадь равнобедренного
треугольника, если его основание
,
а боковая сторона?
Решение:
–равнобедренный,
Рисунок
2.4.4
Проведём
по свойству равнобедренного треугольника
–
медиана и высота. Тогда
В
по
теореме Пифагора:
Находим
площадь треугольника:
Ответ:
Пример
2.4.2.
В
прямоугольном треугольнике биссектриса
острого угла делит противоположный
катет на отрезки длиной 4 и 5 см. Определить
площадь треугольника.[7, c.
78]
Решение:
Пусть
(рисунок 2.4.5). Тогдаи(посколькуBD
–
биссектриса). Отсюда имеем
,
то есть.
Значит,
Рисунок
2.4.5
Ответ:
Пример
2.4.3.
Найти
площадь равнобедренного треугольника,
если его основание равно
,
а длина высоты, проведённой к основанию,
равна длине отрезка, соединяющего
середины основания и боковой стороны.
Решение:
По
условию,
–
средняя линия
(рисунок 2. 4.6). Так какВимеем:
или
,
откудаСледовательно,
Рисунок
2.4.6
Ответ:
формулы и факты. Формула для вычисления площади параллелограмма
Несмотря на то, что математика – царица наук, а арифметика – царица математики, самую большую сложность в изучении у школьников вызывает геометрия. Планиметрия – раздел геометрии, который изучает плоские фигуры. Одной из таких фигур является ромб. Большинство задач по решению четырехугольников сводятся к нахождению их площадей. Систематизируем известные формулы и различные способы расчета площади ромба.
Ромб – это параллелограмм, все четыре стороны которого равны. Напомним, что у параллелограмма есть четыре угла и четыре попарно параллельные равные стороны. Как любой четырехугольник, ромб имеет ряд свойств, которые сводятся к следующим: при пересечении диагонали образуют угол, равный 90 градусов (AC ⊥ BD), точка пересечения делит каждую на два равных отрезка. Диагонали ромба также являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.). Отсюда следует, что они делят ромб на четыре равных прямоугольных треугольника. Сумма длин диагоналей, возведенных во вторую степень, равна длине стороны во второй степени, умноженной на 4, т.е. BD 2 + AC 2 = 4AB 2 .
Существует множество методов, используемых в планиметрии для расчета площади ромба, применение которых зависит от исходных данных. Если известны длина стороны и любой угол, можно воспользоваться следующей формулой: площадь ромба равна квадрату стороны, умноженному на синус угла. Из курса тригонометрии известно, что sin (π – α) = sin α, а значит, в расчетах можно использовать синус любого угла – как острого, так и тупого. Частным случаем является ромб, у которого все углы прямые. Это квадрат. Известно, что синус прямого угла равен единице, поэтому площадь квадрата равна длине его стороны, возведенной во вторую степень.
Если величина сторон неизвестна, воспользуемся длиной диагоналей. В этом случае площадь ромба равна половине произведения большой и малой диагоналей.
При известной длине диагоналей и величине любого угла площадь ромба определяется двумя способами. Первый: площадь – это половина квадрата большей диагонали, умноженная на тангенс половины градусной меры острого угла, т.е. S = 1/2*D 2 *tg(α/2), где D – большая диагональ, α – острый угол. Если вам известен размер меньшей диагонали, воспользуемся формулой 1/2*d 2 *tg(β/2), где d – меньшая диагональ, β – тупой угол. Напомним, что мера острого угла меньше 90 градусов (меры прямого угла), а тупой угол соответственно – больше 90 0 .
Площадь ромба можно отыскать, используя длину стороны (напомним, все стороны у ромба равны) и высоты. Высота – это перпендикуляр, опущенный на противоположную углу сторону или на ее продолжение. Чтобы основание высоты располагалось внутри ромба, ее следует опускать из тупого угла.
Иногда в задаче требуется отыскать площадь ромба, исходя из данных, относящихся к вписанной окружности. В этом случае необходимо знать ее радиус. Существуют две формулы, которыми можно воспользоваться для расчета. Итак, чтобы ответить на поставленный вопрос, можно удвоить произведение стороны ромба и радиуса вписанной окружности. Другими словами, необходимо умножить диаметр вписанной окружности на сторону ромба. Если в условии задачи представлена величина угла, то площадь находится через частное между квадратом радиуса, умноженном на четыре, и синусом угла.
Как видите, существует множество способов для нахождения площади ромба. Конечно, чтобы запомнить каждый из них, потребуется терпение, внимательность и, конечно же, время. Но в дальнейшем вы сможете легко выбрать метод, подходящий для вашей задачи, и убедитесь, что геометрия – это несложно.
Определение ромба
Ромб
— это параллелограмм, в котором все стороны равны друг другу.
Онлайн-калькулятор
Если стороны ромба образуют прямой угол, то получим квадрат
.
Диагонали ромба пересекаются под прямым углом.
![]()
Диагонали ромба являются биссектрисами его углов.
Площадь ромба, как и площади большинства геометрических фигур, можно найти несколькими способами. Разберемся в их сути и рассмотрим примеры решений.
Формула площади ромба по стороне и высоте
Пусть нам дан ромб со стороной a a
a
и высотой h h
h
, проведенной к этой стороне. Так как ромб это параллелограмм, то его площадь мы находим так же, как и площадь параллелограмма.
S = a ⋅ h S=acdot h
S
=
a
⋅
h
A a
a
— сторона;
h h
h
— высота, опущенная на сторону a a
a
.
Решим простой пример.
Пример
Сторона ромба равна 5 (см.). Высота, опущенная к этой стороне, имеет длину 2 (см.). Найти площадь ромба S S
S
.
Решение
A = 5 a=5
a
=
5
h = 2 h=2
h
=
2
Пользуемся нашей формулой и вычисляем:
S = a ⋅ h = 5 ⋅ 2 = 10 S=acdot h=5cdot 2=10
S
=
a
⋅
h
=
5
⋅
2
=
1
0
(см. кв.)
Ответ:
10 см. кв.
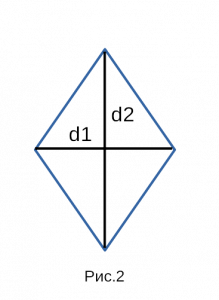
Формула площади ромба через диагонали
Здесь все так же просто. {circ})}approx73.9
S
=
sin
(α
)
4
⋅
r
2
=
sin
(6
0
∘
)
4
⋅
1
6
≈
7
3
.
9
(см. кв.)
Ответ:
73.9 см. кв.
Формула площади ромба по радиусу вписанной окружности и стороне
S = 2 ⋅ a ⋅ r S=2cdot acdot r
S
=
2
⋅
a
⋅
r
A a
a
-сторона ромба;
r r
r
— радиус вписанной окружности в ромб.
Пример
Возьмем условие из предыдущей задачи, но пусть вместо угла нам известна сторона ромба, равная 5 см.
Решение
A = 5 a=5
a
=
5
r = 4 r=4
r
=
4
S = 2 ⋅ a ⋅ r = 2 ⋅ 5 ⋅ 4 = 40 S=2cdot acdot r=2cdot5cdot4=40
S
=
2
⋅
a
⋅
r
=
2
⋅
5
⋅
4
=
4
0
(см. кв.)
Ответ:
40 см. кв.
– это параллелограмм, у которого все стороны равны.
Ромб с прямыми углами называется квадратом и считается частным случаем ромба. Найти площадь ромба можно различными способами, используя все его элементы – стороны, диагонали, высоту. Классической формулой площади ромба считается расчет значения через высоту.
Пример расчета площади ромба по этой формуле очень прост. Необходимо только подставить данные и высчитать площадь.
Площадь ромба через диагонали
Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.
Формула площади ромба через диагонали представляет собой произведение его диагоналей, разделенное на 2.
Рассмотрим пример расчета площади ромба через диагонали. Пусть дан ромб с диагоналями
d1
=5 см и d2
=4. Найдем площадь.
Формула площади ромба через стороны подразумевает и применение других элементов. Если в ромб вписана окружность, то площадь фигуры можно просчитать по сторонам и ее радиусу:
Пример расчета площади ромба через стороны также весьма прост. Требуется только просчитать радиус вписанной окружности. Его можно вывести из теоремы Пифагора и по формуле .
Площади ромба через сторону и угол
Формула площади ромба через сторону и угол используется очень часто.
Рассмотрим пример расчета площади ромба через сторону и угол.
Задача:
Дан ромб, диагонали которого равны d1
=4 см,d2
=6 см. Острый угол равен α
= 30°. Найдите площадь фигуры через сторону и угол.
Для начала найдем сторону ромба. Используем для этого теорему Пифагора. Мы знаем, что в точке пересечения диагонали делятся пополам и образуют прямой угол. Следовательно:
Подставим значения:
Теперь мы знаем сторону и угол. Найдем площадь:
В статье рассмотрим формулу площади ромба
и не одну! На картинках покажем, как легко находиться площадь ромба по простым формулам
.
Существует большое количество заданий на нахождение той или иной величины в ромбе и в этом нам помогут формулы, о которых и пойдет речь.
Ромб относится к отдельному виду четырехугольников, так как у него все стороны равны. Так же представляет частный случай параллелограмма в котором стороны АВ=ВС=СD=АD равны.
Заметка: Если Вам нужна курсовая, контрольная или дипломная работа, тогда вам на webmath. ru. или просто перейдите по ссылке заказать курсовую работу (http://www.webmath.ru/zakaz_kursovye.php).
Ромб обладает следующими свойствами:
У ромба параллельные углы равные,
— сложение двух соседних углов равно 180 градусам,
— Пересечение диагоналей под углом в 90 градусов,
— Биссектрисами ромба, приходятся его же диагонали,
— Диагональ при пересечении делится на равные части.
Ромб обладает следующими признаками:
Если у параллелограмма в котором диагонали встречаются под углом 90 градусов, то он называется ромбом.
— Если у параллелограмма в котором биссектриса это диагональ, то он называется ромбом.
— Если у параллелограмма равные стороны — это ромб.
— Если у четырехугольника равные стороны — это ромб.
— Если у четырехугольника в котором биссектриса это диагональ и диагонали встречаются под углом 90 градусов, то это ромб.
— Если у параллелограмма одинаковые высоты — это ромб.
Из вышеперечисленных признаков можно сделать вывод, что они нужны для того чтобы научиться отделять ромб от других схожих с ним фигур.
Так как в ромбе все стороны одинаковы периметр находится
по следующей формуле:
Р=4а
Площадь ромба формула
Данных формул несколько. Самая простая решается как сложение площадь 2 треугольников, которые получились в результате деления диагоналей.
С помощью второй формулы можно решать задачи с известными диагоналями ромба. В этом случае площадью ромба будет: сумма диагоналей деленная на два.
Очень просто в решении и не забудется.
Третью формулу можно использовать когда знаешь угол между сторон. Зная его можно найти площадь ромба, она будет равна квадрату сторон на синус угла. При чем нет разницы какой угол. так как синус угла имеет единое значение.
Важно помнить что измерение площади происходит в квадратах, а периметра в единицах. Данные формулы очень легко применяются на практике.
Так же могут встретиться задачи на поиск радиуса по вписанной в ромб окружности.
Для этого так же существует несколько формул:
В помощью первой формулы радиус находится как произведение диагоналей поделенное на число полученное от сложения всех сторон. либо равняется половине высоты (r=h/2).
Во второй формуле взят принцип из первой, применяется мы знаем диагонали и стороны ромба.
В третьей формуле радиус выходит из высоты меньшего из треугольников, получившегося в результате пересечения.
Ромб — это особая фигура в геометрии. Благодаря его особым свойствам, существует не одна, а несколько формул, с помощью которых вычисляется площадь ромба. Что это за свойства и какие наиболее распространенные формулы для поиска площади этой фигуры существуют? Давайте разберемся.
Какая геометрическая фигура называется ромбом
Прежде чем выяснить, чему равна площадь ромба, стоит узнать, что же это за фигура.
Ромбом со времен Евклидовой геометрии называется симметричный четырехугольник, все четыре стороны коего являются равными между собою по длине и попарно параллельными.
Происхождение термина
Название этой фигуры пришло в большинство современных языков из греческого, через посредничество латыни. «Прародителем» слова «ромб», стало греческое существительное ῥόμβος (бубен). Хотя жителям двадцатого века, привыкшим к круглым бубнам, тяжело представить их другой формы, но у эллинов эти музыкальные инструменты традиционно изготавливались не круглой, а ромбовидной формы.
В большинстве современных языков данный математический термин употребляется, как и в латыни: rombus. Однако в английском языке иногда ромбы называют diamond (алмаз или диамант). Такое прозвище данная фигура получила из-за своей особой формы, напоминающей драгоценный камень. Как правило, подобный термин используют не для всех ромбов, а только для тех, у которых угол пересечения его двух сторон равен шестидесяти или сорока пяти градусам.
Впервые эта фигура была упомянута в трудах греческого математика, жившего в первом веке новой эры — Герона Александрийского.
Какими свойствами обладает эта геометрическая фигура
Чтобы найти площадь ромба, в первую очередь нужно знать, какими особенностями обладает данная геометрическая фигура.
При каких условиях параллелограмм является ромбом
Как известно, каждый ромб является параллелограммом, но при этом не всякий параллелограмм — это ромб. Чтобы точно утверждать, что представленная фигура действительно является ромбом, а не простым параллелограммом, она должна соответствовать одному из трех основных признаков, выделяющих ромб. Или всем трем сразу.
- Диагонали параллелограмма пересекаются под углом девяносто градусов.
- Диагонали разделяют углы надвое, выступая в качестве их биссектрис.
- Не только параллельные, но и смежные стороны имеют одинаковую длину. В этом, кстати, одно из основных различий между ромбом и параллелограммом, поскольку у второй фигуры одинаковы по длине лишь параллельные стороны, но не смежные.
При каких условиях ромб является квадратом
По своим свойствам в отдельных случаях ромб одновременно может становиться квадратом. Чтобы наглядно подтвердить это утверждение, достаточно просто повернуть квадрат в любую сторону на сорок пять градусов. Получившаяся фигура окажется ромбом, каждый из углов которого равен девяноста градусам.
Также, чтобы подтвердить, что квадрат является ромбом, можно сопоставить признаки этих фигур: в обоих случаях все стороны равны, а диагонали являются биссектрисами и пересекаются под углом в девяносто градусов.
Как узнать площадь ромба с помощью его диагоналей
В современном мире в интернете можно найти практически все материалы для выполнения необходимых расчетов. Так, существует масса ресурсов, оснащенных программами для автоматического вычисления площади той или иной фигуры. Причем, если (как в случае с ромбом) есть несколько формул для этого, то есть возможность выбирать, какой из них удобнее всего будет воспользоваться. Однако, прежде всего, необходимо самим уметь вычислять площадь ромба без помощи компьютера и ориентироваться в формулах. Для ромба их существует немало, но самые известные из них четыре.
Одним из самых простых и распространенных способов узнать площадь этой фигуры, если есть информация о длине его диагоналей. Если в задаче есть эти данные, в таком случаем можно применить следующую формулу для нахождения площади: S = КМ x LN/2 (КМ и LN — это диагонали ромба KLMN).
Можно проверить достоверность этой формулы на практике. Допустим, у ромба KLMN длина одной его диагонали КМ — 10 см, а второй LN — 8 см. Тогда подставляем эти данные в указанную выше формулу, и получаем следующий результат: S = 10 х 8/ 2= 40 см 2 .
Формула для вычисления площади параллелограмма
Существует и другая формула. Как было указано выше в определении ромба, он является не просто четырехугольником, но и параллелограммом, и обладает всеми особенностями данной фигуры. В таком случае для нахождения ее площади вполне целесообразно использовать формулу, применяемую для параллелограмма: S = KL х Z. В данной случае KL — это длинна стороны параллелограмма (ромба), а Z — это длинна высоты, проведенной к данной стороне.
В отдельных задачах длина стороны не предоставлена, зато известен периметр ромба. Поскольку выше была указана формула его нахождения, с ее помощью можно узнать и длину стороны. Итак, периметр фигуры — 10 см. Длину стороны можно узнать, инвертировав формулу периметра и разделив 10 на 4. Результатом окажется 2,5 см — это и есть искомая длина стороны ромба.
Теперь стоит попробовать подставить это число в формулу, зная, что длинна высоты, проведенной к стороне, также равна 2,5 см. Теперь попробуем поставить эти значения в вышеупомянутую формулу площади параллелограмма. Получается, что площадь ромба равна S = 2,5 х 2,5 = 6,25 см 2 .
Другие способы вычисления площади ромба
Те, кто уже освоили синусы и косинусы, могут использовать для нахождения площади ромба формулы, содержащие их. Классическим примером служит следующая формула: S = КМ 2 х Sin KLM. В данном случае площадь фигуры равна произведению двух сторон ромба, умноженному на синус угла между ними. А поскольку в ромбе все стороны одинаковы, то проще сразу произвести одну сторону в квадрат, как и было показано в формуле.
Проверяем на практике данную схему, причем не просто к ромбу, а к квадрату, у которого, как известно, все углы прямые, а значит, равны девяносто градусам. Допустим, одна из сторон равна 15 см. Также известно, что синус угла в 90° равен единице. Тогда, согласно формуле, S = 15 х 15 х Sin 90°= 255х1=255 см 2.
Помимо вышеперечисленных, в отдельных случаях используется еще одна формула, с использованием синуса для определения площади ромба: S = 4 х R 2 /Sin KLM. В данном варианте используется радиус вписанной в ромб окружности. Он возносится в степень квадрата и умножается на четыре. А весь результат делиться на синус угла, близлежащего к вписанной фигуре.
В качестве примера для простоты вычислений возьмем опять квадрат (синус его угла будет всегда равен единице). Радиус вписанного в него круга — 4,4 см. Тогда площадь ромба будет вычисляться так: S= 4 х 4,4 2 / Sin 90 °= 77,44 см 2
Приведенные выше формулы нахождения радиуса ромба — далеко не единственные в своем роде, однако они являются наиболее простыми для понимания и проведения вычислений.
Как найти площадь параллелограмма. Площади фигур. Площадь параллелограмма.
Содержание
- Найти диагональ параллелограммаЗная стороны и угол
- Формула вычисления площади
- Площадь параллелограмма через диагонали
- Зная длину стороны a и длину высоты h
- Формула
- Площади фигур
- Периметр параллелограмма
- Формулы определения длины периметра параллелограмма:
- Через основание и высоту
- Высота
- Формула Герона
- Основные свойства параллелограмма
- Формулы определения длин сторон параллелограмма:
- Через стороны и угол между ними
- Площадь параллелограмма по вписанной окружности и углу между сторонами
- Площадь
- Пример
Найти диагональ параллелограммаЗная стороны и угол
Так как каждая диагональ параллелограмма делит его на два равновеликих треугольника, именно их свойства и будут использованы для выведения формулы диагонали параллелограмма.
В любом треугольнике угол и сторона, лежащие напротив, пропорциональны друг другу. Для параллелограмма это будет значить, что более длинная диагональ будет лежать напротив тупого угла, а более короткая диагональ – напротив острого.С учетом того, что стороны треугольников, полученных в результате проведения диагоналей, одинаковы – это стороны параллелограмма, значение градусной меры угла между данными сторонами определяет чему будет равна длина диагонали,вычисленной по формуле. Другими словами, если в формулудиагонали подставить значение острого угла параллелограмма, то калькулятор вычислит длину короткой диагонали, а если подставить значение тупого угла – то длинной.
Для того чтобы перейти от одного угла к другому, используется разность 180 градусов и заданного угла, таким образом калькулятор одновременно может вычислить обе диагонали.
α=180°-β
Чтобы вывести формулу диагонали параллелограмма, используется теорема косинусов в треугольнике, который диагональ образует со сторонами. В любом из подобных треугольников, диагональ является стороной, противолежащей углу параллелограмма и, соответственно, ее квадрат равен сумме квадратов двух других сторон треугольника (сторон параллелограмма, в данном случае) за вычетом удвоенного произведения тех же сторон на косинус приведенного угла. Чтобы найти длину диагонали параллелограмма, калькулятор вычисляет квадратный корень из данного выражения.
Формула вычисления площади
1. По длине стороны и высоте:
Площадь параллелограмма (S) равняется произведению длины его стороны и высоты, проведенной к ней:
S = a * h
2. По двум сторонам и углу между ними:
Площадь параллелограмма находится путем умножения длин его обеих сторон и синуса угла между ними:
S = a * b * sin α
3. По двум диагоналям и углу между ними:
Площадь параллелограмма равна одной второй произведения длин его диагоналей, умноженного на синус угла между ними:
S = 1/2 * d1 *d2 * sin α
Площадь параллелограмма через диагонали
Формула площади параллелограмма через диагонали позволяет быстро найти значение.
Для вычислений понадобится величина угла, расположенного между диагоналями.
Рассмотрим пример расчета площади параллелограмма через диагонали. Пусть дан параллелограмм с диагоналями D = 7 см, d = 5 см. Угол, лежащий между ними α=30°. Подставим данные в формулу:
Пример расчета площади параллелограмма через диагональ дал нам прекрасный результат – 8,75.
Зная формулу площади параллелограмма через диагональ можно решать множество интересных задач. Давайте рассмотрим одну из них.
Задача:
Дан параллелограмм с площадью 92 кв. см. Точка F расположена на середине его стороны ВС. Давайте найдем площадь трапеции ADFB, которая будет лежать в нашем параллелограмме. Для начала нарисуем все, что получили по условиям.
Приступаем к решению:
По нашим условиям ah =92, а соответственно, площадь нашей трапеции будет равняться
Зная длину стороны a и длину высоты h
Чему равна площадь параллелограмма если сторона
a
а высота
h
Ответ: S =
Чему равна площадь параллелограмма S если известны длина стороны a и длина высоты h, проведенной к этой стороне?
Формула
S = a⋅h
Площади фигур
| Сторона параллелограмма a | |||||||||||
| Сторона параллелограмма b | |||||||||||
| Угол в градусах между этими сторонами α | |||||||||||
| Расчет площади квадрата, прямоугольника, параллелограмма, треугольника, трапеции, ромба, круга (площадь фигур). |
|||||||||||
| Площади фигур | |||||||||||
Периметр параллелограммаОпределение. Периметром параллелограмма называется сумма длин всех сторон параллелограмма. Формулы определения длины периметра параллелограмма:1. Формула периметра параллелограмма через стороны параллелограмма: P = 2a + 2b = 2(a + b) 2. Формула периметра параллелограмма через одну сторону и две диагонали: P = 2a + √2d12 + 2d22 – 4a2 P = 2b + √2d12 + 2d22 – 4b2 3. Формула периметра параллелограмма через одну сторону, высоту и синус угла: Через основание и высоту{S= a cdot h} Формула для нахождения площади параллелограмма через основание и высоту: {S= a cdot h}, где a — основание параллелограмма, h — его высота, проведенная к основанию. ВысотаНижняя сторона параллелограмма называется его основанием, а перпендикуляр, опущенный на основание из любой точки противоположной стороны, – высотой. AD – это основание параллелограмма, h – высота. Высота выражает расстояние между противоположными сторонами, поэтому определение высоты можно сформулировать ещё так: высота параллелограмма – это перпендикуляр, опущенный из любой точки одной стороны на противоположную ей сторону. Формула ГеронаS = √p(p – a)(p – b)(p – c) Формула площади треугольника по двум сторонам и углу между ними Формула площади треугольника по трем сторонам и радиусу описанной окружности Формула площади треугольника по трем сторонам и радиусу вписанной окружности где S – площадь треугольника,
Основные свойства параллелограммаКвадрат, прямоугольник и ромб – есть параллелограммом. 1. Противоположные стороны параллелограмма имеют одинаковую длину: AB = CD, BC = AD 2. Противоположные стороны параллелограмма параллельны: AB||CD, BC||AD 3. Противоположные углы параллелограмма одинаковые: ∠ABC = ∠CDA, ∠BCD = ∠DAB 4. Сумма углов параллелограмма равна 360°: ∠ABC + ∠BCD + ∠CDA + ∠DAB = 360° 5. ∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180° 6. Каждая диагональ делит параллелограмма на два равных треугольника 7. Две диагональ делят параллелограмм на две пары равных треугольников 8. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам:
9. Точка пересечения диагоналей называется центром симметрии параллелограмма 10. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон: AC2 + BD2 = 2AB2 + 2BC2 11. Биссектрисы противоположных углов параллелограмма всегда параллельны 12. Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом (90°) Формулы определения длин сторон параллелограмма:1. a = √d12 + d22 – 2d1d2·cosγ2= √d12 + d22 + 2d1d2·cosδ2 b = √d12 + d22 + 2d1d2·cosγ2= √d12 + d22 – 2d1d2·cosδ2 2. Формула сторон параллелограмма через диагонали и другую сторону: 3. Формула сторон параллелограмма через высоту и синус угла: 4. Через стороны и угол между ними{S= a cdot b cdot sin({alpha})} Формула для нахождения площади параллелограмма через стороны и угол между ними: {S= a cdot b cdot sin({alpha})}, где a и b — стороны параллелограмма, α — угол между сторонами. Площадь параллелограмма по вписанной окружности и углу между сторонамиДанная формула применима только для параллелограммов, в которые можно вписать окружность. Таким параллелограммом может являться только ромб. r – радиус вписанной окружности α° – угол между сторонами Примечание: Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». ПлощадьДля измерения площади параллелограмма можно представить его в виде прямоугольника. Рассмотрим параллелограмм ABCD: Построенные высоты BE и CF образуют прямоугольник EBCF и два треугольника: ΔABE и ΔDCF. Параллелограмм ABCD состоит из четырёхугольника EBCD и треугольника ABE, прямоугольник EBCF состоит из того же четырёхугольника и треугольника DCF. Треугольники ABE и DCF равны (по четвёртому признаку равенства прямоугольных треугольников), значит и площади прямоугольника с параллелограммом равны, так как они составлены из равных частей. Итак, параллелограмм можно представить в виде прямоугольника, имеющего такое же основание и высоту. А так как для нахождения площади прямоугольника перемножаются длины основания и высоты, значит и для нахождения площади параллелограмма нужно поступить также: площадь ABCD = AD · BE Из данного примера можно сделать вывод, что площадь параллелограмма равна произведению его основания на высоту. S = ah где S – это площадь параллелограмма, a – основание, h – высота. ПримерДаны длина прилежащей к высоте стороны параллелограмма (b) и угол, противоположный самой высоте (a).
Пример: Обозначим наш параллелограмм буквами ABCD, высота BE проходит из угла ABC к стороне AD. Длина стороны AB равна 20 см, угол BAD равен 30 градусов. Найдите высоту. Решение:
Ответ: 10 см Источники
|
= , = ?
Найти площадь параллелограмма по сторонам. Площадь параллелограмма
Что такое параллелограмм? Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
1. Площадь параллелограмма вычисляется по формуле:
[ LARGE S = a cdot h_{a}]
где:
a – сторона параллелограмма,
h a – высота, проведенная к этой стороне.
2. Если известны длины двух смежных сторон параллелограмма и угол между ними, то площадь параллелограмма вычисляется по формуле:
[ LARGE S = a cdot b cdot sin(alpha) ]
3. Если заданы диагонали параллелограмма и известен угол между ними, то площадь параллелограмма вычисляется по формуле:
[ LARGE S = frac{1}{2} cdot d_{1} cdot d_{2} cdot sin(alpha) ]
Свойства параллелограмма
В параллелограмме противоположные стороны равны: (AB = CD )
, (BC = AD )
В параллелограмме противоположные углы равны: (angle A = angle C )
, (angle B = angle D )
Диагонали параллелограмма в точке пересечения делятся пополам (AO = OC )
, (BO = OD )
Диагональ параллелограмма делит его на два равных треугольника. {2} )
В параллелограмме угол между высотами равен его острому углу: (angle K B H =angle A )
.
Биссектрисы углов, прилежащих к одной стороне параллелограмма, взаимно перпендикулярны.
Биссектрисы двух противоположных углов параллелограмма параллельны.
Признаки параллелограмма
Четырехугольник будет параллелограммом, если:
(AB = CD )
и (AB || CD )
(AB = CD )
и (BC = AD )
(AO = OC )
и (BO = OD )
(angle A = angle C )
и (angle B = angle D )
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Вывод
формулы площади параллелограмма сводится
к построению прямоугольника, равного
данному параллелограмму по площади.
Примем одну сторону параллелограмма
за основание, а перпендикуляр, проведенный
из любой точки противолежащей стороны
на прямую, содержащую основание будем
называть высотой параллелограмма. Тогда
площадь параллелограмма будет равна
произведению его основания на высоту.
Теорема.
Площадь
параллелограмма равна произведению
его основания на высоту.
Доказательство
.
Рассмотрим параллелограмм
с площадью.
Примем сторонуза
основание и проведем высотыи(рисунок 2.3.1). Требуется доказать, что.
Рисунок
2.3.1
Докажем
сначала, что площадь прямоугольника
также равна.
Трапециясоставлена из параллелограммаи треугольника.
С другой стороны, она составлена из
прямоугольника НВСК и треугольника.
Но прямоугольные треугольникии
равны
по гипотенузе и острому углу (их
гипотенузыиравны как противоположные стороны
параллелограмма, а углы 1 и 2 равны как
соответственные углы при пересечении
параллельных прямыхисекущей),
поэтому их площади равны. Следовательно,
площади параллелограммаи прямоугольникатакже равны, то есть площадь прямоугольникаравна.
По теореме о площади прямоугольника,
но так как,
то.
Теорема
доказана.
Пример
2.3.1.
В
ромб со стороной
и острым углом
вписана окружность. Определить площадь
четырёхугольника, вершинами которого
являются точки касания окружности со
сторонами ромба.
Решение:
Радиус
вписанной в ромб
окружности (рисунок 2.3.2),
поскольку
Четырёхугольникявляется прямоугольником, так как его
углы опираются на диаметр окружности.
Его площадь,
где(катет, лежащий против угла),.
Рисунок
2.3.2
Итак,
Ответ:
Пример
2.3.2.
Дан
ромб
,
диагонали которого равны 3 см и 4 см. Из
вершины тупого угла
проведены высотыиВычислить площадь четырёхугольника
Решение:
Площадь
ромба
(рисунок 2.3.3).
Итак,
Ответ:
Пример
2.3.3.
Площадь
четырёхугольника равна
Найти площадь параллелограмма, стороны
которого равны и параллельны диагоналям
четырёхугольника.
Решение:
Так
как
и(рисунок 2.3.4), то– параллелограмм и, значит,.
Рисунок
2.3.4
Аналогично
получаем
откуда следует, что.
Ответ:
.
2.4 Площадь треугольника
Существует
несколько формул для вычисления площади
треугольника. Рассмотрим те, что изучаются
в школе.
Первая
формула вытекает из формулы площади
параллелограмма и предлагается учащимся
в виде теоремы.
Теорема.
Площадь треугольника равна половине
произведения его основания на высоту
.
Доказательство.
Пусть
– площадь треугольника.
Примем сторонуза основание треугольника и проведем
высоту.
Докажем что:
Рисунок
2.4.1
Достроим
треугольник
до параллелограмматак, как показано на рисунке. Треугольникииравны по трем сторонам (– их общая сторона,икак противоположные стороны параллелограма),
поэтому их площади равны. Следовательно,
площадь S треугольника АВС равна половине
площади параллелограмма,
т.е.
Теорема
доказана.
Важно
обратить внимание учащихся на два
следствия, вытекающих из данной теоремы.
А именно:
площадь
прямоугольного треугольника равна
половине произведения его катетов.
если
высоты двух треугольников равны, то их
площади относятся как основания.
Эти
два следствия играют важную роль в
решении разного рода задач. С опорой на
данную доказывается еще одна теорема,
имеющая широкое применение при решении
задач.
Теорема.
Если
угол одного треугольника равен углу
другого треугольника, то их площади
относятся как произведения сторон,
заключающих равные углы.
Доказательство
.
Пусть
и– площади треугольникови,
у которых углыиравны.
Рисунок
2.4.2
Докажем,
что:
.
Наложим
треугольник
.
на треугольниктак, чтобы вершинасовместилась с вершиной,
а стороныиналожились соответственно на лучии.
Рисунок
2.4.3
Треугольники
иимеют общую высоту,
поэтому,.
Треугольникиитакже имеют общую высоту –,
поэтому,.
Перемножая полученные равенства, получим.
Теорема
доказана.
Вторая
формула.
Площадь
треугольника равна половине произведения
двух его сторон на синус угла между
ними.
Существует несколько способов
доказательства этой формулы, и я
воспользуюсь одним из них.
Доказательство.
Из
геометрии известна теорема о том, что
площадь треугольника равна половине
произведения основания на высоту,
опущенную на это основание:
В
случае остроугольного треугольника
.
В случае тупого угла.
Ho,
а поэтому.
Итак, в обоих случаях.
Подставив вместов геометрической формуле площади
треугольника,
получим тригонометрическую формулу
площади треугольника:
Теорема
доказана.
Третья
формула
для площади треугольника – формула
Герона
,
названа так в честь древнегреческого
ученого Герона Александрийского, жившего
в первом веке нашей эры. Эта формула
позволяет находить площадь треугольника,
зная его стороны. Она удобна тем, что
позволяет не делать никаких дополнительных
построений и не измерять углов. Ее вывод
основывается на второй из рассмотренных
нами формул площади треугольника и
теореме косинусов:
и
.
Прежде
чем перейти к реализации этого плана,
заметим, что
Точно
так же имеем:
Теперь
выразим косинус через
и:
Так
как любой угол в треугольнике больше
и меньше,
то. Значит,.
Теперь
отдельно преобразуем каждый из
сомножителей в подкоренном выражении.
Имеем:
Подставляя
это выражение в формулу для площади,
получаем:
Тема
«Площадь треугольника» имеет большое
значение в школьном курсе математики.
Треугольник – простейшая из геометрических
фигур. Он является «структурным элементом»
школьной геометрии. Подавляющее
большинство геометрических задач
сводятся к решению треугольников. Не
исключение и задача о нахождении площади
правильного и произвольного
n-угольника.
Пример
2.4.1.
Чему
равна площадь равнобедренного
треугольника, если его основание
,
а боковая сторона?
Решение
:
–равнобедренный,
Рисунок
2.4.4
Проведём
по свойству равнобедренного треугольника
–
медиана и высота. Тогда
В
по
теореме Пифагора:
Находим
площадь треугольника:
Ответ:
Пример
2.4.2.
В
прямоугольном треугольнике биссектриса
острого угла делит противоположный
катет на отрезки длиной 4 и 5 см. Определить
площадь треугольника.
Решение:
Пусть
(рисунок 2.4.5). Тогдаи(посколькуBD
–
биссектриса). Отсюда имеем
,
то есть.
Значит,
Рисунок
2.4.5
Ответ:
Пример
2.4.3.
Найти
площадь равнобедренного треугольника,
если его основание равно
,
а длина высоты, проведённой к основанию,
равна длине отрезка, соединяющего
середины основания и боковой стороны.
Решение:
По
условию,
–
средняя линия
(рисунок 2.4.6). Так какВимеем:
или
,
откудаСледовательно,
Прежде чем узнать, как найти площадь параллелограмма, нам необходимо вспомнить, что такое параллелограмм и что называется его высотой. Параллелограмм – четырехугольник, противолежащие стороны которого попарно параллельны (лежат на параллельных прямых). Перпендикуляр, проведенный из произвольной точки противоположной стороны к прямой, содержащей эту сторону называется высотой параллелограмма.
Квадрат, прямоугольник и ромб – это частные случаи параллелограмма.
Площадь параллелограмма обозначается как (S).
Формулы нахождения площади параллелограмма
S=a*h
, где а – это основание, h – это высота, которая проведена к основанию.
S=a*b*sinα
, где a и b – это основания, а α — угол между основаниями а и b.
S =p*r
, где р – это полупериметр, r – это радиус окружности, которая вписана в параллелограмм.
Площадь параллелограмма, который образован векторами a и b равна модулю произведения заданных векторов, а именно:
Рассмотрим пример №1: Дан параллелограмм, сторона которого равна 7 см, а высота 3 см. Как найти площадь параллелограмма, формула для решения нам необходима.
Таким образом, S= 7×3. S=21. Ответ: 21 см 2 .
Рассмотрим пример №2: Даны основания 6 и 7 см, а также дан угол между основаниями 60 градусов. Как найти площадь параллелограмма? Формула, используемая для решения:
Таким образом, сначала найдем синус угла. Синус 60 = 0,5, соответственно S = 6*7*0,5=21 Ответ: 21 см 2 .
Надеюсь, что эти примеры Вам помогут при решении задач. И помните, главное – это знание формул и внимательность
При решении задач по данной теме кроме основных свойств
параллелограмма
и соответственных формул можно запомнить и применять следующее:
- Биссектриса внутреннего угла параллелограмма отсекает от него равнобедренный треугольник
- Биссектрисы внутренних углов прилежащие к одной из сторон параллелограмма взаимно перпендикулярные
- Биссектрисы, выходящие из противоположных внутренних углов параллелограмма, параллельные между собой либо лежат на одной прямой
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними
Рассмотрим задачи, при решении которых используются данные свойства.
Задача 1.
Биссектриса угла С параллелограмма АВСD пересекает сторону АD в точке М и продолжение стороны АВ за точку А в точке Е. Найдите периметр параллелограмма, если АЕ = 4, DМ = 3.
Решение.
1. Треугольник СМD равнобедренный. (Свойство 1). Следовательно, СD = МD = 3 см.
2. Треугольник ЕАМ равнобедренный.
Следовательно, АЕ = АМ = 4 см.
3. АD = АМ + МD = 7 см.
4. Периметр АВСD = 20 см.
Ответ. 20 см.
Задача 2.
В выпуклом четырёхугольнике АВСD проведены диагонали. Известно, что площади треугольников АВD, АСD, ВСD равны. Докажите, что данный четырёхугольник является параллелограммом.
Решение.
1. Пусть ВЕ – высота треугольника АВD, СF – высота треугольника АCD. Так как по условию задачи площади треугольников равны и у них общее основание АD, то высоты этих треугольников равны. ВЕ = СF.
2. ВЕ, СF перпендикулярны АD. Точки В и С расположены по одну сторону относительно прямой АD. ВЕ = СF. Следовательно, прямая ВС || AD. (*)
3. Пусть АL – высота треугольника АСD, BK – высота треугольника BCD. Так как по условию задачи площади треугольников равны и у них общее основание СD, то высоты этих треугольников равны. АL = BK.
4. АL и BK перпендикулярны СD. Точки В и А расположены по одну сторону относительно прямой СD. АL = BK. Следовательно, прямая АВ || СD (**)
5. Из условий (*), (**) вытекает – АВСD параллелограмм.
Ответ. Доказано. АВСD – параллелограмм.
Задача 3.
На сторонах ВС и СD параллелограмма АВСD отмечены точки М и Н соответственно так, что отрезки ВМ и НD пересекаются в точке О;
Решение.
1. В треугольнике DОМ
2. В прямоугольном треугольнике DНС
(
Тогда (Так как в прямоугольном треугольнике катет, который лежит против угла в 30 о, равен половине гипотенузы).
Но СD = АВ. Тогда АВ: НD = 2: 1.
3.
4.
Ответ: АВ: НD = 2: 1,
Задача 4.
Одна из диагоналей параллелограмма длиною 4√6, составляет с основанием угол 60 о, а вторая диагональ составляет с тем же основанием угол 45 о. Найти вторую диагональ.
Решение.
1. АО = 2√6.
2. К треугольнику АОD применим теорему синусов.
АО/sin D = OD/sin А.
2√6/sin 45 о = OD/sin 60 о.
ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6.
Ответ: 12.
Задача 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма. Найдите сумму длин диагоналей.
Решение.
Пусть d 1 , d 2 – диагонали параллелограмма, а угол между диагоналями и меньший угол параллелограмма равен ф.
1. Посчитаем двумя разными
способами его площадь.
S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin ф,
S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin ф.
Получим равенство 5√2 · 7√2 · sin ф = 1/2d 1 d 2 sin ф или
2 · 5√2 · 7√2 = d 1 d 2 ;
2. Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
(АВ 2 + АD 2) · 2 = АС 2 + ВD 2 .
((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2 .
d 1 2 + d 2 2 = 296.
3. Составим систему:
{d 1 2 + d 2 2 = 296,
{d 1 + d 2 = 140.
Умножим второе уравнение системы на 2 и сложим с первым.
Получим (d 1 + d 2) 2 = 576. Отсюда Id 1 + d 2 I = 24.
Так как d 1 , d 2 – длины диагоналей параллелограмма, то d 1 + d 2 = 24.
Ответ: 24.
Задача 6.
Стороны параллелограмма 4 и 6. Острый угол между диагоналями равен 45 о. Найдите площадь параллелограмма.
Решение.
1. Из треугольника АОВ, используя теорему косинусов, запишем соотношение между стороной параллелограмма и диагоналями.
АВ 2 = АО 2 + ВО 2 2 · АО · ВО · cos АОВ.
4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1 /2) · (d 2 /2)cos 45 о;
d 1 2 /4 + d 2 2 /4 – 2 · (d 1 /2) · (d 2 /2)√2/2 = 16.
d 1 2 + d 2 2 – d 1 · d 2 √2 = 64.
2. Аналогично запишем соотношение для треугольника АОD.
Учтем, что
Получим уравнение d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
3. Имеем систему
{d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
{d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
Вычитая из второго уравнения первое, получим 2d 1 · d 2 √2 = 80 или
d 1 · d 2 = 80/(2√2) = 20√2
4. S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2/2 = 10.
Примечание:
В этой и в предыдущей задаче нет надобности, решать полностью систему, предвидя то, что в данной задаче для вычисления площади нам нужно произведение диагоналей.
Ответ: 10.
Задача 7.
Площадь параллелограмма равна 96, а его стороны равны 8 и 15. Найдите квадрат меньшей диагонали.
Решение.
1. S ABCD = AВ · АD · sin ВAD. Сделаем подстановку в формулу.
Получим 96 = 8 · 15 · sin ВAD. Отсюда sin ВAD = 4 / 5 .
2. Найдём cos ВАD. sin 2 ВAD + cos 2 ВАD = 1.
(4 / 5) 2 + cos 2 ВАD = 1. cos 2 ВАD = 9 / 25 .
По условию задачи мы находим длину меньшей диагонали. Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3 / 5.
3. Из треугольника АВD по теореме косинусов найдём квадрат диагонали ВD.
ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos ВАD.
ВD 2 = 8 2 + 15 2 – 2 · 8 · 15 · 3 / 5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Формула для площади параллелограмма
Площадь параллелограмма равна произведению его стороны на высоту, опущенную на эту сторону.
Доказательство
Если параллелограмм — прямоугольник, то равенство выполнено по теореме о площади прямоугольника. Далее считаем, что углы параллелограмма не прямые.
Пусть в параллелограмме $ABCD$ угол $angle BAD$ острый и $AD > AB$. Иначе переименуем вершины. Тогда высота $BH$ из вершины $B$ на прямую $AD$ падает на сторону $AD$, так как катет $AH$ короче гипотенузы $AB$, а $AB
Сравним площадь параллелограмма $ABCD$ и площадь прямоугольника $HBCK$. circ — angle AOD$. Значит, синусы углов при пересечении диагоналей равны $sin alpha$.
$S_{ABCD}=S_{triangle AOB} + S_{triangle BOC} + S_{triangle COD} + S_{triangle AOD}$
по аксиоме измерения площади. Применяем формулу площади треугольника $S_{ABC} = dfrac{1}{2} cdot AB cdot BC sin angle ABC$ для этих треугольников и углов при пересечении диагоналей. Стороны каждого равны половинам диагоналей, синусы также равны. Следовательно, площади всех четырёх треугольников равны $S = dfrac{1}{2} cdot dfrac{AC}{2} cdot dfrac{BD}{2} cdot sin alpha = dfrac{AC cdot BD}{8} sin alpha$. Суммируя всё вышесказанное, получаем
$S_{ABCD} = 4S = 4 cdot dfrac{AC cdot BD}{8} sin alpha = dfrac{AC cdot BD cdot sin alpha}{2}$
Area — Площадь параллелограммов и ромбов
Параллелограммы представляют собой запутанные формы, в основном потому, что в самом слове слишком много слогов. Почему фигура с четырьмя сторонами нуждается в пяти слогах? Давай, геометрия.
К счастью, параллелограммов определяются только тем фактом, что они являются четырехугольниками (не говоря уже о количестве слогов в этом слове), состоящими из двух наборов параллельных линий. Из-за этого простого факта противоположные стороны параллелограмма равны. Но ты знал это.
Как бы замечательно это ни было, это не очень помогает нам найти местность. Когда мы находим площадь, нам нужна длина основания и высота , которая должна быть перпендикулярна основанию. Все, что нам нужно сделать, это перемножить их вместе, и мы получим формулу площади параллелограмма. Итак, наша формула:
A = bh
Ощущение дежавю? Выглядит как площадь прямоугольника или вдвое больше площади треугольника, не так ли? Что ж, на это есть причина.
На самом деле параллелограмм — это просто два треугольника в одном большом плаще, которые притворяются тем, чем они не являются. Так как площадь каждого равна ½ bh , площадь их обоих вместе равна 2 (½ bh ) = bh . Мы можем видеть сквозь их обман.
Если мы также разрежем параллелограмм от верхней вершины вниз к основанию
под прямым углом, мы можем взять треугольник, который мы отрезали, и заполнить
зазор с другой стороны. Это даст нам параллелограмм с четырьмя правыми
углы. Или, знаете, прямоугольник. Вот так:
Поскольку площадь прямоугольника равна A = lw , мы можем использовать эту формулу. Только теперь мы знаем, что l = b и w = h . Замена этих значений дает нам площадь параллелограмма: A = bh . Вам действительно нужны еще доказательства?
Пример задачи
Если основание галактики Центавр А составляет 16 500 световых лет, а высота галактики — 10 000 световых лет, какова площадь этой галактики в форме параллелограмма?
Параллелограмм есть параллелограмм, независимо от того, большой он или маленький. Даже у параллелограмма размером с галактику есть площадь.
a = BH
A = 16 500 световых лет × 10 000 световых лет
A = 165 000 000 световых лет 2
Проблема выборки
Какова область этой параллелиграммы?
Ну мы знаем что основание 10см, а вот высота не сразу понятна. Если мы нарисуем высоту, она образует 30-60-90 треугольник. Как удобно.
Мы можем использовать отношения сторон треугольника, чтобы найти высоту параллелограмма (которая в нашем случае является длинной стороной треугольника 30-60-90). Поскольку мы знаем, что отношение гипотенузы к длинному катету равно , мы можем найти высоту, составив пропорцию.
Теперь, когда у нас есть высота, мы можем найти площадь параллелограмма.
А =
В то время как квадрат и прямоугольник заплатили достаточно, чтобы получить свои собственные сечения, есть еще один тип параллелограмма, о площади которого мы еще не говорили. Это также любимый автомобиль четырехугольника: ромб .
Мы просто шутим. Они предпочитают Феррари.
Мы можем думать о ромбе как о особом параллелограмме, точно так же, как квадрат — это особый тип прямоугольника. У ромба четыре равные стороны и диагонали, перпендикулярные друг другу. В основном они выглядят как бриллианты. Так что, если подумать, ромбы — лучшие друзья девушек.
Поскольку ромбы являются особыми типами параллелограммов, мы можем использовать формулу A = bh , чтобы найти их площади, точно так же, как мы использовали A = lw , чтобы найти площадь квадрата. Однако углы формы не одинаковы. Это означает, что основание и высота ромба будут равны , а не , поэтому мы не можем волей-неволей возводить стороны в квадрат. Нам еще нужно найти основание и высоту ромба.
Что такого особенного в ромбах, если мы должны использовать ту же самую формулу? Ну и их диагонали, разумеется. Особенность ромбов в том, что половина произведения их диагоналей составляет их площадь. Пример задачи Какова площадь ромба?
Иногда проблемы пытаются обмануть вас, используя взаимозаменяемые термины «сторона» и «база». В случае с ромбами длина всех сторон одинакова, поэтому они взаимозаменяемы. Просто помните, что для ромба основание и сторона одинаковы, но высота не является ни тем, ни другим.
Итак, в этом случае b = 4 м и h = 3 м, и это все, что нам нужно. Район, вот и мы.
A = BH
A = 4 M × 3 M
A = 12 M 2
Проверка образца
Тот же ромб ( B = 4 М и H = 3 М. ) имеет диагональ 8 м. Какова длина другой диагонали?
Мы уже нашли площадь ромба. Если бы мы этого не сделали, мы могли бы легко сделать это, используя A = bh = 4 м × 3 м = 12 м 2 . Теперь мы можем использовать формулу с диагоналями и найти длину диагонали, измерения которой у нас нет. Неважно, какая диагональ d 1 , а какая d 2 .
A = ½ D 1 D 2
12 M 2 = ½ × 8 M × D 2
3 M. D 2
3 M = D 2
3 M = D 2
3 M = D 2
3 M = D 2
3 M = D 2
.0007
Другая диагональ имеет длину 3 м.
Площадь ромба. Формула, как найти площадь ромба
Площадь ромба – это площадь, заключенная или охваченная ромбом в двумерной плоскости. Ромб — это особый вид параллелограмма, у которого все стороны равны. Форму можно отличить от квадрата по величине внутреннего угла. Внутренний угол ромба не обязательно должен быть прямоугольным. Площадь ромба можно вычислить по-разному, в зависимости от известных нам параметров.
| 1. |
Что такое площадь ромба? |
| 2. | Площадь ромба Формула |
| 3. | Как вычислить площадь ромба? |
| 4. | Часто задаваемые вопросы по площади ромба |
Что такое площадь ромба?
Площадь ромба можно определить как количество пространства, ограниченного ромбом в двумерном пространстве. Он изображает общее количество единичных квадратов, которые могут в него поместиться, и измеряется в квадратных единицах (например, см 2 , м 2 , в 2 и т.д.). Ромб — параллелограмм, у которого противоположные стороны параллельны, противолежащие углы равны, а прилежащие углы смежны. Ниже приведены свойства формы.
- Ромб является равносторонним четырехугольником, потому что все стороны имеют одинаковую длину.
- Диагонали ромба пересекаются под прямым углом пополам.
- Диагонали являются биссектрисами угла.
- Площадь ромба можно найти разными способами: по основанию и высоте, по диагоналям и по тригонометрии.
Площадь ромба Формула
Для вычисления площади ромба можно использовать разные формулы в зависимости от известных нам параметров. Для вычисления площади ромба используются следующие формулы:
- Используя основание и высоту
- Использование диагоналей
- Использование тригонометрии
Формула площади ромба, если известны основание и высота
Ромб является параллелограммом. Мы знаем, что площадь параллелограмма получается путем умножения основания и высоты на квадратные единицы. То же самое относится и к ромбу.
Площадь ромба = основание × высота кв. единицы
Пример: Найдите площадь ромба, длина стороны которого 7 дюймов, а высота ромба 10 дюймов.
Решение: Как мы знаем, площадь = основание × единицы высоты 2
⇒ Площадь = 7 × 10 дюймов 2
⇒ Площадь = 70 дюймов 2
Формула площади ромба при известных диагоналях
Площадь ромба равна половине произведения длин диагоналей. Формула для вычисления площади ромба с использованием диагоналей дается как,
Площадь = (d 1 × d 2 )/2 кв. ед., где d 1 и d 2 — диагонали ромба.
Рассмотрим ромб ABCD. Пусть Е — точка пересечения двух диагоналей. Мы делаем следующие наблюдения:
- Четыре стороны конгруэнтны.
- Диагонали делят друг друга пополам.
- Четыре внутренних угла с равными противоположными углами. ⇒ ∠ А = ∠ С и ∠ В = ∠ D
- Две диагонали AC и BD.
Площадь ромба ABCD = площадь ∆ ADC + площадь ∆ ABC
Площадь ромба = 2 × площадь ∆ ABC —(1) (∵ ∆ ABC конгруэнтна ∆ ADC)
Площадь ∆ ABC
= 1/2 × основание × высота
= 1/2 × АС × ВЕ
= 1/2 × AC × 1/2 × BD (∵BE = BD/2)
= 1/4 (AC × BD) — (2)
Площадь ромба ABCD
Площадь = 2 × 1/4 × AC × BD = 1/2 × AC × BD (Из (1) и ( 2))
⇒ Площадь = 1/2 × диагональ 1 × диагональ 2
∴ Площадь ромба = 1/2 × диагонали 1 × диагонали 2 единицы 2
Формула площади ромба, когда известны стороны и углы
Мы применяем концепцию тригонометрии при вычислении площади, когда стороны и углы известны. Мы можем использовать любой угол, потому что либо углы равны, либо они являются дополнительными, а дополнительные углы имеют один и тот же синус. Площадь ромба с учетом стороны и угла определяется как
Площадь ромба = сторона 2 × sin(A) кв. единиц, где A — внутренний угол.
Пример: Какова площадь ромба, если длина его стороны 4 м, а один из углов А равен 30º.
Решение: Как известно, площадь ромба = s 2 × sin(30º)
Площадь ромба = s 2 × sin(30º) = 4 2 × 1/2
⇒ Площадь ромба = 16 × 1/2 = 8 кв. ярдов
Как вычислить площадь ромба?
Ниже описаны различные методы вычисления площади ромба. Существует три метода вычисления площади ромба, представленные как:
- Способ 1: использование базы и высоты
- Метод 2: использование диагоналей
- Метод 3: использование тригонометрии
Площадь ромба с учетом основания и высоты
- Шаг 1: Найдите и запишите основание и высоту заданного ромба.
Основание — одна из сторон ромба, а высота — расстояние по перпендикуляру от выбранного основания до противоположной стороны.
- Шаг 2: Умножьте основание и высоту.
Полученное значение даст площадь ромба.
Площадь ромба по диагоналям
Рассмотрим ромб ABCD, имеющий две диагонали, т. е. AC и BD.
- Шаг 1: Найдите длину обеих диагоналей, диагонали 1 и диагонали 2.
- Шаг 2: Умножьте обе длины, d1 и d2.
- Шаг 3: Разделите результат на 2.
Полученное значение даст площадь ромба ABCD.
Площадь ромба с использованием тригонометрии
- Шаг 1: Возведите в квадрат длину любой из сторон.
- Шаг 2: Умножьте его на синус любого из углов.
Полученное значение даст площадь ромба.
Пример: Рассмотрим ромб ABCD. AB, BC, CD, DA — конгруэнтные (равные) стороны. AC и BD — диагонали, и они пересекаются в E. Даны CD = 17 футов и AE = 8 футов. Найдите площадь ABCD.
Теперь мы знаем диагональ 1, AC = 16 футов.
Далее нам нужно рассчитать BD.
BD = BE + ED = 2 × BE
У нас все еще есть неизвестное, BE.
Теорема Пифагора утверждает, что
до н.э. 2 = BE 2 + EC 2
BC = 17 футов (∵ CD =BC, так как все стороны конгруэнтны)
EC = 8 футов (∵ AE = EC, поскольку диагонали делятся пополам)
17 2 = БЭ 2 + 8 2
⇒ БЭ 2 = 289 — 64
= 225
∴ BE = 15 футов и BD = 30 футов
Подставим все значения в области формулы ромба.
Площадь ромба = 1/2 × d 1 × d 2 квадратных единиц
= 1/2 × BD × AC кв. футов
= 1/2 × 30 × 16 кв. футов
⇒ Площадь ромба = 240 квадратных футов
Советы и подсказки:
- Помните, что высота не равна длине стороны ромба.
- Площадь ромба можно найти тремя способами: по диагоналям, по углу и стороне, по углу и высоте.
- Используйте теорему Пифагора, чтобы найти вторую диагональ, если известны меры одной диагонали и стороны.
Примеры на площади ромба
-
Пример 1: Используя формулу площади ромба, найдите площадь ромба, изображенного на рисунке ниже.
Решение:
Площадь ромба = 1/2 × BD × AC
BD = 2 × BE
= 2 × 8
= 16 ярдовAC = 2 × AE = 2 × 10 = 2 ярда
⇒ Площадь = 1/2 × 16 × 20
= 8 × 20
= 160 ярдов 2Ответ: Площадь ромба = 160 ярдов 2
-
Пример 2: Стороны ромба ABCD равны 5 дюймов, а длина его одной диагонали АС равна 8 дюймам. Вычислите его площадь.
Решение:
Зная сторону и диагональ, найдем другую диагональ.
Пусть О — точка пересечения диагоналей.
Площадь = (AC × BD)/2 кв. дюйма
⇒ АС = 8 в
.
⇒ AO = 4 дюйма (∵ AO = 1/2 AC)Чтобы найти другую диагональ BD, рассмотрим AOD.
По теореме Пифагора, AD 2 = AO 2 + OD 2
⇒ 25 2 = 4 2 + ОД 2
⇒ ОД 2 = 25 -16
⇒ ОД 2 = 9
⇒ ОД = 3 в
⇒ BD = 6 дюймов (∵BD = 2 × внешний диаметр)
Площадь = (8 × 6) ÷ 2 квадратных дюйма
Площадь = 24 квадратных дюймаОтвет: Площадь ромба = 24 квадратных дюйма
-
Пример 3: Площадь ромба равна 256 квадратных единиц. Если длина одной из диагоналей равна 8 единицам, найдите длину другой ее диагонали.
Решение:
Мы знаем, что площадь ромба можно вычислить с помощью диагоналей следующим образом: (8 × диагональ 2 )
диагональ 2 = (256 × 2)/8
диагональ 2 = 64Ответ: Длина другой диагонали данного ромба = 64 единицы
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика — это жизненный навык. Помогите своему ребенку усовершенствовать это с помощью реального приложения с Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по площади ромба
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по площади ромба
Какова площадь ромба?
Площадь ромба – это общее количество пространства, заключенного или охваченного ромбом в двухмерной плоскости. Он выражается в квадратных единицах (например, см 2 , м 2 , в 2 и т.д.).
Какая формула нахождения площади ромба?
Для вычисления площади ромба можно использовать разные формулы в зависимости от известных нам параметров. Используя основание и высоту, формула задается следующим образом: площадь ромба = основание × высота в квадратных единицах. Площадь ромба по диагоналям равна: Площадь = (d 1 × d 2 )/2 квадратных единиц, где d 1 и d 2 — диагонали ромба. Применяя концепцию тригонометрии с использованием стороны и угла, мы можем следовать формуле: Площадь ромба = сторона 2 × sin(A) квадратных единиц, где а — внутренний угол.
Как найти сторону ромба по диагоналям?
Площадь ромба можно вычислить, используя длины диагоналей. Формула для нахождения площади в этом случае имеет следующий вид: Площадь = (d 1 × d 2 )/2 квадратных единиц, где d 1 и d 2 — диагонали ромба.
Равны ли площади ромба и квадрата?
Нет, площади ромба и квадрата не равны. Однако их площадь можно было бы рассчитать таким же образом, учитывая их размеры. Площадь ромба или любого параллелограмма = основание × высота. У ромба сторона и высота неодинаковы. Однако площадь квадрата = сторона×сторона, причем стороной может быть и высота квадрата. Квадрат является ромбом, потому что у него четыре стороны, и каждая сторона имеет одинаковую длину. Однако далее квадрат определяется как фигура, имеющая четыре равных угла по 9 градусов. 0 градусов. Следовательно, квадрат — это ромб. Однако ромб не обязательно является квадратом. Поэтому их площади не могут быть одинаковыми.
Как найти площадь ромба, зная сторону и высоту?
Площадь ромба можно вычислить, зная длину основания или стороны и высоту. Здесь под высотой понимается перпендикулярное расстояние между параллельными сторонами, одну из которых мы взяли за основу. Формула для нахождения площади в этом случае дается как площадь ромба = основание × высота кв.
В чем разница между площадью ромба и квадрата?
Площадь квадрата равна квадрату его стороны, т. е. s × s, где s — длина стороны квадрата, тогда как площадь ромба равна ½ × d1 × d2, где d1 и d2 — длины диагоналей.
В чем разница между площадью ромба и прямоугольника?
Площадь прямоугольника равна l × b, где «l» — длина прямоугольника, а «b» — длина прямоугольника, тогда как площадь ромба равна ½ × d1 × d2, где d1 и d2 — длины диагоналей.
В чем разница между площадью ромба и его периметром?
Периметр ромба представляет собой общую меру его границы и рассчитывается путем сложения длин всех его сторон, тогда как площадь ромба или любых параллелограммов является произведением его основания и высоты, т. е. основание × высота. Следовательно, площадь ромба равна половине произведения ts диагоналей, заданных как ½ × d1 × d2, где d1 и d2 — длины диагоналей.
Для чего нужен калькулятор площади ромба?
Калькулятор площади ромба — это онлайн-инструмент, с помощью которого мы можем легко вычислить площадь ромба за считанные секунды. Чтобы определить значение, нам нужно ввести определенные параметры, такие как значение диагоналей. Попробуйте онлайн-калькулятор площади ромба Cuemath для быстрых вычислений и решите свои проблемы, связанные с площадью ромба, за считанные секунды.
Какова высота, если известна площадь ромба?
Чтобы вычислить высоту или высоту, когда дана площадь, нам нужна длина основания. Формула, которая может быть применена для расчета высоты, представлена в виде площади/базовых единиц.
Площадь параллелограмма – формула, определение, примеры
Площадь параллелограмма определяется как область или пространство, покрываемое параллелограммом в двумерной плоскости. Параллелограмм – это особый вид четырехугольника. Если четырехугольник имеет две пары параллельных противоположных сторон, то он называется параллелограммом. Прямоугольник, квадрат и ромб — все это примеры параллелограмма. Геометрия — это все о формах, 2D или 3D. Все эти фигуры имеют разный набор свойств с разными формулами площади. Основное внимание здесь будет полностью сосредоточено на следующем:
- Определение площади параллелограмма
- Формула площади параллелограмма
- Вычисление площади параллелограмма в векторной форме
| 1. | Какова площадь параллелограмма? |
| 2. | Формула площади параллелограмма |
| 3. | Как рассчитать площадь параллелограмма? |
| 4. | Площадь параллелограмма в векторной форме |
| 5. | Часто задаваемые вопросы о площади параллелограмма |
Какова площадь параллелограмма?
Площадь параллелограмма относится к общему количеству единичных квадратов, которые могут поместиться в него, и измеряется в квадратных единицах (например, см 2 , м 2 , 2 и т. д.). Это область, заключенная или охваченная параллелограммом в двумерном пространстве. Напомним определение параллелограмма. Параллелограмм представляет собой четырехстороннюю двумерную фигуру, в которой:
- две равные противоположные стороны,
- две пересекающиеся и не равные диагонали, а
- противоположных углов, равных
В повседневной жизни мы сталкиваемся со многими геометрическими фигурами, помимо прямоугольников и квадратов. Поскольку некоторые свойства прямоугольника и параллелограмма в чем-то похожи, площадь прямоугольника аналогична площади параллелограмма.
Площадь параллелограмма Формула
Площадь параллелограмма можно вычислить, умножив его основание на высоту. Основание и высота параллелограмма перпендикулярны друг другу, как показано на следующем рисунке. Таким образом, формула для вычисления площади параллелограмма может быть представлена следующим образом:
Площадь параллелограмма = b × h квадратных единиц
где,
- b — длина основания
- h это высота или высота
Разберем приведенную выше формулу на примере. Предположим, что PQRS — параллелограмм. Используя сетку, найдем ее площадь, посчитав квадраты.
На рисунке выше:
Общее количество полных квадратов = 16
Общее количество полуквадратов = 8
Площадь = 16 + (1/2) × 8 = 16 + 4 = 20 ед. 2
Также на рисунке видно, что ST ⊥ PQ. Подсчитав квадраты, получим:
Сторона, PQ = 5 шт.
Соответствующая высота, ST=4 шт.
Сторона × высота = 5 × 4 = 20 единиц 2
Таким образом, площадь данного параллелограмма равна основанию, умноженному на высоту.
Давайте выполним задание, чтобы понять площадь параллелограмма.
- Шаг I: Начертите на картоне параллелограмм (PQRS) с высотой (SE) и вырежьте его.
- Шаг II: Вырежьте треугольную часть (PSE).
- Шаг III: Вставьте оставшуюся часть (EQRS) на белую диаграмму.
- Шаг IV: Вставьте треугольную часть (PSE) на белую диаграмму, соединяющую стороны RQ и SP.
Выполнив это задание, мы обнаружили, что площадь прямоугольника равна площади параллелограмма. Кроме того, основание и высота параллелограмма равны длине и ширине прямоугольника соответственно.
Площадь параллелограмма = основание × высота
Как рассчитать площадь параллелограмма?
Площадь параллелограмма можно рассчитать с помощью его основания и высоты. Кроме того, площадь параллелограмма также может быть оценена, если известны две его диагонали вместе с любым из их пересекающихся углов или если известна длина параллельных сторон вместе с любым из углов между сторонами.
Площадь параллелограмма с использованием высоты
Предположим, что «a» и «b» — это набор параллельных сторон параллелограмма, а «h» — это высота (которая представляет собой перпендикулярное расстояние между «a» и «b»), тогда площадь параллелограмма определяется как:
Площадь = Основание × Высота
A = b × h [квадратные единицы]
Пример: Если основание параллелограмма равно 5 см, а высота 4 см, затем найдите его площадь.
Решение: Дано, длина основания = 5 см и высота = 4 см
По формуле Площадь = 5 × 4 = 20 см 2
Площадь параллелограмма с использованием длин сторон
Площадь параллелограмма также может быть рассчитана без учета высоты, если длина соседних сторон и угол между ними известны нам. Мы можем просто использовать площадь формулы треугольника из концепции тригонометрии для этого случая.
Площадь = ab sin (θ)
где,
- a и b = длина параллельных сторон, и,
- θ = угол между сторонами параллелограмма.
Пример: Угол между любыми двумя сторонами параллелограмма равен 90 градусов. Если длина двух параллельных сторон равна 4 и 6 единицам соответственно, то найдите площадь.
Решение:
Пусть a = 4 единицы и b = 6 единиц
θ = 90 градусов
Используя формулу площади параллелограмма,
Площадь = ab sin (θ)
⇒ A = 4 × 6 sin (90º)
⇒ А = 24 грех 90º
⇒ A = 24 × 1 = 24 кв. ед.
Примечание: Если угол между сторонами параллелограмма равен 90 градусов, то параллелограмм становится прямоугольником.
Площадь параллелограмма с использованием диагоналей
Площадь любого заданного параллелограмма также можно вычислить, используя длину его диагоналей. У параллелограмма две диагонали, пересекающиеся друг с другом под определенными углами. Предположим, что этот угол равен x, тогда площадь параллелограмма равна:
Площадь = ½ × d(_1) × d(_2) sin (x)
где,
- d(_1) и d(_2) = длина диагоналей параллелограмма , и
- x = угол между диагоналями.
Площадь параллелограмма в векторной форме
Площадь параллелограмма можно вычислить по разным формулам, даже если стороны или диагонали заданы в векторной форме. Рассмотрим параллелограмм ABCD, как показано на рисунке ниже,
Площадь параллелограмма в векторной форме с использованием смежных сторон равна,
(|overrightarrow{mathrm{a}} × overrightarrow{mathrm{b}}|)
где (overrightarrow{a}) и (overrightarrow{b}) — векторы, представляющие две смежные стороны.
Здесь,
(overrightarrow{a} + overrightarrow{b} = overrightarrow{d_1} ) → i) и,
(overrightarrow{b} + (-overrightarrow{a}) = overrightarrow{d_2} )
или (overrightarrow{b} — overrightarrow{a} = overrightarrow{d_2}) → ii)
⇒ ( overrightarrow{d_1} times overrightarrow{d_2} = (overrightarrow{a} + overrightarrow{b}) (overrightarrow{b} — overrightarrow{a}))
= (overrightarrow{a}) × ((overrightarrow{b}) — (overrightarrow{a})) + (overrightarrow{b}) × ((overrightarrow{b }) — (overrightarrow{а}))
= (overrightarrow{a}) × (overrightarrow{b}) — (overrightarrow{a}) × (overrightarrow{a}) + (overrightarrow{b}) × (overrightarrow{b}) — (overrightarrow{b}) × (overrightarrow{a})
Поскольку (overrightarrow{a}) × (overrightarrow{a}) = 0 и (overrightarrow{b}) × (overrightarrow{b}) = 0
⇒ (overrightarrow{a}) × (overrightarrow{b}) — 0 + 0 — (overrightarrow{b}) × (overrightarrow{a})
Так как ( overrightarrow{a}) × (overrightarrow{b}) = — (overrightarrow{b}) × (overrightarrow{a}),
( overrightarrow{d_1}) × (overrightarrow{d_2}) = (overrightarrow{a}) × (overrightarrow{b}) — (-((overrightarrow{a} ) × (overrightarrow{b})))
= 2((overrightarrow{a}) × (overrightarrow{b}))
Следовательно, площадь параллелограмма, когда диагонали заданы в векторной форме = 1/2 |((overrightarrow{d_1} ) × (overrightarrow{d_2}))|
где (overrightarrow{d_1}) и (overrightarrow{d_2}) — диагонали.
Нестандартное мышление!
- Можно ли назвать воздушного змея параллелограммом?
- Какие элементы трапеции надо изменить, чтобы она стала параллелограммом?
- Может ли быть вогнутый параллелограмм?
- Можно ли найти площадь параллелограмма, не зная его высоты?
Площадь параллелограмма Примеры
-
Пример 1: Смежные стороны параллелограмма равны 10 дюймам и 6 дюймам. Высота, соответствующая стороне 10 дюймов, равна 5 дюймам. Используя формулу площади параллелограмма, найдите площадь и длину высоты, соответствующей сторона.
Решение:
Пусть ABCD будет параллелограммом, где DE⊥AB, AF⊥BC
Используя формулу площади параллелограмма,
Площадь параллелограмма ABCD = (10) × (90) = 078 дюймов 2
Длина BC = 6 в
Длина высоты AF = (50 ÷ 6) = 8,3 дюймаОтвет: Площадь данного параллелограмма = 50 дюймов 2 ; Высота = 8,3 в
-
Пример 2: Вычислите площадь солнечного листа, имеющего форму параллелограмма, учитывая, что размер основания составляет 20 дюймов, а высота — 8 дюймов.
Решение:
Используя формулу площади параллелограмма,
Площадь листа солнечного элемента = B × H = (20) × (8) = 160 дюймов 2Ответ: Площадь листа солнечного элемента = 160 дюймов 2
-
Пример 3: Площадь игровой площадки в форме параллелограмма составляет 2500 дюймов 2 , с одной стороной 250 дюймов. Найдите соответствующую высоту, используя формулу площади параллелограмма.
Решение:
Площадь детской площадки = 2500 в 2
Сторона детской площадки = 250 в
Соответствующая высота = 2500/250 = 10 дюймовОтвет: Соответствующая высота игровой площадки составляет 10 дюймов
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.
Записаться на бесплатный пробный урок
Практические вопросы по области параллелограмма
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади параллелограмма
Какова площадь параллелограмма в математике?
Площадь параллелограмма определяется как область, заключенная или охваченная параллелограммом в двумерном пространстве. Он представлен в квадратных единицах, таких как см 2 , m 2 , in 2 , и т. д.
Как найти площадь параллелограмма без высоты?
Площадь параллелограмма можно вычислить без учета высоты, если известна длина смежных сторон и угол между ними. Формула для нахождения площади для этого случая дается как площадь = ab sin (θ), где «a» и «b» — длины смежных сторон, а θ — угол между ними.
Кроме того, площадь можно рассчитать, зная диагонали и угол их пересечения, по формуле Площадь = ½ × d1 × d2 sin (y), где d1 и d2 — длины диагоналей параллелограмма , а y — угол между ними.
Какая формула нахождения площади параллелограмма?
Площадь параллелограмма можно вычислить, найдя произведение его основания на высоту. Основание и высота параллелограмма всегда перпендикулярны друг другу. Формула для вычисления площади параллелограмма дается как Площадь параллелограмма = квадратные единицы основания × высоты.
Как найти площадь параллелограмма с векторами?
Площадь параллелограмма можно вычислить, если смежные стороны или диагонали заданы в векторной форме. Формула для нахождения площади с использованием смежных сторон вектора задается следующим образом: | (overrightarrow{a}) × (overrightarrow{b})|, где (overrightarrow{a}) и (overrightarrow{b}) — смежные боковые векторы. Кроме того, площадь формулы параллелограмма с использованием диагоналей в векторной форме равна площади = 1/2 |((overrightarrow{d_1}) × (overrightarrow{d_2}))|, где (overrightarrow{d_1 }) и (overrightarrow{d_2}) — диагональные векторы.
Как рассчитать площадь параллелограмма с помощью калькулятора?
Самый простой и быстрый способ определить площадь параллелограмма — это воспользоваться калькулятором площади параллелограмма. Это бесплатный онлайн-инструмент, который поможет вам рассчитать площадь параллелограмма с помощью заданных размеров. Попробуйте калькулятор площади параллелограмма Куэмата, введите значение высоты и основания параллелограмма и получите площадь параллелограмма за несколько секунд.
Какова площадь параллелограмма, если даны диагонали?
Площадь параллелограмма можно вычислить, если известны диагонали и угол их пересечения. Формула задается как площадь = ½ × d1 × d2 sin (x), где «d1» и «d2» — длины диагоналей параллелограмма, а «x» — угол между ними.
Как вычислить площадь параллелограмма, смежные стороны которого заданы?
Чтобы найти площадь параллелограмма, зная длины смежных сторон, нам нужен угол между ними. Формула для нахождения площади для этого случая дается как площадь = ab sin (θ), где «a» и «b» — длины смежных сторон, а θ — угол между сторонами параллелограмма.
Открытие формул для площади – Элементарная математика
Формулы площади
Учащиеся, у которых есть неформальное представление о том, что площадь – это «количество двумерных «вещей»», содержащихся внутри области, могут изобрести для себя большинство формул, которые они используют. часто просят просто запомнить. Каждая формула, которую они заново изобретают, помогает укрепить их понимание (и память) о других формулах, которые они знают. (См. также площадь поверхности.)
Площадь прямоугольников
Выбирая квадрат в качестве единицы площади, мы получаем интуитивное представление о площади прямоугольников. Если мы решим, что площадь этого квадрата равна 1, то прямоугольник, длина которого в 7 раз больше, будет иметь площадь 7 × 1.
Прямоугольник, который в два раза больше высоты, будет иметь вдвое большую площадь, поэтому площадь равна 2 × 7 единиц площади. Мы можем сосчитать два ряда по семь квадратов. Точно так же имеет 3 строки по 7 квадратов (или 7 столбцов по 3 квадрата), всего 7 × 3 квадрата, поэтому его площадь составляет 21 квадратную единицу.
Количество квадратов в одном ряду равно длине прямоугольника. Количество строк равно высоте прямоугольника. Итак, площадь равна длине × высоте.
Поскольку прямоугольник можно нарисовать под наклоном, «высота» определяется как «направление, перпендикулярное основанию», а «основание» определяется как любая сторона, которую вы выберете.
Подходит для подсчета чисел. Это работает даже для дробей. Синий прямоугольник, показанный здесь, имеет высоту в половину единицы длины и ширину в пять с половиной единиц длины. Если мы выберем соответствующий квадрат в качестве нашей единицы площади, мы увидим, что синий прямоугольник содержит пять половинных единиц площади и одну четверть единицы площади, или всего две и три четверти единиц площади. (Розовые части показывают завершение каждой квадратной единицы площади.)
Чтобы включить все чисел, мы определяем площадь прямоугольника равна основания × высоты (где «основание» и «высота» означают длины этих сторон, измеренные в тех же единицах ).
Площадь параллелограмма
Получение идеи
Мы можем вычислить формулу площади параллелограмма, разрезав параллелограмм и переставив части так, чтобы получился прямоугольник. Поскольку параллелограмм и прямоугольник состоят из одних и тех же частей, они обязательно имеют одинаковую площадь. (См. определение площади, чтобы узнать, почему эти области одинаковы.)
Мы видим, что они и имеют точно такую же длину основания (синий) и точно такую же высоту (зеленый). Поскольку Основание × Высота дает площадь прямоугольника, мы можем использовать те же измерения на параллелограмме для вычисления ее площади: . (Как и раньше, «высота» измеряется перпендикулярно основанию, а «основание» — это сторона, которую вы выбрали первой. См. параллелограмм.)
На разрезе, показанном выше, легко увидеть, что длина основания не изменилась. На самом деле перпендикулярный разрез можно сделать в любом месте вдоль основания.
Укрепление дыр
Интуиция и доказательство
Это рассечение дает интуитивное понимание формулы площади параллелограмма, причины того, что он должен быть таким, какой он есть. Но мы не задавались вопросом, действительно ли рассечение «работает». То есть, когда мы разрезаем параллелограмм и переставляем его части, мы ожидают получить и результат, безусловно, выглядит именно так. Но внешность может быть обманчива. Что гарантирует нам, что при перемещении этого треугольника в результате получится прямоугольник? Что, если это больше похоже (хотя и менее преувеличено)? Если результатом не всегда является идеальный прямоугольник, мы не можем использовать наши знания формулы площади прямоугольника для разработки формулы параллелограмма. В старших классах учащиеся смогут доказать, что две части параллелограмма, если их правильно собрать, образуют прямоугольник. В классах К-8 учащиеся по большей части должны опираться на визуальный эксперимент и получать интуитивное ощущение. Узнайте больше о том, почему эти рассечения работают.
Что, если мы выберем короткую сторону в качестве основания?
Мы вольны выбрать любую сторону в качестве базы; «высота» измеряется перпендикулярно стороне, которую мы выбрали в качестве основания. Если мы возьмем короткую сторону (синюю) за основу, показанное выше рассечение будет не таким убедительным. Разрезание по этой высоте и перестановка частей оставляет беспорядок:
В этом конкретном примере мы можем спасти беспорядок, сделав еще один разрез, но что, если бы параллелограмм был еще длиннее и тоньше?
Получается, что любой параллелограмм, каким бы длинным и тонким он ни был, можно разрезать таким образом, чтобы части — возможно, многие из них — можно было переставить в прямоугольник. Но требуется больше работы, чтобы показать, что это всегда можно сделать. Нам нужна другая идея.
Несколько иная идея вскрытия значительно облегчает жизнь в этом случае. (Вы можете самостоятельно показать, что это работает и в исходном случае.)
- Заключите параллелограмм в прямоугольник.
- Две части прямоугольника, равные , а не внутри параллелограмма, являются конгруэнтными треугольниками.
- Сдвиньте один из этих треугольников к другому, пока они не встретятся, чтобы сформировать прямоугольник.
Поскольку общая площадь внешнего прямоугольника не изменилась (это тот же прямоугольник, что и раньше) и желтая область не изменилась (фигуры просто переместились), разница между ними — фиолетовыми областями — должна быть одинаковой. Как и прежде, мы также можем видеть, что размеры прямоугольной фиолетовой области — это основание и высота исходного параллелограмма.
Интуиция и доказательство, повторение: Опять же, рассечение дает существенное понимание, но требуется немного больше усилий, чтобы убедиться, что два желтых треугольника, которые, безусловно, выглядят так, как будто они соединяются, образуя прямоугольник, на самом деле подходят точно, а не только почти .
Почему так важно быть осторожным?
Когда мы будем строить другие формулы площади (см. ниже), мы захотим использовать наш способ нахождения площади параллелограмма, и поэтому мы хотим иметь возможность полагаться на найденное нами правило. Мы может быть уверенным, что перестановка частей не изменит площадь: в конце концов, именно так мы определяем площадь. Но мы также должны быть уверены, что детали подходят друг к другу так, как мы заявляем о , иначе мы не можем полагаться на сделанные нами измерения. И мы должны быть уверены, что правило основания × высоты не зависит от удачного выбора основания.
В большинстве учебных программ учащиеся не имеют достаточной систематической базы геометрических знаний до 8 класса, чтобы убедительно доказать, что эти рассечения работают. Но интуитивного понимания достаточно для объяснения и обоснования формул, а также хорошей основы для последующего изучения геометрии.
Площадь треугольника
Знание того, как найти площадь параллелограмма, поможет нам найти площадь треугольника.
Разрез треугольника
Мы можем разрезать треугольник на две части — одну на треугольник и одну на трапецию — разрезав его параллельно основанию. Если мы разрезаем высоту ровно пополам с помощью этого среза, две части соединятся вместе, чтобы получить параллелограмм с тем же основанием , но вдвое меньше высоты .
Итак, основание × половина высоты дает площадь треугольника. На аналогичном разрезе показаны полубаза × высота . Любой из них сокращается до bh .
Удвоение треугольника и уменьшение полученной площади пополам
Другой способ мышления: две копии треугольника образуют параллелограмм с тем же основанием и той же высотой , что и треугольник.
Площадь параллелограмма равна основание × высота , но это в два раза больше площади треугольника, поэтому площадь треугольника равна основания × высоты , как мы видели с помощью метода рассечения.
(Как всегда, выберите «основание» и измерьте высоту, перпендикулярную этому основанию, от основания до противоположной вершины.)
Площадь трапеции
Удвоение трапеции, а затем уменьшение полученной площади пополам
Как и было с помощью треугольника две копии трапеции можно сложить вместе, чтобы получился параллелограмм.
Высота параллелограмма такая же, как высота трапеции, но его основание равно сумме двух оснований трапеции. Таким образом, площадь параллелограмма равна высоты × ( основание1 + основание2 ). Но эта площадь равна двум трапециям, поэтому нам нужно разрезать ее пополам, чтобы получить площадь трапеции.
Разрез трапеции
Мы также можем разрезать трапецию так же, как разрезали треугольник, с одним срезом, сокращающим ее высоту пополам. Две части соединяются вместе, образуя параллелограмм, основание которого равно сумме двух оснований трапеции, а высота равна половине высоты трапеции.
В случае трапеции основания нельзя выбирать произвольно. Две параллельные стороны являются основаниями, а высота, как всегда, является перпендикулярным расстоянием от одного основания до противоположного.
Площадь этого параллелограмма равна его высоте (половина высоты трапеции), умноженной на его основание (сумма оснований трапеции), поэтому его площадь равна полувысоты × ( основание1 + основание2 ). Поскольку параллелограмм состоит из того же «материала», что и трапеция, это тоже площадь трапеции.
В любом случае площадь трапеции равна × высота × ( основание1 + основание2 ) .
Площадь других специальных четырехугольников
Площадь ромба
Площадь ромба можно найти, разрезав и переставив части так, чтобы получился параллелограмм. Это можно сделать несколькими способами:
- Разрежьте более короткую диагональ (а), чтобы сформировать два конгруэнтных треугольника. Переместите нижнюю половину треугольника рядом с верхней половиной, чтобы сформировать параллелограмм. Более короткая диагональ (a) становится основанием параллелограмма, а половина большей диагонали (b) становится высотой параллелограмма. Таким образом, площадь ромба равна a * b или произведению диагоналей, что является стандартной формулой для ромба.
- Другой подобный способ состоит в том, чтобы разрезать ромб на четыре конгруэнтных треугольника и перестроить их в прямоугольник с более короткой диагональю в качестве основания и половиной большей диагонали в качестве высоты.
- Разрезав ромб на два конгруэнтных треугольника, мы можем вычислить площадь одного из треугольников, которая равна * основание (а) * высота (b) = ab. Затем умножьте на два, так как их два: 2 * ab = ab.
Площадь воздушного змея
Площадь воздушного змея можно найти аналогично площади ромба. Если пересечь более длинную диагональ, получится два равных треугольника. Если мы переставим их, мы можем сформировать параллелограмм с большей диагональю (b) в качестве основания и половиной меньшей диагонали (a) в качестве высоты. Таким образом, площадь становится b * a = ab. Более сложный подход включает в себя немного алгебры. Разрежьте воздушного змея по более короткой диагонали, чтобы сформировать два треугольника с более короткой диагональю (а) в качестве основания. Таким образом, площадь первого треугольника равна * волнистой линии, где волнистая линия — высота. Площадь второго треугольника равна a * (b — волнистая линия), где (b — волнистая линия) — оставшаяся часть большей диагонали. Таким образом, общая площадь становится ( a * волнистой) + ( a * (b — волнистой)). Выделив a, мы имеем a (волнистый + b – волнистый) = ab.
Ну, что ты знаешь. По сути, вам нужно знать только формулу площади параллелограмма, а затем вывести формулы для остальных.
Объяснение урока: Площадь ромба
В этом объяснении мы научимся находить площадь ромба, используя
длины его диагоналей.
Напомним, что ромбом называется любой четырехугольник, у которого все четыре стороны равны
длина. Поскольку ромб также является параллелограммом, его площадь можно вычислить из
длину его основания и высоту перпендикуляра по формуле
площадь=𝑏ℎ.
Альтернативная формула площади ромба, которую мы здесь выводим, вместо этого использует
длины его диагоналей. Диагонали любого параллелограмма делят единицу пополам.
другое, но дополнительное свойство диагоналей ромба состоит в том, что они
перпендикулярны, как показано на рисунке ниже.
Рассмотрим диагональ 𝐵𝐷, которая делит ромб на конгруэнтные
треугольники 𝐴𝐵𝐷 и 𝐶𝐵𝐷. Поскольку треугольники равны, каждая их площадь равна
половина площади ромба. Эквивалентно, мы можем утверждать, что
площадь ромбаплощадьтреугольника𝐴𝐵𝐶𝐷=2×𝐴𝐵𝐷.
Предположим также, что длины диагоналей равны 𝑑 и
𝑑 единиц, как показано на рисунке ниже.
Площадь треугольника 𝐴𝐵𝐷 можно рассчитать по формуле
площадьтреугольника=12𝑏ℎ,
где 𝑏 представляет основание треугольника и
ℎ представляет перпендикулярную высоту. Из рисунка мы
определить, что основание этого треугольника равно
𝐵𝐷, длина которого 𝑑
единицы. Перпендикулярная высота этого треугольника равна
𝐴𝐸. Вспоминая еще раз, что диагонали
ромб делит друг друга пополам, мы
известно, что 𝐴𝐸 составляет половину длины
диагональ 𝐴𝐶 и поэтому имеет длину
𝑑2 ед. Следовательно,
площадь треугольниковквадрата единиц𝐴𝐵𝐷=12×𝑑×𝑑2=𝑑𝑑4.
Следовательно, площадь ромба равна
Площадь ромбаквадрата единиц𝐴𝐵𝐶𝐷=2×𝑑𝑑4=𝑑𝑑2.
Формула: Площадь ромба
Площадь ромба равна половине произведения длин его
диагонали. Для ромба с диагоналями длины 𝑑 и
𝑑 единиц,
площадь ромбаквадрата единиц = 𝑑𝑑2.
В нашем первом примере мы применим эту формулу для вычисления площади
ромб, нарисованный внутри прямоугольника.
Пример 1. Нахождение площади ромба внутри прямоугольника
На рисунке показан ромб внутри прямоугольника. Найдите площадь ромба на
два десятичных знака.
Ответ
При рассмотрении диаграммы мы видим, что каждая вершина ромба
𝑋𝑇𝑍𝑌
находится в середине одной из сторон прямоугольника. Например, вершина
𝑋 находится на середине стороны
𝐴𝐷. Мы знаем это, потому что
𝐴𝑋 и
𝑋𝐷 есть
равной длины. Отсюда можно сделать вывод, что диагональ ромба
𝑋𝑍
параллелен 𝐴𝐵 и
𝐷𝐶, а диагональ
𝑌𝑇 параллелен
𝐴𝐷 и
𝐵𝐶.
Отсюда также следует, что
𝑋𝑍=𝐴𝐵=𝐷𝐶
а также
𝑌𝑇=𝐴𝐷=𝐵𝐶.
Размеры прямоугольника указаны в вопросе и, следовательно,
𝑋𝑍=15,8см и
𝑌𝑇=30,3см.
Теперь вспомним, что площадь ромба равна половине произведения
длины его диагоналей:
площадь ромба=𝑑𝑑2,
где 𝑑 и 𝑑 — длины
диагонали. В этой задаче длины диагоналей равны
30,3 см и
15,8 см,
так что у нас есть
площадьсм𝑋𝑇𝑍𝑌=30,3×15,82=478,742=239.37.
Кратко отметим связь между ромбом
𝑋𝑇𝑍𝑌 и прямоугольник 𝐴𝐵𝐶𝐷 в предыдущем примере. Площадь любого прямоугольника равна произведению его длины на ширину,
или, другими словами, произведение его размеров. В этой задаче
длины диагоналей ромба равны размерам
прямоугольник, а так как площадь ромба равна половине произведения его
диагоналей, это эквивалентно половине произведения
размеры прямоугольника. Это свидетельствует о том, что площадь
ромб, нарисованный внутри прямоугольника так, что каждая вершина ромба
находится в середине одной из сторон прямоугольника, составляет половину площади
окружающего его прямоугольника.
Теперь мы рассмотрели один пример того, как вычислить площадь заданного ромба.
длины двух его диагоналей. Так же возможна работа в др.
направление: если нам дана площадь ромба и длина одного из
его диагоналей, мы можем вычислить длину другой диагонали, составив
и решение уравнения. Зная площадь ромба, мы также можем вычислить
длину одной или обеих диагоналей, если мы явно не знаем
длина любого из них, но мы знаем соотношение между их длинами,
как мы увидим в нашем следующем примере.
Пример 2. Расчет длины диагонали ромба по его площади
Одна диагональ ромба в два раза длиннее другой диагонали. Если площадь
ромба 81 квадратный миллиметр,
какова длина диагоналей?
Ответ
Напомним, что площадь ромба равна половине произведения длин
его диагонали 𝑑 и 𝑑:
area=𝑑𝑑2.
Пусть длина меньшей диагонали равна 𝑑. Так как другая диагональ
в два раза больше первой, имеем 𝑑=2𝑑. Таким образом, мы можем сформировать
уравнение, подставив 𝑑=2𝑑 в приведенную выше формулу и установив это
выражение, равное известной площади:
𝑑×(2𝑑)2=81.
Упрощение выражения в левой части за счет сокращения коэффициента 2 дает
𝑑=81.
Мы находим 𝑑 путем извлечения квадратного корня из каждой части уравнения,
принимая только положительное значение, поскольку 𝑑 представляет длину:
𝑑=√81=9.мм
Мы нашли длину меньшей диагонали 𝑑
быть 9 мм. Вторая диагональ в два раза длиннее, поэтому имеем
𝑑=2𝑑=2×9=18.мм
Длины диагоналей данного ромба равны
9мм и
18 мм.
В следующем примере мы решим задачу на ромб и квадрат
которые имеют одинаковую площадь. Зная периметр квадрата и длину
одной диагонали ромба вычислим длину
другая диагональ ромба.
Пример 3. Нахождение длины диагонали ромба по длине другой диагонали и фигуре с одинаковой площадью
Ромб и квадрат имеют одинаковую площадь. Если периметр квадрата
44 и одна из диагоналей ромба равна 10, какой длины другая
диагональ, до двух знаков после запятой?
Ответ
Чтобы связать две фигуры, нам нужно найти значение или
выражение для каждой из их областей, которые, как нам говорят, равны. Позволять
Начнем с рассмотрения квадрата.
Нам дано, что периметр квадрата равен 44 единицам. Мы помним, что
периметр фигуры — это расстояние вокруг ее края. В случае
квадрат, у которого четыре равные стороны по 𝑠 единиц длины, периметр равен
равно 4𝑠. Установка этого выражения равным 44 дает уравнение, которое
можно решить, чтобы определить длину стороны квадрата:
4𝑠=44𝑠=11.единиц
Площадь квадрата можно рассчитать по длине его стороны с помощью
формула площадь квадрата=𝑠. Замена
𝑠=11 дает
площадь квадратных квадратных единиц = 11 = 121.
Теперь мы знаем, что площадь ромба также равна
121 кв. Напомним, что площадь одного
ромб равен половине произведения длин его диагоналей
𝑑 и 𝑑:
площадь ромба=𝑑𝑑2.
Нам дано, что одна диагональ имеет длину 10 единиц, поэтому мы можем составить уравнение:
10×𝑑2=121.
Чтобы решить это уравнение для 𝑑, мы сначала упростим
в левой части, уменьшив коэффициент 2:
5𝑑=121.
Затем мы делим каждую часть уравнения на 5, чтобы получить
𝑑=1215=24,2.
С точностью до двух знаков после запятой длина другой диагонали ромба равна
24,20 ед.
В предыдущем примере мы использовали наши знания о том, как вычислить площадь
квадрат по длине его стороны. Однако квадрат на самом деле является особым типом
ромба, у которого две диагонали имеют одинаковую длину. Предположим, что каждая диагональ
квадрата имеет длину 𝑑 единиц. Используя формулу площади ромба,
площадь квадрата равна половине произведения длин его
диагонали, ведущие к
площадь квадрата=𝑑×𝑑2=𝑑2.
Формула: площадь квадрата
Площадь квадрата равна половине квадрата длины его диагонали. Для квадрата с диагональю длины 𝑑 единиц,
areaofsquasquareunits=𝑑2.
В нашем следующем примере мы рассмотрим, как найти длину диагонали
шахматной доске, сначала рассмотрев взаимосвязь между площадью и
диагонали меньших квадратов, из которых состоит шахматная доска.
Пример 4. Нахождение длины диагонали квадрата по его площади
Учитывая, что площадь каждой клетки на шахматной доске равна
81 см 2 ,
найдите длину диагонали шахматной доски.
Ответ
Шахматная доска состоит из 64 равных квадратов, расположенных в 8 рядов.
из 8. Заметим, что длина диагонали шахматной доски, которую мы
будет обозначать 𝐷, равно 8-кратной длине диагонали
каждого отдельного квадрата, который мы будем обозначать через 𝑑:
𝐷=8𝑑.
Нам известно, что площадь каждой клетки на шахматной доске равна
81 см 2 . Мы вспоминаем
и что площадь квадрата можно вычислить по длине его
диагональ 𝑑 по формуле
areaofsquare=𝑑2.
Следовательно, мы имеем
𝑑2=81.
Чтобы найти 𝑑, мы начнем с умножения каждой стороны этого
уравнение на 2, что приводит к
𝑑=162.
Затем извлекаем квадратный корень и упрощаем радикал, что дает
𝑑=√162=√81×2=√81×√2=9√2.cm
Наконец, мы можем вычислить длину диагонали
шахматную доску (𝐷), вспомнив, что 𝐷=8𝑑. Следовательно,
𝐷=8×9√2=72√2.cm
В предыдущем примере альтернативный подход состоял бы в том, чтобы
- вычислить длину стороны каждого из меньших квадратов, вспомнив, что
areaofsquare=𝑠, - вычислить длину диагонали каждой из меньших
квадратов по теореме Пифагора, - умножьте это на 8, чтобы получить длину диагонали
шахматная доска.
Несмотря на то, что это вполне допустимый метод, он включает такое же количество шагов
к методу, который мы представили, поэтому он не более или менее эффективен.
В нашем последнем примере мы найдем разницу между площадями
квадрат и ромб, каждый из которых рассчитывается с использованием длин их диагоналей.
Пример 5. Нахождение площадей квадрата и ромба по диагоналям
Определить разность площадей квадрата с диагональю
10 см и ромб
с диагоналями 2см
и 12 см.
Ответ
Начнем с вычисления площади каждой фигуры. Площадь квадрата может
вычислить по длине его диагонали 𝑑 по формуле
areaofsquare=𝑑2.
Следовательно, для квадрата с диагональю 10 см,
площадь квадратасм=10×102=50.
Площадь ромба равна половине произведения длин его
диагонали 𝑑 и 𝑑:
площадь ромба=𝑑𝑑2.
Отсюда для ромба с диагоналями
2 см и
12 см,
площадь ромба см=2×122=12.
Наконец, мы вычисляем разницу в площади, вычитая площадь
меньшего четырехугольника (ромба) из площади большего
четырехугольник (квадрат):
разность вплощадиквадратаплощадьромбасм=−=50−12=38.
Давайте закончим повторением некоторых ключевых моментов.
Ключевые точки
- Площадь ромба равна половине произведения длин его диагоналей.
- Для ромба с диагоналями длины 𝑑 и
𝑑 единиц,
areaofrhombussquareunits=𝑑𝑑2. - Площадь квадрата равна половине квадрата длины его диагонали.
- Для квадрата с диагоналями длины 𝑑 единиц,
площадьквадратных квадратов=𝑑2.
Площадь параллелограммов: определение и формула
Задумывались ли вы, какую форму представляет воздушный змей? Воздушный змей обычно имеет четыре стороны, что делает его типом четырехугольника.
Теперь обратите внимание, как верхняя левая и нижняя правая стороны воздушного змея, показанного ниже, параллельны друг другу. Точно так же верхняя правая и нижняя левая стороны этого воздушного змея параллельны друг другу.
Есть предположения, что это за четырехугольник? Это правильно! Это параллелограмм.
Скажем, вам сказали найти площадь этого воздушного змея. Поскольку это тип параллелограмма, мы могли бы использовать определенную формулу для вычисления площади этого воздушного змея.
Иллюстрация воздушного змея, StudySmarter Originals
В этой статье мы познакомимся с формулой площади параллелограмма и рассмотрим некоторые рабочие примеры, где она применяется.
Резюме по параллелограммам
Прежде чем мы перейдем к нашему основному предмету, давайте проведем краткий обзор параллелограммов, чтобы облегчить себе задачу.
Как следует из названия, параллелограмм имеет параллельные стороны. Таким образом, мы можем определить параллелограмм, как показано ниже.
Параллелограмм — это четырехугольник с двумя парами параллельных противоположных сторон. Параллелограмм является частным случаем четырехугольника.
Четырехсторонняя плоская фигура известна как четырехугольник.
На следующем рисунке показан параллелограмм со сторонами AB, BD, CD и AC.
Иллюстрация параллелограмма, StudySmarter Originals
Свойства параллелограммов
Вернемся к нашему параллелограмму ABCD выше. Давайте посмотрим на некоторые свойства, которые отличают эту форму.
-
Противоположные стороны треугольника ABCD параллельны. В этом случае АВ параллельна CD, а АС параллельна BD. Запишем это как AB // CD и AC // BD,
-
Противоположные углы ABCD равны. Здесь ∠CAB = ∠CDB и ∠ACD = ∠ABD,
-
Диагонали параллелограмма делятся пополам в точке, скажем, M. Тогда AM = MD и BM = MC. Это показано ниже,
Свойство параллелограмма, StudySmarter Originals
Типы параллелограммов
Существуют три типа параллелограммы, которые мы должны рассмотреть на протяжении всей этой программы, а именно
-
прямоугольник
- Формулу площади ромба можно использовать и для нахождения площади воздушного змея.
9029 2 квадрат
7 9027 7024 7024. их друг от друга. Более подробное объяснение параллелограммов можно найти здесь, Параллелограммы.
Площадь определения параллелограмма
Площадь параллелограмма определяется как область, ограниченная параллелограммом в двумерном пространстве.
На приведенной выше диаграмме общая площадь, заключенная в ABCD, является площадью параллелограмма ABCD.
Формула площади параллелограмма
Ссылаясь на наш исходный параллелограмм ABCD, мы добавим к этой фигуре два новых компонента, называемых b и h. Это показано на диаграмме ниже.
Параллелограмм с основанием b и высотой h, Study Smarter Originals
Переменная b называется основанием параллелограмма. Любая из длинных сторон ABCD может быть использована в качестве основания. На приведенной выше диаграмме b может быть либо AB, либо CD. Здесь, здесь мы взяли b = AB.
Обратите внимание, что это понятие является соглашением, а не жестким правилом.
Переменная h называется высотой параллелограмма. Это также можно назвать высотой. Высота — это отрезок, перпендикулярный паре смежных сторон параллелограмма с одной конечной точкой на одной стороне и другой конечной точкой на другой стороне.
Теперь, когда мы определили наши переменные b и h, мы можем представить площадь параллелограмма следующим образом.
Площадь любого параллелограмма определяется формулой
, где b = основание, а h = высота.
Примеры площади параллелограмма
Имея это в виду, давайте теперь рассмотрим следующие рабочие примеры, в которых используется эта формула.
Найдите площадь следующего параллелограмма,
Пример 1, StudySmarter Originals
Решение
Здесь основание равно b = 24 единицы, а высота h = 10 единиц. Используя формулу площади параллелограмма, получаем,
Таким образом, площадь этого параллелограмма составляет 240 единиц 2 .
Параллелограмм высотой 5 единиц длины имеет площадь 20 единиц 2 . Какова длина основания?
Раствор
Здесь нам дана площадь параллелограмма и высота (или высота), то есть
A = 20 и h = 5.
Чтобы найти основание, нам просто нужно подставить эти значения в нашу площадь формулу параллелограмма и переформулируйте уравнение, как показано ниже.
Сделав b предметом, получим
Таким образом, основание этого параллелограмма равно 4 единицам.
Нахождение площади параллелограмма из прямоугольника
Предположим, мы хотим найти площадь параллелограмма, где высота (или высота) неизвестна. Вместо этого нам даны длины двух сторон параллелограмма, а именно длины АВ и АС.
Давайте попробуем рассмотреть этот сценарий графически. Возвращаясь к нашему исходному параллелограмму ABCD, давайте проведем две высоты для каждой пары смежных сторон, AC и AB, а также CD и BD.
Площадь параллелограмма из прямоугольника, StudySmarter Originals
Таким образом, мы получаем две новые точки на этом параллелограмме, а именно S и T. Теперь посмотрим на форму, образованную BTCS. Вам это кажется знакомым? Вот так! Это прямоугольник, который также является разновидностью параллелограмма. Теперь нам нужно найти способ получить длины либо CS, либо BT, чтобы мы могли вывести высоту этого параллелограмма.
Обратите внимание, что из построения этих двух отрезков мы получили пару прямоугольных треугольников, CAS и BDT. Поскольку CS = BT, нам достаточно вычислить только один из них. Рассмотрим треугольник CAS.
Треугольник CAS, StudySmarter Originals
Для простоты мы будем обозначать следующие стороны как: x = AS, y = CS и z = AC. Поскольку это прямоугольный треугольник, мы можем использовать теорему Пифагора, чтобы получить длину CS, которая является высотой параллелограмма ABCD. Учитывая длины AS и AC, мы имеем
x 2 + y 2 = z 2
Преобразовав это и применив квадратный корень, мы получим
Поскольку мы теперь нашли длину CS, мы можем продолжить нахождение площади параллелограмма ABCD по данной формуле. За основание возьмем длину АВ. Таким образом, площадь ABCD равна
Покажем это на примере.
Дан параллелограмм PQRS, найдите его площадь.
Пример 2, StudySmarter Originals
Линия OQ представляет собой высоту смежных сторон PQ и PS. Длины QR, PQ и PO равны 12 единицам, 13 единицам и 5 единицам соответственно.
Решение
Так как QR = PS, мы можем принять основание как QR = 12 единиц. Теперь нам нужно найти высоту этого параллелограмма, чтобы найти его площадь. Это дается отрезком OQ.
Из диаграммы видно, что треугольник QPO является прямоугольным. Поскольку у нас есть длина PO = 5 единиц, мы можем использовать теорему Пифагора, чтобы найти OQ.
Переставляя это и применяя квадратный корень, мы получаем следующее значение для OQ,
Таким образом, высота этого параллелограмма составляет 12 единиц. Теперь мы можем найти площадь PQRS, как показано ниже:
Следовательно, площадь этого параллелограмма составляет 144 единицы 2 .
Параллелограмм, вписанный в прямоугольник Пример
В этом примере мы рассмотрим случай, когда параллелограмм вписан внутрь прямоугольника. Мы хотим определить площадь внутри прямоугольника, не занятую параллелограммом.
На рисунке ниже показан параллелограмм PXRY внутри прямоугольника PQRS. Найдите площадь области, заштрихованной синим цветом.
Пример 3. Исследование Smarter Originals
Отрезок линии XZ представляет собой высоту смежных сторон XP и PY. Здесь QP = RS = XZ, PX = RY и QR = PS. Длины QP, PY и SY равны 19ед., 21 ед. и 7 ед. соответственно.
Решение
Здесь высота прямоугольника PQRS равна h = QP = 19 единиц. Основание равно PS, равному сумме длин PY и SY. Таким образом, основание равно
Таким образом, b = 28 единиц. Формула площади прямоугольника представляет собой произведение его основания и высоты. Таким образом, площадь прямоугольника PQRS равна
Теперь найдем площадь параллелограмма PXRY. Высота параллелограмма равна XZ. Так как XZ = QP, то h = XZ = 19 единиц. База задается длиной PY. Таким образом, b = PY = 21 единица. Используя формулу площади параллелограмма, получаем
Таким образом, площади прямоугольника PQRS и параллелограмма PXRY составляют 532 единицы 2 и 399 единиц 2 соответственно.
Теперь нам нужно найти область, заштрихованную синим цветом, которая не занята параллелограммом внутри прямоугольника. Это можно найти, вычислив разницу между площадями прямоугольника PQRS и параллелограмма PXRY. При этом получаем
Следовательно, площадь оставшейся области, заштрихованной синим цветом, составляет 133 единицы 2 .
Особый случай: площадь ромба
Ромб — это особый тип четырехугольника, площадь которого вычисляется по собственной формуле. Иногда его называют равносторонним четырехугольником. Напомним определение ромба.
Ромб представляет собой параллелограмм, все четыре стороны которого имеют одинаковую длину.
Теперь рассмотрим ромб ниже. На этом параллелограмме построены две диагонали AD (голубая линия) и BC (синяя линия). Диагонали имеют длины d 1 и d 2 соответственно.
Площадь ромба, StudySmarterOriginals
Площадь ромба
Площадь ромба находится по формуле
, где A = площадь, d 1 = длина диагонали AD и d 2 = длина диагонали BC.
Пример площади ромба
Вот пример площади ромба.
Диагонали ромба имеют длины 10 единиц и 15 единиц. Чему равна площадь ромба?
Раствор
Обозначим d 1 = 10 единиц и d 2 = 15 единиц. Применяя формулу выше, получаем
Таким образом, площадь этого ромба равна 75 единицам 2 .
Мы закончим эту статью последним примером, касающимся площади параллелограмма или, точнее, воздушного змея.
Реальный пример площади параллелограмма
Теперь мы вернемся к нашему примеру в начале этой статьи. Поскольку теперь у нас есть базовая формула для вычисления площади параллелограмма, мы можем использовать ее, чтобы найти площадь нашего воздушного змея.
Вы решаете измерить длину двух диагоналей воздушного змея рулеткой. Вы обнаружите, что горизонтальная диагональ и вертикальная диагональ равны 18 дюймам и 31 дюйму соответственно.