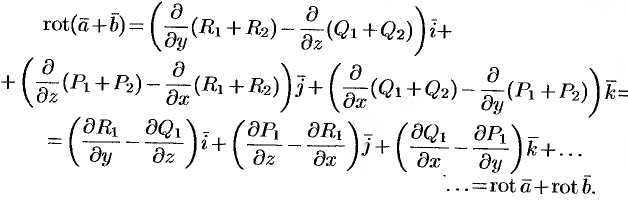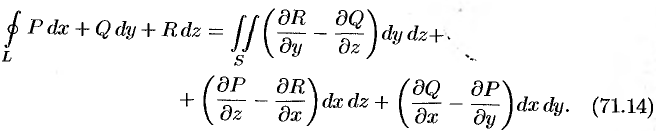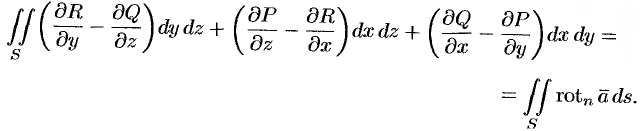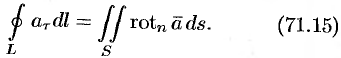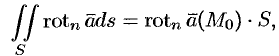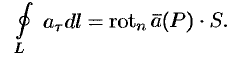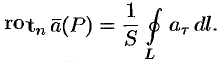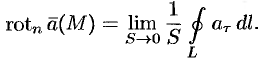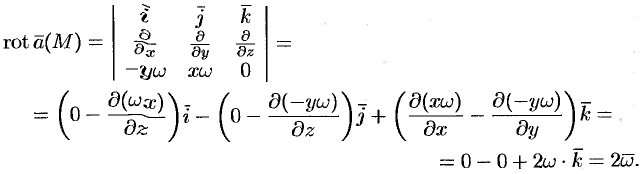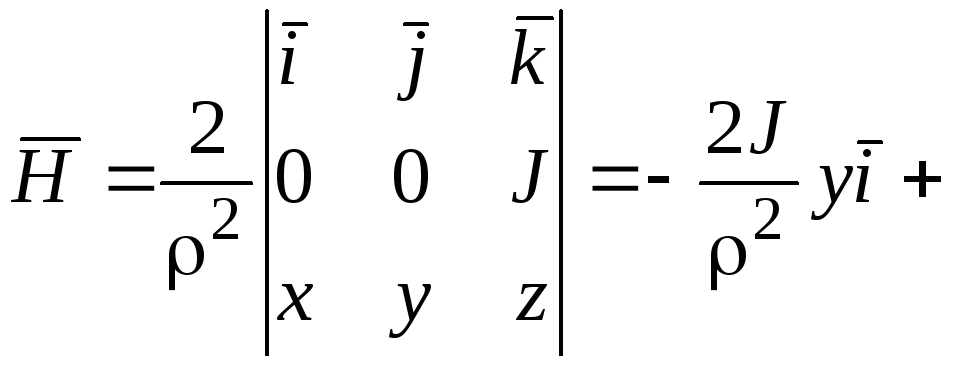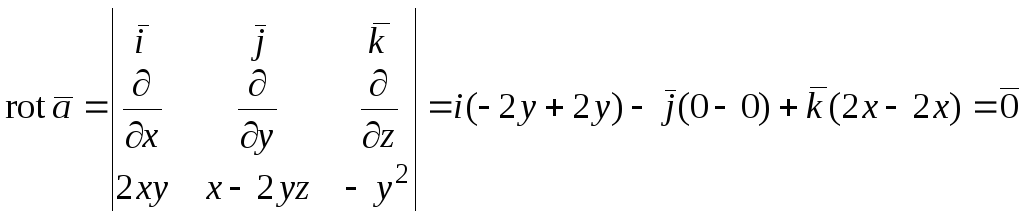У этого термина существуют и другие значения, см. Ротор.
Ро́тор, рота́ция[источник не указан 1010 дней] или вихрь — векторный дифференциальный оператор над векторным полем.
Обозначается разными способами:
Результат действия оператора ротора на конкретное векторное поле 


Поле 


Определение[править | править код]
Ротор 





-
.
Направление обхода контура выбирается так, чтобы, если смотреть в направлении 

Операция, определённая таким образом, существует строго говоря только для векторных полей над трёхмерным пространством. Об обобщениях на другие размерности — см. ниже.
Альтернативным определением может быть непосредственное вычислительное определение дифференциального оператора, сводящееся к
-
,
что может быть записано в конкретных координатах как это показано ниже.
Иногда можно встретиться с таким альтернативным[6] определением[7]
,
- где
— точка, в которой определяется ротор поля
,
— какая-то замкнутая поверхность, содержащая точку
внутри и в пределе стягивающаяся к ней,
— вектор элемента этой поверхности, длина которого равна площади элемента поверхности, ортогональный поверхности в данной точке,
- знаком
обозначено векторное произведение,
— объём внутри поверхности
.
- где
Это последнее определение таково, что даёт сразу вектор ротора, не нуждаясь в определении проекций на три оси отдельно.
Интуитивный образ[править | править код]
Если 

Конкретно 

- Простую иллюстрацию этого факта — см. ниже.
Эта аналогия может быть проведена вполне строго (см. ниже). Основное определение через циркуляцию, данное выше, можно считать эквивалентным полученному таким образом.
Выражение в конкретных координатах[править | править код]
Формула ротора в декартовых координатах[править | править код]
В трёхмерной декартовой системе координат ротор (в соответствии с определением выше) вычисляется следующим образом (здесь 


-
,
или
(что можно считать альтернативным определением, по сути совпадающим с определением в начале параграфа, по крайней мере при условии дифференцируемости компонент поля).
Для удобства можно формально представлять ротор как векторное произведение оператора набла (слева) и векторного поля:
(последнее равенство формально представляет векторное произведение как определитель).
Формула ротора в криволинейных координатах[править | править код]
Удобным общим выражением ротора, пригодным для произвольных криволинейных координат в трёхмерном пространстве, является выражение с использованием тензора Леви-Чивиты (используя верхние и нижние индексы и правило суммирования Эйнштейна):
-
,
где 





Это выражение может быть также переписано в виде:
-
.
Формула ротора в ортогональных криволинейных координатах[править | править код]
-
,
где 
Обобщения[править | править код]
- Обобщением ротора применительно к векторным (и псевдовекторным) полям на пространствах произвольной размерности (при условии совпадения размерности пространства с размерностью вектора поля) является антисимметричное тензорное поле валентности два, компоненты которого равны:
- Эта же формула может быть записана через внешнее произведение с оператором набла:
- Для двумерной плоскости может быть использована аналогичная формула с псевдоскалярным произведением (такой ротор будет псевдоскаляром, и его величина совпадает с проекцией традиционного векторного произведения на нормаль к данной плоскости, если она вложена в трёхмерное евклидово пространство).
-
- ротор и дивергенцию (а они останутся действительными числами) можно записать так:
,
.
Основные свойства[править | править код]
-
.
-
,
.
-
.
-
- Таким образом, различные векторные поля могут иметь одинаковый ротор. При этом различаться они будут обязательно на безвихревое поле (то есть, локально — на градиент некоторого скалярного поля).
- Дивергенция ротора равна нулю (поле ротора бездивергентно):
-
,
.
-
.
- Дивергенция векторного произведения двух векторных полей выражается через их роторы по формуле:
-
- Таким образом, если
и
— безвихревые векторные поля, их векторное произведение будет бездивергентным и локально будет обладать векторным потенциалом. Например, если
, а
, легко найти векторный потенциал для
:
.
- Локально каждое бездивергентное векторное поле в трёхмерной области является векторным произведением двух градиентов.
- Ротор ротора равен градиенту дивергенции минус лапласиан:
-
.
- Ротор векторного произведения полей равен:
-
.
Физическая интерпретация[править | править код]
При движении сплошной среды распределение её скоростей (то есть поле скорости течения жидкости) вблизи точки О задаётся формулой Коши — Гельмгольца:
,
где 


Таким образом, движение сплошной среды вблизи точки 



Применяя к формуле Коши — Гельмгольца операцию ротора, получим, что в точке 

В качестве интуитивного образа, как это описано выше, здесь можно использовать представление о вращении брошенной в поток маленькой пылинки (увлекаемой потоком с собой, без его заметного возмущения) или о вращении помещённого в поток с закреплённой осью маленького (без инерции, вращаемого потоком, заметно не искажая его) колеса с прямыми (не винтовыми) лопастями. Если то или другое при взгляде на него вращается против часовой стрелки, то это означает, что вектор ротора поля скорости потока в данной точке имеет положительную проекцию в направлении на нас.
Формула Кельвина — Стокса[править | править код]
Циркуляция вектора по замкнутому контуру, являющемуся границей некоторой поверхности, равна потоку ротора этого вектора через эту поверхность:
Частный случай формулы Кельвина — Стокса для плоской поверхности — содержание теоремы Грина.
Примеры[править | править код]
- В этой главе будем для единичных векторов по осям (прямоугольных) декартовых координат использовать обозначение
Простой пример[править | править код]
Рассмотрим векторное поле 


.
- В отношении этого примера нетрудно заметить, что
, где
— радиус-вектор, а
, то есть поле
можно рассматривать как поле скоростей точек твёрдого тела, вращающегося с единичной по величине угловой скоростью, направленной в отрицательном направлении оси
(то есть по часовой стрелке, если смотреть «сверху» — против оси
). Интуитивно более или менее очевидно, что поле закручено по часовой стрелке. Если мы поместим колесо с лопастями в жидкость, текущую с такими скоростями (то есть вращающуюся как целое по часовой стрелке), в любое место, мы увидим, что оно начнет вращаться по направлению часовой стрелки. (Для определения направлений используем, как обычно, правило правой руки или правого винта).
-компоненту поля
будем считать равной нулю. Однако если она ненулевая, но постоянная (или даже зависящая только от
) — результат для ротора, получаемый ниже, будет тем же.
Вычислим ротор:
Как и предположили, направление совпало с отрицательным направлением оси 

не зависящим от координат (что естественно для вращения твёрдого тела).
Что замечательно,
Угловая скорость вращения в данном примере одна и та же в любой точке пространства (угол поворота пылинки, приклеенной к твердому телу не зависит от того места, где именно приклеить пылинку). График ротора 
Более сложный пример[править | править код]
Теперь рассмотрим несколько более сложное векторное поле[9]:
-
.
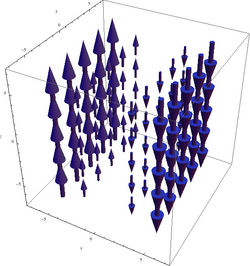
Его график:
Мы можем не увидеть никакого вращения, но, посмотрев повнимательнее направо, мы видим большее поле в, например, точке 



Действительно, ввинчивание происходит в направлении 



Ротор 

Можно заметить, что график этого ротора не зависит от 





Поясняющие примеры[править | править код]
- В смерче ветры вращаются вокруг центра, и векторное поле скоростей ветра имеет ненулевой ротор (где-то) в центральной области. (см. Вихревое движение). (Правда, ближе к краю где-то ротор может принимать и нулевое значение см. ниже).
- Для векторного поля
скоростей движения точек вращающегося твёрдого (абсолютно твёрдого) тела,
одинаков всюду по объёму этого тела и равен (вектору) удвоенной угловой скорости вращения (подробнее — см. выше). В частном случае чисто поступательного движения или покоя, этот ротор может быть равен нулю, как и угловая скорость, тоже для всех точек тела.
- Если бы скорости автомобилей на трассе описывались векторным полем, и разные полосы имели разные ограничения по скорости движения, ротор на границе между полосами был бы ненулевым.
- Закон электромагнитной индукции Фарадея, одно из уравнений Максвелла, просто записывается (в дифференциальной форме) через ротор: ротор электрического поля равен скорости изменения магнитного поля (со временем), взятой с обратным знаком.
- Четвёртое уравнение Максвелла — закон Ампера — Максвелла — также записывается в дифференциальной форме с использованием ротора: ротор напряжённости магнитного поля равен сумме плотностей тока обычного и тока смещения[10].
Важный контринтуитивный пример[править | править код]
Нужно иметь в виду, направление ротора может не соответствовать направлению вращения поля (пусть это поле скоростей жидкости), которое представляется очевидным, соответствующим направлению течения. Он может иметь противоположное течению направление, и, в частности, ротор может оказаться равным нулю, хотя линии тока загибаются или даже представляют собой точные окружности).
Другими словами, направление искривления векторных линий векторного поля никак не связано с направлением вектора ротора этого поля.
Рассмотрим такой пример. Пусть поле скорости течения жидкости 
,
.
Если 



Сказанное означает, что среда как целое может вращаться вокруг наблюдателя в одну сторону, а каждый её маленький объём — в противоположную сторону, или не вращаться вообще.
Примечания[править | править код]
- ↑ Также в немецкой, откуда, по-видимому, это обозначение и попало в русскую, и почти везде в Европе, кроме Англии, где такое обозначение считается «альтернативным» (возможно, из-за неблагозвучности: англ. rot — гниль, гниение)[источник не указан 2709 дней].
- ↑ О. Хэвисайд. The relations between magnetic force and electric current Архивная копия от 22 июля 2016 на Wayback Machine. // The Electrician, 1882.
- ↑ Точнее — если
— псевдовекторное поле, то
— обычное векторное поле (вектор
— полярный), и наоборот, если поле
— поле обычного (полярного) вектора, то
— псевдовекторное поле.
- ↑ Стягивание в точку — обязательное условие, просто стремления
к нулю недостаточно, ведь мы хотим получить характеристику поля в одной конкретной точке.
- ↑ Обычное соглашение, согласованное с определением через векторное произведение с оператором набла.
- ↑ Эквивалентность этих определений, если предел существует и не зависит от способа стягивания точке, видна, если выбрать поверхность
второго определения в виде цилиндрической поверхности с основаниями, полученными параллельным переносом площадки первого определения
на очень маленькое расстояние в двух противоположных направлениях ортогонально к
. В пределе же они должны приближаться к
быстрее, чем уменьшается размер самой
. Тогда выражение второго определения разбивается на два слагаемых, одно, содержащее интеграл по боковой поверхности, совпадает с первым определением, а второе даёт ноль в проекции на нормаль к основаниям, поскольку
на основаниях само ортогонально ему. Можно вместо этого рассмотреть просто маленький параллелепипед в качестве поверхности, тогда не столь легко сразу строго, но в целом понятно аналогичное.
- ↑ Формально сходным с определением дивергенции через поток через поверхность:
.
- ↑ Оговорка о локальности важна для общего случая, когда рассматриваемые здесь поля
и
могут быть определены на пространстве (многообразии) или области нетривиальной топологии, и когда условия
также выполняется вообще говоря на пространстве или области нетривиальной топологии. Для случая евклидова пространства или его односвязной области оговорка о локальности не нужна, поле, ротор которого нуль на всем таком пространстве или односвязной области, будет потенциальным на всем этом пространстве или этой области. То есть тогда найдётся такое скалярное поле
, что
будет верно везде на этом пространстве или этой области.
- ↑ Простейшая физическая реализация такого поля (с точностью до аддитивной константы, которая не влияет на вычисление ротора, поскольку
; кроме того, при желании эта константа может быть обнулена переходом в систему отсчета, связанной с максимально быстро текущей водой в центре струи) — ламинарное течение (вязкой) жидкости между двумя параллельными твердыми плоскостями, перпендикулярными оси
, под действием однородного силового поля (тяжести) или разности давлений. Течение жидкости в трубе круглого сечения даёт такую же зависимости
, поэтому приведённое дальше вычисление ротора применимо и к этому случаю (проще всего взять ось
совпадающей с осью трубы, и хотя зависимость
не будет уже константой, однако
будет нулем при
, как и в основном примере, то есть вычисление и ответ для любой плоскости, проходящей через ось трубы такой же, а это решает задачу).
- ↑ Математический словарь высшей школы. В. Т. Воднев, А. Ф. Наумович, Н. Ф. Наумович
См. также[править | править код]
- Ротор векторного поля. Теорема Стокса. на YouTube
- Вычисление ротора векторного поля. на YouTube
- Векторный анализ
- Теорема Грина
- Формулы векторного анализа
Циркуляция векторного поля. Ротор вектора. Теорема Стокса
Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
Пусть в некоторой области G задано непрерывное векторное поле а ) к и замкнутый ориентированный контур L. Определение 1. Циркуляцией вектора а по замкнутому контуру L называется криволинейный интеграл 2-го рода от оектора а по контуру L Здесь dr — вектор, длина которого равна дифференциалу дуги L, а направление совпадаете направлением касательной к L, оп- Рис. 31 ределяемымориентацией контура (рис. 31); символ f означает, что интеграл берется по зам1«угому контуру L. ь
Пример 1. вычислить циркуляцию векторного поля вдоль эллипса L: По определению циркуляции имеем Параметрические уравнения данного эллипса имеют вид: , и, значит, . Подставляя эти выражения в формулу (2), найдем Циркуляция векторного поля. Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля Правила вычисления ротора 8.1.
Ротор (вихрь) векторного поля Рассмотрим поле вектора Р, Q, R которого непрерывны и имеют непрерывные частные производные первого порядка по всем своим аргументам. Огределенив 2. Ротором вектора »(М) называется вектор, обозначаемый символом rot а и определяемый равенством или, в символической, удобной для запоминания форме, Этот определитель раскрывают по элементам первой строки, при этом операции умножения элементов второй строки на элементы третьей строки понимаются как операции дифференцирования, например,
Определение 3. Если в некоторой области G имеем rot а = 0, то поле вектора а в области G называете я безвихревым. Пример 2. Найти ротор вектора 4 Согласно формуле (3) имеем Так как rot а — вектор, то мы можем рассматривать векторное поле — поле ротора вектора а. Предполагая, что координаты вектора а имеют непрерывные частные производные второго порядка, вычислим дивергенцию вектора rot а. Получим Таким образом, поле вектора rot а соленоида л ьно.
Теорема 7 (Стокса). Циркуляция вектора а вдоль ориентированного замкнутого контура L равна потоку ротора этого вектора через любую поверхность Е, натянутую на контур L, При этом предполагается, что координаты вектора а имеют непрерывные частные производные в некоторой области G пространства, содержащей поверхность Е, и что ориентация орта нормали п° к поверхности ЕС G согласована с ориентацией контура L так, что из конца нормши обход контура в заданном направлении виден совершающимся против часовой стрелки.
Учитывая, что , и пользуясь определением ротора (3), перепишем формулу (4) в следующем виде: Рассмотрим сначала случай, когда гладкая поверхность Е и ее контур L однозначно проектируются на область D плоскости хОу и ее границу — контур А соответственно (рис. 32). Ориентация контура L порождает определенную ориентацию контура А. Для определенности будем считать, что контур L ориентирован так, что поверхность Е остается слева, так что веетор нормали п к поверхности Е составдя етсосью Oz острый угол 7 (cos 7 >0).
Возможно вам будут полезны данные страницы:
Пусть — уравнение поверхности Е и функция ф(х>у) непрерывна и имеет непрерывные частные производные gf и ^ в замкнутой области D.
Рассмотрим интеграл Линия L лежит на поверхности Е. Поэтому, пользуясь уравнением этой поверхности , мы можем заменить г под знаком интеграла на ^(ж, у). Координаты перемсннойточки кривой А равны координатам соответствующей точки на кривой L, а потому интегрирование по L можно заменить интегрированием по А, Применим к интегралу, стоящему справа, формулу Грина.
Имеем Перейдем теперь от интеграла по области D к интегралу по поверхности Е. Так как dS = cos 7 • da, то из формулы (8) получим, что Вектор нормали п° к поверхности Е определяется выражением к. Отсюда видно, что . Поэтому равенсгво (9) можно переписать так: Считая Е гладкой поверхностью, однозначно проектирующейся на все три координатные плоскости, аналогично убеждаемся в справедливости формул Циркуляция векторного поля.
Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля Правила вычисления ротора Складывая равенства почленно, получим формулу Стокса (5), или, короче, Замечание 1. Мы показали, что поле вектора rote — соленоидальное, и потому поток вектора rota не зависит от вида поверхности Е, натянутой на контур L. Замечание 2. Формула (4) выведена в предположении, что поверхность £ однозначно проектируется на все три координатные плоскости. Бели это условие не выполнено, то разбиваем £ на частя так, чтобы каждая часть указанному условию удовлетворяла, а затем пользуемся аддитивностью интегралов.
Пример 3:
Вычислить циркуляцию вектора по линии 1) пользуясь определением; 2) по теореме Стокса. 4 1) Зададим линию L параметрически: Тогда 2) Найдем rota: Натянем на контур L кусок плосхости Тогда . Инвариантное определение ротора поля Из теоремы Стокса можно получить инвариантное определение ротора поля, не связанное с выбором системы координат. Теорема 8.
Проекция ротора а на любое направление не зависит от выбора системы координат и равна поверхностной плотности циркуляции вектора а по контуру площадки, перпендикулярной этому направлению, Здесь (Е) — плоская площадка, перпендикулярная вектору л; 5 — площадь этой площадки; L — контур площадки, ориентированный так, чтобы обход контура был виден из конца вектора п против хода часовой стрелки; (Е) М означает, что площадка (Е) стягивается к точке М, в которой рассматривается вектор rot а, причем вектор нормали п к этой площадке остается все время одним и тем же (рис. 33). 4
Применим сначала к циркуляции (a,dr) вектора а теорему Стокса, а затем к полученному двойному интегралу — теорему о среднем значении: откуда (скалярное произведение берется в некоторой средней точке Мф площадки (Е)). Пристягивании площадки (Е) кточке М средняяточка Л/ср тоже стремится кточ-ке М и, в силу предполагаемой непрерывности частных производных от координат вектора а (а значит, и непрерывности rot а), мы получаем Поскольку проекция вектора rot а на произвольное направление не зависитотвы-бора системы координат,то и сам вектор rota инвариантен относительно этого выбора.
Отсюда получаем следующее инвариантное определение ротора поля: ротор поля есть вектор, длина которого равна наибольшей поверхностной плотности циркуляции в данной точке, направленный перпендикулярно той площадке, на которой эта наибольшая плотность циркуляции достигается; при этом ориентация вектора rota согласуется с ориентацией контура, при которой циркуляция положительна, по правилу правого винта. 8.3.
Физический смысл ротора поля Пустьтвердое
тело вращается вокруг неподвижной оси I с угловой скоростью и. Не нарушая общности, можно считать, что ось I совпадает с осью Oz (рис. 34). Пусть М(г) — изучаемая точка тела, где Вектор угловой скорости в нашем случае равен из = wk, вычислим вектор v линейной скорости точки М, Отсюда Циркуляция векторного поля. Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля.
Правила вычисления ротора
Итак, вихрь поля скоростей вращающегося твердого тела одинаков во всех точках поля, параллелен оси вращения и равен удвоенной угловой скорости вращения. 8.4. Правила вычисления ротора 1. Ротор постоянного вектора с равен нулевому вектору, 2. Ротор обладает свойством линейности постоянные числа. 3. Ротор произведения скалярной функции и<М) на векторную а(М) вычисляется по формуле
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Ротор векторного поля. Формула Стокса
Ротор поля. Формула Стокса
Ротором (или вихрем) векторного поля
называется вектор, обозначаемый 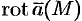
Формулу (71.13) можно записать с помощью символического определителя в виде, удобном для запоминания:
Отметим некоторые свойства ротора.
- Если
— постоянный вектор, то
.
, где
.
, т. e. ротор суммы двух векторов равен сумме роторов слагаемых.
- Если
— скалярная функция, а
— векторная, то
Эти свойства легко проверить, используя формулу (71.13). Покажем, например, справедливость свойства 3:
Используя понятия ротора и циркуляции, векторного поля, запишем известную в математическом анализе (см. п. 58.4) формулу Стокса:
Левая часть формулы (71.14) представляет собой циркуляцию вектора 

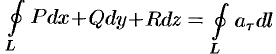
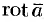


Следовательно, формулу Стокса можно записать в виде
Такое представление формулы Стокса называют ее векторной формой. В этой формуле положительное направление на контуре 

Формула (71.15) показывает, что циркуляция вектора 





Используя формулу (71.14), можно дать другое определение ротора поля, эквивалентное первому и не зависящее от выбора координатной системы.
Для этого применим формулу Стокса (71.15) для достаточно малой плоской площадки 


По теореме о среднем для поверхностного интеграла (п. 57.1, свойство 7) имеем:
где 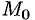

Тогда формулу (71.15) можно записать в виде
Пусть контур 

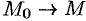
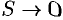
Ротором вектора 




Как видно из определения, ротор вектора 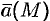
Дадим физическое истолкование понятия ротора векторного поля. Найдем ротор ноля линейных скоростей твердого тела, вращающегося вокруг оси 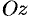
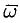
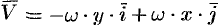
По определению ротора
Ротор этого поля направлен параллельно оси вращения, его модуль равен удвоенной угловой скорости вращения.
С точностью до числового множителя ротор поля скоростей 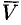
Замечание. Из определения (71.13) ротора вытекает, что направление ротора — это направление, вокруг которого циркуляция имеет наибольшее значение (плотность) по сравнению с циркуляцией вокруг любого направления, не совпадающего с нормалью к площадке 
Так что связь между ротором и циркуляцией аналогична связи между градиентом и производной по направлению (см. п. 70.3).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Элементы теории поля и векторного анализа (стр. 2 )
 |
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 |


Пример 1.2. Найти 
Аналогично, 

Последнее соотношение можно использовать для получения напряженности поля для сферически-симметричных потенциалов, то есть для потенциалов, поверхности уровня которых представляют собой сферы.
1.3 Оператор C
Определение Оператором называется правило, по которому одной функции ставится в соответствие другая функция.
Предположим, мы имеем две функции f и φ.Соотношение f = Tφ, где T – оператор, устанавливает соответствие между ними, Например, если 

Заметим, соотношение (1.3) не зависит от того, какое скалярное поле мы дифференцируем. Эту формулу можно записать компактно, если ввести дифференциальный векторный оператор C (читается «набла»).

В многих случаях с оператором ∇ можно обращаться как с обычным вектором. ∇ = 

Примечание Вообще говоря, не любые три оператора образуют векторный оператор. (Также как не любые три числа образуют вектор.) Компоненты векторных операторов, как и компоненты обычных векторов, при преобразовании системы координат должны преобразовываться определенным образом. Можно провести и более простые рассуждения, показывающие, что ∇ – векторный оператор. В предыдущем разделе мы показали, что grad f = ∇ f – вектор, направленный по нормали к поверхности уровня. Поскольку, формально соотношение (1.6) выглядит как действие оператора на скалярную функцию и в результате получается вектор, то поэтому ∇ – векторный оператор.
Пример 1.3. Вычислить вектор 
Последовательно проводим действия:
1. Находим частные производные от функции



2. Каждую из полученных производных умножаем на соответствующий единичный вектор, полученные векторы складываем и результат умножаем на функцию 

3. Вычисляем полученный вектор в точке (1,2,0):

1.4 Действия с оператором ∇. Дивергенция вектора. Ротор вектора.
Рассмотрим векторное поле A(x, y,z) = Из двух векторов ∇ и A по обычным правилам векторной алгебры можно образовать скалярное произведение:

Эта скалярная величина называется дивергенцией вектора A и обозначается как divA:

Из векторов ∇ и A можно образовать и векторное произведение. Используя обычные правила векторной алгебры, получим:

Эта векторная величина называется ротором вектора A и обозначается как rotA:

Примечание Определения (1.1) и (1.13) даны в прямоугольной системе координат. К независящим от выбора системы координат определениям дивергенции и ротора функции, а также к их смыслу мы вернемся позже.
В различных применениях векторного анализа часто возникает необходимость в вычислении div(Af) и rot(Af), где A – векторное поле, f-скалярное. Получим соответствующие формулы, используя (1.8), (1.10) и (1.12):


Пример 1.4. Вычислить divr, где r = – радиус вектор:
Пример 1.5. Вычислить rotr, где, по-прежнему, r = – радиус вектор:
Пример 1.6. Вычислить div(rφ(r)),где r = – радиус вектор, r – его длина, φ(r) – произвольная дифференцируемая функция от r.
Используя формулу (1.14) и решения примеров 1.2 и 1.4, получаем
Пример 1.7. Вычислить rot(rφ(r)),где r, r и φ(r) определены в примере 1.6.
Используя формулу (1.15) и решения примеров 1.2 и 1.5, получаем:
1.5 Некоторые формулы векторного анализа
До сих пор мы рассматривали действие оператора ∇ на скалярные и векторные поля и их произведения. Сейчас мы получим некоторые часто встречающиеся в приложениях соотношения, в которых оператор ∇ встречается дважды.
1.5.1 Вычисление rot gradf
Пустьf(x, y,z) – некоторое скалярное поле. Тогда, используя формулы (1.3) и (1.10) получим:

Этот же результат можно получить проще, используя, оператор ∇.
rot gradf = [∇,(∇f] = [∇,∇]f = 0, так как векторное произведение вектора самого на себя равно нулю.
1.5.2 Вычисление div rot A
Используя соотношения (1.8) –(1.11) и правила для вычисления смешанного произведения векторов, получаем:

так как в определителе две одинаковых строки.
1.5.2 Вычисление div gradf. Оператор Лапласа.
Используя соотношения (1.6) –(1.9) и правила для вычисления скалярного произведения векторов, получаем:

Оператор 

Оператор Лапласа может действовать и на векторное поле A(x, y,z). По определению:
ΔA = i ΔAx+ j ΔAy+ k ΔAz (1.20)
1.5.3 Вычисление rot rotA.
Для вычисления используем известную формулу для двойного векторного произведения:
где A, B, C– три произвольных вектора.
rot rotA = [∇,[∇A]] = ∇(∇,A)-( ∇,∇)A = grad divA – ΔA (1.21)
Разумеется, эту же формулу мы получим, используя (1.12) и расписывая выражение rot rotA по компонентам.
Последняя строка в этом выражении, сумма слагаемых в которой равна нулю, добавлена для удобства вычислений. Группируя слагаемые со знаком “+”и со знаком “-“ и принимая во внимание равенство смешанных производных, получим:

Примечание Последние вычисления показывают преимущества использования оператора ∇ при рассмотрении различных векторных соотношений, содержащих дифференцирование.
[spoiler title=”источники:”]
http://lfirmal.com/rotor-vektornogo-polya/
http://pandia.ru/text/80/484/8647-2.php
[/spoiler]
Пусть поле
–
дифференцируемое поле (то есть проекции
вектора поля на оси координат являются
дифференцируемыми функциями).
Определение.Вихрем векторного поля(обозначаетсяrot
)
называется вектор, проекция которого
на произвольный векторопределяется как предел отношения
циркуляции поляпо некоторому контуру (L),
содержащему точкуM,
и лежащему в плоскости, перпендикулярной
вектору,
к площади области, ограниченной этим
контуром, при условии, что этот контур
стягивается в точкуM,
а площадь области (S)
стремится к нулю:

(1.13)
В трехмерном
пространстве
через декартовы прямоугольные координаты
векторавыражается следующим образом:
,
(1.14)
или в удобной для
запоминания символической форме

(1.15)
Теорема Стокса.Пусть координаты вектора+
непрерывны и имеют непрерывные частные
производные. Тогда циркуляция векторного
поляпо замкнутому контуру (L)
равна потоку вихрей поля через произвольную
поверхность (S),
натянутую на этот контур:
.
(1.16)
Предполагается,
что ориентация контура (L)
и поверхности (S)
согласованы: при положительном обходе
контура нормаль направлена от “ног к
голове”.
Свойства ротора:
1)
;
2)
.
Определение.Векторное поленазывается безвихревым в данной области
(V), если.
Пример 1.Найти
ротор поля вектора напряженности
магнитного поля.
Решение. Векторв координатной форме:
.
Вычислим ротор по формуле (1.15):
+–
– поле напряженности
– безвихревое поле.
Пример 2.Вычислить циркуляцию векторапо контуру
1)непосредственно, 2)по теореме Стокса.
Р
Рис.5.
ешение. 1)Контур (L)
– окружность радиуса,
лежащая в плоскостиz=3 (см. рис.5). Выберем ориентацию на ней,
как указано на рисунке. Параметрические
уравнения линии,
так что,
.
Для циркуляции вектораимеем:
.
2)Для вычисления циркуляции по теореме
Стокса выберем какую-нибудь поверхность
(S), натянутую на контур
(L).Естественно в
качестве (S) взять
круг, имеющий линию (L)
своей границей. Согласно выбранной
ориентации контура нормальк кругу необходимо взять равной
.
Вычислим ротор:
По теореме Стокса.
Задачи для самостоятельного решения
Найти векторные
линии плоских векторных полей:
1.;2.
;3.
;4.
;
5..
Найти векторные
линии:
6.
;
7.
,
где;
8.
;
9.,
;
10.;
11.;
12.;
13.,
где
–постоянные векторы.
Найти векторные
линии, проходящие через заданную точку:
14.,
;15.
,
.
Вычислить поток
векторного поля, используя поверхностный
интеграл первого рода:
16.,
(S): верхняя сторона
треугольника, ограниченного плоскостями,
.
17.
,
(S): внешняя сторона
параболоида,
ограниченного плоскостью;
18.,
:
боковая поверхность кругового цилиндра,
ограниченного плоскостями;
19.
,
(S): внешняя сторона
части параболоида,
расположенной в первом октанте;
20.,
(S): полная поверхность
конуса,
ограниченного плоскостью;
21.
,
(S): замкнутая поверхность,
ограниченная параболоидоми плоскостьюz= 0;
22.
,
(S): полная поверхность
пирамиды, ограниченной плоскостями,
,
,
;
23.,
(S): сфера.
Вычислить поток,
используя метод проектирования на все
три координатные плоскости.
24.,
(S): верхняя сторона
круга, вырезанного конусомна плоскости
25.,
(S): верхняя сторона
треугольника, полученного пересечением
плоскостис координатными плоскостями;
26.
,
(S): часть плоскости,
ограниченная окружностью,
в направлении орта.
Определить поток
поля, используя формулу Гаусса-Остроградского:
27.,
(S): произвольная
кусочно гладкая замкнутая поверхность;
28.
,
(S): поверхность куба,
,
;
29.,
(S): сфера;
30.
,
(S): часть параболоида,
отсекаемая плоскостью;
в отрицательную сторону осиOx;
31.,
(S): поверхность тела,
,
,
;
32.
,
(S): поверхность тела,
;
33.
,
(S):;
34.;
35.
.
Найти линейный
интеграл вектора на плоскости:
36.
верхняя половина эллипса
от точкиA(a,0),
до точкиB(-a,0);
37.а) отрезок прямойOB;
б) дуга параболы;
в) дуга параболы;
г) ломанаяOAB, гдеA(1,0); д) ломанаяOCB,
гдеC(0,1);
38.
39.от точки (-1, 1) до точки (2, 2).
Вычислить линейный
интеграл:
40.
41.,
отрезок прямой от точки (1,1,1) до точки
(4,4,4);
42.
43.
44.
отрезок прямой от точки (0,0,0) до точки
(1,1,1).
45.Дана
напряженностьсилового поля. Найти работу поля при
перемещении массыmвдоль одного витка винтовой линии,
из точки
в точкуB(t=2);
46.Силовое поле
образовано силой, равной по величине
расстоянию от начала координат до точки
ее приложения и направленной к началу
координат. Найти работу поля по перемещению
единицы массы вдоль дуги параболыот точки с абсциссой
до точки с абсциссой
.
В задачах 47- 51 найти
циркуляцию поля:
47.
в отрицательном направлении;
48.
замкнутая
линия, образованная отрезками осей
координатOxиOyи другой астроиды,
,
лежащей в первом квадранте;
49.
50.
51.линия пересечения параболоида
с координатными плоскостями (в первом
октанте);
52.Твердое тело
вращается с постоянной угловой скоростьювокруг осиOz. Вычислить
циркуляцию поля линейных скоростей
вдоль окружности радиусаR,
центр которой лежит на оси вращения,
если плоскость окружности перпендикулярна
оси вращения (циркуляция рассматривается
в направлении вращения).
53.Найти работу
поляпри перемещении точки единичной массы
вдоль замкнутой линии, состоящей из
трех прямолинейных отрезков, лежащих
в координатных плоскостях, отсекающих
на осях координат отрезки, равные
единице.
Найти дивергенцию
нижеследующих полей:
54..
При какой функциибудет
?
55.
;56.
– линейная скорость точек вращающейся
жидкости– угловая скорость);
57.напряженность магнитного поля,J,
– постоянные;
58.; 59.

60.Вычислитьв точке (1,-1,1).
Найти поток
векторного поля через указанные замкнутые
поверхности: 1) непосредственно, 2) по
теореме Гаусса-Остроградского в векторной
формулировке:
61.
62.
63.
64.;
65.
66.
67.
68.
69.
70.
71.
72.
В задачах 73 и 74
вычислить ротор указанных векторных
полей:
73.74.
75.Показать,
что если координаты вектораимеют непрерывные частные производные
второго порядка, то.
76.Показать,
что еслии
–
постоянные векторы, то.
77.Показать,
что.
78.Показать,
что.
79.Показать,
что векторное полеявляется безвихревым.
80.Показать,
что ротор поля линейных скоростейточек вращающегося твердого тела есть
постоянный вектор, направленный
параллельно оси вращения, модуль которого
равен удвоенной угловой скорости
вращения:.
81.Какова должна
быть функция,
чтобы ротор векторного полясовпадал с вектором
?
Найти циркуляцию
поля по указанным контурам 1)непосредственно,
2)по теореме Стокса в векторной
формулировке:
82.
83.
84.по контуру, образованному пересечением
плоскостис координатными плоскостями;
85.
86.
87.
88.
89.
90.
15.2. Частные случаи
векторных полей. Операции второго
порядка
15.2.1. Потенциальное
векторное поле
Определение.Векторное поленазывается потенциальным полем, если
существует некоторая скалярная функция,
градиент которой образует это поле:
.
(2.1)
Функция uназывается потенциалом векторного поля.
Теорема.Для
того, чтобы поле было потенциальным,
необходимо и достаточно, чтобы оно было
безвихревым:
.
(2.2)
Формула (2.2) есть
критерий потенциальности векторного
поля
.
Свойства
потенциальных полей.
1)
в области непрерывности потенциала
поля u
линейный интеграл не зависит от пути
интегрирования и равняется приращению
потенциала
(2.3)
2)
циркуляция (1.9) вектора
по любому замкнутому контуру, целиком
лежащему в области непрерывности поля,
равна нулю:
.
(2.4)
3)
потенциал
находится по формуле (2.3):
,
(2.5)
где
(AM)
– произвольная кривая, стягивающая
точки A
и M.
Если путь (AM)
взять в виде ломаной, состоящей из
отрезков, параллельных осям координат
(количество таких ломаных равно шести),
то для нахождения потенциала может быть
применена одна из формул, выражающая
потенциал
через определенные интегралы
;
):
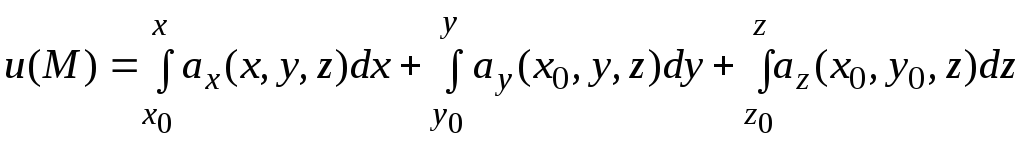
(2.6)
Пример.
Проверить, что поле вектора
является потенциальным и найти его
потенциал.
Решение.
Составим для данного поля критерий
потенциальности (2.2):
–
поле потенциально. Найдем потенциал
по формуле (2.6): за начальную точку удобно
взять точкуA(0,0,0):
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ротор поля. Формула Стокса
Ротором (или вихрем) векторного поля
называется вектор, обозначаемый 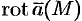
Формулу (71.13) можно записать с помощью символического определителя в виде, удобном для запоминания:
Отметим некоторые свойства ротора.
- Если
— постоянный вектор, то
.
, где
.
, т. e. ротор суммы двух векторов равен сумме роторов слагаемых.
- Если
— скалярная функция, а
— векторная, то
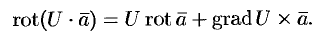
Эти свойства легко проверить, используя формулу (71.13). Покажем, например, справедливость свойства 3:
Используя понятия ротора и циркуляции, векторного поля, запишем известную в математическом анализе (см. п. 58.4) формулу Стокса:
Левая часть формулы (71.14) представляет собой циркуляцию вектора 

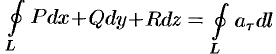
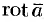


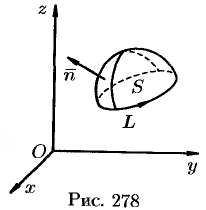
Следовательно, формулу Стокса можно записать в виде
Такое представление формулы Стокса называют ее векторной формой. В этой формуле положительное направление на контуре 

Формула (71.15) показывает, что циркуляция вектора 





Используя формулу (71.14), можно дать другое определение ротора поля, эквивалентное первому и не зависящее от выбора координатной системы.
Для этого применим формулу Стокса (71.15) для достаточно малой плоской площадки 


По теореме о среднем для поверхностного интеграла (п. 57.1, свойство 7) имеем:
где 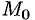

Тогда формулу (71.15) можно записать в виде
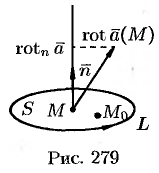
Отсюда:
Пусть контур 

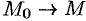
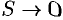
Ротором вектора 




Как видно из определения, ротор вектора 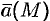
Дадим физическое истолкование понятия ротора векторного поля. Найдем ротор ноля линейных скоростей твердого тела, вращающегося вокруг оси 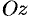
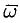
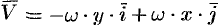
По определению ротора
Ротор этого поля направлен параллельно оси вращения, его модуль равен удвоенной угловой скорости вращения.
С точностью до числового множителя ротор поля скоростей 
Замечание. Из определения (71.13) ротора вытекает, что направление ротора — это направление, вокруг которого циркуляция имеет наибольшее значение (плотность) по сравнению с циркуляцией вокруг любого направления, не совпадающего с нормалью к площадке 
Так что связь между ротором и циркуляцией аналогична связи между градиентом и производной по направлению (см. п. 70.3).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:
Содержание:
- Пример 3:
- Правила вычисления ротора
По этой ссылке вы найдёте полный курс лекций по математике:
Пусть в некоторой области G задано непрерывное векторное поле а ) к и замкнутый ориентированный контур L. Определение 1. Циркуляцией вектора а по замкнутому контуру L называется криволинейный интеграл 2-го рода от оектора а по контуру L Здесь dr — вектор, длина которого равна дифференциалу дуги L, а направление совпадаете направлением касательной к L, оп- Рис. 31 ределяемымориентацией контура (рис. 31); символ f означает, что интеграл берется по зам1«угому контуру L. ь
Пример 1. вычислить циркуляцию векторного поля вдоль эллипса L: По определению циркуляции имеем Параметрические уравнения данного эллипса имеют вид: , и, значит, . Подставляя эти выражения в формулу (2), найдем Циркуляция векторного поля. Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля Правила вычисления ротора 8.1.
Ротор (вихрь) векторного поля Рассмотрим поле вектора Р, Q, R которого непрерывны и имеют непрерывные частные производные первого порядка по всем своим аргументам. Огределенив 2. Ротором вектора »(М) называется вектор, обозначаемый символом rot а и определяемый равенством или, в символической, удобной для запоминания форме, Этот определитель раскрывают по элементам первой строки, при этом операции умножения элементов второй строки на элементы третьей строки понимаются как операции дифференцирования, например,
Определение 3. Если в некоторой области G имеем rot а = 0, то поле вектора а в области G называете я безвихревым. Пример 2. Найти ротор вектора 4 Согласно формуле (3) имеем Так как rot а — вектор, то мы можем рассматривать векторное поле — поле ротора вектора а. Предполагая, что координаты вектора а имеют непрерывные частные производные второго порядка, вычислим дивергенцию вектора rot а. Получим Таким образом, поле вектора rot а соленоида л ьно.
Теорема 7 (Стокса). Циркуляция вектора а вдоль ориентированного замкнутого контура L равна потоку ротора этого вектора через любую поверхность Е, натянутую на контур L, При этом предполагается, что координаты вектора а имеют непрерывные частные производные в некоторой области G пространства, содержащей поверхность Е, и что ориентация орта нормали п° к поверхности ЕС G согласована с ориентацией контура L так, что из конца нормши обход контура в заданном направлении виден совершающимся против часовой стрелки.
Учитывая, что , и пользуясь определением ротора (3), перепишем формулу (4) в следующем виде: Рассмотрим сначала случай, когда гладкая поверхность Е и ее контур L однозначно проектируются на область D плоскости хОу и ее границу — контур А соответственно (рис. 32). Ориентация контура L порождает определенную ориентацию контура А. Для определенности будем считать, что контур L ориентирован так, что поверхность Е остается слева, так что веетор нормали п к поверхности Е составдя етсосью Oz острый угол 7 (cos 7 >0).
Возможно вам будут полезны данные страницы:
Пусть — уравнение поверхности Е и функция ф(х}у) непрерывна и имеет непрерывные частные производные gf и ^ в замкнутой области D.
Рассмотрим интеграл Линия L лежит на поверхности Е. Поэтому, пользуясь уравнением этой поверхности , мы можем заменить г под знаком интеграла на ^(ж, у). Координаты перемсннойточки кривой А равны координатам соответствующей точки на кривой L, а потому интегрирование по L можно заменить интегрированием по А, Применим к интегралу, стоящему справа, формулу Грина.
Имеем Перейдем теперь от интеграла по области D к интегралу по поверхности Е. Так как dS = cos 7 • da, то из формулы (8) получим, что Вектор нормали п° к поверхности Е определяется выражением к. Отсюда видно, что . Поэтому равенсгво (9) можно переписать так: Считая Е гладкой поверхностью, однозначно проектирующейся на все три координатные плоскости, аналогично убеждаемся в справедливости формул Циркуляция векторного поля.
Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля Правила вычисления ротора Складывая равенства почленно, получим формулу Стокса (5), или, короче, Замечание 1. Мы показали, что поле вектора rote — соленоидальное, и потому поток вектора rota не зависит от вида поверхности Е, натянутой на контур L. Замечание 2. Формула (4) выведена в предположении, что поверхность £ однозначно проектируется на все три координатные плоскости. Бели это условие не выполнено, то разбиваем £ на частя так, чтобы каждая часть указанному условию удовлетворяла, а затем пользуемся аддитивностью интегралов.
Пример 3:
Вычислить циркуляцию вектора по линии 1) пользуясь определением; 2) по теореме Стокса. 4 1) Зададим линию L параметрически: Тогда 2) Найдем rota: Натянем на контур L кусок плосхости Тогда . Инвариантное определение ротора поля Из теоремы Стокса можно получить инвариантное определение ротора поля, не связанное с выбором системы координат. Теорема 8.
Проекция ротора а на любое направление не зависит от выбора системы координат и равна поверхностной плотности циркуляции вектора а по контуру площадки, перпендикулярной этому направлению, Здесь (Е) — плоская площадка, перпендикулярная вектору л; 5 — площадь этой площадки; L — контур площадки, ориентированный так, чтобы обход контура был виден из конца вектора п против хода часовой стрелки; (Е) М означает, что площадка (Е) стягивается к точке М, в которой рассматривается вектор rot а, причем вектор нормали п к этой площадке остается все время одним и тем же (рис. 33). 4
Применим сначала к циркуляции (a,dr) вектора а теорему Стокса, а затем к полученному двойному интегралу — теорему о среднем значении: откуда (скалярное произведение берется в некоторой средней точке Мф площадки (Е)). Пристягивании площадки (Е) кточке М средняяточка Л/ср тоже стремится кточ-ке М и, в силу предполагаемой непрерывности частных производных от координат вектора а (а значит, и непрерывности rot а), мы получаем Поскольку проекция вектора rot а на произвольное направление не зависитотвы-бора системы координат,то и сам вектор rota инвариантен относительно этого выбора.
Отсюда получаем следующее инвариантное определение ротора поля: ротор поля есть вектор, длина которого равна наибольшей поверхностной плотности циркуляции в данной точке, направленный перпендикулярно той площадке, на которой эта наибольшая плотность циркуляции достигается; при этом ориентация вектора rota согласуется с ориентацией контура, при которой циркуляция положительна, по правилу правого винта. 8.3.
Физический смысл ротора поля Пустьтвердое
тело вращается вокруг неподвижной оси I с угловой скоростью и. Не нарушая общности, можно считать, что ось I совпадает с осью Oz (рис. 34). Пусть М(г) — изучаемая точка тела, где Вектор угловой скорости в нашем случае равен из = wk, вычислим вектор v линейной скорости точки М, Отсюда Циркуляция векторного поля. Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля.
Правила вычисления ротора
Итак, вихрь поля скоростей вращающегося твердого тела одинаков во всех точках поля, параллелен оси вращения и равен удвоенной угловой скорости вращения. 8.4. Правила вычисления ротора 1. Ротор постоянного вектора с равен нулевому вектору, 2. Ротор обладает свойством линейности постоянные числа. 3. Ротор произведения скалярной функции и{М) на векторную а(М) вычисляется по формуле
Лекции:
- Векторное произведение векторов
- Таблица производных полная: для студентов
- Функции двух переменных. Действия над случайными величинами
- Найти значение выражения
- Исследование графика функции
- Нормальное распределение
- Ранг матрицы: примеры решения
- Найдите объем тела ограниченного
- Разложение вектора по базису
- Умножение матрицы на вектор



![{displaystyle operatorname {rot} mathbf {a} {Big |}_{O}=lim _{Sto O}{frac {oint limits _{S}[dmathbf {S} times mathbf {a} ]}{V}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c631789d553cf032b52b8ebf61355f1e83b446d)














![{displaystyle {}={frac {1}{H_{2}H_{3}}}left[{frac {partial }{partial q_{2}}}(A_{3}H_{3})-{frac {partial }{partial q_{3}}}(A_{2}H_{2})right]mathbf {q_{1}} +}](https://wikimedia.org/api/rest_v1/media/math/render/svg/557abaf775de1ededeeb76c5fe3a4eb87f3e571e)
![{displaystyle {}+{frac {1}{H_{3}H_{1}}}left[{frac {partial }{partial q_{3}}}(A_{1}H_{1})-{frac {partial }{partial q_{1}}}(A_{3}H_{3})right]mathbf {q_{2}} +}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86be3211685bb80dcaf9572b4518a436d4d54423)
![{displaystyle {}+{frac {1}{H_{1}H_{2}}}left[{frac {partial }{partial q_{1}}}(A_{2}H_{2})-{frac {partial }{partial q_{2}}}(A_{1}H_{1})right]mathbf {q_{3}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/57311237c00b0ebb9927cf86cd45db4b397d7e30)































![mathbf{nabla} times mathbf{F} =0 mathbf e_x + 0 mathbf e_y+ left[ {frac{partial}{partial x}}(-x) -{frac{partial}{partial y}} y right] mathbf e_z = -2mathbf e_z](https://wikimedia.org/api/rest_v1/media/math/render/svg/85d5e9400eeb2031c18a73399578b0a22f23fe9f)























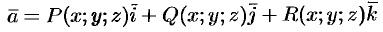
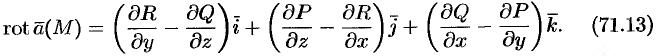
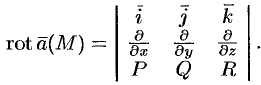
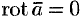 .
.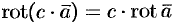 , где
, где 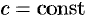 .
.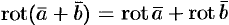 , т. e. ротор суммы двух векторов равен сумме роторов слагаемых.
, т. e. ротор суммы двух векторов равен сумме роторов слагаемых. — скалярная функция, а
— скалярная функция, а