В области (V) задано скалярное поле, если каждой точке (M) из (V) поставлено в соответствие число (uleft(M right)). Скалярное поле (uleft(M right)) называется дифференцируемым в точке (M_{0}) из области (V), если приращение поля (Delta u) в этой точке можно представить в виде: (Delta u=gcdot Delta r+oleft(rho right)), где (rho =rho left(M_{0},M right)) – расстояние между точками (M_{0}) и (M), (Delta u=uleft(M right)-uleft(M_{0} right)). Вектор (gleft(M_{0} right)) называется градиентом дифференцируемого в точке (M_{0}) скалярного поля. В декартовой системе координат [grad u=frac{partial u}{partial x}i+frac{partial u}{partial y}j+frac{partial u}{partial z}k] Если каждой точке (M) из области (V) поставлен в соответствие некоторый вектор (Fleft(M right)), то говорят, что в (V) задано векторное поле. Дивергенция — это линейный дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность достаточно малой окрестности каждой внутренней точки области определения поля. Оператор дивергенции, примененный к полю (F), обозначается (divF) или (bigtriangledown cdot F). [div F=lim_{Vrightarrow 0}frac{P_{F}}{V}] где (P_{F})-поток векторного поля (F) через сферическую поверхность площадью (S), ограничивающую объем (V). Ротор — векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Обозначается (rot) или (curl), вычисляется по формуле (rot F = bigtriangledown times F).
С помощью нашего решебника вы можете вычислить градиент, дивергенцию, ротор векторного поля, выполнить другие операции векторного анализа. Ниже приведены примеры команд. Скопируйте и вставьте в строку решателя или просто наберите ваш пример а затем нажмите кнопку “Решить”.
Вычислить градиент функции
grad sin(x^2 y)
del z e^(x^2+y^2)
grad of a scalar field
Вычислить градиент функции в полярных координатах
grad sqrt(r) cos(theta)
Вычислить дивергенцию векторного поля
div (x^2-y^2, 2xy)
div [x^2 sin y, y^2 sin xz, xy sin (cos z)]
divergence calculator
Вычислить ротор векторного поля
curl [-y/(x^2+y^2), -x/(x^2+y^2), z]
rotor operator
Вычислить Лапласиан функции
Laplace e^x sin y
Laplace x^2+y^2+z^2
laplacian calculator
Вычислить выражения
div (grad f)
curl (curl F)
grad (F . G)
Если вам наших примеров мало, то читайте больше о новых возможностях WoframAlpha, позволяющей решать задачи онлайн в реальном времени.
Похожие публикации: математика
Циркуляция векторного поля. Ротор вектора. Теорема Стокса
Содержание:







По этой ссылке вы найдёте полный курс лекций по математике:
Пусть в некоторой области G задано непрерывное векторное поле а ) к и замкнутый ориентированный контур L. Определение 1. Циркуляцией вектора а по замкнутому контуру L называется криволинейный интеграл 2-го рода от оектора а по контуру L Здесь dr — вектор, длина которого равна дифференциалу дуги L, а направление совпадаете направлением касательной к L, оп- Рис. 31 ределяемымориентацией контура (рис. 31); символ f означает, что интеграл берется по зам1«угому контуру L. ь
Пример 1. вычислить циркуляцию векторного поля вдоль эллипса L: По определению циркуляции имеем Параметрические уравнения данного эллипса имеют вид: , и, значит, . Подставляя эти выражения в формулу (2), найдем Циркуляция векторного поля. Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля Правила вычисления ротора 8.1.
Ротор (вихрь) векторного поля Рассмотрим поле вектора Р, Q, R которого непрерывны и имеют непрерывные частные производные первого порядка по всем своим аргументам. Огределенив 2. Ротором вектора »(М) называется вектор, обозначаемый символом rot а и определяемый равенством или, в символической, удобной для запоминания форме, Этот определитель раскрывают по элементам первой строки, при этом операции умножения элементов второй строки на элементы третьей строки понимаются как операции дифференцирования, например,
Определение 3. Если в некоторой области G имеем rot а = 0, то поле вектора а в области G называете я безвихревым. Пример 2. Найти ротор вектора 4 Согласно формуле (3) имеем Так как rot а — вектор, то мы можем рассматривать векторное поле — поле ротора вектора а. Предполагая, что координаты вектора а имеют непрерывные частные производные второго порядка, вычислим дивергенцию вектора rot а. Получим Таким образом, поле вектора rot а соленоида л ьно.
Теорема 7 (Стокса). Циркуляция вектора а вдоль ориентированного замкнутого контура L равна потоку ротора этого вектора через любую поверхность Е, натянутую на контур L, При этом предполагается, что координаты вектора а имеют непрерывные частные производные в некоторой области G пространства, содержащей поверхность Е, и что ориентация орта нормали п° к поверхности ЕС G согласована с ориентацией контура L так, что из конца нормши обход контура в заданном направлении виден совершающимся против часовой стрелки.
Учитывая, что , и пользуясь определением ротора (3), перепишем формулу (4) в следующем виде: Рассмотрим сначала случай, когда гладкая поверхность Е и ее контур L однозначно проектируются на область D плоскости хОу и ее границу — контур А соответственно (рис. 32). Ориентация контура L порождает определенную ориентацию контура А. Для определенности будем считать, что контур L ориентирован так, что поверхность Е остается слева, так что веетор нормали п к поверхности Е составдя етсосью Oz острый угол 7 (cos 7 >0).
Возможно вам будут полезны данные страницы:
Пусть — уравнение поверхности Е и функция ф(х>у) непрерывна и имеет непрерывные частные производные gf и ^ в замкнутой области D.
Рассмотрим интеграл Линия L лежит на поверхности Е. Поэтому, пользуясь уравнением этой поверхности , мы можем заменить г под знаком интеграла на ^(ж, у). Координаты перемсннойточки кривой А равны координатам соответствующей точки на кривой L, а потому интегрирование по L можно заменить интегрированием по А, Применим к интегралу, стоящему справа, формулу Грина.
Имеем Перейдем теперь от интеграла по области D к интегралу по поверхности Е. Так как dS = cos 7 • da, то из формулы (8) получим, что Вектор нормали п° к поверхности Е определяется выражением к. Отсюда видно, что . Поэтому равенсгво (9) можно переписать так: Считая Е гладкой поверхностью, однозначно проектирующейся на все три координатные плоскости, аналогично убеждаемся в справедливости формул Циркуляция векторного поля.
Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля Правила вычисления ротора Складывая равенства почленно, получим формулу Стокса (5), или, короче, Замечание 1. Мы показали, что поле вектора rote — соленоидальное, и потому поток вектора rota не зависит от вида поверхности Е, натянутой на контур L. Замечание 2. Формула (4) выведена в предположении, что поверхность £ однозначно проектируется на все три координатные плоскости. Бели это условие не выполнено, то разбиваем £ на частя так, чтобы каждая часть указанному условию удовлетворяла, а затем пользуемся аддитивностью интегралов.
Пример 3:
Вычислить циркуляцию вектора по линии 1) пользуясь определением; 2) по теореме Стокса. 4 1) Зададим линию L параметрически: Тогда 2) Найдем rota: Натянем на контур L кусок плосхости Тогда . Инвариантное определение ротора поля Из теоремы Стокса можно получить инвариантное определение ротора поля, не связанное с выбором системы координат. Теорема 8.
Проекция ротора а на любое направление не зависит от выбора системы координат и равна поверхностной плотности циркуляции вектора а по контуру площадки, перпендикулярной этому направлению, Здесь (Е) — плоская площадка, перпендикулярная вектору л; 5 — площадь этой площадки; L — контур площадки, ориентированный так, чтобы обход контура был виден из конца вектора п против хода часовой стрелки; (Е) М означает, что площадка (Е) стягивается к точке М, в которой рассматривается вектор rot а, причем вектор нормали п к этой площадке остается все время одним и тем же (рис. 33). 4
Применим сначала к циркуляции (a,dr) вектора а теорему Стокса, а затем к полученному двойному интегралу — теорему о среднем значении: откуда (скалярное произведение берется в некоторой средней точке Мф площадки (Е)). Пристягивании площадки (Е) кточке М средняяточка Л/ср тоже стремится кточ-ке М и, в силу предполагаемой непрерывности частных производных от координат вектора а (а значит, и непрерывности rot а), мы получаем Поскольку проекция вектора rot а на произвольное направление не зависитотвы-бора системы координат,то и сам вектор rota инвариантен относительно этого выбора.
Отсюда получаем следующее инвариантное определение ротора поля: ротор поля есть вектор, длина которого равна наибольшей поверхностной плотности циркуляции в данной точке, направленный перпендикулярно той площадке, на которой эта наибольшая плотность циркуляции достигается; при этом ориентация вектора rota согласуется с ориентацией контура, при которой циркуляция положительна, по правилу правого винта. 8.3.
Физический смысл ротора поля Пустьтвердое
тело вращается вокруг неподвижной оси I с угловой скоростью и. Не нарушая общности, можно считать, что ось I совпадает с осью Oz (рис. 34). Пусть М(г) — изучаемая точка тела, где Вектор угловой скорости в нашем случае равен из = wk, вычислим вектор v линейной скорости точки М, Отсюда Циркуляция векторного поля. Ротор вектора Теорема Стокса Ротор (вихрь) векторного поля Инвариантное определение ротора поля Физический смысл ротора поля.
Правила вычисления ротора
Итак, вихрь поля скоростей вращающегося твердого тела одинаков во всех точках поля, параллелен оси вращения и равен удвоенной угловой скорости вращения. 8.4. Правила вычисления ротора 1. Ротор постоянного вектора с равен нулевому вектору, 2. Ротор обладает свойством линейности постоянные числа. 3. Ротор произведения скалярной функции и<М) на векторную а(М) вычисляется по формуле
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Ротор векторного поля. Формула Стокса

Ротор поля. Формула Стокса
Ротором (или вихрем) векторного поля
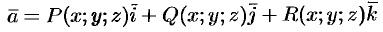
называется вектор, обозначаемый 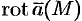 и определяемый формулой
и определяемый формулой
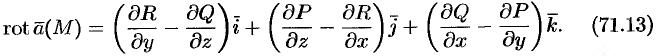
Формулу (71.13) можно записать с помощью символического определителя в виде, удобном для запоминания:
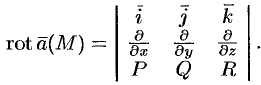
Отметим некоторые свойства ротора.
- Если
 — постоянный вектор, то
— постоянный вектор, то 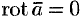 .
. 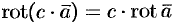 , где
, где 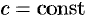 .
.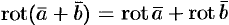 , т. e. ротор суммы двух векторов равен сумме роторов слагаемых.
, т. e. ротор суммы двух векторов равен сумме роторов слагаемых.- Если
 — скалярная функция, а
— скалярная функция, а 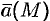 — векторная, то
— векторная, то
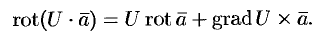
Эти свойства легко проверить, используя формулу (71.13). Покажем, например, справедливость свойства 3:
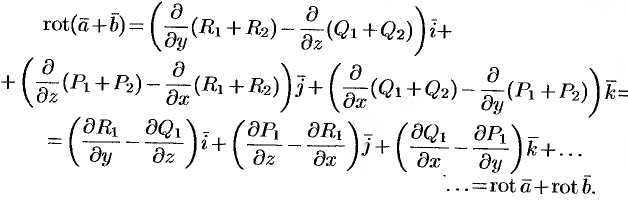
Используя понятия ротора и циркуляции, векторного поля, запишем известную в математическом анализе (см. п. 58.4) формулу Стокса:
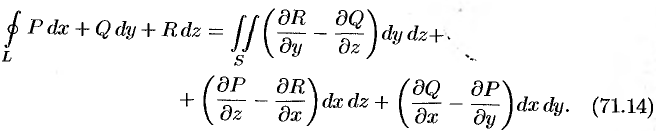
Левая часть формулы (71.14) представляет собой циркуляцию вектора  по контуру
по контуру  , т. е.
, т. е. 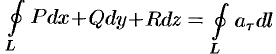 (см. (71.11)). Интеграл в правой части формулы (71.14) представляет собой поток вектора
(см. (71.11)). Интеграл в правой части формулы (71.14) представляет собой поток вектора 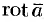 через поверхность
через поверхность  , ограниченную контуром
, ограниченную контуром  (см. (71.3)), т. е.
(см. (71.3)), т. е.
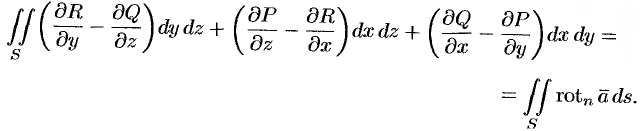
Следовательно, формулу Стокса можно записать в виде
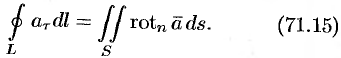
Такое представление формулы Стокса называют ее векторной формой. В этой формуле положительное направление на контуре  и выбор стороны у поверхности
и выбор стороны у поверхности  согласованы между собой так же, как в теореме Стокса.
согласованы между собой так же, как в теореме Стокса.
Формула (71.15) показывает, что циркуляция вектора  вдоль замкнутого контура
вдоль замкнутого контура  равна потоку ротора этого вектора
равна потоку ротора этого вектора  через поверхность
через поверхность  , лежащую в поле вектора
, лежащую в поле вектора  и ограниченную контуром
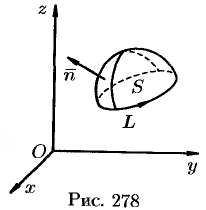
и ограниченную контуром  (натянутую на контур) (см. рис. 278).
(натянутую на контур) (см. рис. 278).
Используя формулу (71.14), можно дать другое определение ротора поля, эквивалентное первому и не зависящее от выбора координатной системы.
Для этого применим формулу Стокса (71.15) для достаточно малой плоской площадки  с контуром
с контуром  , содержащей точку
, содержащей точку  .
.
По теореме о среднем для поверхностного интеграла (п. 57.1, свойство 7) имеем:
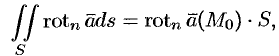
где 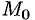 — некоторая (средняя) точка площадки
— некоторая (средняя) точка площадки  (см. рис. 279).
(см. рис. 279).
Тогда формулу (71.15) можно записать в виде
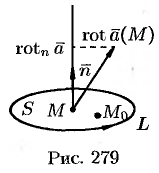
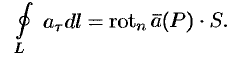
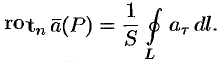
Пусть контур  стягивается в точку
стягивается в точку  . Тогда
. Тогда 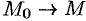 , a
, a 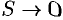 . Перейдя к пределу, получаем:
. Перейдя к пределу, получаем:
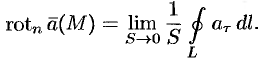
Ротором вектора  в точке
в точке  называется вектор, проекция которого на каждое направление равна пределу отношения циркуляции вектора
называется вектор, проекция которого на каждое направление равна пределу отношения циркуляции вектора  по контуру
по контуру  плоской площадки
плоской площадки  , перпендикулярной этому направлению, к площади этой площадки.
, перпендикулярной этому направлению, к площади этой площадки.
Как видно из определения, ротор вектора 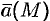 есть векторная величина, образующая собственное векторное поле.
есть векторная величина, образующая собственное векторное поле.
Дадим физическое истолкование понятия ротора векторного поля. Найдем ротор ноля линейных скоростей твердого тела, вращающегося вокруг оси 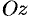 с постоянной угловой скоростью (пример 69.2)
с постоянной угловой скоростью (пример 69.2) 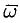 , т. е. ротор вектора
, т. е. ротор вектора 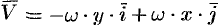 .
.
По определению ротора
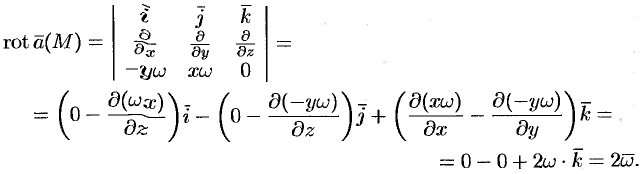
Ротор этого поля направлен параллельно оси вращения, его модуль равен удвоенной угловой скорости вращения.
С точностью до числового множителя ротор поля скоростей 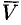 представляет собой угловую скорость вращения твердого тела. С этим связано само название «ротор» (лат. «вращатель»).
представляет собой угловую скорость вращения твердого тела. С этим связано само название «ротор» (лат. «вращатель»).
Замечание. Из определения (71.13) ротора вытекает, что направление ротора — это направление, вокруг которого циркуляция имеет наибольшее значение (плотность) по сравнению с циркуляцией вокруг любого направления, не совпадающего с нормалью к площадке  .
.
Так что связь между ротором и циркуляцией аналогична связи между градиентом и производной по направлению (см. п. 70.3).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:






















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Элементы теории поля и векторного анализа (стр. 2 )
 |
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 |

 , где
, где  – потенциал заряда.
– потенциал заряда.
Пример 1.2. Найти  , где –φ(r) – произвольная дифференцируемая функция от r, где, как и в предыдущем примере, r длина радиус-вектора r.
, где –φ(r) – произвольная дифференцируемая функция от r, где, как и в предыдущем примере, r длина радиус-вектора r.


Аналогично,  ,
,  . В итоге получаем:
. В итоге получаем:

Последнее соотношение можно использовать для получения напряженности поля для сферически-симметричных потенциалов, то есть для потенциалов, поверхности уровня которых представляют собой сферы.
1.3 Оператор C
Определение Оператором называется правило, по которому одной функции ставится в соответствие другая функция.
Предположим, мы имеем две функции f и φ.Соотношение f = Tφ, где T – оператор, устанавливает соответствие между ними, Например, если  , то T – оператор дифференцирования, если
, то T – оператор дифференцирования, если  , то T – интегральный оператор и т. д..
, то T – интегральный оператор и т. д..
Заметим, соотношение (1.3) не зависит от того, какое скалярное поле мы дифференцируем. Эту формулу можно записать компактно, если ввести дифференциальный векторный оператор C (читается «набла»).
 (1.9)
(1.9)
В многих случаях с оператором ∇ можно обращаться как с обычным вектором. ∇ =  . Следует только помнить, что операторная алгебра несколько отличается от векторной. Оператор действует на функцию, написанную справа от оператора. Например, ∇ f и f∇ – зто разные выражения:: ∇ f = grad f – вектор,
. Следует только помнить, что операторная алгебра несколько отличается от векторной. Оператор действует на функцию, написанную справа от оператора. Например, ∇ f и f∇ – зто разные выражения:: ∇ f = grad f – вектор,  – векторный оператор, образно говоря, «жаждущий» подействовать на функцию, которая появится справа от него.
– векторный оператор, образно говоря, «жаждущий» подействовать на функцию, которая появится справа от него.
Примечание Вообще говоря, не любые три оператора образуют векторный оператор. (Также как не любые три числа образуют вектор.) Компоненты векторных операторов, как и компоненты обычных векторов, при преобразовании системы координат должны преобразовываться определенным образом. Можно провести и более простые рассуждения, показывающие, что ∇ – векторный оператор. В предыдущем разделе мы показали, что grad f = ∇ f – вектор, направленный по нормали к поверхности уровня. Поскольку, формально соотношение (1.6) выглядит как действие оператора на скалярную функцию и в результате получается вектор, то поэтому ∇ – векторный оператор.
Пример 1.3. Вычислить вектор  в точке (1,2,0).
в точке (1,2,0).
Последовательно проводим действия:
1. Находим частные производные от функции 
 ;
;  ;
;  .
.
2. Каждую из полученных производных умножаем на соответствующий единичный вектор, полученные векторы складываем и результат умножаем на функцию  :
:
 .
.
3. Вычисляем полученный вектор в точке (1,2,0):
 .
.
1.4 Действия с оператором ∇. Дивергенция вектора. Ротор вектора.
Рассмотрим векторное поле A(x, y,z) = Из двух векторов ∇ и A по обычным правилам векторной алгебры можно образовать скалярное произведение:
 (1.10)
(1.10)
Эта скалярная величина называется дивергенцией вектора A и обозначается как divA:
 (1.11)
(1.11)
Из векторов ∇ и A можно образовать и векторное произведение. Используя обычные правила векторной алгебры, получим:
 (1.12)
(1.12)
Эта векторная величина называется ротором вектора A и обозначается как rotA:
 (1.13)
(1.13)
Примечание Определения (1.1) и (1.13) даны в прямоугольной системе координат. К независящим от выбора системы координат определениям дивергенции и ротора функции, а также к их смыслу мы вернемся позже.
В различных применениях векторного анализа часто возникает необходимость в вычислении div(Af) и rot(Af), где A – векторное поле, f-скалярное. Получим соответствующие формулы, используя (1.8), (1.10) и (1.12):

 (1.14)
(1.14)



 (1.15)
(1.15)
Пример 1.4. Вычислить divr, где r = – радиус вектор:

Пример 1.5. Вычислить rotr, где, по-прежнему, r = – радиус вектор:

Пример 1.6. Вычислить div(rφ(r)),где r = – радиус вектор, r – его длина, φ(r) – произвольная дифференцируемая функция от r.
Используя формулу (1.14) и решения примеров 1.2 и 1.4, получаем

Пример 1.7. Вычислить rot(rφ(r)),где r, r и φ(r) определены в примере 1.6.
Используя формулу (1.15) и решения примеров 1.2 и 1.5, получаем:

1.5 Некоторые формулы векторного анализа
До сих пор мы рассматривали действие оператора ∇ на скалярные и векторные поля и их произведения. Сейчас мы получим некоторые часто встречающиеся в приложениях соотношения, в которых оператор ∇ встречается дважды.
1.5.1 Вычисление rot gradf
Пустьf(x, y,z) – некоторое скалярное поле. Тогда, используя формулы (1.3) и (1.10) получим:
 (1.16)
(1.16)
Этот же результат можно получить проще, используя, оператор ∇.
rot gradf = [∇,(∇f] = [∇,∇]f = 0, так как векторное произведение вектора самого на себя равно нулю.
1.5.2 Вычисление div rot A
Используя соотношения (1.8) –(1.11) и правила для вычисления смешанного произведения векторов, получаем:
 , (1.17)
, (1.17)
так как в определителе две одинаковых строки.
1.5.2 Вычисление div gradf. Оператор Лапласа.
Используя соотношения (1.6) –(1.9) и правила для вычисления скалярного произведения векторов, получаем:
 (1.18)
(1.18)
Оператор  широко используется в приложениях и называется оператором Лапласа или лапласианом и обозначается символом Δ:
широко используется в приложениях и называется оператором Лапласа или лапласианом и обозначается символом Δ:
 (1.19)
(1.19)
Оператор Лапласа может действовать и на векторное поле A(x, y,z). По определению:
ΔA = i ΔAx+ j ΔAy+ k ΔAz (1.20)
1.5.3 Вычисление rot rotA.
Для вычисления используем известную формулу для двойного векторного произведения:
где A, B, C– три произвольных вектора.
rot rotA = [∇,[∇A]] = ∇(∇,A)-( ∇,∇)A = grad divA – ΔA (1.21)
Разумеется, эту же формулу мы получим, используя (1.12) и расписывая выражение rot rotA по компонентам.

Последняя строка в этом выражении, сумма слагаемых в которой равна нулю, добавлена для удобства вычислений. Группируя слагаемые со знаком “+”и со знаком “-“ и принимая во внимание равенство смешанных производных, получим:
 что и требовалось показать.
что и требовалось показать.
Примечание Последние вычисления показывают преимущества использования оператора ∇ при рассмотрении различных векторных соотношений, содержащих дифференцирование.
[spoiler title=”источники:”]
http://lfirmal.com/rotor-vektornogo-polya/
http://pandia.ru/text/80/484/8647-2.php
[/spoiler]
5. Дивергенция векторного поля
Продолжим изучение
характеристик векторных полей.
Определение 23.
Дивергенцией
векторного
поля A
= {Ax,
Ay,
Az},
где
Ax,
Ay,
Az
– функции от x,
y,
z,
называется
.
(107)
Замечание 1.
Из определения видно, что дивергенция
является скалярной
функцией.
Замечание 2.
Слово «дивергенция» означает
«расходимость», так как дивергенция
характеризует плотность источников
данного векторного поля в рассматриваемой
точке.
Рассмотрим формулу
Гаусса-Остроградского с учетом определений
потока и дивергенции векторного поля.
Тогда в левой части формулы (67) стоит
тройной интеграл по объему V
от дивергенции векторного поля {P,
Q,
R},
а в правой – поток этого вектора через
ограничивающую тело поверхность S:
(108)
Докажем, что
величина дивергенции в данной точке не
зависит от выбора системы координат.
Рассмотрим некоторую точку М,
которую окружает трехмерная область
V,
ограниченная поверхностью
S.
Разделим обе части формулы (108) на V
и перейдем к пределу при стягивании
тела V
к точке М.
Получим:
.
(109)
Это равенство
можно считать инвариантным
определением дивергенции,
то есть определением, не зависящим от
выбора координатной системы.
Пример 28.
Определить
дивергенцию и ротор векторного поля
.
Дифференциальные
операции второго порядка
Вспомним определение
градиента скалярной функции
u
= u(x,
y,
z):
grad
u
=
Определим оператор,
стоящий в скобках в правой части этого
равенства, так:
Определение 24.
Оператор
(110)
называется
оператором
Гамильтона или набла-оператором
и обозначается символом
(«набла»).
При применении
оператора Гамильтона удобно рассматривать
его как «символический вектор» и
использовать различные операции над
векторами. Например:
1) если умножить
«вектор» на
скалярную функцию и,
то получим градиент этой функции:
u
= grad
u;
(111)
2) составив скалярное
произведение
на вектор A
= {Ax,
Ay,
Az},
получим дивергенцию вектора A:
· A
=
;
(112)
3) перемножим теперь
векторы
и А
векторным образом.
Результатом будет
ротор вектора А:
А
=
(113)
4) рассмотрим
скалярное произведение векторов
и u
= grad
u:
·
(u)
= div
(grad
u)
= =
Определение 25.
Оператор
Δ
= ·
= ²
=
(114)
называется
оператором
Лапласа и
обозначается символом Δ («дельта»).
Определение 26.
Уравнение
(115)
называется
уравнением
Лапласа, а
функция, удовлетворяющая ему –
гармонической
функцией.
Отметим еще раз,
результатом применения к скалярной
функции
и
оператора Гамильтона является вектор,
а оператора Лапласа – скаляр.
По аналогии с
производной по направлению от скалярной
функции и:
введем понятие
производной по направлению единичного
вектора
от векторной функции:
)
.
(116)
Производная по
направлению любого произвольного
вектора
отличается от производной по направлению
единичного вектора лишь тем, что в нее
входит дополнительный скалярный
множитель:
(117)
Таким образом, с
помощью оператора Гамильтона можно
образовать пять дифференциальных
операций второго порядка:
-
div grad u
= (,)
u
= 2
u
-
rot grad u
= [,]
u
-
grad div
=(,)
(118)
-
div rot
= (,[,])
-
rot rot
=
Кроме того, операцию
2
можно применять и к векторным полям,
рассматривая 2. 2 — вопрос №2998977 — Учеба и наука
2 — вопрос №2998977 — Учеба и наука
Лучший ответ по мнению автора
|
|||||||||||||
Другие ответы
|
||||||||
|
|
|
Посмотреть всех экспертов из раздела Учеба и наука > Математика
Решено
На рисунке изображены графики функций y = f(x) и y = g(x). 2, y=0 ( с графиком)
2, y=0 ( с графиком)
Пользуйтесь нашим приложением
Калькулятор расхождения — eMathHelp
Калькулятор найдет дивергенцию заданного векторного поля с указанием шагов.
Связанные калькуляторы:
Калькулятор частных производных,
Калькулятор скалярного произведения
$$$mathbf{vec{F}}left(x,y,zright)$$$:$$$langle$$$
,
,
$$$rangle$$$
$$$влево(x_{0}, y_{0}, z_{0}вправо)$$$:$$$($$$
,
,
$$$)$$$
Оставьте пустым, если вам не нужна дивергенция в конкретной точке. {z }$$$ (шаги см. в калькуляторе производных). 9{z}$$$A
{z }$$$ (шаги см. в калькуляторе производных). 9{z}$$$A
Калькулятор дивергенции — Найдите дивергенцию векторного поля
Онлайн-калькулятор дивергенции специально разработан для нахождения дивергенции векторного поля только с точки зрения величины потока и без направления . Подобно ротору векторного поля, дивергенция имеет свои специфические свойства, которые делают ее ценным термином в области физических наук.
Если вам интересно узнать больше о физическом явлении этого термина, вы находитесь на правильной платформе.
Что такое дивергенция?
В словаре векторного анализа:
«Векторный оператор, который фактически измеряет норму источника и стока поля через скаляр со знаком, называется дивергенцией»
Типы дивергенции:
В зависимости от Поток потока, дивергенция векторного поля подразделяется на два типа:
Положительная дивергенция:
Точка, из которой поток идет наружу, называется положительной дивергенцией. Точка известна как источник.
Точка известна как источник.
Отрицательное расхождение:
Точка, из которой поток движется внутрь, называется отрицательным расхождением. Здесь точка выступает в роли стока.
Нулевая дивергенция:
Нулевая дивергенция означает, что ничего не теряется. Другими словами, количество приходящего потока эквивалентно количеству уходящего потока.
Вы можете мгновенно определить любой тип дивергенции, используя наш бесплатный онлайн-калькулятор дивергенции.
Дивергенция Формула:
Вычисление дивергенции векторного поля не дает правильного направления выхода. Однако для иллюстрации расхождения можно использовать следующее математическое уравнение:
Расхождение = ∇ . A
Поскольку дельта оператора определяется как:
$$ ∇ = frac{partial}{partial x}P, frac{partial}{partial y}Q, frac{partial} {partial z}R $$
Таким образом, формула для дивергенции выглядит следующим образом:
$$ Расхождение {vec{A}} = left(frac{partial}{partial x}P, frac{partial}{partial y}Q, frac{partial}{ partial z}Rright)cdot {vec{A}} $$
Как рассчитать дивергенцию?
Вы можете использовать наш бесплатный онлайн-калькулятор дивергенции для получения более точных результатов, но очень важно попрактиковаться на нескольких примерах, чтобы понять основную концепцию дивергенции векторного поля. {2} right)} ,sin{left(x y right)},3right) $$ 9{2} right)}+x cos{left(x y right)}+0right) $$
{2} right)} ,sin{left(x y right)},3right) $$ 9{2} right)}+x cos{left(x y right)}+0right) $$
Это требуемый ответ.
Вы также можете использовать наш бесплатный калькулятор расходимости векторного поля для определения потока жидкости или газа с точки зрения величины.
Пример № 02:
Вычислить дивергенцию векторного поля, приведенного ниже:
$$ B = sin{left(x right)},cos{left(y right)},2 z $$
Решение:
Дивергенция векторного поля изображается следующим образом:
Расхождение = ∇ . А
или;
$$ Расхождение {vec{A}} = left(frac{partial}{partial x}, frac{partial}{partial y}, frac{partial}{partial z}right)cdot {vec{A}} $$
Итак, имеем:
$$ Расходимость {vec{A}} = left(frac{partial}{partial x }, frac{partial}{partial y}, frac{partial}{partial z}right)cdot left(sin{left(x right)}, cos{left (y right)}, 2 zright) $$
Записав каждый член отдельно с его частной производной:
$$ Расходимость {vec{A}} = frac{partial}{partial x} left(sin{left(x right)}right) + frac{partial}{ partial y} left(cos{left(y right)}right) + frac{partial}{partial z} left(2 zright) $$
Взятие частных производных каждого член индивидуально:
$$ frac{partial}{partial x} left(sin{left(x right)}right) = cos{left(x right)} $$
$$ frac{partial}{partial y} left(cos{left(y right)}right) = — sin{left(y right)} $$
$$ frac{partial}{partial z} left(2 zright) = 2 $$
(щелкните частную производную, чтобы получить пошаговые расчеты)
Теперь вычисляем дивергенцию, суммируя все следующие члены:
$$ Расходимость {vec{A}} = cos{left(x right)}+ sin{left(y right)}+2 $$
Однако, если вы используете наш бесплатный онлайн-калькулятор дивергенции, шансы на любую неопределенность уменьшаются.
Как работает калькулятор дивергенции?
Наш калькулятор лучший среди всех калькуляторов, которые используются для нахождения дивергенции векторного поля.
Посмотрим, что делать!
Ввод:
- Запишите значения для каждой заданной координаты векторного поля
Теперь, если вы хотите найти расхождение для определенной координаты:
- Запишите желаемое значение координаты
- Нажмите «Рассчитать»
Вывод:
Калькулятор свободных расхождений вычисляет:
- Частные производные каждого члена, входящего в формулу
- Суммируйте все значения, чтобы получить расхождение заданного поля
- Пошаговые расчеты для лучшего понимания
Часто задаваемые вопросы:
Каков реальный пример феномена дивергенции?
В реальной атмосфере дивергенция возникает, когда сильный iwing=d удаляется от более слабого ветра. Когда дивергенция происходит в верхних слоях атмосферы, это приводит к подъему воздуха.
Что говорит нам теорема о дивергенции?
Эта теорема утверждает, что если вы используете тройной интеграл для дивергенции, чтобы определить сумму исходящего потока маленьких битов в объеме, вы получите общий исходящий поток для этого объема. Чтобы определить этот поток, вы можете бесплатно воспользоваться нашим калькулятором теорем дивергенции.
Является ли дивергенция тем же, что и поток?
Да, расходимость векторного поля можно представить как плотность его потока, входящего или выходящего из точки, которую можно легко измерить с помощью бесплатного онлайн-калькулятора расходимости вектора.
Что подразумевается под завитком?
Угловое вращение потока вокруг точки в определенном направлении называется ротором векторного поля.
Заключение:
Дивергенция говорит нам о мгновенном изменении силы векторного поля. Мы можем видеть широкое применение теоремы о дивергенции в области дифференциальных уравнений в частных производных, где они используются для вывода потока тепла и сохранения массы.
Примеры решений задач по теории поля
В этом разделе вы найдете готовые задания разного типа по векторному анализу (теории поля):
Понравилось? Добавьте в закладки
Примеры: базовые понятия теории поля
Задача 1. Проверить, что поле $f=(3x+y^2)i+2xy j$ потенциально и восстановить потенциал.
Задача 2. Найти дивергенцию и ротор векторного поля $overline{a}=(3x-y) overline{i}+(6z+5x) overline{k}$
Задача 3. Дано скалярное поле $u(x,y,z)$ и векторное поле $overline{a}(x,y,z)$. Найти $grad u$, $div overline{a}$, $rot overline{a}$ в точке $M(1;5;-2)$.
$$u=frac{sqrt{x}}{y}-frac{yz}{x+sqrt{y}}, quad
overline{a}=yzoverline{i} +xzoverline{j} +xyoverline{k}$$
Задача 4. Вычислить потенциальную функцию векторного поля
$$overline{a}=left( frac{x}{y}+ycos x right)overline{i} +left(-frac{x^2}{2y^2}+sin xright)overline{j}.$$
Поток поля через поверхность
Задача 5. Найти поток векторного поля $overline{a}=2x overline{i}+y overline{j}-2z overline{k}$ через часть плоскости $P: 2x+y/2+z=1$, расположенную в первом октанте (нормаль образует острый угол с осью $Oz$).
Задача 6. Найти поток векторного поля $overline{a}$ через часть поверхности $S$, вырезаемую плоскостями $P_1, P_2$ (нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями).
$$ overline{a}=(x^3+xy^2)overline{i}+(y^3+x^2y)overline{j}+z^2overline{k},\
S: x^2+y^2=1, P_1^ z=0; P_2: z=3$$
Задача 7. Найти поток векторного поля $overline{a}$ через замкнутую поверхность $S$ (нормаль внешняя).
$$ overline{a}=xoverline{i}+zoverline{j}-yoverline{k},\
S: z=4-2(x^2+y^2), z=2(x^2+y^2).$$
Задача 8. Найти поток векторного поля $overline{a}=x^3overline{i}+y^3overline{j}+z^3overline{k}$ через замкнутую поверхность $S: x^2+y^2+z^2=1$ (нормаль внешняя).
Задача 9. Найти поток векторного поля $overline{a}$ через часть плоскости $S$, вырезанную плоскостью $P: z=1$ непосредственно и с помощью формулы Гаусса-Остроградского (нормаль внешняя к замкнутой поверхности).
$$overline{a}=(x+xy^2) overline{i} + (y-yx^2)overline{j}+(z-3)overline{k}, quad S: x^2+y^2=z^2 (z geq 0).$$
Циркуляция векторного поля
Задача 10. Найти модуль циркуляции векторного поля $overline{a}=xyoverline{i}+yzoverline{j}+zxoverline{k}$ вдоль контура
$$x^2+y^2=9, x+y+z=1.$$
Задача 11. Найдите циркуляцию вектора $overline{a}=(x^2-y) overline{i}+ xoverline{j}+ overline{k}$ по контуру
$$x^2+y^2=1;\
z=1$$
с помощью формулы Стокса и непосредственно (положительным направлением обхода контура считать то, при котором точка перемещается по часовой стрелке, если смотреть из начала координат).
Задача 12. Найти циркуляцию вектора $F$ вдоль ориентированного контура $L$.
$$ overline{F} = (3x-1) overline{i}+ (y-x+z)overline{j}+4z overline{k}, $$
$L$ – контур треугольника $ABCA$, где $A,B,C$ точки пересечения плоскости $2x-y-2z+2=0$ соответственно с осями координат $Ox, Oy, Oz$.
Работа векторного поля
Задача 13. Найдите работу векторного поля $A=(2xy-y; x^2+x)$ по перемещению материальной точки вдоль окружности $x^2+y^2=4$ из $M (2; 0)$ в $К(-2; 0)$.
Задача 14. Вычислить работу векторного поля силы $overline{F} = xz overline{i} -overline{j}+y overline{k}$ при движении материальной точки по пути $L: x^2+y^2+z^2=4$, $z=1 (y ge 0)$ от точки $M(sqrt(3);0;1)$ до точки $N(-sqrt(3);0;1)$.
Типовой расчет по теории поля
Задание 15.
А) Найти поток векторного поля $F$ через внешнюю поверхность пирамиды, отсекаемой плоскостью $(p)$ двумя способами: непосредственно и по формуле Гаусса-Остроградского.
Б) Найти циркуляцию вектора $F$ по контуру треугольника двумя способами: по определению и по формуле Стокса.
$$ overline{F} = z overline{i}+ (x+y)overline{j}+y overline{k}, quad (p): 2x+y+2z=2. $$
Помощь с решением заданий
Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 150 рублей, оформление производится в Word, срок от 1 дня.
Проконсультируем по задачам теории поля
Полезные ссылки
- Учебник с примерами онлайн по теории поля
- Функции нескольких переменных – задачи с решениями
 09.18
09.18 09.18
09.18