Каждый из нас учился в школе. Там человек получает огромное количество тех знаний, которые впоследствии могут понадобиться в жизни. Не все, конечно, могут в полной мере оценить значимость полученных знаний в школьной время, но сейчас речь не об этом.
Математика. Это страшное для многих слово, которое пугало достаточное количество школьников в своё время. Цифры, формулы и расчёты поддавались только самым пытливым. И с каждым годом этот сложный предмет становился всё сложнее и сложнее.
В старших классах появляется геометрия и всё становится ещё сложнее и непонятнее. Возможно, многие хоть раз в жизни, но в сердцах проклинали непонятную им науку и задавались вопросом, зачем это вообще нужно, и понадобится ли это в жизни.
Возможно, в повседневной жизни применить полученные в школе знания не удавалось. Вряд ли требовалось посреди белого дня высчитывать логарифмы и квадратные уравнения или доказывать, что две параллельные никогда не сойдутся. Но, где уж точно могут понадобиться знания геометрии и математике, так это в строительстве и при осуществлении ремонта.
В данной статье речь пойдёт о вычислении прямого угла, что требуется при строительстве зданий. Точность при возведении строений должна быть соблюдена в обязательном порядке, ведь только точные расчёты могут избавить от перекосов и нестабильности организации всего здания. Вычисление прямого угла при строительстве — не такой уж и трудный процесс, при котором потребуется знание и применение некоторых простых правил математики и геометрии. Подробнее об этом будет рассказано ниже.
Действительно ли прямой угол?
Возможно, некоторые читатели, ознакомившиеся с заголовком данной статьи, возразят, что прямой угол можно получить не всегда, и не всегда при строительстве используются именно ровные и точные прямые углы.
И, в принципе, они правы. Получить его весьма сложно, особенно если наблюдается неровность фундамента, на котором осуществляется строительство здания. Но, даже учитывая это обстоятельство, ни в коем случае нельзя делать вывод, что расчёт прямого угла можно делать просто «на глаз». В любом случае, если не представляется возможным вычислить идеальный прямой угол, то требуется достичь наиболее приближённого значения к идеальному углу в 90 градусов. И этого можно добиться, используя незатейливые инструменты и не самые сложные математические знания и познания в геометрии.
Как сделать угол прямым
Все зависит от величины уклонов стен. К незначительным относятся отклонения не более 20 мм. При проведении работ следует придерживаться некоторых правил:
- Выставление вертикальных маяков является обязательным.
- Соблюдение последовательности при нанесении раствора: сначала делается наброска жидким раствором, а после его схватывания производится окончательное выравнивание поверхности стены.
- Нанесение толстого слоя раствора не рекомендуется, так как смесь под собственным весом отвалится, не успев схватиться.
- Первоначально выравнивается правилом по маякам одна стена, затем – вторая.
- При наличии правила в виде большого металлического угольника выравнивание происходит движением инструмента вверх-вниз по маякам. Излишек раствора срезается, а в недостающих местах – набрасывается.
Что понадобится для определения прямого угла?
Итак, какие инструменты понадобится использовать для того, чтобы проверить прямой угол. Сразу стоит отметить, что никаких приборов и серьёзных инструментов для этого не потребуется. Нужно будет использовать весьма простые вещи, которые могут найтись практически в каждом хозяйстве. И даже если их не имеется под рукой, их с лёгкостью можно приобрести в магазине. С этим никаких трудностей не возникнет.
Для вычисления прямого угла нужно взять:
- Карандаш;
- Строительную рулетку.
И всё. Вот так вот всё просто.
Чем проверять и выставлять углы
Угол легко проверить строительным угольником, можно приобрести в магазине, если собираетесь выводить углы, он будет вам необходим.

Строительный угольник необходим для проверки углов
Просто прислоняем угольник к внутреннему углу. Наружные углы мы пока рассматривать не будем, ради понимания самого процесса. После понимания как выравнивать внутренние углы под 90 градусов своими руками, внешние для вас проблем не составят.

Проверяем внутренний угол
Смотрим, что получается. Если всё нормально, зазоров между угольником нет, то расслабьтесь. Если зазор превышает 5 мм, то следует насторожиться и узнать как выровнять такой угол в прямой, что бы и ванна и шкафы висели хорошо. Дело в том, что зазор в 5 мм под небольшим, пускай полуметровым (в длину хотя бы одной грани) угольником, на всю длину стены оказывается довольно крупным и в конце стены может достичь и 5 см.
Делаем угольник самостоятельно
Угольник можно соорудить и самостоятельно, причём любого размера. Удобнее всего делать такой угольник из гипсокартонных профилей 27*28 мм (жёстких или полужёстких).
Пользуемся пра́вилом египетского треугольника, при котором: если катеты угла равны 3 и 4 частям, а гипотенуза 5 частям, то угол будет прямоугольным (прямой угол между катетами).
Надрезаем и сгибаем нужной длины профиль посредине (стороны нашего угольника не обязательно должны быть равны 3 и 4 определённым нами частям, пра́вило нужно лишь для того, чтобы сделать прямой угол). Сгибаем, принимаем за 1 часть, к примеру, 30 см. Чем больше вы сделаете часть, тем «прямее» получится угол.
Отмеряем на одном катете 3 части — 90 см, на втором 4 части — 120 см. Делаем отметки маркером. Далее, сгибая угол, отмеряем строго от отметок гипотенузу — 5 частей — 150 см. Наш угол прямой, осталось его зафиксировать тем же профилем на саморезы. Тут следует быть аккуратным, чтобы не сбить угол, проверьте правильность разметки несколько раз.
Ниже в ролике наглядно показано как соорудить такой угольник.
Проверяем угол с помощью лазерного построителя плоскостей
Лазерные построители плоскостей позволяют с лёгкостью выверять вертикали, горизонтали, отклонения целых площадей, а так же и углы, если такая функция на нём предусмотрена.

Лазерный построитель плоскостей, с функцией построения прямого угла
Не все построители плоскостей подходят, а те которые проецируют две перпендикулярных вертикальных плоскости. С ним работа гораздо облегчается, но стоит такой прибор начиная от 15 тыс. руб. Можно найти и подешевле, особенно в Китае, но у них могут быть и отклонения, хоть часто и не значительные, они как минимум, написаны в паспорте устройства, а на дешёвых моделях отклонения могут и вовсе не совпадать с паспортными. Проверьте это перед использованием с помощью большого угольника, который описан выше или на заведомо прямых углах.
Такие приборы позволяют не только выводить прямые углы, а так же и → штукатурные плоскости и → стяжку пола (по ссылкам рассказано как делать штукатурку по маякам и цементно-песчаную стяжку).
Лазерный построитель плоскостей (нивелир) стоит лишь включить, приставить к углу и прочертить линии на полу, которые он спроецировал. Далее я расскажу как проверить углы и выстроить прямоугольник на площади помещения с помощью угольника и правила, а как работать лазерным построителем плоскостей станет понятно из этого рассказа.
Как можно вычислить прямой угол?
Итак, в этой статье будет описан принцип 3-4-5 при определении угла в 90 градусов. Ничего сложного в этом нет. Потребуется просто лишь чуть пораскинуть мозгами и вникнуть во все расчёты, которые смогут помочь в проверке угла.
Итак, нужно обозначить следующие шаги:
- Для начала стоит разобраться в том, почему принцип так обозначен — 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;
- Итак, потребуется для начала отмерить 3 метра от угла вдоль одной из стен. Тут следует отметить, что 3 метра — предпочтительная длина замера, но в том случае, если комната маленькая, можно отметить всего 30 сантиметров. В месте замера нужно сделать отметку;
- В принципе, можно использовать и другие цифры, но рекомендуется в любом случае использовать пропорционально увеличенные числа, например: 9-12-15 или же 30-40-50;
- После проделанного предварительного замера нужно отмерить 4 метра вдоль другой стены, тоже от угла. Ну или соответственно 40 сантиметров, если комната маленькая. Нужно сделать отметку;
- Теперь остаётся сделать последнее действие, по которому уже можно судить прямой угол или нет. От измеряющего потребуется измерить расстояние между сделанными отметками. По полученным данным можно будет сделать определённые выводы:
- Если расстояние между отметками будет равняться 5 метрам ровно, это будет означать, что угол является прямым;
- В том случае, если измеренное расстояние будет равняться меньше 5 метров, угол будет меньше, чем 90 градусов;
- Ну и, наконец, величина угла будет составлять больше 90 градусов, если полученная величина замера будет равняться больше 5 метров.
Как вывести угол 90 градусов между стенами своими руками
К
ачественный ремонт и отделка подразумевает хорошую геометрию помещения. Без выверенной геометрии, хотя бы в самых нужных местах, хороший ремонт сделать не удастся. Здесь я расскажу как сделать угол 90 градусов между стенами своими руками и о том, где он действительно необходим. Так же можно почитать статью по ссылке → о геометрии помещения и как проверить правильность геометрии, и что будет если геометрия нарушена.
Содержание:
1.
Где нужен угол 90 градусов между стенами.
2.
Чем проверять и выставлять углы.
2.1
Делаем угольник самостоятельно.
2.2
Проверяем угол с помощью лазерного построителя плоскостей.
3.
Делаем разметку под выравнивание прямых углов.
4.
Начинаем разметку от первой стены.
5.
Как вывести углы в ванной: все углы 90 градусов или только два.
5.1
Определяемся с углами.
6.
Проверяем вертикальность стен.
7.
Установка маяков и штукатурка стен.
Вывод
Вот, как просто можно вычислить прямой угол без использования каких-либо строительных инструментов и приборов. Использовать можно самое простое, но в то же время весьма действенное средство, которое вкупе с использованием имеющихся знаний и бесхитростных расчётов, может помочь произвести измерение.
При использовании предложенных величин, ключевым становится финальный замер между двумя отметками, которые были сделаны ранее. Расстояние, которое будет равняться точно 5 метрам, покажется, что он прямой. Если же величина будет больше или меньше 5 метров, это будет означать, что он прямым не является.
Как проверить ровность стен и качество штукатурных работ в жилых помещениях
До начала работ по штукатурке стен надо понимать, что бывает простая штукатурка и высококачественная штукатурка. Для возможности качественной дальнейшей отделки стен применяется именно высококачественная штукатурка стен. Поэтому при заказе работ обратите внимание исполнителей на это. Как проверить ровность стен после штукатурных работ. Для этого вам понадобится правило-уровень желательно новое высотой 2.5 метра, новый строительный уровень.
1.Проверяем отклонения по вертикали и горизонтали. Допускаются перепады плоскости стен от вертикали на 1 метр их длины на 1 миллиметр. На всю высоту помещения не больше 5 миллиметров. Плоскости стен от горизонтали, на 1 метр их длины 1 миллиметр. Проверьте это при помощи двухметрового строительного уровня. Совет! Обязательно проверяйте каждые два метра поверхности стены.
2. Проверяем ровность стен. Поверхность может иметь не более двух неровностей плавных очертаний на 4 квадратных метра глубиной или высотой не более 2 миллиметров. Ровность стен проверяют с помощью нового правила-уровня высотой 2 или лучше 2.5 метра. Его прикладывают к плоскости сначала вертикально, потом горизонтально, и выявляют расстояние между ним и отштукатуренной поверхностью, оно не должно превышать 2 мм. Проверьте ровность поверхности под батареями, на стенах где окна, в районе розеток и выключателей, за стояками отопления, в тех местах куда затруднительно добраться. Внимание! Неродивые строители считают, что идеально ровно должно быть на уровне глаз, и покажут вам именно эти места, поэтому будьте бдительны в этом вопросе и проверяйте везде.
3. Проверяем прочность отштукатуренной поверхности. Осмотрите поверхность. Трещин быть не должно. Ударьте раскрытой ладонью по поверхности в нескольких местах по вашему усмотрению, если услышите гулкий звук от удара и ощутите отслоение, то работы необходимо переделывать. Внимание: Проконтролируйте, чтобы все металлические маяки были удалены из стен.
4. Проверяем углы Если вы договорились с исполнителями о выравнивании углов под 90 градусов, особенно это актуально в местах установки мебели и оборудования, то проверить работу можно следующим образом. Углы проверяются не на ровность, так как ровность дадут металлические уголки, которые устанавливают перед шпаклевкой, а на отклонения в градусах по горизонтали. Например угол в 89,9 градуса дает на стену длиной 5 метров, отклонение около 1 см. Угол 90 градусов между стенами в прямоугольной комнате проще проверить рулеткой. Надо замерить две диагонали помещения и сравнить их. Если они равны, то стены образуют прямоугольник, с прямыми углами и параллельными стенами. Так же прямые углы стен можно проверять с помощью длинного строительного угольника не менее 50 см длинной, проверяйте весь угол от пола до потолка.
5. Проверяем параллельность стен. Если вы заранее договорились о стенах, которые должны быть строго параллельны друг другу, то померьте с помощью рулетки расстояние между ними, в начале и в конце, оно должно быть одинаковое.
6. Проверяем зоны особого внимания. Делаем это так же с помощью строительного уровня-правила. Важно! Дверные наличники, потолочные и половые плинтусы ровные, поэтому зоны примыканий плинтусов и наличников должны быть идеально ровными, что бы не получить в этом месте щель. Отклонения дверных и оконных откосов, арок, столбов, пилястр от горизонтали и вертикали не должны быть свыше 1 миллиметра. Радиусы криволинейных элементов, например арок не должны отклоняться от проектной величины более 5 миллиметров. Это можно проверить с помощью лекала шаблона. Ширина откосов от проектного значения не должна отклоняться свыше, чем на 2 миллиметра. Проверяйте весь периметр откосов.
Внимание! Проверьте, чтобы стены были оштукатурены до самого края дверного проема, так как наличники могут не скрыть оставшуюся поверхность.
Внимание! Проверьте, что бы штукатурка на оконных откосах не мешала свободному ходу оконных створок. Для этого надо открыть окно до упора и посмотреть открывается ли окно полностью.
Внимание! Проконтролируйте, чтобы все металлические уголки, особенно над дверными проемами были предварительно загрунтованы, что бы в последствии при окраске не проступали пятна от коррозии металла.
Как проверить прямой угол: простая технология
На чтение 2 мин Просмотров 308 Обновлено 19.06.2022
Чтобы проверить прямой угол, поможет очень старая и простая столярная хитрость. По сути, эта базовая хитрость и не хитрость вовсе. Она основана на теореме Пифагора, которая гласит «Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы». Звучит сложно? Вовсе нет! Давайте разбираться.

Как проверить прямой угол
Если вы хотите проверить, является ли ваше изделие или какая-то его часть строго прямоугольными, используя математику, сделайте следующее. Выберите один угол и с помощью комбинированного угольника предварительно проверьте, действительно ли он является прямым. Затем с помощью рулетки измерьте длину одной из сторон, составляющей прямой угол, и на калькуляторе умножьте полученное число на само себя (или, иными словами, возведите его в квадрат). Запишите это число или сохраните в памяти калькулятора.
Затем измерьте длину второй стороны, которая составляет прямой угол. Проделайте ту же операцию – умножьте это число на само себя. Затем сложите полученное число с тем, которые вы записали до этого. Одна часть уравнения готова!
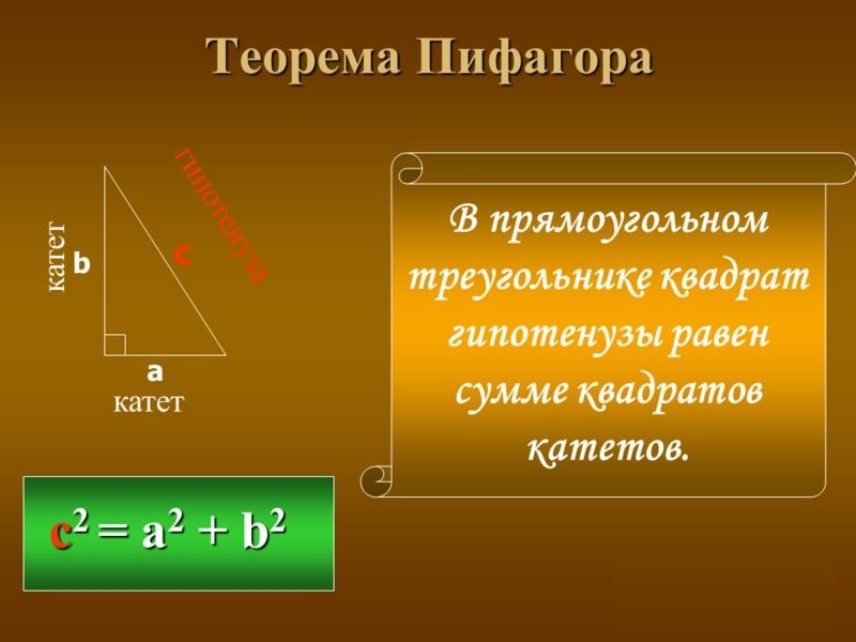
Чтобы получить третью величину, измерьте расстояние от свободного конца одной стороны до свободного конца другой стороны. Это будет гипотенузой. Умножьте длину гипотенузы на саму себя. Если полученное число совпадает с суммой, которую вы получили до этого (когда складывали квадраты двух сторон), то угол действительно прямой.
Читайте также Столярное дело для новичков: главные моменты
Как проверить прямоугольник?
В столярном деле часто используют так называемое «правило 3-4-5». Вы всегда можете использовать его, чтобы определить прямой угол по любой шкале при разметке.
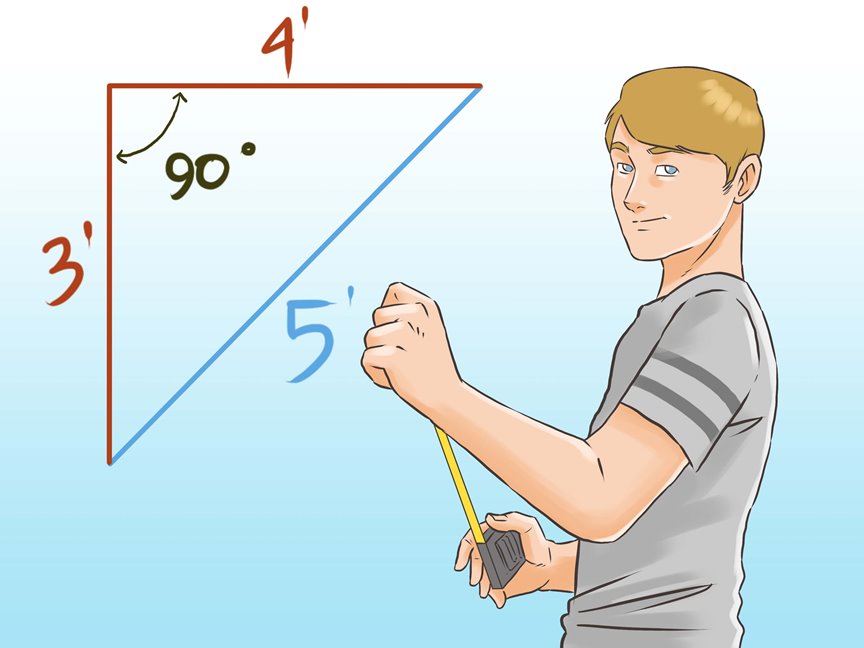
Однако есть более точный (и гораздо более быстрый) способ определить, является ли ваше изделие прямоугольным. Просто измерьте диагонали предполагаемого прямоугольника. Если диагональ, проведённая из левого нижнего в правый верхний угол в точности совпадает по длине с диагональю, проведённой из правого нижнего в левый верхний угол, то элементы действительно составляют прямоугольник.
Читайте также Как правильно забивать гвозди под углом: основные рекомендации
А что же делать, если их длины не совпали? Скорректируйте изделие. Выберите ту диагональ, которая получилась длиннее, и слегка подтолкните один из её углов внутрь. После этого повторите измерения. Продолжайте корректировать положение до тех пор, пока длины диагоналей не буду совпадать.
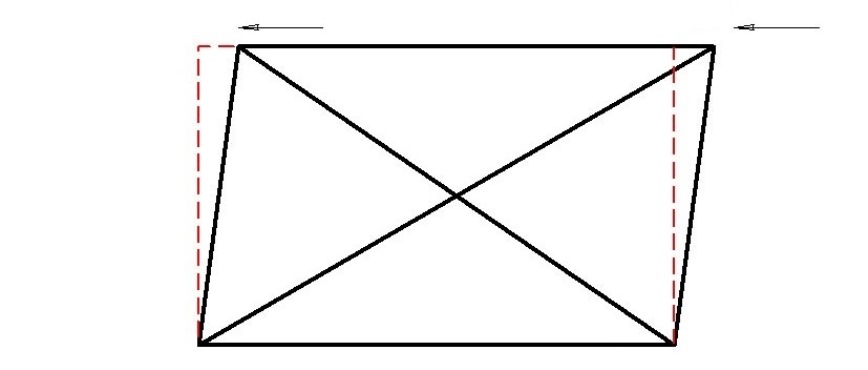
Просто? Конечно! Теперь и вы можете использовать этот способ в своей работе.
Нажмите, пожалуйста, на одну из кнопок, чтобы узнать понравилась статья или нет.

Изучаю инженерное проектирование, механику, архитектуру и дизайн. Люблю создавать вещи своими руками
 Каждый из нас учился в школе. Там человек получает огромное количество тех знаний, которые впоследствии могут понадобиться в жизни. Не все, конечно, могут в полной мере оценить значимость полученных знаний в школьной время, но сейчас речь не об этом.
Каждый из нас учился в школе. Там человек получает огромное количество тех знаний, которые впоследствии могут понадобиться в жизни. Не все, конечно, могут в полной мере оценить значимость полученных знаний в школьной время, но сейчас речь не об этом.
Математика. Это страшное для многих слово, которое пугало достаточное количество школьников в своё время. Цифры, формулы и расчёты поддавались только самым пытливым. И с каждым годом этот сложный предмет становился всё сложнее и сложнее.
- Действительно ли прямой угол?
- Что понадобится для определения прямого угла?
- Как можно вычислить прямой угол?
- Вывод
В старших классах появляется геометрия и всё становится ещё сложнее и непонятнее. Возможно, многие хоть раз в жизни, но в сердцах проклинали непонятную им науку и задавались вопросом, зачем это вообще нужно, и понадобится ли это в жизни.
Возможно, в повседневной жизни применить полученные в школе знания не удавалось. Вряд ли требовалось посреди белого дня высчитывать логарифмы и квадратные уравнения или доказывать, что две параллельные никогда не сойдутся. Но, где уж точно могут понадобиться знания геометрии и математике, так это в строительстве и при осуществлении ремонта.
В данной статье речь пойдёт о вычислении прямого угла, что требуется при строительстве зданий. Точность при возведении строений должна быть соблюдена в обязательном порядке, ведь только точные расчёты могут избавить от перекосов и нестабильности организации всего здания. Вычисление прямого угла при строительстве – не такой уж и трудный процесс, при котором потребуется знание и применение некоторых простых правил математики и геометрии. Подробнее об этом будет рассказано ниже.
Действительно ли прямой угол?
 Возможно, некоторые читатели, ознакомившиеся с заголовком данной статьи, возразят, что прямой угол можно получить не всегда, и не всегда при строительстве используются именно ровные и точные прямые углы.
Возможно, некоторые читатели, ознакомившиеся с заголовком данной статьи, возразят, что прямой угол можно получить не всегда, и не всегда при строительстве используются именно ровные и точные прямые углы.
И, в принципе, они правы. Получить его весьма сложно, особенно если наблюдается неровность фундамента, на котором осуществляется строительство здания. Но, даже учитывая это обстоятельство, ни в коем случае нельзя делать вывод, что расчёт прямого угла можно делать просто “на глаз”. В любом случае, если не представляется возможным вычислить идеальный прямой угол, то требуется достичь наиболее приближённого значения к идеальному углу в 90 градусов. И этого можно добиться, используя незатейливые инструменты и не самые сложные математические знания и познания в геометрии.
Что понадобится для определения прямого угла?
 Итак, какие инструменты понадобится использовать для того, чтобы проверить прямой угол. Сразу стоит отметить, что никаких приборов и серьёзных инструментов для этого не потребуется. Нужно будет использовать весьма простые вещи, которые могут найтись практически в каждом хозяйстве. И даже если их не имеется под рукой, их с лёгкостью можно приобрести в магазине. С этим никаких трудностей не возникнет.
Итак, какие инструменты понадобится использовать для того, чтобы проверить прямой угол. Сразу стоит отметить, что никаких приборов и серьёзных инструментов для этого не потребуется. Нужно будет использовать весьма простые вещи, которые могут найтись практически в каждом хозяйстве. И даже если их не имеется под рукой, их с лёгкостью можно приобрести в магазине. С этим никаких трудностей не возникнет.
Для вычисления прямого угла нужно взять:
- Карандаш;
- Строительную рулетку.
И всё. Вот так вот всё просто.
Как можно вычислить прямой угол?
Итак, в этой статье будет описан принцип 3-4-5 при определении угла в 90 градусов. Ничего сложного в этом нет. Потребуется просто лишь чуть пораскинуть мозгами и вникнуть во все расчёты, которые смогут помочь в проверке угла.
Итак, нужно обозначить следующие шаги:
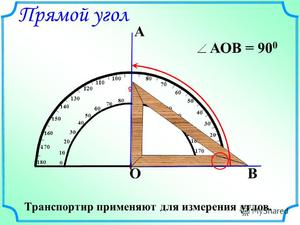 Для начала стоит разобраться в том, почему принцип так обозначен – 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;
Для начала стоит разобраться в том, почему принцип так обозначен – 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;- Итак, потребуется для начала отмерить 3 метра от угла вдоль одной из стен. Тут следует отметить, что 3 метра – предпочтительная длина замера, но в том случае, если комната маленькая, можно отметить всего 30 сантиметров. В месте замера нужно сделать отметку;
- В принципе, можно использовать и другие цифры, но рекомендуется в любом случае использовать пропорционально увеличенные числа, например: 9-12-15 или же 30-40-50;
- После проделанного предварительного замера нужно отмерить 4 метра вдоль другой стены, тоже от угла. Ну или соответственно 40 сантиметров, если комната маленькая. Нужно сделать отметку;
- Теперь остаётся сделать последнее действие, по которому уже можно судить прямой угол или нет. От измеряющего потребуется измерить расстояние между сделанными отметками. По полученным данным можно будет сделать определённые выводы:
- Если расстояние между отметками будет равняться 5 метрам ровно, это будет означать, что угол является прямым;
- В том случае, если измеренное расстояние будет равняться меньше 5 метров, угол будет меньше, чем 90 градусов;
- Ну и, наконец, величина угла будет составлять больше 90 градусов, если полученная величина замера будет равняться больше 5 метров.
Вывод
Вот, как просто можно вычислить прямой угол без использования каких-либо строительных инструментов и приборов. Использовать можно самое простое, но в то же время весьма действенное средство, которое вкупе с использованием имеющихся знаний и бесхитростных расчётов, может помочь произвести измерение.
При использовании предложенных величин, ключевым становится финальный замер между двумя отметками, которые были сделаны ранее. Расстояние, которое будет равняться точно 5 метрам, покажется, что он прямой. Если же величина будет больше или меньше 5 метров, это будет означать, что он прямым не является.
План урока:
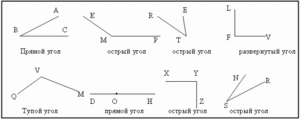
Угол. Виды углов: прямой, тупой, острый
Прямоугольник. Свойство противоположных сторон прямоугольника
Квадрат
Построение прямого угла, прямоугольника, квадрата на бумаге в клетку
Здравствуйте, дорогие ребята!
Приглашаем вас в сказочную страну Геометрию.
Жил-был король Луч. Была у короля маленькая, смешная и забавная дочка Точка. Отец очень любил и баловал принцессу и никогда не наказывал: не ставил в угол за ее шалости.
Угол. Виды углов: прямой, тупой, острый
Ребята, а вы знаете, что такое угол? Какие бывают углы?
Давайте вместе начертим угол. Сначала поставим точку. Затем проведем из этой точки 2 луча. Например, так:

Лучи – это стороны угла. А точка, из которой мы проводили лучи – вершина угла.

Углы бывают прямые, острые и тупые. Острым углом назовем тот, который меньше прямого, а тупым углом – тот, который больше прямого угла.
Изготовим модель прямого угла из кусочка бумаги.

Можно в качестве модели прямого угла использовать угольник. У него обязательно есть один прямой угол.

Ребята, помогите принцессе Точке определить, какие углы являются прямыми, а какие тупыми и острыми! Сосчитайте, сколько на этом чертеже прямых, острых, тупых углов.

Проверь себя!
Прямых – 6 углов, острых – 4 угла, тупых – 2 угла.
Король Луч решил построить для принцессы Точки игровую площадку. Он долго размышлял, чертил на песке разные фигуры. Посмотрите, после дождя остались лишь очертания. Назовите одним словом, что это?

Верно, это углы. Запишите номера углов в 3 столбика: острые, тупые, прямые.
Проверь себя.

Прямоугольник. Свойства противоположных сторон прямоугольника
Ребята, посмотрите на дворец короля и принцессы. Из каких геометрических фигур он состоит?

Давайте сосчитаем все прямоугольники, квадраты, треугольники и круги.
Прямоугольники – 3.
Квадраты – 5.
Треугольники – 3.
Круги – 5.

Найдите среди этих фигур четырехугольники, у которых все углы прямые. Воспользуйтесь моделью прямого угла, которую мы с вами изготовили.

Проверь себя.
Прямоугольники: 1, 3, 5.
Ребята, у принцессы Точки есть для вас вопросы о прямоугольнике. Попробуйте на них ответить.
Вопрос 1. Равны ли у прямоугольника противоположные стороны (они лежат напротив друг друга)?

На чертеже противоположные стороны обозначены одинаковым цветом.
Вопрос 2. Все ли углы прямые у прямоугольника?
Вопрос 3. Могут ли все стороны прямоугольника, а не только противоположные, быть одинаковыми? Например, так:

Подумайте! Возьмите любой прямоугольник, измерьте линейкой стороны фигуры, с помощью модели прямого угла или угольника проверьте углы.
Сравните свои выводы с правильными ответами.
Ответ 1. Противоположные стороны равны.
Ответ 2. Все углы прямые.
Ответ 3.Все стороны прямоугольника могут быть одинаковыми.
Молодцы! Не огорчайтесь, если не все выводы совпали с правильными ответами. Давайте еще раз повторим о прямоугольнике все, что узнали.

Квадрат
Ребята, отвечая на вопрос принцессы Точки, мы сделали вывод о том, что у прямоугольника все стороны могут быть одинаковой длины. Такой прямоугольник будет называться квадратом.

Задача на смекалку от короля. Помогите принцессе Точке ее решить.
Начерти прямоугольник со сторонами 5 см и 4 см. Сделай из него квадрат! Подсказка: «Можно сделать двумя способами: добавить, убрать».
Проверь себя.

Принцесса отлично справилась с задачей. А теперь попробуйте вы самостоятельно выполнить следующее задание.
Найдите среди этих прямоугольников квадраты. Запишите их номера.

Проверь себя.
Квадраты: 1,3.
Поиграем вместе с принцессой Точкой. Она выложила из счетных палочек такую фигуру:

Сколько квадратов вы видите? Уберите одну палочку так, чтобы осталось два квадрата. Сделать это можно разными способами. Какие еще фигуры, кроме двух квадратов, у вас получились?

Проверь себя.
Кроме двух квадратов, на каждом рисунке есть прямоугольник.
Построение прямого угла, прямоугольника, квадрата на клетчатой бумаге
Как вы заметили, король Луч и принцесса Точка любят чертить. Они приглашают нас, ребята, поучаствовать в этом увлекательном занятии. Вооружитесь тетрадью в клеточку, простым карандашом, угольником.
Задание: построить на бумаге в клеточку прямой угол, прямоугольник со сторонами 6 см и 3 см, квадрат со стороной 7 см.
Посмотрите, как получилось у принцессы. Сравните со своими чертежами.

Ставим точку. Откладываем два луча при помощи угольника или линейки.

Ставим точку. Вверх – 3 см, вправо – 6 см. Помним, что противоположные прямоугольника стороны равны. Чертим их – 6 см и 3 см.
Квадрат
А это тетрадь короля. Он чертил квадрат. Сравните со своим чертежом.

Ставим точку. Помним, что у квадрата все стороны равны. Откладываем вверх 7 см, вправо – 7 см. Чертим противоположные стороны по 7 см.
Молодцы, здорово получилось! Если такое занятие было для вас интересным и увлекательным, попробуйте начертить прямой угол, прямоугольник и квадрат на нелинованной бумаге. Сделать это будет гораздо сложнее. Здесь на помощь придет угольник: проверять прямой угол. Можно воспользоваться моделью прямого угла, которую мы изготовили.
Посмотрите, как это получилось у короля и Точки.

После нелегкого занятия король Луч и его дочка присели отдохнуть. Принцесса попросила рассказать интересную сказку. Давайте и мы послушаем!
Сказка
Жил-был на свете Прямоугольник. Фигура важная, спору нет! Люди ценили и уважали Прямоугольника, потому что при изготовлении многих вещей использовали эту фигуру. Всё хорошо у Прямоугольника, но одиноко как-то. Решил он найти своих родственников. Думает: «Если встречу родственников, сразу узнаю, потому что на меня должны быть похожи!».
Однажды встретил Прямоугольник Квадрата и говорит: «Как тебя зовут? Очень ты, брат, на меня похож!». Отвечает Квадрат: «Если найдем не меньше четырех общих признака, значит, родственники». Стали они друг друга рассматривать и обнаружили четыре сходства:
У каждого было по 4 угла, да все прямые, по 4 стороны, да стороны, которые одна напротив другой – одинаковой длины.
Обрадовались родственники, что нашли друг друга. Поспешили вместе отправиться дальше. Встретили однажды Четырехугольника и спрашивают: «Похож ты на нас. Уж не родня ли?».
Говорит им Четырехугольник: «Я был бы очень рад! Если найдем хотя бы два сходства, значит, родственники». Стали опять внимательно друг к другу приглядываться и увидели два общих признака:
- 4 угла.
- 4 стороны.
Обрадовались фигуры и решили не терять друг друга, держаться всегда рядом.
Понравилась вам сказка? Давайте повторим о фигурах все, что узнали.

В сказочное королевство Геометрия мы вернемся еще не раз. А этот урок подошел к концу. Выберите смайлик вашего настроения.

До скорой встречи в королевстве Геометрия! А сейчас проверьте свои знания. Принцесса Точка справилась с заданиями хорошо, допустила одну небольшую ошибку. Будьте внимательны, не спешите!
Информация по назначению калькулятора
Прямоугольник – это двумерная геометрическая фигура, имеющая 4 стороны и 4 угла. Две его стороны сходятся под прямым углом. Таким образом, прямоугольник имеет 4 угла, каждый из которых равен 90 градусов. Противоположные стороны прямоугольника имеют одинаковую длину и параллельны. Две стороны называются параллельными, когда расстояние между ними остается одинаковым во всех точках.
Поскольку все углы прямоугольника равны, его можно назвать равноугольным четырехугольником.
Некоторые свойства прямоугольника отмечены далее:
⇒ Прямоугольник – это четырехугольник.
⇒ Противоположные стороны прямоугольника равны и параллельны друг другу.
⇒ Внутренний угол прямоугольника в каждой вершине равен 90°.
⇒ Сумма всех внутренних углов равна 360°.
⇒ Диагонали делят пополам друг друга.
⇒ Длина диагоналей равна.
⇒ Поскольку стороны прямоугольника параллельны, его также называют параллелограммом.
⇒ Все прямоугольники являются параллелограммами, но не все параллелограммы являются прямоугольниками.
Онлайн калькулятор поможет найти параметры прямоугольника, такие как:
- Длины сторон
- Периметр
- Площадь
- Диагонали
- Углы
- Радиус Описанной окружности
- Диаметр Описанной окружности
- Длина Описанной окружности
- Площадь Описанной окружности
– равен сумме всех 4х сторон (P=AB+BC+CD+DA)
– равна произведению двух сторон (S=AB*BC)
– Диагональ разрезает прямоугольник на 2 прямоугольных треугольника, в которых диагональ образует гипотенузу, а две смежные стороны прямоугольника образуют две другие стороны треугольника.(AC=√(AB2 + BC2))
– всегда равны 90 градусов
Диаметр описанной окружности прямоугольника равен длине его диагонали
