Как найти румб дирекционный прямой

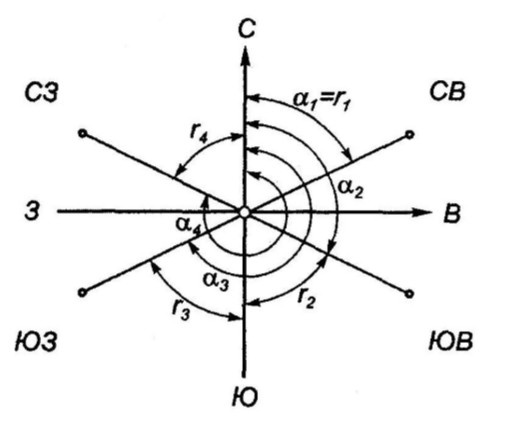
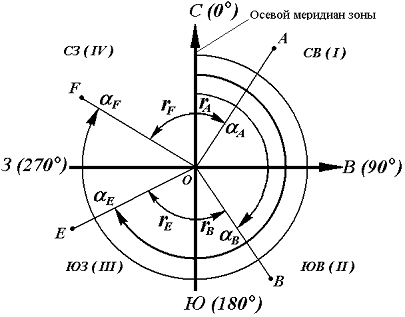
румбом
называется острый горизонтальный угол,
отсчитываемый от ближайшего направления
осевого меридиана (северного или южного)
до данной линии. Румбы обозначают буквой
r с индексом, указывающим четверть, в
которой находится румб.

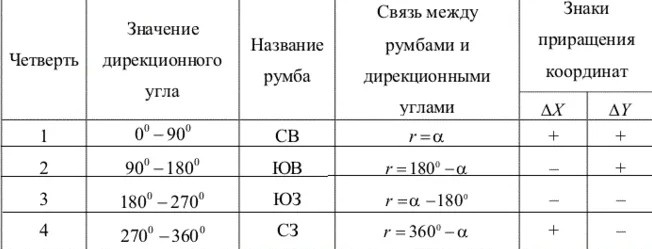
Зависимость
между дирекционными углами и румбами
определяется для четвертей по следующим
формулам:

I
четверть (СВ) r = α

II
четверть (ЮВ) r = 180° – α

III
четверть (ЮЗ) r = α – 180°

IV
четверть (СЗ) r = 360° – α

Румб
в точке М направления ВС называется
прямым, а противоположного направления
СВ – обратным. Прямой и обратный румб
в одной и той же точке данной линии равны
по численному значению, но имеют индексы
противоположных четвертей.

19. Прямая геодезическая задача

В
геодезии часто приходится передавать
координаты с одной точки на другую.
Например, зная исходные координаты
точки А (рис.23), горизонтальное расстояние
SAB от неё до точки В и направление линии,
соединяющей обе точки (дирекционный
угол αAB или румб rAB), можно определить
координаты точки В. В такой постановке
передача координат называется прямой
геодезической задачей.

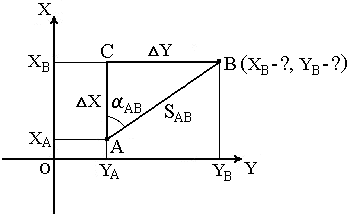
Для
точек, расположенных на сфероиде, решение
данной задачи представляет значительные
трудности. Для точек на плоскости она
решается следующим образом.

Дано:
Точка А( XA, YA ), SAB и αAB. Найти: точку В( XB,
YB ).

Непосредственно
из рисунка имеем:

ΔX
= XB – XA ; ΔY = YB – YA .

Разности
ΔX и ΔY координат точек последующей и
предыдущей называются приращениями
координат. Они представляют собой
проекции отрезка АВ на соответствующие
оси координат. Их значения находим из
прямоугольного прямоугольника АВС:

ΔX
= SAB · cos αAB ;ΔY = SAB · sin αAB .

Так
как в этих формулах SAB всегда число
положительное, то знаки приращений
координат ΔX и ΔY зависят от знаков cos
αAB и sin αAB.

При
помощи румба приращения координат
вычисляют по формулам:

ΔX
= SAB · cos rAB ;ΔY
= SAB · sin rAB .

Знаки
приращениям дают в зависимости от
названия румба. Вычислив приращения
координат, находим искомые координаты
другой точки:

XB
= XA + ΔX ; YB = YA + ΔY .

Таким
образом можно найти координаты любого
числа точек по правилу: координаты
последующей точки равны координатам
предыдущей точки плюс соответствующие
приращения.

Контроль
вычислений координат выполняют по
формуле

20. Обратная геодезическая задача

Обратная
геодезическая задача – это вычисление
дирекционного угла α и длины S линии,
соединяющей два пункта с известными
координатами X1, Y1 и X2, Y2

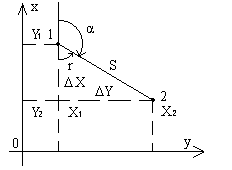
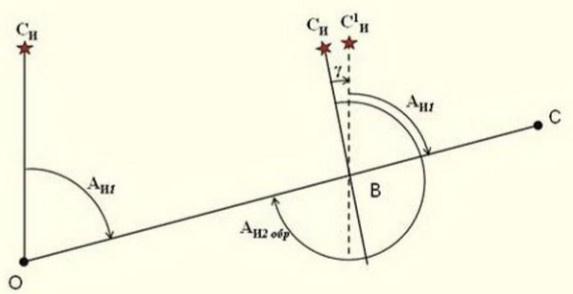
Построим
на отрезке 1-2 как на гипотенузе
прямоугольный треугольник с катетами,
параллельными осям координат. В этом
треугольнике гипотенуза равна S, катеты
равны приращениям координат точек 1 и
2 ( ΔX = X2 – X1, ΔY = Y2 – Y1 ), а один из острых
углов равен румбу r линии 1-2.

Если
Δ X 00 и Δ Y 00, то решаем треугольник по
известным формулам:

Для
данного рисунка направление линии 1-2
находится во второй четверти, поэтому
на основании (1.22) находим:

Общий
порядок нахождения дирекционного угла
линии 1-2 включает две операции:

*
определение номера четверти по знакам
приращений координат Δ>X и ΔY (рис.1.4-а),

*
вычисление α по формулам связи (1.22) в
соответствии с номером четверти.Контролем
правильности вычислений является
выполнение равенства:

Контроль:
d . cos α + XA = XB, d . sin α + YB = YB.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Азимуты

Азимут

Это направление, измеряемое в градусах по часовой стрелке от севера на азимутальной окружности. Азимутальный круг состоит из 360 градусов. Девяносто градусов соответствует востоку, 180 градусов — югу, 270 градусов — западу, а 360 градусов и 0 градусов — северу.

Слово «азимут» иногда используется как синоним азимута для обозначения направления (показания в градусах) от одного объекта к другому. Такое использование корректно только в первом (СВ) квадранте между 0° и 90°.

Азимуты также можно считывать с юга. Национальная геодезическая служба Национального управления океанических и атмосферных исследований (NOAA) (бывшая Береговая и геодезическая служба США) всегда использует юг в качестве нулевого направления. В пожарной службе дикой природы азимут всегда считывается с северной точки.

Направление ветра

Азимут часто используется для обозначения направления ветра. Традиционно направление ветра указывается как одна из восьми точек компаса (С, СВ, В, ЮВ, Ю, ЮЗ, З, СЗ). Однако графики направления ветра и скорости часто дают значение азимута, используя 0° и 360° для севера. Ветры называются по направлению, откуда они дуют. Например, западный ветер дует с запада (или 270°), а юго-восточный ветер дует с юго-востока (135°).

Обратный азимут и обратное визирование

Обратный азимут — это проекция азимута от начала координат до противоположной стороны азимутального круга. В азимутальном круге 360 градусов, поэтому противоположное направление будет 180 градусов (половина 360 градусов) от азимута.

Обратный азимут рассчитывается путем прибавления 180° к азимуту, если азимут меньше 180°, или вычитания 180° из азимута, если он больше 180°. Например, если азимут равен 320°, обратный азимут будет 320° – 180° = 140°. Если азимут равен 30°, обратный азимут будет равен 180° + 30° = 210°.

Обратное прицеливание — это метод прицеливания, в котором используется отсчет азимута, снятый в обратном направлении.

Компас – это инструмент, используемый для навигации и ориентации. Азимутальный компас градуирован/отмечен полным кругом в 360 градусов, который называется азимутальным кругом. Компоненты компаса включают магнитную стрелку, которая всегда указывает на магнитный север, градуированную окружность для откладывания углов от истинного севера и линию визирования для продолжения линии визирования при следовании курсу направления.

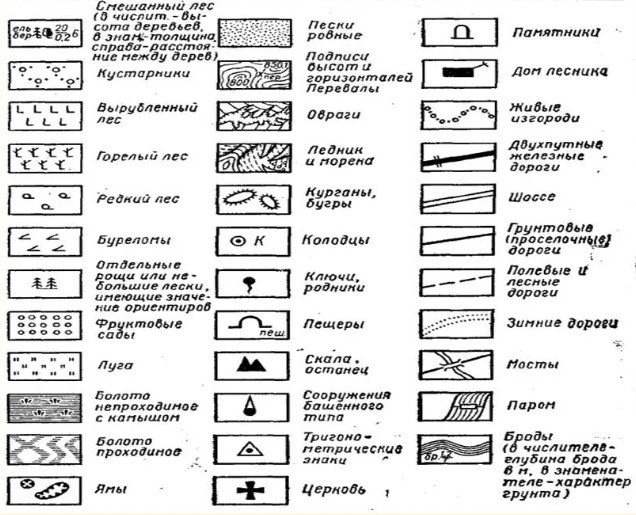
Условные знаки

Дирекционные углы и румбы

Дирекционные углы и румбы используются для ориентирования линий.

Дирекционным углом (α) линии называют угол, отсчитанный по ходу часовой стрелки от северного направления вертикальной линии километровой сетки (осевого меридиана зоны) до направления заданной линии. Пределы изменения дирекционного угла от 0º до 360º.

Румб (r)

Это острый угол от ближайшего направления меридиана (северного или южного) до направления ориентирной линии. Пределы изменения румба от 0º до 90º.

Связь между дирекционными углами и румбами зависит от четверти, в которой находится заданное направление. Перевод дирекционных углов в румбы выполняется согласно таблице ниже.

Пример перевода дирекционных углов в румбы

1. если дирекционный угол α равен 42°15′55″, тогда согласно таблице румб вычисляется по формуле r=α=42°15′55″, а название румба будет СВ;
2. если дирекционный угол α равен 100°45′11″, тогда согласно таблице румб вычисляется по формуле r=180°-α=180°-100°45′11″=79°14′49″, а название румба будет ЮВ;
3. если дирекционный угол α равен 210°17′42″, тогда согласно таблице румб вычисляется по формуле r=α-180°=210°17′42″-180°=30°17′42″, а название румба будет ЮЗ;
4. если дирекционный угол α равен 335°28′32″, тогда согласно таблице румб вычисляется по формуле r=360°-α=360°-335°28′32″=24°31′28″, а название румба будет СЗ.

Решение обратной геодезической задачи

Целью решения обратной геодезической задачи является вычисление длины линии и дирекционного угла линии по известным координатам её конечных точек. Т.е. при известных координатах точек А(X_A, Y_A) и В(X_B, Y_B) необходимо найти длину S_AB и направление линии АВ: осевой румб r_AB и дирекционный угол a_AB (рис. 10).

Координаты точекА(X_A, Y_A) и В(X_B, Y_B) определяют при решении предыдущей задачи (см. п.1.4.2).

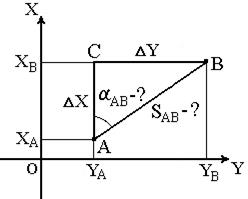
Данная задача решается следующим образом.

Сначала находим приращения координат

Рис. 10. Обратная геодезическая задача

Величину осевого румба r_AB определяем из отношения

.

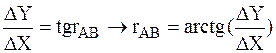
По знакам приращений координат определяем четверть, в которой располагается румб, и её название (см. табл.1).

Знаки приращений координат ΔX и ΔY

Приращения координат	Четверть окружности, в которую направлена линия
I (СВ)	II (ЮВ)	III (ЮЗ)	IV (СЗ)
ΔX	+	–	–	+
ΔY	+	+	–	–

Используя зависимость между дирекционными углами и осевыми румбами (рис. 11), находим a_AB.

Рис. 11. Осевые румбы и дирекционные углы

Зависимость между дирекционными углами и румбами определяется для четвертей по следующим формулам:

I четверть (СВ) r = a ,

II четверть (ЮВ) r = 180° – a ,

III четверть (ЮЗ) r = a – 180° ,

IV четверть (СЗ) r = 360° – a .

Расстояние S_AB определяем по формуле

.

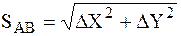
Для контроля расстояние S_AB вычисляют дважды по формулам:

,

.

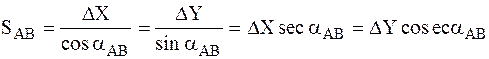
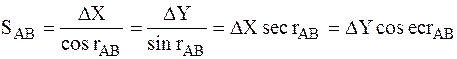
Пример.Координаты точек:А(5998.650 км, 2396.750 км);

В(6000.150 км, 2395.250 км).

Вычисляем осевой румб r_AB из отношения

,

.

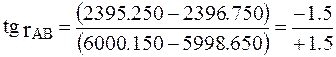
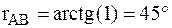
По знакам приращений координат ΔX>0 и ΔY

Лучшие изречения:

80% успеха — это появиться в нужном месте в нужное время. © Вуди Аллен
==> читать все изречения. 167 — | 158 —

Источник

Решение обратной геодезической задачи

Основой решения является расчетная схема рис.1.5.

1. Выписать исходную информацию (расчетная схема соответствует рис.1.10).

2. Вычислить приращения координат по формулам (1.6).

3. На микрокалькуляторе вычислить румб и длину линии по формулам (1.7)-(1.8).

4. По знакам приращений определить название румба в соответствии с рис.1.6.

5. От румба перейти к дирекционному углу по формулам связи (рис.1.4).

6. Сравнить вычисленные значения с измеренными. Расхождения не должны превышать 2 мм в длине линии и 1 0 в дирекционном угле.

Задача решается на микрокалькуляторе. Но при этом непосредственно определить угол  по формуле:=arc tg(у/х), вытекающей из уравнений (1.4), невозможно из-за неоднозначного решения задачи. Так прих отрицательном,у положительном их положительном,у отрицательном получим одинаковые значения. Для контроля вычисления можно выполнить через радианы. Связь между градусами и радианами:

r рад =r 0 / 57.29578 ;r 0 =r рад 57.29578. (1.10)

2. Приращения координат: x=X_B -X_A=6064410 — 6065675 = -1265 м,y=У_В— У_А= -188318–(- 188030) = — 288 м.

3. Румб линии через градусы, установив программу DEG:

/r/ = arc tg ( Δу / Δх )=”288” : ” 1265” = ”2ndF» tg -1 ” = 12.826 0 = 12 0 50′ .

Длина линии (программа DEG):

d=x/Cosr=“12.826“Cos”2ndF“1/x”×”1265”=1297 м. Второе вычисление:d=y/Sinr=“12.826“Sin”2ndF“1/x”×”288” = 1297 м. Расхождений в вычислениях не должно быть.

4. В соответствии со знаками приращений румб r = ЮЗ:12 0 50′.

5. Дирекционный угол = 192 0 50′.

6. Расхождение в длине линии 3 м, в румбе 10′. Расхождения допустимы.

Пример вычисления румба через радианы. Программа RAD:

arctg(Δу/Δх )=”288”:”1265“=“2ndF»tg -1 ”=»×»57.2958″=12.826 0 =12 0 50′.

Вычисления следует выполнять по разным формулам. Так, решение прямой задачи выполняется через дирекционные углы по формулам (1.4) и через румбы по формулам (1.5), кроме первой четверти. В северо-восточной части r= , контроля не будет. В этом случае, как и при решении обратной задачи, вычисления следует вести через градусы и через радианы.

Определение отметок точек

Отметки точек определяют по правилам, см. фрагмент листа карты (рис.1.1).

1. Точка лежит на горизонтали. Отметка точки равна отметке горизонтали: Н₁=152.5 м.

2. Точка лежит между разноименными горизонталями. Отметка точки определяется графической интерполяцией на глаз: Н₂=150+2.5/3=150.8 м.

3. Седловина. Отметка точки равна отметке ближней горизонтали ± полсечения рельефа: Н₃=152.5+h/2=153.8 м или 155 – h/2 = 153.8 м.

4. Определяемая точка лежит между горизонталью и точкой с подписанной на карте отметкой. Отметка определяется графической интерполяцией: Н₄=155+(156.9–155)/2=155.7 м.

5. Точка лежит на полугоризонтали: Н₅ = 155 +h/ 2 = 156.2 м.

6 и 7. Отметки вершин: H₆ =155 +h/ 2 = 156.2 м;H₇ = 156.25 (полугоризонталь)+h/4=156.8 м.

Источник

Тема 3. Прямая и обратная геодезическая задача.

При производстве строительных работ создается разбивочная основа в виде строительной сетки. Пункт Государственной геодезической сети выносится на территорию строительства для обеспечения исходными данными всех геодезических работ. Решение прямой геодезической задачи позволяет определить координаты всех точек, расположенных в зоне строительства.

В геодезии принята система плос­ких прямоугольных координат, в которой относительно оси XX , совпадающей с направлением меридиана, и оси YY , перпендику­лярной к оси XX , определяют положение каждой точки, т. е. её координаты х и у; при этом счет четвертей идет по ходу часовой стрелки, согласно возрастанию азимутов и дирекционных углов .

При составлении планов ситуацию накладывают от опорных точек и линий, их соединяющих. Поэтому на бумагу сначала на­носят опорные точки по их координатам. Так как число этих точек весьма велико, то при геодезических работах часто решают прямую задачу на координаты. Она состоит в том, что по извест­ным координатам данной точки, а также дирекционному углу и горизонтальному проложению линии от этой точки до определяе­мой вычисляют координаты определяемой точки.

Решить прямую геодезическую задачу, т.е Пример

определить прямоугольные координаты точки 2 через координаты точки 1 по следующим данным:

Кординаты точки 1 — X, = 4250 м. У,=6730 м;

Расстояние между точками d =120,10 м; направление линии, т.е дирекционный угол 48°30′ =r.

Для определения координат точки 2 сначала нужно найти приращение координат –ΔХ и ΔУ,затем сами координаты Х₂;У_{2 .}

1.Определяем приращение координат ΔХ =d . cosr = 120,10 . 0,6626 =79,51 м

ΔУ= d . sinr =12,10 . 0,7490 =89,95 м

ΔУ

х₂ 2

r d

х₁ 1

2. Определяем координаты точки 2

В практике прикладной геодезии для нужд проектирования и выноса проекта на местность приходиться определять значения дирекционного угла и длинны стороны по известным координатам её конечных точек. Это и составляет сущность решения обратной геодезической задачи.

Решение обратной геодезической задачи состоит в том, что, зная координаты опорных точек, можно вычислить дирекционный угол и расстояние между данными точками.

Пример.

Решить обратную геодезическую задачу, т.е. найти расстояниеd между точками и направление этой линии ( румб, азимут), если координаты точки1 Х₁= 320,5 м, У₁ = 780,2 м; координаты т очки 2 Х₂= 230,7 м, У₂ =900,1 м.

1. Определяем приращение координатΔХ = Х₂-Х₁ = 230,7 -320,5 = -89,8 м

ΔХ = У₂ –У₁ =900,1 – 780,2 = 119,9 м

Знаки приращений говорят, что линия расположена во второй четверти (ЮВ)

Знаки приращения координат можно определить по следующей схеме:

СЗ С х

З +ΔХ — ΔУ +ΔХ + ΔУ В

у -ΔХ — ΔУ -ΔХ + ΔУ у

Они зависят от четверти, в которой расположена линия.

2. Величина румба определяется по формуле

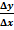
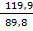
tg r= = = 1, 3352

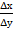
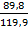
ctgr = = = 0,74,89

По таблицам Брадиса находим величину румба — 53⁰ 10ʹ

3. Расстояние между точками найдем по теореме Пифагора:

d= 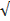ΔХ 2 + ΔУ 2 = 89,8 2 + 119,9 2 = 22440,05 = 149,8 м

Контрольные вопросы:

1. Какие знаки у приращения координат ΔХ и ΔУ, если наименование румба ЮЗ?

а) –ΔХ, –ΔУ; б)+ ΔХ, +ΔУ; в)–ΔХ,+ΔУ; г))+ ΔХ,–ΔУ;

2. Найдите координаты точки 2, если координаты точки 1 Х= 10, У=5 и приращение ΔХ = 20, ΔУ =15.

а) 30, 20; б) 20, 30; в) 20, 40; г) 30, 40;

3. Решить обратную геодезическую задачу: найти расстояние между двумя точками и румб линии, если координаты начала и конца линии Х₁= 320,5 м, У₁ = 780,2 м; Х₂ 230,7 м,

а); 160,7 м, 60⁰ 20ʹ; б)149,8 м, 53⁰ 10ʹ; в) 120, 9 м, 58⁰ 45ʹ; г) 456,7м, 45⁰ 15ʹ;

4. Решить прямую геодезическую задачу: определить прямоугольные координаты точки 2 через координаты точки 1 по следующим данным: Х₁ = 4250м, У₁= 6730м, расстояние d – 120, 1 м, дирекционный угол — 48⁰30ʹ.

Какие слова нужно вставить в место точек в определении «Дирекционным углом лини называют угол, отсчитанный от. до данной прямой по направлению часовой стрелки?»

Азимут лини находится в пределах 90°-180 каково градусное значение румба?

Каково название румба линии и его величина , если азимут её определён по формуле А°-З60-r°

№	Вопросы (задания)	Ответы	Код
I	Осевого меридиана зоны	1
Ближайшего направления меридиана	2
Южного направления магнитного меридиана	3
Северного направления географического меридиана	4
II	Азимут лини находиться в пределах от 180°-270°	Сз	1
каково наименование румба?	Юв	2
Юз	3
Св	4
III	r°=А°	1
r°=180°-А°	2
r°=А°-180°	3
r°=360°-А°	4
IV	каково градусное значение азимута (А°) линии для ЮВ:r	А°=180°+r°	1
А о =360°-r°	2
А°=180°-r°	3
А°=r°	4
V	Сз:r°	1
Юз:r°	2
Юв:r°	3
Св:r°	4

Азимут лини находится в пределах 270°-360° каково градусное значение румба?

Каково название румба линии и его величина, если азимут её определён по формуле А°- 180°+r°

№	Вопросы (задания)	Ответы	Код
I	Какие слова нужно вставить в место точек в определении «Дирекционным углом лини называют угол, отсчитанный от. до данной прямой по направлению часовой стрелки?»	Северного направления географического меридиана	1
Осевого меридиана зоны	2
Южного	3
направления магнитного
меридиана
Ближайшего	4
направления меридиана
И	Азимут лини находиться в пределах от 0°-90° каково наименование румба?	Сз	1
Юв	2
Юз	3
Св	4
III	r°=А°	1
r°=180°-А°	2
r°=А°-180°	3
r°=360°-А°	4
IV	каково градусное значение азимута (А°) линии для Юз:ч°	А°=180°-r°	1
А°-360°-r°	2
A°=180W	3
А°=r°	4
V	Сз:r°	1
Юз:r°	2
Юв:r°	3
Св:r°	4

Азимут лини находится в пределах 180°-270° каково градусное значение румба?

Каково название румба линии и его величина , если азимут её определён по формуле А°-360°-r°

№	Вопросы (задания)	Ответы	Код
I	Какие слова нужно вставить в место точек в определении «Дирекционным углом лини называют угол, отсчитанный от. до данной прямой по направлению часовой стрелки?»	Северного направления географического меридиана	1
Южного
направления магнитного	2
меридиана
Ближайшего
направления меридиана	3
Осевого	4
меридиана зоны
И	Азимут лини находиться в пределах 90°-180 каково	Сз	8
наименование румба?	Юв	9
Юз	1
Св	2
III	r°=А°	3
r°=180°-А°	4
r°=А°-180°	5
r°=360°-А°	6
IV	каково градусное значение азимута (А°) линии для румба св: r°	А°=180°-r°	7
А°=360°-r°	8
А°=180°+r°	9
А°=r°	1
V	Сз:r°	2
Юз:r°	3
Юв:r°	4
Св:r°	5

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Источник

Координаты – это величины, которые отображают местоположение конкретной точки в пространстве. Они определяются путем проведения геодезических измерений, к которым относится триангуляция, а также построение тахеометрического и теодолитного хода.

На плоскости координаты можно вводить неисчислимым количеством способов и через различные математические задачи создавать координатные системы. Благодаря вычислению координаты точек теодолитного хода на карту или план наносятся как эти самые пункты, так и жесткие объекты в зоне их видимости.

Общие понятия о системах координат в геодезии

Столь глубокие познания о строении и форме Земли, которые человек осваивал на протяжении веков, сегодня позволяют создавать невероятно точные координатные системы и картографические проекции.

Координатные системы заданы двумя направлениями на плоскости, а в пространстве – тремя. Осевые направления всегда перпендикулярны друг другу, а ориентированы горизонтально и вертикально. Их пересечение и определяет местоположение точки в заданной системе.

В геодезии координатные системы разделены на следующие две группы:

1. Прямолинейные прямоугольные. К ним причисляют проекцию Гаусса-Крюгера, индивидуальные референцные и местные системы.
2. Полярные. Это геодезические, географические, астрономические, а также геоцентрические и топоцентрические координаты.

Теодолитный ход можно считать самым распространённым плановым обоснованием. Он не требует дорогостоящего и высокоточного оборудования, но помогает создать надежную плановую основу на территориях со сложной местностью. Его развивают от пунктов государственных геодезических сетей (ГГС) и сетей сгущения с уже установленными координатами.

Вычисляются координаты точек замкнутого и разомкнутого теодолитного хода посредством нахождения дирекционных углов его сторон и решения прямой геодезической задачи. Но перед этим следует проверить, соответствуют ли измерения нормативным требованиям.

Исходные данные для расчетов

Теодолитный ход может быть проложен в виде замкнутой фигуры или ломаной линии. Это зависит от характера снимаемой местности. Он является отличной геодезической основой для многих инженерных изысканий.

По итогу проведенных измерений составляется план или карта местности, а все вычисления заносятся в специальные ведомости. В нее заносятся следующие данные:

– горизонтальные углы пунктов;

– измеренное расстояние между ними;

– координаты пункта ГГС или опорной сети;

– значение исходного дирекционного угла.

Для привязки хода к пункту ГГС или опорной сети необходимо определить местоположение одной его точки относительно этого пункта. Это можно сделать, измерив расстояние и горизонтальный примычной угол между ними. Такая процедура называется передачей координат и дирекционных углов.

Уравнивание измерений

Не существует еще методов, позволяющих без погрешностей выполнить измерения, но уравнивание позволит свести их к минимуму. Для замкнутого хода первым делом рассчитывается невязка:

(f_{beta}=sum beta _{изм}-sum beta_{теор})

где:

(sum beta _{изм}=beta _{1}+beta _{2}+…beta _{n}) – сумма углов пунктов;

(sum beta _{теор}) – теоретическая сумма, определяемая выражением:

(sum beta _{теор}=180^{circ}cdot (n-2))

(n) – количество углов.

Вычисленная невязка допустима, если соответствует требованию:

(beta _{испр}=pm 1,5sqrt{n})

Когда полученное значение не превышает допуск, то невязку разбрасываются между углами с противоположным знаком равномерно. Можно также распределить ее только между самыми короткими сторонами. Учитывая поправки и их знак, вычисляют исправленные углы:

(beta _{испр}=beta _{изм}+delta _{beta })

(delta _{beta }) – поправка.

Правильность уравнивания подтверждается следующим условием:

(sum beta _{теор}=beta _{испр})

Поскольку разомкнутый ход является ломаной линией, математические расчеты для него проводятся как для хода, в котором две исходные стороны и дирекционных угла. Для него применяют следующие выражения:

для левых углов:

(sum beta _{теор}=alpha _{кон}-alpha _{нач}+ncdot 180^{circ})

правых:

(sum beta _{теор}=alpha _{нач}-alpha _{кон}+ncdot 180^{circ})

Для упрощения дальнейших вычислений поправки могут быть распределены с целью округления десятых долей минут в углах до целых минут.

Вычисление дирекционных углов вершин

В геодезии за дирекционный угол ((alpha )) принимают угол, который начинают отсчитывать от северного направления осевого меридиана и до заданной стороны. Он измеряется от 0 до 360°. Вычислить его значение для правой стороны хода можно по формуле ниже:

(alpha _{n}=alpha _{n-1}+eta )

(eta=180^{circ} -beta _{пр.испр})

(a _{n}=alpha _{n-1}+180^{circ}-beta _{пр.испр})

Для левой стороны это выражение будет иметь такой вид:

(alpha _{n}=alpha _{n-1}+eta )

(eta=beta _{лев.исп.}-180^{circ} )

(a _{n}=alpha _{n-1}-180^{circ}+beta _{лев.исп.})

где:

(alpha _{n-1}) – дирекционный угол предыдущей стороны, а (n) – последующей;

(beta _{пр.исп.}) – значение правого исправленного угла между сторонами отрезка, а (beta _{лев.исп.})– левой стороны.

Вычисления выполнены верно при равенстве заданного α и начальной стороны теодолитного хода. Если дирекционный угол больше 360° или имеет отрицательное значение, то это говорит об ошибке в расчетах.

После дирекционных углов необходимо найти румбы – острые углы, отсчитываемые от 0 до 90°. Они берут свое начало от ближайшего окончания осевого меридиана до ориентирной линии.

Четверть румба	Название четверти	Пределы изменения α	Формула румба	Знаки приращения
ΔХ	ΔУ
I	С.В. (северо-восток)	0° – 90°	r = α	+	+
II	Ю.В. (юго-восток)	90°-180°	r = 180° – α	–	+
III	Ю.З. (юго-запад)	180°-270°	r = α – 180°	–	–
IV	С.З. (северо-запад)	270°-360°	r = 360° – °α	+	–

Таблица 1. Связь дирекционного угла и румба

Вычисление румбов и их знаков приращений зависит от четверти геодезических прямоугольных координат, в которой находится линия ориентирования.

Решение прямой и обратной геодезической задачи

Суть прямой геодезической задачи состоит в том, чтобы определить координатные значения вершины при заданных координатах соседней. Это возможно при известной горизонтальном проложении между ними и дирекционным углом линии. Для ее решения используются следующие формулы:

(Delta X=dcdot cos alpha )

(Delta Y=dcdot sin alpha )

где:

Создавайте будущее вместе с нами

Присоединяйтесь к нашей команде: мы создаем финтех-сервисы для 28 млн клиентов и опережаем рынок на 5 лет. Работаем на результат и делаем больше, чем от нас ждут.

(d)–расстояния между соседними пунктами.

(alpha ) – значение дирекционного угла.

Знаки приращений зависят от четверти, определяемой дирекционным углом направления. Координатные значения конечной точки линии равняется сумме координаты начальной и приращения между ними. Из этого следует следующие выражение:

(X_{2}=X_{1}+Delta X)

(Y_{2}=Y_{1}+Delta Y)

(X_{2}=X_{1}+d_{1-2}cdot cosalpha _{1-2})

(Y_{2}=Y_{1}+d_{1-2}cdot sinalpha _{1-2})

Стоит также упомянуть и обратную геодезическую задачу, которая позволяет определить дирекционный угол, румб и горизонтальное проложение при установленных координатах пунктов теодолитного хода. Вычисления имеют такую последовательность:

(Delta X=X_{2}-X_{1})

(Delta Y=Y_{2}-Y_{1})

определяется румб линии (r_{1-2}):

(tgr=frac{Delta Y}{Delta X})

из этого выходит, что:

(r=arctgfrac|{Delta Y}{Delta X}|)

По знакам приращения определяют четверть, в котором находится направление и по уже известному румбу вычисляют дирекционный угол. Определение горизонтального проложения будет завершающим этапом в решении обратной задачи:

(d=frac{Delta X}{cosalpha })

(d=frac{Delta Y}{sinalpha })

(d=sqrt{Delta X^2+Delta Y^2})

Приращение координат и их увязка

Приращением называют величины, на которые будут увеличены координаты предыдущей точки для вычисления последующей. В основу этих расчетов берется уже знакомая формула прямой задачи:

(Delta X=dcdot cos alpha )

(Delta Y=dcdot sin alpha )

Полученные значения также необходимо уровнять, чтобы равномерно распределить погрешности и получить наиболее точный результат. Начинают расчеты с определения невязок. Поскольку сумма проекций в сторонах многоугольной замкнутой фигуры равняется нулю, для вычисления невязок пунктов замкнутого хода используют следующую формулу:

(f_{X}=sum Delta X_{выч}-sum Delta X_{теор};sum Delta X_{теор}=0)

(f_{Y}=sum Delta Y_{выч}-sum Delta Y_{теор};sum Delta Y_{теор}=0)

(sum Delta X_{выч},sum Delta Y_{выч}) – суммы приращений, рассчитанные с учетом знаков для замкнутого и разомкнутого хода;

(sum Delta X_{теор},sum Delta Y_{теор}) – теоретические суммы приращений.

Если невязки не находятся в допуске, необходимы повторные расчеты, чтобы определить ошибку и устранить ее. В противном случае проводятся повторные измерения на участке.

Вследствие влияния погрешностей на ход, он будет разомкнут на величину , которая представляет собой абсолютную невязку в его периметре. По этому причине проверяется соответствие условию допустимости его невязок.

1. Абсолютное значение:

(f_{p}=sqrt{f_{x}^2+f_{y}^2})

1. Относительное

(f_{отн}=frac{f_{абс}}{P})

P – периметр хода, полученный суммированием всех его сторон.

Допустимая невязка должна удовлетворять условие 1/2000, а при соответствии выражению (|f_{отн}|leq |f_{доп}|) выполняют ее распределение с противоположным знаком. Однако перед этим рассчитывают поправки приращений, которые определяют для каждой стороны:

(delta _{x_{i}}=-frac{f_{x}d_{i}}{P});(delta _Delta {y_{i}}=-frac{f_{y}d_{i}}{P})

(delta _{x_{i}},delta _{y_{i}})– значения поправок в приращениях.

Чтобы упростить дальнейшие расчеты поправки, необходимо округлить их до 0,01 м.

Для разомкнутого хода за теоретическую сумму приращений берется разность между двумя соседними точками.

(f_{X}=sum Delta X_{выч}-sum Delta X_{теор};   sum Delta X_{теор}=x_{B}-x_{A})

(f_{Y}=sum Delta Y_{выч}-sum Delta Y_{теор};   sum Delta Y_{теор}=y_{B}-y_{A})

Для обоих ходов поправки имеют противоположный приращению знак. Уравнивание выполнено верно, если сумма исправленных приращений равна или максимально приближена к нулю.

Как вычислить координаты точек хода

Вычисляют значения координат вершин замкнутого и разомкнутого теодолитного хода сначала для опорного пункта, а потом уже для остальных его вершин.

Значение следующего пункта хода вычисляют суммированием предыдущего пункта и исправленного приращения. Это наглядно отображено в формуле:

(X_{n}=X_{n-1}+Delta X _{n-1(испр)})

(Y_{n}=Y_{n-1}+Delta Y _{n-1(испр)})

(X_{n-1},Y_{n-1}) – координатные значения предыдущего пункта

(Delta X_{теор}=x_{B}-x_{A},Delta Y_{теор}=y_{B}-y_{A}) – исправленные приращения.

В данных формулах применяется алгебраическая сумма, поэтому знаки также необходимо учитывать при расчетах. Если в конце вычислений получены координатные значения начальной точки, то они выполнены правильно.

Нанесение точек на план и его оформление

После завершения обработки измерений, которые были проведены на местности, составляется ее контурный или ситуационный план. Построение плана теодолитного хода происходит поэтапно и состоит из следующих этапов:

1. Создание координатной сетки. Ход необходимо равномерно отобразить на плане, поэтому сначала определяют середину листа. Через весь лист проводят два диагональных отрезка, от которых и будет строиться сетка, состоящая из отрезков по 10 см. Допускается погрешность не более 0,2 мм. Определить их количество можно по формуле:

(N_{X}=(x_{max}-x_{min})/200)

(N_{Y}=(y_{max}-y_{min})/200)

(x_{max},y_{max}) – наибольшие значения координат, увеличенные до большего значения, которое кратное 200.

(x_{min},y_{min}) – наименьшее значение, но уменьшенное и кратное 200.

200 – длина стороны квадрата в метрах , которая в плане равна 10 см.

1. Обозначение точек на плане. Лучше всего подходят для нанесения координат пунктов на план циркуль и масштабная линейка. Соседние вершины должны иметь такое же расстояние и дирекционный угол, как записано в ведомости.
2. Нанесение ситуации на план. Участки снимаемой местности в процессе полевых работ отображают на специальном схематическом бланке – абрисе. В дальнейшем их используют для переноса контуров, линий и вершин точек. Ситуация изображается на планах и картах специальными обозначениями – условными знаками.
3. Оформление плана в соответствии с требованиями. Все топографические материалы должны строго соответствовать нормативным документам. В частности, нужно выдерживать заданные очертания и их размеры. Должны присутствовать пояснительные надписи, легенда, а также указан масштаб.

Сегодня координаты замкнутого теодолитного хода вычисляются значительно проще, а создание всех графических материалов выполняется при помощи специализированных программ автоматически. Это значительно ускорило процесс выполнения геодезических работ и других инженерных изысканий.

При выполнении
геодезических работ на местности, работ с картой или чертежом необходимо
определить положение линии (ориентировать линию) относительно стран света или
какого-нибудь направления, принимаемого за исходное.

Ориентирование
заключается в том, что определяют угол между исходным направлением и
направлением данной линии. За исход­ное направление для ориентирования
принимают истинный (гео­графический), магнитный меридианы или ось абсцисс прямо­угольной
системы координат плана. В качестве углов, определя­ющих направление линии,
служат истинный и магнитный азиму­ты, румбы и дирекционные углы.

Азимутом называется угол между северным направлением ме­ридиана и
направлением данной линии MN.
Азимут из­меряется от севера через восток, юг и запад, т.е. по направлению
движения часовой стрелки, и может иметь значения 0… 360°. Ази­мут А, измеряемый
относительно истинного меридиана, называ­ется истинным.      

Азимуты и румбы

В
геодезии принято различать прямое и обратное направления линии. Если
направление линии MN от точки М к точке N считать прямым, то NM— обратное направление той же линии. В соответ­ствии с этим угол А₁
— прямой азимут линии MN в точке М, а А₂ — обратный азимут этой же
линии в точке N.

Меридианы разных
точек не параллельны между собой, так как они сходятся в точках полюсов. Отсюда
азимут линии в разных ее точках имеет разное значение.

Угол между
направлениями двух ме­ридианов называется сближением
меридианов и обозначается γ. Зави­симость между прямым и
обратным азимутами линии MN выражает следующая формула: A₂ = A_t + 180⁰ + γ .

Истинные
азимуты линий местности определяются путем астрономических наблюдений или с
помощью приборов — гиротеодолитов.

Иногда для
ориентирования линии местности пользуются не азимутами, а румбами.

Румбом называется острый угол между ближайшим (северным С или
южным Ю) направлением меридиана и направ­лением данной линии.

Румбы
обозначают буквой r с индексами, указывающими чет­верть, в которой находится
румб. Названия четвертей составлены из соответствующих обозначений стран света.
Так, I четверть —
северо-восточная (СВ), II — юго-восточная (ЮВ), III — юго-западная (ЮЗ), IV — северо-западная (СЗ). Соответственно
обо­значают румбы в четвертях, например: в первой — г_св, во второй —
г_юв. Румбы измеряют в градусах (0… 90°).

В прямоугольной системе координат ориентирование линии
про­изводят относительно оси абсцисс. Углы, отсчитываемые в направ­лении хода
часовой стрелки от положительного (северного) направления оси абсцисс до линии, на­правление которой определяется, на­зываются дирекционными.
   Дирекцион­ные углы обозначаются буквой ά и по­добно азимуту изменяются от 0 до 360⁰. Дирекционный угол какого-либо направления непосредственно на мест­ности не измеряют, его значение мож­но вычислить, если для данного направления определен истинный азимут (рис. 2). В
данном случае у — сближе­ние меридианов —
представляет собой угол между истинным
меридианом М и осью абсцисс в этой точке.

Зависимость между дирекционным углом и истинным азимутом линии

Ось абсцисс параллельна осевому
меридиану зоны, в которой расположена линия MN. Как видно из рисунка, =А – γ. Также как и для азимута, различают прямой и обратный
дирекционные углы:  — прямой, ά — обратный дирекционные углы линии MN: ά =  + 180°.

Румбы
дирекционных углов обозначают и вычисляют так же, как румбы истинных азимутов,
только отсчитывают от северного и южного направлений оси абсцисс (табл.).

Четверть	А,0	r
I   (СВ)	0…90	А
II (ЮВ)	90.. .180	180°-А
III (ЮЗ)	180…270	А -180°
IV (СЗ)	270… 360	360° -А