Актуальные цены на услуги геодезистов в Москве и Московской области в 2022 году.
Решение обратной геодезической задачи онлайн
Обратная геодезическая задача заключается в том, что при известных координатах точек А( XA, YA ) и В( XB, YB ) необходимо найти длину SAB и направление линии АВ: румб rAB и дирекционный угол αAB
Ниже представлена форма в которую можно ввести исходные значения и получить искомые данные. Это простое решение, которым может воспользоваться любой кому лень разбираться с формулами.
Если же говорить о сути решения задачи, то обратная геодезическая задача решается следующим образом.
Сначала находим приращения координат:
ΔX = XB – XA ;
ΔY = YB – YA .
Величину угла rAB определяем из отношения
По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим αAB.
Для контроля расстояние SAB дважды вычисляют по формулам:
Прямая
геодезическая задача
В
геодезии часто приходится передавать
координаты с одной точки на другую.
Например, зная исходные координаты
точки А (рис.23),
горизонтальное расстояние SABот
неё до точки В и
направление линии, соединяющей обе
точки (дирекционный угол αAB или
румб rAB),
можно определить координаты точки В.
В такой постановке передача координат
называется прямой
геодезической задачей.
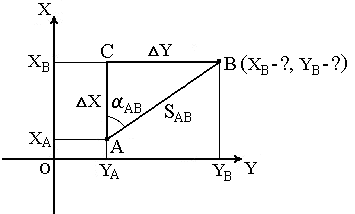
Рис.
23. Прямая геодезическая задача
Для
точек, расположенных на сфероиде, решение
данной задачи представляет значительные
трудности. Для точек на плоскости она
решается следующим образом.
Дано:
Точка А(
XA,
YA ), SAB и αAB.
Найти:
точку В(
XB,
YB ).
Непосредственно
из рисунка имеем:
ΔX
= XB –
XA ;
ΔY
= YB –
YA .
Разности ΔX и ΔY координат
точек последующей и предыдущей называются
приращениями координат. Они представляют
собой проекции отрезка АВ на
соответствующие оси координат. Их
значения находим из прямоугольного
прямоугольника АВС:
ΔX
= SAB · cos
αAB ;
ΔY
= SAB · sin
αAB .
Так
как в этих формулах SAB всегда
число положительное, то знаки приращений
координат ΔX и ΔY зависят
от знаков cos
αAB и sin
αAB.
Для различных значений углов
знаки ΔX и ΔY представлены
в табл.1.
Таблица
1.
Знаки
приращений координат ΔX и ΔY
|
Приращения |
Четверть |
|||
|
I (СВ) |
II (ЮВ) |
III (ЮЗ) |
IV (СЗ) |
|
|
ΔX |
+ |
– |
– |
+ |
|
ΔY |
+ |
+ |
– |
– |
При
помощи румба приращения координат
вычисляют по формулам:
ΔX
= SAB · cos
rAB ;
ΔY
= SAB · sin
rAB .
Знаки
приращениям дают в зависимости от
названия румба.
Вычислив
приращения координат, находим искомые
координаты другой точки:
XB =
XA + ΔX ;
YB =
YA + ΔY .
Таким
образом можно найти координаты любого
числа точек по правилу: координаты
последующей точки равны координатам
предыдущей точки плюс соответствующие
приращения.
Обратная
геодезическая задача
Обратная
геодезическая задача заключается
в том, что при известных координатах
точек А(
XA,
YA ) и В(
XB,
YB ) необходимо
найти длину SAB и
направление линииАВ: румб rAB
и дирекционный угол αAB (рис.24).
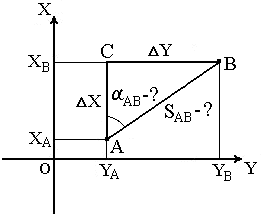
Рис.
24. Обратная геодезическая задача
Даннная
задача решается следующим образом.
Сначала
находим приращения координат:
ΔX
= XB –
XA ;
ΔY
= YB –
YA .
Величину
угла rAB определем
из отношения
|
ΔY |
= tg |
|
ΔX |
.
По
знакам приращений координат вычисляют
четверть, в которой располагается румб,
и его название. Используя зависимость
между дирекционными углами и румбами,
находим αAB.
Для
контроля расстояние SAB дважды
вычисляют по формулам:
|
SAB= |
ΔX |
= |
ΔY |
= ΔX · sec |
|
cos αAB |
sin αAB |
|
SAB= |
ΔX |
= |
ΔY |
= ΔX · sec |
|
cos rAB |
sin rAB |
Расстояние SAB можно
определить также по формуле
![]() .
.
Топографические
съемки.
Топографи́ческая
съёмка — совокупность работ по созданию
топографических карт или планов местности
посредством измерений расстояний,
высот, углов и т. п. с помощью различных
инструментов (наземная съёмка), а также
получение изображений земной поверхности
с летательных аппаратов (аэрофотосъёмка,
космическая съёмка).
Наземные съемки
бывают плановые, высотные и комбинированные.
При Плановой (теодолитной) получается
топографическая карта, но без учёта
рельефа, т.е. только ситуация (совокупность
объектов местности). Топографическая
(тахеометрическая) съёмка , особенно
крупных масштабов, является наиболее
востребованным видом геодезических
работ. Потребности в ней могут возникнуть
при изысканиях, обновлении топокарт,
составлении генпланов, составления
рабочих чертежей, для решения вертикальной
планировки и проектировании ландшафтного
дизайна. На основе топографической
съёмки возможно построить цифровую
модель местности. При Высотной (нивелирной)
съемке выполняется определение высотного
(вертикального) положения характерных
точек рельефа и конструктивных элементов
зданий.
Топографические
работы сильно облегчились после появления
специальных геодезических GPS и ГЛОНАСС
приёмников, совмещённых с компьютером
и синхронизированных между собой по
радиоканалу.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Обратная геодезическая задача.
Дано: Из прямоугольного
XA; YA треугольника АВС
XB; YB имеем:
1. X = XB – XA; Y = YB – YA;
АВ – ? ; SАВ – ? 2. tg (rАВ) = ΔY : ΔX ;
3. rАВ = аrctg(rАВ);
Для вычисления румба в градусной мере необходимо выполнить на микрокалькуляторе следующие операции:
делением ΔY на ΔX находим tg(rАВ), далее нажимаем клавиши 2ndF и tan над которой стоит символ (tan-1), получаем значение румба в градусах, желательно до семи знаков после запятой. Для перевода румбического значения в градусы минуты секунды (° ´ ´´) необходимо нажать клавишу 2ndF и клавишу DEG над которой стоит символ (D.MS ). Название румба определяется в зависимости от того в какой четверти находится данная линия. Четверть определяется по знакам
ΔY и ΔX (рис.2) .
4. Дирекционный угол линии АВ (αАВ) вычисляется с учётом четверти, в которой находится данная линия (рис.2), а четверть определяется по знакам приращений координат (ΔX , ΔY).
Рис. 1
X
IV I
ΔX ΔY ΔX ΔY
+ – + +
Y
III II
ΔX ΔY ΔX ΔY
– – – +
Рис. 2
- Формулы для вычисления дирекционного угла линии по румбу.
Первая четверть: αАВ = rАВ ; (название румба СВ)
Вторая четверть: αАВ = 180° – rАВ; (название румба ЮВ)
Третья четверть: αАВ = 180° + rАВ; (название румба ЮЗ)
Четвёртая четверть: 360° – rАВ; (название румба СЗ)
6. S(AB)= ΔX : Cosα(АВ) ;
7. S(AB)= ΔY : Sinα(АВ) ;
8. .
9. SAB ср. вычисляется, как среднее из трёх
полученных значений расстояния АВ.
Пример.
Дано: Решение:
XA = 28359.109 м 1. X = XB – XA=29007.458 – 28359.109 = 648.349м.
YA = 29408.251 м 2. Y = YB – YA=29903.074 – 29408.251 = 494.823м.
XB = 29007.458 м 3. tg (rАВ) = ΔY : ΔX = 0.7632047;
YB = 29903.074 м 4. rАВ = СВ : 37˚ 21´ 03.´´8 ;
5. АВ = 37˚ 21´ 03.´´8 ;
АВ – ? ; SАВ – ? 6. S(AB)= ΔX : Cosα(АВ) = 815.602 ;
7. S(AB)= ΔY : Sinα(АВ) = 815.602 ;
8. = 815.602 ; 9. SAB ср. = 815.602 ;
Образец формуляра №1 для решения обратной геодезической задачи.
|
XB |
28359.109 |
YB |
29903.074 |
|
XA |
29007.458 |
YA |
29408.251 |
|
X |
– 648.349 |
Y |
494.823 |
|
tg (rАВ) = |
0.7632047 |
rАВ = |
ЮВ : 37˚ 21´ 03.´´8 |
|
АВ = |
142˚ 38´ 56.´´2 |
Вторая четверть |
|
|
S(AB)= ΔX : Cosα(АВ)= |
815.602 |
S(AB)= ΔY : Sinα(АВ)= |
815.602 |
|
|
815.602 |
SAB ср. = |
815.602 |
Образец формуляра №2 для решения нескольких обратных геодезических задач.
|
Обозначения |
Решение задач |
|||
|
А – В |
В – С |
С – Д |
Д – Е |
|
|
XA |
||||
|
YA |
||||
|
XB |
||||
|
YB |
||||
|
X |
||||
|
Y |
||||
|
tg( r) |
||||
|
r |
||||
|
r |
||||
|
Cos () |
||||
|
Sin () |
||||
|
S1 |
||||
|
S2 |
||||
|
Sср. |
||||
В.С. Воронович
В помощь студенту.
Г Е О Д Е З И Я
Обратная геодезическая задача
Краснодар
2008
