Как найти ряд фурье для системы

Как найти ряд фурье для системы

Ряд Фурье́ — представление функции f с периодом tau в виде ряда

{displaystyle f(x)={frac {a_{0}}{2}}+sum limits _{k=1}^{+infty }A_{k}cos left(k{frac {2pi }{tau }}x+theta _{k}right)}

Этот ряд может быть также записан в виде

{displaystyle f(x)=sum limits _{k=-infty }^{+infty }{hat {f}}_{k}e^{ik{frac {2pi }{tau }}x},}

где

A_k — амплитуда k-го гармонического колебания,
{displaystyle k{frac {2pi }{tau }}=komega } — круговая частота гармонического колебания,
theta_k — начальная фаза k-го колебания,
hat{f}_k — k-я комплексная амплитуда

В более общем виде, рядом Фурье элемента некоторого пространства функций называется разложение этого элемента по полной системе ортонормированных функций или другими словами по базису, состоящему из ортогональных функций. В зависимости от используемого вида интегрирования говорят о рядах Фурье — Римана, Фурье — Лебега и т. п.[1]

Существует множество систем ортогональных многочленов и других ортогональных функций (например, функции Хаара, Уолша и Котельникова), по которым может быть произведено разложение функции в ряд Фурье.

Разложение функции в ряд Фурье является мощным инструментом при решении самых разных задач благодаря тому, что ряд Фурье прозрачным образом ведёт себя при дифференцировании, интегрировании, сдвиге функции по аргументу и свёртке функций.

Существуют многочисленные обобщения рядов Фурье в различных разделах математики. Например, любую функцию на конечной группе можно разложить в ряд, аналогичный ряду Фурье, по матричным элементам неприводимых представлений этой группы (теорема полноты).

История[править | править код]

Ряд Фурье назван в честь французского математика Жана-Батиста Жозефа Фурье (1768—1830), внесшего важный вклад в изучение тригонометрических рядов после предварительных исследований Леонарда Эйлера, Жана Лерона д’Аламбера и Даниила Бернулли[2]. Фурье представил ряд с целью решения уравнения теплопроводности в металлической пластине, написав свои первоначальные результаты в своем «Воспоминании о распространении тепла в твердых телах» («Трактат о распространении тепла в твердых телах») и опубликовав в Аналитической теории тепла (Théorie analytique de la chaleur) в 1822 году. В Воспоминании приведен анализ Фурье, в частности ряд Фурье. Благодаря исследованиям Фурье был установлен факт того, что произвольная (непрерывная)[3] функция может быть представлена ​​тригонометрическим рядом. Первое объявление об этом великом открытии было сделано Фурье в 1807 году перед Французской академией[4]. Ранние идеи разложения периодической функции на сумму простых осциллирующих функций относятся к 3 веку до нашей эры, когда древние астрономы предложили эмпирическую модель движения планет, основанную на семействах и эпициклах.

Уравнение теплопроводности является уравнением в частных производных. До работы Фурье в общем случае не было известно решение уравнения теплопроводности, хотя были известны конкретные решения, если бы источник тепла вел себя простым образом, в частности, если источником тепла была волна синуса или косинуса. Эти простые решения теперь иногда называют собственными решениями. Идея Фурье состояла в том, чтобы смоделировать сложный источник тепла как суперпозицию (или линейную комбинацию) простых синусоидальных и косинусных волн и записать решение как суперпозицию соответствующих собственных решений. Эта суперпозиция или линейная комбинация называется рядом Фурье.

С современной точки зрения, результаты Фурье несколько неформальны из-за отсутствия точного понятия функции и интеграла в начале девятнадцатого века. Позднее Петер Густав Лежён Дирихле[5] и Бернхард Риман[6][7][8] выразили результаты Фурье с большей точностью и формальностью.

Хотя первоначальной мотивацией было решение уравнения теплопроводности, позже стало очевидно, что те же методы можно применять к широкому кругу математических и физических задач, особенно тех, которые включают линейные дифференциальные уравнения с постоянными коэффициентами, для которых собственные решения являются синусоидами. Ряд Фурье имеет много применений в области электротехники, вибрации анализа, акустики, оптики, обработки сигналов, обработки изображений, квантовой механики, эконометрики[9], теории перекрытия-оболочки[10] и т. д.

Тригонометрический ряд Фурье[править | править код]

Тригонометрическим рядом Фурье функции {displaystyle fin {mathcal {L}}([-pi ,pi ])} (то есть функции, суммируемой на промежутке {displaystyle ([-pi ,pi ])}, или её периодического продолжения на вещественную прямую) называют функциональный ряд вида

{displaystyle f(x)={frac {a_{0}}{2}}+sum _{n=1}^{infty }(a_{n}cos nx+b_{n}sin nx),} (1)

где

a_0= frac{1}{pi}intlimits_{-pi}^{pi}f(x)dx,
a_n= frac{1}{pi}intlimits_{-pi}^{pi}f(x)cos(nx)dx,
b_n= frac{1}{pi}intlimits_{-pi}^{pi}f(x)sin(nx)dx,

Числа a_{0}, a_n и b_n (n = 1, 2, ldots) называются коэффициентами Фурье функции f. Формулы для них можно объяснить следующим образом. Предположим, что мы хотим представить функцию {displaystyle fin {mathcal {L}}([-pi ,pi ])} в виде ряда (1) и нам надо определить неизвестные коэффициенты a_{0}, a_n и b_n. Если умножить правую часть (1) на cos(kx) и проинтегрировать по промежутку [-pi,pi], то все слагаемые в правой части, благодаря ортогональности синусов и косинусов на этом промежутке, обратятся в нуль, кроме одного. Из полученного равенства легко выражается коэффициент a_{k}. Аналогично для b_{k}.

Ряд (1) для функции f из пространства {displaystyle {mathcal {L}}_{2}([-pi ,pi ])} сходится в этом пространстве. Иными словами, если обозначить через S_k(x) частичные суммы ряда (1):

S_k(x)=frac{a_0}{2} + sum^{k}_{n=1} (a_n cos nx + b_n sin nx),

то их среднеквадратичное отклонение от функции f будет стремиться к нулю:

limlimits_{krightarrow infty}intlimits_{-pi}^{pi}(f(x)-S_k(x))^2dx=0.

Несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно.

Часто при работе с рядами Фурье бывает удобнее в качестве базиса использовать вместо синусов и косинусов экспоненты мнимого аргумента. Мы рассматриваем пространство {displaystyle {mathcal {L}}^{2}([-pi ,pi ],mathbb {C} )} комплекснозначных функций со скалярным произведением

langle f,grangle := intlimits_{-pi}^{pi}f(x)overline{g(x)}dx.

Мы также рассматриваем систему функций

varphi_k(x)=e^{ikx}=cos(kx)+isin(kx), kinmathbb{Z}.

Как и прежде, эти функции являются попарно ортогональными и образуют полную систему, и, таким образом, любая функция {displaystyle fin {mathcal {L}}^{2}([-pi ,pi ],mathbb {C} )} может быть разложена по ним в ряд Фурье:

f(x) = sumlimits_{k=-infty}^{+infty} hat{f}_k e^{ikx},

где ряд в правой части сходится к f по норме в L^2([-pi,pi],mathbb{C}). Здесь

hat{f}_k= frac{1}{2pi}intlimits_{-pi}^{pi}f(x)e^{-ikx}dx.

Коэффициенты hat{f}_k связаны с классическими коэффициентами Фурье следующими соотношениями:

hat{f}_k = (a_k-ib_k)/2, k>0
hat{f}_0 = a_0/2
hat{f}_k = (a_{|k|}+ib_{|k|})/2, k<0
a_k = hat{f}_k+hat{f}_{-k}, k>0
b_k = i(hat{f}_k-hat{f}_{-k}), k>0

Для вещественнозначной функции коэффициенты hat{f}_k и hat{f}_{-k} комплексно сопряжены.

Обобщения[править | править код]

Ряды Фурье в гильбертовом пространстве[править | править код]

Описанную выше конструкцию можно обобщить со случая пространства L^2[-pi,pi] с тригонометрической системой на произвольное гильбертово пространство. Пусть даны ортогональная система {varphi_1, varphi_2, ..., varphi_n, ...} в гильбертовом пространстве H
и f — произвольный элемент из H. Предположим, что мы хотим представить f в виде (бесконечной) линейной комбинации элементов {varphi_k}:

{displaystyle f=sum _{n=1}^{infty }c_{n}varphi _{n}.}

Домножим это выражение на varphi_k. С учётом ортогональности системы функций {varphi_k} все слагаемые ряда обращаются в ноль, кроме слагаемого при n=k:

{displaystyle (f,varphi _{k})=c_{k}|varphi _{k}|^{2}.}

Числа

{displaystyle c_{k}={frac {(f,varphi _{k})}{|varphi _{k}|^{2}}}}

называются координатами, или коэффициентами Фурье элемента f по системе {varphi_k}, а ряд

sum_k c_k varphi_k

называется рядом Фурье элемента f по ортогональной системе {varphi_k}.

Ряд Фурье любого элемента f по любой ортогональной системе сходится в пространстве H, но его сумма не обязательно равна f. Для ортонормированной системы {varphi_k} в сепарабельном гильбертовом пространстве следующие условия эквивалентны:

{displaystyle sum _{k=1}^{infty }|c_{k}|^{2}=|f|^{2}}.

Если эти условия не выполняются, то сумма ряда Фурье элемента f равна его ортогональной проекции на замыкание линейной оболочки элементов varphi_1, varphi_2, ..., varphi_n, .... В этом случае вместо равенства Парсеваля справедливо неравенство Бесселя:

{displaystyle sum _{k=1}^{infty }c_{k}^{2}leqslant |f|^{2}.}

Двойственность Понтрягина[править | править код]

При обобщении теории рядов Фурье на случай гильбертовых пространств теряются свойства, выражающие связь рядов Фурье со свёрткой — то, что коэффициенты Фурье свертки функций являются почленными произведениями их коэффициентов Фурье, и наоборот, коэффициенты Фурье произведения представляются сверткой коэффициентов Фурье сомножителей. Эти свойства являются ключевыми для приложений теории Фурье к решению дифференциальных, интегральных и других функциональных уравнений. Поэтому большой интерес представляют такие обобщения теории рядов Фурье, при которых эти свойства сохраняются. Таким обобщением является теория двойственности Понтрягина. Она рассматривает функции, заданные на локально-компактных абелевых группах. Аналогом ряда Фурье такой функции будет функция, заданная на двойственной группе.

Сходимость ряда Фурье[править | править код]

Обзор результатов о сходимости ряда Фурье[править | править код]

Обозначим через S_N(f,x) частичные суммы ряда Фурье функции f(x):

S_N(f,x):=sumlimits_{k=-N}^Nhat{f}_ke^{ikx}.

Далее обсуждается сходимость последовательности функций S_N(f,x) к функции f(x) в различных смыслах. Функция f предполагается 2pi -периодической (если она задана только на промежутке [-pi,pi], её можно периодически продолжить).

  • Если fin L_2([-pi,pi]), то последовательность S_N(f,x) сходится к функции f(x) в смысле L_{2}. Кроме того, S_N(f,x) являются наилучшим (в смысле расстояния в L_{2}) приближением функции f тригонометрическим многочленом степени не выше N.
  • Сходимость ряда Фурье в заданной точке x_{0} — локальное свойство, то есть, если функции f и g совпадают в некоторой окрестности x_{0}, то последовательности S_N(f,x_0) и S_N(g,x_0) либо одновременно расходятся, либо одновременно сходятся, и в этом случае их пределы совпадают. (Принцип локализации).
  • Если функция f дифференцируема в точке x_{0}, то её ряд Фурье в этой точке сходится к f(x_{0}). Более точные достаточные условия в терминах гладкости функции f задаются признаком Дини.
  • Функция, непрерывная в точке x_{0}, может иметь расходящийся в ней ряд Фурье. Однако, если он сходится, то непременно к f(x_{0}). Это следует из того, что для непрерывной в x_{0} функции f последовательность S_N(f,x_0) сходится по Чезаро к f(x_{0}).
  • Если функция f разрывна в точке x_{0}, но имеет пределы в этой точке справа и слева {displaystyle f(x_{0}+0)neq f(x_{0}-0),} то при некоторых дополнительных условиях S_N(f,x_0) сходятся к (f(x_0+0)+f(x_0-0))/2. Подробнее см. модифицированный признак Дини.
  • Теорема Карлесона: если fin L_2([-pi,pi]), то её ряд Фурье сходится к ней почти всюду. Это верно и если fin L_p([-pi,pi]), p>1. Однако, существуют функции из L_1([-pi,pi]), ряд Фурье которых расходится во всех точках (пример такой функции построен Колмогоровым[11]).
  • Зафиксируем точку x_0in(-pi,pi). Тогда множество всех непрерывных функций, ряд Фурье которых сходится в этой точке, является множеством первой категории в пространстве C([-pi,pi]). В некотором смысле это означает, что «типичная» непрерывная функция имеет расходящийся ряд Фурье.

Убывание коэффициентов Фурье и аналитичность функции[править | править код]

Существует фундаментальная связь между аналитичностью функции и скоростью убывания её коэффициентов Фурье. Чем «лучше» функция, тем быстрее её коэффициенты стремятся к нулю, и наоборот. Степенное убывание коэффициентов Фурье присуще функциям класса C^{(k)}, а экспоненциальное — аналитическим функциям. Примеры такого рода связи:

См. также[править | править код]

  • Преобразование Фурье
  • Быстрое преобразование Фурье
  • Тригонометрический ряд
  • Признак Жордана
  • Признак Дини
  • Числовой ряд
  • АТС-теорема
  • Натуральный звукоряд
  • Явление Гиббса[en]

Примечания[править | править код]

  1. ↑ Математический энциклопедический словарь. — М.: «Сов. энциклопедия », 1988. — С. 619.
  2. ↑ Fetter, Alexander L. Theoretical Mechanics of Particles and Continua / Alexander L. Fetter, John Dirk Walecka. — Courier, 2003. — P. 209—210. — ISBN 978-0-486-43261-8. Архивная копия от 18 апреля 2021 на Wayback Machine
  3. ↑ Stillwell, John  (англ.) (рус.. Logic and the philosophy of mathematics in the nineteenth century // Routledge History of Philosophy / Ten, C. L.. — Routledge, 2013. — Т. Volume VII: The Nineteenth Century. — С. 204. — ISBN 978-1-134-92880-4. Архивная копия от 16 мая 2020 на Wayback Machine
  4. ↑ Florian Cajori. A History of Mathematics. — Macmillan, 1893. — С. 283.
  5. ↑ Lejeune-Dirichlet, Peter Gustav  (англ.) (рус.. Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données (фр.) // Journal für die reine und angewandte Mathematik. — 1829. — Vol. 4. — P. 157—169. — arXiv:0806.1294.
  6. ↑ Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe (неопр.). Habilitationsschrift, Göttingen; 1854. Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, vol. 13, 1867. Published posthumously for Riemann by Richard Dedekind. Архивировано 20 мая 2008 года.
  7. ↑ Mascre, D. & Riemann, Bernhard (1867), Posthumous Thesis on the Representation of Functions by Trigonometric Series, in Grattan-Guinness, Ivor, Landmark Writings in Western Mathematics 1640–1940, Elsevier, 2005, <https://books.google.com/books?id=UdGBy8iLpocC>
  8. ↑ Remmert, Reinhold. Theory of Complex Functions: Readings in Mathematics (англ.). — Springer, 1991. — P. 29. Архивная копия от 16 мая 2020 на Wayback Machine
  9. ↑ Nerlove, Marc; Grether, David M.; Carvalho, Jose L. Analysis of Economic Time Series. Economic Theory, Econometrics, and Mathematical Economics (англ.). — Elsevier, 1995. — ISBN 0-12-515751-7.
  10. ↑ Flugge, Wilhelm. Statik und Dynamik der Schalen (нем.). — Berlin: Springer-Verlag, 1957. Архивная копия от 14 мая 2020 на Wayback Machine
  11. ↑ В. М. Тихомиров, В. В. Успенский. Пеpвые филдсовские лауpеаты и советская математика 30-х годов. I. — Матем. просв., сер. 3, 2, МЦНМО, М., 1998, 21-40.

Литература[править | править код]

  • Жук В. В., Натансон Г. И. Тригонометрические ряды Фурье и элементы теории аппроксимации. — Л.: Изд-во Ленингр. ун-та, 1983. — 188 с.
  • Рудин У. Основы математического анализа. — 1976.
  • Пискунов Н. С. Дифференциальное и интегральное исчисления для ВТУЗов. — М.: «Наука», 1964. — Т. 2.
  • Зигмунд А. Тригонометрические ряды. — М.: «Мир», 1965. — Т. 1.
  • Харди Г. Х., Рогозинский В. В.ruen. Ряды Фурье. — М.: Физматгиз, 1959.

Ссылки[править | править код]

  • Представление периодических сигналов. Ряд Фурье.
  • Некоторые свойства разложения периодических сигналов в ряд Фурье.
Источник

  1. Ортогональные системы функций.

    Начать изучение

  2. Ряд Фурье по ортогональной системе.

    Начать изучение

  3. Ряд Фурье абсолютно интегрируемой функции.

    Начать изучение

Ортогональные системы функций.

Определение 1.

Система непрерывных на отрезке ([a, b]) функций называется ортогональной на отрезке ([a, b]), если
$$
intlimits_{a}^{b} varphi_{n}(x) varphi_{m} dx = 0 mbox{для} n, m in mathbb{N} mbox{и} n neq m.label{ref1}
$$
Если, кроме того,
$$
intlimits_{a}^{b} varphi_{n}^{2}(x) dx = 1 mbox{для} n in mathbb{N},label{ref2}
$$
то система функций ({varphi_{n}}) называется ортонормированной на отрезке ([a, b]).

Например, тригонометрическая система
$$
frac{1}{2},quad cos frac{pi x}{l},quad sin frac{pi x}{l},quad ldots,quad cos frac{npi x}{l},quad sin frac{npi x}{l}, ldotslabel{ref3}
$$
ортогональна на отрезке ([-l, l]) (ранее мы уже разбирали этот пример).

Так как
$$
2intlimits_{-l}^{l} left(frac{1}{2}right)^{2} dx = intlimits_{-l}^{l} cos^{2} frac{npi x}{l} = intlimits_{-l}^{l} sin^{2} frac{npi x}{l} = l, n in mathbb{N},label{ref4}
$$
то, поделив все функции тригонометрической системы eqref{ref3} на (sqrt{l}), а первую из этих функций на (sqrt{l/2}), получим ортонормированную на отрезке ([-l, l]) тригонометрическую систему
$$
frac{1}{sqrt{2l}},quad frac{1}{sqrt{l}} cos frac{pi x}{l},quad frac{1}{sqrt{l}} sin frac{pi x}{l}, ldotslabel{ref5}
$$

При (l = pi) тригонометрическая система eqref{ref3} имеет особенно простой вид
$$
frac{1}{2},quad cos x,quad sin x,quad ldots,quad cos nx,quad sin nx,quad ldotslabel{ref6}
$$
и ортогональна на отрезке ([-pi, pi]).

Пример 1.

Многочлены Лежандра
$$
L_{n}(x) = frac{1}{2^{n}n!} frac{d^{n}}{dx^{n}}(x^{2}-1)^{n},quad n in mathbb{N},quad L_{0}(x) = 1,label{ref7}
$$
образуют ортогональную систему функций на отрезке [—1,1].

Решение.

(vartriangle) Доказательство ортогональности многочленов Лежандра на отрезке [—1,1] сводится к проверке при (n > m) тождества
$$
J = intlimits_{-1}^{1} frac{d^{n}}{dx^{n}}(x^{2}-1)^{n} frac{d^{m}}{dx^{m}}(x^{2}-1)^{m} dx = 0.nonumber
$$

Воспользуемся тем, что (x = 1) и (x = -1) есть нули кратности (n) многочлена ((x^{2}-1)^{n}). Поэтому все производные многочлена ((x^{2}-1)^{n}) до порядка (n-1) включительно обращаются в нуль в точках (x = 1) и (x = -1).

Интегрируя выражение (J) по частям, получаем, что
$$
J = -intlimits_{-1}^{1} frac{d^{n-1}}{dx^{n-1}}(x^{2}-1)^{n} frac{d^{m + 1}}{dx^{m + 1}}(x^{2}-1)^{m} dx = ldots \ ldots = (-1)^{n} intlimits_{-1}^{1}(x^{2}-1)^{n} frac{d^{n + m}}{dx^{n + m}}(x^{2}-1)^{m} dx = 0,nonumber
$$
так как (n + m > 2m), многочлен ((x^{2}-1)^{m}) имеет степень (2m), а производная от многочлена порядка, более высокого, чем степень многочлена, тождественно равна нулю. (blacktriangle)

Ряд Фурье по ортогональной системе.

Пусть функция (f(x)) непрерывна на отрезке ([a, b]), а ({varphi_{k}(x)}) — ортогональная на ([a, b]) система непрерывных функций, причем ни одна из функций (varphi_{k}(x)) не обращается тождественно в нуль на отрезке ([a, b]).

Определение 2.

Говорят, что функция (f(x)) разложена на отрезке ([a, b]) в сходящийся ряд по ортогональной системе функций ({varphi_{k}(x)}), если найдется такая числовая последовательность ({a_{k}}), что функциональный ряд (sum_{k=1}^{infty} a_{k}varphi_{k}(x)) сходится и его сумма равна (f(x)), то есть
$$
f(x) = sum_{k=1}^{infty} a_{k}varphi_{k}(x),quad x in [a, b].label{ref8}
$$

Лемма 1.

Если функциональный ряд eqref{ref8} сходится равномерно на отрезке ([a, b]), то справедливы следующие выражения для коэффициентов этого ряда:
$$
a_{n} = dfrac{displaystyle intlimits_{a}^{b} f(x)varphi_{n}(x) dx}{displaystyleintlimits_{a}^{b} varphi_{n}^{2}(x) dx}, n in mathbb{N}.label{ref9}
$$

Доказательство.

(circ) Так как функция (varphi_{n}(x)) непрерывна на отрезке ([a, b]), то она ограничена на этом отрезке (теорема Вейерштрасса). Если равномерно сходящийся ряд умножить на ограниченную функцию, то получим равномерно сходящийся ряд (это непосредственно следует из определения равномерной сходимости функционального ряда). Поэтому, умножая ряд eqref{ref8} на функцию (varphi_{n}(x)), получаем
$$
f(x)varphi_{n}(x) = sum_{k=1}^{infty} a_{k}varphi_{k}(x)varphi_{n}(x), n in mathbb{N},label{ref10}
$$
причем ряд в правой части равенства eqref{ref10} сходится равномерно на отрезке ([a, b]).

Воспользовавшись теоремой о законности почленного интегрирования равномерно сходящегося ряда и ортогональностью функций (varphi_{k}(x)) на отрезке ([a, b]), получаем
$$
intlimits_{a}^{b} f(x)varphi_{n}(x) dx = intlimits_{a}^{b} left(sum_{k=1}^{infty} a_{k}varphi_{k}(x)right)varphi_{n}(x) dx =\= sum_{k=1}^{infty} a_{k} intlimits_{a}^{b} varphi_{k}(x)varphi_{n}(x) dx = a_{n} intlimits_{a}^{b} varphi_{n}^{2}(x) dx.label{ref11}
$$
Так как функция (varphi_{n}(x)) не равна тождественно нулю на отрезке ([a, b]) и непрерывна, то (displaystyleintlimits_{a}^{b} varphi_{n}^{2}(x) dx > 0). Поэтому из равенства eqref{ref11} следует формула eqref{ref9} для коэффициентов (a_{n}). (bullet)

Числа (a_{n}) называются коэффициентами Фурье, а ряд eqref{ref8} — рядом Фурье функции (f(x)) по ортогональной на ([a, b]) системе функций ({varphi_{k}(x)}).

Ряд Фурье функции (f(x)) по тригонометрической системе на отрезке ([-l, l]) будем записывать в виде
$$
f(x) = frac{a_{0}}{2} + sum_{k=1}^{infty} left(a_{k} cos frac{kpi x}{l} + b_{k} sin frac{kpi x}{l}right)label{ref12}
$$
и называть тригонометрическим рядом Фурье функции (f(x)) на отрезке ([-l, l]).

Коэффициенты (a_{k}) и (b_{k}) можно вычислить, если подставить в формулы eqref{ref9} выражения для тригонометрических функций и воспользоваться формулами eqref{ref4}:
$$
a_{0} = frac{1}{l} intlimits_{-l}^{l} f(x) dx,quad a_{n} = frac{1}{l} intlimits_{-l}^{l} f(x) cos frac{npi x}{l} dx,\ b_{n} = frac{1}{l} intlimits_{-l}^{l} f(x) sin frac{npi x}{l} dx, n in mathbb{N}.label{ref13}
$$
В частности, при (l = pi) получаем
$$
a_{0} = frac{1}{pi} intlimits_{-pi}^{pi} f(x) dx,quad a_{n} = frac{1}{pi} intlimits_{-pi}^{pi} f(x) cos nx dx,\b_{n} = frac{1}{pi} intlimits_{-pi}^{pi} f(x) sin nx dx, n in mathbb{N}.label{ref14}
$$

Ряд Фурье абсолютно интегрируемой функции.

Коэффициенты Фурье могут быть вычислены при помощи формулы eqref{ref9} для любой абсолютно интегрируемой на отрезке ([a, b]) функции (f(x)), если функции (varphi_{k}(x)) непрерывны и не обращаются тождественно в нуль на отрезке ([a, b]).

В самом деле, пусть (displaystyleintlimits_{a}^{b} |f(x)| dx) сходится как несобственный интеграл. Тогда
$$
|f(x)varphi_{n}(x)| leq k_{n}|f(x)|, k_{n} = sup_{x in [a, b]} |varphi_{n}(x)|.nonumber
$$

По признаку сравнения интеграл (displaystyleintlimits_{a}^{b} f(x)varphi_{n}(x) dx) сходится абсолютно. Следовательно, все коэффициенты Фурье могут быть вычислены при помощи формулы eqref{ref9}.

Ряд (displaystylesum_{n=1}^{infty} a_{n}varphi_{n}(x)), где (a_{n}) — коэффициенты Фурье абсолютно интегрируемой на ([a, b]) функции (f(x)), будем называть рядом Фурье функции (f(x)) по ортогональной системе функций ({varphi_{n}(x)}). Так как этот ряд может оказаться расходящимся, то будем писать
$$
f(x) sim sum_{n=1}^{infty} a_{n}varphi_{n}(x).label{ref15}
$$
В частности, для тригонометрической системы eqref{ref3} формула eqref{ref15} имеет следующий вид:
$$
f(x) sim frac{a_{0}}{2} + sum_{n=1}^{infty} a_{n} cos frac{npi x}{l} + b_{n} sin frac{npi x}{l}.label{ref16}
$$

Запись eqref{ref15} означает, что (sum_{n=1}^{infty} a_{n}varphi_{n}(x)) есть ряд Фурье функции (f(x)) по ортогональной системе ({f_{n}(x)}).

Источник

Если Lконечномерное
евклидово пространство с базисомто любой элементможно разложить по этому базису, то естьгде.

В случае бесконечномерного евклидова
пространства Е разложение элемента
по бесконечной ортонормированной
системе называется рядом Фурье.

Пусть (1.2) является ортонормированной
системой в евклидовом пространстве Е.

Определение 3.2. Рядом
Фурье элементапо ортонормированной системе (1.2)
называется ряд

(5.2)

где
Числаназываются коэффициентами Фурье или
координатами элементав системе (1.2). Выражениеназываетсяn-й частичной
(или просто частичной) суммой ряда Фурье
(5.2).

Определение 4.2. Говорят,
что ряд Фурье (5.2) сходится в среднем
(или по норме Е), еслитакая, что

(6.2)

Если выполнено равенство (6.2), то будем
говорить, что ряд (5.2) сходится в среднем
к элементу
и писать

Основной целью параграфа является
изучение вопроса о том, в каких случаях
ряд Фурье элемента
сходится кв среднем.

Исследуем для начала вопрос о просто
сходимости ряда Фурье.

Теорема 1.2. Если Е-гильбертово
пространство, то ряд Фурье (5.2) элементасходится для любой ортонормированной
системы (1.2).

Для доказательства теоремы нам
потребуется вспомогательное утверждение
относительно свойств ортонормированных
систем в евклидовых пространствах.

Лемма 1.2. Если Е-евклидово
пространство и (1.2) ортонормированная
система в Е, тоимеет место соотношение (равенство
Бесселя):

(7.2)

а также равенство

(8.2)

которое называется неравенством Бесселя.
Здесь
– коэффициенты Фурье элемента.

Доказательство.

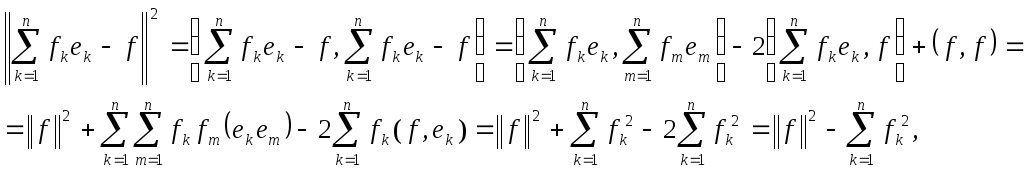
поскольку система {}
– ортонормированна.

Равенство Бесселя (7.2) доказано. Из
него, в частности, следует, что

Следовательно, все частичные суммы
ряда в (8.2) ограничены. Поэтому этот ряд
сходится. Переходя в последнем неравенстве
к пределу при
,
получим неравенство (8.2) . Лемма доказана.

Замечание 3.2. Из неравенства
Бесселя, в частности следует, что ряд
слева в (8.2) сходится и, значит, коэффициенты
Фурьедля любого элемента.

Доказательство теоремы 1.2.

Докажем, что последовательность
фундаментальна в Е. Имеем при

гдеостаток рядаИз неравенства Бесселя следует, что
этот ряд сходится и, значит,Поэтому

Следовательно,
таких, что.
Таким образом, {}
фундаментальная последовательность.
А так как Е полное пространство, тотакая, что.
Теорема доказана.

4. Замкнутые системы в евклидовых пространствах.

Рассмотрим еще одно важное свойство
ряда Фурье.

Теорема 3.2. Если (1.2) есть
ортонормированная система в пространстве
Е, тоиимеет место неравенство

(9.2)

где
есть-я
частичная сумма ряда Фурье функции.

Доказательство.

Так как система
ортонормированна, то

согласно равенству Бесселя. Теорема
доказана.

Замечание 4.2. Неравенство (9.2)
называется минимальным свойством
коэффициентов Фурье. Оно означает, что
частичные суммы ряда Фурьенаилучшим образом приближают в среднем
элементв линейной оболочке первыхвекторов системы (1.2).

Определение 5.2.Система
векторов (1.2) называется замкнутой в
нормированном пространстве Е, еслиисуществует конечный набор чиселтакой, что

.
(10.2)

Если через
обозначить замыкание по норме Е множества
всех конечных линейных комбинаций
системы (1.2) (линейной оболочки),
то определение (5.2) можно переформулировать
так: системазамкнута в Е, если Е.

Следующие теоремы описывают свойства
замкнутых систем.

Теорема 4.2. Если (1.2) ортонормированная
система в евклидовом пространстве Е,
то следующие условия эквивалентны:

1. Система (1.2) замкнута в Е;

  1. Для
    неравенство Бесселя превращается в
    неравенство (Парсеваля)

где(11.2)

  1. Для
    ряд Фурье элементасходится в среднем к,
    то есть

в среднем. (12.2)

Доказательство.

1.2.
Возьмеми.
Так как система (1.2) замкнута, тотакие, что.

Используя равенство Бесселя, и минимальное
свойство коэффициентов ряда Фурье
(9.2), выведем:

Если в этом неравенстве перейти к пределу
при
и воспользоваться неравенством Бесселя,
то получим

Отсюда следует равенство Парсеваля
(11.2).

2.3.
Для,
воспользовавшись равенством Парсеваля,
получим

А это и означает (12.2).

3.1.
Из (12.2) следует

Поэтому система (1.2) замкнута. Теорема
доказана.

Замечание 5.2. Из теоремы 4.2 следует,
что замкнутая ортонормированная система
в бесконечномерном пространстве.

Задача 2.2. Если (1.2) есть замкнутая
ортонормированная система в евклидовом
пространстве,
тоимеет место равенство (обобщённое
равенство Парсеваля)гдеесть коэффициенты Фурье элементовисоответственно.

Утверждение 2.2.Если (1.2)
замкнутая ортонормированная система
в,
то вне
существует ненулевого элемента, у
которого все коэффициенты Фурье равны
0. (системы с таким свойством называются
полными).

Доказательство.

Действительно, если
при всех,
то из равенства Парсеваля следует.
Утверждение доказано.

Следствие 1.2.Для всякой замкнутой
ортонормированной системы вдва различных элемента не могут иметь
одинаковые ряды Фурье.

Действительно, если элементы
иимеют одинаковые ряды Фурье, то у разностивсе коэффициенты Фурье равны 0.
Следовательно,.

Следствие 2.2. Если (1.2) есть
замкнутая ортонормированная система
ви для элементав смысле сходимости в среднем имеет
место равенство,
тоесть коэффициенты Фурье функции,
то есть.

Доказательство.

Пусть
есть коэффициенты Фурье.
Тогда из условия и утвержденияIIIтеоремы 4.2 следует:.
Учитывая ортонормированность системы
(1.2), отсюда выведем.
Это означает, чтои.
Следствие доказано.

Мы рассмотрели вопрос о разложении
векторов в ряд Фурье в произвольном
бесконечномерном Евклидовом пространстве.
Ряды Фурье являются эффективным аппаратом
при решении различных задач математической
физики и математики. При этом в качестве
евклидовых пространств берутся
функциональные пространства с
соответствующими ортонормированными
системами. Примерами таких систем
являются полиномы Лежандра, полиномы
Чебышева, система Хаара, система
Радемахера, функция Бесселя и другие.

В следующем параграфе мы подробно
рассмотрим вопрос о разложении функций
в ряд Фурье по тригонометрической
системе.

Соседние файлы в папке ЛекцииТФДП

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Ряды Фурье – способ представления сложной функции суммой более простых, хорошо известных.
Синус и косинус – это периодические функции. Еще они образуют ортогональный базис. Это свойство можно объяснить по аналогии с осями XX и YY на координатной плоскости. Точно так же, как мы можем описать координаты точки относительно осей, мы можем описать любую функцию относительно синусов и косинусов. Тригонометрические функции хорошо изучены и их легко применять в математике.

Представить синусы и косинусы можно в виде таких волн:

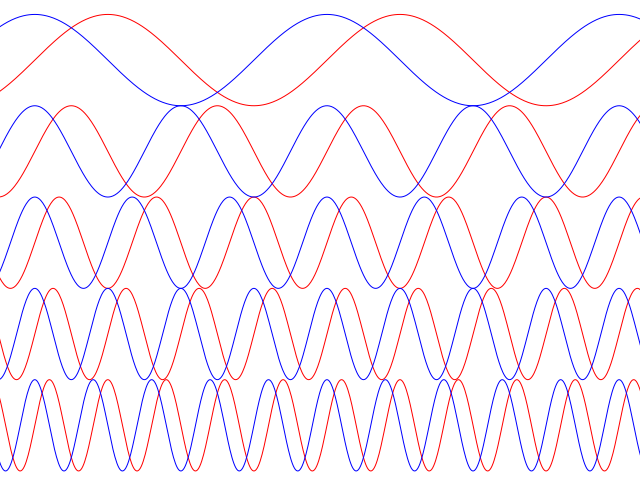
ряды фурье волны синус и косинус
Синие – это косинусы, красные – синусы. Еще такие волны называют гармониками. Косинусы – четными, синусы – нечетными. Термин гармоника пришел еще из античности и связан с наблюдениями о взаимосвязи высот звуков в музыке.

Что такое ряд Фурье

Такой ряд, где в качестве простейших используются функции синуса и косинуса, называется тригонометрическим. Назван он в честь своего изобретателя Жана Батиста Жозефа Фурье, в конце XVIII–начале XIX в. доказавшего, что любую функцию можно представить в виде комбинации таких гармоник. И чем больше их взять, тем точнее это представление будет. Для примера картинка ниже: можно заметить, что с большим количеством гармоник, т. е. членов ряда Фурье, красный график становится все ближе к синему – исходной функции.

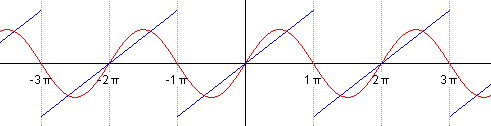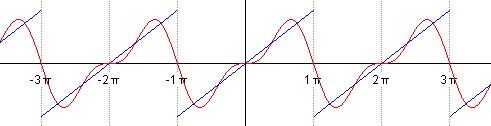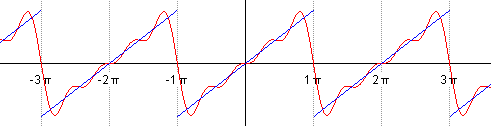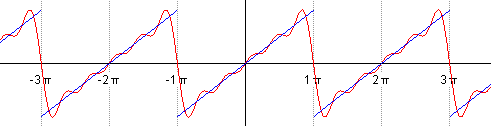
фурье пример построения в гиф.gif

Практическое применение в современном мире

А вообще нужны ли эти ряды сейчас? Где они могут применяться практически и использует ли их кто-то кроме математиков-теоретиков? Оказывается, Фурье потому и знаменит на весь мир, что практическая польза его рядов буквально неисчислима. Их удобно применять там, где есть какие-либо колебания или волны: акустика, астрономия, радиотехника и т. д. Самый простой пример его использования: механизм работы фотоаппарата или видеокамеры. Если объяснять вкратце, эти устройства записывают не просто картинки, а коэффициенты рядов Фурье. И работает это везде – при просмотре картинок в интернете, фильма или прослушивании музыки. Именно благодаря рядам Фурье вы сейчас можете прочитать эту статью со своего мобильного телефона. Без преобразования Фурье нам не хватило бы никакой пропускной способности интернет-соединений, чтобы просто посмотреть видео на YouTube даже в стандартном качестве.

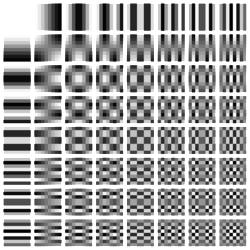
двухмерное преобразование

На этой схеме двухмерное преобразование Фурье, которое используется для разложения изображения на гармоники, т. е. базисные составляющие. На этой схеме черным закодировано значение -1, белым 1. Вправо и вниз по графику увеличивается частота.

Разложение в ряд Фурье

Наверное, вы уже устали читать, поэтому перейдем к формулам.
Для такого математического приема, как разложение функций в ряд Фурье, придется брать интегралы. Много интегралов. В общем виде ряд Фурье записывают в виде бесконечной суммы:

f(x)=A+∑n=1∞(ancos⁡(nx)+bnsin⁡(nx))f(x) = A + displaystylesum_{n=1}^{infty}(a_n cos(nx)+b_n sin(nx))
где
A=12π∫−ππf(x)dxA = frac{1}{2pi}displaystyleintlimits_{-pi}^{pi} f(x)dx
an=1π∫−ππf(x)cos⁡(nx)dxa_n = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} f(x)cos(nx)dx
bn=1π∫−ππf(x)sin⁡(nx)dxb_n = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} f(x)sin(nx)dx

Если мы каким-то образом сможем посчитать бесконечное количество ana_n и bnb_n (они и называются коэффициентами разложения Фурье, AA – это просто постоянная этого разложения), то полученный ряд в результате будет на 100% совпадать с исходной функцией f(x)f(x) на отрезке от −π-pi до πpi. Такой отрезок обусловлен свойствами интегрирования синуса и косинуса. Чем больше nn, для которого мы рассчитаем коэффициенты разложения функции в ряд, тем точнее будет это разложение.

Пример

Возьмем простую функцию y=5xy=5x
A=12π∫−ππf(x)dx=12π∫−ππ5xdx=0A = frac{1}{2pi}displaystyleintlimits_{-pi}^{pi} f(x)dx = frac{1}{2pi}displaystyleintlimits_{-pi}^{pi} 5xdx = 0
a1=1π∫−ππf(x)cos⁡(x)dx=1π∫−ππ5xcos⁡(x)dx=0a_1 = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} f(x)cos(x)dx = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} 5xcos(x)dx = 0
b1=1π∫−ππf(x)sin⁡(x)dx=1π∫−ππ5xsin⁡(x)dx=10b_1 = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} f(x)sin(x)dx = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} 5xsin(x)dx = 10
a2=1π∫−ππf(x)cos⁡(2x)dx=1π∫−ππ5xcos⁡(2x)dx=0a_2 = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} f(x)cos(2x)dx = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} 5xcos(2x)dx = 0
b2=1π∫−ππf(x)sin⁡(2x)dx=1π∫−ππ5xsin⁡(2x)dx=−5b_2 = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} f(x)sin(2x)dx = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} 5xsin(2x)dx = -5

И так далее. В случае с такой функцией мы можем сразу сказать, что все an=0a_n=0, коэффициенты bnb_n придется вычислять. Если мы возьмем первые четыре члена разложения в ряд Фурье для функции y=5xy=5x, получим:

5x≈10⋅sin⁡(x)−5⋅sin⁡(2⋅x)+103⋅sin⁡(3⋅x)−52⋅sin⁡(4⋅x)5x approx 10 cdot sin(x) – 5 cdot sin(2 cdot x) + frac{10}{3} cdot sin(3 cdot x) – frac{5}{2} cdot sin (4 cdot x)

График получившейся функции будет выглядеть следующим образом:

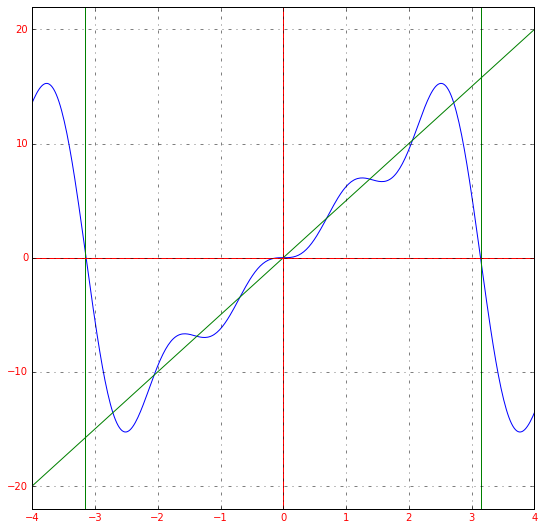
полученный график.png
Получившееся разложение в ряд Фурье приближается к нашей исходной функции. Если мы возьмем большее количество членов ряда, например, 15, то увидим уже следующее:

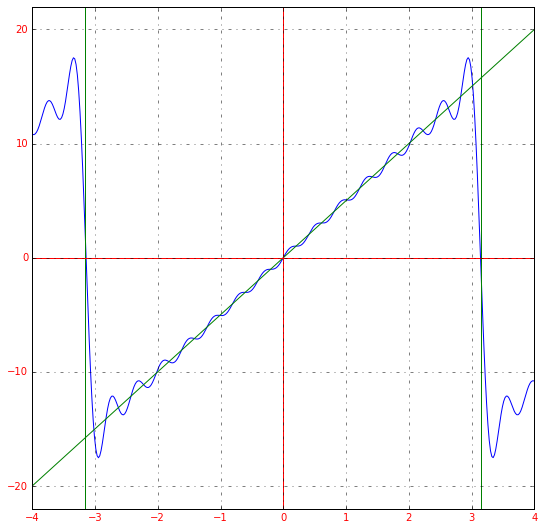
полученный график 2 пример.png
Чем больше членов разложения в ряд, тем выше точность.
Если мы немного изменим масштаб графика, сможем заметить еще одну особенность преобразования: ряд Фурье – это периодическая функция с периодом 2π2pi.

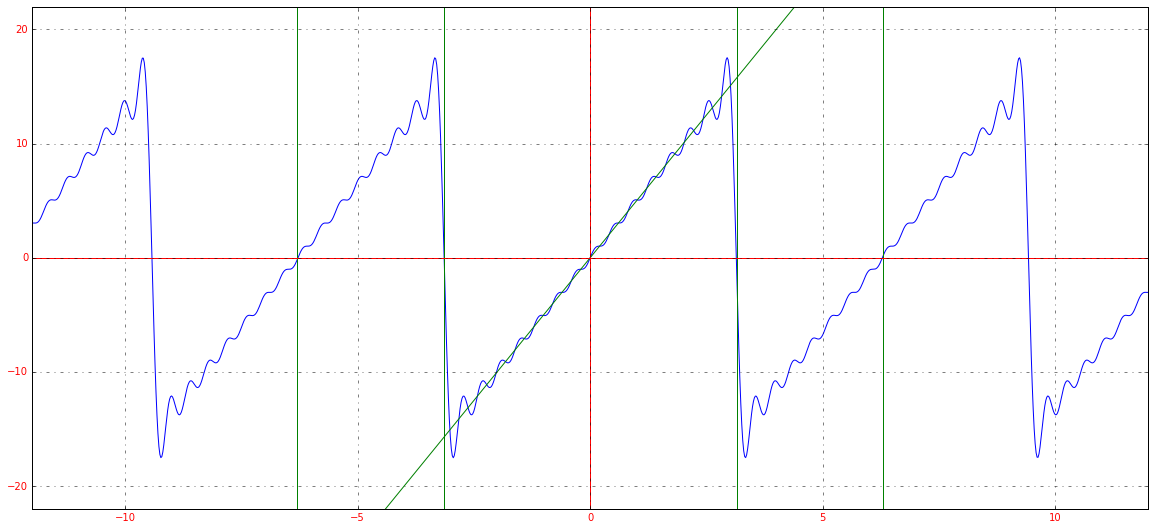
полученный график 3 итоговый пример

Таким образом, можно представлять любую функцию, которая является непрерывной на отрезке [−π;π][-pi;pi]. Все это нужно для того, чтобы облегчить анализ каких-то явлений, которые описываются сложными функциями. Не всегда возможно аналитически (т. е. по формуле) посчитать производную, а в случае с набором синусов и косинусов такой проблемы не возникнет. Собственно разложение в ряд Фурье показывает, что зачастую задачи можно решать аналитически на упрощенных моделях, одним из примеров которых и является ряд Фурье.

Тест по теме «Ряды Фурье»

Источник

Добавить комментарий