Как найти ряд фурье по графику

Ряды Фурье – способ представления сложной функции суммой более простых, хорошо известных.
Синус и косинус – это периодические функции. Еще они образуют ортогональный базис. Это свойство можно объяснить по аналогии с осями XX и YY на координатной плоскости. Точно так же, как мы можем описать координаты точки относительно осей, мы можем описать любую функцию относительно синусов и косинусов. Тригонометрические функции хорошо изучены и их легко применять в математике.

Представить синусы и косинусы можно в виде таких волн:

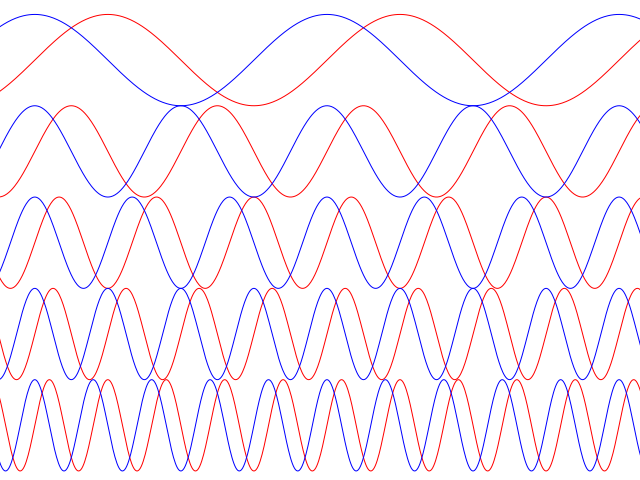
Синие – это косинусы, красные – синусы. Еще такие волны называют гармониками. Косинусы – четными, синусы – нечетными. Термин гармоника пришел еще из античности и связан с наблюдениями о взаимосвязи высот звуков в музыке.

Что такое ряд Фурье

Такой ряд, где в качестве простейших используются функции синуса и косинуса, называется тригонометрическим. Назван он в честь своего изобретателя Жана Батиста Жозефа Фурье, в конце XVIII–начале XIX в. доказавшего, что любую функцию можно представить в виде комбинации таких гармоник. И чем больше их взять, тем точнее это представление будет. Для примера картинка ниже: можно заметить, что с большим количеством гармоник, т. е. членов ряда Фурье, красный график становится все ближе к синему – исходной функции.

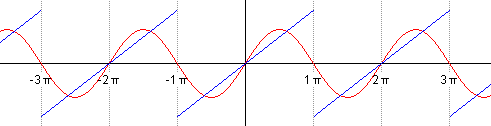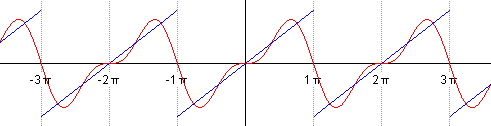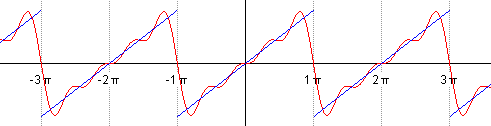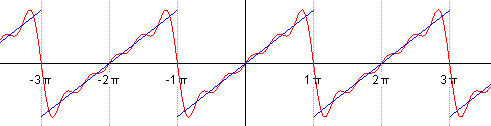
Практическое применение в современном мире

А вообще нужны ли эти ряды сейчас? Где они могут применяться практически и использует ли их кто-то кроме математиков-теоретиков? Оказывается, Фурье потому и знаменит на весь мир, что практическая польза его рядов буквально неисчислима. Их удобно применять там, где есть какие-либо колебания или волны: акустика, астрономия, радиотехника и т. д. Самый простой пример его использования: механизм работы фотоаппарата или видеокамеры. Если объяснять вкратце, эти устройства записывают не просто картинки, а коэффициенты рядов Фурье. И работает это везде – при просмотре картинок в интернете, фильма или прослушивании музыки. Именно благодаря рядам Фурье вы сейчас можете прочитать эту статью со своего мобильного телефона. Без преобразования Фурье нам не хватило бы никакой пропускной способности интернет-соединений, чтобы просто посмотреть видео на YouTube даже в стандартном качестве.

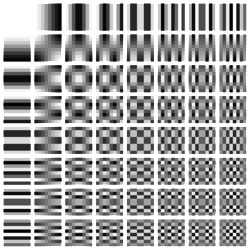
На этой схеме двухмерное преобразование Фурье, которое используется для разложения изображения на гармоники, т. е. базисные составляющие. На этой схеме черным закодировано значение -1, белым 1. Вправо и вниз по графику увеличивается частота.

Разложение в ряд Фурье

Наверное, вы уже устали читать, поэтому перейдем к формулам.
Для такого математического приема, как разложение функций в ряд Фурье, придется брать интегралы. Много интегралов. В общем виде ряд Фурье записывают в виде бесконечной суммы:

f(x)=A+∑n=1∞(ancos⁡(nx)+bnsin⁡(nx))f(x) = A + displaystylesum_{n=1}^{infty}(a_n cos(nx)+b_n sin(nx))
где
A=12π∫−ππf(x)dxA = frac{1}{2pi}displaystyleintlimits_{-pi}^{pi} f(x)dx
an=1π∫−ππf(x)cos⁡(nx)dxa_n = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} f(x)cos(nx)dx
bn=1π∫−ππf(x)sin⁡(nx)dxb_n = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} f(x)sin(nx)dx

Если мы каким-то образом сможем посчитать бесконечное количество ana_n и bnb_n (они и называются коэффициентами разложения Фурье, AA – это просто постоянная этого разложения), то полученный ряд в результате будет на 100% совпадать с исходной функцией f(x)f(x) на отрезке от −π-pi до πpi. Такой отрезок обусловлен свойствами интегрирования синуса и косинуса. Чем больше nn, для которого мы рассчитаем коэффициенты разложения функции в ряд, тем точнее будет это разложение.

Пример

Возьмем простую функцию y=5xy=5x
A=12π∫−ππf(x)dx=12π∫−ππ5xdx=0A = frac{1}{2pi}displaystyleintlimits_{-pi}^{pi} f(x)dx = frac{1}{2pi}displaystyleintlimits_{-pi}^{pi} 5xdx = 0
a1=1π∫−ππf(x)cos⁡(x)dx=1π∫−ππ5xcos⁡(x)dx=0a_1 = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} f(x)cos(x)dx = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} 5xcos(x)dx = 0
b1=1π∫−ππf(x)sin⁡(x)dx=1π∫−ππ5xsin⁡(x)dx=10b_1 = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} f(x)sin(x)dx = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} 5xsin(x)dx = 10
a2=1π∫−ππf(x)cos⁡(2x)dx=1π∫−ππ5xcos⁡(2x)dx=0a_2 = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} f(x)cos(2x)dx = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} 5xcos(2x)dx = 0
b2=1π∫−ππf(x)sin⁡(2x)dx=1π∫−ππ5xsin⁡(2x)dx=−5b_2 = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} f(x)sin(2x)dx = frac{1}{pi}displaystyleintlimits_{-pi}^{pi} 5xsin(2x)dx = -5

И так далее. В случае с такой функцией мы можем сразу сказать, что все an=0a_n=0, коэффициенты bnb_n придется вычислять. Если мы возьмем первые четыре члена разложения в ряд Фурье для функции y=5xy=5x, получим:

5x≈10⋅sin⁡(x)−5⋅sin⁡(2⋅x)+103⋅sin⁡(3⋅x)−52⋅sin⁡(4⋅x)5x approx 10 cdot sin(x) – 5 cdot sin(2 cdot x) + frac{10}{3} cdot sin(3 cdot x) – frac{5}{2} cdot sin (4 cdot x)

График получившейся функции будет выглядеть следующим образом:

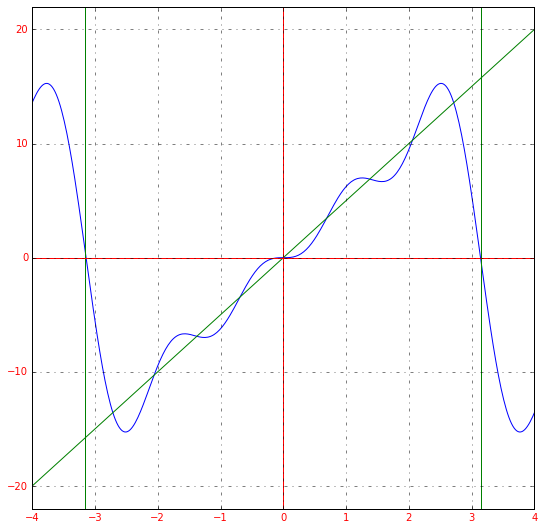
Получившееся разложение в ряд Фурье приближается к нашей исходной функции. Если мы возьмем большее количество членов ряда, например, 15, то увидим уже следующее:

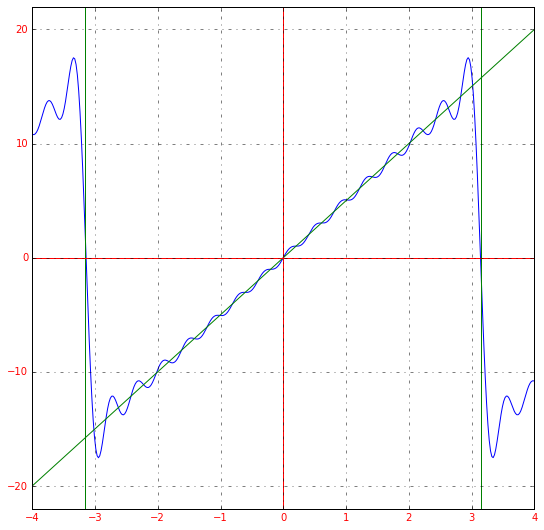
Чем больше членов разложения в ряд, тем выше точность.
Если мы немного изменим масштаб графика, сможем заметить еще одну особенность преобразования: ряд Фурье – это периодическая функция с периодом 2π2pi.

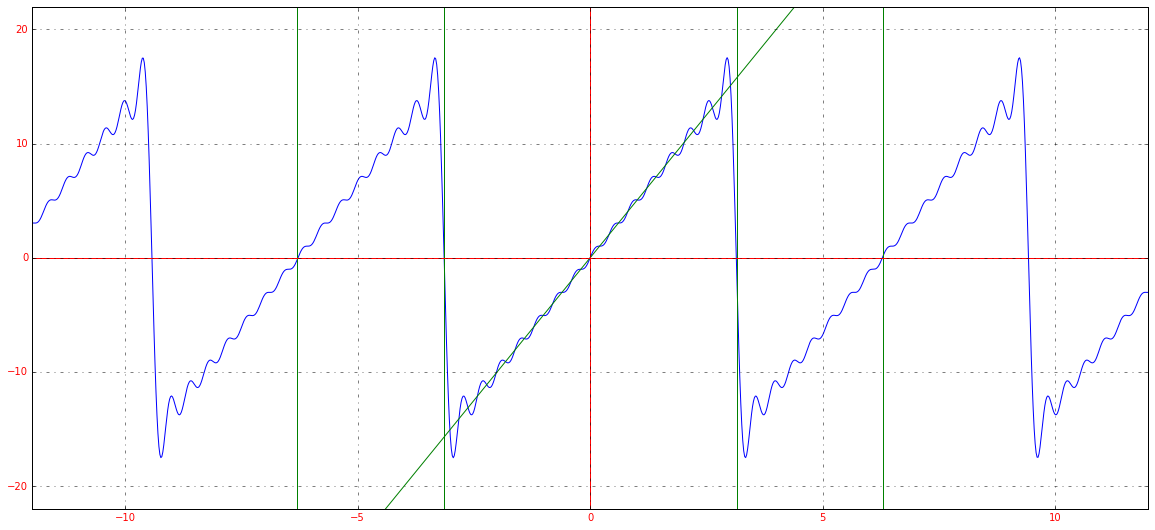
Таким образом, можно представлять любую функцию, которая является непрерывной на отрезке [−π;π][-pi;pi]. Все это нужно для того, чтобы облегчить анализ каких-то явлений, которые описываются сложными функциями. Не всегда возможно аналитически (т. е. по формуле) посчитать производную, а в случае с набором синусов и косинусов такой проблемы не возникнет. Собственно разложение в ряд Фурье показывает, что зачастую задачи можно решать аналитически на упрощенных моделях, одним из примеров которых и является ряд Фурье.

Тест по теме «Ряды Фурье»

Начнем
с простого замечания: если заданная на
отрезке

интегрируемая функция

является нечетной, то есть для всех

выполняется
равенство
,
то

.

Для
четной функции

справедливо

.

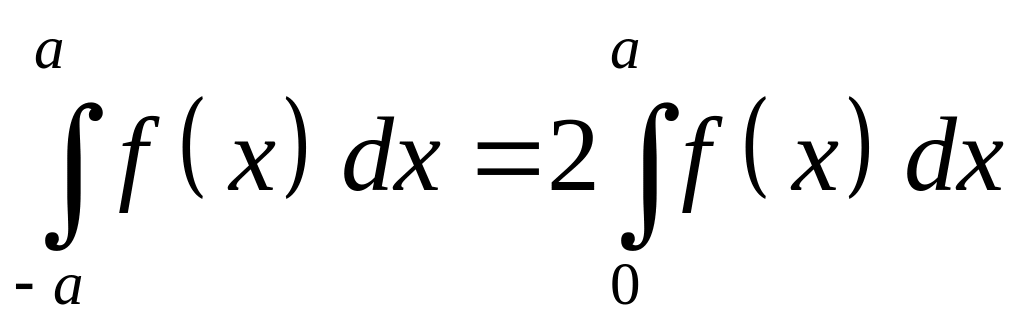
Напомним
некоторые свойства четных и нечетных
функций на

:

1. Произведение
   двух четных или двух нечетных функций
   есть функция четная;

2. Произведение
   четной и нечетной функций есть нечетная
   функция.

Утверждение.
Пусть

определена и интегрируема на

,
а

-ее
коэффициенты Фурье. Тогда

1. если

   -нечетная,
   то

,
а ряд Фурье имеет вид

.

1. если

   –
   четная, то

,
а
ряд Фурье имеет вид
.

Допустим,
что функция

задана
на отрезке

.
Если
мы хотим найти разложение

на
этом отрезке в ряд Фурье, то сначала
продолжим

на
симметричный промежуток

произвольным образом, а потом воспользуемся
формулами для коэффициентов Фурье.

Если
продолжить функцию четным образом, то
получим разложение только по косинусам,
а если продолжить нечетным образом, то
– только по синусам. При этом в первом
случае продолженная функция

будет
иметь вид

,

а
во втором случае

4.6. Разложение в ряд Фурье функции, заданной на произвольном промежутке

Пусть

задана
на отрезке

,
и
на этом отрезке она кусочно-гладкая.
Рассмотрим периодическую кусочно-гладкую
функцию

с
периодом

,

которая
совпадает с

на

,
а

-произвольная
кусочно-гладкая функция.

Таким
образом,

была продолжена на симметричный отрезок.
Теперь для

существует разложение в ряд Фурье. Сумма
этого ряда совпадает с

во
всех точках непрерывности отрезка

,
то
есть функция

разложена
в ряд Фурье на

.

Алгоритм
разложения функции
в
тригонометрический ряд Фурье:

1. выяснить
   формально ряд Фурье по заданию функции;

2. найти
   коэффициенты ряда Фурье;

3. используя
   теорему о достаточном условии сходимости
   ряда Фурье, найти сумму ряда, построить
   график

   и
   
   .
   Выяснить, в каких точках

   совпадает
   с

   .

4.7. Контрольные вопросы и задания.

1. Какая
   функция называется периодической?
   Является ли функция Дирихле
   

   периодической?
   Чему равен период? Имеет ли эта функция
   основной период?

1. Что
   такое тригонометрический ряд?

2. Какой
   тригонометрический ряд называется
   рядом Фурье?

1. Являются
   ли тригонометрические ряды
   

   и
   

   рядами Фурье?

1. Сформулировать
   достаточные условия поточечной
   сходимости ряда Фурье.

2. Записать
   равенство Парсеваля и неравенство
   Бесселя для тригонометрического ряда
   Фурье.

3. Какой
   вид имеет ряд Фурье для нечетной
   интегрируемой функции?

4. Какой
   вид имеет ряд Фурье для
   
   -периодической
   функции?

4.8. Образцы решения типовых задач

При
нахождении коэффициентов Фурье полезно
помнить:

.

Пример
1.
Разложить функцию

в ряд
Фурье
на интервале

.
Построить
график суммы ряда Фурье. Вычислить суммы
получающихся рядов, полагая

.

Построим
график данной функции:

Продолжим
данную функцию периодически с периодом

на
всю прямую.

Построим
график суммы ряда Фурье

Найдём
коэффициенты ряда
Фурье.
Так как

нечётная на

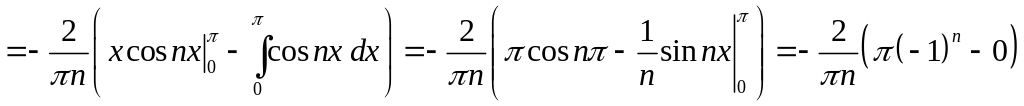
Итак,

.

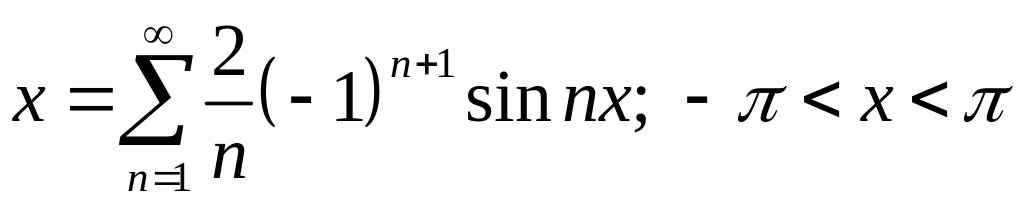
Используя
полученное разложение с учётом вида
графика суммы
ряда
Фурье,
из которого видно, к чему сходится ряд
в точках разрыва, найдём суммы некоторых
числовых рядов.

При

получим

.

При

получим

.

При

получим

.

Пример
2.
Разложить в ряд
Фурье
по косинусам функцию

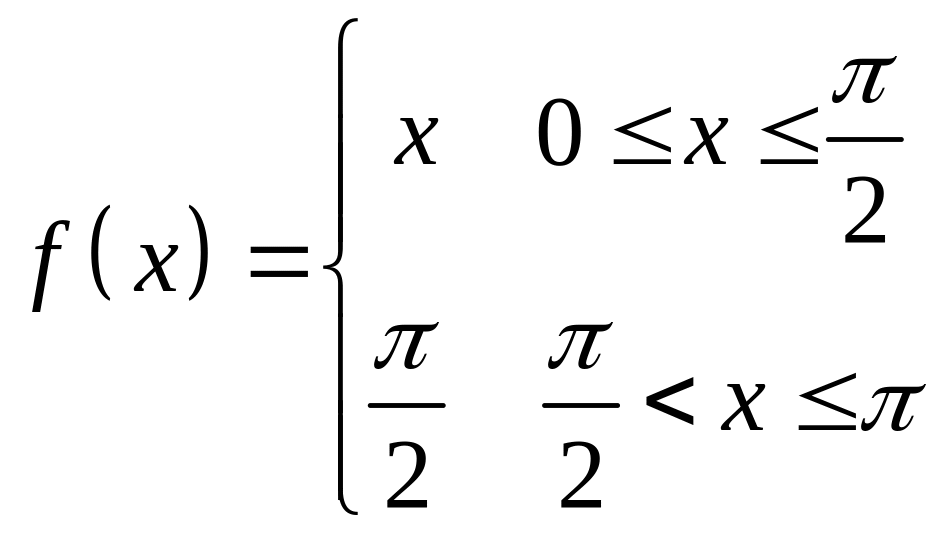
(полупериод
функции равен

)

Изобразим
график заданной функции

Продолжим
функцию чётным образом на промежутке

,
тогда коэффициенты

.

Продолжим
полученную функцию с периодом

на
всю прямую. Так как продолжение будет
непрерывной функцией, то для

график
суммы ряда Фурье совпадает с графиком
продолженной функции

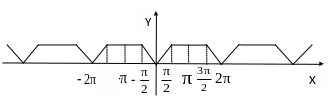
Вычислим
коэффициенты ряда
Фурье

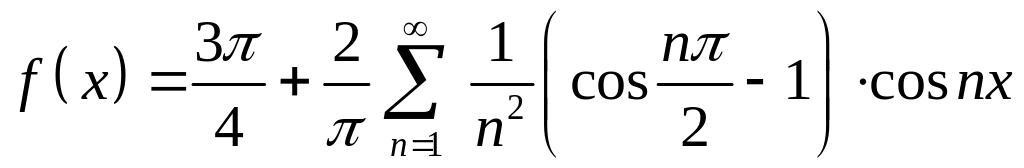
при

.

Пример
3.
Разложить в ряд
Фурье
по синусам функцию

(полупериод
функции равен

)

Разложение
функции в ряд по синусам – это ряд Фурье
нечётного продолжения функции с
промежутка

на
промежуток

.

Изобразим
график суммы ряда Фурье

Имеем

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание:

1. Примеры с решением

Разложения функции в ряд Фурье

Существует несколько теорем, содержанием которых является перечень достаточных условий разложения функции в ряд Фурье.

В вузовском курсе математики чаше других используется теорема Дирихле.

Теорема Дирихле. Пусть периодическая с периодом функция удовлетворяет на промежутке условиям:

Тогда ряд Фурье функции сходится на всей числовой оси. При этом сумма ряда Фурье равна:

1) значению в точках непрерывности функции

2) если в точке функция терпит разрыв;

Заметим, что требование кусочной монотонности на промежутке означает, что эта функция может иметь на промежутке лишь конечное число точек экстремума.

Очевидно, периодическая с периодом функция.

Из теоремы Дирихле следует, что класс функций, которые разлагаются в ряд Фурье, довольно широк.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Примеры с решением

Пример 1.

Разложить в ряд Фурье периодическую с периодом функцию, значения которой на промежутке совпадают со значениями функции

Решение:

Применяя метод интегрирования по частям, получим:

По теореме Дирихле в точках непрерывной функции , в частности, на интервале будем иметь

В точках сумма ряда будет равна:

Это же значение будет принимать функция во всех других точках разрыва функции, которая является периодическим продолжением функции на всю числовую ось. График функции изображен на рис. 1.

Рисунок иллюстрирует, что функция имеет только точки разрыва 1-го рода и кусочно-монотонна, это означает, что применение теоремы Дирихле было возможно.

Возможно вам будут полезны данные страницы:

В частном случае при будем иметь

Так как получим

Заметим, что ряды Фурье часто используются при суммировании числовых рядов. И еще одно замечание. В данном примере функция была задана на с помощью двух аналитических выражений. В математике и се приложениях таким образом заданные функции встречаются довольно часто. Разложение их в ряд Фурье является универсальным средством представления таких функций единым аналитическим выражением.

Можно ли пользоваться теоремой Дирихле, если функция удовлетворяет условиям теоремы на промежутке и является периодическои? Как в этом случае вычисляются коэффициенты ряда Фурье?

Так как интеграл от периодической функции по любому промежутку, длина которого равна периоду, всегда имеет одно и то же значение (это очевидно даже из геометрических соображений), это означает, что периодическую с периодом функцию можно разлагать в ряд Фурье но любому промежутку длины если на этом промежутке выполнены условия теоремы Дирихле. В случае промежутка вычислительные формулы для коэффициентов Фурье будут иметь вид:

Какой особенностью обладают ряды Фурье для четных и нечетных функции?

Напомним, что если четная функция, то

если функция нечетная. тогда

Если функция четная, тогда четная функция, а функция нечетная. Если же нечетная функция, тогда нечетная, четная функция. Отсюда следует:

1. Коэффициенты ряда Фурье четной функции будут вычисляться по формулам

Таким образом, ряд Фурье четной функции содержит только косинусы и имеет вид:

2. Если же функция нечетная,

Следовательно, ряд Фурье нечетной функции содержит только синусы, т. е. только нечетные функции.

Можно ли разложить в ряд Фурье функцию, заданную на промежутке

Можно. С этой целью заданную функцию произвольным образом доопределяют на промежутке таким образом, чтобы для этой функции были выполнены условия теоремы Дирихле. Далее разлагают в ряд функцию, которая является периодическим продолжением на всю числовую ось функции

В частных случаях, если доопределить функцию так, чтобы оказалась четной функцией (рис. 2), получим ряд, содержащий только косинусы, если продолжить функцию на промежуток нечетным образом (рис. 3), получим ряд Фурье, содержащий только синусы.

Очевидно, существует бесконечно много способов доопределения функции . Соответственно будем получать ряды, которые на промежутке будут вести себя по-разному, но при этом в любой точке из интервала значение суммы ряда будет одним и тем же при любой функции Очевидно, это значение будет определяться только поведением функции на интервале

Пример 2.

Периодическую с периодом функцию, значения которой на вычисляются по формуле разложить в ряд Фурье на промежутке доопределив функцию на отрезке двумя способами (рис. 4, рис. 5):

Во втором случае функция доопределена нечетным образом.

Решение:

Разложение в ряд функции было получено при решении примера 1. Следовательно, разложение в ряд функции на будет иметь вид:

Получим разложение в ряд функции Так как функция нечетная,

(интегрировали методом по частям).

Разложение на будет иметь вид:

В первом случае (см. пример 1), во втором случае

Полученные для одной и той же функции разложения в ряд на различны. Посмотрим, как ведут себя полученные разложения, например, в точке Так как все слагаемые разложения функции содержащие косинусы. при равны нулю, будем иметь

Так как получим

Во втором случае

Так как

будем иметь

Таким образом, используя два различных разложения в ряд Фурье функции па промежутке полагая в них . мы получили один и тот же результат.

Напомним, что в теории степенных рядов было получено разложение в ряд Тейлора функции

Так как будем иметь тог же результат, который мы получили, используя разложение совсем другой функции в ряд Фурье:

Можно ли разложить в ряд Фурье периодическую функцию с периодом (отличным от )?

Да, можно. Пусть функция задана на промежутке Введем переменную по формуле Тогда функция будет периодической функцией аргумента с периодом Если эта функция разлагается в ряд Фурье на промежутке то этот ряд будет иметь вид:

где

Возвращаясь к прежней переменной полагая

будем иметь

И тогда ряд Фурье функции с периодом 21 будет иметь вид:

Заметим, что вся изложенная выше теория рядов Фурье для периодических функций с периодом имеет место и для периодических функций с периодом

Пример 3.

Разложить в ряд Фурье периодическую функцию с периодом совпадающую на интервале с функцией

и равную 0 в точках разрыва (рис. 6).

Решение:

Заданная функция удовлетворяет условиям теоремы Дирихле, следовательно, разлагается в ряд Фурье, который сходится на всей числовой оси. Функция нечетная, поэтому

Сумма ряда Фурье будет иметь вид:

Значения будут совпадать со значениями периодической функции, изображенной на рис. 6 во всех точках числовой оси.

На рис. 7 показано, как частичные суммы ряда с увеличением все точнее и точнее представляют функцию

Пример 4.

Функцию разложить в ряд Фурье на интервале (0,2п). Пользуясь полученным разложением, найти суммы рядов

Решение:

Функция не является периодической. Введем вспомогательную функцию с периодом которая на интервале будет совпадать с а на остальной части оси будет ее периодическим продолжением. В точках разрыва функцию примем равной полусумме ее односторонних пределов, т. е. График схематично изображен на рис. 8.

Функция удовлетворяет всем условиям теоремы Дирихле. Найдем ее разложение в ряд Фурье

Дважды используя метод интегрирования по частям, получим:

Аналогично, дважды интегрируя по частям, найдем

Таким образом,

Полагая в первом разложении и получим соответственно

Заметим, что так как можно было подставить и в разложение функции Складывая почленно два полученных сходящихся ряда, получим еще один интересный результат:

Пример 5.

Разложить в ряд Фурье периодическую с периодом функцию, совпадающую на промежутке с функцией

Решение:

В данной задаче функция имеет период где Очевидно, что данная функция нечетная, так как

Функция удовлетворяет условиям Дирихле, следовательно, разлагается в сходящийся на всей оси ряд Фурье. В данном случае коэффициенты Фурье будут вычисляться по формулам

При будем иметь:

Интегрируя два раза по частям, получим:

Так как окончательно будем иметь

Тогда

для В точках , согласно теореме Дирихле будем иметь

Это же значение сумма (рис. 9) полученного ряда будет принимать во всех остальных точках разрыва заданной периодической функции.