Идея представления функции в виде многочлена с остаточным слагаемым основана на разложении функции в степенной ряд.
Ряды Тейлора и Маклорена
Бесконечно дифференцируемую в точке x0x_0 функцию действительной переменной f(x)f(x) можно разложить в ряд по степеням двучлена (x−x0)(x-x_0):
f(x)=f(x0)+f′(x0)1!(x−x0)+f′′(x0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=f(x)=f(x_0)+dfrac{f{‘}(x_0)}{1!}(x-x_0) +dfrac{f{”}(x_0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =
=∑k=0∞f(k)(x0)k!(x−x0)k=sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
Этот ряд называют рядом Тейлора.
В случае x0=0x_0=0, полученный степенной ряд:
f(x)=f(0)+f′(0)1!x+f′′(0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=f(x)=f(0)+dfrac{f{‘}( 0)}{1!} x +dfrac{f{”}(0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =
=∑k=0∞f(k)(x0)k!(x−x0)k=sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
называют рядом Маклорена.
Запишем разложения основных элементарных функций в ряд Маклорена, укажем соответствующие интервалы сходимости и приведем примеры их определения.
- Показательная функция:
ex=1+x1!+x22!+x33!+…+xnn!+…=∑k=1∞xnn!,∣x∣<∞e^x=1+dfrac{x}{1!} +dfrac{x^2}{2!} +dfrac{x^3}{3!}+ldots+dfrac{x^n}{n!}+ldots=sumlimits_{k=1}^{infty} dfrac{x^n}{n!},quad |x|<infty
- Тригонометрические функции:
sinx=x1!−x33!+x55!−x77!+…+(−1)n+1x2n−1(2n−1)!+…=∑k=1∞(−1)k+1x2k−1(2k−1)!,∣x∣<∞sin x=dfrac{x}{1!} -dfrac{x^3}{3!} +dfrac{x^5}{5!} -dfrac{x^7}{7!} +ldots+dfrac{(-1)^{n+1}x^{2n-1}}{(2n-1)!}+ldots=sumlimits_{ k =1}^{infty} dfrac{(-1)^{ k +1}x^{2 k -1}}{(2 k -1)!},quad |x|<infty
cosx=1−x22!+x44!−x66!+…+(−1)n+1x2n(2n)!+…=∑k=0∞(−1)kx2k(2k)!,∣x∣<∞cos x=1 -dfrac{x^2}{2!} +dfrac{x^4}{4!} -dfrac{x^6}{6!} +ldots+dfrac{(-1)^{n+1}x^{2n}}{(2n)!}+ldots=sumlimits_{ k =0}^{infty} dfrac{(-1)^{k}x^{2 k }}{(2 k)!},quad |x|<infty
arctgx=x−x33+x55−x77+…+(−1)nx2n+12n+1+…=∑k=0∞(−1)kx2k+12k+1,∣x∣≤1arctg x=x-dfrac{x^3}{3} +dfrac{x^5}{5} -dfrac{x^7}{7} +ldots+dfrac{(-1)^{n}x^{2n+1}}{2n+1}+ldots=sumlimits_{ k =0}^{infty} dfrac{(-1)^{ k }x^{2 k +1}}{2 k +1},quad |x|le{1}
- Логарифмическая функции:
ln(1+x)=x1!−x22!+x33!−x44!+…+(−1)n+1xnn!+…=∑k=1∞(−1)k+1xkk!,x∈(−1;1]ln (1+x)=dfrac{x}{1!} -dfrac{x^2}{2!} +dfrac{x^3}{3!} -dfrac{x^4}{4!} +ldots+dfrac{(-1)^{n+1}x^{n}}{n!}+ldots=sumlimits_{ k =1}^{infty} dfrac{(-1)^{ k +1}x^{ k }}{ k!},quad xin (-1;1]
- Степенная функции:
(1+x)α=1+α1!x+α(α−1)2!x2+α(α−1)(α−2)3!x3+…+α(α−1)…(α−n+1)n!xn+…=(1+x)^alpha=1+dfrac{alpha }{1!}x+dfrac{alpha (alpha -1)}{2!}x^2 +dfrac{alpha (alpha -1)( alpha -2)}{3!} x^3 +ldots+dfrac{alpha (alpha -1) ldots ( alpha-n+1)} {n!} {x^n}+ldots=
=∑k=0∞α(α−1)…(α−k+1)k!xk=sumlimits_{ k =0}^{infty} dfrac{alpha (alpha -1) ldots ( alpha-k+1)}{ k!} {x^ k }
11−x=1+x+x2+…+xn+…=∑k=0∞xk,∣x∣<1dfrac{1}{1-x}=1+x+x^2+ldots+x^n+ldots =sumlimits_{ k =0}^{infty}x^{ k },quad |x|<1
Пример 1
Найдем для функции:
f(x)=sinxf(x)=sin x
интервал сходимости ряда:
f(x)=sinx==∑n=1∞(−1)n+1x2n−1(2n−1)!f(x)=sin x==sumlimits_{n=1}^{infty} dfrac{(-1)^{n+1}x^{2n-1}}{(2n-1)!}
Воспользуемся признаком Даламбера:
limn→∞∣an+1an∣=limn→∞∣x2n+1/(2n+1)!x2n−1/(2n−1)!∣=x2limn→∞12n(2n+1)=0limlimits_{n to infty } left | dfrac {a_{n+1}}{a_n} right | = limlimits_{n to infty } left | dfrac {x^{2n+1}/{(2n+1)!}}{ x^{2n-1}/{(2n-1)!}} right | =x^2 limlimits_{n to infty } dfrac {1} {2n(2n+1)}=0
Полученный результат говорит о том, что предел равен нулю для любого xx, и, следовательно, интервалом сходимости ряда является вся числовая ось.
Пример 2
Найдем интервал сходимости ряда для функции
f(x)=arctgx=∑n=0∞(−1)nx2n+12n+1,∣x∣≤1f(x)=arctg x= sumlimits_{n=0}^{infty} dfrac{(-1)^{n}x^{2n+1}}{2n+1}, quad |x|le{1}
Воспользовавшись признаком Даламбера применительно к степенному ряду, получаем:
limn→∞∣an+1an∣=limn→∞∣x2n+1/(2n+1)x2n−1/(2n−1)∣=x2limn→∞2n−12n+1=x2limn→∞2−1n2+1n=x2limlimits_{n to infty } left | dfrac {a_{n+1}}{a_n} right | = limlimits_{n to infty } left | dfrac {x^{2n+1}/(2n+1)}{ x^{2n-1}/(2n-1)} right | =x^2 limlimits_{n to infty } dfrac {2n-1} {2n+1}=x^2 limlimits_{n to infty } dfrac {2-dfrac{1}{n}}{2+dfrac{1}{n}}= x^2
Условие сходимости по этому признаку имеет вид:
x2<1x^2<1
В граничных точках x=±1x=pm1 получаем знакопеременный ряд вида:
∑n=0∞anx2n+1sumlimits_{n=0}^{infty} a_n x^{2n+1},
где ∣an∣=1n+1|a_n|=dfrac {1}{n+1}
Заметим, что
limn→∞∣an∣=0limlimits_{n to infty } |a_n|=0
и, согласно признаку Лейбница, знакопеременный ряд сходится. Таким образом, интервалом сходимости исходного ряда является: ∣x∣≤1|x| le 1.
Применение формулы и рядов Маклорена
Вычисление значений функций
Идея использования рядов для приближенного вычисления примечательна тем, что можно добиться требуемой точности, т.е. фактически найти требуемое значение со сколь угодно высокой точностью.
Пример
Вычислим значение числа ee с точностью до второго знака после запятой. Воспользуемся разложением в ряд Маклорена функции f(x)=exf(x)=e^x при x=1x=1, вычислив сумму до шестого члена в разложении и с остаточным членом в форме Лагранжа:
e1=1+11!+12!+13!+14!+15!+ec6!,0≤c≤1e^1=1+dfrac {1}{1!} +dfrac {1}{2!} +dfrac {1}{3!} +dfrac {1}{4!} +dfrac {1}{5!} +dfrac {e^c}{6!},quad 0le c le 1
Далее:
e1=16360!+ec6!≈2.716+ec6!,0≤c≤1e^1=dfrac {163}{60!} +dfrac {e^c}{6!}approx 2.716+dfrac {e^c}{6!},quad 0le c le 1
Учитывая, что ec6!<0.0014dfrac {e^c}{6!}<0.0014 получаем результат e≈2.72e approx 2.72
Вычисление пределов функций
На практике часто встречаются такие пределы, которые нельзя найти, используя первый и второй замечательные пределы, правило Лопиталя или другие способы вычислений. В этих случаях можно воспользоваться разложением элементарных функций в степенной ряд Маклорена и уже затем найти сам предел.
Пример
Вычислим:
limx→0e2x−1−2x−2x2x−sinxlimlimits_{x to 0 } dfrac {e^{2x}-1-2x-2x^2}{x-sin {x}}
Заменим exe^x и sinxsin{x} их разложениями в степенные ряды, находим:
limx→0e2x−1−2x−2x2x−sinx=limx→0(1+2x+4×22!+8×33!+…)−1−2x−2x2x−(x−x33!+x55!−…)=limlimits_{x to 0 } dfrac {e^{2x}-1-2x-2x^2}{x-sin {x}}=limlimits_{x to 0 } dfrac {left( 1+2x+dfrac{4x^2}{2!}+dfrac{8x^3}{3!}+ldots right)-1-2x-2x^2}{x-left( x-dfrac{x^3}{3!}+dfrac{x^5}{5!}-ldots right)}=
=limx→08×33!+16×44!+…x33!−x55!+…=limx→083!+16×4!+…13!−x25!+…=8=limlimits_{x to 0 } dfrac {dfrac{8x^3}{3!}+dfrac{16x^4}{4!}+ldots} {dfrac{x^3}{3!} -dfrac{x^5}{5!}+ldots} = limlimits_{x to 0 } dfrac {dfrac{8}{3!}+dfrac {16x}{4!} +ldots} {dfrac{1}{3!} -dfrac{x^2}{5!}+ldots}=8
Вычисление определенных интегралов
Конечно, на практике лучше всего вычислять точное значение определенного интеграла. Но очень часто соответствующие неопределенные интегралы является «неберущимися». Поэтому для приближенного вычисления определенного интеграла используется разложение подынтегральной функции в ряд Маклорена.
Пример
Вычислим с точностью до третьего знака после запятой:
∫01x3e−xdxdisplaystyle intlimits_0^1 sqrt[3] x e^{-x} dx
Для приближенного вычисления этого определенного интеграла используется разложение функции f(x)=sqrt[3]xe−xf(x)= sqrt[3] x e^{-x} в ряд Маклорена:
f(x)=sqrt[3]xe−x=x1/3−x4/3+12×7/3−16×10/3+…f(x)= sqrt[3] x e^{-x}=x^{1/3}-x^{4/3}+dfrac{1}{2}x^{7/3}-dfrac{1}{6}x^{10/3}+ldots
Интервал, заданный пределами интегрирования: 0≤x≤10 le x le 1 входит в радиус сходимости полученного ряда (−∞;+∞)(-infty;+infty).
Интегрируя почленно, получаем:
∫01f(x)=∫01×1/3dx−∫01×4/3dx+12∫01×7/3dx−16∫01×10/3dx+…=displaystyleintlimits_0^1 f(x)= intlimits_0^1 x^{1/3}dx-intlimits_0^1 x^{4/3}dx+dfrac{1}{2}intlimits_0^1 x^{7/3}dx-dfrac{1}{6}intlimits_0^1 x^{10/3}dx+ldots=
=34×4/3∣01−37×7/3∣01+32⋅10×10/3∣01−36⋅13×13/3∣01+…= dfrac{3}{4} Biggl. x^{4/3}Biggr |_0^1-dfrac{3}{7} Biggl. x^{7/3}Biggr |_0^1+dfrac{3}{2 cdot 10} Biggl. x^{10/3}Biggr |_0^1-dfrac{3}{6 cdot 13} Biggl. x^{13/3}Biggr|_0^1+ldots
и с учетом требуемой точности:
∫01x3e−xdx≈34−37+32⋅10−36⋅13≈928+29260≈197455≈0,433displaystyleintlimits_0^1 sqrt[3] x e^{-x} dx approx dfrac{3}{4}-dfrac{3}{7}+dfrac{3}{2 cdot 10}-dfrac{3}{6 cdot 13}approx dfrac{9}{28}+dfrac{29}{260} approx dfrac{197}{455} approx 0,433
Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций. Частный случай разложения в ряд Тейлора в нулевой точке называется рядом Маклорена.
Ряд Тейлора был известен задолго до публикаций Брука Тейлора[1] — его использовали ещё в XIV веке в Индии[2], а также в XVII веке Грегори и Ньютон.
Ряды Тейлора применяются при аппроксимации функции многочленами.
В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Обобщением понятия ряда Тейлора в функциональном анализе является ряд Фантапье.
Определение[править | править код]
1. Многочленом Тейлора функции 



,
используемая в приближённых вычислениях, как обобщение следствия теоремы Лагранжа о среднем значении дифференцируемой функции:
- при
верно
.
При записи суммы использованы обозначение 


2. Рядом Тейлора в точке 



с общим членом
, зависящим от параметра
.
Другими словами, рядом Тейлора функции 


.[3]
Как указано ниже в примерах, наличия бесконечной дифференцируемости функции 


3. Рядом Тейлора в точке 


удовлетворяющей в некоторой окрестности 

называется степенной ряд
.
В отличие от вещественного случая, из условий следует, что найдётся такое значение радиуса 


4. В случае 
называется рядом Маклорена.
Аналитическая функция[править | править код]
1. Функция 








то есть 


Функция называется аналитической на промежутке (на множестве), если она является аналитической в каждой точке этого промежутка (множества).
2. Степенной ряд 


Если в 



Таким образом, для аналитической в точке 




Следствие. Функция 




3. Вопрос: будет ли для произвольной бесконечно дифференцируемой в точке 






Ответ: нет.
Существуют бесконечно дифференцируемые функции вещественной переменной, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности

Примеры. Функции вещественной переменной 

являются бесконечно дифференцируемыми в точке 
Следовательно, ряды Тейлора всех этих функций с параметром 
Однако, для любого 


в которых функции отличны от 
Таким образом, эти функции не являются в точке 
Доказательство
Доказательство проведём для функции 
Функция 
для всех 
Для 

Функция 



дополненная пределами слева
и справа 

Найдём производную функции 

По определению:

Поскольку для 

то
докажем, что для произвольного 

Применение правила Лопиталя непосредственно к частям
не приводит к результату.
Выполним замену переменной: 

Пусть 
Применяя правило Лопиталя 




.
Таким образом,
.
Найдём (для 
производных функции 
И так далее. Во всех случаях, очевидно,
получается произведение
на сумму целых отрицательных степеней

Конечная сумма
бесконечно малых является бесконечно малой.
Таким образом,

Вычисляя последовательно по определению (как выше) производные 

обнаруживаем, что все производные в
точке 
Область сходимости ряда Тейлора[править | править код]
Ряд Тейлора, являясь степенным рядом, имеет в качестве области сходимости круг (с центром в точке 
и интервал (с центром в точке 
1. Например, функция 





2. Радиус сходимости ряда Тейлора можно определить, например, по формуле Даламбера:
.
3. Рассмотрим для примера экспоненциальную функцию 



4. От параметра — точки разложения 
Например, разложим в общем случае (для произвольного 


Можно доказать с помощью формулы суммы геометрической прогрессии, что данный ряд, как функция аргумента 


Действительно,
.
Область сходимости ряда может быть задана неравенством 





Формула Тейлора[править | править код]
Предположим, что функция 









Достаточно легко доказать, что такой многочлен имеет вид 








Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
Теорема:
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).
Различные формы остаточного члена[править | править код]
В форме Лагранжа:
В форме Коши:
В интегральной форме:
Ослабим предположения:
- В асимптотической форме (форме Пеано, локальной форме):
Критерий аналитичности функции[править | править код]
Основной источник: [5]
Предположим, что некоторую функцию 



Во-первых, необходимым условием аналитичности функции является сходимость ряда Тейлора в некоторой непрерывной области. Действительно, если ряд Тейлора сходится всего в одной точке, то это точка 

Во-вторых, по формуле Тейлора в ряд Тейлора с остаточным членом может быть разложена любая (а не только аналитическая) функция, бесконечно дифференцируемая в окрестности, содержащей точку 





Очевидно, что функция 






В качестве примера рассмотрим экспоненциальную функцию 



Остаточный член разложения этой функции в форме Лагранжа имеет вид 



Здесь используется, что на фиксированном промежутке экспонента ограничена некоторым числом 
Причем, как видно, предел остаточного члена равен нулю для любых 

Ряды Маклорена некоторых функций[править | править код]
- Гиперболические функции[6][10]:
- Обратные гиперболические функции[6][11]:
Формула Тейлора для функции двух переменных[править | править код]
Пусть функция 


Введём дифференциальный оператор
.
Тогда разложение (формула Тейлора) функции 



где 
Следует иметь в виду, что операторы 
в 



Аналогичным образом формула строится для функций любого числа переменных, меняется только число слагаемых в операторе 
В случае функции одной переменной 
Формула Тейлора многих переменных[править | править код]
Для получения формулы Тейлора функции 



Тогда разложение (формула Тейлора) функции по степеням 

где 

Для функции 


В другой форме ряд Тейлора можно записать таким образом:

Пример разложения в ряд Маклорена функции трёх переменных[править | править код]
Найдём выражение для разложения в ряд Тейлора функции трёх переменных 




Разложение в ряд Тейлора запишется в виде
Учитывая, что
получим
Например, при 
Примечания[править | править код]
- ↑ Taylor, Brook, Methodus Incrementorum Directa et Inversa [Direct and Reverse Methods of Incrementation] (London, 1715), pages 21-23 (Proposition VII, Theorem 3, Corollary 2). Translated into English in D. J. Struik, A Source Book in Mathematics 1200—1800 (Cambridge, Massachusetts: Harvard University Press, 1969), pages 329—332.
- ↑ Gupta R. C. The Madhava-Gregory series, Math. Education 7 (1973), B67-B70.
- ↑ Запорожец Г. И. «Руководство к решению задач по математическому анализу» — С. 371
- ↑ Н.С. Пискунов. Дифференциальное и интегральное исчисления. — Мифрил, 1996. — С. Том 1, глава 4, параграф 6.
- ↑ Н.С. Пискунов. Дифференциальное и интегральное исчисления для втузов. — тринадцатое. — МОСКВА “НАУКА”, 1985. — С. Том 2, глава 16, параграф 16.
- ↑ 1 2 3 4 5 6 Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. — 4-е изд. — М.: Наука, 1963.
- ↑ Цукер Р. Тригонометрические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 37—43. — 832 с. — 50 000 экз.
- ↑ Цукер Р. Обратные тригонометрические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 44—47. — 832 с. — 50 000 экз.
- ↑ При значении x, близком к 1, эта расчётная формула сходится медленно, т.е. даёт большую погрешность при приближении функции суммой первых нескольких членов ряда. Поэтому можно воспользоваться формулой
где
- ↑ Цукер Р. Гиперболические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 48—49. — 832 с. — 50 000 экз.
- ↑ Цукер Р. Обратные гиперболические функции // Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — С. 50—53. — 832 с. — 50 000 экз.
Литература[править | править код]
- Ильин В. А., Садовничий В. А., Сендов Б. Х. Математический анализ, ч. 1, изд. 3, ред. А. Н. Тихонов. М.: Проспект, 2004.
- Камынин Л. И. Математический анализ. Т. 1, 2. — 2001.
- Киселёв В. Ю., Пяртли А. С., Калугина Т. Ф. Высшая математика. Первый семестр, Интерактивный компьютерный учебник.
- Маркушевич А. И. Теория аналитических функций. В 2 т. — Изд. 2-е. — М.: Наука, 1967. — Т. 1: Начала теории. — 486 с.
- Нарасимхан Р. Анализ на действительных и комплексных многообразиях. — пер. с англ. Е. М. Чирки. — М.: Мир, 1971. — 232 с.
- Петрова С. С., Романовска Д. А. К истории открытия ряда Тэйлора. // Историко-математические исследования. — М.: Наука, 1980. — № 25. — С. 10—24.
- Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов. В 2 т. — Изд. 13-е. — М.: Наука, Главная редакция физико-математической литературы, 1985. — Т. 1. — 432 с.
- Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов. В 2 т. — Изд. 13-е. — М.: Наука, Главная редакция физико-математической литературы, 1985. — Т. 2. — 560 с.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. В 3 т. — Изд. 8-е. — М.: ФИЗМАТЛИТ, 2003. — Т. I. — 680 с. — ISBN ISBN 5-9221-0156-0.
Лекция 16. Ряды Тейлора и Маклорена
16.1. Разложение элементарных
функций в ряды Тейлора и
Маклорена
Покажем,
что если произвольная функция
задана на множестве
, в окрестности точки
имеет множество производных и является
суммой степенного ряда:
,
то
можно найти коэффициенты этого ряда.
Подставим
в степенной ряд
.
Тогда
.
Найдем
первую производную функции
:
При
:
.
Для
второй производной получим:
При
:
.
Продолжая
эту процедуру n
раз получим:
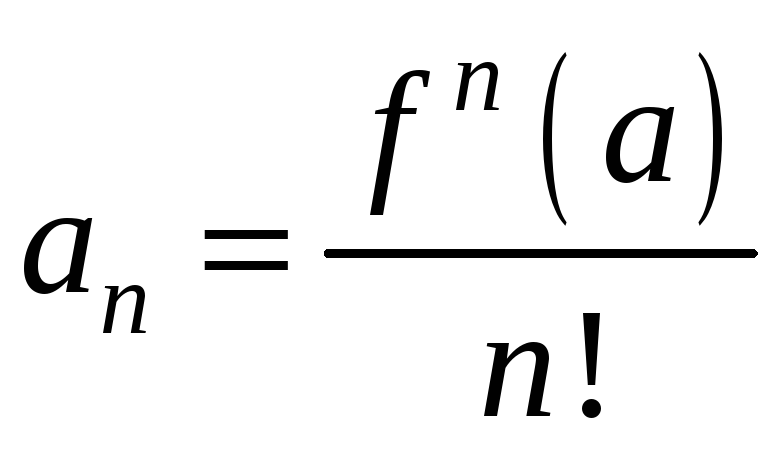
Таким
образом, получили степенной ряд вида:
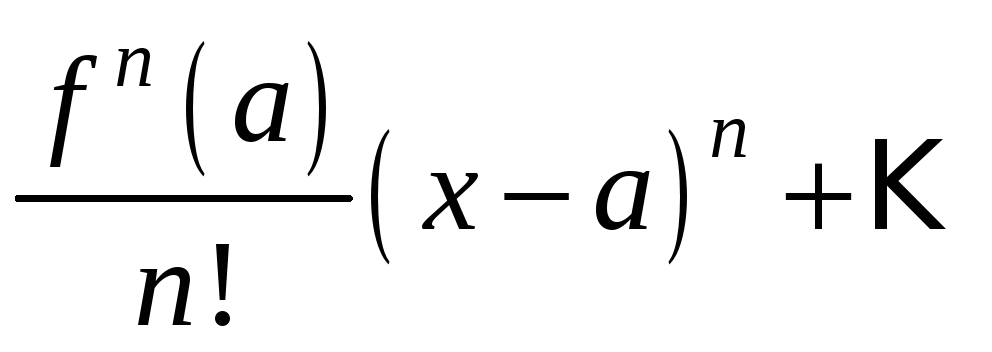
который
называется рядом Тейлора
для функции
в окресности точки
.
Частным
случаем ряда Тейлора является ряд
Маклорена
при
:
Остаток
ряда Тейлора (Маклорена) получается
отбрасыванием от основных рядов n
первых членов и обозначается как
.
Тогда функцию
можно записать как сумму n
первых членов ряда
и остатка
:
,
то
есть
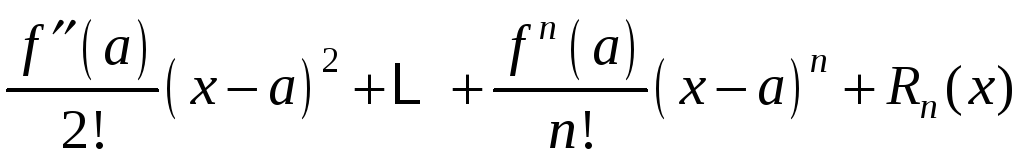
Остаток
обычно
выражают разными формулами.
Одна
из них в форме Лагранжа:
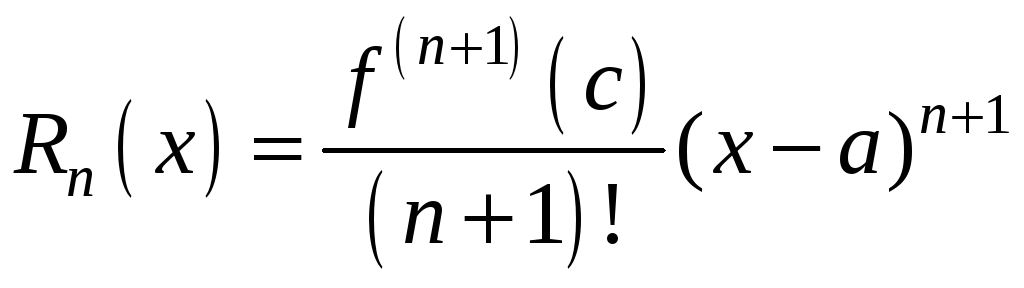
где
.
.
Заметим,
что на практике чаще используется
ряд Маклорена. Таким
образом, для того, чтобы записать функцию
в виде суммы степенного ряда
необходимо:
1)
найти коэффициенты ряда Маклорена
(Тейлора);
2)
найти область сходимости полученного
степенного ряда;
3)
доказать, что данный ряд сходится
к функции
.
Теорема
1
(необходимое и достаточное условие
сходимости ряда Маклорена). Пусть радиус
сходимости ряда
.
Для того, чтобы этот ряд сходился
в интервале
к функции
,
необходимо
и достаточно, чтобы выполнялось условие:
в указанном интервале.
Теорема
2. Если производные любого порядка
функции
в некотором промежутке
ограниченны по абсолютной величине
одним и тем же числом M,
то есть
,
то в этом промежутке функцию
можно разложить в ряд
Маклорена.
Пример
1. Разложить в
ряд Тейлора в окрестности
точки
функцию
.
Решение.
Находим
значение функции и ее производных при
.
,
;
,
;
,
;
,
;
,
………………………………………………………………………………………………………………………
,
;
Подставляем
эти значения в ряд. Получаем:
,
или
.
Область сходимости
.
Пример
2. Разложить
функцию
в ряд Тейлора в окрестности
точки
.
Решение:
Находим
значение функции и ее производных при
.
,
;
,
;
………..……………………………
,
.
Подставляем
эти значения в ряд. Получаем:
или
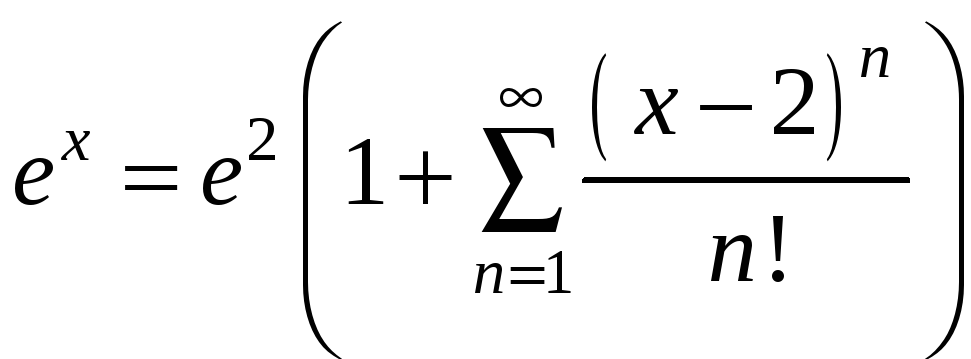
Найдем
область сходимости этого ряда. По
признаку Даламбера ряд сходится,
если
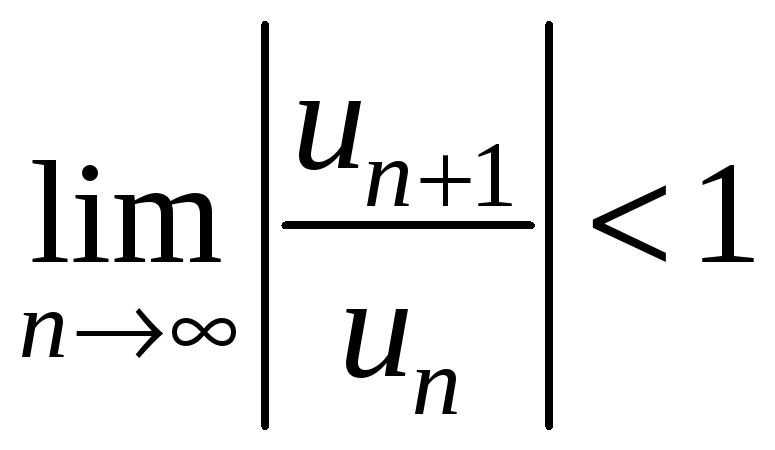
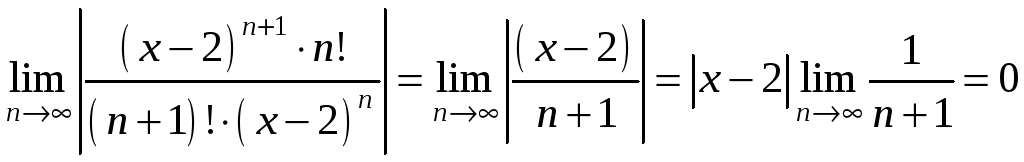
Следовательно,
при любом
этот предел менее 1, а
потому область сходимости ряда будет:
.
Рассмотрим
несколько примеров разложения
в ряд Маклорена основных элементарных
функций. Напомним, что ряд Маклорена:
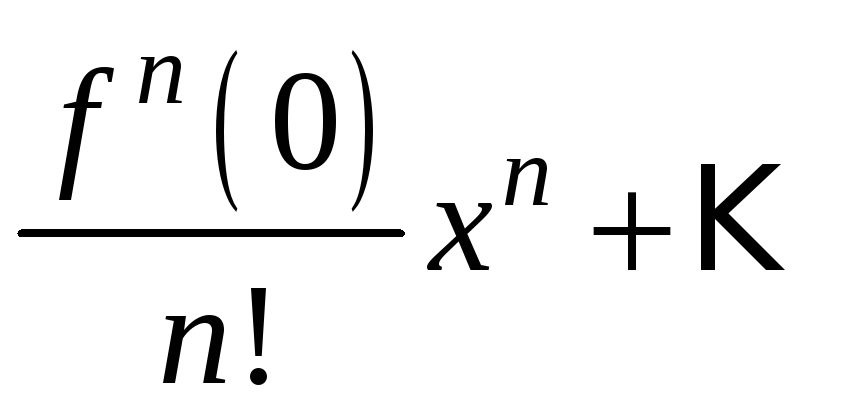
сходится
на интервале
к функции
.
Отметим,
что для разложения функции
в ряд необходимо:
а)
найти коэффициенты ряда Маклорена для
данной функции;
б)
вычислить радиус сходимости
для полученного ряда;
в)
доказать, что полученный ряд сходится
к функции
.
Пример
3. Рассмотрим функцию
.
Решение.
Вычислим
значение функции и ее производных при
.
.
Тогда числовые коэффициенты ряда
имеют вид:
для
любого n. Подставим найденные
коэффициенты в ряд Маклорена и получим:
Найдем
радиус сходимости полученного ряда, а
именно:
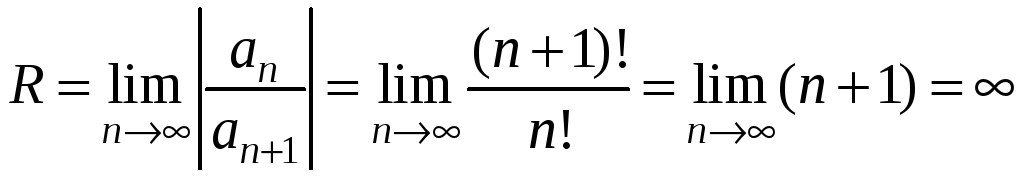
Следовательно,
ряд сходится на
интервале
.
Этот
ряд сходится к функции
при любых значениях
,
потому что на любом
промежутке
функция
и ее производные по
абсолютной величине
ограничены числом
.
Пример
4. Рассмотрим
функцию
.
Решение.
Найдем
значение функции и ее производных при
:
Нетрудно
заметить, что производные четного
порядка,
а производные нечетного
порядка
.
Подставим найденные коэффициенты в ряд
Маклорена и получим
разложение:
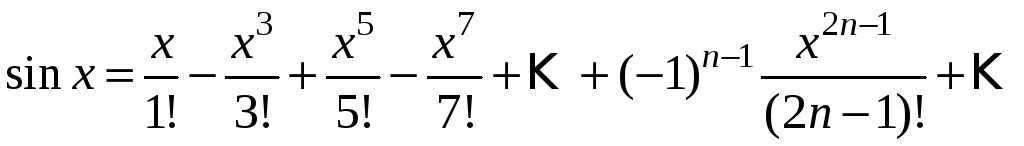
Найдем
интервал сходимости данного ряда. По
признаку Даламбера:
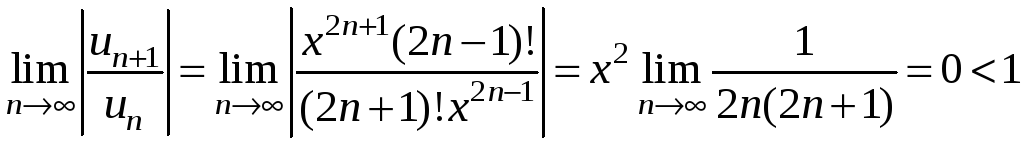
для
любого
.
Следовательно, ряд сходится
на интервале
.
Этот
ряд сходится к функции
,
потому что все ее производные
ограничены единицей.
Пример
5.
.
Решение.
Найдем
значение функции и ее производных при
:
Таким
образом, коэффициенты данного ряда:
и
,
следовательно:
Аналогично
с предыдущим рядом область сходимости
.
Ряд сходится к функции
,
потому что все ее
производные ограничены единицей.
Обратим
внимание, что функция
нечетная и разложение
в ряд по нечетным
степеням, функция
– четная и разложение в ряд по четным
степеням.
Пример
6. Биномиальный
ряд :.
Решение.
Найдем
значение функции и ее производных при
:
Отсюда
видно, что:
Подставим
эти значения коэффициентов в ряд
Маклорена и получим разложение данной
функции в степенной ряд:
Найдем
радиус сходимости этого ряда:
Следовательно,
ряд сходится на интервале
.
В предельных точках при
и
ряд может сходится или нет в зависимости
от показателя степени
.
Исследованный
ряд сходится на интервале
к функции
,
то есть сумма ряда
при
.
Пример
7. Разложим в
ряд Маклорена функцию
.
Решение.
Для
разложения в ряд этой
функции используем биномиальный ряд
при
.
Получим:
На
основе свойства степенных рядов
(степенной ряд можно интегрировать в
области его сходимости) найдем интеграл
от левой и правой частей данного ряда:
Найдем
область сходимости данного ряда:
,
то
есть областью сходимости данного ряда
является интервал
.
Определим сходимость ряда на концах
интервала. При
получим числовой ряд с общим членом
.
Этот ряд является гармоничным рядом,
то есть расходится. При
получим числовой ряд с общим членом
.
Ряд
по признаку Лейбница сходится. Таким
образом, областью сходимости данного
ряда является промежуток
.
16.2. Применение
степенных рядов степеней в приближенных
вычислениях
В
приближенных вычислениях степенные
ряды играют исключительно большую роль.
С их помощью составлены таблицы
тригонометрических функций, таблицы
логарифмов, таблицы значений других
функций, которые используют в разных
областях знаний, например в теории
вероятностей и математической статистике.
Кроме того, разложение
функций в степенной ряд полезно для их
теоретического исследования. Главным
вопросом при использовании степенных
рядов в приближенных вычислениях
является вопрос оценки погрешности при
замене суммы ряда суммой его первых n
членов.
Рассмотрим
два случая:
-
функция
разложена в знакочередующийся ряд; -
функция
разложена в знакопостоянный ряд.
Вычисление с помощью знакочередующихся
рядов
Пусть
функция
разложена в знакочередующийся степенной
ряд. Тогда при вычислении этой функции
для конкретного значения
получаем числовой ряд, к которому можно
применить признак Лейбница. В соответствии
с этим признаком, если сумму ряда заменить
суммой его первых n членов, то
абсолютная погрешность не превышает
первого члена остатка этого ряда, то
есть:.
Пример
8. Вычислить
с точностью до 0,0001.
Решение.
Будем
использовать ряд Маклорена для
,
подставив значение угла в радианах:
Если
сравнить первый и второй члены ряда с
заданной точностью, то:
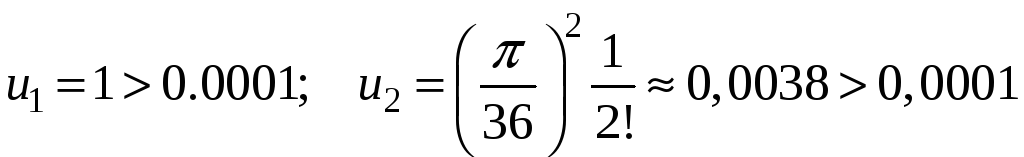
Третий
член разложения:
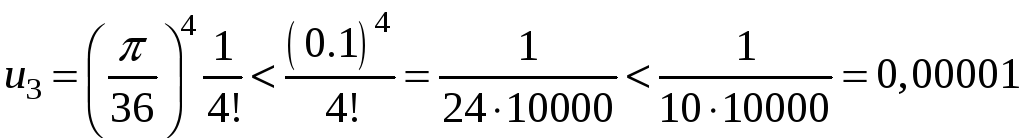
меньше
заданной точности вычисления.
Следовательно, для вычисления
достаточно оставить два члена ряда, то
есть
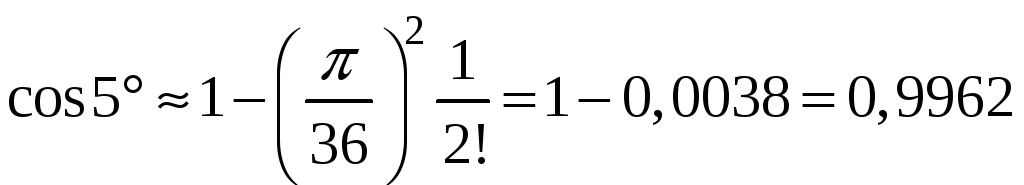
Таким
образом
.
Пример
9. Вычислить
с точностью 0,001.
Решение.
Будем
использовать формулу биномиального
ряда. Для этого запишем
в виде:
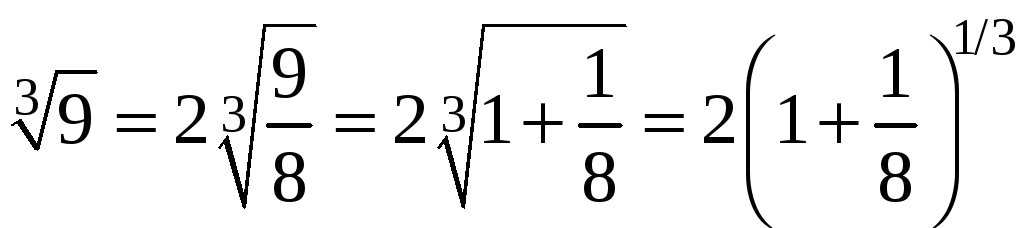
В
этом выражении
,
Сравним
каждый из членов ряда с точностью,
которая задана. Видно, что
.
Следовательно, для вычисления
достаточно оставить три члена ряда.
или
.
Вычисление с помощью
знакоположительных
рядов
Пример
10. Вычислить
число
с точностью до 0,001.
Решение.
В
ряд для функцїї
подставим
.
Получим:
Оценим
погрешность, которая возникает при
замене суммы ряда суммой первых
членов. Запишем очевидное неравенство:
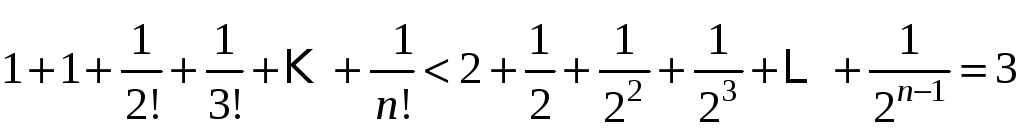
то
есть 2<<3.
Используем формулу остаточного члена
ряда в форме Лагранжа:
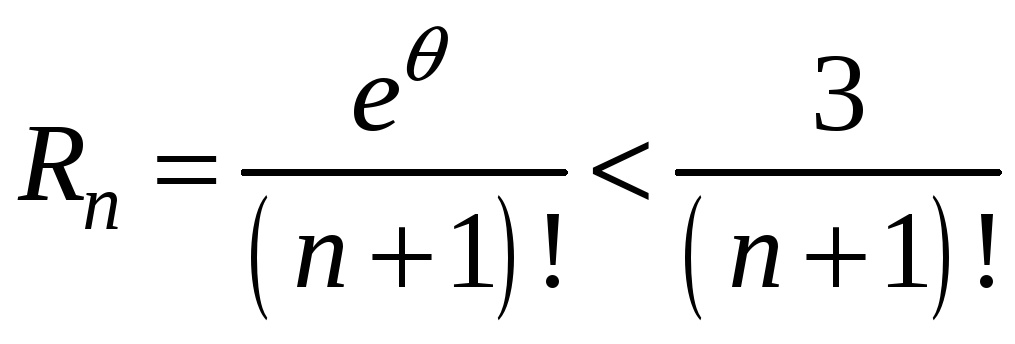
.
По
условию задачи нужно найти n
такое, чтобы выполнялось неравенство:
или
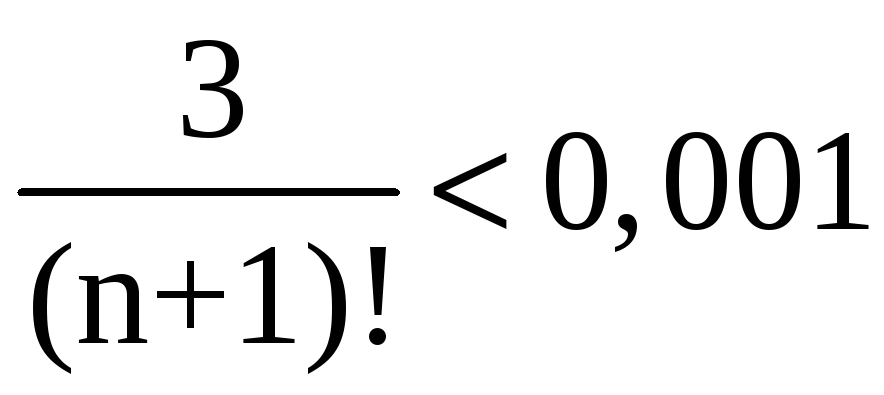
Легко
проверить, что при n
= 6:

Следовательно,
.
Отсюда
Пример
11. Вычислить
с точностью 0,0001.
Решение.
Заметим,
что для вычисления логарифмов можно
было бы применить ряд для функции
,
но этот ряд очень медленно сходится и
для достижения заданной точности нужно
было бы взять 9999 членов! Поэтому для
вычисления логарифмов, как правило,
используется ряд для функции
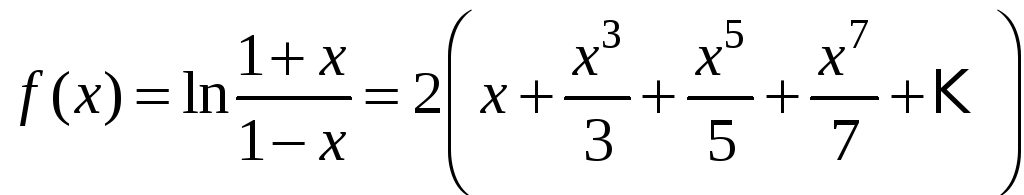
который сходится на интервале
.
Вычислим
с помощью этого ряда. Пусть
,
тогда
.
Следовательно,
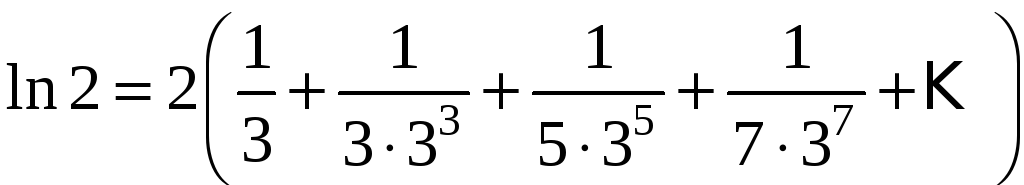
или
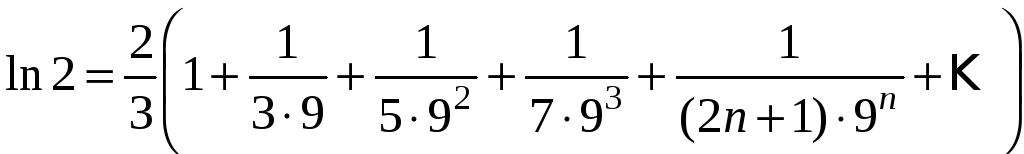
Для
того, чтобы вычислить
с заданной точностью, возьмем сумму
первых четырех членов:
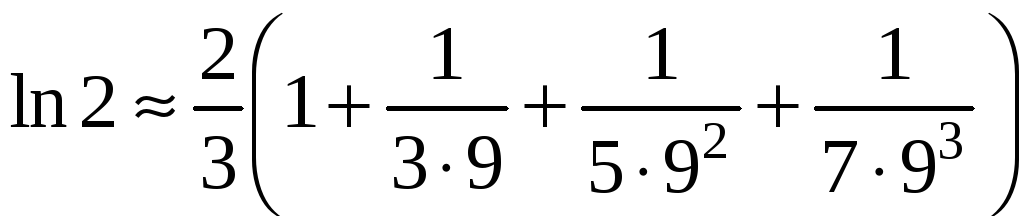
Остаток
ряда
отбросим. Оценим погрешность. Очевидно,
что
или 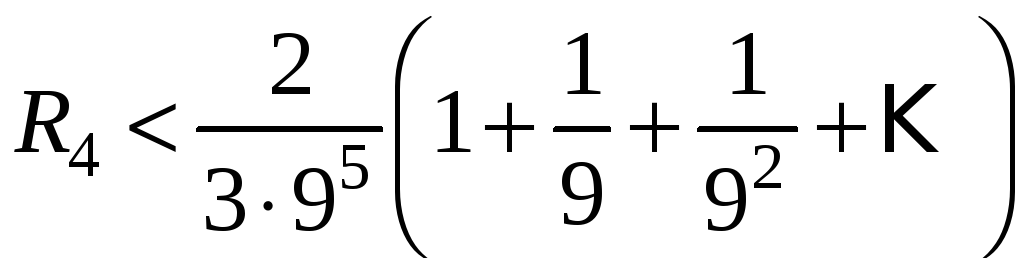
Отсюда
Таким
образом, в ряду, который был использован
для вычисления, достаточно было взять
только четыре первые
слагаемые вместо 9999 в ряду для функции
.
Вопросы для самодиагностики
1.
Что такое ряд Тейлора?
2.
какой вид имеел ряд Маклорена?
3.
Сформулировать теорему о разложении
функции в ряд Тейлора.
4.
Записать разложение в ряд Маклорена
основных функций.
5.
Указать области сходимости рассмотренных
рядов.
6.
Как выполнить оценку погрешности в
приближенных вычислениях с помощью
степенных рядов?
11
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Эта статья будет полезна студентам младших курсов технических направлений и учащимся старших классов, которые собираются принять участие в различных олимпиадах.
В математике часто используется декомпозиция объекта для представления его в другой вид. Например, разложение дробей на рациональные для их интегрирования, разложение матрицы и др. Но в математике также существует разложение многочлена (или функции) в некоторый ряд. Этот ряд называется рядом Тейлора. Что же такое ряд Тейлора? Ряд Тейлора – это представление многочлена (функции) в виде бесконечной суммы степенных функций. В общем виде теорема Тейлора звучит так: если функция f(x) определена и дифференцируема в окрестности некоторой точки x, находящейся на отрезке (a;b), и на этом отрезке функция имеет производную до (n+1)-ого порядка, тогда выполняется бесконечный ряд Тейлора:
Теперь разберемся, что такое ряд Маклорена. Ряд Маклорена – это частный случай ряда Тейлора, при котором x₀ = 0. Давайте разберем для примера некоторую функцию. Пусть эта функция f(x) = 4^x
Вот разложение некоторых элементарных функций в ряд Маклорена:
Содержание:
- Разложение в ряд Маклорена некоторых функций
- Рассмотрим геометрический ряд
- Пример с решением
Предположим, что функция 


Выразим коэффициенты ряда через 


Полагая в полученных равенствах х=0. получим 
Подставляя значения коэффициентов 

По этой ссылке вы найдёте полный курс лекций по высшей математике:
Следует отметить, что не все функции могут быть разложены в рад Маклорена- Может оказаться, что ряд Маклорена, составленный формально для функции 

Так же как и для числовых рядов, сумму
ряда Маклорена можно представить в виде (13.9)
где 

Тогда на основании свойства 4 сходящихся рядов (см. §13.1) можно сформулировать теорему.
Теорема. Для того чтобы ряд Маклорена сходился к функции 


Возможно вам будут полезны данные страницы:
Можно доказать, что если функция 
Замечание. Ряд Маклорена является частным случаем рядо Тейлора
Ряд Тейлора тесно связан с формулой Тейлора:
где 


Очевидно, что при выполнении условия (14.7) остаток 

Разложение в ряд Маклорена некоторых функций
1.
Имеем
По формуле (13.6)


2.
Имеем 


Очевидно, что производные четного порядка 


3. 

4. 





Рад (14.11) называется биномиальным. Если 

5.
Получить разложение для этой функции можно проще, ие вычисляя непосредственно коэффициенты ряда (14.6) с помощью производных.
Рассмотрим геометрический ряд




Интегрируя почленно равенство (14.12) в интервале (0; х), где



Можно доказать, что рады, приведенные в формулах (14.8) — (14.13), сходятся к функциям, для которых они составлены.
При разложении более сложных функций используют непосредственно формулу (14.6) либо таблицу простейших разложений (14.8) – (14.13).
Пример с решением
Разложить в ряд функции:
Решение:
а) Так как по (14.8)
то, заменяя 






Теперь

Лекции:
- Полное приращение и полный дифференциал функции многих переменных
- Производная косинуса
- Решение задачи Коши
- Дифференциальные уравнения
- Алгебраические комплексные числа
- Логарифмы: примеры и решения
- Производная и дифференциал
- Правило Лопиталя: пример решения
- Ряд тейлора примеры решения
- Каноническое уравнение эллипса


















![{displaystyle R_{n}(x)={(x-a)^{n+1} over (n+1)!}f^{(n+1)}[a+theta (x-a)]qquad p=n+1;qquad 0<theta <1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a9581ea19ed64de9723d6f3725f0470e9a0f23c)
![{displaystyle R_{n}(x)={(x-a)^{n+1}(1-theta )^{n} over n!}f^{(n+1)}[a+theta (x-a)]qquad p=1;qquad 0<theta <1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/616cdc3cb043af06990a174a073b35ea0e3fbee1)

![{displaystyle R_{n}(x)=o[(x-a)^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7eca3be3644e41dedb8f25e26357ddb9a08386d)



![R_n(x,y)=dfrac {mathrm{T}^{(n+1)} f(xi,zeta)} {(n+1)!}, xi in [x_0,x], zeta in [y_0,y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/144e134c30b8d4c579305c2bbaf6591647deb6c9)












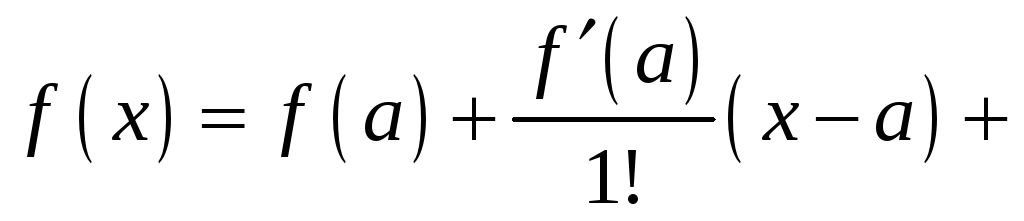
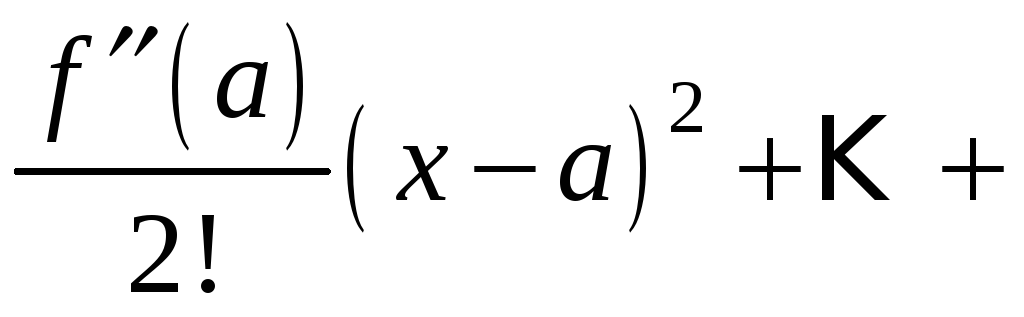
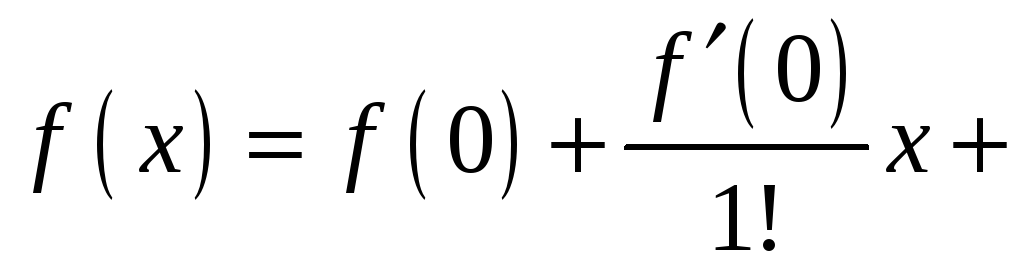
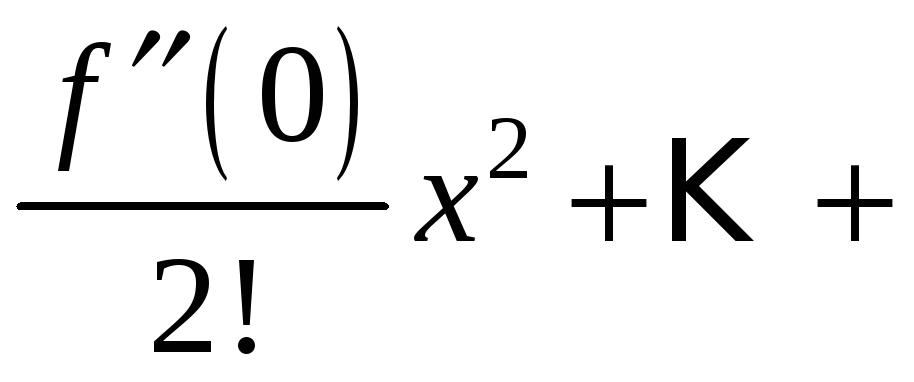
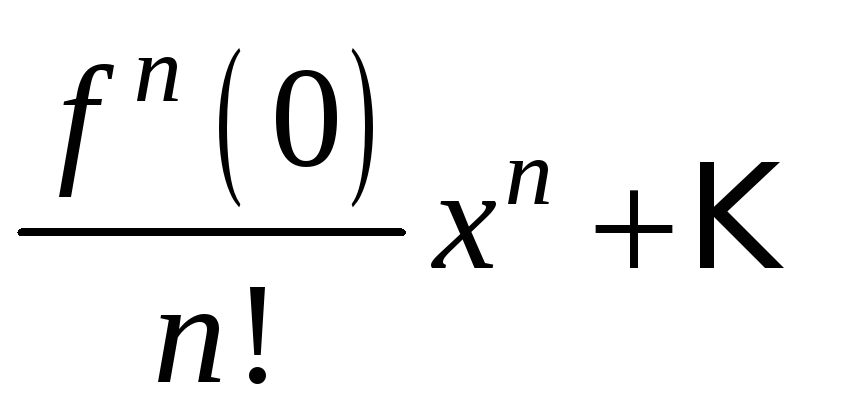
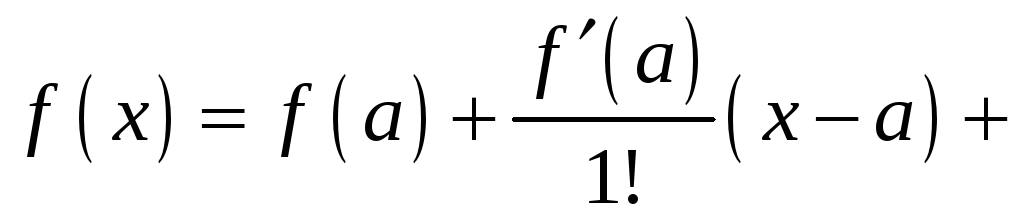
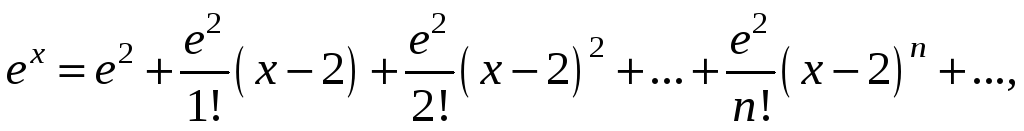
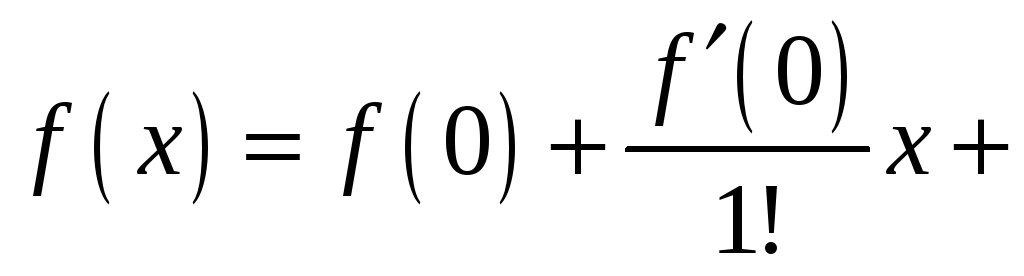
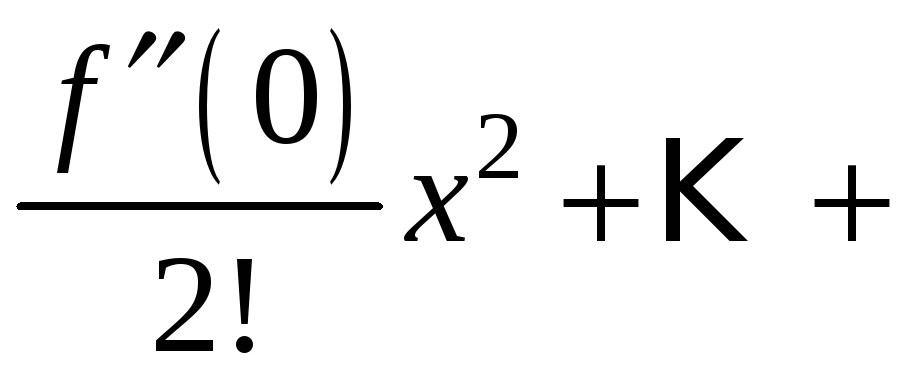
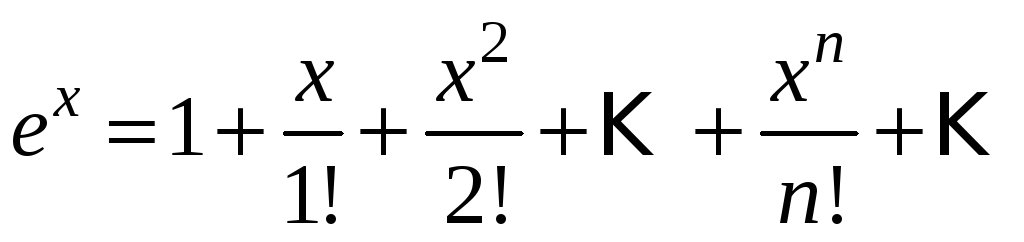
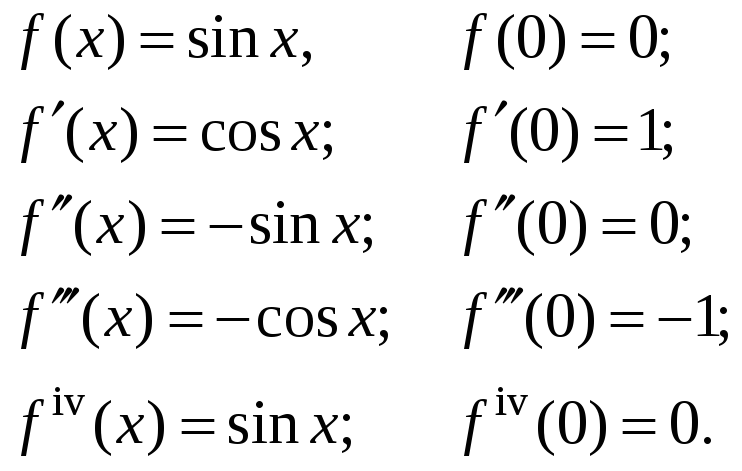
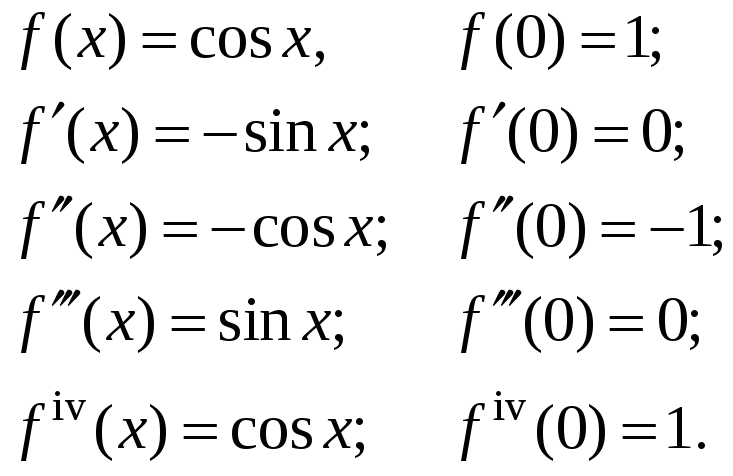
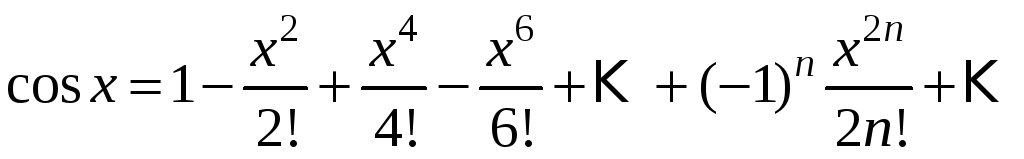
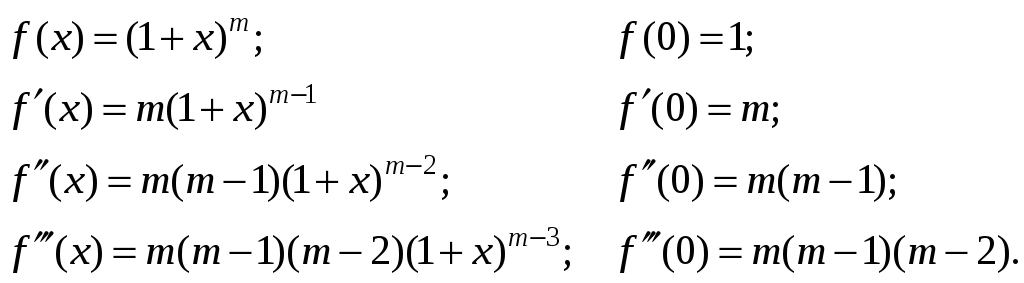

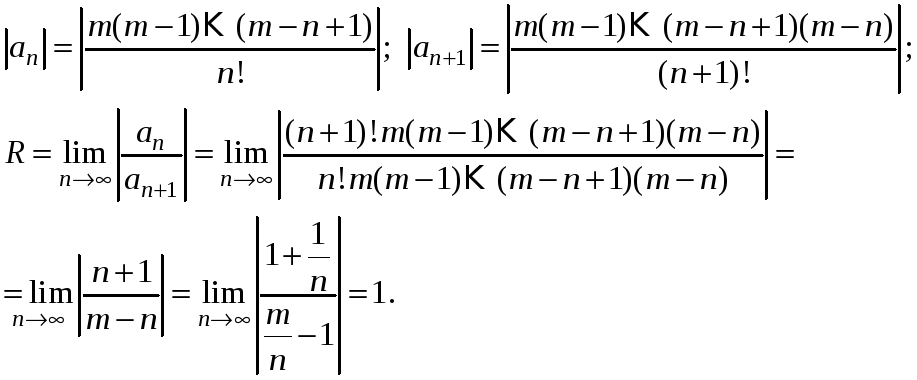
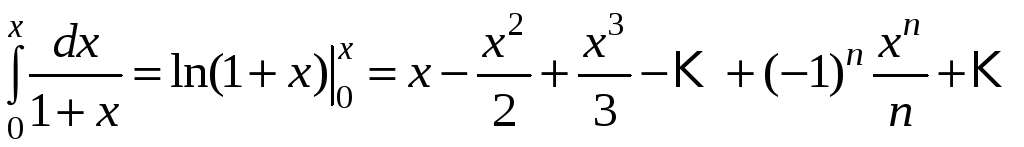
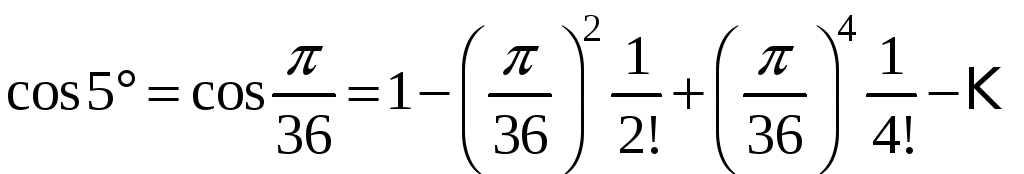
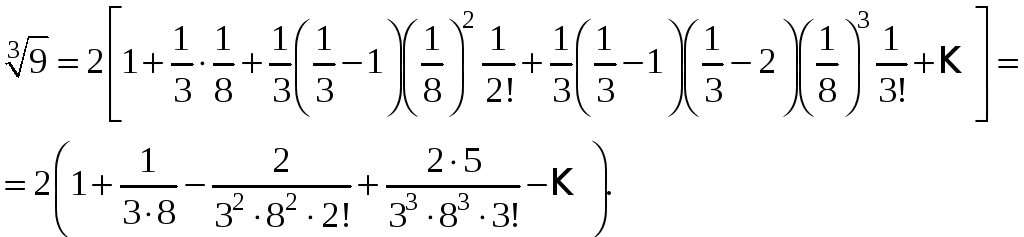
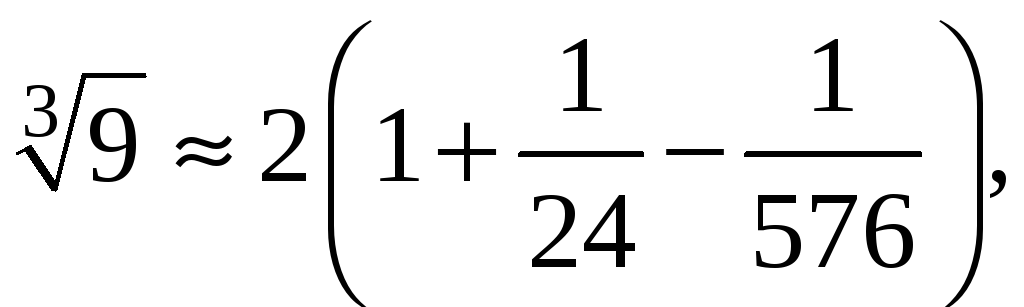
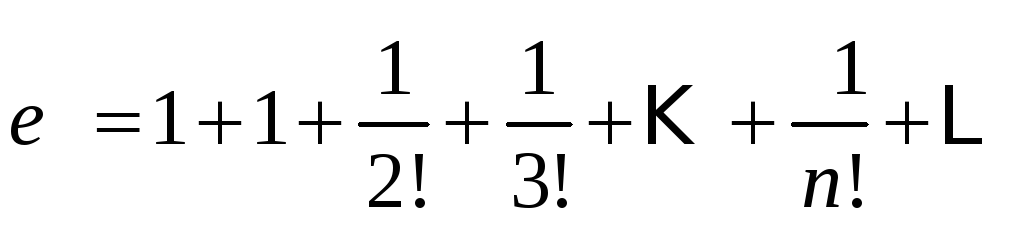
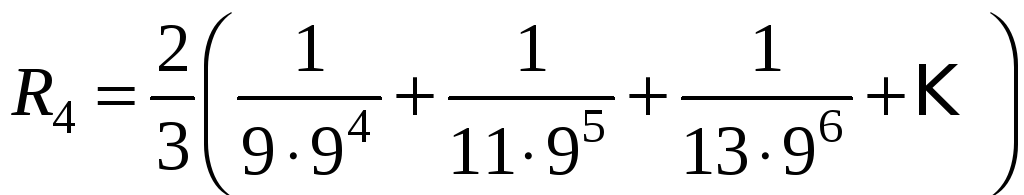
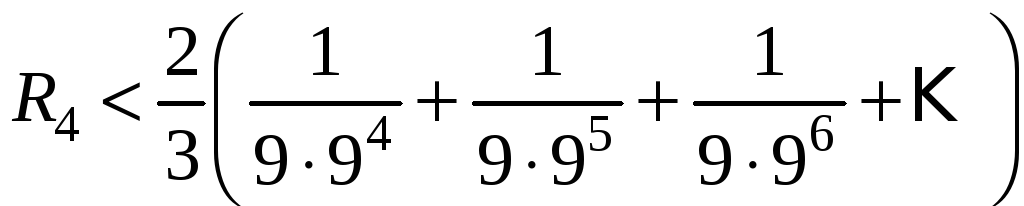
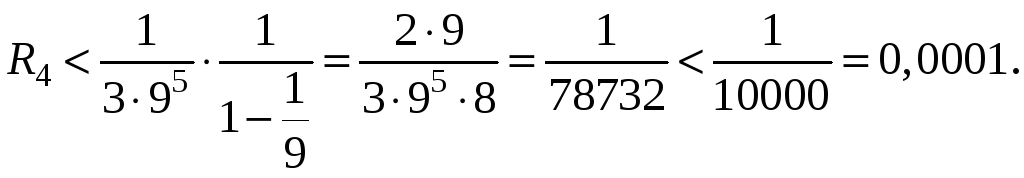



 ряда Маклорена можно представить в виде (13.9)
ряда Маклорена можно представить в виде (13.9)
















