Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом.
Другими словами, последовательность (аn) – арифметическая прогрессия, если для любого натурального числа n выполняется условие аn+1=аn+d, где d – некоторое число. Из данного равенства следует, что можно найти это число d, если вычесть из последующего члена предыдущий, то есть d = аn+1–аn. Число d называют разностью арифметической прогрессии.
Арифметической прогрессией, например, является ряд чисел 3; 8; 13; 18….., так как разница между числами равна 5, мы видим, что каждое последующее на 5 больше предыдущего.
Если известен первый член арифметической прогрессии a1 и разность d, то можно вычислить любой член арифметической прогрессии:
a2 = a1 + d;
a3 = a2 + d = a1+2d;
a4 = a3 + d = a1+3d.
Этот ряд можно продолжать до бесконечности, поэтому надо запомнить, что n-ый член арифметической прогрессии можем получить быстрее, если к первому члену прогрессии добавить (n−1) разностей, то есть:
Формула n-ого члена арифметической прогрессии
an = a1 + d(n−1)
где n – порядковый номер члена арифметической прогрессии, a1 – первый член прогрессии, d – разность арифметической прогрессии
Формулу используют, чтобы вычислить заданный член арифметической прогрессии (например, пятнадцатый, двухсотый и т.д.), если известны первый член последовательности и ее разность. Рассмотрим на примерах применение данной формулы.
Пример №1. Найти а20 арифметической прогрессии (аn), если а1=14, d=5. Составляем формулу для а20 и подставляем в нее данные: а20= a1 + d(20−1)=14+5(20−1)=109. Таким образом, мы вычислили, что на 20-ом месте в данной арифметической прогрессии стоит число 109.
Найти а7 арифметической прогрессии (аn), если а1=−8, d=−3. Аналогично работаем, составляя формулу и подставляя в нее данные значения (обращаем внимание на знаки чисел, чтобы не допустить ошибок): а7= a1 + d(7−1)= −8−3(7−1)= −26.
Дана арифметическая прогрессия 10; 12; 14;…… Найти а12. Здесь для нахождения а12 надо сначала найти разность d: d=12−10=2, то есть из последующего вычтем предыдущее. Можно было 14−12, порядок здесь не имеет значения, главное берем два соседних члена прогрессии. Теперь можем составлять формулу и находить а12: а12= a1 + d(12−1)=10+2(12−1)=32.
Утверждение
Любая арифметическая прогрессия может быть задана формулой вида an=kn+b, где k и b некоторые числа. Верно и обратное утверждение: если последовательность чисел задана формулой вида an=kn+b, где k и b некоторые числа, то она является арифметической.
Так, например, формула an=5n+1 задает арифметическую прогрессию, в которой разность d равна 1; по данной формуле можно найти любой член последовательности, например, найдем 20-ый член, подставляя в формулу число 20: a20=5×20+1=101.
Свойство арифметической прогрессии
Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предыдущего и последующего членов. Формула:
аn=(аn-1+ аn+1):2
Другими словами, используя данное свойство, мы можем найти член арифметической прогрессии, стоящий между двумя известными членами, без использования разности d. Рассмотрим это на примерах.
Пример №2. Найти а10 арифметической прогрессии (аn), если а9=24; а11=38. Здесь используем свойство, так как видим, что у а10 известны соседние члены. Значит, а10=(а9+а11):2=(24+38):2=31. Таким образом, десятый член равен 31.
Дана арифметическая прогрессия …..23; х; 35. Найти х. Применяем свойство для нахождения х: х=(23+35):2=29. Для наглядности запишем, что ряд чисел выглядит так: …23; 29; 35.
Формулы суммы n первых членов арифметической прогрессии
Для нахождения суммы (обозначим ее буквой S) большого количества членов арифметической прогрессии существует формула, позволяющая это сделать быстро.
Формула суммы членов арифметической прогрессии с известными членами
Sn=
(a1+an
)n2
В данной формуле мы видим, что для нахождения суммы нужны первый и последний член прогрессии. Но встречаются случаи, когда аn не известно, но известна разность. Тогда для нахождения суммы применяют вторую формулу.
Формула суммы членов арифметической прогрессии с первым членом и разностью
Sn=2a1+d(n−1)2n
Рассмотрим на примерах применение данных формул.
Пример №3. Найти сумму первых пятидесяти членов арифметической прогрессии (аn), если а1=11, а50=39.
Для решения лучше использовать первую формулу, так как здесь есть первый и последний члены: а1=11, а50=39. Поэтому составляем формулу, подставляем в нее данные значения и вычисляем:
S50=(a1+a50
)502=(11+39)502=25002=1250
Найти сумму первых десяти членов арифметической последовательности 3; 18; …. В данном случае задание можно выполнить двумя способами, как по первой формуле, так и по второй, а затем выяснить, какой способ короче, а значит, рациональнее.
Способ №1 (по первой формуле): надо найти разность d, затем десятый член прогрессии, а затем сумму:
d=18-3=15; а10=3+15(10-1)=138
S10=(a1+a10
)102=(3+138)102=705
Способ №2 (по второй формуле): надо знать разность d, d=18-3=15. Теперь подставим значения во вторую формулу и сосчитаем результат:
S10=2a1+d(10−1)210=2×3+15(10−1)210=705
Результаты в обоих случаях получились у нас одинаковые. А если сравнить два способа, то видно, что второй способ быстрее, тем более что в большинстве случаев разность арифметической прогрессии можно вычислить устно.
Таким образом, выбор формулы для нахождения суммы n первых членов арифметической прогрессии зависит от заданного условия.
Задание OM1420223
Миша решил заказать себе такси. Подача машины и первые пять минут поездки в совокупности стоят 159 рублей, а стоимость каждой последующей минуты поездки фиксирована. Стоимость поездки с 6 по 15 минуту (включительно) составила 80 рублей, а с 6 по 25 минуту – 160 рублей. Найти итоговую стоимость поездки, если она длилась 1 час.
Выпишем, что мы имеем по условию задачи в левый столбец, а в правый запишем то, что из этого следует
| Известно | Решение |
| Подача и первые 5 минут – 159 руб | – |
| Стоимость с 6 по 15 минуту – 80 рублей
Стоимость с 6 по 25 минуту – 160 рублей. |
Разница во времени 10 минут стоит 80 руб |
| Значит, 1 минута стоит 8 руб (80:10=8) | |
| 1 час – ? руб | 1 час=60 мин; убираем 5 минут, которые включены в подачу машины, значит, надо найти стоимость 55 минут: 55•8=440 руб
Прибавляем стоимость подачи: 440+159=599 рублей |
Ответ: 599
pазбирался: Даниил Романович | обсудить разбор
Задание OM1420221
В амфитеатре 12 рядов. В первом ряду 18 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?
Из условия задачи видно, что имеем дело с арифметической прогрессией, так как сказано, что в каждом следующем на 2 места больше, чем в предыдущем.
Выписываем, что нам известно и определяем, что нужно найти: всего 12 рядов, значит n=12; в первом ряду 18 мест, значит, а1=18; так как в каждом последующем ряду мест на 2 больше, то разность арифметической прогрессии d=2. Надо найти, сколько всего мест в амфитеатре, т.е. найти сумму арифметической прогрессии S12.
Для нахождения суммы имеем формулу Sn=a1+an2×n, то есть для нашей задачи S12=a1+a122×12. У нас нет а12, найдем его по формуле n-ого члена арифметической прогрессии: a12=a1+d(n-1)=18+2(12-1)=18+22=40. Подставим данные в формулу суммы:
S12=18+402×12=348
Следовательно, 348 мест всего в амфитеатре.
Проверка: можно проверить решение следующим способом, просто прибавляя по 2 места в каждый ряд до 12-ого, а затем сложить количество мест. Записать можно так: 18+20+22+24+26+28+30+32+34+36+38+40=348. Этим же способом, кстати, можно решить задачу, если от волнения забыли про арифметическую прогрессию.
Ответ: 348
pазбирался: Даниил Романович | обсудить разбор
Задание 14OM21R
При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 80С. Найдите температуру вещества (в градусах Цельсия) через 6 минут после начала проведения опыта, если его начальная температура составляла -60С.
Можно решить данную задачу логическим путем, т.е. без формулы. Так как начальная температура была -6, а потом уменьшалась на 8 градусов в течение 6 минут, то можно сделать следующее:
-6-8=-14 через 1 минуту
-14-8=-22 через 2 минуты
-22-8=-30 через 3 минуты
-30-8=-38 через 4 минуты
-38-8=-46 через 5 минут
-46-8=-54 через 6 минут
Значит, наш ответ -540С
Вторым способом является решение по формуле n-ого члена арифметической прогрессии, которая есть также и в справочном материале, т.е. an=a1+d(n – 1). В данном случае a1=-6; d=-8, n=7 (так как ЧЕРЕЗ 6 минут). Подставим значения в формулу: a7=-61-8(7 – 1). Вычислим: a6=-6-8∙5=-6-48=-54.
Ответ: -54
pазбирался: Даниил Романович | обсудить разбор
Задание OM1407
К концу 2008 года в городе проживало 38100 человек. Каждый год число жителей города возрастало на одну и ту же величину. В конце 2016 года в городе проживало 43620 человек. Какова была численность населения этого города к концу 2012 года?
Содержание данной задачи говорит нам о том, что здесь есть арифметическая прогрессия, так как число жителей города возрастало на одну и ту же величину.
Рассмотрим данные:
2008 г – 38100 человек
2012 г – ? человек
2016 г. – 43620 человек
Удобно решить данную задачу способом по формуле связи между любыми двумя членами арифметической прогрессии: d=an−akk−n , где k>n. Число d (разность прогрессии) будет являться ежегодным приростом населения.
Итак, можно вычислить прирост населения с 2008 по 2016 ежегодно:
(43620 – 38100):(2016 – 2008)= 5520:8=690 человек.
Теперь можно найти, сколько человек проживало в конце 2012 года.
38100+690(2016 – 2012)= 40860 человек
Ответ: 40860
pазбирался: Даниил Романович | обсудить разбор
Задание OM1406
Митя играет в компьютерную игру. Он начинает с 0 очков, а для перехода на следующий уровень ему нужно набрать не менее 30000 очков. После первой минуты игры добавляется 2 очка, после второй – 4 очка, после третьей – 8 очков и так далее. Таким образом, после каждой следующей минуты игры количество добавляемых очков удваивается. Через сколько минут Митя перейдет на следующий уровень?
Анализируя содержание задачи, можно сказать, что мы имеем дело с геометрической прогрессией, так как после первой минуты игры добавляется 2 очка, после второй – 4 очка, после третьей – 8, а это значит, что с каждой последующей минутой количество очков удваивается. То есть знаменатель геометрической прогрессии q равен 2, b1=2 по условию (после 1 минуты 2 очка). Так как очки суммируются, то будем использовать формулу суммы n первых членов геометрической прогрессии Sn=b1(qn−1)q−1, где Sn>30000, так как для перехода на следующий уровень ему нужно набрать не менее 30000 очков.
Подставляем наши данные в формулу: 2(2n−1)2−1>30000
Упрощаем выражение: так как в знаменателе дроби получается 1, то получим 2(2n-1)>30000; делим обе части на 2: 2n-1>15000; переносим 1 в правую часть и получим: 2n>15001. Теперь надо подобрать число n, при котором будет верно наше неравенство. Делать это можно постепенно, возводя 2 в степени, а можно запомнить, что 210=1024. Тогда легко будет добраться до числа, которое меньше 15001, а это 214=16384, где 16384<15001. Следовательно, наш ответ 14 минут.
Ответ: 14
pазбирался: Даниил Романович | обсудить разбор
Задание OM1405
В течение 25 банковских дней акции компании дорожали ежедневно на одну и ту же сумму. Сколько стоила акция компании в последний день этого периода, если в 7-й день акция стоила 777 рублей, а в 12-й день – 852 рубля?
В содержании задачи есть фраза, что акции дорожали ежедневно на одну и ту же сумму, следовательно, имеем арифметическую прогрессию. Итак, определяем, что известно: в 7-й день акция стоила 777 рублей, это а7=777; в 12-й день – 852 рубля, это а12=852. Известно, что акции дорожали 25 дней, а найти надо стоимость акции в последний, т.е. в 25-ый день, значит, будем искать а25.
1 способ:
В данной арифметической прогрессии нет первого члена, не идет речь про сумму, поэтому воспользуемся формулой аn=ak+d(n – k), где n>k. Числа n и k – это порядковые номера. Составим формулу для наших данных и подставим в неё значения: а12=а7+d(12-7); 852=777+d(12 – 7). Упростим выражение и найдем разность d, 852–777= d(12 – 7); 75= d∙5; отсюда d=75:5=15. Итак, мы нашли, что акции ежедневно дорожали на 15 рублей.
Теперь, зная число d, мы можем найти а25 через, например, а12, используя всё ту же формулу. Получаем: а25=а12+d(25-12); а25=852+15(25-12)=852+15∙13= 852+195=1047. Значит, 1047 рублей стоила акция в последний день.
2 способ:
Можно решить данную задачу другим способом по формуле связи между любыми двумя членами арифметической прогрессии: d=an−akk−n , где k>n. Составим формулу для наших а12 и а7, а затем подставим в нее данные: d=a12−a712−7; d=852−77712−7=15. Теперь по этой же формуле найдем а25, связывая его с а12: d=a25−a1225−12; 15=a25−85213; найдем отсюда а25, а25=15∙13+852=1047.
Ответ: 1047
pазбирался: Даниил Романович | обсудить разбор
Задание OM1404
Грузовик перевозит партию щебня массой 176 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что в первый день было перевезено 6 тонн щебня. Определите, сколько тонн щебня было перевезено в последний день, если вся работа была выполнена за 11 дней.
В условии задачи встречаются слова, что норма увеличивалась на одно и то же число. И это значит, что мы имеем арифметическую прогрессию, в которой а1=6, так как в первый день перевезли 6 тонн. Далее, известно, что вся работа была выполнена за 11 дней, значит число n=11. Так как масса всего щебня равна 176, то это число является суммой нашей прогрессии, т.е. S11=176. Требуется найти, сколько тонн было перевезено в последний день, а он – 11, значит, найти надо а11.
Итак, если нам встретилась сумма арифметической прогрессии, значит, нам надо воспользоваться формулой суммы n первых членов арифметической прогрессии Sn=а1+аn2∙n, куда мы и подставим все данные: 176=6+а112∙11.
Разделим обе части на 11, получим 16= 6+а112 ; умножим 16 на 2 (правило пропорции): 32=6+а11. Отсюда найдем а11=32–6=26. Итак, мы нашли, что 26 тонн щебня было перевезено в последний день.
Ответ: 26
pазбирался: Даниил Романович | обсудить разбор
Задание OM1403
Для получения витамина D могут быть рекомендованы солнечные ванны. Загорать лучше утром до 10 часов или вечером после 17 часов. Михаилу назначили курс солнечных ванн. Михаил начинает курс с 15 минут в первый день и увеличивает время этой процедуры в каждый следующий день на 15 минут. В какой по счету день продолжительность процедуры достигнет 1 часа 15 минут?
Из содержания данной задачи видно, что время процедуры увеличивалось с каждым днем на одно и то же количество времени – на 15 минут, следовательно, это арифметическая прогрессия. Так как в первый день курс был 15 минут, то а1=15; так как время ежедневно увеличивалось на 15 минут, то значит разность d=15; зная, что продолжительность процедуры должна достигнуть 1 ч 15 мин, т.е. достигнуть 75 минут (1 час=60 мин, плюс 15 минут), то это число 75 и будет являться n членом арифметической прогрессии. Требуется найти, в какой по счету день продолжительность процедуры достигнет этих 75 минут, т.е. найдем число n.
Теперь берем формулу n члена арифметической прогрессии аn=a1+d(n – 1) и подставляем в неё наши данные: 75=15+15(n – 1); упростим данное выражение: 75-15=15(n – 1); 60=15(n – 1); разделим на 15 обе части: 4=n – 1; найдем отсюда, что n=5. Таким образом, на пятый день продолжительность процедуры достигнет 75 минут.
Ответ: 5
pазбирался: Даниил Романович | обсудить разбор
Задание OM1402
Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же расстояние меньше, чем в предыдущий день. Известно, что за первый и последний дни улитка проползла в сумме 7,5 метров. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 60 метрам.
Анализируя содержание задачи, мы видим, что улитка проползала ежедневно на одно и то же расстояние меньше, чем в предыдущий день. А это значит, что имеем арифметическую прогрессию. По условию определяем данные: так как в первый и последний дни она проползла 7,5 м, то имеем, что а1+аn=7,5. Так как расстояние между деревьями равно 60 м, то имеем сумму n первых членов прогрессии, т.е. Sn=60. Так как найти надо количество дней, которое она потратила на весь путь, то искомым числом будет число n.
Зная формулу суммы n первых членов арифметической прогрессии
Sn=а1+аn2∙n, имеем 60=7,5 ∙ n2. Отсюда находим n, умножая сначала 60 на 2 (по определению пропорции), затем 120 делим на 7,5 и получаем, что n=16. Таким образом, улитка потратила на весь путь 16 дней.
Ответ: 16
pазбирался: Даниил Романович | обсудить разбор
Задание OM1401
При проведении химической реакции в растворе образуется нерастворимый осадок. Наблюдения показали, что каждую минуту образуется 0,2 г осадка. Найдите массу осадка (в граммах) в растворе спустя семь минут после начала реакции.
При анализе содержания задачи мы видим, что каждую минуту количество осадка увеличивается на одно и то же число, на 0,2 г. А это значит, что имеем арифметическую прогрессию, в которой первый член равен 0,2, так как по условию в первую минуту образовалось 0,2 г осадка. Разность арифметической прогрессии равна также 0,2, так как каждую минуту на это количество увеличивается количество осадков. Найти нужно седьмой член последовательности.
Итак, имеем а1=0,2; d=0,2. Ищем а7. По определению n-ого члена арифметической прогрессии имеем формулу аn=a1+d(n – 1). Подставим в нее наши данные: а7=a1+d(7 – 1)=0,2+0,2·6=1,4
Ответ: 1,4
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 8.1k
Skip to content
В этом руководстве показано, как использовать ИНДЕКС и ПОИСКПОЗ в Excel и чем они лучше ВПР.
В нескольких недавних статьях мы приложили немало усилий, чтобы объяснить основы функции ВПР новичкам и предоставить более сложные примеры формул ВПР опытным пользователям. А теперь я постараюсь если не отговорить вас от использования ВПР, то хотя бы показать вам альтернативный способ поиска нужных значений в Excel.
- Краткий обзор функций ИНДЕКС и ПОИСКПОЗ
- Как использовать формулу ИНДЕКС ПОИСКПОЗ
- ИНДЕКС+ПОИСКПОЗ вместо ВПР?
- Поиск справа налево
- Двусторонний поиск в строках и столбцах
- ИНДЕКС ПОИСКПОЗ для поиска по нескольким условиям
- Как найти среднее, максимальное и минимальное значение
- Что делать с ошибками поиска?
Для чего это нужно? Потому что функция ВПР имеет множество ограничений, которые могут помешать вам получить желаемый результат во многих ситуациях. С другой стороны, комбинация ПОИСКПОЗ ИНДЕКС более гибкая и имеет много замечательных возможностей, которые во многих отношениях превосходят ВПР.
Функции Excel ИНДЕКС и ПОИСКПОЗ — основы
Поскольку целью этого руководства является демонстрация альтернативного способа выполнения поиска в Excel с использованием комбинации функций ИНДЕКС и ПОИСКПОЗ, мы не будем подробно останавливаться на их синтаксисе и использовании. Тем более, что это подробно рассмотрено в других статьях, ссылки на которые вы можете найти в конце этого руководства. Мы рассмотрим лишь минимум, необходимый для понимания общей идеи, а затем подробно рассмотрим примеры формул, раскрывающие все преимущества использования ПОИСКПОЗ и ИНДЕКС вместо ВПР.
Функция ИНДЕКС
Функция ИНДЕКС (в английском варианте – INDEX) возвращает значение в массиве на основе указанных вами номеров строк и столбцов. Синтаксис функции ИНДЕКС прост:
ИНДЕКС(массив,номер_строки,[номер_столбца])
Вот простое объяснение каждого параметра:
- массив – это диапазон ячеек, именованный диапазон или таблица.
- номер_строки — это номер строки в массиве, из которого нужно вернуть значение. Если этот аргумент опущен, требуется следующий – номер_столбца.
- номер_столбца — это номер столбца, из которого нужно вернуть значение. Если он опущен, требуется номер_строки.
Дополнительные сведения см. в статье Функция ИНДЕКС в Excel .
А вот пример формулы ИНДЕКС в самом простом виде:
=ИНДЕКС(A1:C10;2;3)
Формула выполняет поиск в ячейках с A1 по C10 и возвращает значение ячейки во 2-й строке и 3-м столбце, т. е. в ячейке C2.
Очень легко, правда? Однако при работе с реальными данными вы вряд ли когда-нибудь будете заранее знать, какие строки и столбцы вам нужны. Здесь вам пригодится ПОИСКПОЗ.
Функция ПОИСКПОЗ
Она ищет нужное значение в диапазоне ячеек и возвращает относительное положение этого значения в диапазоне.
Синтаксис функции ПОИСКПОЗ следующий:
ПОИСКПОЗ(искомое_значение, искомый_массив, [тип_совпадения])
- искомое_значение — числовое или текстовое значение, которое вы ищете.
- диапазон_поиска – диапазон ячеек, в которых будем искать.
- тип_совпадения — указывает, следует ли искать точное соответствие или наиболее близкое совпадение:
- 1 или опущено — находит наибольшее значение, которое меньше или равно искомому значению. Требуется сортировка массива поиска в порядке возрастания.
- 0 — находит первое значение, точно равное искомому значению. В комбинации ИНДЕКС/ПОИСКПОЗ вам почти всегда нужно точное совпадение, поэтому вы чаще всего устанавливаете третий аргумент вашей функции в 0.
- -1 — находит наименьшее значение, которое больше или равно искомому значению. Требуется сортировка массива поиска в порядке убывания.
Например, если диапазон B1:B3 содержит значения «яблоки», «апельсины», «лимоны», приведенная ниже формула возвращает число 3, поскольку «лимоны» — это третья по счету запись в этом диапазоне:
=ПОИСКПОЗ(“лимоны”;B1:B3;0)
Дополнительные сведения см . в статье Функция ПОИСКПОЗ в Excel .
На первый взгляд полезность функции ПОИСКПОЗ может показаться сомнительной. Кого волнует положение значения в диапазоне? Что мы действительно хотим определить, так это само значение.
Однако, относительная позиция искомого значения (т. е. номера строки и столбца, в которых оно находится) — это именно то, что нам нужно указать для аргументов номер_строки и номер_столбца функции ИНДЕКС. Как вы помните, ИНДЕКС может найти значение на пересечении заданной строки и столбца, но сама не может определить, какую именно строку и столбец ей нужно выбрать.
Вот поэтому совместное использование ИНДЕКС и ПОИСКПОЗ открывает перед нами массу возможностей для поиска в Excel.
Как использовать формулу ИНДЕКС ПОИСКПОЗ в Excel
Теперь, когда вы знаете основы, я считаю, что вы уже начали понимать, как ПОИСКПОЗ и ИНДЕКС работают вместе. Короче говоря, ИНДЕКС извлекает нужное значение по номерам столбцов и строк, а ПОИСКПОЗ предоставляет ей эти номера. Вот и все!
Для вертикального поиска вы используете функцию ПОИСКПОЗ только для определения номера строки, указывая диапазон столбцов непосредственно в самой формуле:
ИНДЕКС ( столбец для возврата значения ; ПОИСКПОЗ ( искомое значение ; столбец для поиска ; 0))
Все еще не совсем понимаете эту логику? Возможно, будет проще разобрать на примере. Предположим, у вас есть список национальных столиц и их население:

Чтобы найти население определенной столицы, скажем, Индии, используйте следующую формулу ПОИСКПОЗ ИНДЕКС:
=ИНДЕКС(C2:C10; ПОИСКПОЗ(“Индия”;A2:A10;0))
Теперь давайте проанализируем, что на самом деле делает каждый компонент этой формулы:
- Функция ПОИСКПОЗ ищет искомое значение “Индия” в диапазоне A2:A10 и возвращает число 2, поскольку это слово занимает второе место в массиве поиска.
- Этот номер поступает непосредственно в аргумент номер_строки функции ИНДЕКС, предписывая вернуть значение из этой строки.
Таким образом, приведенная выше формула превращается в ИНДЕКС(C2:C10;2), которая означает, что нужно искать в ячейках от C2 до C10 и извлекать значение из второй ячейки в этом диапазоне, то есть из C3, потому что мы начинаем отсчет со второй строки.
Но указывать название города в формуле не совсем правильно, так как для каждого нового поиска придется корректировать эту формулу. Введите его в какую-нибудь отдельную ячейку, скажем, F1, укажите ссылку на ячейку для ПОИСКПОЗ, и вы получите формулу динамического поиска:
=ИНДЕКС(C2:C10;ПОИСКПОЗ(F1;A2:A10;0))

Важное замечание! Количество строк в аргументе массив функции ИНДЕКС должно совпадать с количеством строк в аргументе просматриваемый_массив в ПОИСКПОЗ, иначе формула выдаст неверный результат.
Вы спросите: «А почему бы нам просто не использовать обычную формулу ВПР? Какой смысл тратить время на то, чтобы разобраться в хитросплетениях ИНДЕКС ПОИСКПОЗ в Excel?»
Вот как это будет выглядеть:
=ВПР(F1; A2:C10; 3; 0)
Конечно, так проще. Но этот наш элементарный пример предназначен только для демонстрационных целей, чтобы вы поняли, как именно функции ИНДЕКС и ПОИСКПОЗ работают вместе. Действительно, ВПР была бы здесь более уместна. Другие примеры, которые вы найдёте ниже, покажут вам реальную силу этой комбинации, которая легко справляется со многими сложными задачами, когда ВПР будет бессильна.
ИНДЕКС+ПОИСКПОЗ вместо ВПР?
Решая, какую функцию использовать для вертикального поиска, большинство знатоков Excel сходятся во мнении, что ПОИСКПОЗ+ИНДЕКС намного лучше, чем ВПР. Однако многие до сих пор остаются с ВПР, во-первых, потому что это проще, а, во-вторых, потому что они не до конца понимают все преимущества использования формулы ПОИСКПОЗ ИНДЕКС в Excel. Без такого понимания никто не захочет тратить свое время на изучение более сложного синтаксиса.
Ниже я укажу на ключевые преимущества ИНДЕКС ПОИСКПОЗ перед ВПР, а уж вам решать, является ли это достойным дополнением к вашему арсеналу знаний в Excel.
4 основные причины использовать ИНДЕКС ПОИСКПОЗ вместо ВПР
- Поиск справа налево. Как известно любому образованному пользователю, ВПР не может искать влево. Это означает, что искомое значение всегда должно находиться в крайнем левом столбце таблицы. А извлекать нужное значение мы будем из столбца, который находится правее. ИНДЕКС+ПОИСКПОЗ может легко выполнять поиск влево! Здесь это показано в действии: Как выполнить поиск значения слева в Excel .
- Можно безопасно вставлять или удалять столбцы. Формулы ВПР не работают или выдают неверные результаты, когда новый столбец удаляется из таблицы поиска или добавляется в нее, поскольку синтаксис ВПР требует указания порядкового номера столбца, из которого вы хотите извлечь данные. Естественно, когда вы добавляете или удаляете столбцы, этот номер в формуле автоматически не меняется, а нужный столбец уже оказывается на новом месте.
С функциями ИНДЕКС и ПОИСКПОЗ вы указываете диапазон возвращаемых столбцов, а не номер одного из них. В результате вы можете вставлять и удалять столько столбцов, сколько хотите, не беспокоясь об обновлении каждой связанной с ними формулы.
- Нет ограничений на размер искомого значения. При использовании функции ВПР общая длина ваших критериев поиска не может превышать 255 символов, иначе вы получите ошибку #ЗНАЧ!. Таким образом, если ваш набор данных содержит длинные строки, ИНДЕКС ПОИСКПОЗ — единственное работающее решение.
- Более высокая скорость обработки. Если ваши таблицы относительно небольшие, вряд ли будет какая-то существенная разница в производительности Excel. Но если ваши рабочие листы содержат сотни или тысячи строк и, следовательно, сотни или тысячи формул, ИНДЕКС ПОИСКПОЗ будет работать намного быстрее, чем ВПР. Причина в том, что Excel будет обрабатывать только столбцы поиска и возврата, а не весь массив таблицы.
Влияние ВПР на производительность Excel может быть особенно заметным, если ваша книга содержит сложные формулы массива. Чем больше значений содержит ваш массив и чем больше формул массива содержится в книге, тем медленнее работает Excel.
ИНДЕКС ПОИСКПОЗ в Excel – примеры формул
Уяснив, почему все же стоит изучать ИНДЕКС ПОИСКПОЗ, давайте перейдем к самому интересному и посмотрим, как можно применить теоретические знания на практике.
Формула для поиска справа налево
Как уже упоминалось, ВПР не может получать значения слева от столбца поиска. Таким образом, если ваши значения поиска не находятся в самом левом столбце, нет никаких шансов, что формула ВПР принесет вам желаемый результат. Функция ПОИСКПОЗ ИНДЕКС в Excel более универсальна и не имеет особого значения, где расположены столбцы поиска и возврата.
Для этого примера мы добавим столбец «Ранг» слева от нашей основной таблицы и попытаемся выяснить, какое место занимает столица России по численности населения среди других перечисленных столиц.
Записав искомое значение в G1, используйте следующую формулу для поиска в C2:C10 и возврата соответствующего значения из A2:A10:
=ИНДЕКС(A2:A10; ПОИСКПОЗ(G1;C2:C10;0))

Совет. Если вы планируете использовать формулу ПОИСКПОЗ ИНДЕКС более чем для одной ячейки, обязательно зафиксируйте оба диапазона абсолютными ссылками (например, $A$2:$A$10 и $C$2:$C$10), чтобы они не изменялись при копировании формулы.
Двусторонний поиск в строках и столбцах
В приведенных выше примерах мы использовали ИНДЕКС ПОИСКПОЗ вместо классической функции ВПР, чтобы вернуть значение из точно указанного столбца. Но что, если вам нужно искать в нескольких строках и столбцах? То есть, сначала нужно найти подходящий столбец, а уж потом извлечь из него значение? Другими словами, что, если вы хотите выполнить так называемый матричный или двусторонний поиск?
Это может показаться сложным, но формула очень похожа на базовую функцию ПОИСКПОЗ ИНДЕКС в Excel, но с одним отличием.
Просто используйте две функции ПОИСКПОЗ, вложенных друг в друга: одну – для получения номера строки, а другую – для получения номера столбца.
ИНДЕКС(массив; ПОИСКПОЗ(значение_поиска1 ; столбец_поиска ; 0); ПОИСКПОЗ(значение_поиска2 ; столбец_поиска ; 0))
А теперь, пожалуйста, взгляните на приведенную ниже таблицу и давайте составим формулу двумерного поиска, чтобы найти население (в миллионах) в данной стране за данный год.
С целевой страной в G1 (значение_поиска1) и целевым годом в G2 (значение_поиска2) формула принимает следующий вид:
=ИНДЕКС(B2:D11; ПОИСКПОЗ(G1;A2:A11;0); ПОИСКПОЗ(G2;B1:D1;0))

Как работает эта формула?
Всякий раз, когда вам нужно понять сложную формулу Excel, разделите ее на более мелкие части и посмотрите, что делает каждая отдельная функция:
ПОИСКПОЗ(G1;A2:A11;0); – ищет в A2:A11 значение из ячейки G1 («США») и возвращает его позицию, которая равна 3.
ПОИСКПОЗ(G2;B1:D1;0) – просматривает диапазон B1:D1, чтобы получить позицию значения из ячейки G2 («2015»), которая равна 3.
Найденные выше номера строк и столбцов становятся соответствующими аргументами функции ИНДЕКС:
ИНДЕКС(B2:D11, 3, 3)
В результате вы получите значение на пересечении 3-й строки и 3-го столбца в диапазоне B2:D11, то есть из D4. Несложно?
ИНДЕКС ПОИСКПОЗ для поиска по нескольким условиям
Если у вас была возможность прочитать наши материалы по ВПР в Excel, вы, вероятно, уже протестировали формулу для ВПР с несколькими условиями . Однако существенным недостатком этого подхода является необходимость добавления вспомогательного столбца. Хорошей новостью является то, что функция ПОИСКПОЗ ИНДЕКС в Excel также может выполнять поиск по нескольким условиям без изменения или реструктуризации исходных данных!
Вот общая формула ИНДЕКС ПОИСКПОЗ с несколькими критериями:
{=ИНДЕКС( диапазон_возврата; ПОИСКПОЗ (1; ( критерий1 = диапазон1 ) * ( критерий2 = диапазон2 ); 0))}
Примечание. Это формула массива , которую необходимо вводить с помощью сочетания клавиш Ctrl + Shift + Enter.
Предположим, что в таблице ниже вы хотите найти значение на основе двух критериев: Покупатель и Товар.
Следующая формула ИНДЕКС ПОИСКПОЗ отлично работает:
=ИНДЕКС(C2:C10; ПОИСКПОЗ(1; (F1=A2:A10) * (F2=B2:B10); 0))
Где C2:C10 — это диапазон, из которого возвращается значение, F1 — это критерий1, A2:A10 — это диапазон для сравнения с критерием 1, F2 — это критерий 2, а B2:B10 — это диапазон для сравнения с критерием 2.
Не забудьте правильно ввести формулу, нажав Ctrl + Shift + Enter, и Excel автоматически заключит ее в фигурные скобки, как показано на скриншоте ниже:

Рис5
Если вы не хотите использовать формулы массива, добавьте в формулу в F4 еще одну функцию ИНДЕКС и завершите ее ввод обычным нажатием Enter:
=ИНДЕКС(C2:C10; ПОИСКПОЗ(1; ИНДЕКС((F1=A2:A10) * (F2=B2:B10); 0; 1); 0))
Разберем пошагово, как это работает.
Здесь используется тот же подход, что и в обычном сочетании ИНДЕКС ПОИСКПОЗ, где просматривается один столбец. Чтобы оценить несколько критериев, вы создаете два или более массива значений ИСТИНА и ЛОЖЬ, которые представляют совпадения и несовпадения для каждого отдельного критерия, а затем перемножаете соответствующие элементы этих массивов. Операция умножения преобразует ИСТИНА и ЛОЖЬ в 1 и 0 соответственно и создает массив, в котором единицы соответствуют строкам, которые удовлетворяют всем условиям. Функция ПОИСКПОЗ со значением поиска 1 находит первую «1» в массиве и передает ее позицию в ИНДЕКС, которая возвращает значение в этой позиции из указанного столбца.
Вторая формула без массива основана на способности функции ИНДЕКС работать с массивами. Второй вложенный ИНДЕКС имеет 0 в номер_строки , так что он будет передавать весь массив столбцов в ПОИСКПОЗ.
Среднее, максимальное и минимальное значение при помощи ИНДЕКС ПОИСКПОЗ
Microsoft Excel имеет специальные функции для поиска минимального, максимального и среднего значения в диапазоне. Но что, если вам нужно получить значение из другой ячейки, связанной с этими значениями? Например, получить название города с максимальным населением или узнать товар с минимальными продажами? В этом случае используйте функцию МАКС , МИН или СРЗНАЧ вместе с ИНДЕКС ПОИСКПОЗ.
Максимальное значение.
Предположим, нам нужно в списке городов найти столицу с самым большим населением. Чтобы найти наибольшее значение в столбце С и вернуть соответствующее ему значение из столбца В, находящееся в той же строке, используйте эту формулу:
=ИНДЕКС(B2:B10; ПОИСКПОЗ(МАКС(C2:C10); C2:C10; 0))
Скриншот с примером находится чуть ниже.
Минимальное значение
Теперь найдём город с самым маленьким населением в списке. Чтобы найти наименьшее число в столбце С и получить соответствующее ему значение из столбца В:
=ИНДЕКС(B2:B10; ПОИСКПОЗ(МИН(C2:C10); C2:C10; 0))
Ближайшее к среднему
Теперь мы находим город, население которого наиболее близко к среднему значению. Чтобы вычислить позицию, наиболее близкую к среднему значению показателя, рассчитанному из D2:D10, и получить соответствующее значение из столбца C, используйте следующую формулу:
=ИНДЕКС(B2:B10; ПОИСКПОЗ(СРЗНАЧ(C2:C10); C2:C10; -1 ))
В зависимости от того, как организованы ваши данные, укажите 1 или -1 для третьего аргумента (тип_совпадения) функции ПОИСКПОЗ:
- Если ваш столбец поиска (столбец D в нашем случае) отсортирован по возрастанию , поставьте 1. Формула вычислит наибольшее значение, которое меньше или равно среднему значению.
- Если ваш столбец поиска отсортирован по убыванию , введите -1. Формула вычислит наименьшее значение, которое больше или равно среднему значению.
- Если ваш массив поиска содержит значение , точно равное среднему, вы можете ввести 0 для точного совпадения. Никакой сортировки не требуется.
В нашем примере данные в столбце D отсортированы в порядке убывания, поэтому мы используем -1 для типа соответствия. В результате мы получаем «Токио», так как его население (13 189 000) является ближайшим, превышающим среднее значение (12 269 006).

Что делать с ошибками поиска?
Как вы, наверное, заметили, если формула ИНДЕКС ПОИСКПОЗ в Excel не может найти искомое значение, она выдает ошибку #Н/Д. Если вы хотите заменить это стандартное сообщение чем-то более информативным, оберните формулу ПОИСКПОЗ ИНДЕКС в функцию ЕСНД . Например:
=ЕСНД(ИНДЕКС(C2:C10; ПОИСКПОЗ(F1;A2:A10;0)); “Не найдено”)
И теперь, если кто-то вводит значение, которое не существует в диапазоне поиска, формула явно сообщит пользователю, что совпадений не найдено:

Если вы хотите перехватывать все ошибки, а не только #Н/Д, используйте функцию ЕСЛИОШИБКА вместо ЕСНД:
=ЕСЛИОШИБКА(ИНДЕКС(C2:C10; ПОИСКПОЗ(F1;A2:A10;0)); “Что-то пошло не так!”)
Пожалуйста, имейте в виду, что во многих ситуациях было бы не совсем правильно скрывать все такие ошибки, потому что они предупреждают вас о возможных проблемах в вашей формуле.
Итак, еще раз об основных преимуществах формулы ИНДЕКС ПОИСКПОЗ.
-
Возможен ли “левый” поиск?
-
Повлияет ли на результат вставка и удаление столбцов?
Вы можете вставлять и удалять столько столбцов, сколько хотите. На результат ИНДЕКС ПОИСКПОЗ это не повлияет.
-
Возможен ли поиск по строкам и столбцам?
Можно сначала найти подходящий столбец, а уж потом извлечь из него значение. Общий вид формулы:
ИНДЕКС(массив; ПОИСКПОЗ(значение_поиска1 ; столбец_поиска ; 0); ПОИСКПОЗ(значение_поиска2 ; столбец_поиска ; 0))
Подробную инструкцию смотрите здесь. -
Как сделать поиск ИНДЕКС ПОИСКПОЗ по нескольким условиям?
Можно выполнять поиск по двум или более условиям без добавления дополнительных столбцов. Вот формула массива, которая решит проблему:
{=ИНДЕКС( диапазон_возврата; ПОИСКПОЗ (1; ( критерий1 = диапазон1 ) * ( критерий2 = диапазон2 ); 0))}
Вот как можно использовать ИНДЕКС и ПОИСКПОЗ в Excel. Я надеюсь, что наши примеры формул окажутся полезными для вас.
Вот еще несколько статей по этой теме:
ВВЕДЕНИЕ
Методическое пособие предназначено для
преподавателей математики в техникумах, а также
для студентов второго курса, всех
специальностей.
В данной работе излагаются основные понятия
теории рядов. Теоретический материал
соответствует требованиям Государственного
образовательного стандарта среднего
профессионального образования (Министерство
образования Российской Федерации. М., 2002г.).
Изложение теоретического материала по всей
теме сопровождается рассмотрением большого
количества примеров и задач, ведется на
доступном, по-возможности строгом языке. В конце
пособия приведены примеры и задания, которые
студенты могут выполнять в режиме самоконтроля.
Пособие предназначено для студентов заочной и
дневной форм обучения.
Учитывая уровень подготовки учащихся
техникума, а также крайне ограниченное число
часов (12 часов + 4 ф.), отводимое программой для
прохождения высшей математики в техникумах,
строгие выводы, представляющие большие
трудности для усвоения, опущены, ограничиваясь
рассмотрением примеров.
ОСНОВНЫЕ ПОНЯТИЯ
Решение задачи, представленной в
математических терминах, например, в виде
комбинации различных функций, их производных и
интегралов, нужно уметь “довести до числа”,
которое чаще всего и служит окончательным
ответом. Для этого в различных разделах
математики выработаны различные методы.
Раздел математики, позволяющий решить любую
корректно поставленную задачу с достаточной для
практического использования точностью,
называется теорией рядов.
Даже если некоторые тонкие понятия
математического анализа появились вне связи с
теорией рядов, они немедленно применялись к
рядам, которые служили как бы инструментом для
испытания значимости этих понятий. Такое
положение сохраняется и сейчас.
Выражение вида
![]() ,
,
где ![]() ;
;![]() ;
;![]() ;…;
;…;![]() ;… – члены ряда;
;… – члены ряда; ![]() – n-ый или общий член
– n-ый или общий член
ряда, называется бесконечным рядом (рядом).
Если члены ряда :
- числа, то ряд называется числовым;
- числа одного знака, то ряд называется
знакопостоянным; - числа разных знаков, то ряд называется
знакопеременным; - положительные числа, то ряд называется
знакоположительным; - числа, знаки которых строго чередуются, то ряд
называется знакочередующимся; - функции, то ряд называется функциональным;
- степени
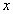 , то ряд
, то ряд
называется степенным; - тригонометрические функции, то ряд называется
тригонометрическим.
I. Числовой ряд
1.1. Основные понятия числового ряда.
Числовым рядом называется сумма вида
![]() , (1.1)
, (1.1)
где ![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…, называемые членами ряда,
,…, называемые членами ряда,
образуют бесконечную последовательность; член![]() называется
называется
общим членом ряда.
Суммы
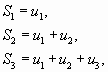
…………..
![]() ,
,
составленные из первых членов ряда (1.1),
называются частичными суммами этого ряда.
Каждому ряду можно сопоставить
последовательность частичных сумм ![]() .
.
Если при бесконечном возрастании номера n
частичная сумма ряда ![]() стремится к пределу
стремится к пределу![]() , то ряд называется сходящимся, а
, то ряд называется сходящимся, а
число ![]() –
–
суммой сходящегося ряда, т.е.
![]() и
и ![]() .
.
Эта запись равносильна записи
![]() .
.
Если частичная сумма ![]() ряда (1.1) при неограниченном
ряда (1.1) при неограниченном
возрастании n не имеет конечного предела
(стремится к ![]()
или ![]() ), то
), то
такой ряд называется расходящимся.
Если ряд сходящийся, то значение ![]() при достаточно
при достаточно
большом n является приближенным
выражением суммы ряда S.
Разность ![]()
называется остатком ряда. Если ряд сходится, то
его остаток стремится к нулю, т.е.![]() , и наоборот, если остаток
, и наоборот, если остаток
стремится к нулю, то ряд сходится.
1.2. Примеры числовых рядов.
Пример 1. Ряд вида
![]() (1.2)
(1.2)
называется геометрическим ![]() .
.
Геометрический ряд образован из членов
геометрической прогрессии.
Известно, что сумма её первых n членов ![]() . Очевидно: это n-ая
. Очевидно: это n-ая
частичная сумма ряда (1.2).
Возможны случаи:
![]() :
:
![]() .
.
Ряд (1.2) принимает вид:
![]() ,
,
![]() , ряд
, ряд
расходится;
![]()
Ряд (1.2) принимает вид:
![]() ,
,
![]()
![]() не имеет
не имеет
предела, ряд расходится.
![]() ,
,
![]() – конечное
– конечное
число, ряд сходится.
![]() ,
,
![]() – ряд
– ряд
расходится.
Итак, данный ряд сходится при ![]() и расходится при
и расходится при ![]() .
.
Пример 2. Ряд вида
![]() (1.3)
(1.3)
называется гармоническим.
Запишем частичную сумму этого ряда:
![]() .
.
Сумма ![]() больше суммы,
больше суммы,
представленной следующим образом:
![]()
или ![]() .
.
Если ![]() , то
, то ![]() , или
, или ![]() .
.
Следовательно, если ![]() , то
, то ![]() ,
,
т.е. гармонический ряд расходится.
Пример 3. Ряд вида
![]() (1.4)
(1.4)
называется обобщенным гармоническим.
Если ![]() , то
, то
данный ряд обращается в гармонический ряд,
который является расходящимся.
Если ![]() , то
, то
члены данного ряда больше соответствующих
членов гармонического ряда и, значит, он
расходится. При ![]() имеем геометрический ряд, в котором
имеем геометрический ряд, в котором ![]() ; он является
; он является
сходящимся.
Итак, обобщенный гармонический ряд сходится
при ![]() и
и
расходится при ![]() .
.
1.3. Необходимый и достаточные признаки
сходимости.
Необходимый признак сходимости ряда.
Ряд ![]() может
может
сходиться только при условии, что его общий член ![]() при
при
неограниченном увеличении номера ![]() стремится к нулю:
стремится к нулю: ![]() .
.
Если ![]() , то
, то
ряд ![]()
расходится – это достаточный признак
расходимости ряда.
Достаточные признаки сходимости ряда с
положительными членами.
Признак сравнения рядов с положительными
членами.
Исследуемый ряд сходится, если его члены не
превосходят соответствующих членов другого,
заведомо сходящегося ряда; исследуемый ряд
расходится, если его члены превосходят
соответствующие члены другого, заведомо
расходящегося ряда.
Признак Даламбера.
Если для ряда с положительными членами
![]()
![]()
выполняется условие ![]() , то ряд сходится при
, то ряд сходится при ![]() и расходится при
и расходится при ![]() .
.
Признак Даламбера не дает ответа, если ![]() . В этом случае
. В этом случае
для исследования ряда применяются другие приемы.
Упражнения.
Записать ряд по его заданному общему члену:
![]() ;
;
![]() ;
;
![]() .
.
Решение.
Полагая ![]() ,
,![]() ,
,![]() ,…, имеем бесконечную
,…, имеем бесконечную
последовательность чисел:
![]() ,
,![]() ,
,![]() . Сложив его члены, получим
. Сложив его члены, получим
ряд
![]() .
.
Поступая так же, получим ряд
![]() .
.
Придавая![]() значения
значения
1,2,3,… и учитывая, что![]() ,
,![]() ,
,![]() ,…, получим ряд
,…, получим ряд
![]() .
.
Найти n-ый член ряда по его данным первым
членам:
![]() ;
;
![]() .
.
Решение.
Знаменатели членов ряда, начиная с первого,
являются четными числами; следовательно, n-ый
член ряда имеет вид ![]() .
.
Числители членов ряда образуют натуральный ряд
чисел, а соответствующие им знаменатели –
натуральный ряд чисел, а соответствующие им
знаменатели – натуральный ряд чисел, начиная с 3.
Знаки чередуются по закону ![]() или по закону
или по закону ![]() . Значит, n-й член ряда
. Значит, n-й член ряда
имеет вид ![]() .
.![]() или
или ![]() .
.
Исследовать сходимость ряда, применяя
необходимый признак сходимости и признак
сравнения:
![]() ;
;
![]() ;
;
![]() .
.
Решение.
Находим ![]() .
.
Необходимый признак сходимости ряда
выполняется, но для решения вопроса о сходимости
нужно применить один из достаточных признаков
сходимости. Сравним данный ряд с геометрическим
рядом
![]() ,
,
который сходится, так как![]() .
.
Сравнивая члены данного ряда, начиная со
второго, с соответствующими членами
геометрического ряда, получим неравенства
![]()
т.е. члены данного ряда, начиная со второго,
соответственно меньше членов геометрического
ряда, откуда следует, что данный ряд сходится.
Имеем
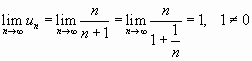 .
.
Здесь выполняется достаточный признак
расходимости ряда; следовательно, ряд
расходится.
Находим ![]() .
.
Необходимый признак сходимости ряда
выполняется. Сравним данный ряд с обобщенным
гармоническим рядом
![]() ,
,
который сходится, поскольку![]() , следовательно, сходится и
, следовательно, сходится и
данный ряд.
Исследовать сходимость ряда, используя признак
Даламбера:
![]() ;
;
![]()
![]() .
.
Решение.
Подставив в общий член ряда ![]() вместо n число n+1, получим
вместо n число n+1, получим
![]() . Найдем
. Найдем
предел отношения ![]() -го члена к n-му члену при
-го члена к n-му члену при ![]() :
:
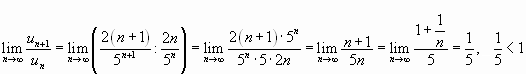 .
.
Следовательно, данный ряд сходится.
Имеем
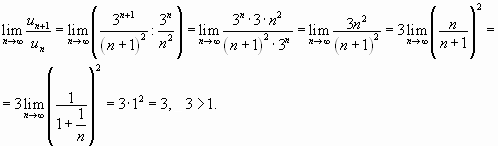
Значит, данный ряд расходится.
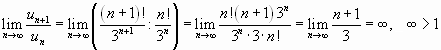 , т.е. ряд
, т.е. ряд
расходится.
II. Знакопеременный ряд
2.1 Понятие знакопеременного ряда.
Числовой ряд
![]()
называется знакопеременным, если среди
его членов имеются как положительные, так и
отрицательные числа.
Числовой ряд называется знакочередующимся,
если любые два стоящие рядом члена имеют
противоположные знаки.
![]() ,
,
где ![]() для
для
всех ![]() (т.е. ряд,
(т.е. ряд,
положительные и отрицательные члены которого
следуют друг за другом поочередно). Например,
![]() ;
;
![]() ;
;
![]() .
.
Для знакочередующихся рядов имеет место
достаточный признак сходимости (установленный в
1714г. Лейбницем в письме к И.Бернулли).
2.2 Признак Лейбница. Абсолютная и условная
сходимость ряда.
Теорема (Признак Лейбница).
Знакочередующийся ряд сходится, если:
Последовательность абсолютных величин членов
ряда монотонно убывает, т.е. ![]() ;
;
Общий член ряда стремится к нулю:![]() .
.
При этом сумма S ряда удовлетворяет
неравенствам
![]() .
.
Замечания.
Исследование знакочередующегося ряда вида
![]()
(с отрицательным первым членом) сводится путем
умножения всех его членов на ![]() к исследованию ряда
к исследованию ряда ![]() .
.
Ряды, для которых выполняются условия теоремы
Лейбница, называются лейбницевскими (или
рядами Лейбница).
Соотношение ![]() позволяет получить простую и удобную
позволяет получить простую и удобную
оценку ошибки, которую мы допускаем, заменяя
сумму S данного ряда его частичной суммой ![]() .
.
Отброшенный ряд (остаток) представляет собой
также знакочередующийся ряд ![]()
![]() , сумма которого по модулю меньше
, сумма которого по модулю меньше
первого члена этого ряда, т.е.![]() . Поэтому ошибка меньше модуля первого из
. Поэтому ошибка меньше модуля первого из
отброшенных членов.
Пример. Вычислить приблизительно сумму ряда ![]() .
.
Решение: данный ряд Лейбницевского типа. Он
сходится. Можно записать:
![]() .
.
Взяв пять членов, т.е. заменив![]() на
на
![]() , сделаем
, сделаем
ошибку, меньшую,
чем![]() . Итак,
. Итак,![]() .
.
Для знакопеременных рядов имеет место
следующий общий достаточный признак сходимости.
Теорема. Пусть дан знакопеременный ряд
![]() .
.
Если сходится ряд
![]() ,
,
составленный из модулей членов данного ряда, то
сходится и сам знакопеременный ряд.
Признак сходимости Лейбница для
знакочередующихся рядов служит достаточным
признаком сходимости знакочередующихся рядов.
Знакопеременный ряд называется абсолютно
сходящимся, если сходится ряд, составленный
из абсолютных величин его членов, т.е. всякий
абсолютно сходящийся ряд является сходящимся.
Если знакопеременный ряд сходится, а
составленный из абсолютных величин его членов
ряд расходится, то данный ряд называется условно
(неабсолютно) сходящимся.
2.3. Упражнения.
Исследовать на сходимость (абсолютную или
условную) знакочередующийся ряд:
![]() ;
;
Решение.
Члены данного ряда по абсолютной величине
монотонно убывают:
![]() и
и
![]()
Следовательно, согласно признаку Лейбница, ряд
сходится. Выясним, сходится ли этот ряд абсолютно
или условно.
Ряд ![]() ,
,
составленный из абсолютных величин данного ряда,
является гармоническим рядом, который,
расходится. Поэтому данный ряд сходится условно.
![]()
Решение.
Члены данного ряда по абсолютной величине
монотонно убывают:
![]() , но
, но
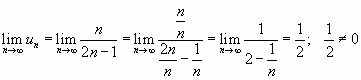 .
.
Ряд расходится, так как признак Лейбница не
выполняется.
![]() ;
;
Решение.
Используя признак Лейбница, получим
![]() ;
;![]() ,
,
т.е. ряд сходится.
Рассмотрим ряд, составленный из абсолютных
величин членов данного ряда:
![]() .
.
Это геометрический ряд вида![]() , где
, где![]() , который сходится. Поэтому данный ряд
, который сходится. Поэтому данный ряд
сходится абсолютно.
![]() ;
;
Решение.
Используя признак Лейбница, имеем
![]() ;
;
![]() , т.е. ряд
, т.е. ряд
сходится.
Рассмотрим ряд, составленный из абсолютных
величин членов данного ряда:
![]() , или
, или
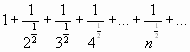 .
.
Это обобщенный гармонический ряд, который
расходится, так как![]() . Следовательно, данный ряд сходится
. Следовательно, данный ряд сходится
условно.
III. Функциональный ряд
3.1. Понятие функционального ряда.
Ряд, членами которого являются функции от ![]() , называется функциональным:
, называется функциональным:
![]() .
.
Придавая ![]()
определенное значение ![]() , получим числовой ряд
, получим числовой ряд
![]() ,
,
который может быть как сходящимся, так и
расходящимся.
Если полученный числовой ряд сходится, то точка
![]() называется точкой
называется точкой
сходимости функционального ряда; если же ряд
расходится – точкой расходимости
функционального ряда.
Совокупность числовых значений аргумента ![]() , при которых
, при которых
функциональный ряд сходится, называется его областью
сходимости.
В области сходимости функционального ряда его
сумма является некоторой функцией от ![]() :
:![]() .
.
Определяется она в области сходимости
равенством
![]() , где
, где
![]() – частичная
– частичная
сумма ряда.
Пример. Найти область сходимости ряда ![]() .
.
Решение. Данный ряд является рядом
геометрической прогрессии со знаменателем ![]() . Следовательно,
. Следовательно,
этот ряд сходится при ![]() , т.е. при всех
, т.е. при всех ![]() ; сумма ряда равна
; сумма ряда равна ![]() ;
;
![]() , при
, при ![]() .
.
3.2. Степенные ряды.
Степенным рядом называется ряд вида
![]() ,
,
где числа ![]()
называются коэффициентами ряда, а член ![]() – общим членом
– общим членом
ряда.
Областью сходимости степенного ряда
называется множество всех значений ![]() , при которых данный ряд
, при которых данный ряд
сходится.
Число![]() называется радиусом
называется радиусом
сходимости степенного ряда, если при ![]() ряд сходится и
ряд сходится и
притом абсолютно, а при ![]() ряд расходится.
ряд расходится.
Радиус сходимости ![]()
найдем, используя признак Даламбера:
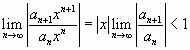 (
(![]() не зависит от
не зависит от![]() ),
),
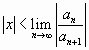 ,
,
т.е. если степенной ряд сходится при любых ![]() ,
,
удовлетворяющих данному условию и расходится
при 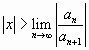 .
.
Отсюда следует, что если существует предел
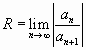
![]() ,
,
то радиус сходимости ряда![]() равен этому пределу и степенной
равен этому пределу и степенной
ряд сходится при ![]() , т.е. в промежутке
, т.е. в промежутке ![]() , который называется промежутком
, который называется промежутком
(интервалом) сходимости.
Если ![]() , то
, то
степенной ряд сходится в единственной точке ![]() .
.
На концах промежутка ряд может сходиться
(абсолютно или условно), но может и расходиться.
Сходимость степенного ряда при ![]() и
и ![]() исследуется с помощью
исследуется с помощью
какого-либо из признаков сходимости.
3.3. Упражнения.
Найти область сходимости ряда:
![]() ;
;
Решение. Найдем радиус сходимости данного
ряда:
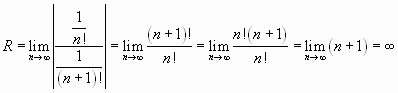 .
.
Следовательно, данный ряд абсолютно сходится
на всей числовой оси.
![]()
Решение. Воспользуемся признаком Даламбера.
Для данного ряда имеем:
![]() ,
,![]() ,
,
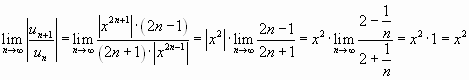 .
.
Ряд абсолютно сходится, если ![]() или
или ![]() . Исследуем поведение ряда на
. Исследуем поведение ряда на
концах интервала сходимости.
При ![]() имеем
имеем
ряд ![]() , который
, который
сходится по признаку Лейбница.
При ![]() имеем
имеем
ряд![]() – это тоже
– это тоже
сходящийся Лейбницевский ряд. Следовательно,
областью сходимости исходного ряда является
отрезок![]() .
.
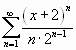 .
.
Решение. Найдем радиус сходимости ряда:
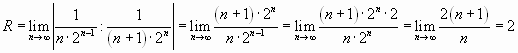 .
.
Следовательно, ряд сходится при![]() , т.е. при
, т.е. при![]() .
.
При![]() имеем
имеем
ряд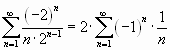 , который
, который
сходится по признаку Лейбница.
При![]() имеем
имеем
расходящийся ряд
![]() .
.
Следовательно, областью сходимости исходного
ряда является промежуток![]() .
.
IV. Разложение элементарных функций в ряд
Маклорена.
Для приложений важно уметь данную функцию![]() разлагать в
разлагать в
степенной ряд, т.е. функцию ![]() представлять в виде суммы
представлять в виде суммы
степенного ряда.
Рядом Тейлора для функции ![]() называется степенной ряд
называется степенной ряд
вида
![]() .
.
Если ![]() , то
, то
получим частный случай ряда Тейлора
![]() ,
,
который называется рядом Маклорена.
Степенной ряд внутри его промежутка сходимости
можно почленно дифференцировать и интегрировать
сколько угодно раз, причем полученные ряды имеют
тот же промежуток сходимости, что и исходный ряд.
Два степенных ряда можно почленно складывать и
умножать по правилам сложения и умножения
многочленов. При этом промежуток сходимости
полученного нового ряда совпадает с общей частью
промежутков сходимости исходных рядов.
Для разложения функции ![]() в ряд Маклорена необходимо:
в ряд Маклорена необходимо:
Вычислить значения функции и ее
последовательных производных в точке ![]() , т.е.
, т.е.![]() ,
,![]() ,
,![]() ,…,
,…,![]() ;
;
Составить ряд Маклорена, подставив значения
функции и ее последовательных производных в
формулу ряда Маклорена;
Найти промежуток сходимости полученного ряда
по формуле
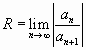 ,
, ![]() .
.
Таблица, содержащая разложения в ряд
Маклорена некоторых элементных функций:
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]()
Пример 1. Разложить в ряд Маклорена функцию![]() .
.
Решение. Так как ![]() , то, заменяя
, то, заменяя![]() на
на ![]()
в разложении ![]() ,
,
получим:
![]() ,
, ![]() .
.
Пример 2. Выписать ряд Маклорена функции ![]() .
.
Решение. Так как ![]() , то воспользовавшись формулой
, то воспользовавшись формулой ![]() , в которой
, в которой
заменим ![]() на
на ![]() , получим:
, получим:
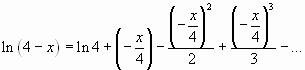 ,
,
или
![]() ,
,
если
![]() , т.е.
, т.е.![]() .
.
Пример 3. Разложить в ряд Маклорена функцию ![]() .
.
Решение. Воспользуемся формулой ![]() . Так как
. Так как
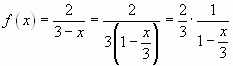 , то
, то
заменив![]() на
на![]() получим:
получим:
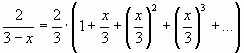 , или
, или
![]() ,
,
где ![]() , т.е.
, т.е. ![]() .
.
V. Практические задания для самоконтроля
студентов.
При помощи признака сравнения рядов установить
сходимость
или расходимость рядов:
![]()
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
Исследовать по признаку Даламбера сходимость
рядов:
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
Исследовать на сходимость (абсолютную или
условную) знакочередующийся ряд:
![]() .;
.;
![]() .;
.;
![]() .;
.;
![]() .;
.;
![]() .
.
Найти промежутки сходимости нижеследующих
рядов и выяснить вопрос об их сходимости на
концах промежутков сходимости:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
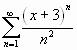 .
.
Используя разложения в ряд Маклорена функции![]() ,
,![]() ,
,![]() ,
,![]() ,
,
разложить степенные ряды функции:
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
VI. Ответы
I.
- сходится;
- расходится;
- сходится;
- сходится;
- расходится;
- сходится;
- сходится;
- расходится;
- сходится;
- сходится.
II.
- cходится абсолютно;
- cходится абсолютно;
- cходится условно;
- cходится условно;
- cходится абсолютно.
III.
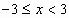 ;
; ;
;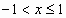 ;
;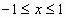 ;
;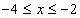 .
.
IV.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
VII. Историческая справка.
Решение многих задач сводится к вычислению
значений функций и интегралов или к решению
дифференциальных уравнений, содержащих
производные или дифференциалы неизвестных
функций.
Однако точное выполнение указанных
математических операций во многих случаях
оказывается весьма затруднительным или
невозможным. В этих случаях можно получить
приближенное решение многих задач с любой
желаемой точностью при помощи рядов.
Ряды представляют собой простой и совершенный
инструмент математического анализа для
приближенного вычисления функций, интегралов и
решений дифференциальных уравнений.
Теория рядов создавалась в тесной связи с
теорией приближенного представления функций в
виде многочленов. Впервые это сделал И. Ньютон (1642
– 1727). в 1676г. В его письме к секретарю Лондонского
Королевского Общества появилась формула:
![]() ,
,
которую мы знаем как формулу бинома Ньютона.
Здесь мы видим функцию ![]() , представленную в виде
, представленную в виде
многочлена. Но если число![]() не является натуральным, в
не является натуральным, в
правой части равенства получается не полином, а
бесконечная сумма слагаемых, то есть ряд.
Развивая идею Ньютона, английский математик
Брук Тейлор (1685 – 1731) в 1715г. доказал, что любой
функции, имеющей в точке ![]() производные всех порядков, можно
производные всех порядков, можно
сопоставить ряд:
![]() .
.
Мы не можем пока поставить знак равенства между
функцией ![]() ,
,
принимающей конечное значение для любого
значения ![]() , и
, и
стоящим справа функциональным рядом.
Для того, чтобы вместо знака “![]() ” можно было поставить
” можно было поставить
знак равенства, необходимо провести некоторые
дополнительные рассуждения, связанные именно с
бесконечностью числа слагаемых в правой части
равенства и касающиеся области сходимости ряда.
При ![]()
формула Тейлора принимает вид, в котором
называется формулой Маклорена:
![]() .
.
Колин Маклорен (1698 – 1746), ученик Ньютона, в
работе “Трактат о флюксиях” (1742) установил, что
степенной ряд, выражающий аналитическую функцию,
– единственный, и это будет ряд Тейлора,
порожденный такой функцией. В формуле бинома
Ньютона коэффициенты при степенях ![]() представляют собой
представляют собой
значения ![]() ,
,
где ![]() .
.
Итак, ряды возникли в XVIII в. как способ
представления функций, допускающих бесконечное
дифференцирование. Однако функция,
представляемая рядом, не называлась его суммой, и
вообще в то время не было еще определено, что
такое сумма числового или функционального ряда,
были только попытки ввести это понятие.
Например, Л. Эйлер (1707-1783), выписав для функции
соответствующий ей степенной ряд, придавал
переменной ![]()
конкретное значение ![]() . Получался числовой ряд. Суммой этого
. Получался числовой ряд. Суммой этого
ряда Эйлер cчитал значение исходной функции в
точке ![]() . Но это
. Но это
не всегда верно.
О том, что расходящийся ряд не имеет суммы,
ученые стали догадываться только в XIX в., хотя в
XVIII в. многие, и прежде всего Л. Эйлер, много
работали над понятиями сходимости и
расходимости. Эйлер называл ряд ![]() сходящимся, если его общий
сходящимся, если его общий
член ![]()
стремится к нулю при возрастании ![]() .
.
В теории расходящихся рядов Эйлер получил
немало существенных результатов, однако
результаты эти долго не находили применения. Еще
в 1826г. Н.Г. Абель (1802 – 1829) называл расходящиеся
ряды “дьявольским измышлением”. Результаты
Эйлера нашли обоснование лишь в конце XIX в.
В формировании понятия суммы сходящегося ряда
большую роль сыграл французский ученый О.Л. Коши
(1789 – 1857); он сделал чрезвычайно много не только в
теории рядов, но и теории пределов, в разработке
самого понятия предела. В 1826г. Коши заявил, что
расходящийся ряд не имеет суммы.
В 1768г. французский математик и философ Ж.Л.
Д’Аламбер исследовал отношение последующего
члена к предыдущему в биномиальном ряде и
показал, что если это отношение по модулю меньше
единицы, то ряд сходится. Коши в 1821г. доказал
теорему, излагающую в общем виде признак
сходимости знакоположительных рядов, называемых
теперь признаком Д’Аламбера.
Для исследования сходимости знакочередующихся
рядов используется признак Лейбница.
Г.В. Лейбниц (1646 – 1716), великий немецкий
математик и философ, наряду с И. Ньютоном
является основоположником дифференциального и
интегрального исчисления.
Список литературы:
Основная:
- Богомолов Н.В., Практические занятия по
математике. М., “Высшая школа”, 1990 – 495 с.; - Тарасов Н.П., Курс высшей математики для
техникумов. М., “Наука”, 1971 – 448 с.; - Зайцев И.Л., Курс высшей математики для
техникумов. М., государственное издательство
техникумов – теоретической литературы, 1957 – 339 с.; - Письменный Д.Т., Курс лекций по высшей
математике. М., “Айрис Пресс”, 2005, часть 2 – 256 с.; - Выгодский М.Я., Справочник по высшей математике.
М., “Наука”, 1975 – 872 с.;
Дополнительная:
- Гусак А.А., Высшая математика. В 2-х т., Т.2: Учебное
пособие для студентов вузов. Мос.,
“ТетраСистемс”, 1988 – 448 с.; - Григулецкий В.Г., Лукьянова И.В., Петунина И.А.,
Математика для студентов экономических
специальностей. Часть 2. Краснодар, 2002 – 348 с.; - Григулецкий В.Г. и др. Задачник-практикум по
математике. Краснодар. КГАУ, 2003 – 170 с.; - Григулецкий В.Г., Степанцова К.Г., Гетман В.Н.,
Задачи и упражнения для студентов
учетно-финансового факультета. Краснодар. 2001 – 173
с.; - Григулецкий В.Г., Ященко З.В., Высшая математика.
Краснодар, 1998 – 186 с.; - Малыхин В.И., Математика в экономике. М.,
“Инфра-М”, 1999 – 356с.
Соседние места в концертном зале
Хотите готовиться со мной к ЕГЭ?
Пишите: ydkras@mail.ru
Немного обо мне.
Язык Питон позволяет решать задачи ЕГЭ по информатике существенно проще, чем другие языки, которые можно использовать на ЕГЭ.
Рассмотрим задачу 26 варианта 1 с сайта Полякова:
(№ 4214) Организация купила для своих сотрудников все места в нескольких
подряд идущих рядах на концертной площадке. Известно, какие места уже
распределены между сотрудниками. Найдите ряд с наибольшим номером, в
котором есть два соседних места, таких что слева и справа от них в том
же ряду места уже распределены (заняты). Гарантируется, что есть хотя бы
один ряд, удовлетворяющий условию.
Входные данные представлены в файле 26-59.txt
следующим образом. В первой строке входного файла находится одно число:
N – количество занятых мест (натуральное число, не превышающее 10
000). В следующих N строках находятся пары чисел: ряд и место
выкупленного билета, не превышающие 100000. В ответе запишите два целых
числа: номер ряда и наименьший номер места из найденных в этом ряду
подходящих пар.
Пример входного файла:10
5 5
5 9
5 6
16 9
16 3
16 6
20 23
20 28
20 35
20 40В
данном примере есть следующие свободные места, удовлетворяющие условию:
7 и 8 в ряду 5, 4 и 5 в ряду 16, а также 7 и 8 в ряду 16. Выбираем
наибольший номер ряда: 16 и наименьший номер места: 4. В ответе нужно
указать: 16 4.
Упакуем номер ряда и номер места в одно целое число. Для этого умножим номер ряда на число, заведомо превышающее число мест в одном ряду, и сложим результат с номером места. Так как номер места не превышает 100 тысяч, то в качестве множителя возьмём миллион: этого заведомо достаточно.
Для примера входной информации в условии задачи получаем следующие числа:
[5000005, 5000009, 5000006, 16000009, 16000003, 16000006, 20000023, 20000028, 20000035, 20000040]
Чтобы получить номер ряда, нужно разделить нацело число на миллион (x//1000000), а номер места – взять остаток от деления числа на миллион (x%1000000).
Отсортируем полученный массив по возрастанию. Теперь соседние числа – это максимально близкие проданные места. Если они находятся в одном ряду, то их разность – это количество непроданных мест между проданными плюс 1. (Так как мы взяли множитель с солидным запасом, то исключаются ситуации,
когда разность между первым местом в ряду и последним местом в
предыдущем ряду будет мала.) Таким образом, нам достаточно рассмотреть весь массив и найти пары, разность между которыми равна трем.
Проще всего отсортировать массив, воспользовавшись встоенной в Питон операцией sort.
Теперь просматриваем массив и ищем соседние элементы, разность между которыми равна трем. Если пара найдена, получаем номер ряда. Если номер ряда больше, чем найденный ранее, то запоминаем новый номер ряда и номер места. Номер места на единицу больше, чем номер левого из занятых вокруг свободной пары мест.
Приведем полный текст программы, решающей данную задачу:
f=open(“in.txt”)
rm=[]
n=int(f.readline())
for i in range(n):
r,m = map(int, f.readline().split())
rm.append(r*1000000+m)
rm.sort()
r=0
m=0
for i in range(n-1):
if rm[i+1] – rm[i] == 3 and rm[i]//1000000 > r:
r=rm[i]//1000000
m=rm[i]%1000000 + 1
print(r,m)
(c) Ю.Д.Красильников, 2021-2022 г.
Сразу отметим, что единой универсальной методики для решения задач на числовые ряды нет. Закономерности, по которым числа следуют друг за другом, могут быть самыми разными, и научиться быстро решать такого рода задачи можно только путём практики – прорешав большое количество других задач на ряды.
Рассмотрим самые простые случаи.
Надо продолжить ряд
1) 2 4 6 8 …
В этом случае всё просто – каждое следующее число на 2 больше предыдущего (т.е. это ряд чётных чисел, или арифметическая прогрессия с шагом 2), поэтому следующее число будет 10
2) 4 8 16 32 …
Тут каждое следующее число в 2 раза больше предыдущего (геометрическая прогрессия), поэтому следующим будет число 64
3) 6 11 17 24 …
Этот случай уже чуть сложнее. В этом числовом ряду разница между соседними числами на 1 больше, чем разница между предыдущими
11 – 6 = 5
17 – 11 = 6
24 -17 = 7
Как видим, шаг (разница) между соседними числами каждый раз увеличивается на 1.
Соответственно, после 24 будет число, которое на 8 больше, то есть 32
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Пример 1
Ряд: 18 10 6 4 …
Взглянув на этот ряд, можно достаточно быстро понять, что разница между соседними числами с каждым шагом сокращается в 2 раза
18 – 10 = 8
10 – 6 = 4 (8:4 = 2)
6 – 4 = 2 (4:2 = 2)
Следовательно, следующий шаг – это 2:2 = 1, то есть число будет 4-1 = 3
Пример 2
Ряд: 7 15 31 63
Этот ряд противоположен предыдущему. Тут разница между соседними числами с каждым шагом увеличивается в 2 раза
15 – 7 = 8
31 – 15 = 16 (16:8 = 2)
63 – 31 = 32 (32:16 = 2)
Следующий шаг будет 32∙2 = 64, соответственно, следующее число будет 63 + 64 = 127
Ответ: 127
Пример 3
Ряд: 2 4 8 10 20 22 44 46 92 94
Взглянем на этот ряд подробнее.
4 – 2 = 2
8:4 = 2
10 – 8 =2
20:10 = 2
То есть одно число на 2 больше предыдущего, а следующее – в 2 раза больше предыдущего.
Далее опять – на 2 больше, и потом в два раза больше.
Следующие числа в этом ряду:
22 – 20 = 2
44:22 = 2
46 – 44 = 2
92:46 = 2
94 – 92 = 2
Соответственно, следующее число будет в 2 раза больше, чем 94. Т.е. это будет 94∙2 = 188
Ответ: 188
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Пример 4
Ряд: 1 2 3 5 7 11 13 17 19
В этом ряду бесполезно искать закономерности, насколько соседние числа отличаются друг от друга. Все числа в этом ряду – простые, то есть без остатка делятся только на 1 и на само себя. Соответственно, следующим в ряду будет следующее после 19 простое число, то есть 23.
После того, как вы поняли, что это ряд простых чисел, то вы поняли, почему иные закономерности в этом ряду искать бесполезно – ведь математики до сих пор не нашли закона, по которому распределяются простые числа, и как можно по формуле (а не путём перебора) найти следующее простое число, зная предыдущие.
Ответ: 23
Дата публикации
02.05.2020
