Лучший ответ
electro
Профи
(975)
13 лет назад
немного подредактировал
условия схема для удобства подсчета и наглядности

оцените пожалуйста
Остальные ответы
Krab Вark
Просветленный
(32266)
13 лет назад
С мыслями вслух? Два параллельных R сводим к одному R/2. Четыре параллельных R сводим к одному R/4. Получили три последовательно включенных сопротивления. Суммируем их: R/2+R+R/4=1¾ R = (1¾)*4=7 кОм
ДриоДынъ
Мастер
(2035)
13 лет назад
Сначала первый блок – оба R соединены параллельно
R0 = R*R/(R+R)
Потом третий блок, аналогично
Потом все это вместе соединено последовательно R = R1+R2+R3
валерий лопатинский
Высший разум
(115532)
13 лет назад
 это для тех кто в бронепоезде
это для тех кто в бронепоезде
Введение
Решение задач – неотъемлемая часть обучения
физике, поскольку в процессе решения задач
происходит формирование и обогащение физических
понятий, развивается физическое мышление
учащихся и совершенствуется их навыки
применения знаний на практике.
В ходе решения задач могут быть поставлены и
успешно реализованы следующие дидактические
цели:
- Выдвижение проблемы и создание проблемной
ситуации; - Обобщение новых сведений;
- Формирование практических умений и навыков;
- Проверка глубины и прочности знаний;
- Закрепление, обобщение и повторение материала;
- Реализация принципа политехнизма;
- Развитие творческих способностей учащихся.
Наряду с этим при решении задач у школьников
воспитываются трудолюбие, пытливость ума,
смекалка, самостоятельность в суждениях, интерес
к учению, воля и характер, упорство в достижении
поставленной цели. Для реализации перечисленных
целей особенно удобно использовать
нетрадиционные задачи.
§1. Задачи по расчету электрических
цепей постоянного тока
По школьной программе на рассмотрение данной
темы очень мало отводится времени, поэтому
учащиеся более или менее успешно овладевают
методами решения задач данного типа. Но часто
такие типы задач встречаются олимпиадных
заданиях, но базируются они на школьном курсе.
К таким, нестандартным задачам по расчету
электрических цепей постоянного тока можно
отнести задачи, схемы которых:
1) содержат большое число элементов –
резисторов или конденсаторов;
2) симметричны;
3) состоят из сложных смешанных соединений
элементов.
В общем случае всякую цепь можно рассчитать,
используя законы Кирхгофа. Однако эти законы не
входят в школьную программу. К тому же, правильно
решить систему из большого числа уравнений со
многими неизвестными под силу не многим учащимся
и этот путь не является лучшим способом тратить
время. Поэтому нужно уметь пользоваться
методами, позволяющими быстро найти
сопротивления и емкости контуров.
§2. Метод эквивалентных схем
Метод эквивалентных схем заключается в том, что
исходную схему надо представить в виде
последовательных участков, на каждом из которых
соединение элементов схемы либо
последовательно, либо параллельно. Для такого
представления схему необходимо упростить. Под
упрощением схемы будем понимать соединение или
разъединение каких-либо узлов схемы, удаление
или добавление резисторов, конденсаторов,
добиваясь того, чтобы новая схема из
последовательно и параллельно соединенных
элементов была эквивалентна исходной.
Эквивалентная схема – это такая схема, что при
подаче одинаковых напряжений на исходную и
преобразованную схемы, ток в обеих цепях будет
одинаков на соответствующих участках. В этом
случае все расчеты производятся с
преобразованной схемой.
Чтобы начертить эквивалентную схему для цепи
со сложным смешанным соединением резисторов
можно воспользоваться несколькими приемами. Мы
ограничимся рассмотрением в подробностях лишь
одного из них – способа эквипотенциальных узлов.
Этот способ заключается в том, что в
симметричных схемах отыскиваются точки с
равными потенциалами. Эти узлы соединяются между
собой, причем, если между этими точками был
включен какой-то участок схемы, то его
отбрасывают, так как из-за равенства потенциалов
на концах ток по нему не течет и этот участок
никак не влияет на общее сопротивление схемы.
Таким образом, замена нескольких узлов равных
потенциалов приводит к более простой
эквивалентной схеме. Но иногда бывает
целесообразнее обратная замена одного узла
несколькими узлами с равными потенциалами, что
не нарушает электрических условий в остальной
части.
Рассмотрим примеры решения задач эти методом.
З а д а ч а №1
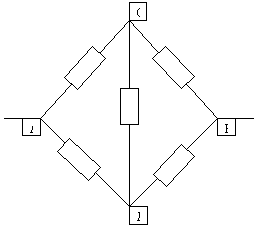
Рассчитать сопротивление между точками А и В
данного участка цепи. Все резисторы одинаковы и
их сопротивления равны r.
Решение:
В силу симметричности ветвей цепи точки С И Д
являются эквипотенциальными. Поэтому резистор
между ними мы можем исключить. Эквипотенциальные
точки С и Д соединяем в один узел. Получаем очень
простую эквивалентную схему:
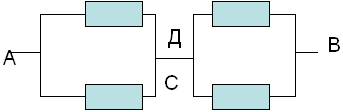
Сопротивление которой равно:
RАВ=Rac+Rcd=r*r/r*r+r*r/r+r=r.
З а д а ч а № 2
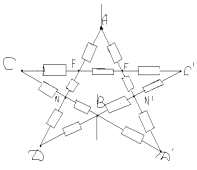
Решение:
В точках F и F` потенциалы равны, значит
сопротивление между ними можно отбросить.
Эквивалентная схема выглядит так:
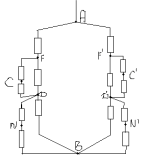
Сопротивления участков DNB;F`C`D`; D`, N`, B`; FCD равны
между собой и равны R1:
1/R1=1/2r+1/r=3/2r
R1=2/3*r
С учетом этого получается новая эквивалентная
схема:
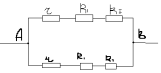
Ее сопротивление и сопротивление исходной цепи
RАВ равно:
1/RАВ=1/r+R1+R1+1/r+R1+R1=6/7r
RАВ=(7/6)*r.
З а д а ч а № 3.
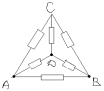
Решение:
Точки С и Д имеют равные потенциалы.
Исключением сопротивление между ними. Получаем
эквивалентную схему:
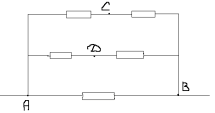
Искомое сопротивление RАВ равно:
1/RАВ=1/2r+1/2r+1/r=2/r
RАВ=r/2.
З а д а ч а № 4.
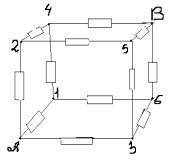
Решение:
Как видно из схемы узлы 1,2,3 имеют равные
потенциалы. Соединим их в узел 1. Узлы 4,5,6 имеют
тоже равные потенциалы- соединим их в узел 2.
Получим такую эквивалентную схему:
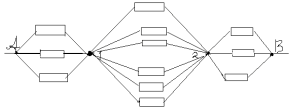
Сопротивление на участке А-1, R 1-равно
сопротивлению на участке 2-В,R3 и равно:
R1=R3=r/3
Сопротивление на участке 1-2 равно: R2=r/6.
Теперь получается эквивалентная схема:
![]()
Общее сопротивление RАВ равно:
RАВ= R1+ R2+ R3=(5/6)*r.
З а д а ч а № 5.
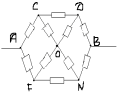
Решение:
Точки C и F-эквивалентные. Соединим их в один
узел. Тогда эквивалентная схема будет иметь
следующий вид:
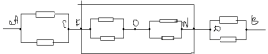
Сопротивление на участке АС:
Rас=r/2
Сопротивление на участке FN:
RFN = ![]()
Сопротивление на участке DB:
RDB =r/2
Получается эквивалентная схема:
![]()
Искомое общее сопротивление равно:
RAB= r.
Задача №6
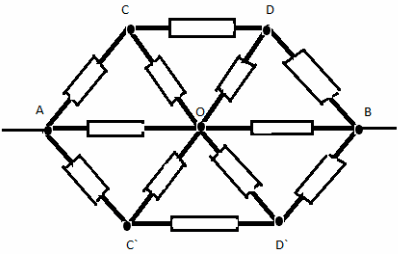
Решение:
Заменим общий узел О тремя узлами с равными
потенциалами О, О1 , О2. Получим
эквивалентную систему:
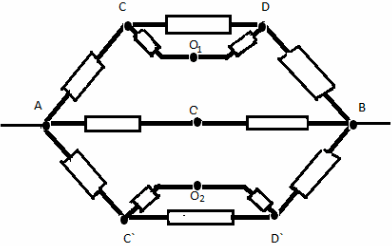
Сопротивление на участке ABCD:
R1=(3/2)*r
Сопротивление на участке A`B`C`D`:
R2= (8/3)*r
Сопротивление на участке ACВ
R3 = 2r.
Получаем эквивалентную схему:
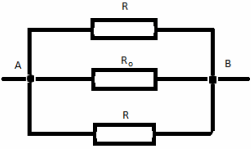
Искомое общее сопротивление цепи RAB
равно:
RAB= (8/10)*r.
Задача №7.
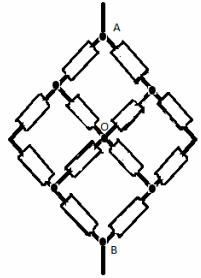
Решение:
“Разделим” узел О на два эквипотенциальных
угла О1 и О2. Теперь схему можно
представить, как параллельные соединение двух
одинаковых цепей. Поэтому достаточно подробно
рассмотреть одну из них:
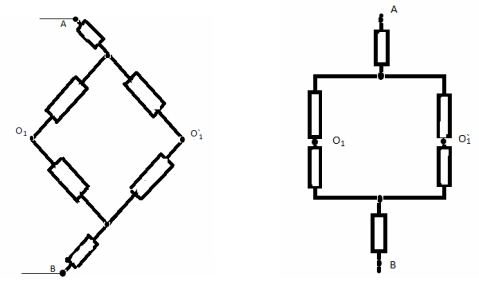
Сопротивление этой схемы R1 равно:
R1 = 3r
Тогда сопротивление всей цепи будет равно:
RAB = (3/2)*r
З а д а ч а №8
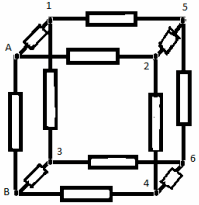
Решение:
Узлы 1 и 2 – эквипотенциальные, поэтому соединим
их в один узел I. Узлы 3 и 4 также эквипотенциальные
– соединимих в другой узел II. Эквивалентная
схема имеет вид:
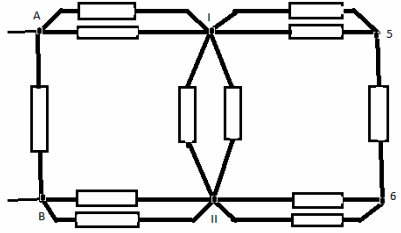
Сопротивление на участке A- I равно
сопротивлению на участке B- II и равно:
RI =![]()
Сопротивление участка I-5-6- II равно:
RII = 2r
Cопротивление участка I- II равно:
RIII = ![]()
Получаем окончательную эквивалентную схему:
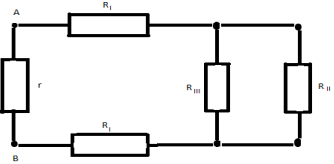
Искомое общее сопротивление цепи RAB=(7/12)*r.
З а д а ч а №9
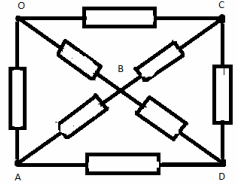
В ветви ОС заменим сопротивление на два
параллельно соединенных сопротивления по 2r.
Теперь узел С можно разделить на 2
эквипотенциальных узла С1 и С2.
Эквивалентная схема в этом случае выглядит так:
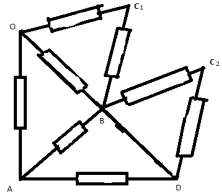
Сопротивление на участках ОСIB и DCIIB
одинаковы и равны, как легко подсчитать 2r. Опять
чертим соответствующую эквивалентную схему:
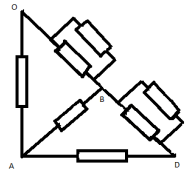
Сопротивление на участке AOB равно
сопротивлению на участке ADB и равно (7/4)*r. Таким
образом получаем окончательную эквивалентную
схему из трех параллельно соединенных
сопротивлений:
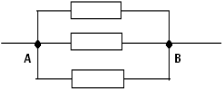
Ее общее сопротивление равно RAB= (7/15)*r
З а д а ч а № 10
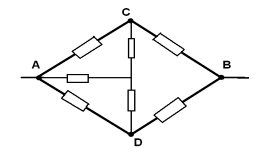
Точки СОD имеют равные потенциалы – соединим их
в один узел ОI .Эквивалентная схема
изображена на рисунке :
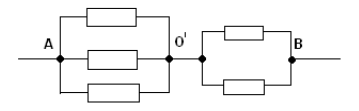
Сопротивление на участке А ОI равно ![]() . На участке
. На участке
ОIВ сопротивление равно ![]() .Получаем совсем
.Получаем совсем
простую эквивалентную схему:
![]()
ЕЕ сопротивление равно искомому общему
сопротивлению
RAB=(5/6)*r
Задачи № 11 и № 12 решаются несколько иным
способом, чем предыдущие. В задаче №11 для ее
решения используется особое свойство
бесконечных цепей, а в задаче № 12 применяется
способ упрощения цепи.
Задача № 11
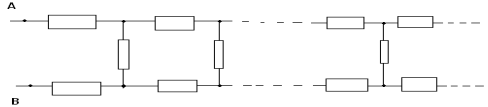
Решение
Выделим в этой цепи бесконечно повторяющееся
звено, оно состоит в данном случае из трех первых
сопротивлений. Если мы отбросим это звено, то
полное сопротивление бесконечной цепи R не
измениться от этого , так как получится точно
такая же бесконечная цепь. Так же ничего не
измениться, если мы выделенное звено подключим
обратно к бесконечному сопротивлению R, но при
этом следует обратить внимание , что часть звена
и бесконечная цепь сопротивлением R соединены
параллельно. Таким образом получаем
эквивалентную схему :
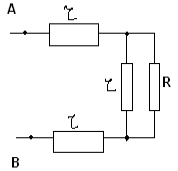
Получается уравнения
RAB=2ч +![]()
RAB = R
Решая систему этих уравнений, получаем:
R=ч (1+ ![]() ).
).
§3. Обучение решению задач по расчету
электрических цепей способом эквипотенциальных
узлов
Задача – это проблема, для разрешения которой
ученику потребуются логические рассуждения и
выводы. Строящиеся на основе законов и методов
физики. Таким образом, с помощью задач происходит
активизация целенаправленного мышления
учащихся.
В то же время. Теоретические знания можно
считать усвоенными только тогда, когда они
удачно применяются на практике. Задачи по физике
описывают часто встречающиеся в жизни и на
производстве проблемы, которые могут быть решены
с помощью законов физики и, если ученик успешно
решает задачи, то можно сказать, что он хорошо
знает физику.
Для того, чтобы ученики успешно решали задачи,
недостаточно иметь набор методов и способов
решения задач, необходимо еще специально учить
школьников применению этих способов.
Рассмотрим план решения задач по расчету
электрических цепей постоянного тока методом
эквипотенциальных узлов.
- Чтение условия.
- Краткая запись условия.
- Перевод в единицы СИ.
- Анализ схемы:
- установить, является ли схема симметричной;
- установить точки равного потенциала;
- выбрать, что целесообразнее сделать –
соединить точки равных потенциалов или же,
наоборот, разделить одну точку на несколько
точек равных потенциалов; - начертить эквивалентную схему;
- найти участки только с последовательным или
только с параллельным соединением и рассчитать
общее сопротивление на каждом участке по законам
последовательного и параллельного соединения; - начертить эквивалентную схему, заменяя участки
соответствующими им расчетными сопротивлениями; - пункты 5 и 6 повторять до тех пор, пока не
останется одно сопротивление, величина которого
и будет решением задачи. - Анализ реальности ответа.
Подробнее об анализе схемы
а) установить, является ли схема симметричной.
Определение. Схема симметрична, если одна ее
половина является зеркальным отражением другой.
Причем симметрия должна быть не только
геометрической, но должны быть симметричны и
численные значения сопротивлений или
конденсаторов.
Примеры:
1)
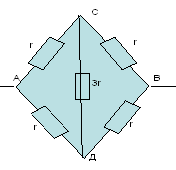
Схема симметричная, так как ветви АСВ и АДВ
симметричны геометрически и отношение
сопротивления на одном участке АС:АД=1:1 такое же,
как и на другом участке СД:ДВ=1:1.
2)
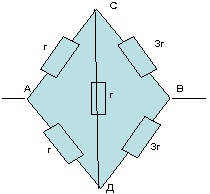
Схема симметричная, так как отношение
сопротивлений на участке АС:АД=1:1 такое же, как и
на другом участке СВ:ДВ=3:3=1:1
3)
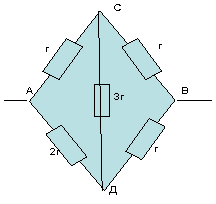
Схема не симметрична, так как отношения
сопротивлений численно
не симметричны -1:2 и 1:1.
б) установить точки равных потенциалов.
Пример:
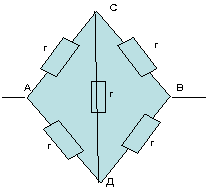
Из соображений симметрии делаем вывод, что в
симметричных точках потенциалы равны. В данном
случае симметричными точками являются точки С и
Д. Таким образом, точки С и Д – эквипотенциальные
точки.
в) выбрать, что целесообразно сделать –
соединить точки равных потенциалов или же,
наоборот, разделить одну точку на несколько
точек равных потенциалов.
Мы видим в этом примере, что между точками
равных потенциалов С и Д включено сопротивление,
по которому ток не будет течь. Следовательно, мы
можем отбросить это сопротивление, а точки С и Д
соединить в один узел.
г) начертить эквивалентную схему.
Чертим эквивалентную схему. При этом получаем
схему с соединенными в одну точку точками С и Д.
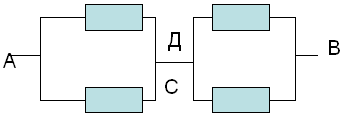
д) найти участки только с последовательным или
только с параллельным соединением и рассчитать
общее сопротивление на каждом таком участке по
законам последовательного и параллельного
соединения.
Из полученной эквивалентной схемы видно, что на
участке АС мы имеем два параллельно соединенных
резистора. Их общее сопротивление находится по
закону параллельного соединения:
1/ Rобщ=1/R1+1/R2+1/R3+…
Таким образом 1/RAC=1/r+1/r=2/r,откуда RAC= r/2.
На участке СВ картина аналогичная:
1/RCB= 1/r+1/r =2/r, откуда RCB=r/2.
е)начертить эквивалентную схему, заменяя
участки соответствующими им расчетными
сопротивлениями.
Чертим эквивалентную схему подставляя в нее
рассчитанные сопротивления участков RAC и RCB:
![]()
ж)пункты д) и е) повторять до тех пор, пока
останется одно сопротивление, величина которого
и будет решением задачи.
Повторяем пункт д): на участке АВ имеем два
последовательно соединенных сопротивления. Их
общее сопротивление находим по закону
последовательного соединения:
Rобщ= R1+R2+R3+… то есть, RAB=RAC+RCB = r/2+r/2 =2r/2 = r.
Повторяем пункт е): чертим эквивалентную
схему:

Мы получили схему с одним сопротивлением,
величина которого равна сопротивлению исходной
схемы. Таким образом, мы получили ответ RAB = r.
Далее, для проверки усвоения данного материала
можно учащимся предложить задания для
самостоятельной работы, взятые из
дидактического материала. (см. приложение)
Литература
- Балаш. В.А. задачи по физике и методы их решения. –
М: Просвещение,1983. - Лукашик В.И. Физическая олимпиада.- М:
Просвещение, 2007 - Усова А.В., Бобров А.А. Формирование учебных
умений и навыков учащихся на уроках физики.- М:
Просвещение,1988 - Хацет А. Методы расчета эквивалентных схем
//Квант. - Чертов А. Г. Задачник по физике. – М.: Высшая
школа,1983 - Зиятдинов Ш.Г., Соловьянюк С.Г. (методические
рекомендации) г. Бирск,1994г - Марон А.Е., Марон Е.А. Физика. Дидактические
материалы. Москва, “Дрофа”, 2004г
Equivalent resistance is defined as the total resistance of the circuit for the resistors connected in series or parallel combination. Resistors are electrical devices that limit the current flow in a circuit and obey Ohm’s law, V = IR. A circuit may have more than one resistor present due to which equivalent resistance is evaluated accordingly. The value of current and voltage depends on the orientation of resistors in the circuit.
In this article, we will learn about the Equivalent Resistance Formula in Series and Parallel combinations in detail.
What is the Equivalent Resistance?
Equivalent Resistance is the total resistance of the combination of all the resistances in the circuit. Suppose there are n resistance added in the circuit either in series or in parallel combination and if we replace all the resistance with a single resistance such that the current and the voltage difference in the circuit do not change it is called equivalent resistance.
Unit of Equivalent Resistance
Equivalent resistance is denoted by the symbol Req. SI unit of the measurement of Equivalent Resistance is Ohm (Ω) and the dimensional formula of the Equivalent Resistance [M1L2A−2T−3].
Formula for Equivalent Resistance
Equivalent Resistance is calculated using the Equivalent Resistance Formula, and the equivalent resistance formula is different in series and parallel combinations, i.e., we have two different equivalent resistance formulas they are,
- Equivalent Resistance Formula for Series Combination.
- Equivalent Resistance Formula for Parallel Combination.
Now, let’s learn about both formulas in detail in this article,
Equivalent Resistance Formula for Series Combination
In a series circuit of resistors, n resistors (n > 1) are connected adjacently one after the other, such that the collection of these resistors can be replaced by a single equivalent resistor to give the same resistance value. Here, the sum of the individual resistances will be the equivalent resistance of a series of resistors. The current through each resistor is the same but the voltage gets divided into n parts among the resistors.
.png)
Req = R1 + R2 + R3 + ….. + Rn
where,
Req is the equivalent resistance,
R1 is the resistance of the first resistor,
R2 is the resistance of the second resistor,
R3 is the resistance of the third resistor,
Rn is the resistance of the nth resistor,
Equivalent Resistance Formula for Parallel Combination
In a parallel circuit of resistors, n resistors (n > 1) are connected parallelly via wires that start from a common point. Here, the sum of the reciprocals of individual resistances equals the reciprocal of the equivalent resistance. The voltage through each resistor is the same but the current gets divided into n parts among the resistors.
.png)
1/Req = 1/R1 + 1/R2 + 1/R3 + ….. + 1/Rn
where,
Req is the equivalent resistance,
R1 is the resistance of the first resistor,
R2 is the resistance of the second resistor,
R3 is the resistance of the third resistor,
Rn is the resistance of the nth resistor,
How to find Equivalent Resistance?
The equivalent resistance of any circuit can easily be calculated using the steps given below,
Step 1: Study the electric circuit and mark all the resistance in the circuit along with the voltage of the battery.
Step 2: Check whether the resistance added is in series or parallel combination or both.
Step 3: Use the Equivalent Resistance Formula for Series Combination or Parallel combination accordingly.
Step 4: Simplify the formula in step 3 to get the Equivalent Resistance.
Read, More
- Electrical Resistance and Resistivity
- Temperature Dependence of Resistance
- Electrical Resistance Formula
Solved Examples on Equivalent Resistance Formula
Example 1: What is the equivalent resistance if three resistances of 4 Ω, 2 Ω, and 5 Ω are connected in series?
Solution:
We have,
R1 = 4 Ω
R2 = 2 Ω
R3 = 5 ΩUsing the formula we get,
Req = R1 + R2 + R3
= 4 + 2 + 5
= 11 Ω
Example 2: Find the unknown resistance if three resistances of 2 Ω, 5 Ω, and x Ω are connected in series to give an equivalent resistance of 10 Ω.
Solution:
We have,
R1 = 2 Ω
R2 = 5 ΩReq = 10 Ω
Using the formula we get,
Req = R1 + R2 + R3
10 = 2 + 5 + x
10 = 7 + x
x = 3 Ω
Example 3: Find the unknown resistance if three resistances of 7 Ω, 3 Ω, and X Ω are connected in series to give an equivalent resistance of 15 Ω.
Solution:
We have,
R1 = 7 Ω
R2 = 3 ΩReq = 15 Ω
Using the formula we get,
Req = R1 + R2 + R3
15 = 7 + 3 + X
15 = 10 +
x = 5 Ω
Example 4: What is the equivalent resistance if three resistances of 6 Ω, 3 Ω, and 8 Ω are connected in parallel?
Solution:
We have,
R1 = 6 Ω
R2 = 3 Ω
R3 = 8 ΩUsing the formula we get,
1/Req = 1/R1 + 1/R2 + 1/R3
1/Req = 1/6 + 1/3 + 1/8
1/Req = (4+8+3)/24
1/Req = 15/24
Req = 24/15 Ω = 1.6 Ω
Example 5: Find the unknown resistance if three known resistances of 4 Ω, 2 Ω, and 1 Ω connected in series with an unknown resistance of X Ω give an equivalent resistance of 0.5 Ω.
Solution:
We have,
R1 = 4 Ω
R2 = 2 Ω
R3 = 1 ΩReq = 0.5 Ω
Using the formula we get,
1/Req = 1/R1 + 1/R2 + 1/R3 + 1/R4
1/0.5 = 1/4 + 1/2 + 1/1 + 1/R4
1/R4 = 1/4 + 1/2 + 1/1 – 1/0.5
1/R4 = 1/4
R4 = 4 Ω
FAQs on Equivalent Resistance Formula
Question 1: What is the “equivalent resistance” formula in the Series combination?
Answer:
The “equivalent resistance” formula in the Series combination is given below,
Req = R1 + R2 + R3 + ….. + Rn
Question 2: What is the condition for the series combination of resistance?
Answer:
For the resistor to be connected in series combination the important conditions are,
- The current passing through each resistor is the must be same.
- The resistors are connected in a linear manner.
Question 3: What is the “equivalent resistance” formula in the Parallel combination?
Answer:
The “equivalent resistance” formula in the Parallel combination is given below,
1/Req = 1/R1 + 1/R2 + 1/R3 + ….. + 1/Rn
Question 4: What is the condition for the parallel combination of resistance?
Answer:
For the resistor to be connected in parallel combination the important conditions are,
- The voltage difference across each resistor is the same.
- The resistors are connected parallel to each other.
Last Updated :
21 Mar, 2023
Like Article
Save Article

Вы видели ее везде: на одежде, сумках, автомобилях, татуированных людях, в интернете, в рекламе по телевизору. Возможно, даже в учебнике. Стивен Хокинг включил в свою книгу только ее, единственную, а одна поп-певица назвала этой формулой свой альбом. Интересно, знала она при этом, в чем смысл формулы? Хотя вообще, это дело не наше, и дальше не об этом.
Как вы поняли, речь ниже пойдет о самой эпичной и знаменитой формуле Эйнштейна:
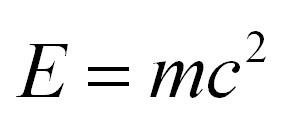
Пожалуй, это самая популярная физическая формула. Но в чем ее смысл? Уже знаете? Отлично! Тогда предлагаем ознакомиться с другими, не такими известными, но не менее полезными формулами, которые действительно могут пригодиться при решении разных задач.
А тем, кто хочет узнать смысл формулы Эйнштейна быстро и без копания в учебниках, добро пожаловать в нашу статью!
Формула Эйнштейна – самая знаменитая формула
Альберт Эйнштейн (1879-1955) опубликовал специальную теорию относительности в 1905 году. Именно в этой работе фигурировала знаменитая формула, а сам Эйнштейн был 26-летним служащим патентного бюро.

Интересно, что Эйнштейн не был преуспевающим учеником и даже имел проблемы с получением аттестата зрелости. Когда его спрашивали, как он смог придумать теорию относительности, физик отвечал: “Нормальный взрослый человек вообще не задумывается над проблемой пространства и времени. По его мнению, он уже думал об этой проблеме в детстве. Я же развивался интеллектуально так медленно, что пространство и время занимали мои мысли, когда я стал уже взрослым. Естественно, я мог глубже проникать в проблему, чем ребёнок с нормальными наклонностями”.
1905 год называют годом чудес, так как именно тогда была заложена основа для научной революции.
Что есть что в формуле Эйнштейна
Вернемся к формуле. В ней всего три буквы: E, m и c. Если бы все в жизни было так просто!
Каждый школьник в шестом классе уже знает, что:
- m – это масса. В ньютоновской механике – скалярная и аддитивная физическая величина, мера инертности тела.
- с в формуле Эйнштейна – скорость света. Максимальная возможная скорость в мире, считается фундаментальной физической константой. Скорость света равна 300000 (примерно) километров в секунду.
- E – энергия. Фундаментальная мера взаимодействия и движения материи. В этой формуле фигурирует не кинетическая и не потенциальная энергия. Здесь E – энергия покоя тела.
Важно понимать, что в теории относительности механика Ньютона – частный случай. Когда тело движется со скоростью, близкой к с, масса изменяется. В формуле m обозначает массу покоя.
Так вот, формула связывает эти три величины и называется еще законом или принципом эквивалентности массы и энергии.
Масса – мера содержания энергии в теле.
Смысл формулы Эйнштейна: связь энергии и массы
Как это работает? Например: жаба греется на солнце, девушки в бикини играют в волейбол, вокруг красота. Почему все это происходит? Прежде всего, из-за термоядерного синтеза, который протекает внутри нашего Солнца.
Там атомы водорода сливаются, образуя гелий. На других звездах протекают такие же реакции или реакции с более тяжелыми элементами, но суть остается той же. В результате реакции выделяется энергия, которая летит к нам в виде света, тепла, ультрафиолетового излучения и космических лучей.
Откуда берется эта энергия? Дело в том, что масса двух вступивших в реакцию атомов водорода больше, чем масса образовавшегося в результате атома гелия. Эта разница масс и превращается в энергию!
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один пример – механизм работы ядерного реактора.
Термоядерный синтез на Солнце неуправляемый. Люди уже освоили этот тип синтеза на Земле и построили водородную бомбу. Если бы мы могли замедлить реакцию и получить управляемый термоядерный синтез, у нас был бы практически неиссякаемый источник энергии.
О материи и энергии
Итак, мы выяснили смысл формулы и рассказали о принципе эквивалентности массы и энергии.
Массу можно превратить в энергию, а энергии соответствует некоторая масса.
При этом важно не путать понятия материи и энергии и понимать, это это разные вещи.
Фундаментальный закон природы – закон сохранения энергии. Он гласит, что энергия ниоткуда не берется и никуда не девается, ее количество во Вселенной постоянно, изменяется только форма. Закон сохранения массы является частным случаем для закона сохранения энергии.
Что есть энергия, а что – материя? Посмотрим на вещи с вот такой стороны: когда частица движется со скоростью, близкой к скорости света, она рассматривается как излучение, то есть энергия. Покоящаяся или движущаяся с медленной скоростью частица определяется как материя.
В момент Большого Взрыва материи не существовало, была лишь энергия. Потом Вселенная остыла, и часть энергии перешла в материю.
Сколько энергии заключено в материи? Зная массу тела, мы можем рассчитать, чему равна энергия этого тела согласно формуле Эйнштейна. Скорость света сама по себе немаленькая величина, а ее квадрат – и подавно. Это значит, что в очень маленьком кусочке материи заключена огромная энергия. Подтверждение тому – атомная энергетика.
Таблетка ядерного топлива (на АЭС используется обогащенный уран) весит 4,5 грамма. Но дает энергию, эквивалентную энергии от сжигания 400 килограммам угля. Хороший КПД, не так ли?
Итак, самая знаменитая формула физики говорит о том, что материю можно преобразовать в энергию и наоборот. Энергия никуда не исчезает, а лишь изменяет свою форму.
Не будем приводить вывод формулы Эйнштейна – там нас ждут гораздо более сложные формулы, а они могут отбить у начинающих ученых весь интерес к науке. Наш студенческий сервис готов оказать помощь в решении вопросов по учебе. Сохраните энергию и силы с помощью наших экспертов!
Содержание материала
- Последовательное соединение элементов
- Последовательное соединение элементов
- Определение эквивалентного сопротивления
- Параллельное соединение резисторов. Калькулятор для расчета
- Основные преимущества
- Физические формулы и примеры вычислений
- Практическое применение
- Простое соединение
- Комбинированный контур
- Емкость в цепи переменного тока
- Виды устройств и их особенности
- Основные популярные типы
- Как рассчитать сложные схемы соединения резисторов
- Параллельное соединение
Последовательное соединение элементов
В случае последовательного подключения все приборы соединяются последовательно друг с другом, а собранная цепь не имеет разветвлений.
При таком подключении сила тока, проходящая через каждый резистор, будет одинаковая, а общее падение напряжения складывается из суммарных падений напряжения на каждом из приборов.
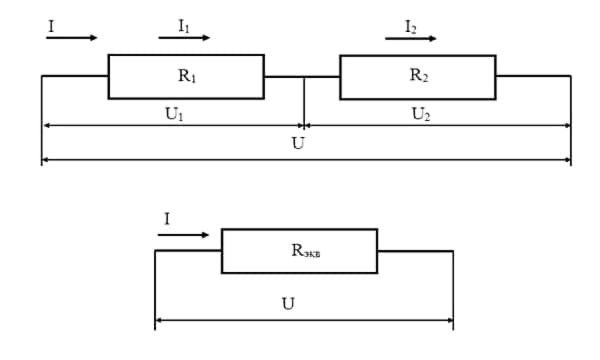
Последовательное подключение приборов
Чтобы определить суммарное значение в этом случае, воспользуемся законом Ома, который записывается следующим образом:
I = U/R.
Из вышестоящего выражения получаем значение R:
R = U/I (1).
Поскольку при последовательном соединении:
- I = I1 = I2 =…= IN (2),
- U = U1 + U2 +…+ UN (3),
формула для расчёта эквивалентного сопротивления (Rобщ или Rэкв) из (1) – (3) будет иметь вид:
- Rэкв = (U1 + U2 + …+ UN)/I,
- Rэкв = R1 + R2 + … + RN (4).
Таким образом, если имеется N последовательно соединённых одинаковых элементов, то их можно заменить на одно устройство, у которого:
Rобщ = N·R (5).
Последовательное соединение элементов
Подобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.
Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи.
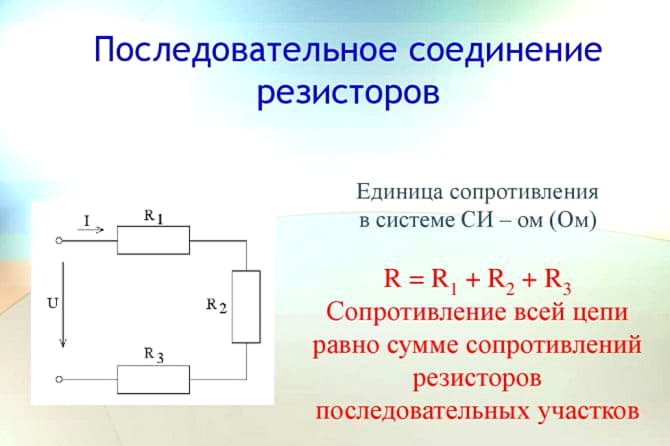
В случае постоянного тока формула закона Ома для отрезка цепи имеет вид:
Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула:
Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности.
Проходящий по цепи ток везде одинаковый:
Прикладываемое напряжение является суммой напряжений на каждом резисторе:
Следовательно, рассчитать можно общее:
Rэкв.= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.
Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R.
Определение эквивалентного сопротивления
При рассмотрении схем любых электрических или электронных устройств можно увидеть, что такие компоненты, как резисторы, имеют разные типы соединений между собой. Чтобы определить эквивалентное соединение, необходимо рассматривать два элемента, включенных в определённом порядке. Несмотря на то, что на чертеже их может быть несколько десятков, и соединены они по-разному, есть только два типа включения их друг с другом: последовательное и параллельное. Остальные конфигурации – это лишь их вариации.
Параллельное соединение резисторов. Калькулятор для расчета
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
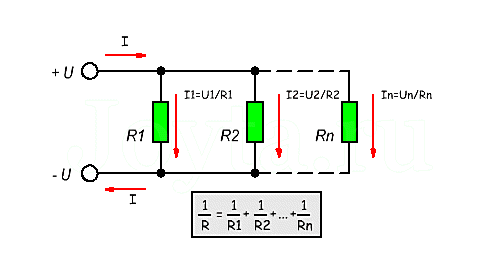
Основные преимущества
Светодиодные лампы Т8 значительно превосходят альтернативные образцы практически по всем показателям. К достоинствам приборов следует отнести:
- эффективность, высокие значения светового потока;
- экономичность;
- длительный срок службы;
- освещение имеет направленный характер, что позволяет организовать более эффективный и комфортный режим подсветки;
- подключение происходит мгновенно, чего не наблюдается у люминесцентных ламп;
- ровный, без мерцания режим работы;
- есть возможность работы при нестабильности напряжения в сети;
- не создают электромагнитных помех;
- нет вредного излучения в ультрафиолетовом диапазоне;
- попадание частиц жира или иных взвесей, находящихся в воздухе, не создает опасность перегрева и взрыва лампы, характерных для альтернативных конструкций;
- утилизация светодиодных устройств не требует специализированных мероприятий и может быть произведена обычным способом;
- подключать такие светильники можно напрямую к сети 220 В, без промежуточных устройств.

Помимо этих преимуществ, необходимо отметить широкие возможности выбора цветовой температуры ламп. Этот параметр позволяет создать в помещении определенную обстановку, позволяющую повысить концентрацию и увеличивающую работоспособность сотрудников. Такой результат достигается подключением ламп с холодным белым светом.
Если необходимо обеспечить более расслабленную, комфортную обстановку, выбирают экземпляры с теплым светом. Кроме этого, светодиоды хорошо переносят низкие температуры, что позволяет использовать их в неотапливаемых переходах, коридорах и прочих помещениях со сложными условиями эксплуатации.
Физические формулы и примеры вычислений
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.
Практическое применение
 Чаще всего на практике расчёт общего сопротивления цепи выполняют для того, чтобы узнать потребляемую мощность той или иной схемы. При этом, зная общее сопротивление, можно найти и такие важные параметры цепи, как ток и напряжение. Поэтому и рисуют эквивалентную схему электрической цепи. Простые цепи состоят только из последовательных или параллельных участков, но чаще встречаются комбинированные соединения.
Чаще всего на практике расчёт общего сопротивления цепи выполняют для того, чтобы узнать потребляемую мощность той или иной схемы. При этом, зная общее сопротивление, можно найти и такие важные параметры цепи, как ток и напряжение. Поэтому и рисуют эквивалентную схему электрической цепи. Простые цепи состоят только из последовательных или параллельных участков, но чаще встречаются комбинированные соединения.
Перед тем как приступить к расчёту эквивалентного сопротивления, вся электрическая цепь разделяется на простые контуры. Как только импеданс каждого такого контура будет подсчитан, схема перерисовывается, но вместо контуров рисуется уже резистор. Затем всё повторяется, и это происходит до тех пор, пока не останется один элемент.
Простое соединение
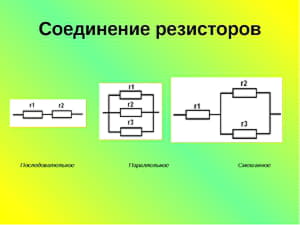 Пусть будет дана схема, состоящая из трёх резисторов, включённых последовательно. При этом сопротивление R1и R2 одинаковое и равно 57 Ом, а сопротивление R3 составляет один килоОм. Для расчёта общего сопротивления цепи сначала понадобится привести значение R3 согласно Международной системе единиц.
Пусть будет дана схема, состоящая из трёх резисторов, включённых последовательно. При этом сопротивление R1и R2 одинаковое и равно 57 Ом, а сопротивление R3 составляет один килоОм. Для расчёта общего сопротивления цепи сначала понадобится привести значение R3 согласно Международной системе единиц.
R3 = 1 кОм = 1000 Ом.
Так как соединение последовательное, используется формула: Ro = R1+R2+R3. Подставив известные значения, рассчитывается эквивалентное значение: Ro = 57+57+1000 = 1114 Ом.
Если же те же самые резисторы будут расположены параллельно друг другу, то для расчёта общего сопротивления уже используется другое выражение:
1/Ro = 1/R1 + 1/R2 +1/R3.
Ro = R1*R2*R3 / (R1*R2+R2*R3+R1*R3).
Подставив исходные данные в эту формулу, получим:
Ro = 57*57*1000/ (57*57 +57*1000+ 57*1000) = 3249000/117249 = 27,7 Ом.
Комбинированный контур
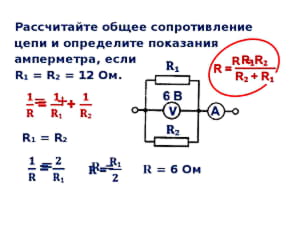 Необходимо вычислить мощность и эквивалентное сопротивление смешанной цепи, состоящей из четырёх резисторов. Резистор R1 =R2 =5 Ом, R3= 10 Ом, R4 =3 Ом. На схему подаётся питание пять вольт.
Необходимо вычислить мощность и эквивалентное сопротивление смешанной цепи, состоящей из четырёх резисторов. Резистор R1 =R2 =5 Ом, R3= 10 Ом, R4 =3 Ом. На схему подаётся питание пять вольт.
Первоначально понадобится упростить схему. Сопротивления R3 и R4 включены относительно друг друга параллельно. Поэтому находится их объединённое сопротивление:
Rp = (R3*R4)/(R3+R4).
Rp = (10*3)/ (10+3) = 2,3 Ом.
Теперь схему можно перерисовать в виде трёх последовательно включённых резисторов и найти общее сопротивление путём сложения их величин:
Ro = R1+R2+Rp = 5+5+2,3 = 12,3 Ом.
Зная эквивалентное сопротивление, используя закон Ома, несложно вычислить силу тока в цепи и мощность эквивалентного резистора:
I = U/R = 5/2,3 = 2,2 A.
P = I*U = 2,2*5= 11 Вт.
Таким образом, путём постепенного упрощения схемы можно свести цепь из последовательно и параллельно соединённых резисторов к одному элементу. А затем рассчитать его сопротивление и требуемую мощность.
Емкость в цепи переменного тока
При подаче на конденсатор постоянного напряжения он постепенно зарядится до максимальной разности потенциалов на его обкладках. После этого ток через электронный компонент прекратится и, не считая ничтожной утечки, будет равняться нулю. Поэтому в цепи постоянного тока конденсатор имеет огромное сопротивление. При расчетах его величину принимают равной бесконечности.
Реактивное сопротивление имеет вполне исчисляемое значение. Его можно измерить с помощью осциллографа, генератора и постоянного резистора. Для этого потребуется собрать схему. В ней конденсатор образует с резистором делитель напряжения. С помощью осциллографа будет измеряться потенциал, который образуется на выводах ёмкости.
Для данной схемы вычисления имеют следующий вид.
Формула косвенного измерения
Здесь:
- Ur – разность потенциалов на резисторе, В;
- Uc – напряжение на обкладках, В;
- R – сопротивление резистора, ом;
- Xc – сопротивление ёмкости, ом;
- I – ток, протекающий в цепи, А.
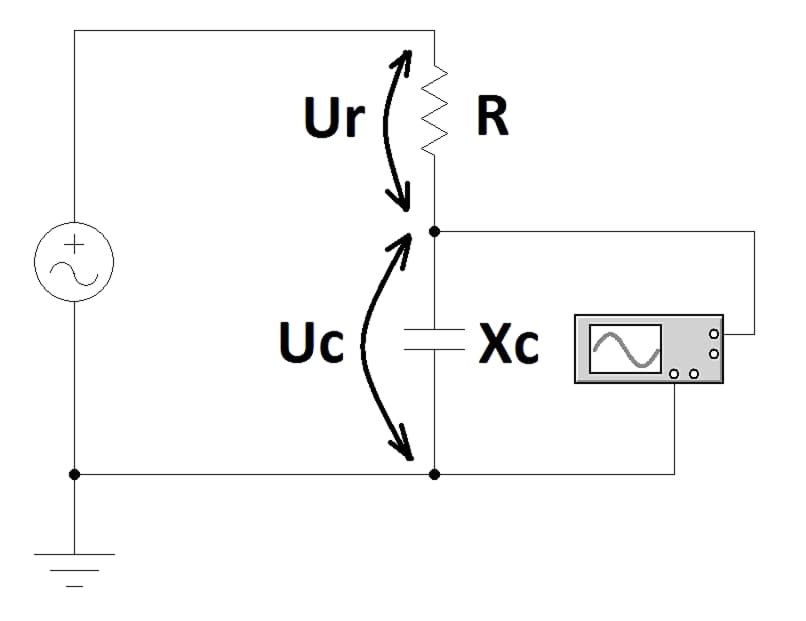 Косвенное измерение
Косвенное измерение
Важно! Электрический кабель также обладает ёмкостью. Поэтому после снятия напряжения на нём остаётся некоторый заряд
Данное явление опасно для человека, особенно, если проводник до отключения находился под потенциалом 1000 В и выше.
Виды устройств и их особенности
Разновидностей штепсельных розеток и блоков довольно много. У каждого типа свои конструктивные особенности и предназначение.
- Скрытые приборы монтируют прямо в стену — в специальные подрозетники.
- Открытые устройства выпускают для тех квартир, где электропроводка не спрятана в стену.
- Выдвижные розеточные блоки монтируют в стол или другую мебель. Их удобство в том, что после эксплуатации приборы легко спрятать от посторонних глаз и шаловливых детских рук.
Приборы отличаются методом зажима контактов. Он бывает винтовым и пружинным. В первом случае проводник фиксируют винтом, во втором — с помощью пружины. Надежность последних больше, однако в продаже их найти не так просто. На стенах устройства закрепляют тремя способами — лапками с зубчатыми краями, саморезами или специальной пластиной — суппортом, который облегчает как установку, так и демонтаж розетки.
Помимо обычных, недорогих устройств существуют модели, оснащенные заземляющими контактами. Это лепестки располагаются в верхней и нижней части, к ним крепят провод заземления. Для обеспечения безопасности выпускают розетки, оборудованные шторкам либо защитными крышками.
Основные популярные типы
К ним относятся:
- вид «С», он имеет 2 контакта — фазу и ноль, обычно покупается, если предназначен для техники малой либо средней мощности;
- тип «F», помимо традиционной пары оснащается еще одним контактом — заземляющим, эти розетки становятся более популярными, так как для квартир в новостройках заземляющий контур стал нормой;
- Вид «Е», отличающийся от предыдущего только формой контакта заземления, это штырь, такой же, как и элементы вилки розетки.
Последний тип встречается реже остальных, так как он менее удобен в эксплуатации: разворот штепселя на 180° при такой розетке невозможен.
Защищенность корпуса — следующее различие моделей. Степень безопасности обозначают индексом IP и двухзначным числом, следующим за этими буквами. Первая цифра обозначает класс защиты от пыли, твердых тел, вторая — от влаги.
- Для обычных жилых комнат достаточно моделей класса IP22 либо IP33.
- IP43 рекомендуют покупать для детских, так как эти розетки оснащены крышками/шторками, блокирующими гнезда, когда техника не используется.
- IP44 — тот минимум, что необходим для ванных комнат, кухонь, бань. Угрозой в них может быть не только сильная влажность, но и брызги воды. Подойдут они для монтажа в подвалах без отопления.
Установка розетки на открытом балконе — достаточное основание для покупки изделия с большей степенью защиты, это как минимум IP55.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
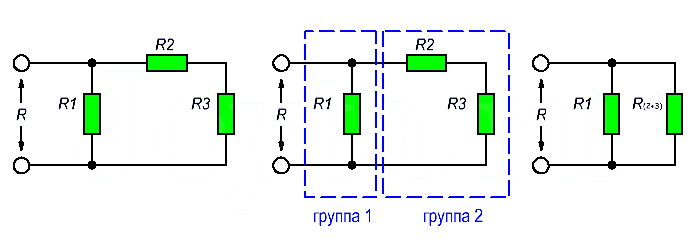 Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения. Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения. Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Параллельное соединение
Реактивное сопротивление
При таком подключении входы от всех устройств соединены в одной точке, выходы – в другой точке. Эти точки в физике и электротехнике называются узлами. На электрических схемах узлы представляют собой места разветвления проводников и обозначаются точками.
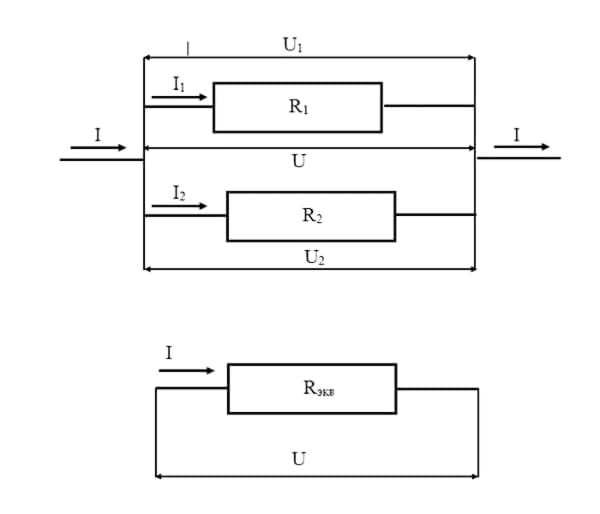
Параллельное соединение
Расчет эквивалентного сопротивления также выполняем с помощью закона Ома.
В этом случае общее значение силы тока складывается из суммы сил токов, протекающих по каждой ветви, а величина падения напряжения для каждого устройства и общее напряжение одинаковые.
Если имеются N резистивных устройств, подключенных таким образом, то:
I = I1 + I2 + … + IN (6),
U = U1 = U2 = … = UN (7).
Из выражений (1), (6) и (7) имеем:
- Rобщ = U/(I1 + I2 + …+ IN),
- 1/Rэкв = 1/R1 + 1/R2 +…+ 1/RN (8).
Если имеется N одинаковых резисторов, имеющих подключение данного типа, то формула (8) преобразуется следующим образом:
Rобщ = R · R / N·R = R / N (9).
Если соединены несколько катушек индуктивности, то их суммарное индуктивное сопротивление рассчитывается так же, как и для резисторов.
