Как найти с какой силой давит вода

Пловец, нырнувший глубоко, ощущает боль в ушах. На барабанные перепонки воздействует сила давления воды.

Корабль в воде не тонет благодаря выталкивающей силе. Вода способна легко изменять свою форму, она воздействует на поверхности тел при соприкосновении с ними.

Чему равна сила давления воды и что это такое, расскажем в статье.

Что это такое?

В сосуде, заполненном водой, на дно давит сила, равная весу столба жидкости. Это вызванное силой тяжести давление называется гидростатическим.

Оно определяется отношением силы к площади, то есть его физический смысл – это сила, действующая на единицу площади (см2).

Законы гидростатики описал Блез Паскаль. В 1648 г. он удивил горожан опытом, демонстрирующим свойства воды.

Вставив в бочку, заполненную водой, длинную узкую трубку, он налил в нее несколько кружек воды, и бочку разорвало.

Согласно закону Паскаля, приложенное к H2O усилие распространяется равномерно во всем объеме. Это объясняется тем, что вода почти не сжимается. В гидравлических прессах используют это свойство.

Плотность воды все же растет при высоком давлении. Это учитывается при расчетах конструкций глубоководных аппаратов.

Факторы, влияющие на показатель

При отсутствии внешнего воздействия, играют роль два фактора:

• высота столба;
• плотность.

Выше уровень воды, налитой в сосуд, — выше напор на дно. Если в одной емкости ртуть, а в другой вода и при этом уровни жидкостей одинаковы, то в первом случае давление на дно больше, так как ртуть имеет большую плотность.

Сверху на содержимое сосуда давит также атмосферный воздух. Поэтому в сообщающихся сосудах уровень одинаков, ведь в каждом из них над поверхностью атмосфера одна и та же.

Если же к поверхности приложить поршень и давить на него, то напор будет складываться из:

• внешней силы;
• веса воды.

При этом форма сосуда не определяет размер усилия, создаваемого столбом. Оно будет одним и тем же при равной высоте столба, хотя стенки емкости могут расширяться кверху или сужаться.

На дно и стенку сосуда – в чем разница?

Вода, заполняющая емкость, оказывает давление по направлению всегда перпендикулярно поверхности твердого тела, по всей площади соприкосновения с дном и стенками.

Усилие на дно распределено равномерно, то есть оно одинаково в любой точке. Заполнив водой сито, можно увидеть, что струи, текущие через отверстия, равны по напору.

Наполнив сосуд, имеющий отверстия одного диаметра в стенках на разной высоте, можно наблюдать различный напор вытекающей струи. Чем выше отверстие – тем слабее струя. То есть, давление на стенки емкости тем больше, чем ближе ко дну.

Единицы измерения

Давление воды измеряют в:

• паскалях – Па;
• метрах водяного столба – м. в. ст.
• атмосферах – атм.

Практически достаточно знать, что 1 атмосфера равна 10 метрам водяного столба или 100000 Па (100кПа).

Формулы расчета

Давление на дно сосуда рассчитывается делением силы на площадь, то есть оно равно произведению плотности воды, высоты столба и ускорения свободного падения g (величина постоянная, равна 9,8 м/с2).

Пример расчета: бак наполнен водой (плотность 1000 кг/м3) до высоты 1,2 м. Нужно найти, какое давление испытывает дно бака. Решение: P = 1000*1, 2*9, 8 = 11760 Па, или 11, 76 кПа.

Для расчета давления на стенки сосуда применяют все ту же формулу напора, приведенную выше. При расчете берется глубина от точки, в которой нужно рассчитать напор, до поверхности воды.

Пример расчета: на глубине 5 м на стенку резервуара с водой будет оказываться давление P=1000 *5 * 9, 8=49000 кПа, что составляет 0,5 атмосферы.

Расчет давления воды на дно и стенки сосуда в видео:

Применение на практике

Примеры использования знаний свойств воды:

1. Подбирая насос для водоснабжения дома высотой 10 м, понимают, что напор должен быть минимум 1 атм.
2. Водонапорная башня снабжает водой дома ниже ее по высоте, напор в кране у потребителей обеспечен весом столба воды в баке.
3. Если в стенках бочки появились отверстия, то, чем ниже они расположены, тем более прочным должен быть материал для их заделки.
4. Замеряют дома напор холодной воды в кране манометром. Если он менее чем 0,3 атм (установлено санитарными нормами), есть основания для претензий к коммунальщикам.

Используя гидравлический пресс, можно получить большое усилие, при этом приложив малую силу. Примеры применения:

• выжимка масла из семян растений;
• спуск на воду со стапелей построенного судна;
• ковка и штамповка деталей;
• домкраты для подъема грузов.

Заключение

Такие свойства воды, как текучесть и несжимаемость, дают возможность использовать силу ее давления для самых различных целей.

Опасность этого явления учитывают при расчетах на прочность корпусов подводных лодок, стенок и днищ резервуаров, в которых хранят воду. Сила давления воды совершает полезную работу, она же способна и разрушать.

Как вы уже знаете, согласно закону Паскаля, давление в жидкостях распространяется одинаково во всех направлениях. Что же необходимо знать, чтобы рассчитать это давление? От чего зависит давление жидкости?

Взгляните на рисунок 1.

Как вы думаете, в каком сосуде больше жидкости? А будет ли одинаково давление, оказываемое на дно сосудов? С этими вопросами нам и предстоит разобраться. 

Вывод формулы

Выведем формулу для расчета давления жидкости на дно сосуда, имеющего форму прямоугольного параллелепипеда (рисунок 2).

Давление жидкости $p$ рассчитывается по формуле: $p = frac{F}{S}$, где $F$ — это сила, действующая на дно сосуда, а $S$ — это площадь дна сосуда.

1. Сила $F$ в данном случае равна весу $P$ жидкости, которая находится в сосуде;
2. Как узнать вес жидкости? Необходимо знать массу $m$ жидкости;
3. Массу $m$ мы можем вычислить по известной нам формуле: 
   $m = rho V$;

1. Так как нам известна жидкость, находящаяся в сосуде, мы знаем ее плотность . Остается вычислить объем $V$ жидкости. Обозначим высоту столба жидкости буквой $h$, площадь дна сосуда — $S$. Тогда объем можно вычислить по формуле:
   $V = Sh$;

1. Итак, подставляем наши данные в формулу для вычисления массы и получаем:
   $m = rho Sh$;

1. Таким образом, возвращаемся к весу жидкости и получаем, что: 
   $P = mg$, где $g$ — ускорение свободного падения, или $P = g rho Sh$.

С другой стороны, мы знаем, что вес столба жидкости равен силе, с которой жидкость давит на дно сосуда. Поэтому если мы разделим вес $P$ на площадь $S$, то получим искомое давление жидкости:
$p = frac{P}{S}$,
или $p =frac{g rho Sh}{S}$,

То есть:

$p = rho gh$.

Рассмотрим измерительные величины, которые мы будем использовать в данной формуле: плотность мы будем выражать в килограммах на кубический метр ($frac{кг}{м^3}$), $g = 9.8 frac{H}{кг}$, высоту столба жидкости  — в метрах ($м$). Тогда давление $p$ будет выражено в паскалях ($Па$).

Выводы

Так мы с вами вывели формулу для расчета давления жидкости на дно сосуда. Какие выводы мы можем сделать? 

От каких величин зависит давление жидкости на дно сосуда?

Давление жидкости не зависит от формы сосуда, оно зависит только от плотности жидкости и высоты ее столба.

Обратите внимание, что во многих случаях, когда говорят о высоте столба жидкости, говорят о глубине.

По какой формуле рассчитывают давление жидкости на стенки сосуда, давление внутри жидкости?

По формуле $p = rho gh$ можно вычислить давление на стенки сосуда или внутри жидкости, так как на одной глубине давление в жидкости будет одинаково во всех направлениях.

Вопросы и пример задачи

Посмотреть ответ

Скрыть

Посмотреть ответ

Скрыть ответ

Дано:
$rho = 800 frac{кг}{м^3}$
$h = 8 space м$

$p — ?$

Посмотреть решение и ответ

Скрыть

Упражнения

Дано:
$h = 0.6 space м$
$rho_1 = 1000 frac{кг}{м^3}$
$rho_2 = 800 frac{кг}{м^3}$
$rho_3 = 13600 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$

$p_1 — ?$
$p_2 — ?$
$p_3 — ?$

Показать решение и ответ

Скрыть

Дано:
$h = 10 space 900 space м$
$rho = 1030 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$

$p — ?$

Показать решение и ответ

Скрыть

Дано:
$m = 5 space кг$
$h = 1 space м$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$

$S — ?$

Показать решение и ответ

Скрыть

Задания

Показать ответ

Скрыть

Дано:
$h = 0.086 space м$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$

$p — ?$

Показать решение и овет

Скрыть

Условие задачи:

Аквариум наполнен доверху водой. С какой средней силой давит вода на стенку аквариума длиной 50 см и высотой 30 см?

Задача №3.2.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(a=50) см, (h=30) см, (P_{ст}-?)

Решение задачи:

Так как давление – это сила, действующая на единицу площади, то искомую силу (P_{ст}) можно найти по формуле:

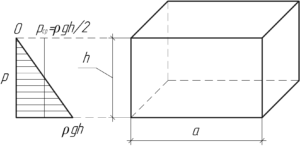
[{P_{ст}} = {p_{ст}}{S_{ст}};;;;(1)]

Давление воды линейно зависит от давления: на уровне поверхности оно равно нулю, на уровне дна аквариума – величине (rho gh). Поэтому среднее давление на стенку аквариума можно найти таким образом:

[{p_{ст}} = rho gfrac{h}{2};;;;(2)]

Так как аквариум заполнен доверху, то площадь боковой стенки, на которую давит вода, равна:

[{S_{ст}} = ah;;;;(3)]

Подставим (2) и (3) в (1), получим:

[{P_{ст}} = rho gfrac{h}{2}ah]

[{P_{ст}} = rho gfrac{{a{h^2}}}{2}]

Переведем геометрические размеры аквариума в систему СИ:

[50;см = frac{{50}}{{100}};м = 0,5;м]

[30;см = frac{{30}}{{100}};м = 0,3;м]

Численно сила давления на стенку аквариума равна:

[{P_{ст}} = 1000 cdot 10 cdot frac{{0,5 cdot {{0,3}^2}}}{2} = 225;Н]

Ответ: 225 Н.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.2.4 Аквариум имеет форму куба со стороной 0,6 м. До какой высоты следует налить в него
3.2.6 В сосуд, имеющий форму прямоугольной призмы, шириной 15 см и длиной 35 см налита
3.2.7 На сколько отличается давление столбика ртути высотой 10 мм от давления столбика

С какой силой давит вода на иллюминатор батискафа на глубине 1,5 км, если иллюминатор имеет форму круга диаметром 400 мм?