Скорость, время и высота свободного падения
- Главная
- /
- Физика
- /
- Скорость, время и высота свободного падения
Чтобы посчитать скорость свободного падения, а также время или расстояние (высоту) свободного падения, воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Скорость свободного падения
Если известно время падения
Ускорение свободного падения g =
Время падения
t =
Расстояние h =
0
Скорость свободного падения
V =
0
/
Округление ответа:
Если известно расстояние (высота падения)
Ускорение свободного падения g =
Расстояние h =
Время падения
t =
0
Скорость свободного падения
V =
0
/
Округление ответа:
Расстояние и время свободного падения
Ускорение свободного падения g =
Скорость свободного падения
V =/
Расстояние h =
0
Время падения
t =
0
Округление ответа:
Просто введите данные, и получите ответ.
Стоит обратить внимание, на то, что данный калькулятор не учитывает сопротивление воздуха (атмосферы) и других сил способных повлиять на скорость падения тела, кроме силы тяжести.
Теория
Ускорение свободного падения
Ускорение свободного падения (g) – ускорение, которое придаёт падающему телу сила тяжести. У каждого небесного тела своё значение ускорения свободного падения, например, у планеты Земля оно составляет g = 9,80665 м/с².
Для небесных тел солнечной системы ускорение свободного падения имеет следующие значения:
- Земля – 9,80665 м/с²
- Луна – 1,62 м/с²
- Меркурий – 3,7 м/с²
- Венера – 8,87 м/с²
- Марс – 3,711 м/с²
- Сатурн – 10,44 м/с²
- Юпитер – 24,79 м/с²
- Нептун – 11,15 м/с²
- Уран – 8,87 м/с²
- Плутон – 0,617 м/с²
- Ио – 1,796 м/с²
- Европа – 1,315 м/с²
- Ганимед – 1,428 м/с²
- Каллисто – 1,235 м/с²
- Солнце – 274,0 м/с²
Как найти скорость свободного падения
Скорость свободного падения V можно рассчитать, зная расстояние (высоту) падения h или время падения t.
Зная время падения:
Формула
V = g⋅t
Пример
Для примера, рассчитаем с какой скоростью врежется в землю монета, брошенная из окна небоскрёба, если известно, что она упала за 5 секунд:
V = 9.8 ⋅ 5 = 49 м/с
Монетка ударилась об землю на скорости 49 м/с
Зная высоту падения:
Формула
V = √2⋅h⋅g
Пример
Для примера, определим скорость при ударе об землю ядра скинутого с 100 метровой вышки:
V = √2 ⋅ 100 ⋅ 9.8 = √1960 ≈ 44 м/с
Ядро ударится об землю на скорости 44 м/с
Время свободного падения
Время свободного падения – время, которое потребуется телу для того чтоб упасть на землю под действием силы тяжести. Чтобы рассчитать время свободного падения t необходимо знать высоту падения h или скорость в конце падения V.
Зная высоту падения:
Формула
t = √2h⁄g
Пример
Посчитаем чему будет равно время свободного падения t тела упавшего с высоты h = 100 метров:
t = √2⋅100⁄9.8 = √20.4 ≈ 4.5 с
Время свободного падения данного тела составит 4.5 секунды.
Зная скорость в конце падения:
Формула
t = V⁄g
Пример
Если тело после падения ударилось об землю со скоростью V = 50 м/с, то сколько секунд оно падало?
t = 50 ÷ 9.8 = 5.1 с
Время падения данного тела составило 5.1 секунды.
Высота свободного падения
Высота падения – высота с которой сбросили тело, численно равная расстоянию, которое пролетает тело за время падения. Чтобы рассчитать высоту падения h необходимо знать время падения t или скорость в конце падения V.
Зная время падения:
Формула
h = gt²⁄2
Пример
Для примера определим с какой высоты сбросили тело, если известно, что время его падения составило t = 5с:
h = 9.8 ⋅ 5² ÷ 2 = 122.5 м
Тело сбросили с высоты в 122.5 метров.
Зная скорость в конце падения:
Формула
h = V²⁄2g
Пример
Если тело после падения ударилось об землю со скоростью V = 60 м/с, то с какой высоты оно упало?
h = 60² ÷ 2⋅9.8 = 3600 ÷ 19.6 = 183.67 м
Тело упало с высоты в 183.67 метра.
См. также
1.6 Свободное падение.
Теория:Свободным падением называется движение тела под действием силы тяжести.
Ускорение свободного падения g = 9,8 м/с2 ≈ 10 м/с2 (на ОГЭ принемаем g = 10 м/с2)
В случае свободного падения v0 = 0 м/с, тогда скорость и высота падения находится по формулам:
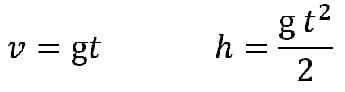
Если же тело бросили вверх (вниз) тогда скорость и высота падения находится по формулам:
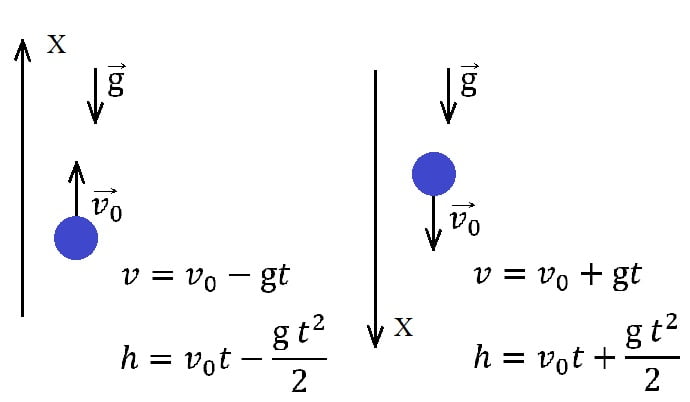
Задание фипи: Камень свободно падает из состояния покоя. Определите путь, пройденный камнем за третью секунду от начала движения. Ответ выразите в метрах.
| Дано: | СИ | Решение: |
|---|---|---|
|
t1 = 2c. t2 = 3c. |
. |
Найдем пройденный путь за 2 секунды свободного падения h1=gt2/2=10·22/2=20 м Путь за 3 секунды свободного падения h2=gt2/2=10·32/2=45 м Путь, пройденный камнем за третью секунду от начала движения: S=h2-h1=45-20=25 м. Ответ: 25 м. |
| S – ? |
Задание ОГЭ по физике: Через 3 с после начала свободного падения из состояния покоя тело оказалось на высоте 2 м отностительно поверхности земли. Какую скорость v имело тело в этот момент, и с какой высоты h оно начало падать? Сопротивлением воздуха пренебречь.
Решение: Воспользуемся формулой для нахождения скорости тела при свободном падении: v=gt, найдем скорость v=10·3=30 м/с, так же по формуле для нахождения пройденного пути при свободном падении найдем пройденный путь: S=gt2/2=10·32/2=45 м
, за 3 с тело преодалело путь в 45 м и оказалось на высоте 2 м, значит что бы найти высоту с которой упало тело надо сложить две величины: h=S+2=45+2=47 м.
Ответ: v=30 м/с , h=47 м.
Предыдущая тема Следующая тема
Знакомства в Израиле доска объявлений Израиля Знакомства.
Условие задачи:
С какой высоты падало тело, если за последние 2 с прошло путь 60 м? Сколько времени падало тело?
Задача №1.4.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(t_1=2) с, (S=60) м, (H-?), (t-?)
Решение задачи:
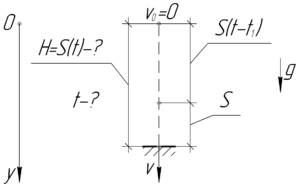 Итак, данный в условии задачи путь 60 м, пройденный за последние (t_1=2) секунды можно определить как разность пути за все время падения тела (t) и пути за время ((t-t_1)).
Итак, данный в условии задачи путь 60 м, пройденный за последние (t_1=2) секунды можно определить как разность пути за все время падения тела (t) и пути за время ((t-t_1)).
[S = Sleft( t right) – Sleft( {t – {t_1}} right)]
Поскольку движение тела является равноускоренным (с ускорением (g)) без начальной скорости, то указанные пути можно записать в виде общеизвестных формул:
[Sleft( t right) = frac{{g{t^2}}}{2}]
[Sleft( {t – {t_1}} right) = frac{{g{{left( {t – {t_1}} right)}^2}}}{2}]
В итоге имеем:
[S = frac{{g{t^2}}}{2} – frac{{g{{left( {t – {t_1}} right)}^2}}}{2}]
Раскроем скобки и выразим искомое полное время падения (t).
[frac{{g{t^2}}}{2} – frac{{g{t^2}}}{2} + gt{t_1} – frac{{gt_1^2}}{2} – S = 0]
[gt{t_1} – frac{{gt_1^2}}{2} – S = 0]
[t = frac{{S + frac{{gt_1^2}}{2}}}{{g{t_1}}}]
[t = frac{{2S + gt_1^2}}{{2g{t_1}}}]
Мы получили красивый ответ на второй вопрос задачи.
[t = frac{S}{{g{t_1}}} + frac{{{t_1}}}{2}]
Понятно, что рассчитать высоту, с которой падало тело, не составит большего труда, если использовать приведенную выше формулу.
[H = Sleft( t right) = frac{{g{t^2}}}{2}]
[H = frac{g}{2}{left( {frac{S}{{g{t_1}}} + frac{{{t_1}}}{2}} right)^2}]
Теперь мы получили ответ и ко второму вопросу. Подсчитаем численные ответы по полученным двум формулам.
[t = frac{{60}}{{10 cdot 2}} + frac{2}{2} = 4; с ]
[H = frac{{10}}{2}{left( {frac{{60}}{{10 cdot 2}} + frac{2}{2}} right)^2} = 80; м ]
Ответ: 4 с; 80 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.4.25 С вертолета, находящегося на высоте 500 м, упал камень. Через какое время
1.4.27 Свободно падающее тело прошло последние 30 м за 0,5 с. С какой высоты
1.4.28 Тело падает с высоты 10 м. За какое время тело прошло последний метр пути?
Что такое свободное падение? Это падение тел на Землю при отсутствии сопротивления воздуха. Иначе говоря – падение в пустоте. Конечно, отсутствие сопротивления воздуха – это вакуум, который нельзя встретить на Земле в нормальных условиях. Поэтому мы не будем брать силу сопротивления воздуха во внимание, считая ее настолько малой, что ей можно пренебречь.
Ускорение свободного падения
Проводя свои знаменитые опыты на Пизанской башне Галилео Галилей выяснил, что все тела, независимо от их массы, падают на Землю одинаково. То есть, для всех тел ускорение свободного падения одинаково. По легенде, ученый тогда сбрасывал с башни шары разной массы.
Ускорение свободного падения – ускорение, с которым все тела падают на Землю.
Ускорение свободного падения приблизительно равно 9,81 мс2 и обозначается буквой g. Иногда, когда точность принципиально не важна, ускорение свободного падения округляют до 10 мс2.
Земля – не идеальный шар, и в различных точках земной поверхности, в зависимости от координат и высоты над уровнем моря, значение g варьируется. Так, самое большое ускорение свободного падения – на полюсах (≈9,83 мс2), а самое малое – на экваторе (≈9,78 мс2).
Свободное падение тела
Рассмотрим простой пример свободного падения. Пусть некоторое тело падает с высоты h с нулевой начальной скоростью. Допустим мы подняли рояль на высоту h и спокойно отпустили его.
Свободное падение – прямолинейное движение с постоянным ускорением. Направим ось координат от точки начального положения тела к Земле. Применяя формулы кинематики для прямолинейного равноускоренного движения, можно записать.
h=v0+gt22.
Так как начальна скорость равна нулю, перепишем:
h=gt22.
Отсюда находится выражение для времени падения тела с высоты h:
t=2hg.
Принимая во внимание, что v=gt, найдем скорость тела в момент падения, то есть максимальную скорость:
v=2hg·g=2hg.
Движение тела, брошенного вертикально вверх
Аналогично можно рассмотреть движение тела, брошенного вертикально вверх с определенной начальной скоростью. Например, мы бросаем вверх мячик.
Пусть ось координат направлена вертикально вверх из точки бросания тела. На сей раз тело движется равнозамедленно, теряя скорость. В наивысшей точки скорость тела равна нулю. Применяя формулы кинематики, можно записать:
v=v0-gt.
Подставив v=0, найдем время подъема тела на максимальную высоту:
t=v0g.
Время падения совпадает со временем подъема, и тело вернется на Землю через t=2v0g.
Максимальная высота подъема тела, брошенного вертикально:
h=v022g.
Взглянем на рисунок ниже. На нем приведены графики скоростей тел для трех случаев движения с ускорением a=-g. Рассмотрим каждый из них, предварительно уточнив, что в данном примере все числа округлены, а ускорение свободного падения принято равным 10мс2.
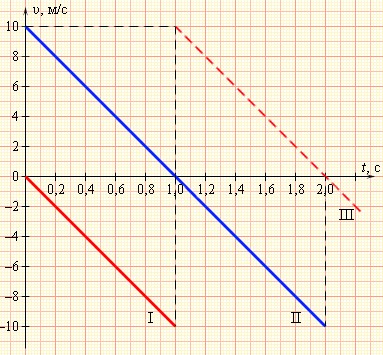
Первый график – это падение тела с некоторой высоты без начальной скорости. Время падения tп=1с. Из формул и из графика легко получить, что высота, с которой падало тело, равна h=5м.
Второй график – движение тела, брошенного вертикально вверх с начальной скоростью v0=10 мс. Максимальная высота подъема h=5м. Время подъема и время падения tп=1с.
Третий график является продолжением первого. Падающее тело отскакивает от поверхности и его скорость резко меняет знак на противоположный. Дальнейшее движение тела можно рассматривать по второму графику.
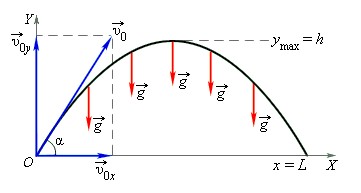
Движение тела, брошенного под углом к горизонту
С задачей о свободном падении тела тесно связана задача о движении тела, брошенного под определенным углом к горизонту. Так, движение по параболической траектории можно представить как сумму двух независимых движений относительно вертикальной и горизонтальной осей.
Вдоль оси OY тело движется равноускоренно с ускорением g, начальная скорость этого движения – v0y. Движение вдоль оси OX – равномерное и прямолинейное, с начальной скоростью v0x.
Условия для движения вдоль оси ОХ:
x0=0; v0x=v0cosα; ax=0.
Условия для движения вдоль оси OY:
y0=0; v0y=v0sinα; ay=-g.
Приведем формулы для движения тела, брошенного под углом к горизонту.
Время полета тела:
t=2v0sinαg.
Дальность полета тела:
L=v02sin2αg.
Максимальная дальность полета достигается при угле α=45°.
Lmax=v02g.
Максимальная высота подъема:
h=v02sin2α2g.
Отметим, что в реальных условиях движение тела, брошенного под углом к горизонту, может проходить по траектории, отличной от параболической вследствие сопротивления воздуха и ветра. Изучением движения тел, брошенных в пространстве, занимается специальная наука – баллистика.
2016-11-18 ![]()
В последнюю секунду свободного падения с нулевой начальной скоростью тело прошло путь вдвое больший, чем в предыдущую секунду. С какой высоты упало тело?
Решение:

Обозначим через 0 ту точку, из которой тело начало движение. Начало системы координат помещаем в точку О. Так как тело движется вниз, ось у целесообразно направить также вниз (в этом случае значения координат тела по оси у будут положительными). Движение одномерное вдоль оси у, и оси х на рисунке нет (в любой момент времени координата тела по оси х равна нулю).
Отмечаем на рисунке положение тела в те моменты времени, о которых в задаче идет речь. Таких моментов времени четыре:
1) начальный момент времени $t = 0$ — ему соответствует точка 0;
2) начало предыдущей секунды $t_{1}$ ($t_{1}$ — время, которое показывает секундомер, включенный в момент $t = 0$, в тот момент, когда началась предыдущая секунда);
3) конец предыдущей — начало последней секунды $t_{2}$;
4) конец последней секунды (касание тела с поверхностью земли) $t_{3}$.
Запишем основное уравнение теории:
$y = y_{0} + v_{0y}t + frac{a_{y}t^{2}}{2}$,
применительно к условиям настоящей задачи. При этом учтем, что $y_{0} = 0$ в силу выбора начала системы отсчета; $v_{0y} = 0$ по условию задачи ($v_{0} = 0$); $a_{y} = g$, поскольку ось у направлена вниз. Таким образом, получаем:
$y = frac{gt^{2}}{2}$. (1)
Уравнение (1) записываем для всех тех моментов времени, о которых идет речь в условии задачи:
$y_{1} = frac{gt_{1}^{2}}{2}$, (2)
$y_{2} = frac{gt_{2}^{2}}{2}$, (3)
$y_{3} = frac{gt_{3}^{2}}{2}$, (4)
где через $y_{1}, y_{2}, y_{3}$ обозначены соответствующие данным моментам времени координаты.
Следующий шаг: информацию, содержащуюся в условии задачи в виде текста, следует записать с помощью математических соотношений.
В условии сказано, что пути, пройденные телом в последнюю и предыдущую секунды отличаются в два раза. Из рисунка видно, что путь за предыдущую секунду равен $y_{2} – y_{1}$, а за последнюю — $y_{3} – y_{2}$.
Следовательно:
$y_{3} – y_{2} = 2(y_{2}-y_{1})$ (5)
Кроме того, согласно тексту условия задачи:
$t_{2}-t_{1} = Delta t$ (6)
$t_{3} – t_{2} = Delta t$, (7)
где $Delta t = 1 с$.
На этом заканчивается «физический» этап решения. Переходим к «математическому» этапу. В задаче требуется найти высоту, с которой упало тело. Обращаясь к чертежу, видим, что эта высота есть уз — величина, которая непосредственно входит в систему уравнений.
Анализируем ситуацию: имеем систему из 6 уравнений (2—7) с 6-ю неизвестными $y_{1}, y_{2}, y_{3}, t_{1}, t_{2}, t_{3}$, из которой, следовательно, можно вычислить $y_{3}$.
Подставим $y_{1}, y_{2}$, и $y_{3}$ из (2, 3, 4) в (5) и воспользуемся разложением разности квадратов двух чисел:
$frac{g}{2}(t_{3}+t_{2})(t_{3}-t_{2}) = frac{g}{2} 2 (t_{2}+t_{1})(t_{2}-t_{1})$. (8)
С учетом (6) и (7), из (8) находим
$t_{3} + t_{2} = 2 (t_{1} + t_{2})$ или $t_{3} – t_{2} = 2t_{1}$.
С учетом (7), отсюда получаем:
$t_{1} = frac{ Delta t}{2}$,
$t_{2} = t_{1} + Delta t = frac{3}{2} Delta t$,
$t_{3} = t_{2} + Delta t = frac{5}{2} Delta t$.
Наконец, окончательно находим:
$y_{3} = frac{g left ( frac{5}{2} Delta t right )^{2}}{2} = frac{10 left ( frac{5}{2} right )^{2}}{2} = 31,25 м$.
