Как найти с окруж ответ

ГДЗ Решебники и ответы к Окружающему миру

Выберите класс

1 класс

Гдз по Окружающему миру 1 класс Рабочая тетрадь

Авторы:

Ивченкова Г.Г.,
Потапов М.К.,
…

Гдз по Окружающему миру 1 класс Рабочая тетрадь

Авторы:

Плешаков А.А.,

Гдз по Окружающему миру 1 класс Учебник

Авторы:

Плешаков А.А.,

Гдз по Окружающему миру 1 класс Рабочая тетрадь

Авторы:

Плешаков А.А.,

Гдз по Окружающему миру 1 класс Рабочая тетрадь

Авторы:

Плешаков А.А.,
Новицкая М.Ю.,
…

Гдз по Окружающему миру 1 класс Учебник

Авторы:

Плешаков А.А.,

Гдз по Окружающему миру 1 класс Тетрадь для самостоятельной работы

Авторы:

Федотова О.Н.,
Трафимов С.А.,
…

Гдз по Окружающему миру 1 класс Рабочая тетрадь

Авторы:

Вахрушев А.А.,
Бурский О.В.,
…

Гдз по Окружающему миру 1 класс Рабочая тетрадь

Авторы:

Виноградова Н.Ф.,

Гдз по Окружающему миру 1 класс Рабочая тетрадь

Авторы:

Дмитриева В.Ф.,
Казаков А.Н.,
…

Гдз по Окружающему миру 1 класс Проверочные работы

Авторы:

Плешаков А.А.,

2 класс

Гдз по Окружающему миру 2 класс Контрольно-измерительные материалы (КИМ)

Авторы:

Яценко И.Ф.,

Гдз по Окружающему миру 2 класс Тесты

Авторы:

Плешаков А.А.,
Гара Н.Н.,
…

Гдз по Окружающему миру 2 класс Рабочая тетрадь

Авторы:

Виноградова Н.Ф.,

Гдз по Окружающему миру 2 класс Рабочая тетрадь

Авторы:

Дмитриева В.Ф.,
Казаков А.Н.,
…

Гдз по Окружающему миру 2 класс Учебник

Авторы:

Плешаков А.А.,

Гдз по Окружающему миру 2 класс Рабочая тетрадь

Авторы:

Плешаков А.А.,

Гдз по Окружающему миру 2 класс Рабочая тетрадь

Авторы:

Плешаков А.А.,

Гдз по Окружающему миру 2 класс Рабочая тетрадь

Авторы:

Плешаков А.А.,
Новицкая М.Ю.,
…

Гдз по Окружающему миру 2 класс Тетрадь для самостоятельной работы

Авторы:

Федотова О.Н.,
Трафимова Г.В.,
…

Гдз по Окружающему миру 2 класс Проверочные и контрольные работы

Авторы:

Вахрушев А.А.,
Бурский О.В.,
…

Гдз по Окружающему миру 2 класс Рабочая тетрадь

Авторы:

Вахрушев А.А.,
Бурский О.В.,
…

Гдз по Окружающему миру 2 класс Учебник

Авторы:

Плешаков А.А.,

Гдз по Окружающему миру 2 класс Проверочные работы

Авторы:

Плешаков А.А.,

3 класс

Гдз по Окружающему миру 3 класс Контрольно-измерительные материалы (КИМ)

Авторы:

Тихомирова Е.М.,

Гдз по Окружающему миру 3 класс Контрольно-измерительные материалы (КИМ)

Авторы:

Яценко И.Ф.,

Гдз по Окружающему миру 3 класс Проверочные и диагностические работы

Авторы:

Потапов М.К.,
Калинина О.Б.,
…

Гдз по Окружающему миру 3 класс Проверочные и контрольные работы

Авторы:

Вахрушев А.А.,
Бурский О.В.,
…

Гдз по Окружающему миру 3 класс Рабочая тетрадь

Авторы:

Ивченкова Г.Г.,
Потапов М.К.,
…

Гдз по Окружающему миру 3 класс Рабочая тетрадь

Авторы:

Вахрушев А.А.,
Бурский О.В.,
…

Гдз по Окружающему миру 3 класс Проверочные работы

Авторы:

Плешаков А.А.,

Гдз по Окружающему миру 3 класс Рабочая тетрадь

Авторы:

Виноградова Н.Ф.,
Калинова Г.С.,
…

Гдз по Окружающему миру 3 класс Рабочая тетрадь

Авторы:

Плешаков А.А.,
Новицкая М.Ю.,
…

Гдз по Окружающему миру 3 класс Рабочая тетрадь

Авторы:

Плешаков А.А.,

Гдз по Окружающему миру 3 класс Рабочая тетрадь

Авторы:

Поглазова О.Т.,
Шилин В.Д.,
…

Гдз по Окружающему миру 3 класс Рабочая тетрадь

Авторы:

Соколова Н.А.,

Гдз по Окружающему миру 3 класс Рабочая тетрадь

Авторы:

Федотова О.Н.,
Трафимова Г.В.,
…

Гдз по Окружающему миру 3 класс Тесты и самостоятельные работы

Авторы:

Потапов М.К.,

Гдз по Окружающему миру 3 класс Тесты

Авторы:

Плешаков А.А.,
Гара Н.Н.,
…

Гдз по Окружающему миру 3 класс Тетрадь для проверочных работ

Авторы:

Виноградова Н.Ф.,
Калинова Г.С.,
…

Гдз по Окружающему миру 3 класс Тетрадь для самостоятельной работы

Авторы:

Чуракова Р.Г.,
Трафимова Г.В.,
…

Гдз по Окружающему миру 3 класс Учебник

Авторы:

Плешаков А.А.,

Гдз по Окружающему миру 3 класс Тетрадь для самостоятельной работы

Авторы:

Федотова О.Н.,
Трафимова Г.В.,
…

4 класс

Гдз по Окружающему миру 4 класс Контрольно-измерительные материалы (КИМ)

Авторы:

Тихомирова Е.М.,

Гдз по Окружающему миру 4 класс Контрольно-измерительные материалы (КИМ)

Авторы:

Яценко И.Ф.,

Гдз по Окружающему миру 4 класс Проверочные работы

Авторы:

Потапов М.К.,
Калинина О.Б.,
…

Гдз по Окружающему миру 4 класс Тесты

Авторы:

Плешаков А.А.,
Гара Н.Н.,
…

Гдз по Окружающему миру 4 класс Рабочая тетрадь

Авторы:

Вахрушев А.А.,
Бурский О.В.,
…

Гдз по Окружающему миру 4 класс Рабочая тетрадь

Авторы:

Виноградова Н.Ф.,
Калинова Г.С.,
…

Гдз по Окружающему миру 4 класс Тетрадь для проверочных работ

Авторы:

Виноградова Н.Ф.,

Гдз по Окружающему миру 4 класс Рабочая тетрадь

Авторы:

Ивченкова Г.Г.,
Потапов М.К.,
…

Гдз по Окружающему миру 4 класс Рабочая тетрадь

Авторы:

Плешаков А.А.,
Крючкова Е.А.,
…

Гдз по Окружающему миру 4 класс Рабочая тетрадь

Авторы:

Плешаков А.А.,
Новицкая М.Ю.,
…

Гдз по Окружающему миру 4 класс Тесты и самостоятельные работы для текущего контроля

Авторы:

Потапов М.К.,
Калинина О.Б.,
…

Гдз по Окружающему миру 4 класс Рабочая тетрадь

Авторы:

Соколова Н.А.,

Гдз по Окружающему миру 4 класс Тетрадь для самостоятельной работы

Авторы:

Федотова О.Н.,
Трафимова Г.В.,
…

Гдз по Окружающему миру 4 класс Тетрадь для самостоятельной работы

Авторы:

Чуракова Р.Г.,
Трафимова Г.В.,
…

Гдз по Окружающему миру 4 класс Проверочные и контрольные работы

Авторы:

Вахрушев А.А.,
Бурский О.В.,
…

Гдз по Окружающему миру 4 класс Проверочные работы

Авторы:

Плешаков А.А.,
Крючкова Е.А.,
…

Гдз по Окружающему миру 4 класс Учебник

Авторы:

Плешаков А.А.,
Крючкова Е.А.,
…

Гдз по Окружающему миру 4 класс Рабочая тетрадь

Авторы:

Поглазова О.Т.,
Шилин В.Д.,
…

Гдз по Окружающему миру 4 класс Тетрадь для практических работ

Авторы:

Тихомирова Е.М.,

Окружающий мир – это область, которая непосредственно влияет на формирование у юных исследователей духовно-нравственных ценностей. Также из основного учебника они узнают о роли каждого в обществе, о его влиянии на внешнюю среду. Помимо этого, ребята научатся классифицировать объекты живой и неживой природы по особым признакам. Также здесь начинается изучение экологии и развитие навыков наблюдения за природными явлениями. Казалось бы, уж с таким интересным предметом не должно возникнуть никаких проблем. Но на практике ученики сталкиваются с серьезными сложностями. Причины кроются в обилие многообразной информации и довольно непростых вопросах. В процессе учебы от учащихся требуется творческий подход. Среди параграфов, которые будут рассматриваться на занятиях: границы России; карта часовых поясов; рельеф и недра, климат; богатство внутренних вод; почвы, природно-хозяйственные зоны; народы и религии. После каждого из них обязательно нужно отвечать на вопросы, требующие глубокого погружения в главу, а также выполнять номера из рабочей тетради, предполагающих заполнение таблиц, развернутых ответов на вопросы, заполнения карт и практических, лабораторных, тестов. Чтобы успешно справиться со всеми сложностями и получить углубленные знания, пригодится такая специализированная литература, как ГДЗ. Причем мы говорим не о тяжелых печатных справочниках, которые придется искать по всем магазинам города. На нашем уникальном сайте собраны виртуальные помощники, пользоваться которыми очень удобно!

Что собой представляют наши онлайн-гдз по окружающему миру

Все вопросы и упражнения разделены по главам и соответствуют программе, которая нацелена на проверку практических умений обучающегося. Много заданий на рассуждение и сравнение. Самое трудное — тесты как в ГИА и ЕГЭ, завершающие каждый раздел. Все это требует определённых усердий. Поэтому д/з вызывает у многих учеников затруднения. В таких ситуациях надо обращаться к онлайн-сборнику, который поможет усвоить предмет без проблем. Ко всем урокам прилагаются правильные ответы в форме описаний – короткого алгоритма. Задания соответствуют всем стандартам образования, и представлены в определенном виде, позволяющем привить интерес к учебе у школьников. Пособие доступно на сайте онлайн в любое время суток для детей и их родителей. Предназначение сборника – оказать квалифицированную помощь в решении упражнений, а также содействовать школьникам при выполнении следующих действий:

• изучении нового материала;
• поиске верных ответов;
• подготовке к уроку;
• разборе сложных и непонятных моментов;
• ликвидации пробелов в знаниях.

Почему все выбирают именно эти пособия на гдз.мода

Оно содержит в себе множество разобранных задач, требующих наличия творческой жилки и мышления. Подробно объясняют все тонкости выполнения заданий квалифицированные и опытные специалисты, а именно: Новицкая, Вахрушев, Глаголева, Архипова, Плешаков, Гара, Назарова, Ивченкова, Потапов. Школьник без труда сможет разобраться в материале, полученном на уроке. Вместе с тем при возникновении трудностей сборником может воспользоваться каждый родитель, неравнодушный к успехам своего чада в школе. Используя книгу, взрослый подскажет верное направление решения упражнений и проконтролирует правильность написанной работы. Только тогда произойдет полное усвоение знаний, и ребенок будет готов продемонстрировать их на классных занятиях. Здесь есть информация для учащегося абсолютно любой ступени образования – от начальной школы и до самой старшей.

Центральные и вписанные углы

О чем эта статья:

Центральный угол и вписанный угол

Окружность — замкнутая линия, все точки которой равноудалены от ее центра.

Определение центрального угла:

Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF

Определение вписанного угла:

Вписанный угол — это угол, вершина которого лежит на окружности.

Вписанный угол равен половине дуги, на которую опирается.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC

Свойства центральных и вписанных углов

Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

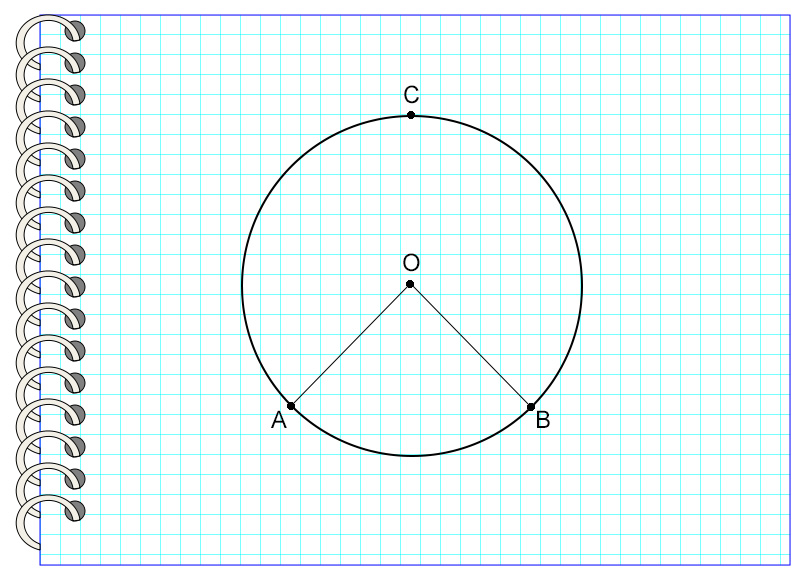
• Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:

Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.

• Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:

• Вписанные углы окружности равны друг другу, если опираются на одну дугу:

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

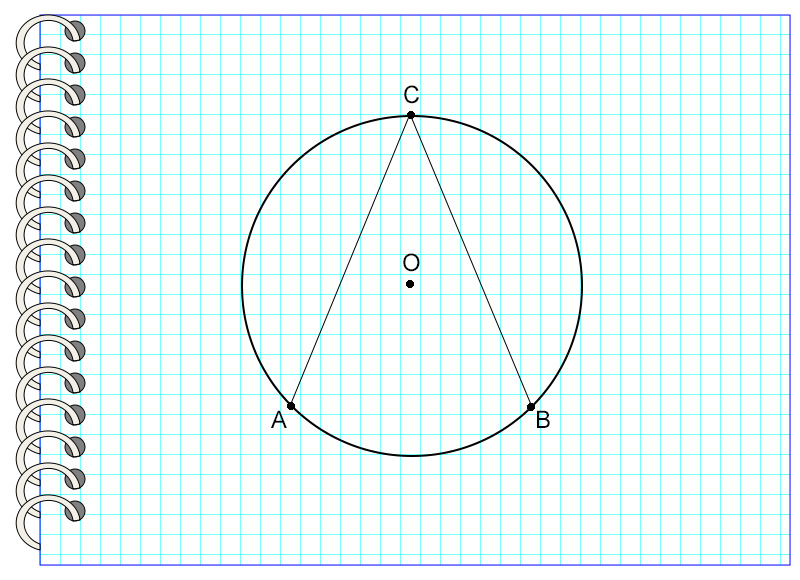
• Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.

Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.

Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Хорда — отрезок, соединяющий две точки на окружности.

• Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.

AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.

• Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

• Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.

ㄥBAC + ㄥBDC = 180°

Примеры решения задач

Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.

Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?

Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°

Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°

Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?

СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°

Углы в окружности, центральный и вписанный. Свойства и способы нахождения

Планиметрия – это раздел геометрии, изучающий свойства плоских фигур. К ним относятся не только всем известные треугольники, квадраты, прямоугольники, но и прямые и углы. В планиметрии также существуют такие понятия, как углы в окружности: центральный и вписанный. Но что они означают?

Что такое центральный угол?

Для того чтобы понять, что такое центральный угол, нужно дать определение окружности. Окружность – это совокупность всех точек, равноудаленных от данной точки (центра окружности).

Очень важно отличать ее от круга. Нужно запомнить, что окружность – это замкнутая линия, а круг – это часть плоскости, ограниченная ею. В окружность может быть вписан многоугольник или угол.

Центральный угол – это такой угол, вершина которого совпадает с центром окружности, а стороны пересекают окружность в двух точках. Дуга, которую угол ограничивает точками пересечения, называется дугой, на которую опирается данный угол.

Рассмотрим пример №1.

На картинке угол AOB – центральный, потому что вершина угла и центр окружности – это одна точка О. Он опирается на дугу AB, не содержащую точку С.

Чем вписанный угол отличается от центрального?

Однако кроме центральных существуют также вписанные углы. В чем же их различие? Так же как и центральный, вписанный в окружность угол опирается на определенную дугу. Но его вершина не совпадает с центром окружности, а лежит на ней.

Приведем следующий пример.

Угол ACB называется углом, вписанным в окружность с центром в точке О. Точка С принадлежит окружности, то есть лежит на ней. Угол опирается на дугу АВ.

Чему равен центральный угол

Для того чтобы успешно справляться с задачами по геометрии, недостаточно уметь различать вписанный и центральный углы. Как правило, для их решения нужно точно знать, как найти центральный угол в окружности, и уметь вычислить его значение в градусах.

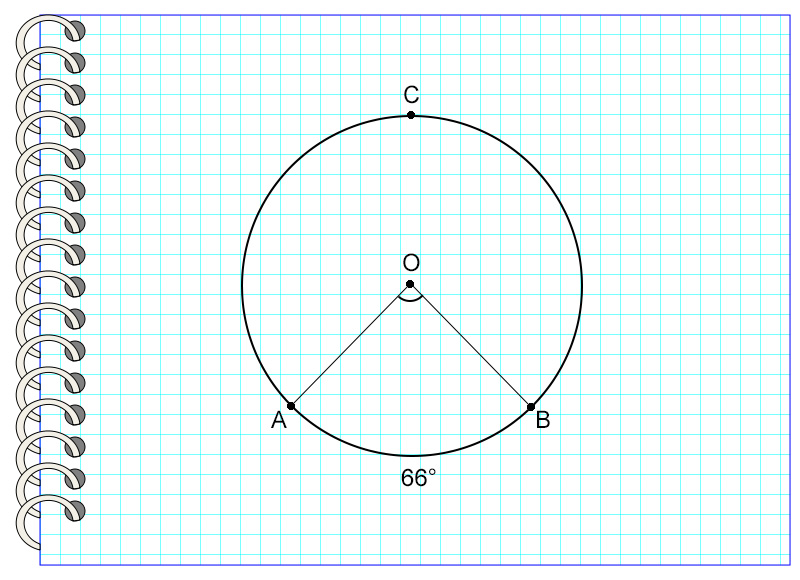
Итак, центральный угол равен градусной мере дуги, на которую он опирается.

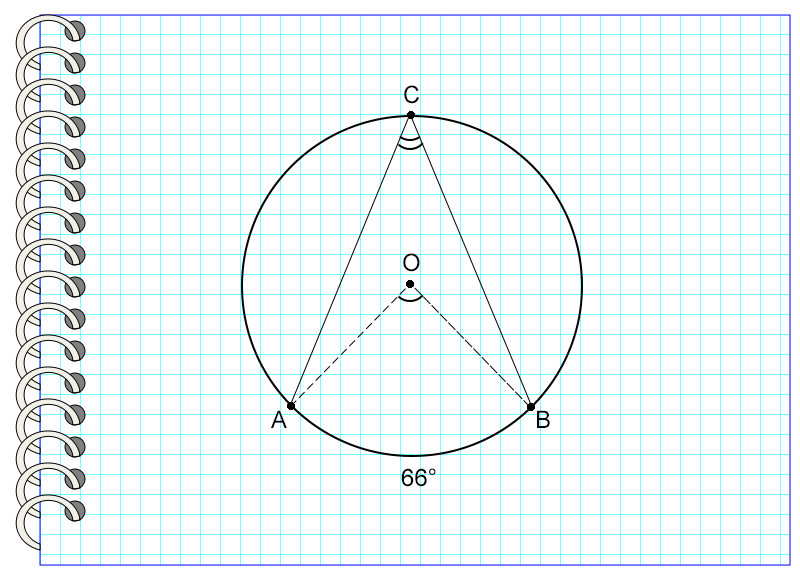
На картинке угол АОВ опирается на дугу АВ, равную 66°. Значит, угол АОВ также равен 66°.

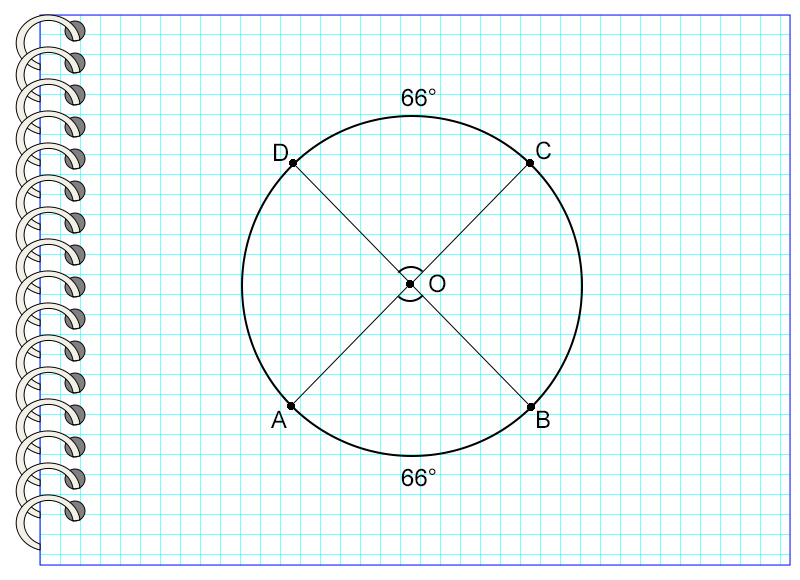
Таким образом, центральные углы, опирающиеся на равные дуги, равны.

На рисунке дуга DC равна дуге AB. Значит, угол АОВ равен углу DOC.

Как найти вписанный угол

Может показаться, что угол, вписанный в окружность, равен центральному углу, который опирается на ту же дугу. Однако это грубая ошибка. На самом деле, даже просто посмотрев на чертеж и сравнив эти углы между собой, можно увидеть, что их градусные меры будут иметь разные значения. Так чему же равен вписанный в окружность угол?

Градусная мера вписанного угла равна одной второй от дуги, на которую он опирается, или половине центрального угла, если они опираются на одну дугу.

Рассмотрим пример. Угол АСВ опирается на дугу, равную 66°.

Значит, угол АСВ = 66° : 2 = 33°

Рассмотрим некоторые следствия из этой теоремы.

• Вписанные углы, если они опираются на одну и ту же дугу, хорду или равные дуги, равны.
• Если вписанные углы опираются на одну хорду, но их вершины лежат по разные стороны от нее, сумма градусных мер таких углов составляет 180°, так как в этом случае оба угла опираются на дуги, градусная мера которых в сумме составляет 360° (вся окружность), 360° : 2 = 180°
• Если вписанный угол опирается на диаметр данной окружности, его градусная мера равна 90°, так как диаметр стягивает дугу равную 180°, 180° : 2 = 90°
• Если центральный и вписанный углы в окружности опираются на одну дугу или хорду, то вписанный угол равен половине центрального.

Где могут встретиться задачи на эту тему? Их виды и способы решения

Так как окружность и ее свойства – это один из важнейших разделов геометрии, планиметрии в частности, то вписанный и центральный углы в окружности – это тема, которая широко и подробно изучается в школьном курсе. Задачи, посвященные их свойствам, встречаются в основном государственном экзамене (ОГЭ) и едином государственном экзамене (ЕГЭ). Как правило, для решения этих задач следует найти углы на окружности в градусах.

Углы, опирающиеся на одну дугу

Этот тип задач является, пожалуй, одним из самых легких, так как для его решения нужно знать всего два простых свойства: если оба угла являются вписанными и опираются на одну хорду, они равны, если один из них – центральный, то соответствующий вписанный угол равен его половине. Однако при их решении нужно быть крайне внимательным: иногда бывает сложно заметить это свойство, и ученики при решении таких простейших задач заходят в тупик. Рассмотрим пример.

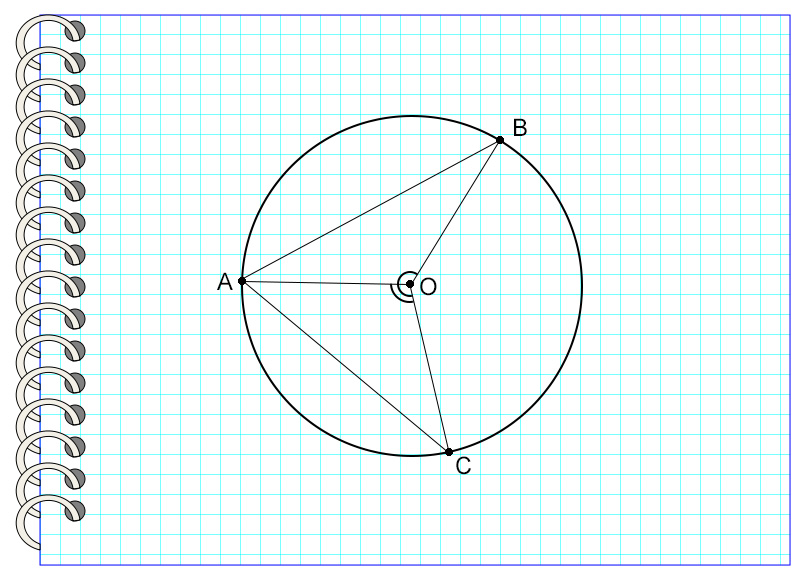
Дана окружность с центром в точке О. Угол АОВ равен 54°. Найти градусную меру угла АСВ.

Эта задача решается в одно действие. Единственное, что нужно для того, чтобы найти ответ на нее быстро – заметить, что дуга, на которую опираются оба угла – общая. Увидев это, можно применять уже знакомое свойство. Угол АСВ равен половине угла АОВ. Значит,

1) АОВ = 54° : 2 = 27°.

Углы, опирающиеся на разные дуги одной окружности

Иногда в условиях задачи напрямую не прописана величина дуги, на которую опирается искомый угол. Для того чтобы ее вычислить, нужно проанализировать величину данных углов и сопоставить их с известными свойствами окружности.

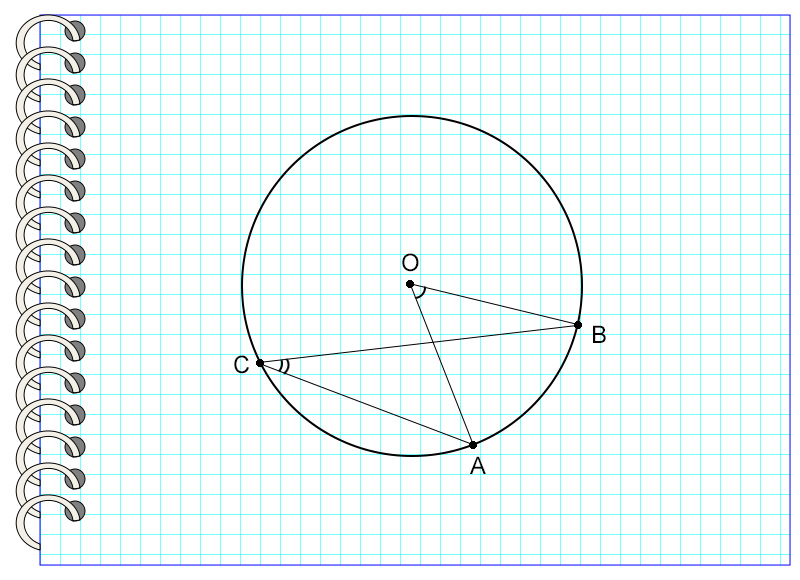
В окружности с центром в точке О угол АОС равен 120°, а угол АОВ – 30°. Найдите угол ВАС.

Для начала стоит сказать, что возможно решение этой задачи с помощью свойств равнобедренных треугольников, однако для этого потребуется выполнить большее количество математических действий. Поэтому здесь будет приведен разбор решения с помощью свойств центральных и вписанных углов в окружности.

Итак, угол АОС опирается на дугу АС и является центральным, значит, дуга АС равна углу АОС.

Точно так же угол АОВ опирается на дугу АВ.

Зная это и градусную меру всей окружности (360°), можно с легкостью найти величину дуги ВС.

ВС = 360° – АС – АВ

ВС = 360° – 120° – 30° = 210°

Вершина угла САВ, точка А, лежит на окружности. Значит, угол САВ является вписанным и равен половине дуги СВ.

Угол САВ = 210° : 2 = 110°

Задачи, основанные на соотношении дуг

Некоторые задачи вообще не содержат данных о величинах углов, поэтому их нужно искать, исходя только из известных теорем и свойств окружности.

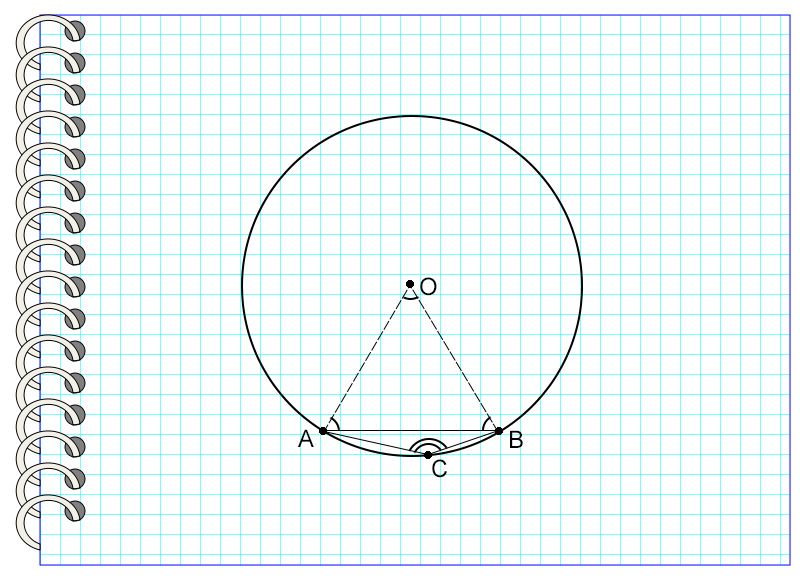
Найдите угол, вписанный в окружность, который опирается на хорду, равную радиусу данной окружности.

Если мысленно провести линии, соединяющие концы отрезка с центром окружности, то получится треугольник. Рассмотрев его, можно заметить, что эти линии являются радиусами окружности, а значит, все стороны треугольника равны. Известно, что все углы равностороннего треугольника равны 60°. Значит, дуга АВ, содержащая вершину треугольника, равна 60°. Отсюда найдем дугу АВ, на которую опирается искомый угол.

АВ = 360° – 60° = 300°

Угол АВС = 300° : 2 = 150°

В окружности с центром в точке О дуги соотносятся как 3:7. Найдите меньший вписанный угол.

Для решения обозначим одну часть за Х, тогда одна дуга равна 3Х, а вторая соответственно 7Х. Зная, что градусная мера окружности равна 360°, составим уравнение.

По условию, нужно найти меньший угол. Очевидно, что если величина угла прямо пропорциональна дуге, на которую он опирается, то искомый (меньший) угол соответствует дуге, равной 3Х.

Значит, меньший угол равен (36° * 3) : 2 = 108° : 2 = 54°

В окружности с центром в точке О угол АОВ равен 60°, а длина меньшей дуги – 50. Вычислите длину большей дуги.

Для того чтобы вычислить длину большей дуги, нужно составить пропорцию – как меньшая дуга относится к большей. Для этого вычислим величину обеих дуг в градусах. Меньшая дуга равна углу, который на нее опирается. Ее градусная мера составит 60°. Большая дуга равна разности градусной меры окружности (она равна 360° вне зависимости от остальных данных) и меньшей дуги.

Большая дуга равна 360° – 60° = 300°.

Так как 300° : 60° = 5, то большая дуга в 5 раз больше меньшей.

Большая дуга = 50 * 5 = 250

Итак, конечно, существуют и другие подходы к решению подобных задач, но все они так или иначе основаны на свойствах центральных и вписанных углов, треугольников и окружности. Для того чтобы успешно их решать, необходимо внимательно изучать чертеж и сопоставлять его с данными задачи, а также уметь применять свои теоретические знания на практике.

Геометрия

План урока:

Центральный угол и градусная мера дуги

Любые две точки на окружности разбивают ее на две дуги. Чтобы отличать эти дуги, на каждой из них ставят точку, которую и указывают в обозначении дуги:

Здесь красным цветом показана⋃АСВ, а синим – ⋃ADB. Однако иногда для простоты указывают только концы дуги, то есть используют обозначение ⋃AВ. Это делается тогда, когда ясно, о какой дуге окружности идет речь. Обычно всегда подразумевается та дуга, которая меньше.

Можно заметить, что дуги отличаются по размеру, поэтому возникает потребность их измерения. Для этого используют такое понятие, как градусная мера дуги.

Для ее определения необходимо соединить концы дуги с центром окруж-ти. В результате получаются радиусы, которые пересекаются в центре окружности. Угол между ними именуется центральным углом окруж-ти.

Для каждой дуги можно построить единственный центральный угол, поэтому логично измерять дугу с помощью такого угла. Правда, обратное неверно. На рисунке видно, что центральному углу ∠АОВ соответствует сразу две дуги: ⋃АСВ и ⋃АDB:

Поэтому условно считают, градусная мера той из двух дуг, которая меньше, как раз и равна центральному углу:

Дуги, также как отрезки или углы, можно складывать или вычитать. Например, пусть есть две дуги, ⋃AВ и ⋃ВС, чьи градусные меры составляют 40° и 30°.

Как найти ⋃АС? Ей соответствует центральный угол ∠АОС, который в свою очередь равен сумме ∠АОВ и ∠ВОС:

Диаметр делит окруж-ть на две равные друг другу дуги, которые называются полуокружностями. При этом диаметр окружности можно рассматривать как угол между двумя радиусами, равный 180°. Получается, что градусная мера полуокружности составляет 180°:

Вместе две полуокружности образуют полную окруж-ть. Получается, что градусная мера всей окруж-ти составляет 180° + 180° = 360°.

Этот факт известен и из жизни – когда кто-то делает полный оборот вокруг своей оси, говорят, что он повернулся на 360°. Теперь мы можем вернуться к случаю, когда две точки делят окруж-ть на две неравные друг другу дуги. Градусная мера меньшей из них будет равна величине соответствующего центрального угла (обозначим его как α). В сумме две дуги должны дать 360°. Значит, градусная мера большей дуги будет составлять 360° – α:

Задание. Точки А, В, С и D лежат на одной окруж-ти. Известно, что ⋃АСВ составляет 107°. Какова величина ⋃ADB?

Решение. Вместе дуги ⋃АСВ и ⋃АDВ образуют полную окруж-ть, поэтому их сумма равна 360°. Это позволяет составить уравнение и найти из него ⋃АDB:

Задание. Найдите величину ∠АОС на рисунке, если известны ⋃AВ и ⋃ВС:

Решение. Сначала найдем ⋃АС, учтя, что все три дуги, показанные на рисунке, в сумме составляют 360°:

Для доказательства построим две одинаковые хорды AВ и СD в окруж-ти и соединим их концы с центром:

В результате получились ∆АОВ и ∆ОСD. У них равны все три стороны, значит, сами эти треугольники равны. Тогда

∠COD = ∠AOB

Но эти углы – центральные для дуг ⋃AВ и ⋃CD. Получается, что у этих дуг одинаковы их градусные меры, поэтому они также равны, ч. т. д.

Примечание. Всякая хорда окружности разбивает ее на две дуги – большую и меньшую. В данном правиле говорится именно равенстве меньших дуг.

Задание. На окруж-ти отмечены точки А, В и С так, что хорды AВ, ВС и АС равны. Найдите угол между радиусами окружности АО и ВО.

Дуги ⋃AВ, ⋃ВС и ⋃АС стянуты равными хордами AВ, ВС и АС. Значит, они одинаковы. Но в сумме эти три дуги образуют окруж-ть величиной в 360°. Значит, каждая из этих дуг втрое меньше:

⋃AВ = ⋃BC = ⋃AC = 360°:3 = 120°

∠АОВ – центральный для ⋃AВ, значит, он равен ее градусной мере, то есть он составляет 120°.

Вписанный угол

В окруж-ти можно построить ещё один угол, который именуют вписанным углом. Его отличие от центрального заключается в том, что его вершина лежит на окруж-ти, а не в ее центре. Сторонами же вписанного угла являются хорды окруж-ти.

Здесь дуга ⋃ВС находится внутри угла, а ее концы лежат на его сторонах. В таких случаях говорят, что ∠ВАС опирается на дугу ВС. Оказывается, что между величиной вписанного угла и дугой, на которую он опирается, есть взаимосвязь.

Обозначим вписанный угол ∠СAВ буквой α. Так как радиусы АО и ОС одинаковы, то ∆АОС – равнобедренный, и тогда углы при его основании будут одинаковы:

∠СОВ – внешний для ∆АОС. Напомним, что такой угол равен сумме тех 2 углов треуг-ка, которые с ним не смежны. В частности, в данном случае можно записать

∠СОВ = ∠OCA = ∠OAC = α + α = 2α

Но этот же угол – центральный, и его величина равна ⋃ВС:

Получается, что дуга вдвое больше вписанного угла.

Далее рассмотрим случай, когда диаметр, проведенный из вершины вписанного угла, делит его на две части:

В этом случае вписанный угол ∠СAВ можно представить как сумму углов ∠САD (обозначен как α)и ∠ВАD (обозначен как β). Мы уже доказали, что дуги, на которые опираются эти углы, вдвое больше самих углов:

Осталось рассмотреть третий случай, при котором обе стороны вписанного угла ∠ВАС лежат по одну сторону от диаметра:

Если здесь обозначить ∠САD как α, а ∠ВАD как β, то интересующий нас ∠СAВ можно представить как их разность:

Итак, во всех трех возможных случаях вписанный угол оказывается вдвое меньше дуги, на которую он опирается.

Задание. Найдите ∠ВАС на рисунке:

Задание. Найдите вписанный ∠AВС, сели прилегающие к нему дуги ⋃AВ и ⋃ВС равны 100° и 128°.

Решение. В сумме дуги ⋃АС, ⋃ВС и ⋃AВ образуют окруж-ть, поэтому их сумма составляет 360°. Тогда можно найти ⋃АС:

Задание. Найдите дугу ⋃SM на рисунке:

Решение. Сначала найдем дугу ⋃MN, она вдвое больше соответствующего ей вписанного угла:

⋃NM = 2*∠NSM = 2*35° = 70°

Заметим, что ⋃SN– это полуокружность, то есть она составляет 180°. При этом ⋃SM и ⋃MN вместе как раз образуют эту полуокружность, то есть их сумма также составляет 180°. Значит, ⋃МS можно найти, вычтя из полуокружности ⋃MN:

⋃MS = ⋃SN – ⋃MN = 180° – 70° = 110°

Заметим, что для одной дуги можно построить несколько вписанных углов. Каждый из них будет равен половине дуги, то есть все эти углы окажутся одинаковыми.

Задание. Найдите ∠АСD на рисунке:

Решение. Так как ∠ACD и ∠ABD опираются на одну дугу ⋃AD, то они должны быть одинаковыми:

∠ACD = ∠ABD = 63°

Задание. Докажите, что две дуги, находящиеся между двумя параллельными секущими окруж-ти, равны друг другу.

Нам надо доказать, что ⋃AВ и ⋃CD равны, если АС||BD. Проведем секущую ВС:

∠СВD и ∠АСВ равны, ведь они накрест лежащие. Получается, что ⋃AВ и ⋃CD являются основаниями равных вписанных углов. Отсюда вытекает, что эти дуги должны быть равными.

Напомним, что диаметр разбивает окруж-ть на две дуги по 180°. Отсюда можно сделать вывод – любой угол, опирающийся на полуокружность, должен составлять 180°:2 = 90°:

Задание. Диаметр окруж-ти AВ равен 17. Хорда ВС имеет длину 8. Какова длина хорды АС?

Так как ∠АСВ опирается на диаметр AВ, то он прямой. Значит, и ∆АСВ – прямоугольный, причем диаметр AВ в нем – гипотенуза. Неизвестный катет можно найти по теореме Пифагора:

Задание. Окруж-ть разбита на две дуги, ⋃AВС и ⋃СDA. Известно, что ∠AВС = 72°. Найдите ∠ADC.

Зная ∠AВС, мы легко найдем дугу ⋃ADC, она вдвое больше опирающегося на нее вписанного угла:

Углы между хордами и секущими

До этого мы рассматривали простые углы в окруж-ти, вершины которых лежали либо на самой окруж-ти, либо в ее центре. Однако иногда хорды и секущие пересекаются в другой точке, либо внутри, либо вне окруж-ти. Рассмотрим подобные задачи.

Более прост случай, когда необходимо найти угол между двумя пересекающимися хордами. Пусть хорды при пересечении образовали дуги ⋃AВ и ⋃СD величиной α и β. Каков угол между ними?

Проведем ещё одну хорду АD. В результате получим вписанные ∠САD и ∠ADB, которые будут равны половинам от соответствующих дуг, то есть α/2 и β/2. Интересующий нас ∠СPD оказывается внешним для ∆APD, и потому равен сумме двух углов в ∆APD (тех, которые с ним не смежны), то есть он составляет величину α/2 + β/2:

Величину α/2 + β/2 можно записать и иначе, вынеся множитель 1/2 за скобки:

Эту величину можно назвать полусуммой дуг, на которые опирается интересующий нас угол.

Задание. Найдите ∠МКВ на рисунке:

Решение. Интересующий нас угол опирается на хорды величиной 38° и 42°. Значит, он равен половине от их суммы:

∠MKB = (42° + 38°)/2 = 80°/2 = 40°

В более сложном случае необходимо найти угол между секущими, которые пересекаются вне окруж-ти. При этом известны дуги, образованные этими секущими:

Снова проведем хорду АD, чтобы у нас получились два вписанных угла, ∠ADB и ∠СAD, которые соответственно будут иметь величину β/2 и α/2:

Теперь уже ∠САD оказывается внешним для ∆ADK, а потому он является суммой двух других углов:

В итоге получили, что угол между секущими составляет половину от разности дуг, которые они отсекают от окруж-ти.

Задание. Найдите на рисунке величину∠К, если ⋃AВ и ⋃СD соответственно равны 42° и 130°:

Решение. В этой задаче просто используем доказанную теорему об углах между секущими. Искомый угол составляет половину от разности дуг, заключенных между секущими:

∠K = (130° – 42°):2 = 88°/2 = 44°

Теорема о произведении отрезков хорд

Можно заметить, что при пересечении двух хорд образуется пара подобных треугольников. Пусть хорды ADи ВС пересекаются в точке K. Добавим хорды AВ и СD и получим ∆AВК и ∆КСD:

На дугу ⋃BD опираются вписанные углы∠А и ∠С, значит, они одинаковы. Также на одну дугу АС опираются ∠D и∠В, поэтому и они одинаково. Равенство двух углов уже означает, что треугольники подобны по первому признаку подобия (дополнительно можно заметить, что ∠АКВ и ∠СКD равны как вертикальные углы).

Из подобия ∆AВК и ∆СКD вытекает пропорция между их сторонами:

Перемножив члены пропорции крест накрест, получим соотношение:

В результате нам удалось доказать следующее утверждение:

Задание. Хорды AВ и CD пересекаются в точке М. Известны, что АМ = 9, МВ = 3, МС = 2. Какова длина отрезка МD?

Хорда AВ разбивается на отрезки АМ и МВ, а хорда CD – на отрезки СМ и МD. Произведения этих отрезков одинаковы:

Подставим в это равенство известные величины

Рассмотрим ещё одну геометрическую конструкцию. Пусть из некоторой точки А к окруж-ти проведена как касательная к окружности АК, так и секущая, пересекающая окруж-ть в точках В и С:

Какие здесь есть взаимосвязи между углами и длинами отрезков? Для начала проведем хорды ВК и СК, а также радиусы ОК и ОВ. Обозначим буквой α угол ∠ВСК. Он вписанный, поэтому дуга, на которую он опирается (это ⋃ВК), вдвое больше и равна 2α. Тогда и центральный угол ∠ВОК также составляет 2α:

Теперь исследуем ∆ВОК. Он равнобедренный (ВО и ОК – одинаковые радиусы), поэтому углы при его основании совпадают:

Итак, углы при основании ∆ОВК, в частности ∠ОКВ, равны 90° – α. Заметим, что ∠ОКА – прямой, так как образован радиусом ОК и касательной АК, при этом он состоит из двух углов, ∠АКВ и ∠ВКО. Это позволяет найти ∠АКВ:

В результате мы получили важный промежуточный результат – угол между касательной и хордой, проведенной из точки касания, вдвое меньше образующейся при этом дуги.

Вернемся к картинке с секущей. Изначально как α мы обозначили ∠ВСК, но в результате получили, что и ∠АКВ = α.

Рассмотрим ∆AВК и ∆САК. У них есть общий∠А, а также одинаковые ∠AКВ и ∠ВСК, которые отмечены буквой α. Значит, ∆AВК и ∆САК подобны, поэтому мы имеем право записать пропорцию между его сторонами:

Здесь отрезок АС можно назвать секущей, а AВ – ее внешней частью. Тогда выведенное отношение можно сформулировать так:

Решение. Сначала находим длину всей секущей, пользуясь доказанной теоремой:

Решение. Проведем из точки А ещё и касательную АК к окруж-ти:

Величину квадрата касательной АК можно найти, используя секущую АС. Сначала вычислим длину АС:

Задачи на квадратной решетке

Рассмотрим несколько несложных задач, часто встречающихся на экзаменах.

Задание. Найдите ∠AВС на рисунке:

Решение. Здесь следует заметить, что расстояние между А и С составляет 8 клеток, при этом в окруж-ть как раз можно вписать квадрат со стороной 8.

Такой квадрат разобьет окруж-ть на 4 дуги, причем так как эти дуги опираются на хорды одинаковой длины, то они и сами равны. Вся окруж-ть составляет 360°, значит, каждая из этих дуг составляет 360°:4 = 90°. ∠AВС – вписанный, то есть он составляет половину дуги, на которую он опирается, а это⋃АС, равная 90°. Тогда

Задание. Найдите ∠AВС, используя рисунок:

Решение. Используя рассуждения из предыдущей задачи, легко определить, что∠А составляет 45°.При этом ∆AВС – равнобедренный, и ВС – его основание. Это следует хотя бы из того факта, что высота АН делит сторону ВН пополам.

Углы∠В и ∠С одинаковы, так как лежат при основании равнобедренного треуг-ка. Найдем их, используя тот факт, что все 3 угла в ∆AВС составляют в сумме 180°:

Задание. Вычислите ∠AВС:

Решение. Снова в окруж-ть можно вписать квадрат со стороной 8 клеток. Из этого следует что ⋃АВС составляет 90° (показана фиолетовым цветом):

Но ∠АВС опирается на синюю дугу. Так как вместе фиолетовая и синяя дуга составляют окружность, равную 360°, то синяя дуга должна быть равна 360° – 90° = 270°. ∠АВС как вписанный будет вдвое меньше, то есть он равен 270°:2 = 135°.

Задание. Чему равен ∠AВС на рисунке?

Если вписать в окруж-ть квадрат то он разобьет окруж-ти на дуги по 90°. В свою очередь точка А является серединой такой дуги, то есть она разбивает ее на две дуги по 45°.

∠AВС как вписанный будет вдвое меньше, то есть он равен 22,5°.

[spoiler title=”источники:”]

http://fb.ru/article/445770/uglyi-v-okrujnosti-tsentralnyiy-i-vpisannyiy-svoystva-i-sposobyi-nahojdeniya

http://100urokov.ru/predmety/urok-10-ugly-v-okruzhnosti

[/spoiler]

Природная зона – это территория, для которой характерны какие-либо климатические условия, особенности растительности, почвы и животного мира. От количества влаги, тепла и света, которые они получают, зависят особенности природных зон. В каждой природной зоне обитают свои животные и растут определённые виды растений.

В разных природных зонах находится территория России, при этом основных зон – семь:

• арктические пустыни;
• тундра;
• тайга;
• широколистные и смешанные леса;
• степи;
• пустыни;
• субтропики.

Ну а теперь вернёмся к вопросу… На карте буквами отмечены следующие природные зоны:

Название природной зоны А: Тундра;

Название природной зоны Б: Тайга.

На фотографиях изображены следующие животные:

• 1) соболь;
• 2) полярная сова;
• 3) песец;
• 4) бурый медведь.

На территории природной зоны А (Тундра) обитают: 2) полярная сова и 3) песец;

На территории природной зоны Б (Тайга) обитают: 1) соболь и 4) бурый медведь.