
Фрагмент физической карты Карелии
Для того, чтобы определить расстояние между двумя точками (пунктами, местами) используя физическую карту, можно воспользоваться простым способом: взять циркуль (им лучше, потому что он чётко фиксирует интервал) и затем с помощью линейки узнать, сколько это будет в сантиметрах.
Если линия криволинейная (например, морское побережье), можно воспользоваться курвиметром – специальным приспособлением с колёсиком, “считывающим” дистанцию.
После этого, соотносим получившееся значение с масштабом карты и пересчитываем см (мм) в километры.
Например, если масштаб 1:500000, это значит, что в 1 см – 5 км, и именно на это число нужно умножать.
Конечно, есть ряд составляющих погрешности даже при мелком масштабе карты, но тем не менее, полученное расстояние всё же будет относительно точным.
Таким образом, занимательная физическая карта, с отображёнными на ней континентами, горами, морями, реками…, позволяет не только увидеть многообразие и красоту нашей Земли, хоть и на бумаге, но и “дотянуться” до них из своего места
Download Article
Download Article
Maps provide you with an accurate picture of a geographic area so you can determine how far it is from one place to another. Maps provide a fractional scale that tells you the ratio between the distance on the map and the real-world distance. With the fractional scale, you simply have to multiply the map distance by the scale value to find the real-world distance. However, fractional scales don’t work for digital maps that can change size, such as maps you might pull up on a smartphone or tablet. For those maps, use the bar scale located at the bottom of the map to measure the distance from one place to another.[1]
-

1
Mark the 2 points on the edge of a sheet of paper. Take a blank sheet of paper and line up the edge between the 2 points that you want to measure the straight-line distance between. Make a tick mark on the paper for the first point, then another tick mark for the second point.[2]
- It’s helpful to label each of the 2 points so you remember which tick mark goes where, but this isn’t strictly necessary since the distance will be the same in either direction.
-

2
Place your paper underneath the map’s bar scale. The bar scale is a black or gray bar, typically at the bottom of the map. Place the tick mark for the first point directly under the 0 on the bar scale.[3]
- The 0 might not be all the way on the left edge of the bar scale. Some bar scales include fractional distances to the left of the 0.
- Bar scales typically have distance measurements in both kilometers and miles, so make sure you’re on the right one. The units used locally will likely be the most helpful since road signs would be in the same units. However, if you’re not familiar with that system, you might want to get a measurement with both.[4]
Advertisement
-

3
Read the distance between the 2 points on the scale. Locate the tick mark you made for the second point on your piece of paper and look at the bar scale. The number above that tick mark on the bar scale is the real-world distance between the 2 points.[5]
- For example, suppose you have a 10-kilometer bar scale that’s marked off in 2-kilometer segments. The number over your tick mark is 8. Therefore, your 2 points are 8 kilometers apart.
- If there isn’t a number directly over the tick mark, you’ll have to estimate. Some bar scales have fractional distances to the left of the 0 that will help you to estimate. For example, suppose you have a 10-kilometer scale that isn’t segmented, but your tick mark is halfway between the 0-point and the end. Your points are approximately 5 kilometers apart.
-

4
Create segments if your distance is longer than the bar scale. Most distances you try to measure will be longer than the bar scale, but you can still measure them. Make a tick mark on your paper where the bar scale ends and write the distance underneath it. Then, slide your paper over so the tick mark you just made is directly under the 0 on the bar scale.[6]
- If the second point is still further than the scale, make another tick mark and move the paper over again. Keep going like that until you reach your destination.
-

5
Add up your segments to determine the total distance. For distances that are longer than the bar scale on the map, take the distance represented by each of the segments you made and add them all together. That tells you the total distance from the first point to the second point.[7]
- For example, suppose you have a 10-kilometer bar scale. You’ve measured 3 10-kilometer segments and one segment you estimate to be half of the bar scale, or 5 kilometers. Your total distance between the points would be 35 kilometers (10 + 10 + 10 + 5).
Advertisement
-

1
Look for the fractional scale on the map. A fractional scale, as the name implies, is expressed as a fraction, typically at the bottom of the map. Sometimes, it’s also expressed as a ratio, but the calculations are the same regardless.[8]
- Maps have different scales for different purposes. For example, a road map is typically drawn at a 1:250,000 scale. It shows a larger area with roads and towns, more suitable for driving. A walking map, on the other hand, might be drawn at a 1:25,000 scale, providing more detail about paths and landmarks in a smaller area.
-

2
Measure the map distance between the 2 points. Use a ruler as a straight edge between the 2 points you want to find the straight-line distance between. Place the 0-edge of the ruler at the first point, then mark the measurement listed at the second point.[9]
- Since you’re using a fractional scale, the number you find becomes the numerator, or top number, of your fraction. If you’re using a road map drawn to a 1/250,000 scale, and the distance between your 2 points is 5, your 5 takes the position of the 1 on the scale. Then, you’ll have to find the total ground distance that represents.
-

3
Cross-multiply by the scale to find the ground measurement. Set up your fraction so that the unit measurement you found is the numerator and “x” is your denominator. Multiply the denominator of the scale by the unit measurement you found to determine the ground measurement.[10]
- To continue with the previous example, if you found 5 as the distance between your 2 points, you would multiply 5 by 250,000 to get 1,250,000. So if you used inches, the 2 points are 1,250,000 inches apart from each other. Similarly, if you used centimeters, the 2 points are 1,250,000 centimeters apart from each other. The unit makes no difference.
-

4
Convert your answer into the unit of your choice. The fractional scale tells you the real-world distance in centimeters or inches. To make your answer more usable, divide centimeters by 100 for meters or 100,000 for kilometers. If you’re working in inches, divide by 12 to find feet or 63,360 to find kilometers.[11]
- For example, you would be unlikely to say that 2 points were 1,250,000 centimeters apart. Instead, you would likely want to convert those centimeters to meters or kilometers. When you did so, you would find that the 2 points are 12,500 meters (1,250,000/100) or 12.5 kilometers (1,250,000/100,000).
- Similarly, if you used inches, the 2 points would be 1,250,000 inches apart, which converts to approximately 104,167 feet (1,250,000/12) or 19.7 miles (1,250,000/63,360).
Advertisement
-

1
Identify the road or roads between the 2 points. Place your finger on the starting point and find a road that goes in the direction of your ending point. Trace your finger down the road to find the route you would need to take between the 2 points.
- You may need to take more than one road — especially if the 2 points are far away from each other. To keep track of your route, trace it in pencil or take notes on a separate sheet of paper.
-

2
Place a string along the route. Put the end of the string at the first point and lay it down directly over the roads you would take if you were traveling to the other point. For curves, hold the string to follow the curve and then move your finger to the furthest point.[12]
- It can help if you have a friend with you to help you hold the string. However, you don’t need to hold it down all the way from the beginning. If you’re going around a curve, just make sure you’re holding down the string at the furthest spot you’ve gone so far.
-

3
Measure the total length of your string. Hold the string at the point where it reaches the second point. The length of the string from the end to that spot represents the road distance on the map. Use a ruler or tape measure to get the total length of the string.[13]
- You can also mark the string with a pen or use a piece of tape. That way, you don’t have to worry about dropping the string and losing your spot.
-

4
Use the bar scale to measure your string if you don’t have a ruler. Get something to take notes so you can keep track of segments, then place the start of the string at the 0-point of the map’s bar scale. Extend the string to the end of the bar scale and place your finger there. Right down the distance represented by the full length of the bar scale, then move the place where your finger is to the 0-point of the bar scale and do it again. Keep going until you reach the place on your string that marked your destination.[14]
- For example, suppose the map has a bar scale that’s 8 kilometers long. Your string has 4 segments the length of the bar scale, plus another segment about half the length of the bar scale before you reach the spot on the string for your destination. The distance between the 2 points is 36 kilometers (8 x 4 + 4).
- Be careful not to stretch the string any tighter than you did when you were measuring, or your final distance measurement will be off.
-

5
Calculate the distance using the map’s scale. If you measured your string with a ruler, use the map’s fractional scale to find out the real-world distance by multiplying the string’s measurement by the number in the denominator of the fraction or right side of the ratio. Then, convert that number to a larger unit, such as miles or kilometers.[15]
- For example, suppose you found your string is 7 centimeters long and the map you’re using has a scale of 1:250,000. Multiplying 7 by 250,000 gives you a real-world distance of 1,750,000 centimeters, which is likely not very helpful. If you divide that number by 100,000, however, you find that your points are 17.5 kilometers apart.
- If you used the bar scale to find the length of your string, you don’t need to do this step because you already have the real-world distance.
-

6
Use a piece of paper to measure segments if you don’t have string. A string is ideal to measure a curvy road because it can follow the curves of the road. If you don’t have a string handy, take a piece of paper and make a tick mark on the edge at your starting point. Then, follow the road until it curves. Place a tick mark at the curve, then pivot the paper until it’s following the road again, holding it in place where you marked the curve. Mark the spot where it curves again and follow the same procedure until you reach the endpoint on the map, always keeping the edge of your paper against the road edge.[16]
- When you get done, you’ll have multiple tick marks on the edge of your sheet of paper. Hold these to the scale to find the distance for each segment. Then, add them together to find the distance between the 2 points.
- This method may not be as accurate as the string method, but in a pinch, it’s better than nothing.
Advertisement
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
If you’re looking at a map that doesn’t have a scale, look for something you know the size of, such as a football field, then measure its length on the map. Once you have those 2 distances, you can find the scale for the map.[17]
Thanks for submitting a tip for review!
Advertisement
-
If you’re looking at a digital copy of a map on a smartphone or tablet, any fractional scale listed won’t be valid because the size of the map has changed from the original. However, the bar scale will still be valid.[18]
Advertisement
References
About This Article
Thanks to all authors for creating a page that has been read 31,608 times.
Did this article help you?
Задача простая. Нужно вычислить расстояние между двумя точками на карте, при этом известны только их географические координаты, то есть широта и долгота. Для примера вычислим расстояние между Москвой и Питером, но данная методика, конечно же, будет применима и к другим двум точкам местности. В наше время у многих людей есть такие компасы, например при смартфонах, которые показывают не только направление, но и географические координаты.
Итак, задача: вычислить расстояние между двумя городами. Известно только одно – географические координаты, то есть широта и долгота. Посмотрим эти данные в справочнике, ну или в Википедии.
Итак, что нам известно: координаты Москвы:
55,7522 град. с.ш., 37.6156 град. в.д.
Координаты Петербурга:
59,89444 град. с.ш., 30,26417 град. в.д.
Построим с помощью Excel трапецию:
Итак, у нас есть трапеция ABCD. На ней точка D – это Москва, точка B – это Петербург. Отрезок AB проходит по меридиану Петербурга, BC – по параллели Петербурга, CD – по меридиану Москвы и AD – по параллели Москвы.
Что нам известно? Во-первых известны все географические координаты каждой из точек:
A: 55,7522, 30,26417;
B: 59,89444, 30,26417;
C: 59,89444, 37,6156;
D: 55,7522, 37,6156.
Вычислить AB и CD достаточно просто. На меридианах в градусе примерно одинаковое число километров. Это расстояние можно взять из справочных данных, и оно составляет примерно 111,1 км в каждом градусе.
Нужная нам разница в градусах – это 59,89444-55,7522, или 4,14224. А это значит, что разница в километрах – это 4,14224*111,1=460,2029 км.
Что же касается оснований трапеции, там тоже все достаточно просто. Экватор – это ноль градусов северной широты, и длина каждого градуса на экваторе около 111,3 км. Поскольку косинус ноля – это единица, то для любой параллели верна следующая формула: длина каждого градуса равна произведению 111,3 на косинус того угла, который числится в градусах северной широты (ну или южной, если это происходит южнее экватора).
Итак, с помощью Excel вычислим нужные нам косинусы:
- cos(55.7522) = 0,562773
- cos(59.89444) = 0,501595
Это значит, что 1 градус в верхнем основании нашей трапеции =111,3*0,501595=55,82749 км, а один градус в нижнем основании трапеции =111,3*0,562773=62,6366 км. Поскольку число градусов одинаково как в верхнем, так и в нижнем основаниях трапеции и составляет 37,6156-30,26417, то есть 7,35143 градуса. Но число километров в верхнем и нижнем основаниях трапеции не одинаковое.
Рассчитаем эти расстояния в километрах. BC=7,35143*55,82749=410,4119 км.
AD=7,35143*62,6366=460,469 км.
Теперь проведем высоту BH в нашей трапеции:
В прямоугольном треугольнике ABH нам известно, что гипотенуза равна 460,2029 км, малый катет тоже известен (это половина разницы между длинами оснований трапеции, то есть 0,5*[460,469-410,4119], то есть 0,5*50,05711, или 25,02856 км).
Итак, найдем высоту трапеции ABCD, ее можно вычислить с помощью теоремы Пифагора. Напомню, что мы знаем и длину гипотенузы, и длину наименьшего из катетов.
- Квадрат гипотенузы: 211786,7
- Квадрат известного катета: 626,4
- Разность между этими числами: 211160,2
Корень из этой разности – 459,5218 км. Это и есть наша высота трапеции, то есть BH.
Задача почти решена. Для нахождения расстояния между Москвой и Питером нам нужно вычислить диагональ трапеции, то есть BD. Нарисуем эту линию:
Итак, у нас есть треугольник BHD. BH мы только что вычислили (459,5218 км), HD тоже известно (нужно от большего основания трапеции отнять AH. 460,469-25,02856=435,4404).
Два катета известны, нужно найти гипотенузу. По той же теореме Пифагора, и мы увидим, что гипотенуза будет равна 633,0629 км. Это и есть расстояние от Питера до Москвы.
Проверим наши вычисления, спросив у Яндекса, сколько составляет расстояние от Питера до Москвы.
Мы увидим ответ – 634 км. При вычислениях по нашей методике получилось чуть больше, чем 633 км. Это значит, что погрешность при данном виде вычислений достаточна мала. Но если учесть, что крупные города – это не маленькие точки, а большие расстояния с севера на юг и с запада на восток, то можно сказать, что мы вычислили все правильно.
А на этом пока всё, подписывайтесь на мой канал и до новых встреч!
Чтобы
определить по карте расстояние между
точками местности (предметами, объектами),
пользуясь численным масштабом, надо
измерить на карте расстояние между
этими точками в сантиметрах и умножить
полученное число на значение масштаба
(рис. 20).
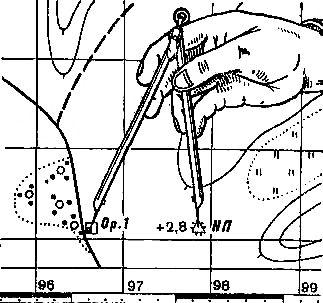

Рис.
20. Измерение расстояний на карте
циркулем-измерителем
по
линейному
масштабу
Например,
на карте масштаба 1 : 50 000 (значение
масштаба 500 м) расстояние между двумя
ориентирами составляет 4,2 см.
Следовательно,
искомое расстояние между этими ориентирами
на местности будет равно 4,2·500 = 2100 м.
Небольшое
расстояние между двумя точками по прямой
линии проще определять, пользуясь
линейным масштабом (см. рис. 20). Для этого
достаточно циркуль-измеритель, раствор
которого равен расстоянию между заданными
точками на карте, приложить к линейному
масштабу и снять отсчет в метрах или
километрах. На рис. 20 измеренное расстояние
равно 1250 м.
Большие
расстояния между точками по прямым
линиям измеряют обычно с помощью длинной
линейки или циркуля-измерителя. В первом
случае для определения расстояния по
карте с помощью линейки пользуются
численным масштабом. Во втором случае
раствор («шаг») циркуля-измерителя
устанавливают так, чтобы он соответствовал
целому числу километров, и на измеряемом
по карте отрезке откладывают целое
число «шагов». Расстояние, не укладывающееся
в целое число «шагов» циркуля-измерителя,
определяют с помощью линейного масштаба
и прибавляют к полученному числу
километров.
Таким
способом измеряют расстояния по
извилистым линиям. В этом случае «шаг»
циркуля-измерителя следует брать 0,5 или
1 см в зависимости от длины и степени
извилистости измеряемой линии (рис.
21).

Рис.
21. Измерение расстояний по извилистым
линиям
Для
определения длины маршрута по карте
применяют специальный прибор, называемый
курвиметром. Он удобен для измерения
извилистых и длинных линий. В приборе
имеется колесико, которое соединено
системой передач со стрелкой. При
измерении расстояния курвиметром нужно
установить его стрелку на нулевое
деление, а затем прокатить колесико
вдоль маршрута так, чтобы показания
шкалы возрастали. Полученный отсчет в
сантиметрах умножают на значение
масштаба и получают расстояние на
местности.
Точность
определения расстояний по карте зависит
от масштаба карты, характера измеряемых
линий (прямые, извилистые), выбранного
способа измерения рельефа местности и
других факторов.
Наиболее
точно определить расстояние по карте
можно по прямой линии. При измерении
расстояний с помощью циркуля–измерителя
или линейки с миллиметровыми делениями
среднее значение ошибки измерения на
равнинных участках местности обычно
не превышает 0,5–1 мм в масштабе карты,
что составляет для карты масштаба 1 :
25 000 – 12,5–25 м, масштаба 1 : 50 000 – 25–50 м,
масштаба 1 : 100 000 – 50–100 м. В горных районах
при большой крутизне скатов ошибки
будут больше. Это объясняется тем, что
при съемке местности на карту наносят
не длину линий на поверхности Земли, а
длину проекций этих линий на плоскость.
При
крутизне ската 20° и расстоянии на
местности 2120 м его проекция на плоскость
(расстояние на карте) составляет 2000 м,
т. е. на 120 м меньше. Подсчитано, что при
угле наклона (крутизне ската) 20° полученный
результат измерения расстояния по карте
следует увеличивать на 6% (на 100 м прибавлять
6 м), при угле наклона 30° – на 15%, а при
угле 40° – на 23%.
При
определении длины маршрута по карте
следует учитывать, что расстояния по
дорогам, измеренные на карте с помощью
циркуля или курвиметра, получаются
короче действительных расстояний. Это
объясняется не только наличием спусков
и подъемов на дорогах, но и некоторым
обобщением извилин дорог на картах.
Поэтому получаемый по карте результат
измерения длины маршрута следует с
учетом характера местности и масштаба
карты умножить на коэффициент, указанный
в табл. 3.
Таблица
3
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
1.1.Масштабы карт
(Статья: 1.1.Масштабы карт)
Масштаб карты
показывает, во сколько раз длина линии на карте меньше соответствующей ей длины на местности. Он выражается в виде отношения двух чисел. Например, масштаб 1:50 000 означает, что все линии местности изображены на карте с уменьшением в 50000 раз, т. е. 1 см на карте соответствует 50000 см (или 500 м) на местности.

Полезно запомнить правило: если в правой части отношения зачеркнуть два последних нуля, то оставшееся число покажет, сколько метров на местности соответствует 1 см на карте, т. е. величину масштаба.
При сравнении нескольких масштабов более крупным будет тот, у которого число в правой части отношения меньше. Допустим, что на один и тот же участок местности имеются карты масштабов 1:25000, 1:50000 и 1:100000. Из них масштаб 1:25000 будет самым крупным, а масштаб 1:100 000-самым мелким. Чем крупнее масштаб карты, тем подробнее на ней изображена местность. С уменьшением масштаба карты уменьшается и количество наносимых на нее деталей местности
Подробность изображения местности на топографических картах зависит от ее характера: чем меньше деталей содержит местность, тем полнее они отображаются на картах более мелких масштабов.
В нашей стране и многих других странах в качестве основных масштабов топографических карт приняты: 1:10000, 1:25000, 1: 50000, 1: 100000, 1: 200000, 1: 500000 и 1:1000000.
Используемые в войсках карты подразделяются на крупномасштабные, среднемасштабные и мелкомасштабные.
| Масштаб карты | Наименование карты | Классификация карт | |
| по масштабам | по основному назначению | ||
| 1:10 000 (в 1 см 100 м) | десятитысячная | крупномасштабные | тактические |
| 1:25 000 (в 1 см 250 м) | двадцатипятитысячная | ||
| 1:50 000 (в 1 см 500 м) | пятитысячная | ||
| 1:100 000 ( в 1 см 1 км) | стотысячная | среднемасштабные | |
| 1:200 000 (в 1 см 2 км) | двухсоттысячная | оперативные | |
| 1:500 000 (в 1 см 5 км) | пятисоттысячная | мелкомасштабные | |
| 1:1 000 000 ( в 1 см 10 км) | миллионная |
Определение расстояний по топографическим картам с помощью графических масштабов.
При создании топографических карт, спроецированные на уровенную поверхность линейные размеры всех объектов местности уменьшают в определенное количество раз. Степень такого уменьшения называется масштабом карты. Масштаб карты может быть выражен в численной форме (численный масштаб) или в графической (линейный, поперечный масштабы), в виде графика.
Расстояния по карте измеряют, пользуясь обычно численным или линейным масштабом. Более точные измерения выполняются с помощью поперечного масштаба.
На шкале линейного масштаба оцифрованы отрезки, соответствующие расстояниям на местности в метрах или километрах. Это облегчает процесс измерения расстояний, так как не требуется производить вычисления.
Определение по карте расстояний и площадей. Измерение расстояний.
При пользовании численным масштабом расстояние, измеренное на карте в сантиметрах, умножают на знаменатель численного масштаба в метрах.
Например, расстояние от пункта ГГС отм. 174,3 (кв. 3909 ) до развилки дорог (кв. 4314) на карте составляет 13,96 см, на местности оно будет: 13,96 х 500 = 6980 м. (карта масштаба 1: 50 000 У-34-85-А).
Если расстояние, измеренное на местности надо отложить на карте, то его надо разделить на знаменатель численного масштаба. Например, расстояние, измеренное на местности, равно 1550 м., на карте масштаба 1: 50 000 оно будет 3,1 см.
Измерения по линейному масштабу выполняют с помощью циркуля-измерителя. Раствором циркуля соединяют две контурные точки на карте, между которым надо определить расстояние, затем прикладывают к линейному масштабу и получают расстояние на местности. Криволинейные участки определяют по частям или при помощи курвиметра.
В практике наиболее часто применяют численный, линейный и поперечный масштабы.
Численный масштаб
обозначается в виде дроби:
1 : М = 1 : 25 000.
Например, 1 : М = 1 : 25 000 означает, что расстояние, равное 1 см на карте, соответствует 250 м горизонтального проложения линии на местности. При этом М – это знаменатель численного масштаба. Знаменатель численного масштаба показывает степень уменьшения горизонтальных проложений линий местности, при этом чем больше знаменатель масштаба, тем мельче масштаб.
Точность масштаба t
. На карте можно различить невооруженным глазом отрезок длиной не менее 0,1 мм. В соответствии с этим точность масштаба определяется как горизонтальное проложение линии местности, соответствующее расстоянию в 0,1 мм на карте данного масштаба. Например, для масштаба 1 : 5 000 точность составляет 0,5 м (t = 0,5 м); для масштаба 1 : 10 000 – t = 1 м.
Масштаб используется для измерения длин линий на карте и для построения на карте линии, длина которой на местности известна.
Пример 1. Надо отложить на карте масштаба 1 : 10 000 по заданному направлению горизонтальное проложение S = 346 м.
Из определения следует, что длина отрезка на карте найдется из соотношения:
D = S / M (1.1)
или
D = 346 : 10 000 = 3,46 см.
Пример 2. На карте масштаба 1 : 10 000 измерена длина линии d = 2,17 см, длина этой линии на местности будет равна:
S = d · M (1.2)
или
S = 2,17 · 10 000 = 217 м.
Работа с численным масштабом требует вычислений.
Поэтому во избежание значительных работ по вычислениям, применяют графические масштабы – линейный и поперечный.
Линейный масштаб
строится следующим образом. На прямой линии откладываются несколько отрезков [а] одинаковой длины, которые называются
основанием линейного масштаба
(рис. 1.16). Обычно основание принимается равным 2 см. Длина основания масштаба соответствует целому числу сотен метров на местности. Горизонтальное проложение линии местности, соответствующее основанию, называется
ценой основания масштаба
.
Например, для масштаба 1 : М = 1 : 5 000 цена основания масштаба при значении а = 2 см равна 100 м.

Конец первого отрезка подписывается знаком «0», а следующим придается оцифровка для определенного численного масштаба. Так, для 1 : М = 1: 5 000 необходимо подписать 100, 200 м и т. д. Крайний слева отрезок от нулевого штриха основания масштаба делится на более мелкие части (обычно 10 или 20). Горизонтальное проложение линии местности, соответствующее наименьшему делению основания масштаба, называют ценой деления масштаба
. На рис. 1.16 основание разделено на 10 делений, поэтому цена наименьшего деления составляет 10 м.

Для определения расстояния по линейному масштабу
необходимо приложить ножки измерителя так, чтобы правая ножка измерителя попадала на штрих графика, обозначающий целое основание, а левая – находилась между малыми делениями Расстояние, измеренное по карте, на рис. 1.16 будет складываться из числа целых оснований и малых делений (Sизм = 200 + 5,8 · 10 = 258 м).
Точность линейного масштаба равна половине наименьшего деления основания поперечного масштаба.
Чтобы отложить на карте, например, 257 м, нужно одну ножку циркуля поставить на отрезке 200 м, а вторую разместить так, чтобы было 57 м, т. е. 5 малых делений и 0,7 деления (оценивается на глаз).
Поперечный масштаб
является более точным, в отличие от линейного, который не обеспечивает достаточной точности. Поперечный масштаб создан для повышения точности отсчитывания долей основания.
Поперечный масштаб представляет собой систему взаимно-перпенди-кулярных линий, образующих номограмму длиной 12 или 20 см и высотой 3 см. Для измерений используются специальные масштабные линейки. Вертикальные линии проведены через расстояния, равные основанию масштаба. Номограмма разделена по высоте на равные m делений. Крайнее основание масштаба разделено по горизонтали на n равных частей. Кроме того, на номограмме отображаются трансверсали
– наклонные линии, служащие для более точного измерения расстояний. Для масштаба 1 : 25 000 с основанием равным АВ = 500 м при m = 10 и n = 10 наименьшее деление поперечного масштаба составит 5 м.
Для определения расстояний по поперечному масштабу
измеритель укладывают так, чтобы правая ножка измерителя находилась на целом обозначении основания масштаба, и ее поднимают одновременно с левой ножкой до тех пор, пока последняя не пересечет трансверсаль. Измеряемая линия складывается из трех частей; первая равна количеству целых оснований масштаба; вторая – количеству целых малых делений (n) по крайнему основанию; третья часть определяется по количеству m делений.
Пример. На карте масштаба 1: 10 000 нужно отложить отрезок, равный 258,6 м. Определяем, что при а = 2 см наименьшее деление поперечного масштаба составит 2 м.
Тогда ножки циркуля должны быть расположены так, как показано на рис. 1.17.

Рис. 1.17
1.2.2. Последовательность выполнения задания
1. Определить точность линейного масштаба.
Точность масштаба карты (плана) можно определить по формуле:
t = 0.1 мм · М, (1.4)
где М – знаменатель численного масштаба.
Начертить и зарисовать в соответствии с заданным численным масштабом поперечный масштаб.
2. Нанести на карту точки 1 и 2 по заданным прямоугольным координатам, точки 3 и 4 по заданным географическим координатам.
3. Определить географические координаты точек 1 и 2 и прямоугольные координаты точек 3 и 4.
4. Определить для точки 3 прямоугольные координаты в соседней зоне. Показать на чертеже, на сколько километров и с какой стороны от осевого меридиана она расположена.
5. Измерить расстояния в четырехугольнике 1-2-3-4 на карте (1-2, 2-3, 3-4, 4-1), пользуясь линейным и поперечным масштабами; результаты выразить в метрах и занести в табл. 1.1; объяснить полученные расхождения двух измерений одной и той же линии.
6. Дать описание ситуации на карте по маршруту в полосе шириной 4 см. Описание ситуации оформить в табл. 1.2.
1.2. Измерение по карте прямых и извилистых линий
(Статья: 1.2. Измерение по карте прямых и извилистых линий)
Чтобы определить по карте расстояние между точками местности (предметами, объектами), пользуясь численным масштабом, надо измерить на карте расстояние между этими точками в сантиметрах и умножить полученное число на величину масштаба.
Пример, на карте масштаба 1:25000 измеряем линейкой расстояние между мостом и ветряной мельницей (рис. 2); оно равно 7,3 см, умножаем 250 м на 7,3 и получаем искомое расстояние; оно равно 1825 метров (250х7,3=1825).

Небольшое расстояние между двумя точками по прямой линии проще определить, пользуясь линейным масштабом (рис. 3). Для этого достаточно циркуль-измеритель, раствор которого равен расстоянию между заданными точками на карте, приложить к линейному масштабу и снять отсчет в метрах или километрах. На рис. 3 измеренное расстояние равно 1070 м.
Рис. 3. Измерение на карте расстояний циркулем-измерителем по линейному масштабу Рис. 4. Измерение на карте расстояний циркулем-измерителем по извилистым линиям
Большие расстояния между точками по прямым линиям измеряют обычно с помощью длинной линейки или циркуля-измерителя.
В первом случае для определения расстояния по карте с помощью линейки пользуются численным масштабом (см. рис. 2).
Во втором случае раствор «шаг» циркуля-измерителя устанавливают так, чтобы он соответствовал целому числу километров, и на измеряемом по карте отрезке откладывают целое число «шагов». Расстояние, не укладывающееся в целое число «шагов» циркуля-измерителя, определяют с помощью линейного масштаба и прибавляют к полученному числу километров.
Таким же способом измеряют расстояния по извилистым линиям (рис. 4). В этом случае «шаг» циркуля-измерителя следует брать 0,5 или 1 см в зависимости от длины и степени извилистости измеряемой линии.

Для определения длины маршрута по карте применяют специальный прибор, называемый курвиметром (рис. 5), который особенно удобен для измерения извилистых и длинных линий.
В приборе имеется колесико, которое соединено системой передач со стрелкой.
При измерении расстояния курвиметром нужно установить его стрелку на деление 99. Держа курвиметр в вертикальном положении вести его по измеряемой линии, не отрывая от карты вдоль маршрута так, чтобы показания шкалы возрастали. Доведя до конечной точки, отсчитать измеренное расстояние и умножить его на знаменатель численного масштаба. (В данном примере 34х25000=850000, или 8500 м)
Определение расстояний по карте различными способами
Масштабы карт и пользование ими
При создании топографических карт, спроецированные на уровенную поверхность линейные размеры всех объектов местности уменьшают в определенное количество раз. Степень такого уменьшения называется масштабом карты. Масштаб карты может быть выражен в численной форме (численный масштаб) или в графической (линейный, поперечный масштабы), в виде графика.
Расстояния по карте измеряют, пользуясь обычно численным или линейным масштабом. Более точные измерения выполняются с помощью поперечного масштаба.
На шкале линейного масштаба оцифрованы отрезки, соответствующие расстояниям на местности в метрах или километрах. Это облегчает процесс измерения расстояний, так как не требуется производить вычисления.
Определение по карте расстояний и площадей.Измерение расстояний.
При пользовании численным масштабом расстояние, измеренное на карте в сантиметрах, умножают на знаменатель численного масштаба в метрах.
Например, расстояние от пункта ГГС отм. 174,3 (кв. 3909 ) до развилки дорог (кв. 4314) на карте составляет 13,96 см, на местности оно будет: 13,96 х 500 = 6980 м. (карта масштаба 1: 50 000 У-34-85-А).
Если расстояние, измеренное на местности надо отложить на карте, то его надо разделить на знаменатель численного масштаба. Например, расстояние, измеренное на местности, равно 1550 м., на карте масштаба 1: 50 000 оно будет 3,1 см.
Измерения по линейному масштабу выполняют с помощью циркуля-измерителя. Раствором циркуля соединяют две контурные точки на карте, между которым надо определить расстояние, затем прикладывают к линейному масштабу и получают расстояние на местности. Криволинейные участки определяют по частям или при помощи курвиметра.
Определение площадей.
Площадь участка местности определяют по карте чаще всего подсчетом квадратов координатной сетки, покрывающих этот участок. Величину долей квадратов определяют на глаз или с помощью специальной палетки. Каждый квадрат, образуемый линиями координатной сетки, соответствует : 1: 25 000 и 1: 50 000 – 1 км.кв., 1: 100 000 – 4 км.кв., 1: 200 000 – 16 км.кв.
Полезно помнить, следующие соотношение 2 х 2 мм., соответсвуют для масштабов:
1: 25 000 – 0,25 га = 0,0025 км.кв.
1: 50 000 – 1 га = 0, 01 км.кв.
1: 100 000 – 4 га = 0, 04 км.кв.
1: 200 000 – 16 га = 0, 16 км.кв.
Определение площадей отдельных участков проводится при отчуждении земельных участков для Министерства обороны.
Точность определения расстояний по карте. Поправка в длину маршрута.
Точность измерения линий, площадей по топографической карте. Приобрести седельные тягачи и грузовики по самым лучшим ценам, вы сможете на сайте auto-holland.ru. Все грузовые автомобили прошли предпродажную подготовку и инспекционный контроль (инструментальный, компьютерный и визуальный).
Точность измерения линий и площадей, в первую очередь, зависит от масштаба карты. Чем крупнее масштаб карты, тем точнее определяются по ней длины линий и площади. При этом точность зависит не только от точности измерений, но и от погрешности самой карты, неизбежно при ее составлении и печати. Ошибки могут достигать для равнинных районов 0, 5, а в горах до 0, 7 мм. Источником ошибок измерений также является деформация карты и сами измерения.
Абсолютно с такой же погрешностью определяются плоские прямоугольные координаты по топографическим картам вышеперечисленных масштабов.
Поправка в расстояние за наклон линии.
Например, расстояние между двумя пунктами, измеренное по карте, на местности с углом наклона 12 градусов равно 9270 м. Действительное же расстояние между этими пунктами будет 9270 х 1.02 = 9455 м. Таким образом, при измерении расстояний по карте, необходимо вводить поправки за наклон линий (рельеф).
Прямолинейные расстояния большой протяженности в одной шестиградусной зоне могут быть рассчитаны по формуле:
Этот способ определения расстояния используется в основном при подготовке стрельбы артиллерии и при пуске ракет по наземным целям.
1.3. Точность измерения расстояний по карте. Поправки на расстояние за наклон и извилистость линий
(Статья: 1.3. Точность измерения расстояний по карте. Поправки на расстояние за наклон и извилистость линий)
Точность определения расстояний по карте
зависит от масштаба карты, характера измеряемых линий (прямые, извилистые), выбранного способа измерения, рельефа местности и других факторов.
Наиболее точно определить расстояние по карте можно по прямой линии.
При измерении расстояний с помощью циркуля-измерителя или линейкой с миллиметровыми делениями средняя величина ошибки измерения на равнинных участках местности обычно не превышает 0,7-1 мм в масштабе карты, что составляет для карты масштаба 1:25000 — 17,5-25 м, масштаба 1:50000 – 35-50 м, масштаба 1:100000 – 70-100 м.
В горных районах при большой крутизне скатов ошибки будут больше. Это объясняется тем, что при съемке местности на карту наносят не длину линий на поверхности Земли, а длину проекций этих линий на плоскость.
Например, При крутизне ската 20° (рис. 6) и расстоянии на местности 2120 м его проекция на плоскость (расстояние на карте) составляет 2000 м, т. е. на 120 м меньше.
Подсчитано, что при угле наклона (крутизне ската) 20° полученный результат измерения расстояния по карте следует увеличивать на 6% (на 100 м прибавлять 6 м), при угле наклона 30° — на 15%, а при угле 40° — на 23%.
Рис. 6. Проекция длины ската на плоскость (карту)
При определении длины маршрута по карте следует учитывать, что расстояния по дорогам, измеренные на карте с помощью циркуля или курвиметра, в большинстве случаев получаются короче действительных расстояний.
Это объясняется не только наличием спусков и подъемов на дорогах, но и некоторым обобщением извилин дорог на картах.
Поэтому получаемый по карте результат измерения длины маршрута следует с учетом характера местности и масштаба карты умножить на коэффициент, указанный в таблице.
| Характер местности | Коэффициент увеличения длины маршрута, измеренного по карте масштаба | ||
| 1: 50000 | 1: 100000 | 1: 200000 | |
| Горная (сильнопересеченная) | 1,15 | 1,20 | 1,25 |
| Холмистая (среднепересеченная) | 1,05 | 1,10 | 1,15 |
| Равнинная (слабопересеченная) | 1,00 | 1,00 | 1,05 |
Основные способы измерения расстояний на местности и по карте.
При выполнении различных задач в разведке, при наблюдении за полем боя, при целеуказании и ориентировании на местности, при подготовке данных для стрельбы и т.д. возникает необходимость быстро определять расстояние до ориентиров, местных предметов, целей в других объектов.
Существуют различные способы и приборы для определения расстояний на местности: по карте, аэрофотоснимку, с помощью дальномера и т.д. Но существуют и более простые способы измерения, такие как:
— определение расстояний на глаз;
— по угловым и линейным размерам предметов;
— промером шагами;
— по времени движения;
— по соотношению скоростей света и звука;
— на слух.
а) Глазомер. Это способ является наиболее распространенным и доступен каждому, так как расстояния определяются без применения каких — либо приборов, что очень важно в условиях боевой обстановки. Основные приёмы глазомерного определения — по отрезкам местности, по степени видимости предмета (цели).
По отрезкам местности. Этот приём заключается в способности наблюдателя мысленно представлять на местности привычные расстояния, например 100, 200, 300, 400м, Запечатлев эти отрезки в своей памяти, наблюдатель мысленно откладывает нужный отрезок в глубину столько раз, сколько он уложится до наблюдаемого предмета.
По степени видимости предмета. Определяя расстояние этим приёмом, нужно учитывать, на каком фоне местности находится предмет (цель) и вблизи каких других предметов он расположен.Определяя расстояние по степени видимости предметов, необходимо также учитывать что:
— мелкие предметы (кусты, бугры, камни), а также отдельные фигуры людей кажутся дальше, чем находящихся на том же расстоянии крупные предметы (лес, высота, населённый пункт, колонна);
— одноцветный, однообразный фон местности (луг, снег, пашня) как бы приближает находящиеся на нем предметы; разноцветный фон, наоборот, маскирует и как бы удаляет их;
— предметы легких цветов лучше видны, чем предметы тёмного цвета;
— при наблюдении ночью предметы, освещённые искусственным светом, кажутся ближе, а не освещённые —
дальше, чем в действительности.
Практикой установлено, что погрешность точности глазомерного определения расстояний до 1000 м при наличии некоторого опыта может быть в пределах 10- 15 % длины измеряемого отрезка. При измерении расстояний более 1000м и недостаточной опытности, наблюдается ошибка, она может достигать 30 и даже 50%.
Для определения расстояний по степени видимости и кажущейся величины предметов (целей) рекомендуется воспользоваться таблицей 1 (см. приложение №1).
Определение расстояний по линейным размерам предметов даёт более точные результаты, чем глазомер, но для этого нужно знать действительные размеры наблюдаемого предмета и иметь линейку с миллиметровыми делениями.
Сущность этого способа состоит в том, что держа линейку на расстоянии наблюдаемого предмета.
Затем действительную высоту (ширину) предмета в см делят на измеренную по линейки высоту (ширину) предметов мм и умножают на постоянное число 5, Полученный результат и будет искомым расстоянием в метрах.
Например. Телеграфный столб высотой 6,4м закрывается 10 мм на линейке, Следовательно, до него:
640
Д = —
“ 5 = 320м
10
Средние размеры наиболее часто встречающихся предметов приводятся в таблице 2 (см. приложение №2).
б) Определение расстояний по угловым размерам предметов основано на зависимости между угловыми и линейными величинами. Эта зависимость состоит в том, что длина 1/6000 любой окружности равна 1/1000 её радиуса.
Угол при центре окружности, соответствующей 1/6000 её дуги, принимается за единицу при условных измерениях вместо градусной меры. Эта единица называется тысячной. Тысячные читаются и записываются так: одна тысячная пишется “0-01”, читается “ноль ноль один”; двадцать пять тысячных — “0-25” — “ноль двадцать пять”; сто двадцать пять тысячных — “1-25”- “один двадцать пять”.
Высота предмета, выраженная в тысячных, может быть измерена биноклем с угломерной сеткой, линейкой с миллиметровыми делениями, а также с помощью подручных предметов, примеры которых в тысячных известны. Расстояние до предмета вычисляется по формуле:
В
Д= — ” 1000, м
У
где: В — высота (ширина) предмета, м;У — угловая величина предмета в тысячных.
Например, наблюдаемая в бинокль цель, высота которой равна 2,5м, покрывается делением сетки бинокля, равным 0-0,5. Следственно расстояние до цели:
2.5
S
= 5 ” 1000 = 500
м
Измерение углов с миллиметровыми делениями производится также измерением высоты (ширины) цели, удерживая линейку на расстоянии 50см от глаз, при этой каждая миллиметровое деление будет соответствовать двум тысячным (0-0,8), а каждый сантиметр — двадцати тысячным (0-20).
Точность определения расстояний по линейному и угловыми величинам составляет 5-10% длины измеренного отрезка.
в) Измерение расстояния шагамипо сравнению с другими способами применяются ограниченно, только в тех случаях, когда позволяет обстановка.
При измерении расстояний шаги считаются парами. Чтоб измеренное расстояние перевести в метры, надо знать длину шага. Она определяется из промера шагами линии, длина известна или точно измерена заранее. Если пройденное расстояние достаточно определить приближённо, то принимают, что расстояние в метрах равно числу пар шагов, увеличенному в полтора раза, так как пара шагов в среднем равна 1т5м.
Скорость своего движения и имея часы, легко подсчитать пройденное расстояние. Этот способ особенно полезен при движении на лыжах. Ошибка в измерениях расстояний шагами обычно составляет 2-4% от длины измеренного расстояния.
Определение расстояний по соотношению скорости света и звука. Скорость звука приблизительно равно 330м/сек, т.е. округлено 1км в 3сек. Скорость света равна 300000 км/сек, можно считать мгновенной. Таким образом расстояние в километрах до места вспышки равна числу секунд, прошедших от момента вспышки до того момента, когда наблюдатель услышал звук выстрела, деленному на три.
Определение расстояний на звук. Ночью и в условиях плохой видимости приблизительно расстояние до объектов, от которых издается звук или шум, можно оценить на слух. При нормальном случае и благоприятных условиях примерная дальность слышимости показана в таблице 1
Таблица 1
| Род войск или вид техники | Характер звука | Дальность слышимости, м | |
| При движении по грунтовой дороге | При движении по шоссе | ||
| Подразделения в пешем строю Автомобили Артиллерия Танки | Ровный глухой шум шагов Ровный, глухой шум моторов Шум моторов, тягачей, лязг гусениц Резкий рокот моторов, лязг гусениц | 1000-2000 | 2000-3000 3000-4000 |
1.4. Простейшие способы измерения площадей по карте
(Статья: 1.4. Простейшие способы измерения площадей по карте)
Приближенную оценку размеров площадей производят на глаз по квадратам километровой сетки, имеющейся на карте. Каждому квадрату сетки карт масштабов 1:10000 — 1:50000 на местности соответствует 1 км2 , квадрату сетки карт масштаба 1:
100000 — 4 км2, квадрату сетки карт масштаба 1:200000 — 16 км2.
Более точно площади измеряют палеткой
, представляющей собой лист прозрачного пластика с нанесенной на него сеткой квадратов со стороной 10 мм (в зависимости от масштаба карты и необходимой точности измерений).
Наложив такую палетку на измеряемый объект на карте, подсчитывают по ней сначала число квадратов, полностью укладывающихся внутри контура объекта, а затем число квадратов пересекаемых контуром объекта. Каждый из неполных квадратов принимаем за половину квадрата. В результате перемножения площади одного квадрата на сумму квадратов получают площадь объекта.
По квадратам масштабов 1:25000 и 1:50000 площади небольших участков удобно измерять офицерской линейкой, имеющей специальные вырезы прямоугольной формы. Площади этих прямоугольников {в гектарах ) указаны на линейке для каждого масштаба гарты.
Как измерить расстояние между точками на Гугл Картах
В зависимости от ситуации пользователь смартфона может измерить расстояние на карте Гугл с помощью веб-версии на сайте или в приложение на мобильном устройстве. Из-за особенностей интерфейса и разных принципов управления подходы также отличаются.
На ПК
Наиболее удобный путь — использование веб-версии Гугл Карт. Сделайте следующие шаги:
- Войдите по ссылке google.ru/maps и сразу обратите внимание на тип софта. Если включен упрощенный режим, линейка на карте Google будет недоступной.
- Перемещайтесь по изображению и найдите место, которое вас интересует. Начинайте с места, от которого необходимо начать измерение.
- Жмите по выбранному месту правой кнопкой мышки и кликните на пункт Измерить расстояние. Сразу после этого на Гугл карте появляется небольшой круг с черным ободом и белым пространством внутри. Вы можете выбрать любую позицию, будь это город или местность вне населенного пункта.

- Найдите на картинке пункт назначения, до которого необходимо выполнить измерение. После этого вы видите Гугл Карту с линейкой онлайн. При этом система сразу показывает расстояние.
При необходимости вы можете перемещать вторую и первую точку по все стороны на 360 градусов. Это удобно, если при задании первичных данных вы вдруг ошиблись. В случае, когда необходимо измерить расстояние к дополнительному участку, найдите его и еще раз кликните левой кнопкой мышки. В этом случае сведения о километраже появляются возле новой отметки. Как и в прошлом случае, все точки можно перемещать путем их зажатия левой кнопкой мышки, чтобы точно измерить путь.
Для удаления отметки кликните по ней один раз левой кнопкой мышки. Если вам больше не нужен инструмент для измерений, жмите на крестик в специальном окне внизу. В этом случае все нарисованные линии будет удалены без возможности возврата. Интересно, что расстояние в специальном окне внизу указывается в километрах и милях.
Разобраться в вопросе, как померить расстояние в Гугл Картах, не трудно. Интерфейс понятен и прост, поэтому измерить путь сможет даже новичок.
На телефоне
При желании можно использовать Гугл Карты и линейку на телефоне, где доступен почти такой же набор возможностей. Алгоритм действий для смартфонов с iOS или Android немного иной. Сделайте следующее:
- Войдите в Плей Маркет и установите приложение Карты Гугл, если этого еще не сделано ранее. Без выполнения этого шага измерить расстояние не получится.
- Откройте приложение и коснитесь нужного места. Удерживайте палец до тех пор, пока не появится красный значок на экране и блок с координатами.
- Жмите на название места, расположенное в специальном блоке внизу экрана.
- Выберите пункт Измерить расстояние.

- Сразу после этого появляется точка в черном ободке. Учтите, что расстояние от точки до точки в Гугл Картах происходит в режиме реального времени. При этом данные обновляются каждый раз после перемещения изображения. Конечный пункт всегда отмечен темной иконкой и находится в центральной части.

- Кликните на кнопку Добавить на нижней панели возле расстояния, чтобы закрепить новую позицию и измерить полный путь Добавляйте столько точек, сколько необходимо.
- Убирайте ненужные позиции путем нажатия на стрелку справа вверху. Здесь же доступен вход в меню (спрятан под тремя точками). Там можно нажать на пункт Очистить и тем самым обнулить информацию. Остаются только данные по начальной отметке.
Чтобы посмотреть метраж или километраж между заданными точками, обратите внимание на нижнюю часть экрана (там стоит необходимая цифра). Перед тем как замерить расстояние на карте Гугл, определитесь с начальной и конечной позицией, чтобы в дальнейшем не тратить время на поиски.
Азимуты и дирекционный угол. Магнитное склонение, сближение меридианов и поправка направления
(Статья: 2. Азимуты и дирекционный угол. Магнитное склонение, сближение меридианов и поправка направления)
Истинный азимут
(Аи) — горизонтальный угол, измеряемый по ходу часовой стрелки от 0° до 360° между северным направлением истинного меридиана данной точки и направлением на объект (см. рис. 7).
Магнитный азимут
(Ам) — горизонтальный угол, измеряемый по ходу часовой стрелки от 0е до 360° между северным направлением магнитного меридиана данной точки и направлением на объект.
Дирекционный угол
(α; ДУ) — горизонтальный угол, измеряемый по ходу часовой стрелки от 0° до 360° между северным направлением вертикальной линии координатной сетки данной точки и направлением на объект.
Магнитное склонение
(δ; Ск) — угол между северным направлением истинного и магнитного меридианов в данной точке.
Если магнитная стрелка отклоняется от истинного меридиана к востоку, то склонение восточное (учитывается со знаком +), при отклонении магнитной стрелки к западу — западное (учитывается со знаком -).

Сближение меридианов
(γ; Сб) — угол между северным направлением истинного меридиана и вертикальной линией координатной сетки в данной точке. При отклонении линии сетки к востоку – сближение меридиана восточное (учитывается со знаком +), при отклонении линии сетки к западу — западное (учитывается со знаком -).
Поправка направления
(ПН) — угол между северным направлением вертикальной линии координатной сетки и направлением магнитного меридиана. Она равна алгебраической разности магнитного склонения и сближения меридианов:
Подготовка по карте данных для движения по азимутам
(Статья: 4. Подготовка по карте данных для движения по азимутам)
Движение по азимутам
– это основной способ ориентирования на местности, бедной ориентирами, особенно ночью и при ограниченной видимости.
Сущность его заключается в выдерживании на местности направлений, заданных магнитными азимутами, и расстояний, определенных по карте между поворотными пунктами намеченного маршрута. Направления движения выдерживают с помощью компаса, расстояния измеряют шагами или по спидометру.
Исходные данные для движения по азимутам (магнитные азимуты и расстояния) определяют по карте, а время движения – по нормативу и оформляют в виде схемы (рис. 11) или вписывают в таблицу (табл. 1). Данные в таком виде выдают командирам, которые не имеют топографических карт. Если командир имеет свою рабочую карту, то исходные данные для движения по азимутам он оформляет непосредственно на рабочей карте.
Рис. 11. Схема для движения по азимуту
Маршрут движения по азимутам выбирают с учетом проходимости местности, ее защитных и маскировочных свойств, чтобы он обеспечивал в боевой обстановке быстрый и скрытный выход к указанному пункту.
В маршрут обычно включают дороги, просеки и другие линейные ориентиры, которые облегчают выдерживание направления движения. Поворотные пункты выбирают у ориентиров, легко опознаваемых на местности (например, постройки башенного типа, перекрестки дорог, мосты, путепроводы, геодезические пункты и т. п.).
Опытным путем установлено, что расстояния между ориентирами на поворотных пунктах маршрута не должны превышать 1 км при движении днем в пешем порядке, а при движении на машине – 6–10 км.
Для движения ночью ориентиры намечаются по маршруту чаще.
Чтобы обеспечить скрытный выход к указанному пункту, маршрут намечают по лощинам, массивам растительности и другим объектам, обеспечивающим маскировку движения. Необходимо избегать передвижений по гребням возвышенностей и открытым участкам.
Расстояния между выбранными на маршруте движения ориентирами на поворотных пунктах измеряют по прямым линиям с помощью циркуля-измерителя и линейного масштаба или возможно точнее – линейкой с миллиметровыми делениями. Если маршрут намечен по холмистой (горной) местности, то в измеренные по карте расстояния вводят поправку за рельеф.
Таблица 1
| № точки | Участок пути | Ам, градусов | Расстояние, м | Время, мин | Расстояние, пары шагов |
| 1 | Сарай — курган | 35 | 675 | 10 | 450 |
| 2 | Курган — развилка просеки и дороги | 338 | 750 | 11 | 500 |
| 3 | Развилка просеки и дороги — башня | 47 | 930 | 14 | 633 |
| 4 | Башня — труба под дорогой | 346 | 980 | 15 | 653 |
Измерение расстояний на поверхности Земли. Изображение расстояний на бумаге. Масштаб
Как измеренное расстояние отмечают на бумаге? Что такое масштаб?
1. Способы измерения расстояний. Чтобы нанести земную поверхность на план местности, недостаточно знать только взаимное расположение предметов. Необходимо определить их размеры и расстояния между ними. Расстояние измеряют мерной лентой, полевым циркулем и другими измерительными приборами. Приблизительное расстояние можно определить и шагами. Длина шагов человека зависит от его возраста и роста, поэтому каждый должен узнать среднюю длину своего шага. Для этого нужно отмерить расстояние длиной 100 м на ровной поверхности, пройти его обычным шагом 3 раза, сосчитать шаги и взять среднюю величину. Например, 100 м пройдено первый раз за 154 шага, второй раз — за 153, третий раз — за 155. 154+153+155 = 492 : 3 =154 шага. Отсюда средняя длина одного шага равна 100 м : 154 = 0,65 м. Во время прогулки на дальнее расстояние удобнее измерить пройденный путь парами шагов. При этом нужно начинать с левой ноги, счет будет приходиться на правую. Чтобы привыкнуть, вначале при шаге левой ногой, нужно говорить «и». Например «и раз, и два, и три и т. д.». Иногда расстояние можно определить на глаз. Для этого воспользуйтесь данными приведенной ниже таблицы:
| Предмет или объект на поверхности Земли | Видимое расстояние |
| Отдельно стоящий дом | 5 км |
| Окно дома | 4 км |
| Труба на крыше | 3 км |
| Отдельно стоящее дерево или человек | 2 км |
| Рама окна | 500 м |
| Деревянные балки крыши | 200 м |
| Глаза, нос, пальцы человека | 60-70м |
| Белки глаз | 20 м |
2. Масштаб и его виды. Вам известно, что для того чтобы нанести на бумагу любое измеренное расстояние на поверхности Земли, необходимо уменьшить его в несколько раз. Масштаб (по-немецки мае — измерить, штаб — палка) — пропорция, которая показывает степень уменьшения длины линии на глобусе, карте или плане по сравнению с действительным расстоянием, то есть во сколько раз уменьшено измеренное расстояние на местности при нанесении его на бумагу. Числитель масштаба всегда равен единице, знаменатель соответствует величине уменьшения.
Например, масштаб равен 1:10 ООО, это значит, что расстояние на местности уменьшено в 10 ООО раз.
Масштаб, записанный в виде дробных чисел, называется численным масштабом. Чем больше число в знаменателе, тем масштаб считается мельче, и наоборот, чем меньше число в знаменателе, тем масштаб становится крупнее. Например, масштаб 1 : 10 ООО будет более крупным, чем 1: 50 000. Масштаб плана или карты можно записывать с пояснением. Например, масштаб 1:10 000 будет иметь в 1 см — 100 м (если перевести 10 000 см в метры, то будет 100 м). Масштаб, записанный в таком виде, называется именованным масштабом. На карте или плане расстояние между двумя точками измеряют в сантиметрах. Число, взятое в масштабе, умножается на сантиметры расстояния.
Например, масштаб карты составляет 1:100 000. Согласно этому масштабу 1 см соответствует 1 км. Допустим, что длина отрезка на карте — 5,5 см. Тогда 1км х 5,5 см = 5 км 500 м.
Рис. 14. Виды масштабов.
Такие расчеты затрудняют использование карты. Поэтому вместо того, чтобы измерять на плане или карте расстояние в сантиметрах, затем переводить в метры и километры, лучше использовать линейный масштаб (рис. 14). Он представляет собой две параллельные линии, которые разделены на равные отрезки. Каждый из них соответствует определенному значению именованного масштаба. Крайний отрезок слева делится еще на равные мелкие части. Это — самое наименьшее деление линейного масштаба. Для измерения длины отрезка на плане или карте используют циркуль-измеритель, одна ножка которого устанавливается на конец целого отрезка, другая — на маленькие деления. Тогда вправо от нуля отмечают целые числа, соответствующие численному масштабу, слева — меньшие значения чисел. Длина отрезка на рисунке 15 равна 1850 м.
Рис. 15. Измерение расстояния на карте по масштабу.
Чтобы нанести местность на карту, выбирают различные масштабы. Карту небольшой территории изображают в крупном масштабе. Такими картами пользуются в повседневной хозяйственной деятельности. Небольшие территории изображают на планах (в масштабах 1:5000, 1:2000, 1:1000 и крупнее) и топографических картах (от 1:10 000 до 1:100 000).
1. Какими способами измеряют расстояние на местности?
2. Как определить среднюю длину шага?
3. Определите среднюю длину своих шагов.
4. Какие отличия между численным и именованным масштабами!
5. Используя линейный масштаб, показанный на рис. 14, начертите и обозначьте в тетради следующие расстояния: 1 км 200 м, 2 км 400 м, 4 км 500 м.
6. Пользуясь данными таблицы, определите некоторые расстояния пути в школу и из школы, во время экскурсии. По возможности полученные величины расстояния проверьте, пройдя их шагами.
7*. Длина отрезка на топографической карте масштабом 1:50000 составляет 5,45 см. Вычислите, чему равно расстояние на земной поверхности, соответствующее этому отрезку.
