Если вы думаете, что ничего не знаете о кругах Эйлера, вы ошибаетесь. На самом деле вы наверняка не раз с ними сталкивались, просто не знали, как это называется. Где именно? Схемы в виде кругов Эйлера легли в основу многих популярных интернет-мемов (растиражированных в сети изображений на определенную тему).
Давайте вместе разберемся, что же это за круги, почему они так называются и почему ими так удобно пользоваться для решения многих задач.
Происхождение термина
Круги Эйлера – это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью.
Пока не очень понятно, верно? Посмотрите на этот рисунок:
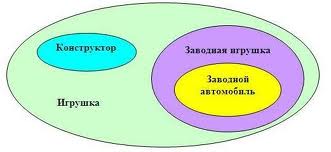
На рисунке представлено множество – все возможные игрушки. Некоторые из игрушек являются конструкторами – они выделены в отдельный овал. Это часть большого множества «игрушки» и одновременно отдельное множество (ведь конструктором может быть и «Лего», и примитивные конструкторы из кубиков для малышей). Какая-то часть большого множества «игрушки» может быть заводными игрушками. Они не конструкторы, поэтому мы рисуем для них отдельный овал. Желтый овал «заводной автомобиль» относится одновременно к множеству «игрушки» и является частью меньшего множества «заводная игрушка». Поэтому и изображается внутри обоих овалов сразу.
Ну что, так стало понятнее? Именно поэтому круги Эйлера – это тот метод, который наглядно демонстрирует: лучше один раз увидеть, чем сто раз услышать. Его заслуга в том, что наглядность упрощает рассуждения и помогает быстрее и проще получить ответ.
Автор метода – ученый Леонард Эйлер (1707-1783). Он так и говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». Эйлер считается немецким, швейцарским и даже российским математиком, механиком и физиком. Дело в том, что он много лет проработал в Петербургской академии наук и внес существенный вклад в развитие российской науки.
До него подобным принципом при построении своих умозаключений руководствовался немецкий математик и философ Готфрид Лейбниц.
Метод Эйлера получил заслуженное признание и популярность. И после него немало ученых использовали его в своей работе, а также видоизменяли на свой лад. Например, чешский математик Бернард Больцано использовал тот же метод, но с прямоугольными схемами.
Свою лепту внес также немецкий математике Эрнест Шредер. Но главные заслуги принадлежат англичанину Джону Венну. Он был специалистом в логике и издал книгу «Символическая логика», в которой подробно изложил свой вариант метода (использовал преимущественно изображения пересечений множеств).
Благодаря вкладу Венна метод даже называют диаграммами Венна или еще Эйлера-Венна.
СЛОЖНА-А-А 🙀 Ты же знаешь, что если не разобраться в теме сейчас, то потом придется исправлять оценки. Беги на бесплатное онлайн-занятие с репетитором (подробности тут + 🎁).
Зачем нужны круги Эйлера?
Круги Эйлера имеют прикладное назначение, то есть с их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике, менеджменте и не только.
Если говорить о видах кругов Эйлера, то можно разделить их на те, что описывают объединение каких-то понятий (например, соотношение рода и вида) – мы их рассмотрели на примере в начале статьи.
А также на те, что описывают пересечение множеств по какому-то признаку. Таким принципом руководствовался Джон Венн в своих схемах. И именно он лежит в основе многих популярных в интернете мемов. Вот вам один из примеров таких кругов Эйлера:

Забавно, правда? И главное, все сразу становится понятно. Можно потратить много слов, объясняя свою точку зрения, а можно просто нарисовать простую схему, которая сразу расставит все по местам.
Кстати, если вы не можете определиться, какую профессию выбрать, попробуйте нарисовать схему в виде кругов Эйлера. Возможно, чертеж вроде этого поможет вам определиться с выбором:
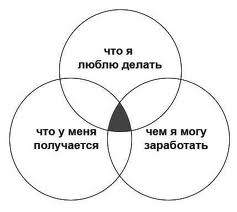
Те варианты, которые окажутся на пересечении всех трех кругов, и есть профессия, которая не только сможет вас прокормить, но и будет вам нравиться.
Решение задач с помощью кругов Эйлера
Давайте рассмотрим несколько примеров задач, которые можно решить с помощью кругов Эйлера.
Вот на этом сайте – http://logika.vobrazovanie.ru/index.php?link=kr_e.html Елена Сергеевна Саженина предлагает интересные и несложные задачи, для решения которых потребуется метод Эйлера. Используя логику и математику, разберем одну из них.
Задача про любимые мультфильмы
Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым – «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».
Решение:
Так как по условиям задачи у нас даны три множества, чертим три круга. А так как по ответам ребят выходит, что множества пересекаются друг с другом, чертеж будет выглядеть так:
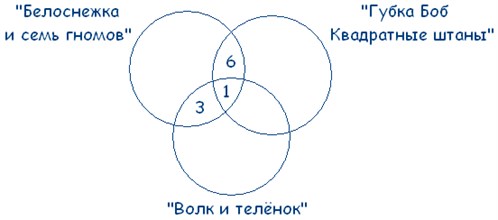
Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу:
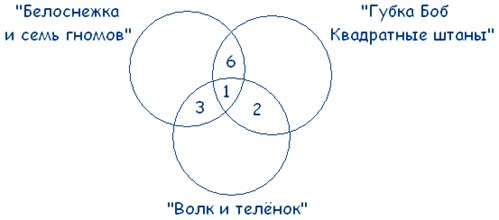
Выходит, что:
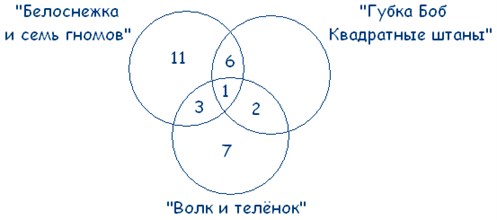
21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».
13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».
Осталось только разобраться, сколько шестиклассников двум другим вариантам предпочитает мультфильм «Губка Боб Квадратные Штаны». От всего количества учеников отнимаем всех тех, кто любит два других мультфильма или выбрал несколько вариантов:
38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».
Теперь смело можем сложить все полученные цифры и выяснить, что:
мультфильм «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек. Это и есть ответ на поставленный в задаче вопрос.
А еще давайте рассмотрим задачу, которая в 2011 году была вынесена на демонстрационный тест ЕГЭ по информатике и ИКТ (источник – http://eileracrugi.narod.ru/index/0-6).
Условия задачи:
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.
| Запрос | Найдено страниц (в тысячах) |
| Крейсер | Линкор | 7000 |
| Крейсер | 4800 |
| Линкор | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор?
Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.
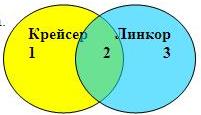
Опираясь на условия задачи, составим уравнения:
- Крейсер | Линкор: 1 + 2 + 3 = 7000
- Крейсер: 1 + 2 = 4800
- Линкор: 2 + 3 = 4500
Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:
4800 + 3 = 7000, откуда получаем 3 = 2200.
Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:
2 + 2200 = 4500, откуда 2 = 2300.
Ответ: 2300 – количество страниц, найденных по запросу Крейсер & Линкор.
Как видите, круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.
Заключение
Полагаю, нам удалось убедить вас, что круги Эйлера – не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Причем не только абстрактных задач на школьный уроках, но и вполне себе житейских проблем. Выбора будущей профессии, например.
Вам еще наверняка будет любопытно узнать, что в современной массовой культуре круги Эйлера нашли отражение не только в виде мемов, но и в популярных сериалах. Таких, как «Теория большого взрыва» и «4исла».
Используйте это полезный и наглядный метод для решения задач. И обязательно расскажите о нем друзьям и одноклассникам. Для этого под статьей есть специальные кнопки.
Молодец! Раз ты дочитал это до конца, вероятно, ты все отлично усвоил. Но если вдруг что-то еще непонятно – попробуй онлайн-занятие с репетитором (подробности тут + 🎁).
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
На самом деле изучение Кругов Эйлера, готовит восприятие обучающегося к работе с базовыми логическими элементами в электронике.
Я не буду вдаваться в определения, а сразу перейду к делу.
Пусть у нас есть класс, назовём его 10 “Б”. Это полное множество учеников и всего там 32 школьника. Обозначим его просто прямоугольником.
Далее мы знаем, что в нём учатся 18 мальчиков и обозначим их в нем как множество А- синим кругом.
Получается, что все школьники не в круге – это девочки и их будет 14. Таким образом у нас есть множество А – 18 мальчиков. И множество НЕ А(инверсия, обозначенная лиловым) – 14 девочек.
Ну а мы продолжим, в этом классе есть дети, которые занимаются плаванием – это будет множество B. Таких будем 16 человек. Сюда будут входить и мальчики и девочки, но графически это будет выглядеть так:
Предположим, что мы знаем количество мальчиков пловцов у нас 9. На картинке это будет сегмент синего круга внутри белой окружности. Тогда остальная часть в белой окружности будут пловцы девочки и их число равно 7.
Теперь мы видим, что пересечением множеств будет принадлежность к двум множествам или выполнение двух условий. Первое условие он мальчик, второе – пловец. Данное пересечение соответствует логическому “И”.
А теперь рассмотрим пример объединение множеств по признакам. Например в бассейн на соревнования по плаванию школу могут представлять мальчики или все те кто занимается плаванием. Получается это будет любой человек, который входи в множество А ИЛИ В. На картинке это будет выделено серым:
Получается что инверсией для того множества будут девочки, которые не занимаются плаванием.
Стоит отметить, что логическая сумма множества А и его инверсии, всегда будет равна 1.
Теперь переключаемся на логические элементы и смотрим как базовые логические элементы связаны с кругами Эйлера.
Логическое И – это пересечение А и В или логическое умножение. и цвет указывает на ту область, которая одновременно принадлежит и А и В.
Для каждой картинки и логического элемента есть своя таблица истинности.
Для начала проще запоминать через Круги Эйлера, а в дальнейшем эти таблицы будут очевидными.
Теперь пример задачи, которую проще решать как раз через Круги Эйлера.
В штате одной IT компании работает группа разных специалистов, среди них много программистов. 28 человек владеют и пишут на языке “C++”, на Python пишут 15 человек. На Java – 10 человек. Двумя языками владеют 8 человек – C++ и Python. На С++ и Java пишут код 6 человек.На Python и Java пишут 5 человек. . Есть ещё два человека, которые знают все три перечисленных языка. При этом оставшиеся 41 сотрудник не владеют ни одним из языков. Сколько всего сотрудников в штате?
Прежде чем решать, я просто нарисую круг и Эйлера и соберу картинку целиком.
Через круги Эйлера видно, что нужно просто подсчитать количество людей в выделенных сегментах и тех что снаружи.
Но некоторые области, на пересечении множеств будут входить два раза. Это нужно просто учесть.
Сейчас перерисую области со вспомогательными числами.
Теперь просто надо сложить нужные сегменты и получим решение.
41 +(28- 6)+(15-3)+(10- 4) – 2 – 2 = 77.
Немного поясню.
41 – это число остальных сотрудников.
(28 – 6) вычитание производим тех сотрудников, которые знают два языка, чтобы не учитывать их два раза. Аналогично будет и с двумя другими группами (15 – 3) и (10 – 4).
-2 и -2 это два раза вычитаем тех программистов, которые учтены во всех группах и знают три языка. После всех простых операций, понимаем, что в компании трудится 77 человек.
Если желаете, что-то добавить, то пишите в комментариях.
——————————————————————————–
99 товаров для электронщика.
Также несколько моделей мультиметров, которые можно заказать найдёте в общей теме: создал недавно тему, в которую собираю все товары с Алика, могут быть полезны тем, кто увлекается электроникой.
99 товаров для электронщика. ————————————————————————————————
Тема»Решение
задач с помощью кругов Эйлера»
Содержание.
. Введение.
1. Исторические сведения.
2. Изображение множества чисел с
помощью кругов Эйлера.
3. Решение задач с помощью кругов
Эйлера.
4 Применение
кругов Эйлера.
5. Заключение.
6 Список использованной литературы
Введение.
1 Исторические сведения
Один из величайших математиков
петербургский академик Леонард Эйлер за свою долгую жизнь (он родился в 1707
г., а умер в 1783 г.) написал более 850 научных работ. В одной из них и появились
эти круги. А впервые он их использовал в письмах к немецкой принцессе. Эйлер
писал тогда, что «круги очень подходят для того, чтобы облегчить наши
размышления». Позднее аналогичный прием использовал ученый Венн и его назвали
«диаграммы Венна». Эйлер писал тогда, что «они очень подходят для того, чтобы
облегчить наши размышления». При решении целого ряда задач Леонард
Эйлер использовал идею изображения множеств с помощью кругов и они
получили название «круги Эйлера».

2 Изображение множества чисел с
помощью кругов Эйлера.
Этот метод даёт ещё более
наглядное представление о возможном способе изображения условий, зависимости,
отношений в логических задачах.
Множество всех действительных
чисел Эйлер изобразил с помощью этих кругов: N-множество натуральных чисел, Z –
множество целых чисел, Q – множество рациональных чисел, R – множество вех
действительных чисел.
Актуальность. В наше время вокруг нас
собрано огромное количество информации и разобраться в ней бывает непросто.
Находить логические связи между явлениями и понятиями помогают «Круги Эйлера» –
это практичный и удобный метод решения логических задач. Многие слышали о них,
но не все могут объяснить, что это такое. Круги Эйлера находят широкое
применение, как в повседневной жизни, так и в науке, поэтому ими стоит уметь
пользоваться каждому.
цель работы –
познакомиться с методом решения задач теории множеств с использованием кругов
Эйлера и составить сборник задач, которые можно решить с помощью кругов Эйлера.
задачи:
изучить
основные понятия теории множеств,
рассмотреть
основные операции, которые можно производить с множествами,
рассмотреть
понятие кругов Эйлера и изучить возможность их применения для решения задач,
разработать
сборник задач, решаемых методом кругов Эйлера
найти
практическое применение кругов Эйлера.
Объектом исследованияявился процесс изучения
раздела математики – теории множеств.
Предмет исследования
– задачи из теории множеств, решаемые с использованием кругов Эйлера.
Гипотеза исследования: изучение
темы «Элементы теории множеств» и разработка задач, решаемых с использованием
кругов Эйлера, способствует повышению уровня математических знаний и развитию
логического мышления учащихся.
Новизна работы заключается в авторском
составлении задач по теме исследования и нахождении практического использования
кругов Эйлера в современном мире.
3 Решение
логических задач с помощью кругов Эйлера
Круги Эйлера –
задачи на пересечение или объединение множеств Это новый тип задач, в которых
требуется найти некоторое пересечение множеств или их объединение, соблюдая
условия задачи.
Круги Эйлера — геометрическая
схема, с помощью которой можно изобразить отношения между подмножествами.
Используется в математике, логике, менеджменте и других прикладных
направлениях. А впервые Эйлер их использовал в письмах к немецкой принцессе.
Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить
наши размышления». При решении целого ряда задач Леонард Эйлер использовал
идею изображения множеств с помощью кругов, и они получили название «круги
Эйлера».
Задача 1. В
классе 35 учеников. Из них 20 человек занимаются в математическом кружке, 11 —
в биологическом, 10 ребят не посещают эти кружки. Сколько биологов увлекаются
математикой?
Изобразим эти кружки на рисунке. Можем, например, начертить в
школьном дворе большой круг, а в нем два поменьше. В левый круг, обозначенный
буквой М, поместим всех математиков, а в правый, обозначенный
буквой Б, всех биологов. Очевидно, в общей части кругов,
обозначенной буквами МБ, окажутся те самые
биологи-математики, которые нас интересуют. Остальных ребят класса, а их 10,
попросим не выходить из внешнего круга, самого большого. Теперь посчитаем:
всего внутри большого круга 35 ребят, внутри двух меньших 35 — 10 = 25 ребят.
Внутри «математического» круга М находятся 20 ребят, значит, в
той части «биологического» круга, которая расположена вне круга М, находятся
25 — 20 = 5 биологов, не посещающих математический кружок. Остальные биологи,
их 11 — 5= = 6 человек, находятся в общей части кругов МБ. Таким
образом, 6 биологов увлекаются математикой.

Задача
2. .В классе 38 человек. Из них 16 играют в баскетбол, 17 –
в хоккей, 18 – в футбол. Увлекаются двумя видами спорта – баскетболом и хоккеем
– четверо, баскетболом и футболом – трое, футболом и хоккеем – пятеро. Трое не
увлекаются ни баскетболом, ни хоккеем, ни футболом.
|
|
Сколько ребят увлекаются одновременно тремя
видами спорта?
Сколько
ребят увлекается лишь одним из этих видов спорта?
Решение.
Воспользуемся кругами Эйлера. Пусть большой круг изображает всех учащихся
класса, а три меньших круга Б, Х и Ф изображают соответственно баскетболистов,
хоккеистов и футболистов. Тогда фигура Z, общая часть кругов Б, Х и Ф,
изображает ребят, увлекающихся тремя видами спорта. Из рассмотрения кругов
Эйлера видно, что одним лишь видом спорта – баскетболом занимаются 16 – (4 + z
+ 3) = 9 – z; одним лишь хоккеи 17 – (4 + z + 5) = 8 – z;
одним
лишь футболом 18 – (3 + z + 5) = 10 – z.
Составляем
уравнение, пользуясь тем, что класс разбился на отдельные группы ребят;
количества ребят в каждой группе обведены на рисунке рамочкам:
3 + (9
– z) + (8 – z) + (10 – z) + 4 + 3 + 5 + z = 38,
z = 2.
Таким
образом, двое ребят увлекаются всеми тремя видами спорта.
Складывая
числа 9 – z, 8 – z и 10 – z, где z = 2, найдем количество ребят, увлекающихся
лишь одним видом спорта: 21 человек.
Ответ.
Двое
ребят увлекаются всеми тремя видами спорта человека.
Увлекающихся
лишь одним видом спорта: 21 человек.
. Решение задач с помощью
кругов Эйлера

Задача №1
В летнем лагере было 70 ребят. 27 из них
занимаются в драмкружке, 32 – поют в хоре, 22 – спортсмены. В драмкружке 10
ребят из хора, в хоре – 6 спортсменов, в драмкружке – 8 спортсменов. 3
спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не
увлекаются спортом и не занимаются в драмкружке? Сколько ребят увлекаются
спортом?
27 – (10 + 5) = 12 (ребят) — занимаются в драмкружке,
в хоре: 32 – (110 + 3) = 19 (ребят);
занимаются спортом: 22 – (8 + 3) = 11 (ребят);
70 – (27 + 19 + 3 + 11) = 10 (ребят) – не занимаются ничем.
Ответ : не увлечены ничем 10 ребят; увлечены спортом 11 ребят.

Задача №2
Часть жителей одного города умеют говорить
только по-русски, часть – только по-узбекски, и часть умеет говорить на обоих
языках. По-узбекски говорят 85% всех жителей, а по-русски – 75%. Сколько %
жителей говорят на обоих языках?
75 % + 85 % = 160 %;
160 % – 100 % = 60 %,
или 100 % – 85 % = 15 % – говорят только по-русски;
75 % – 15 % = 60 % – говорят на обоих языках.
Ответ: 60%.

Задача №3
В классе несколько мальчиков собирали марки. 15
человек собирали марки России, 11 человек собирали иностранные марки, из них 6
человек собирали и марки России, и иностранные марки. Сколько мальчиков в
классе собирали марки? Сколько мальчиков в классе собирали только марки России,
и сколько мальчиков собирали только иностранные марки?
15 – 6 = 9 (мальчиков) – собирали только марки России,
11 – 6 = 5 (мальчиков) – собирали только иностранные марки;
(15 + 11) – 6 = 20 Мальчиков) – всего собирали марок.
Ответ: 20; 9; 5.

Задача №4
В школе зимой работали 3 спортивные секции –
лыжная, хоккейная и конькобежная. В них занимались 38 человек. Известно, что в
лыжной секции занимался 21 человек, среди которых 3 человека занимались ещё в
конькобежной секции, 6 человек – ещё в хоккейной секции и 1 человек занимался
одновременно во всех трёх секциях. В конькобежной секции занимались 13 человек,
среди которых 5 человек занимались одновременно в двух секциях. Сколько человек
занимались в хоккейной секции?
Только коньками занимались: 13 – 2 – 2 – 1 = 8 (человек);
тогда только хоккеем занимались: 38 – 21 – 8 – 2 = 7 (человек);
всего хоккеем занимались: 7+ 5 + 1 + 2 = 15 (человек).
Ответ: 15 человек.

Задача №5
В магазине побывало 65 человек. Известно, что
они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили
и холодильник и микроволновку, 19 – и микроволновку, и телевизор, 15
холодильник и телевизор, а все три покупки совершили 3 человека. Был ли среди
них посетитель, не купивший ничего.
Купили только холодильники: 35 – (20 – 3) – (15 – 3) -3 = 4
Купили только микроволновки: 36 – (20 – 3) – (19 – 3) = 0
Купили только телевизоры: 37 -(15 – 3) -(19 – 3) = 6
Тогда всего покупателей было: 4 + 17 +3 +16+ 12 + 6 = 58
65 – 58= 7 посетителей магазина не купили ничего.
Ответ: 7.

Задача №6
В классе 35 учеников. Из них: 20 школьников
занимаются в математическом кружке, 11 – в экологическом, 10 ребят не посещают
эти кружки. Сколько экологов увлекается математикой?
35 – 10 = 25 (учеников) – посещают кружки,
25 – 20 = 5 (учеников) – посещают экологический кружок,
11 – 5 = 6 (учеников) – посещают оба кружка.
Ответ: 6 экологов увлекаются математикой.
4 Применение кругов Эйлера
в информатике
В таблице приведены запросы и количество найденных по ним
страниц некоторого сегмента сети интернет.
|
Запрос |
Найдено |
|
Кот | |
7000 |
|
Кот |
4800 |
|
Мышь |
4500 |
Какое количество страниц (в тысячах) будет найдено по запросуКот
& Мышь?
Считается, что все вопросы выполняются практически одновременно,
так что набор страниц, содержащих все искомые слова, не изменялся за время
выполнения запросов.
Опираясь на условия задачи, составим уравнения:
Кот | Мышь: 1 + 2 + 3 = 7000; Кот: 1 + 2 = 4800; Мышь: 2 + 3 =
4500
Чтобы найти Кот
& Мышь (обозначенный на чертеже как область 2),
подставим уравнение (2) в уравнение (1) и выясним, что:
4800 + 3 = 7000, откуда получаем 3 = 2200.
Теперь этот результат мы можем подставить в уравнение (3) и
выяснить, что:
2 + 2200 = 4500, откуда 2 = 2300. Ответ: 2300.
в маркетинге и рекламе
В данных областях круги Эйлера могут самым наглядным способом
передать важнейшую информацию.
в обучении и воспитании детей
Круги Эйлера очень хорошо использовать для ускоренного обучения
и развития детей, когда восприятие еще не связано шаблонами мышления и
информация легко усваивается на подсознательном уровне.
Примером может быть игровой построение кругов Эйлера, например,
в песочнице При этом развивается логика и ускоряется процесс обучения.
Круги Эйлера: птицы – домашние животные; ответ:
домашние птицы
5
Заключение
В процессе
выполнения данной работы были получены следующие результаты:
1.
Выделены основные понятия из теории множеств. К ним относятся понятие
множества, понятия конечного и бесконечного множества, понятие пустого
множества, понятие мощности множества, способы задания множества, понятия
подмножества.
2. Изучены
основные операции, которые можно производить над множествами. К ним относятся
операции пересечения, объединения, разности множеств.
3.
Рассмотрены круги Эйлера как средство визуализации понятий теории множеств.
4.Проиллюстрировано
применение кругов Эйлера для решения различных задач.
5.
Составлены задачи, иллюстрирующие отношения между множествами.
выводы:
1. Теория
множеств – один из основных разделов математики.
2.
Использование кругов Эйлера позволяет более наглядно изучить основные понятия
теории множеств.
3.
Изучение теории множеств с использованием кругов Эйлера помогает не только
лучше понять математику, но и развивает логическое мышление.
4. Круги
Эйлера можно использовать как способ решения задач в различных областях
деятельности человека. К ним относятся не только математика, но и логика,
статистика, биология, логистика, управление, а также философия и социология.
Таким
образом, поставленные в ходе исследования задачи решены, гипотеза подтверждена,
цель исследования достигнута.
6
Список использованной литературы
1Виленкин
Н.Я. Рассказы о множествах. 3-е издание. — М.: МЦНМО, 2005.
2 Кантор
Георг. Труды по теории множеств. Под ред. А.Н.Колмогорова и А.П.Юшкевича. –2015г..
3Кузовенко
Л.А. Методика обучения элементам теории множеств в курсе алгебры основной
школы. Тольяттинский государственный университет. – Тольятти. 2016.
4 Математика
XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх
томах. 1998г.
5 Математическая
составляющая / Редакторы-составители Н.Н. Андреев, С.П. Коновалов, Н.М.
Панюшкин. – М.: Фонд «Математические этюды» 2015 г. .
6 Мордкович
А.Г.Школьный курс математики: Краткий справочник. М.: Школа-Пресс, 2015.
7 Презентация
«Круги Эйлера» для проведения факультативных занятий «Занимательная
информатика». //
https://infourok.ru/prezentaciya-krugi-eylera-dlya-provedeniya-fakultativnih-zanyatiy-zanimatelnaya-informatika-
8Юшкевич
А. П. Леонард Эйлер. Жизнь и творчество // Развитие идей Леонарда Эйлера и
современная наука. Сб. статей. 2008.
Что это такое? Диаграмма Эйлера кажется чем-то очень сложным на первый взгляд. Однако на самом деле это круги, накладываемые друг на друга при решение определенных задач. Их применяют в алгебре, информатике и даже в жизни, столкнувшись с каким-то выбором.
Как строить? Для начала нужно представить универсальное множество в виде прямоугольника. Внутри него будут эллипсы или круги, которые могут пересекаться, а могут и нет. Их можно дополнять, объединять, пересекать. Давайте рассмотрим все это на примере ниже.
В статье рассказывается:
- Что собой представляет диаграмма Эйлера
- Разница между диаграммой Эйлера и диаграммой Эйлера-Венна
- Задачи, решаемые диаграммой Эйлера
- Принцип построения диаграммы
- Применение диаграмм для доказательства логических равенств
- Пример решения задачи с помощью кругов Эйлера
-
Пройди тест и узнай, какая сфера тебе подходит:
айти, дизайн или маркетинг.Бесплатно от Geekbrains
Что собой представляет диаграмма Эйлера
Так называется геометрическое изображение, которое используют, чтобы смоделировать множества и схематично отразить отношения между ними. На диаграмме Эйлера наглядно показаны утверждения о данных множествах.
При этом универсальное множество обозначено прямоугольником, а подмножества изображены в виде кругов. Поэтому диаграмму называют также «круги Эйлера». Такое схематичное изображение применяют при решении математических и логических задач, а также в менеджменте и различных прикладных целях.
Автор этого способа – математик XVIII века Леонард Эйлер, который хотел таким образом помочь размышлениям. Автором кругов является известный математик Леонард Эйлер, который считал, что они необходимы, чтобы облегчить размышления человека. Диаграмма Эйлера стала признанным методом с момента своего появления.
Биография Леонарда Эйлера связана со Швейцарией, Пруссией и Россией. Этот учёный оказал огромное влияние на развитие математики, механики, физики. Его научные работы (более 850 трудов) затрагивают теорию чисел, теорию музыки, оптику, баллистику, небесную механику. Среди его трудов имеется ряд основополагающих монографий. Около половины жизни Эйлер провёл в России, работал в Петербургской Академии наук и много вложил в развитие российской науки.
Скачать файл
В дальнейшем в работах многих учёных используется диаграмма Эйлера для множеств: это математики Бернард Больцано и Эрнест Шредер; философ и логик Джон Венн и другие. В наши дни эту методику применяют для развития мышления как при очном обучении, так и на различных онлайн-курсах.
Разница между диаграммой Эйлера и диаграммой Эйлера-Венна
Диаграммы Эйлера-Венна – это частный случай кругов Эйлера, который показывает все 2π{displaystyle 2^{n}} комбинаций π{displaystyle n} свойств, то есть конечную булеву алгебру. При π = 3 диаграмма Эйлера-Венна обычно выглядит как три круга, имеющих одинаковый радиус, их центры совпадают с вершинами равностороннего треугольника, стороне которого приблизительно равны радиусы.
Если определённая комбинация свойств соответствует пустому множеству, на схеме эту область закрашивают. Диаграммы Эйлера могут быть не типичны, а иногда эквивалентны диаграммам Венна. Закрашенный участок схемы указывает на то, что это множество не содержит элементов, то есть пустое.
Задачи, решаемые диаграммой Эйлера
Прикладное значение, которое имеет диаграмма Эйлера: задачи на соотношение множеств в математике, логике, информатике, статистике становятся понятнее при её использовании. Круги Эйлера можно применять и в жизни, находя с их помощью взаимосвязи и отвечая на возникающие насущные вопросы.

Круги Эйлера можно разделить на такие группы:
- равнозначные;
- пересекающиеся;
- подчиненные;
- соподчиненные;
- противоречащие;
- противоположные.

Читайте также
Выполняя упражнения на развитие мышления, чаще всего можно столкнуться с двумя их видами:
- Круги, изображающие объединяющиеся понятия и вложенные один в другой, чтобы это показать.
- Круги, иллюстрирующие пересечения различных множеств, которые имеют те или иные общие признаки.
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда

Подборка 50+ ресурсов об IT-сфере
Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT
ТОП 50+ сервисов и приложений от Geekbrains
Безопасные и надежные программы для работы в наши дни
Уже скачали 20818
Приведём пример использования кругов при выборе профессии. Можно перебирать варианты, обдумывая наиболее подходящий, а можно начертить схему, изобразив в виде кругов то, что вам нравится делать, что вы умеете, и что хорошо оплачивается. Получится диаграмма Эйлера. Пересечение этих трёх кругов и показывает, что будет наиболее вам подходить.
Метод прост в применении и подходит для всех. Его используют и при работе с дошкольниками в детском саду с 4-5 лет, и при обучении студентов (например, можно увидеть подобные задачи в ЕГЭ по информатике), и в научной среде.
Принцип построения диаграммы
При построении диаграммы Эйлера сначала рисуют большой прямоугольник, обозначающий универсальное множество U. Внутри этого прямоугольника располагают фигуры, которые являются изображением множеств: круги (если их не больше трёх) или круги и эллипсы (когда множеств четыре и больше). Фигуры пересекаются различными способами, в зависимости от условий задачи.
Допустим, у нас имеется выражение А. Изображаем на диаграмме круг, обозначающий множество А. Пространство внутри круга показывает значения, при которых выражение А будет истинным, а область снаружи обозначает ложь. Чтобы отобразить на схеме логическую операцию, заштрихуем те части диаграммы, в которых значения истинны. В результате мы отмечаем область, где множества пересекаются.

Можно доказать любой закон алгебры, представив его в виде графической схемы при помощи диаграммы Эйлера. Алгоритм действий таков:
- Сначала чертим диаграмму и заштриховываем все множества, которые находятся с левой стороны от знака «равно».
- Затем нужно начертить другую диаграмму и на ней заштриховать множества, находящиеся справа от знака равенства.
- Если на диаграммах окажется заштрихованной одна и та же область, тождество будет истинным.
Сильнее углубимся в тему.
Дополнение множества
Дополнением к множеству A будет множество Его элементы не относятся к множеству А.
= {x | x ∉ A}
Но в включаются не все элементы, не относящиеся к А. По условиям применения диаграммы Эйлера, все множества, о которых идёт речь в задаче, будут включены в универсальное множество U, то есть являются его подмножествами. С учётом этого дополнение будет определяться так:
=U∖A
Объединение множеств
Объединением двух множеств (назовём их А и В) будет множество A ∪ B, состоящее из элементов, которые включаются хотя бы в одно из них.
Это можно записать так:
A ∪ B={x |x ∈ A или x ∈ B}
Пересечение множеств
Пересечение множеств A и B это множество A ∩ B. Оно состоит из элементов, которые входят и в множество А, и в то же время в множество В.
Только до 18.05
Скачай подборку тестов, чтобы определить свои самые конкурентные скиллы
Список документов:
 Тест на определение компетенций
Тест на определение компетенций
 Чек-лист «Как избежать обмана при трудоустройстве»
Чек-лист «Как избежать обмана при трудоустройстве»
 Инструкция по выходу из выгорания
Инструкция по выходу из выгорания
Чтобы получить файл, укажите e-mail:
Подтвердите, что вы не робот,
указав номер телефона:

Уже скачали 7503
Записывается пересечение множеств так:
A ∩ B = {x | x ∈ A и x ∈ B}
Симметричная разность множеств
Симметричная разность – это множество A B, в которое включаются элементы, которые входят только в одно из множеств А и В, но не в оба сразу.
Запись симметричной разности выглядит таким образом:
A △ B = (A ∖ B) ∪ (B ∖ A)
Разность множеств
Разностью A B являются элементы множества A, не входящие в B.
Записанная разность множеств выглядит так:
A ∖ B = {x | x ∈ A и x ∉ B}
Применение диаграмм для доказательства логических равенств
Давайте рассмотрим, как применяется диаграмма Эйлера на примере доказательства логического равенства.

Представим, что мы имеем конъюнкцию множеств A ∧ B.
Сначала работаем с левой частью равенства. Нужно с помощью диаграммы Эйлера построить множества А и В, заштриховать оба круга цветом и таким образом выделим дизъюнкцию.
Дальше нужно показать инверсию с помощью штриховки области за пределами этих множеств.
Теперь переключаемся на правую часть равенства. Сперва показываем цветной штриховкой за пределами круга А инверсию этого множества.
То же самое действие выполняем для множества В.
Штрихуем чёрным цветом все области пересечения и получаем графическое отображение конъюкции инверсий множеств А и В.
Сравнивая области, отображающие правую и левую части равенства, убеждаемся, что они равны. Таким образом, истинность логического равенства доказана при помощи диаграммы Эйлера.
Пример решения задачи с помощью кругов Эйлера
В демонстрационном тесте ЕГЭ по информатике и ИКТ была представлена задача, которую мы решим с применением этого метода.
Условия задачи:
В языке запросов поискового применяется символ «|» для логической операции «или» и символ «&», чтобы обозначить логическую операцию «и».
Таблица, приведённая ниже, отражает запросы в некотором сегменте сети Интернет и количество найденных страниц по этим запросам.
| Запрос | Найдено страниц (в тысячах) |
| Крейсер | Линкор | 7000 |
| Крейсер | 4800 |
| Линкор | 4500 |
Вопрос: какое количество страниц (в тысячах) найдётся, если запрос будет сформулирован в виде Крейсер & Линкор?
Принимаем версию, что все запросы выполняются в один отрезок времени, поэтому набор страниц, которые включают искомые слова, остался неизменным.
Решение:
Покажем условие задачи при помощи диаграммы Эйлера. Используем цифры 1, 2 и 3 для обозначения полученных областей.

Читайте также
Используя условия задачи, составляем уравнения:
- Крейсер | Линкор: 1 + 2 + 3 = 7000
- Крейсер: 1 + 2 = 4800
- Линкор: 2 + 3 = 4500
Искомая область Крейсер & Линкор обозначенная на чертеже цифрой 2, находится путём подстановки уравнения (2) в уравнение (1). Получаем следующее:
4800 + 3 = 7000, откуда получаем область 3, равную 2200.
Полученный результат мы подставляем в уравнение (3). Получаем результат:
Область 2 + 2200 = 4500, значит, она равна 2300.
Ответ: будет найдено 2300 страниц по запросу Крейсер & Линкор.
Этот пример показывает, что можно решать с помощью диаграммы Эйлера задачи, являющиеся достаточно сложными или запутанными.

Можно сделать вывод, что круги Эйлера не просто занимательный, но и полезный в плане решения учебных и бытовых задач метод. Многие вещи можно представить в виде множеств, а поможет наглядно представить их пересечение или объединение диаграмма Эйлера.
Любопытно, что современная массовая культура применяет круги Эйлера для создания мемов, а также их можно встретить в таких сериалах, как «Теория большого взрыва» и «4исла».
Советуем применять этот метод для решения задач и непременно поделитесь этим полезным и наглядным способом с друзьями.
Сегодня разберём задачи на круги Эйлера в информатике.
Леонард Эйлер – швейцарский, немецкий и российский математик и механик, сыгравший огромную роль в развитии этих наук.
Задача (Простая)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Пушкин | 3500 |
| Лермонтов | 2000 |
| Пушкин | Лермонтов | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Пушкин & Лермонтов? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
Видим, что по запросу “Пушкин” в поисковике нашлось 3500 страниц. По запросу “Лермонтов” – 2000 страниц.
Запрос “Пушкин | Лермонтов” обозначает, что поисковик выдаст страницы, где есть слова про “Пушкина”, и страницы, где есть слова про “Лермонтова”, а так же могут быть страницы, где написано и про “Пушкина”, и про “Лермонтова” одновременно.
Если сложить страницы, в которых написано про “Пушкина” и про “Лермонтова” получается 3500 + 2000 = 5500 страниц. Но почему же при запросе “Пушкин | Лермонтов” получается меньше страниц, всего 4500 ?
Этот факт обозначает то, что когда мы подсчитывали страницы про “Пушкина” (3500 страниц), мы подсчитали и те страницы, где было написано и про “Пушкина”, и про “Лермонтова” одновременно.
Тоже самое и для количества страниц, где написано про “Лермонтова” (2000 страниц). В этом числе находятся и те, в которых одновременно упоминается и про “Пушкина”, и про “Лермонтова”.
В вопросе спрашивается, сколько страниц будет по запросу “Пушкин & Лермонтов“. Это обозначает, что как раз нужно найти количество страниц, где будет одновременно написано и про “Пушкина”, и про “Лермонтова”.
Отсюда получается:
Пушкин & Лермонтов = (3500 + 2000) – 4500 = 5500 – 4500 = 1000 страниц.
Это и будет ответ!
Теперь решим эту задачу с помощью Кругов Эйлера!
У нас всего есть две сущности: “Пушкин” и “Лермонтов”. Поэтому рисуем два пересекающихся круга, желательно разными цветами.
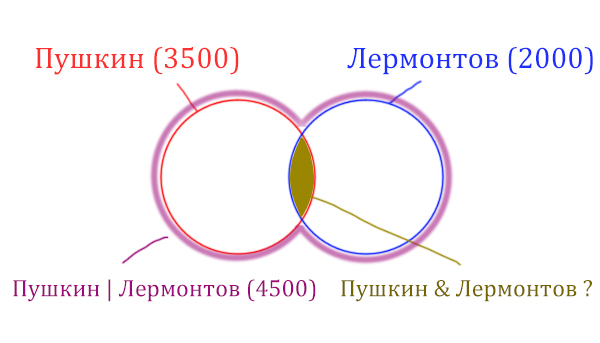
Объединение двух кругов в общую фигуру (показано фиолетовым цветом), показывает операцию “Пушкин | Лермонтов”. Эта операция всегда стремится увеличить площадь, объединить площади других фигур!
Обратите внимание, что круги пересекаются, из-за этого сумма площадей двух кругов по отдельности (3500 + 2000 = 5500) больше чем у фигуры, которая характеризует логическую операцию «ИЛИ» “Пушкин | Лермонтов” (4500).
Нужно найти площадь фигуры Пушкин & Лермонтов, которая закрашена золотистым цветом. Данная логическая операция «И» стремится уменьшить площадь. Она обозначает общую площадь других фигур.
Найдём сначала заштрихованную часть синего круга. Она равна: площадь фиолетовой фигуры (4500) минус площадь красного круга (3500).
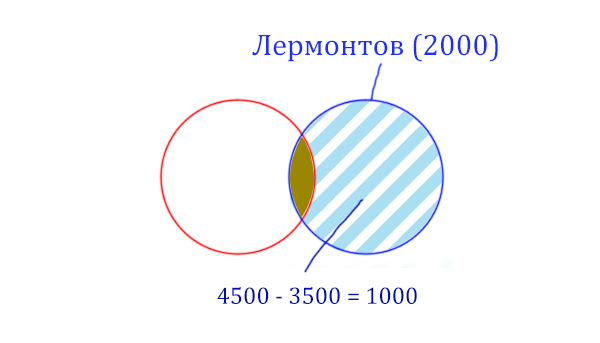
Теперь легко найти площадь золотистой фигуры. Для этого нужно от площади синего круга вычесть площадь заштрихованной части. Получается:
Пушкин & Лермонтов (Количество страниц) = 2000 – 1000 = 1000
Получается, что по запросу Пушкин & Лермонтов будет найдено 1000 страниц.
Ответ: 1000
Рассмотрим ещё одну не сложную разминочную задачу.
Задача (Разминочная)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Кокос | Ананас | 3400 |
| Кокос & Ананас | 900 |
| Кокос | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Ананас?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
У нас две сущности: Кокос и Ананас. Нарисуем два круга Эйлера, которые пересекаются между собой. Так же отменим все имеющееся данные.
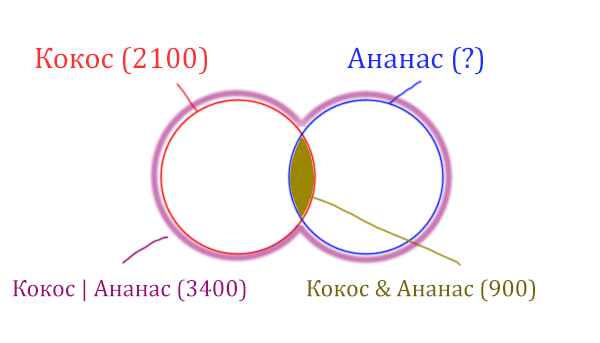
Найдём заштрихованную часть красного круга.
Весь красный круг 2100. Золотистая область равна 900. Заштрихованная часть равна 2100 – 900 = 1200.
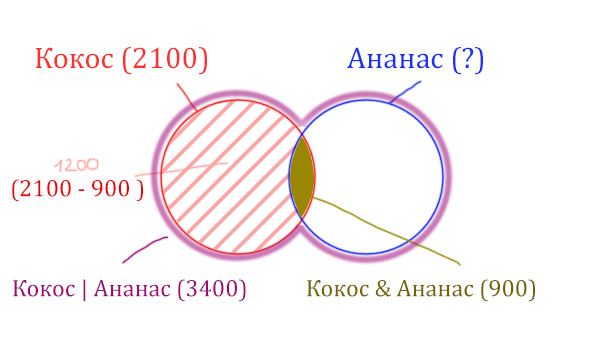
После того, как нашли заштрихованную часть (такой полумесяц), можно найти уже площадь синего круга. Для этого нужно от площади фиолетовой фигуры отнять площадь заштрихованной части!
Ананас (Количество страниц) = 3400 – 1200 = 2200
Ответ: 2200
Разберём классическую задачу из информатики по кругам Эйлера.
Задача (Классическая)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| (Космос & Звезда) | (Космос & Планета) | 1100 |
| Космос & Планета | 600 |
| Космос & Планета & Звезда | 50 |
Какое количество страниц (в тыс.) будет найдено по запросу Космос & Звезда?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
В этой задаче у нас три сущности: Космос, Планета, Звезда. Поэтому рисуем три круга Эйлера, которые пересекаются между собой.
Могут ли круги не пересекаться ? Могут! Если мы докажем, что площади по отдельности двух кругов в сумме дают площадь фигуры, которая получается при применении операции логического “ИЛИ”.
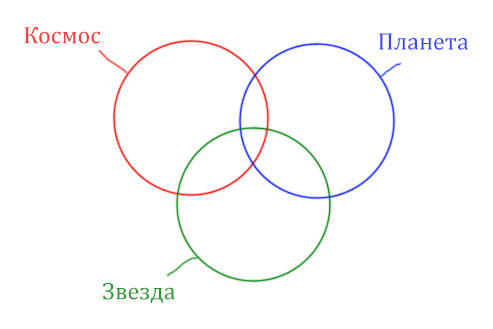
Теперь отметим на нашем рисунке запрос (Космос & Звезда) | (Космос & Планета).
Сначала отменим для себя то, что находится в скобках. Первое Космос & Звезда
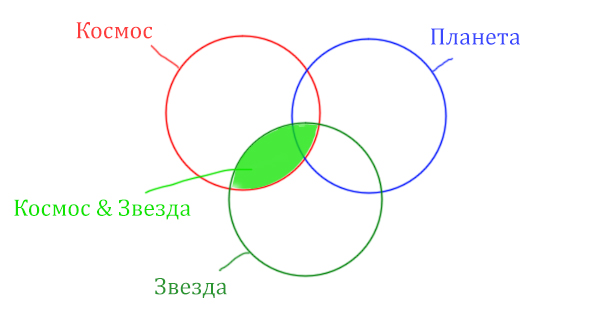
Теперь отметим вторую скобку Космос & Планета.
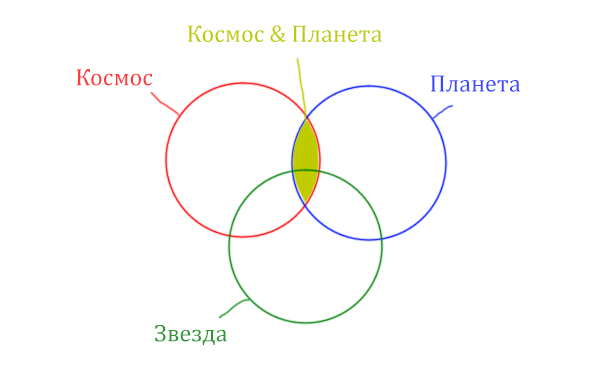
В выражении (Космос & Звезда) | (Космос & Планета) две скобки соединяет знак логического “ИЛИ”. Значит, эти две области нужно объединить! Область (Космос & Звезда) | (Космос & Планета) отмечена фиолетовым цветом!
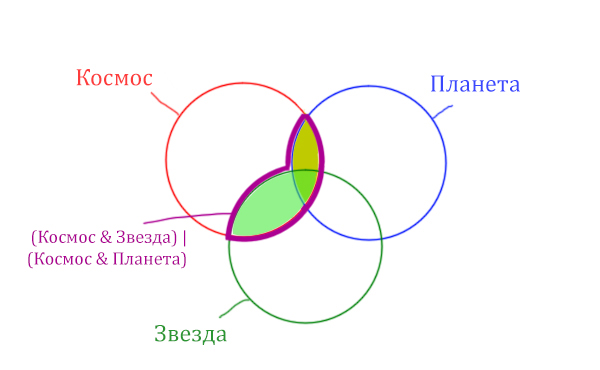
Отметим Космос & Планета ещё раз, т.к. для этого выражения известно количество страниц.
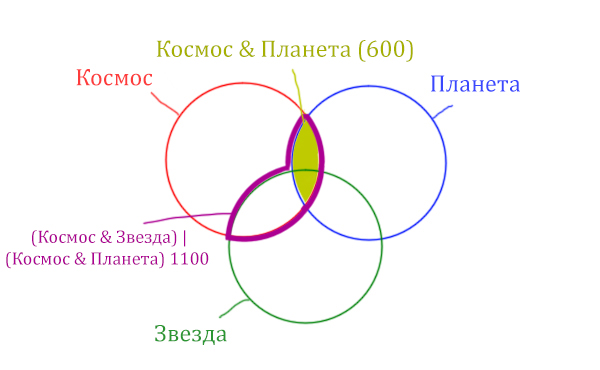
Площадь фигуры для выражения Космос & Планета & Звезда будет очень маленькая. Это общая часть для всех трёх кругов. Отметим её оранжевым цветом! Каждая точка этой фигуры должна одновременно быть в трёх кругах!
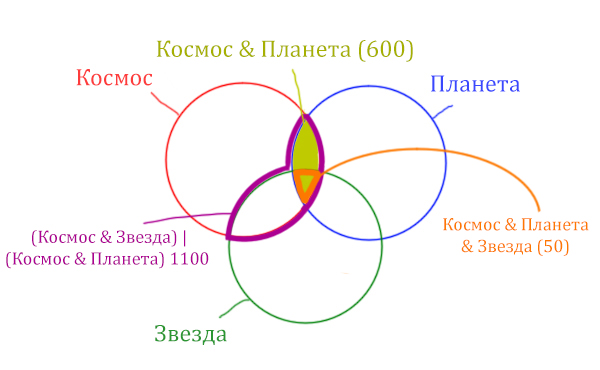
Найти нужно Космос & Звезда. Отменим на рисунке чёрным цветом ту область, которую нужно найти. Мы эту область уже отмечали салатовым цветом.
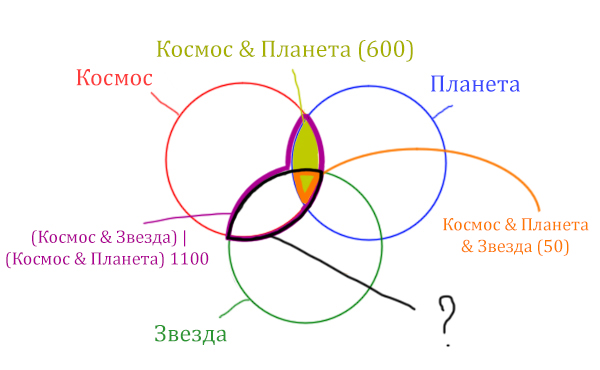
Теперь у нас есть все компоненты, чтобы решить эту задачу.
Найдём заштрихованную область.
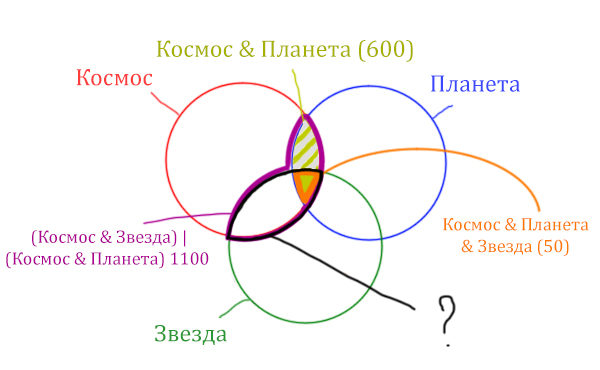
Вся область Космос & Планета равна 600. А заштрихованная часть равна: область Космос & Планета (600) минус оранжевая область (50).
Количество страниц в заштрихованной части = 600 – 50 = 550
Тогда черная область легко находится: фиолетовая область (1100) минус заштрихованная область (550).
Количество страниц (при запросе Космос & Звезда) = 1100 – 550 = 550
Ответ: 550
Закрепляем материал по задачам на Круги Эйлера.
Задача (На закрепление)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Море & Солнце | 290 |
| Море & Пляж | 355 |
| Море & (Пляж | Солнце) | 465 |
Какое количество страниц (в тысячах) будет найдено по запросу Море & Пляж & Солнце? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
В задаче используются три сущности: Море, Пляж, Солнце. Поэтому нарисуем три пересекающихся круга Эйлера.
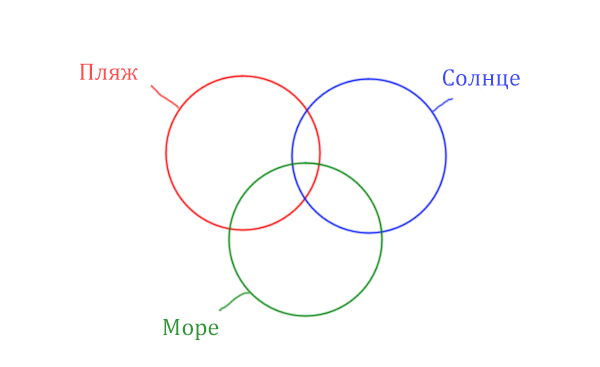
Отметим все области для которых нам даны количество страниц.
В начале отметим Море & (Пляж | Солнце). Для начало нарисуем область, которая в скобках (Пляж | Солнце)
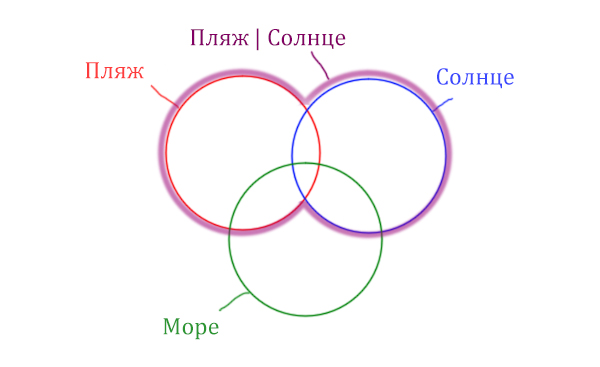
Теперь нужно очертить общую часть фиолетовой области и зелёного круга и получится Море & (Пляж | Солнце). Отметим оранжевым цветом.
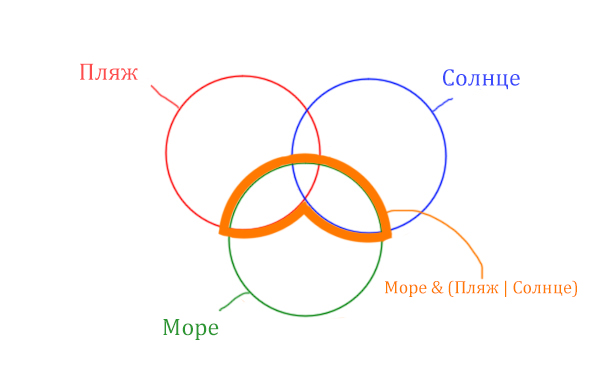
Теперь отметим Море & Пляж.
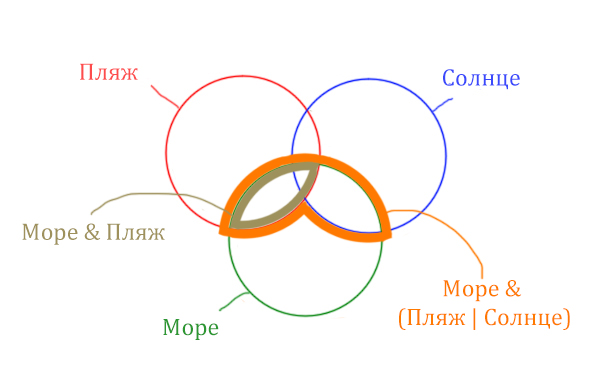
Теперь отметим Море & Солнце.
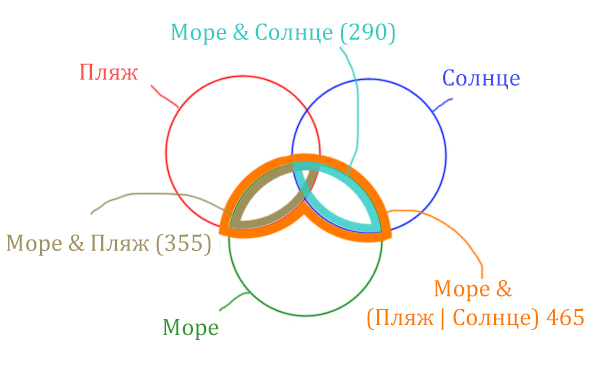
Найти нужно ту область, которая получается в результате выделения общей части для всех трёх кругов! Обозначим её чёрным цветом!
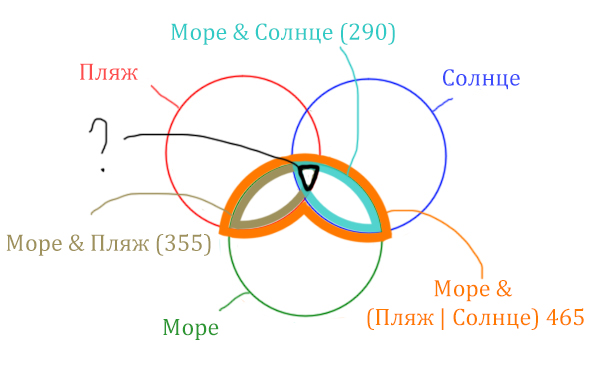
Найдём заштрихованную область!
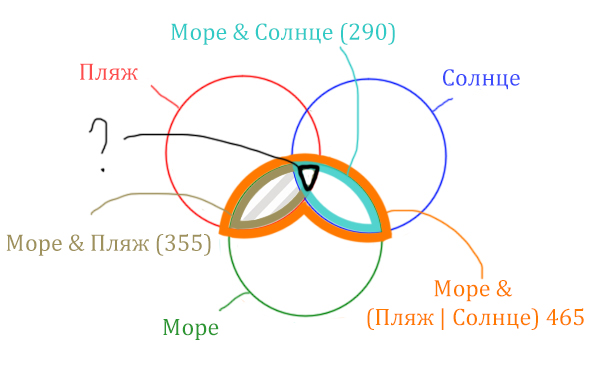
Количество страниц (в заштрихованной области) =
= Количество страниц (В оранжевой области) – Море & Солнце =
= 465 – 290 = 175
Чтобы найти искомую чёрную область, нужно из Море & Пляж (355) вычесть заштрихованную область (175).
Количество страниц (Море & Пляж & Солнце) =
= Море & Пляж (355) – Количество страниц (в заштрихованной области) 175 =
= 355 – 175 = 180
Ответ: 180
Решим ещё одну тренировочную задачу из информатики на Круги Эйлера.
Задача (с 4 сущностями)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Англия & (Уэльс & Шотландия | Ирландия) | 450 |
| Англия & Уэльс & Шотландия | 213 |
| Англия & Уэльс & Шотландия & Ирландия | 87 |
Какое количество страниц (в тысячах) будет найдено по запросу
Англия & Ирландия?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
Нужно нарисовать 4 пересекающихся круга. Сначала нарисуем три круга, как обычно, оставив немного места для четвёртого круга.
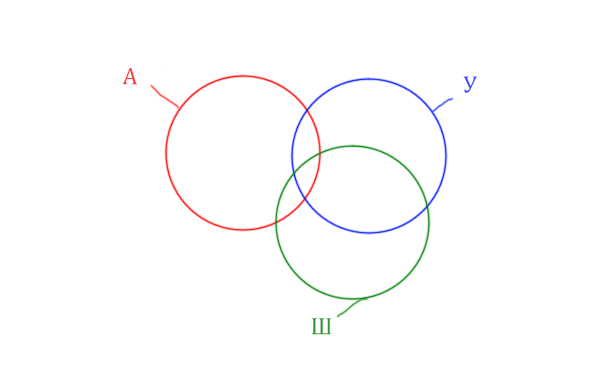
Четвёртый круг для Ирландии нужно нарисовать так, чтобы он проходил через область (Англия & Уэльс & Шотландия). Это нам подсказывает сама таблица, где есть количество страниц для Англия & Уэльс & Шотландия, а так же для Англия & Уэльс & Шотландия & Ирландия.
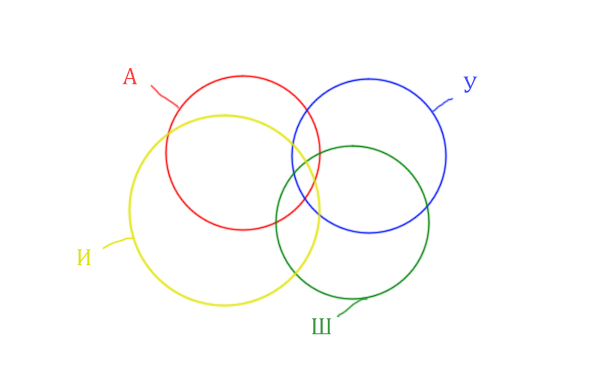
Нужно отметить на рисунке Англия & (Уэльс & Шотландия | Ирландия). Это будем делать, как всегда поэтапно.
Область Уэльс & Шотландия выглядит так:
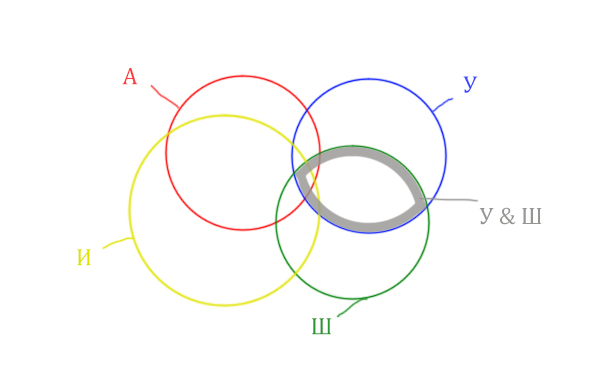
Добавим к этой области Ирландию через логическое “ИЛИ”. Получается область (Уэльс & Шотландия | Ирландия). Произошло объединение серой области и жёлтого круга!
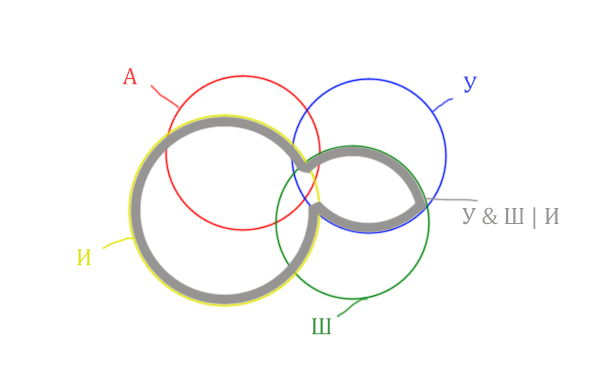
Теперь нужно сделать операцию логического “И” получившийся области с “Англией”. Тогда область Англия & (Уэльс & Шотландия | Ирландия) примет вид:
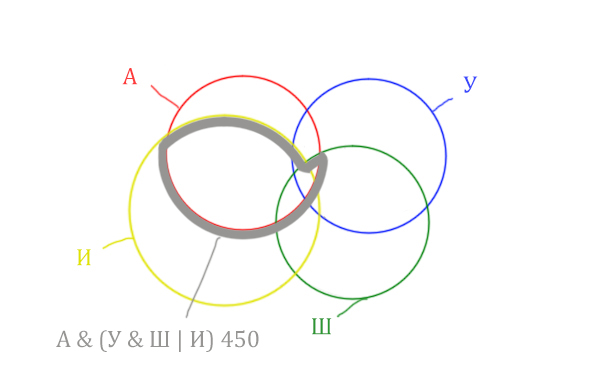
Т.е. это общее между предыдущем серым контуром и красным кругом!
Отметим Англия & Уэльс & Шотландия – это общая территория трёх кругов: Красного, Синего и Зелёного. Отмечено оранжевым цветом.
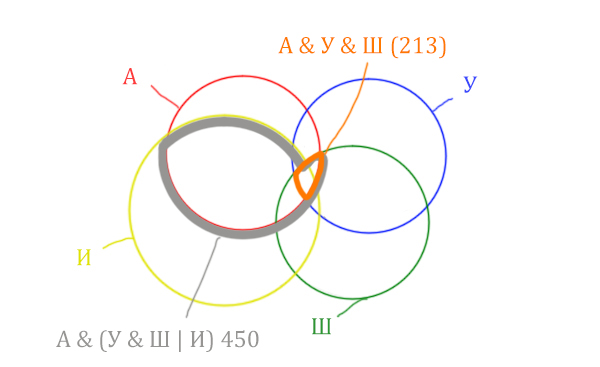
Отметим Англия & Уэльс & Шотландия & Ирландия – это общая территория четырёх кругов. Область получается ещё меньше. Если взять точку в этой области, то мы будем находится сразу в четырёх кругах одновременно. Отмечено фиолетовым цветом.
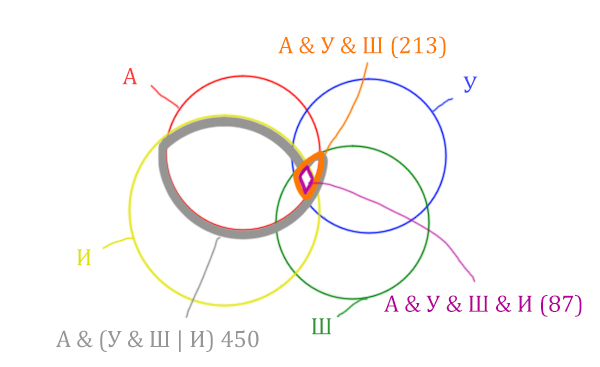
Отметим то, что нужно найти Англия & Ирландия чёрным цветом.
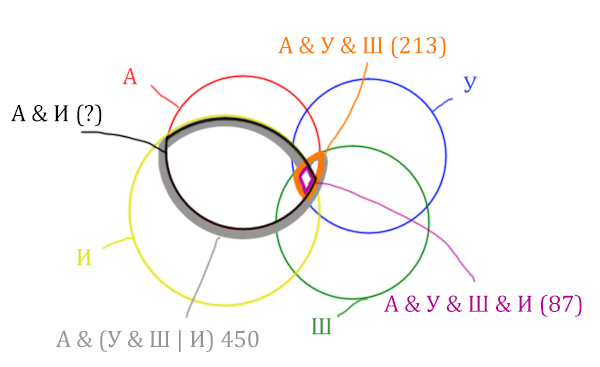
Искомую чёрную область легко найти, если из серой области вычесть кусочек, окрашенный в бирюзовый цвет!
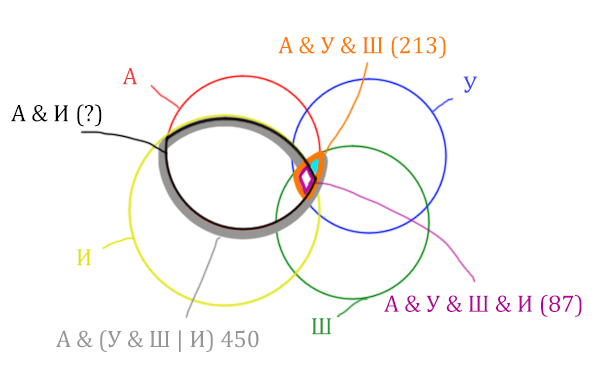
Найдём, сколько страниц приходится на бирюзовый кусочек:
Количество страниц (для бирюзового кусочка) =
= Англия & Уэльс & Шотландия (213) – Англия & Уэльс & Шотландия & Ирландия (87) =
= 213 – 87 = 126
Найдём искомую чёрную область.
Количество станиц (для чёрной области) =
= Англия & (Уэльс & Шотландия | Ирландия) (450) – Количество (для бирюзового кусочка) =
450 – 126 = 324
Это и будет ответ!
Ответ: 324.
Разберём задачу из реального экзамена по информатике, которая была в 2019 году в Москве! (Сейчас в 2021 задачи не встречаются на Круги Эйлера)
Задача (ЕГЭ по информатике, 2019, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Суфле | 450 |
| Корзина | 200 |
| Эклер | 490 |
| Суфле & Корзина | 70 |
| Суфле & Эклер | 160 |
| Корзина & Эклер | 0 |
Сколько страниц (в тысячах) будет найдено по запросу
Суфле | Корзина | Эклер
Решение:
Видим, что у нас три поисковых разных слова, поэтому будет три разных круга Эйлера!
Так же видим, что логическое “И” между словами Корзина и Эклер даёт 0 страниц. Это значит, что эти круги не пересекаются! Так же круги бы не пересекались, если бы операция логического “ИЛИ” совпадала бы с суммой этих кругов.
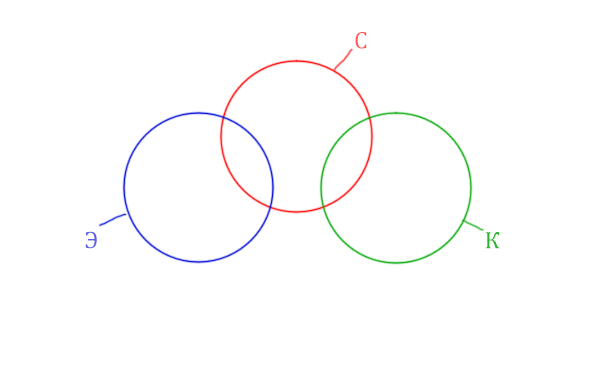
Видим, что Суфле имеет с двумя кругами пересечения, а Корзина и Эклер не пересекаются.
Отметим всё, что нам дано в условии.
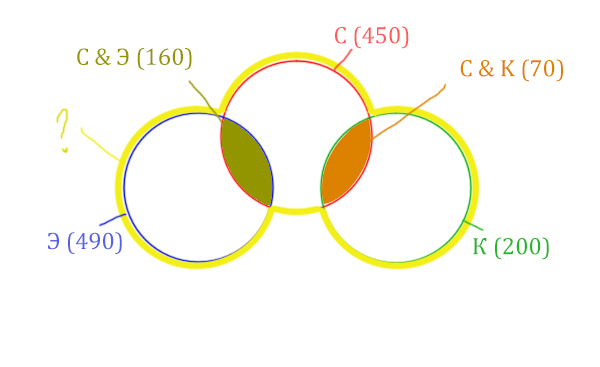
Жёлтым цветом отмечено Суфле | Корзина | Эклер . Объединение всех трёх кругов. Это то, что нужно найти.
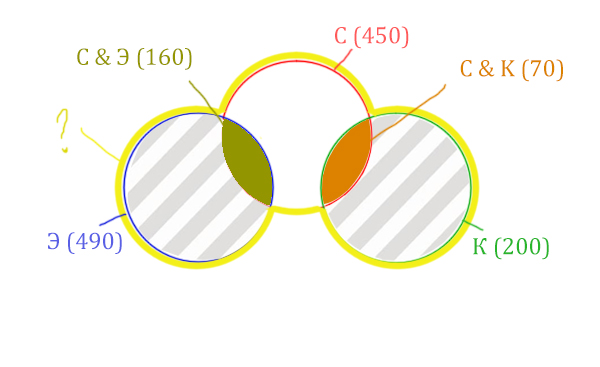
Искомая жёлтая фигура складывается из заштрихованных областей и красного круга! Площадь красного круга мы знаем. Нужно найти площади заштрихованных частей.
Левая заштрихованная область находится просто:
Количество страниц (лев. заштрих. область) =
= Эклер (490) – Суфле & Эклер (160) = 330
Так же найдём площадь правой заштрихованной области:
Количество страниц (прав. заштрих. область) =
= Корзина (200) – Суфле & Корзина (70) = 130
Теперь можно найти искомую жёлтую область
Количество страниц (Суфле | Корзина | Эклер) =
= Красный круг (450) + лев. заштрих. область (310) + прав. заштрих. область (130) =
= 450 + 330 + 130 = 910
Задача решена, можно писать ответ.
Ответ: 910
Разберём ещё одну задачу из реального ЕГЭ уже 2020 года
Задача (ЕГЭ по информатике, 2020, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Аврора | 50 |
| Крейсер | 45 |
| Заря | 23 |
| Аврора & Заря | 9 |
| Заря & Крейсер | 0 |
| Заря | Крейсер | Аврора | 93 |
Сколько страниц (в тысячах) будет найдено по запросу
Аврора & Крейсер
Решение:
Количество страниц при запросе Заря & Крейсер равно нулю. Значит, эти два круга не будут пересекаться.
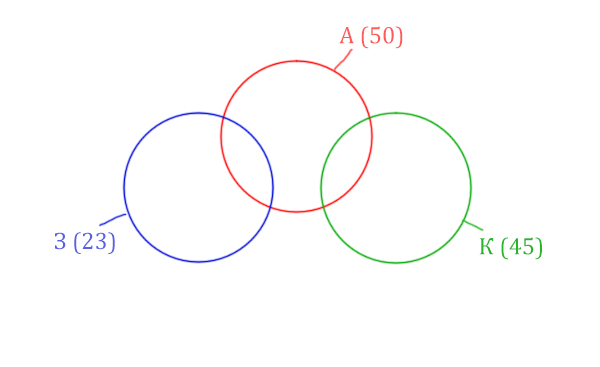
Нарисуем все данные на рисунке.
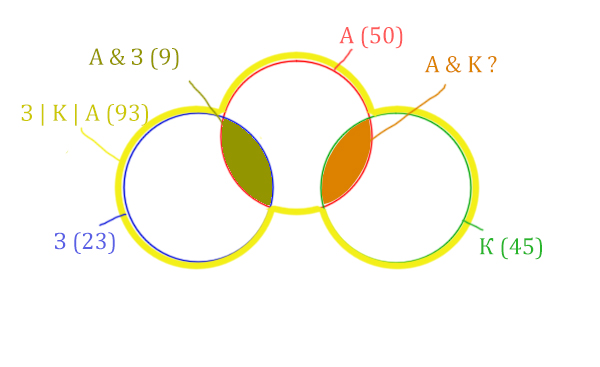
Нужно найти для начала заштрихованную правую часть.
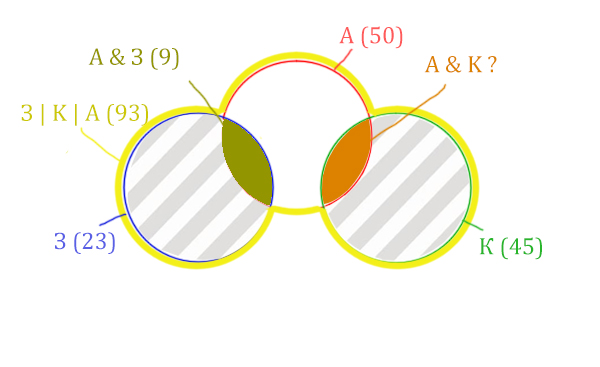
Количество страниц (для двух заштрих. частей) =
З | К | А (93) – Красный круг (50) = 43
Левую заштрихованную область легко найти.
Количество страниц (для левой заштрих. части) =
Синий круг (23) – А & З (9) = 14
Тогда для правой заштрихованной области получается:
Колич. страниц (для правой заштрих. части) =
Колич. страниц (для двух заштрих. частей) (43) – Колич. страниц (для лев. заштрих. части) (14) =
= 43 – 14 = 29
Тогда искомую область легко найти:
Колич. страниц (А & K) =
Зелёный круг (45) – Колич. страниц (для правой заштрих. части) (29) =
45 – 29 = 16
Ответ: 16
На этом всё! Надеюсь, вы теперь будете с удовольствием решать задачи по информатике с помощью Кругов Эйлера.
Интересно…
как быть , когда идет произведение3 предметов + произведниее 3 педметов..
ОГРОМНОЕ СПАСИБО за Ваш труд!!! Всё очень понятно и доходчиво. +++++++++++++++





