Как найти с помощью угольника острый угол

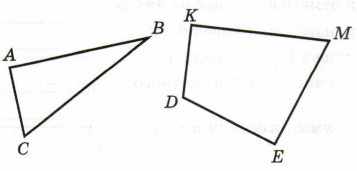
Найди с помощью угольника острые, прямые и тупые углы многоугольников:

Острые углы:
Прямые углы:
Тупые углы:

Определение.

Острый угол — это угол, меньший прямого.

Градусная мера острого угла больше нуля, но меньше 90 градусов.

Например,

∠ABC, ∠MNK, ∠DEF — острые углы.

Чтобы построить острый угол заданной градусной меры, пользуются транспортиром.

Пример.

Построить с помощью транспортира угол 72º.

1) Отмечаем точку — вершину угла.

2) От точки проводим луч — сторону угла.

3) Совмещаем вершину угла с отметкой в центре транспортира (у разных моделей транспортира положение этой отметки может быть разным) так, чтобы отметка 0º была расположена на стороне угла.

4) Находим 72º на той шкале, где находится 0º, и ставим точку.

5) От вершины угла через отмеченную точку проводим луч — вторую сторону угла.

На рисунках изображено построение угла 72º с началом отсчёта по нижней шкале и с началом отсчёта по верхней шкале.

Чтобы определить по рисунку, является ли угол острым, можно воспользоваться угольником. Если приложить вершину угольника к вершине угла так, чтобы сторона угольника прошла через одну сторону угла, то другая сторона угольника закроет вторую сторону угла:

Добрый день, уважаемые гости!

Сегодня, я хотел бы описать полезный совет, как очень быстро построить или измерить любой угол с помощью обычного строительного угольника, когда других инструментов попросту нет под рукой.

Нам сейчас совершенно не потребуются ни угломеры, ни транспортиры и построение угла будет произведено угольником всего лишь в три шага.

1. Построение

Шаг №1

Как мы знаем, угол — это место на плоскости между двумя пересекающимися линиями (или сторонами какого-либо предмета), которые выходят из одной точки, называемой вершиной угла.

Итак, при построении угла, ставим угольник делением “0” (ноль) см. в вершину будущего угла и от этой точки проводим прямую в нужном вам направлении, от которой необходимо построить угол (эта прямая может являться одной из граней или сторон детали, заготовки или фигуры).

После чего, на этой прямой откладываем 10 см и ставим точку (штрих).

Отметив 10 см, из этой точки проводим к прямой перпендикуляр:

Шаг №2

Для примера, мне нужно построить угол 26°! В вашем же случае он может быть любым: 13°, 25°, 49°, 74° и пр.

Берем смартфон, заходим в приложение “калькулятор”, переводим его в инженерный режим и вводим нужный вам угол. Я ввел “26″.

Далее, нажимаем кнопку “tan” или “tg”, которая обозначает “вычислить тангенс угла”.

Машина мне вывела число 0,487. Из школы мы знаем, что тангенс угла — это отношение противолежащего нашему углу катета к прилежащему. И, зная один катет 10 см и отношение катетов 0,487, мы за одну секунду вычисляем второй катет, который равен 4,87 см.

Скорее, вы теперь поняли, для чего я взял первый катет именно 10 единиц.

Для простоты вычислений! На 10 проще всего умножать, переставив запятую на один разряд вправо.

Шаг №3

Я округляю 4,87 до десятых и на перпендикуляре отмечаю 4,9 см.

Чертим гипотенузу и получаем искомый угол!

Я решил перепроверить построенный угол и приложил угольник Свенсона:

Всё верно! Получил 26°.

2. Измерение

Сейчас мы построили угол, а при измерении угла — производим все то же самое, только в обратном порядке. Измеряя угол, мы будем знать оба катета, а соответственно и их отношение. Вводим в калькуляторе значение отношения противолежащего катета к прилежащему и нажимаем кнопку “arctg”, “atg” или “tan -1”, которая обозначает обратную тангенсу функцию — арктангенс.

На дисплее калькулятора мы увидим значение нашего угла!

…написано много, а на деле все занимает не более одной минуты…

Спасибо за внимание!

Вопрос Найди с помощью угольника и выпиши прямые, тупые и острые углы?, расположенный на этой странице сайта, относится к
категории Математика и соответствует программе для 1 – 4 классов. Если
ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска
похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему.
Для этого ключевые фразы введите в строку поиска, нажав на кнопку,
расположенную вверху страницы. Воспользуйтесь также подсказками посетителей,
оставившими комментарии под вопросом.

Математика, 2 класс

Урок № 33. Угол. Виды углов: прямой, острый, тупой

Перечень вопросов, рассматриваемых в теме:

– Какие бывают углы?

– Как распознавать углы?

Глоссарий по теме:

Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом.

Острый угол – это угол, который меньше прямого.

Тупой угол – это угол, который больше прямого.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова, Г.В.Бельтюкова и др. – 5-е изд. – М.: Просвещение, 2014. – с.8-9.
2. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова – 6-е изд., дораб. – М.: Просвещение, 2016. – с.3.
3. Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. М. И. Моро, С. И. Волкова – 9-е изд. – М.: Просвещение, 2014. – с.16.

Теоретический материал для самостоятельного изучения

Рассмотрите фигуры и выберите лишнюю.

Лишняя фигура под номером 2. Она образована незамкнутой линией.

Она называется угол.

Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом.

Посмотрите на рисунки: по-разному открытый веер, образует разные углы.

У каждого угла есть две стороны и вершина. Углы бывают прямые, острые и тупые. Углы определить можно помощью чертежного угольника.

Прямой угол определяем с помощью чертежного угольника.

Угол, который меньше прямого угла называется острым углом.

Угол, который больше прямого угла называется тупым углом.

Посмотрите, как из обычного листа бумаги можно сделать модель прямого угла. Моделью можно воспользоваться, если у вас нет чертежного угольника. Возьмите лист бумаги и перегните его 2 раза, как показано на рисунках 1 и 2. И получите модель прямого угла.

Разверните лист. Линии сгиба образовали 4 прямых угла.

Чтобы определить, какой угол начерчен, на него накладывают угольник или модель прямого угла.

Вывод: Углы могут быть прямыми и непрямыми. Чтобы определить прямой угол или нет, нужно взять особый инструмент – угольник. Если, приложив угольник к углу, вершиной к вершине, стороны совпадут, то угол – прямой. Не совпадут – непрямой. Непрямые углы делятся на: тупые и острые. Угол, величина которого меньше величины прямого – острый, а, если величина угла больше величины прямого – тупой.

Тренировочные задания.

1.Посмотрите на крыши домов и домиков. Какие углы ты видишь на рисунке? Соотнесите вид угла с изображением домика.

Правильные ответы:

2. Выберите цифры, в записи которых присутствуют только прямые углы.

Правильные ответы: