Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем  .
.



 |
(1) |
 |
(2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
 .
.
Пример 1. Известны стороны треугольника ABC:  Найти
Найти  (Рис.1).
(Рис.1).
Решение. Из формул (1) и (2) находим:
И, наконец, находим угол C:
Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:
 .
.
 .
.
Далее, из формулы
 .
.
 . . |
(3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:
 .
.
Пример 2. Известны две стороны треугольника ABC:  и
и  (Рис.2). Найти сторону c и углы A и B.
(Рис.2). Найти сторону c и углы A и B.
Решение. Иcпользуя теорму косинусов найдем сторону c:
 ,
,
Из формулы (3) найдем cosA:
 .
.
Поскольку уже нам известны два угла то находим третий:
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:
 .
.
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Пример 3. Известна одна сторона треугольника ABC:  и углы
и углы  (Рис.3). Найти стороны b и c и угол С.
(Рис.3). Найти стороны b и c и угол С.
Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:


Найдем сторону с. Из теоремы синусов имеем:
Свойства сторон и углов треугольника
Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.
Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .
Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.
a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.
Сумма углов треугольника равна 180°
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Величина большего угла треугольника не может быть меньшей, чем 60°.
 ,
,
где α – больший угол треугольника.
Величина меньшего угла треугольника не может быть большей, чем 60°.
 ,
,
где β – меньший угол треугольника.
 ,
,
| Фигура | Рисунок | Формулировка |
| Треугольник |  |
|
| Большая сторона треугольника |  |
Против большей стороны треугольника лежит больший угол |
| Больший угол треугольника | Против большего угла треугольника лежит большая сторона | |
| Меньшая сторона треугольника |  |
Против меньшей стороны треугольника лежит меньший угол |
| Меньший угол треугольника | Против меньшего угла треугольника лежит меньшая сторона | |
| Длины сторон треугольника |  |
|
| Углы треугольника |  |
|
| Внешний угол треугольника |  |
|
| Больший угол треугольника |  |
|
| Меньший угол треугольника |  |
|
| Теорема косинусов |  |
|
| Теорема синусов |  |
Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.
Определение . Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .
Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.
a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.
Сумма углов треугольника равна 180°
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Величина большего угла треугольника не может быть меньшей, чем 60°.
 ,
,
где α – больший угол треугольника.
Величина меньшего угла треугольника не может быть большей, чем 60°.
 ,
,
где β – меньший угол треугольника.
 ,
,
| Треугольник | |
 |
|
| Большая сторона треугольника | |
 |
Против большей стороны треугольника лежит больший угол |
| Больший угол треугольника | |
 |
Против большего угла треугольника лежит большая сторона |
| Меньшая сторона треугольника | |
 |
Против меньшей стороны треугольника лежит меньший угол |
| Меньший угол треугольника | |
 |
Против меньшего угла треугольника лежит меньшая сторона |
| Длины сторон треугольника | |
 |
|
| Углы треугольника | |
 |
|
| Внешний угол треугольника | |
 |
|
| Больший угол треугольника | |
 |
|
| Меньший угол треугольника | |
 |
|
| Теорема косинусов | |
 |
|
| Теорема синусов | |
 |
| Треугольник |
 |
Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.
Определение . Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .
Большая сторона треугольника

Свойство большей стороны треугольника:
Против большей стороны треугольника лежит больший угол
Больший угол треугольника

Свойство большего угла треугольника:
Против большего угла треугольника лежит большая сторона
Меньшая сторона треугольника

Свойство меньшей стороны треугольника:
Против меньшей стороны треугольника лежит меньший угол
Меньший угол треугольника

Свойство меньшего угла треугольника:
Против меньшего угла треугольника лежит меньшая сторона
Длины сторон треугольника

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.
a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.
Углы треугольника

Свойство углов треугольника:
Сумма углов треугольника равна 180°
Внешний угол треугольника


Свойство внешнего угла треугольника:
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Больший угол треугольника

Свойство большего угла треугольника:
Величина большего угла треугольника не может быть меньшей, чем 60°.
 ,
,
где α – больший угол треугольника.
Меньший угол треугольника

Свойство меньшего угла треугольника:
Величина меньшего угла треугольника не может быть большей, чем 60°.
 ,
,
где β – меньший угол треугольника.
Теорема косинусов

Теорема синусов

Свойство меньшего угла треугольника:
 ,
,
Все формулы для треугольника
1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c – стороны произвольного треугольника
α , β , γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b – катеты
c – гипотенуза
α , β – острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
4. Найти длину высоты треугольника
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.
H – высота треугольника
a – сторона, основание
b, c – стороны
β , γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
[spoiler title=”источники:”]
http://www.resolventa.ru/demo/obsh/diagege.htm
http://www-formula.ru/2011-10-09-11-08-41
[/spoiler]
|
Как проверить, существует ли треугольник, если известны три его стороны?
Необходимым и достаточным условием существования треугольника является выполнение следующих неравенств: a+b>c, a+c>b, b+c>a, (a>0, b>0, c>0), где a, b и с – длины сторон треугольника. Другими словами, треугольник существует тогда и только тогда, когда сумма любых двух его сторон больше третьей стороны.
автор вопроса выбрал этот ответ лучшим
Kuzmich291192 9 лет назад Условие существования треугольника можно представить в следующем виде: пусть a b c стороны треугольника. Тогда, что бы треугольник существовал необходимо, что бы сумма двух любых его сторон была больше третьей стороны a+b>c или a+c>b или b+c>a (если сумма будет равна какой-либо стороне, то такой треугольник называется вырожденным). Рассмотрим пример: пусть дан треугольник со сторонами 3, 6, 5. Возьмём две любые стороны, например, 3 и 6. Проверим условие существования: 3+6=9>5, следовательно треугольник существует. Так же условие сущесвтвования треугольника можно представить в виде векторной суммы. Пусть вектора a b c задают стороны треугольника(и эти вектора не равны нуль-вектору), тогда треугольник существует, если векторная сумма a+b+c=0.
Mefody66 9 лет назад Kuzmich291192 написал в общем, все правильно, но с одним маленьким уточнением: нужно взять самую большую сторону, и проверить, что сумма двух других сторон больше, чем эта большая сторона. Возьмем, например, числа 1, 2 и 10. Если мы сложим 1 + 10 > 2, 2 + 10 > 1, значит, треугольник существует? НЕТ! 1 + 2 < 10. Поэтому треугольник не существует.
У м к а 6 лет назад В геометрии есть теорема под названием “Неравенство треугольника”, которая гласит о том, что любая из сторон треугольника не будет превосходить по своему значению сумму двух других его сторон. Примечательно, что данная теорема также имеет доказательство.
Таким образом, вам необходимо всего лишь поочерёдно просуммировать по две стороны треугольника и сравнить полученное значение с размером третьей стороны, которая не участвовала с сложении.
Galina7v7 4 года назад Когда такой вопрос конкретно задаётся, причём, в цифрах, то нужно проверить величину каждой стороны, чтобы на была меньше суммы двух других сторон. Вот треугольник со сторонами 3,4, и 5 существует, а изменив только одну из сторон, например, 5 см на 7 см, то такого треугольника не существует, так 3 + 4 = 7, а не больше, как положено для существования треугольника. Начинать проверку нужно для большей стороны, и если она меньше суммы двух меньших сторон, то этот треугольник существует. Требование к углам треугольника тоже не маловажное, потому что если даны углы треугольника, и сумма их не равна 180 градусам, то треугольник не существует.
Если известны длины трех сторон треугольника, то еще до его построения можно определить может ли такой треугольник существовать реально. Есть даже простенькая программа для вычисления этого на компьютере, но все что нам надо это найти самую длинную сторону из заданных и проверить является ли сумма двух других сторон больше. Примерно так: заданы три сторона а, в, с, причем в сторона самая длинная. Условием возможности существования треугольника будет выполнение неравенства в<а+с. Если большая сторона будет равна сумме двух других сторон, то это случай вырожденного треугольника, когда все вершины лежат на одной прямой:
Azamatik 6 лет назад Имеем треугольник АВС, где АВ, ВС и СА – это три его стороны. Треугольник существует в тех случаях, когда АВ + ВС > СА; АВ + СА > ВС; ВС + СА > АВ, то есть в том случае, если сложить любые две стороны любого треугольника, сумма должна быть больше третьей его стороны. Например, АВ = 5 см, ВС = 6 см, СА = 8 см – треугольник существует. И другой пример: АВ = 4 см, ВС = 3 см, СА = 9 см. Получается, что одна сторона больше суммы двух других – треугольник не существует.
moreljuba 6 лет назад Чтобы проверить существование треугольника нужно сложить все три угла треугольника ивот если они в сумме не дадут 180-ти градусов, то такого треугольника просто как раз не существует. А также треугольника не существует в том случае, когда одна сторона будет по длине больше чем длина в сумме двух других сторон.
Помощни к 6 лет назад Если одна из сторон треугольника будет больше (по длине), чем две других стороны, то из этих катетов не получится сделать один треугольник. Получится фигура, напоминающая флажок, состоящая из треугольника и присоединенной линии. Любая сторона не может быть больше сумму двух оставшихся сторон треугольника.
Smiledimasik 6 лет назад Самое главное во всех правилах существования треугольника то, что сума двух меньших сторон треугольника или как называются они “катеты” должна быть больше самой большой стороны треугольника. Если сума этих сторон совпадет с самой большой стороной, то это будет обычная прямая с точками на ней.
MarkTolkien 6 лет назад Длина каждой из сторон треугольника должна быть меньше сумы остальных двух сторон, иначе этот треугольник не сложится. Углы треугольника в сумме дают 180 градусов, это еще один критерий для проверки, позволяющий вычислить, существует ли треугольник.
Roxrite 9 лет назад Если одна сторона треугольника окажется больше суммы двух остальных сторон, то такого треугольника не существует. Если сумма всех 3-х углов треугольника не будет равна 180°, то такого треугольника не существует. Знаете ответ? |
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
|||
|
углы тр-ка относятся как 9:5:4,а медиана проведенная к болшей стороне равна 12,5.Найти большую сторону . подскажите ребят как решаются такого типа задачи учитель не успел объяснить )))
|
||
| Вернуться к началу |
|
||
|
Alexander N |
Заголовок сообщения: Re: Найти большую сторону треугольника
|
|
radix писал(а): radix писал(а): Треугольник-то прямоугольный. Большая сторона – гипотенуза. Медиана, проведенная к гипотенузе равна… … медиана, проведенная к гипотенузе, равна половине гипотенузы. Все на свете забыл. Кажется это следствие теоремы косинусов?
|
|
| Вернуться к началу |
|
| За это сообщение пользователю Alexander N “Спасибо” сказали: mad_math, radix |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найти сторону треугольника
в форуме Геометрия |
sorokinaM501 |
4 |
355 |
28 мар 2014, 10:22 |
|
Найти 3 сторону треугольника
в форуме Аналитическая геометрия и Векторная алгебра |
Anies |
2 |
307 |
17 дек 2015, 15:16 |
|
Найти сторону треугольника
в форуме Геометрия |
fedorovdanilo |
3 |
668 |
11 июн 2013, 01:06 |
|
Найти сторону прямоугольного треугольника
в форуме Геометрия |
belinum |
1 |
353 |
21 окт 2013, 13:47 |
|
Найти сторону равностороннего треугольника
в форуме Геометрия |
Serj1257839076 |
2 |
1298 |
04 дек 2016, 22:03 |
|
Найти сторону треугольника по медиане и стороне
в форуме Геометрия |
marie_t |
7 |
757 |
26 мар 2014, 13:44 |
|
Найти сторону треугольника по косинусу прилежащего угла
в форуме Геометрия |
maks242 |
4 |
204 |
12 мар 2019, 21:32 |
|
Найти сторону треугольника к которому восстановлен перпендик
в форуме Геометрия |
Milkaa |
1 |
180 |
14 фев 2017, 18:58 |
|
Найдите боковую сторону треугольника
в форуме Геометрия |
D1mkas777 |
2 |
224 |
13 сен 2020, 11:35 |
|
Найти большую полуось эллипса
в форуме Аналитическая геометрия и Векторная алгебра |
ANASTASIA9999 |
1 |
503 |
24 ноя 2014, 16:12 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 7 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:
- Найти все стороны треугольника.
- Найти все углы треугольника.
- Найти площадь (S) и периметр (P) треугольника.
- Найти радиус (r) вписанной окружности.
- Найти радиус (R) описанной окружности.
- Найти высоту (h) треугольника.
Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
Сторона треугольника (или длина сторон) может быть найдена различными методами.
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.
Как найти длину стороны треугольника?
Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
Для прямоугольного треугольника:
1) Найти катет через гипотенузу и другой катет


где a и b – катеты, с – гипотенуза.
2) Найти гипотенузу по двум катетам


где a и b – катеты, с – гипотенуза.
3) Найти катет по гипотенузе и противолежащему углу


где a и b – катеты, с – гипотенуза,α° и β° – углы напротив катетов.
4) Найти гипотенузу через катет и противолежащий угол


где a и b – катеты, с – гипотенуза,α° и β°- углы напротив катетов.
Для равнобедренного треугольника:
1) Найти основание через боковые стороны и угол между ними


где a – искомое основание, b – известная боковая сторона,α° – угол между боковыми сторонами.
2) Найти основание через боковые стороны и угол при основании


где a – искомое основание,b – известная боковая сторона,β° – угол при осноавнии.
3) Найти боковые стороны по углу между ними


где b – искомая боковая сторона, a – основание,α° – угол между боковыми сторонами.
4) Найти боковые стороны по углу при основании


где b – искомая боковая сторона, a – основание,β° – угол при осноавнии.
Для равностороннего треугольника:
1) Найти сторону через площадь


где a – искомая сторона, S – площадь треугольника.
2) Найти сторону через высоту


где a – искомая сторона,h – высота треугольника.
3) Найти сторону через радиус вписанной окружности


где a – искомая сторона,r – радиус вписанной окружности.
4) Найти сторону через радиус описанной окружности


где a – искомая сторона,R – радиус описанной окружности.
Для произвольного треугольника:
1) Найти сторону через две известные стороны и один угол (теорема косинусов)


где a – искомая сторона, b и с – известные стороны, α° – угол напротив неизвестной стороны.
2) Найти сторону через одну известную сторону и два угла (теорема синусов)


где a – искомая сторона, b – известная сторона, α° и β° известные углы.
Скачать все формулы в формате Word
Углы и стороны в треугольниках
85. Построим равнобедренный ∆ABC (чер. 92), у которого AB = BC. Тогда мы знаем, что его углы при основании равны, т. е. ∠A = ∠C. Пронумеруем эти углы, – тогда ∠1 = ∠2. Станем теперь строить новые треугольники ABC’, ABC” и т. д. так, чтобы сторона AB и ∠B оставались неизменными, но сторона BC увеличивалась. Тогда угол A должен увеличиваться (что очевидно), а угол C станет уменьшаться: мы видим, что ∠3 < ∠2, ∠4 < ∠3 и т. д., потому что ∠2 есть внешний угол для ∆ACC’ и, следов., ∠2 > ∠3 или ∠3 < ∠2, также ∠3 есть внешний угол ∆AC’C” и, след., ∠3 > ∠4 или ∠4 < ∠3 и т. д. (уменьшение угла C видно еще из того, что сумма углов треугольника всегда равна 2d: угол B не изменяется, угол A увеличивается, – след., ∠C должен уменьшаться).
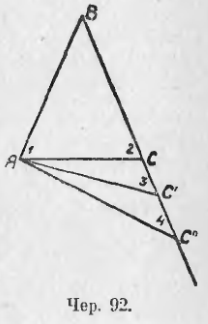
Из этих построений мы вправе сделать заключения:
1) Если в треугольнике две стороны равны, то против них лежат равные углы.
2) Если в треугольнике две стороны не равны, то против большей из них лежит и больший угол.
86. Теперь, наоборот, построим: 1) треугольник с двумя равными углами и 2) треугольник с двумя неравными углами и сравним стороны, противолежащие этим углам. Для решения вопросов, здесь возникающих, воспользуемся способом рассуждения, часто употребляемым в математике.
1) Пусть ∆ABC (чер. 93) постоен так, что ∠A = ∠C. Сравнить стороны BC и BA.
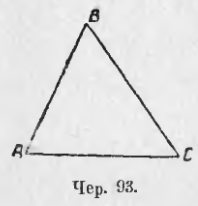
Пока, не зная ничего про стороны AB и BC, мы можем сделать об них 3 предположения: 1) AB = BC, 2) AB > BC и 3) AB < BC – иных предположений быть не может. Рассматривая эти предположения, мы можем заметить, что два из них не годятся, так как противоречат предыдущему. В самом деле, 2-е предположение, что AB > BC должно, на основании предыдущего п., повлечь за собою следствие, что ∠C > ∠A, а у нас построено: ∠C = ∠A. Следовательно, это предположение должно быть вычеркнуто. Также из 3-го предположения, что AB < BC следует, что ∠A > ∠C, что также противоречит нашему построению. Следовательно, и это предположение должно быть вычеркнуто. Остается поэтому лишь одно предположение, что AB = BC, которое и должно быть верно, так как иных сделать нельзя. Поэтому имеем:
Если в треугольнике два угла равны, то против них лежат равные стороны.
2) Пусть ∆ABC (чер. 93) постоен так, что ∠A > ∠C. Сравнить стороны BA и BC.
Опять мы можем сделать 3 предположения: 1) AB = BC, 2) AB > BC и 3) AB < BC. Теперь видим, что первое предположение не годится, так как на основании п. 85 из него вытекало бы, что ∠C = ∠A, что противоречит нашему построению; также найдем, что 2-е предположение, что AB > BC не годится, так как из него вытекало бы, что ∠C > ∠A, что противоречит построению. Остается лишь 3-е предположение, что AB < BC, которое и должно быть верно. Поэтому имеем:
Если два угла в треугольнике неравны, то против большего из них лежит большая сторона.
Теперь легко решаются вопросы: 1) какая из сторон прямоугольного треугольника самая большая? 2) Какая из сторон тупоугольного треугольника самая большая?
87. В двух предыдущих пп. мы имели дело с двумя положениями: 1) против большей стороны лежит больший угол и 2) против большего угла лежит большая сторона. Мы нашли, что эти мысли справедливы для одного треугольника. Возникает вопрос, справедливы ли они для двух треугольников? Несомненно справедливы для двух равных треугольников, так как равные треугольники можно наложением слить в один треугольник. Но, вообще говоря, к двум различным (не равным) треугольникам эти положения не могут быть применимы: мы можем построить два таких треугольника ∆ABC и ∆A’B’C’ (чер. 94), чтобы ∠B был > ∠B’, но AC была бы < A’C’. Чертеж пояснений не требует. Но есть один случай, когда указанные мысли применимы и к двум различным треугольникам).
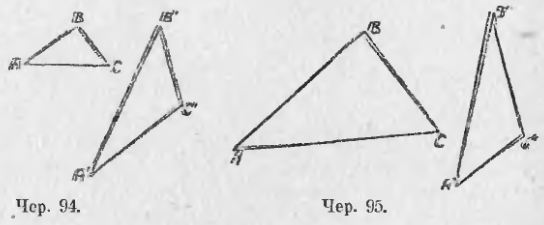
Этот случай легко уясняется наглядно. Возьмем две палочки AB и BC (чер. 95 bis) и сложим их концами (в точке B). Если вращать палочку BC около точки B по стрелке, то ∠B станет увеличиваться: сторона BC будет менять свое положение (пусть одно из них есть BC’), но все время BC останется равным самому себе; не изменяется также и отрезок AB. Обратим внимание, что точками A и C определяется еще отрезок AC, на чертеже не изображенный. При вышеуказанном вращении точка C меняет свое место и нам ясно, что этот отрезок AC, не изображенный на чертеже, должен увеличиваться (напр. AC’ > AC), т. е., если 2 стороны треугольника не изменяются, а угол между ними увеличивается, то третья сторона так же увеличивается. В тексте этот случай выяснен без помощи такого наглядного представления.
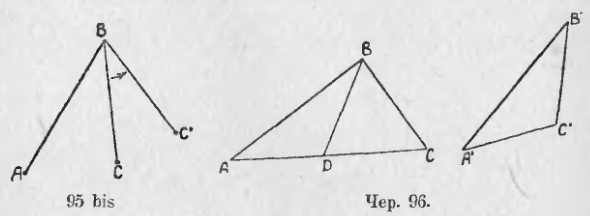
Построим два таких треугольника, чтобы у них было по две равных стороны, но чтобы углы между ними не были равны. Пусть в ∆ABC и в ∆A’B’C’ (чер. 95) имеем AB = A’B’, BC = B’C’, но ∠B > ∠B’. Сравним стороны AC и A’C’, лежащие против неравных углов. Для этого наложим ∆A’B’C’ на ∆ABC так, чтобы сторона A’B’ совпала с равною ей стороною AB. Тогда сторона B’C’ должна пойти внутри ∠B, потому что ∠B’ < ∠B, но где кончится эта сторона, т. е., где расположится точка C’, неизвестно. Может быть, она расположится как раз на стороне AC, может быть, расположится вне ∆ABC, а может быть внутри этого треугольника. Разберем эти три случая отдельно.
1) Пусть ∆A’B’C’ расположится так, что займет положение ∆ABD (чер. 96), так что точка C’ попадет в D, на сторону AC; тогда, очевидно, AD < AC или A’C’ < AC (AD есть та же сторона A’C’, только перенесенная в другое место).
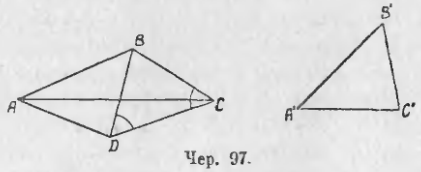
2) Пусть ∆A’B’C’ при наложении займет положение ∆ABD (чер. 97), т. е. точка C’ расположится в точке D, вне ∆ABC. Тогда, соединив точки C и D, получим ∆BCD, у которого BC = BD, так как, по построению, B’C’ = BC, а BD есть та же сторона B’C’, лишь перенесенная в другое место. Поэтому ∆BCD – равнобедренный, и ∠BCD = ∠BDC. Рассмотрим теперь ∆ACD; про два его угла, а именно про ∠C (или ∠ACD) и про ∠D (или ∠ADC) легко сообразить, пользуясь отмеченными равными углами равнобедренного треугольника, какой из них больше другого. В самом деле, мы видим, что ∠ACD < отмеченного угла BCD при основании равнобедренного треугольника, а ∠ADC > отмеченного угла BDC при основании равнобедренного треугольника. Но ∠BCD = ∠BDC, следовательно, ∠ADC > ∠ACD. Поэтому на основании п. 86 (применяя его к ∆ACD) имеем AC > AD, но AD есть сторона A’C’, перенесенная в другое место, – следовательно, AC > A’C’.
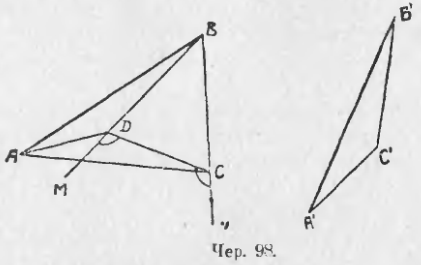
3) Пусть ∆A’B’C’ при наложении займет положение ∆ABD (чер. 98), т. е. точка C’ расположится внутри ∆ABC. Тогда, соединив точки C и D, получим равнобедренный ∆CBD (BD = BC, ибо BD есть сторона B’C’, перенесенная в другое положение, а B’C’ = BC по построению) и, следовательно, ∠BCD = ∠BDC. Если продолжить стороны BD и BC по направлениям DM и CN, то получим два внешних угла этого равнобедренного треугольника ∠MDC и ∠NCD, но ∠MDC = ∠NCD, следовательно, ∠ADC > ∠ACD, а поэтому, на основании п. 86, имеем AC > AD, или AC > A’C’ (AD есть сторона A’C’, перенаправленная в другое положение).
Итак, во всех трех случаях оказалось, что
AC > A’C’,
т. е., если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, но углы между ними не равны, то против большого угла лежит большая сторона.
88. Разберем обратный вопрос. Пусть построены ∆ABC и ∆A’B’C’ (чер. 95) так, что AB = A’B’, BC = B’C’, но AC > A’C’, т. е. два треугольника имеют по две равных стороны, но третьи стороны их не равны. Сравнить ∠B и ∠B’.
Воспользуемся тем же способом рассуждения, как в п. 86.
Пока мы можем об углах B и B’ сделать три предположения: 1) ∠B = ∠B’, 2) ∠B > ∠B’ и 3) ∠B < ∠B’.
Первое предположение не годится, так как тогда наши треугольники, имея по построению по две равных стороны и равные углы между ними, были бы равны, и, следовательно, AC’ = A’C’, а это противоречит построению. Третье предположение, что ∠B < ∠B’ также не годится, так как тогда к этим треугольникам был бы применим результат, найденный в предыдущем п., на основании которого имели бы AC < A’C’, что также противоречит построению. Остается второе предположение, что ∠B > ∠B’, которое и должно быть верно. Итак:
Если две стороны одного треугольника равны соответственно двум сторонам другого, но третьи стороны этих треугольников не равны, то против большей стороны лежит и больший угол.







