Как найти самый маленький период функции - Сайт, где вы сможете решить свои вопросы

Как найти наименьший период функции

Функция, значения которой повторяются через определенное число, называется периодической. То есть сколько бы периодов вы ни прибавили к значению х, функция будет равна одному и тому же числу. Любое исследование периодических функций начинается с поиска наименьшего периода, чтобы не выполнять лишнюю работу: достаточно изучить все свойства на отрезке, равном периоду.

Инструкция

Воспользуйтесь определением периодической функции. Все значения х в функции замените на (х+Т), где Т – наименьший период функции. Решите полученное уравнение, считая Т неизвестным числом.

В результате вы получите некое тождество, из него попробуйте подобрать минимальный период. Например, если получилось равенство sin(2T)=0,5, следовательно, 2Т=П/6, то есть Т=П/12.

Если равенство получается верным только при Т=0 или параметр Т зависит от х (например, получилось равенство 2Т=х), делайте вывод о том, что функция не периодична.

Для того чтобы узнать наименьший период функции, содержащей лишь одно тригонометрическое выражение, воспользуйтесь правилом. Если в выражении стоит sin или cos, периодом для функции будет 2П, а для функций tg, ctg ставьте наименьший период П. Учтите при этом, что функция не должна быть возведена в какую-либо степень, а переменная под знаком функции не должна быть умножена на число, отличное от 1.

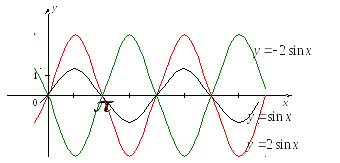
Если cos или sin внутри функции возведены в четную степень, уменьшите период 2П в два раза. Графически вы можете увидеть это так: график функции, расположенный ниже оси ох, симметрично отразится вверх, поэтому функция будет повторяться в два раза чаще.

Чтобы найти наименьший период функции при том, что угол х умножен на какое либо число, действуете так: определите стандартный период этой функции (например, для cos это 2П). Затем разделите его на множитель перед переменной. Это и будет искомый наименьший период. Уменьшение периода хорошо видно на графике: он сжимается ровно во столько раз, на сколько умножен угол под знаком тригонометрической функции.

Обратите внимание, если перед х стоит дробное число меньше 1, период увеличивается, то есть график, напротив, растягивается.

Если в вашем выражении две периодические функции умножены друг на друга, найдите наименьший период для каждой по отдельности. Затем определите наименьший общий множитель для них. Например, для периодов П и 2/3П наименьший общий множитель будет 3П (он делится без остатка как на П, так и на 2/3П).

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Периодичность функций

Функция
называетсяпериодической,
если существует такое число
,
что для любого значениях
из области определения выполняется
равенство

число
Т
называется периодом
функции.

Примеры
периодических функций:
,,,.

Заметим,
что периодическую функцию достаточно
исследовать в пределах одного периода,
т.е. при
.

Пример.
Найти наименьший период функции
.

Решение.
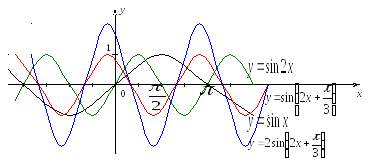
Период для функций
иравен.
Функцияимеет период в 3 раза меньше, т.е.,.
Наименьший период суммыдолжен быть таким, чтобыипомещались в нем целое число раз. В
данном случае.

Задание 3. Найти наименьший период функции

1)	16)
2)	17)
3)	18)
4)	19)
5)	20)
6)	21)
7)	22)
8)	23)
9)	24)
10)	25)
11)	26)
12)	27)
13)	28)
14)	29)
15)	30)

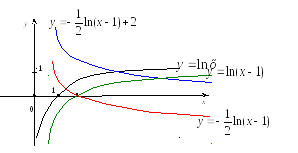
Простейшие преобразования графиков

Пусть
в данной системе координат вычерчен
график некоторой функции

Из
этого графика с помощью специальных
приемов легко получить график сходных
функций; таких как

а
также более общего вида

где
– некоторые константы.

График
функции

получается растяжением
или сжатиемвm
раз исходного графика вдоль оси Оy.

Если
же
,
то, построив сначала график функции,
затем строим симметричный с ним
относительно осиОх
искомый график функции
.

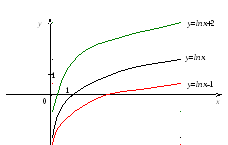
График
функции

получается с помощью параллельного
переноса (сдвига) графика
вдоль осиОy
вверх
или внизнаn
единиц.

График
функции

получается из графика
сжатиемили растяжениемего ва
раз вдоль оси Ох.
(т.е. к оси Оy).

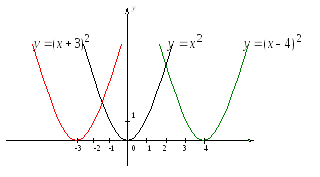
График
функции y=f(x+b)
получается из графика y=f(x)
с помощью параллельного переноса
(сдвига) его вдоль оси Ох
влево (b>0)
или вправо (b<0)
на b
единиц.

Построение
графиков подобного рода в общем случае

сводится
к проведению в соответствующем порядке
операций 1-4.

Пример.
Построить график функции
.

Решение.

Строим
график
;
сжимаем
его вдоль осив
2 раза, получаем график;
сдвигаем
график
влево наи получаем график;
растягиваем
график
вдоль осив 2 раза и получаем требуемый график.

Пример.
Построить график функции
.

Решение.

1)
строим график
;

2)
сдвигаем его влево по осина 1, получаем график функции;

3)
сжимаем график
вдоль осив
2 раза и строим симметричный ему
относительно оси,
получаем график;

4)
поднимаем график функции
по оси Оy
вверх на две единицы, получаем искомый
график.

Задание
4.

Методом
деформации и сдвигов построить график
функции

№ зад № вар	1	2	3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

С периодическими функциями мы встречаемся в школьном курсе алгебры. Это функции, все значения которых повторяются через определенный период. Как будто мы копируем часть графика — и повторяем этот паттерн на всей области определения функции. Например, — периодические функции.

Дадим определение периодической функции:

Функция y=f(x) называется периодической, если существует такое число , не равное нулю, что для любого из ее области определения

Другими словами, это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого фиксированного ненулевого числа . Число называется периодом функции. Как правило, говоря о периоде, мы имеем в виду наименьший положительный период функции.

Например, — периодические функции.

Для функций и период T = 2pi ,

Для функций tg x и период T = pi.

Но не только тригонометрические функции являются периодическими. Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задачи:

1. Периодическая функция определена для всех действительных чисел. Ее период равен двум и Найдите значение выражения

График функции может выглядеть, например, вот так:

Отметим точку М (1; 5), принадлежащую графику функции . Поскольку период функции равен 2, значения функции в точках будут также равны пяти. Здесь k — целое число.

Как ведет себя функция в других точках — мы не знаем. Но знаем, что ее график состоит из повторяющихся элементов длиной 2, что и нарисовано.

Значения функции в точках -3 и 7 равны пяти. Мы получим:

2. График четной периодической функции совпадает с графиком функции на отрезке от 0 до 1; период функции равен 2. Постройте график функции и найдите f(4 ).

Построим график функции при

Поскольку функция четная, ее график симметричен относительно оси ординат. Построим часть графика при симметричную части графика от 0 до 1.

Период функции равен 2. Повторим периодически участок длины 2, который уже построен.

Найдем f(4)

3. Найдите наименьший положительный период функции

Наименьший положительный период функции равен 2pi.

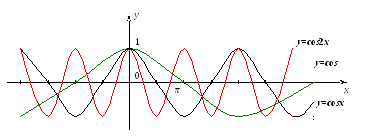
График функции получается из графика функции сжатием в 3 раза по оси X (смотри тему «Преобразование графиков функций).

Значит, у функции частота в 3 раза больше, чем у функции , а наименьший положительный период в 3 раза меньше и равен $frac{{rm 2}pi }{{rm 3}}$ . Значит, на отрезке 2pi укладывается ровно 3 полных волны функции

Рассуждая аналогично, получим, что для функции наименьший положительный период равен $frac{{rm 2}pi }{{rm 5}}.$ На отрезке 2pi укладывается ровно 5 полных волн функции

Числа 3 и 5 — взаимно простые. Поэтому наименьший положительный период функции равен 2pi .

4. Период функции равен 12, а период функции равен 8. Найдите наименьший положительный период функции

По условию, период функции равен 12. Это значит, что все значения повторяются через 12, через . Если мы выберем любую точку x_0 на графике функции то через значение функции будет такое же, как и в точке x_0.

Аналогично, все значения функции повторяются через . В этих точках значения будут такие же, как и в точке x_0.

На каком же расстоянии от точки x_0 расположена точка, в которой значение функции такое же, что и в точке x_0 ? Очевидно, на расстоянии Это значит, что число делится и на 12, и на 8, то есть является их наименьшим общим кратным. Значит, T = 24 .

Наименьший положительный период суммы функций равен наименьшему общему кратному периодов слагаемых.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Периодические функции» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
07.05.2023

Источник

Если cos илиsin внутри функции возведены в четную степень, уменьшите период 2П в два раза. Графически вы можете увидеть это так: график функции, расположенный ниже оси ох, симметрично отразится вверх, поэтому функция будет повторяться в два раза чаще.

Источник

В этой статье обсуждаем периодичность функций: как определить, периодична ли функция, и каков ее период.

Функция периодична, если некоторый набор ее значений повторяется раз за разом, и точки с одинаковыми значениями функции расположены на числовой оси с равными промежутками. Это расстояние и будем называть периодом. Периодичная функция может иметь и несколько периодов, самый маленький положительный из них будем называть основным.

Тогда, если мы знаем период, мы можем, зная все значения функции на протяжении данного периода, достроить функцию, либо узнать ее значения в любой точке числовой оси – то есть при любом аргументе.

period1

Периодичная функция

Пример 1: функция f(x) имеет период, равный 2: T=2 и при . Найдите значение выражения .

Раз наша функция принимает форму части параболы на отрезке [-2; 0] при периоде, равном 2, значит, такую же форму она будет иметь и на следующем отрезке – [0;2], и на отрезке [2;4]. Изобразим ее:

period2

Определение значения периодичной функции

Видно, что функция принимает одинаковые значения в точках, отстоящих друг от друга на 2, 4, 6 единиц и т.д., тогда . Найдем эти значения функции. В точке (-1) функция принимает значение , в точке (3,5) функция принимает значение .

Теперь найдем значение искомого выражения: .

Строго говоря, функция периодична, если есть такое число Т, что .

Попробуем научиться определять, периодична ли функция или нет. Для этого рассмотрим несколько примеров.

Пример 2. Проверим, периодична ли функция .

Установим, выполняется ли условие: , то есть ? Очевидно, что данное условие не выполняется. Значит, функция непериодична.

Пример 3. Проверим, периодична ли функция .

Функцию для удобства представим в виде: .

Установим, выполняется ли условие: , то есть ? Очевидно, что данное условие не выполняется: . Значит, функция непериодична.

Пример 4. Проверим, периодична ли функция . Если функция периодична, то будет выполняться условие: , то есть . Поскольку нам все равно, в какой точке числовой оси мы проведем свое исследование, то очень удобно начать с точки x=0 . Тогда , или . Это означает, что либо cos T=1 , либо , то есть либо T=2{pi} , либо T={pi} , а так как главным считается наименьший положительный период, то T={pi} .

period3

Определение периода функции

В данном примере делать проверку необязательно, но проверка бывает очень полезна в более сложных задачах, поэтому сделаем ее здесь для тренировки: .

Пример 5. Определить периодичность функции .

Если Т – период, то .

В это равенство подставим какие-нибудь «удобные» точки, например, . Получим:

Далее есть два пути отыскания периода, первый – решение этого уравнения, второй – составление еще одного уравнения такого же вида. Если функция имеет период Т, то верно и следующее: . Подставим «удобную» точку :

Пользуясь четностью косинуса и нечетностью синуса можем записать:

Имеем систему:

Уравнения сложим, и получим

, откуда

, при n=1 получим T={pi} – ведь нам нужен наименьший период.

Теперь испробуем второй путь, решим это уравнение: . Из основного тригонометрического тождества:

${sqrt{1-{sin {2T}}^2}}+2{sin {2T}}=1$

Оставим в левой части только корень:

$sqrt{1-{sin {2T}}^2}=1-2{sin {2T}}$

Возведем в квадрат:

$1-(sin {2T})^2=1-4sin 2T+4(sin {2T})^2$

$5(sin {2T})^2-4sin {2T}=0$

Тогда либо , либо и .

Это уравнение имеет два решения, одно из которых (второе) – посторонний корень, появившийся при возведении в квадрат. Проверка подстановкой его в исходное уравнение позволит нам выявить его и отбросить. Таким образом, получаем:

и наименьшим будет период при n=1 , то есть T={pi} .